Dynamics Analysis of a Discrete-Time Commensalism Model with Additive Allee for the Host Species
Abstract
:1. Introduction
2. Dynamics Analysis of Map (6)
2.1. The Existence of Fixed Point
2.2. The Stability of Fixed Points , and
- (1)
- When and , the map (6) has two positive fixed points and :
- (i)
- If , then .
- (ii)
- If , then .
- (2)
- Moreover, when and :
- (i)
- If , then .
- (ii)
- If , then .
- (3)
- When and or , then .
3. Dynamics Analysis of Map (5)
3.1. Existence and Local Stability of Fixed Points
- (1)
- If then ;
- (2)
- If then
- (3)
- If then
- (1)
- A sink if and and it is locally asymptotically stable;
- (2)
- A source if and and it is unstable;
- (3)
- A saddle if and (or and
- (4)
- Non-hyperbolic if either .
- (1)
- is always a source since two eigenvalues are and
- (2)
- Two eigenvalues of are and . Then, is:
- (i)
- A saddle when
- (ii)
- A source when
- (iii)
- Non-hyperbolic when
- (1)
- A source if
- (2)
- A saddle if
- (3)
- Non-hyperbolic if .
- (1)
- A sink if and only if and ;
- (2)
- A source if and only if and ;
- (3)
- A saddle if and only if and or and ;
- (4)
- Non-hyperbolic if or .
- (1)
- When and the boundary fixed point exists in the map (5), and the eigenvalues of are and . So, the fixed point is always a source.
- (2)
- When the boundary fixed point exists, the eigenvalues of are and . So, the fixed point is always a saddle.
- (3)
- When and the boundary fixed point exists in the map (5), and the eigenvalues of are and Consequently, is always non-hyperbolic.
- (1)
- If , we havewhere
- (2)
- If , we have , which is equivalent to .
- (1)
- When exists, it is:
- (i)
- A saddle if and only if and ;
- (ii)
- A source if and only if and or ;
- (iii)
- Non-hyperbolic if and only if and , where
- (2)
- When exists, it is:
- (i)
- A sink if and only if and ;
- (ii)
- A saddle if and only if and or ;
- (iii)
- Non-hyperbolic if and only if and , where
- (3)
- When exists and , it is always non-hyperbolic, where
3.2. Global Stability of Positive Fixed Point
3.3. Bifurcation Analysis of a Codimension of One
3.3.1. Bifurcation at the Fixed Point
- (1)
- A transcritical bifurcation when parameters hold;
- (2)
- A pitchfork bifurcation when holds.
3.3.2. Bifurcation around Boundary Fixed Point
- (i)
- A transcritical bifurcation or a pitchfork bifurcation, whose boundary fixed point is non-hyperbolic, if parameter or , respectively;
- (ii)
- A flip bifurcation if .
3.3.3. Bifurcation Analysis of Positive Fixed Point
- (a)
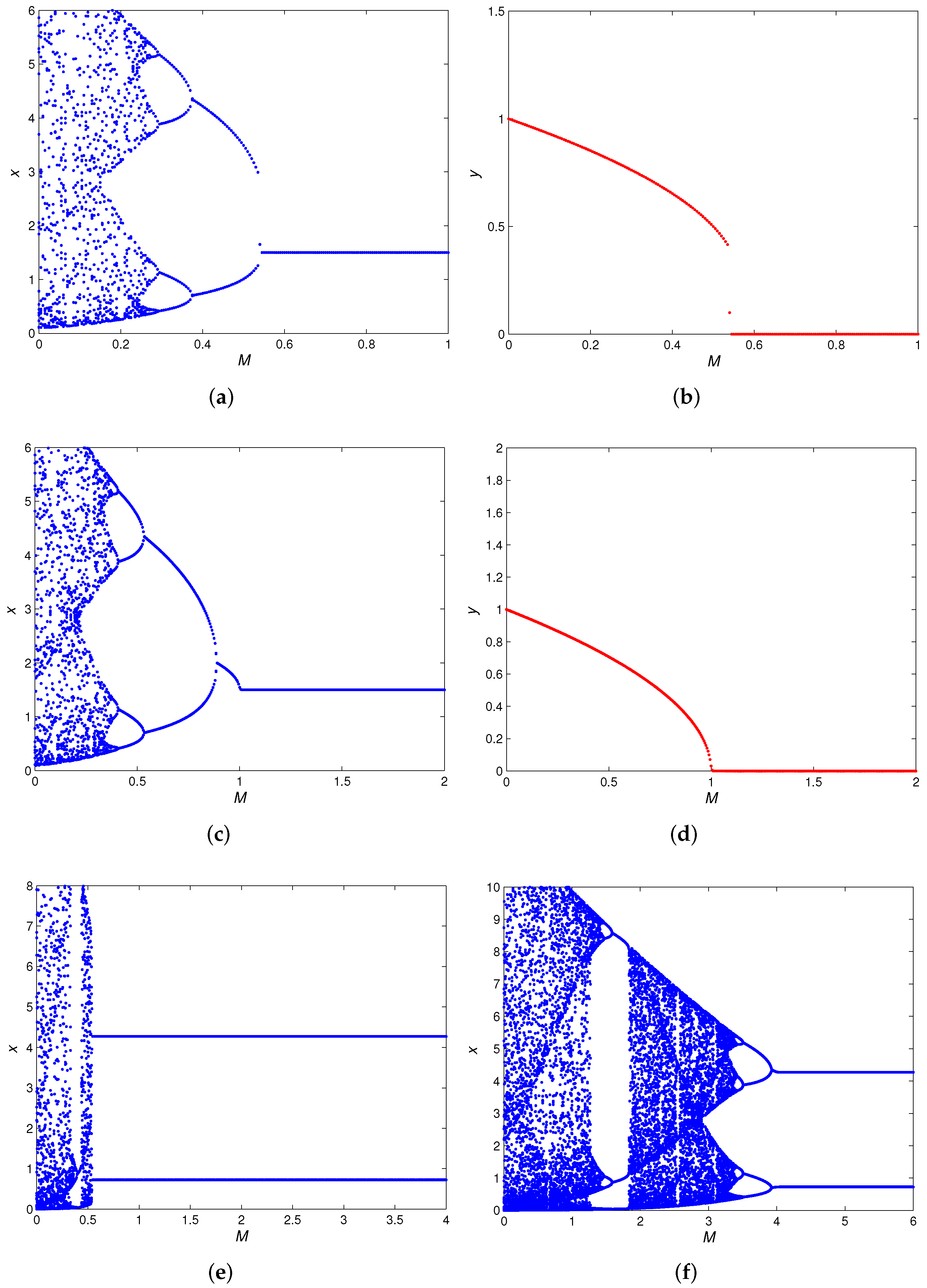
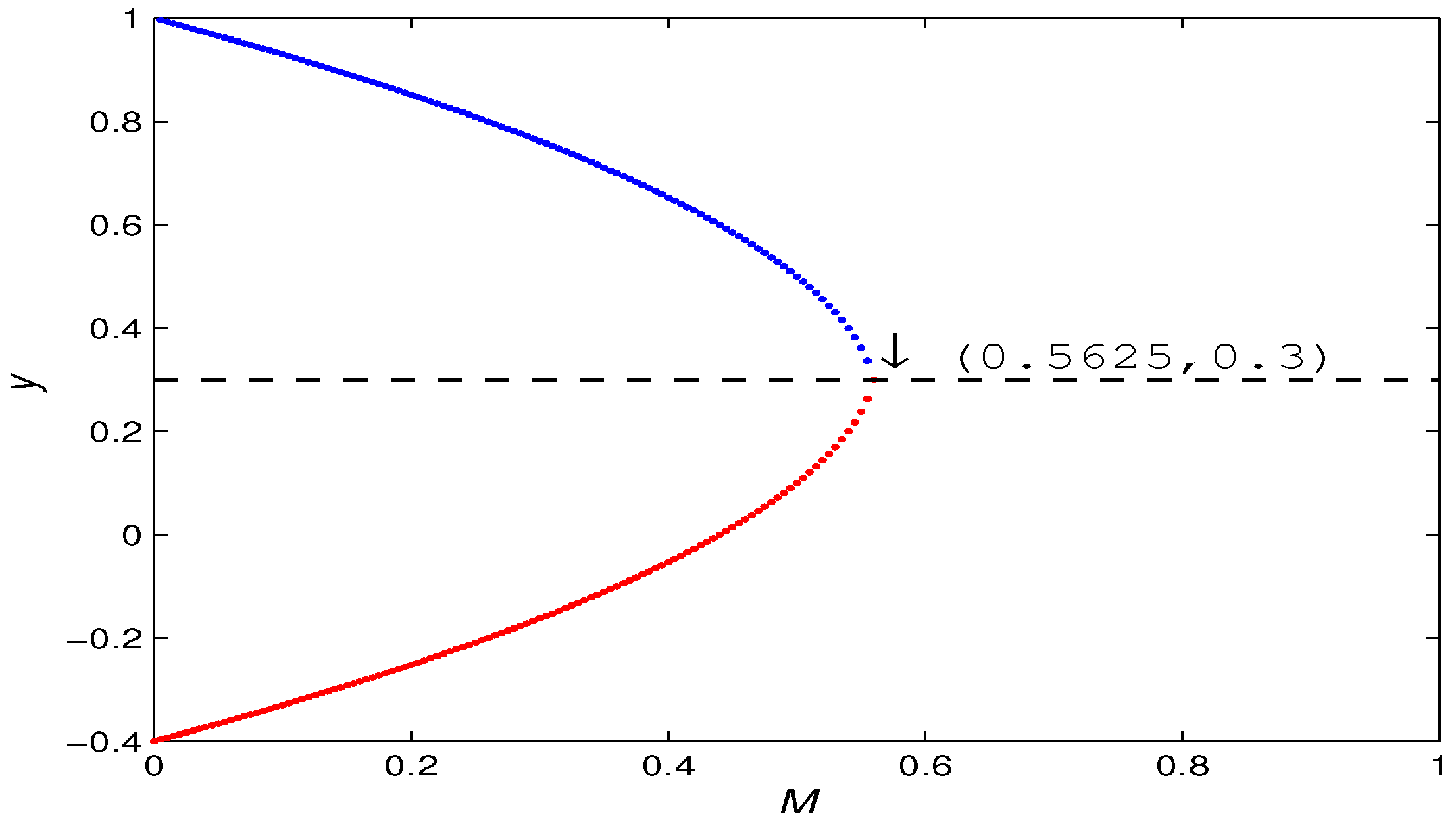
- A flip bifurcation for parameter at .
- (b)
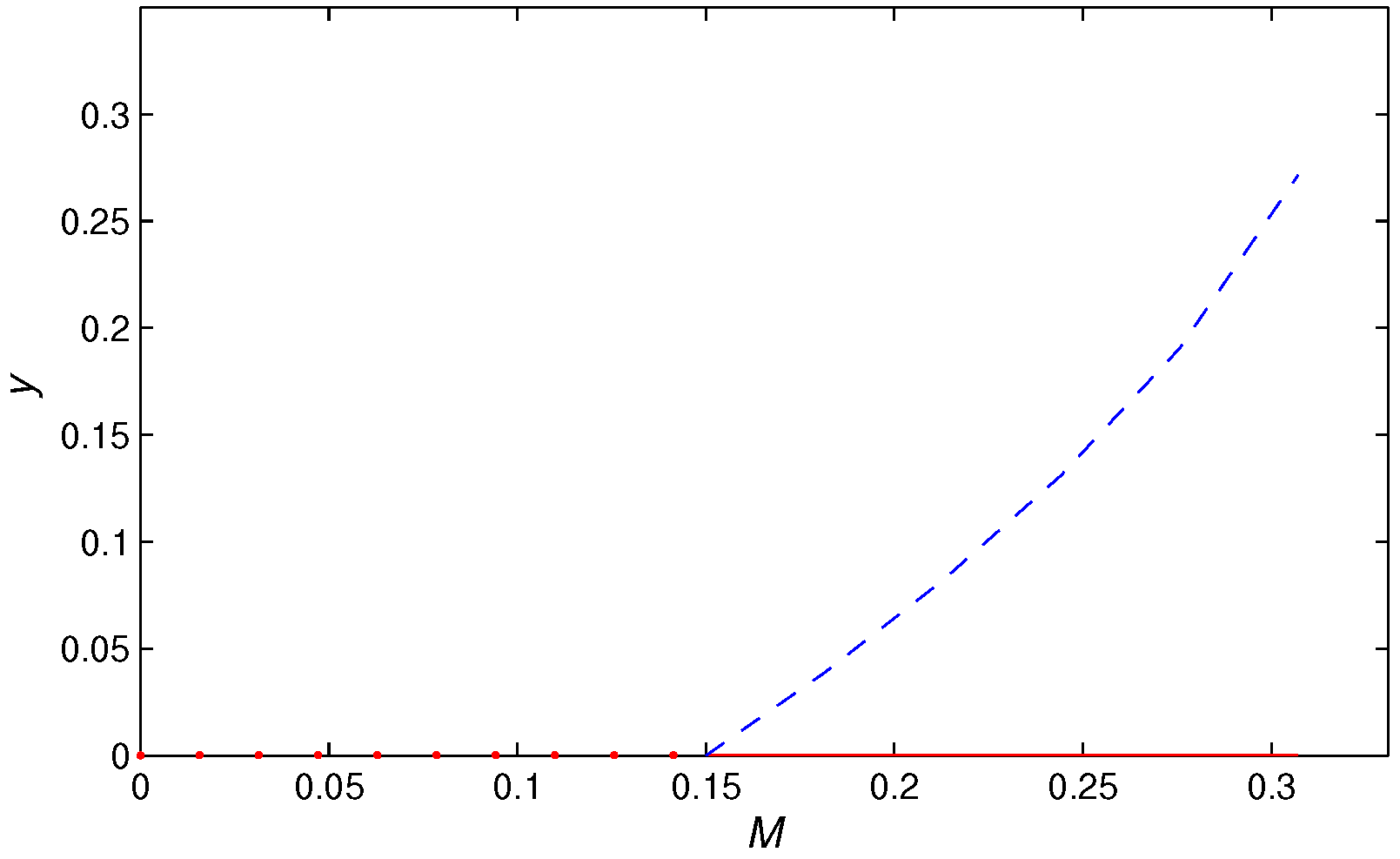
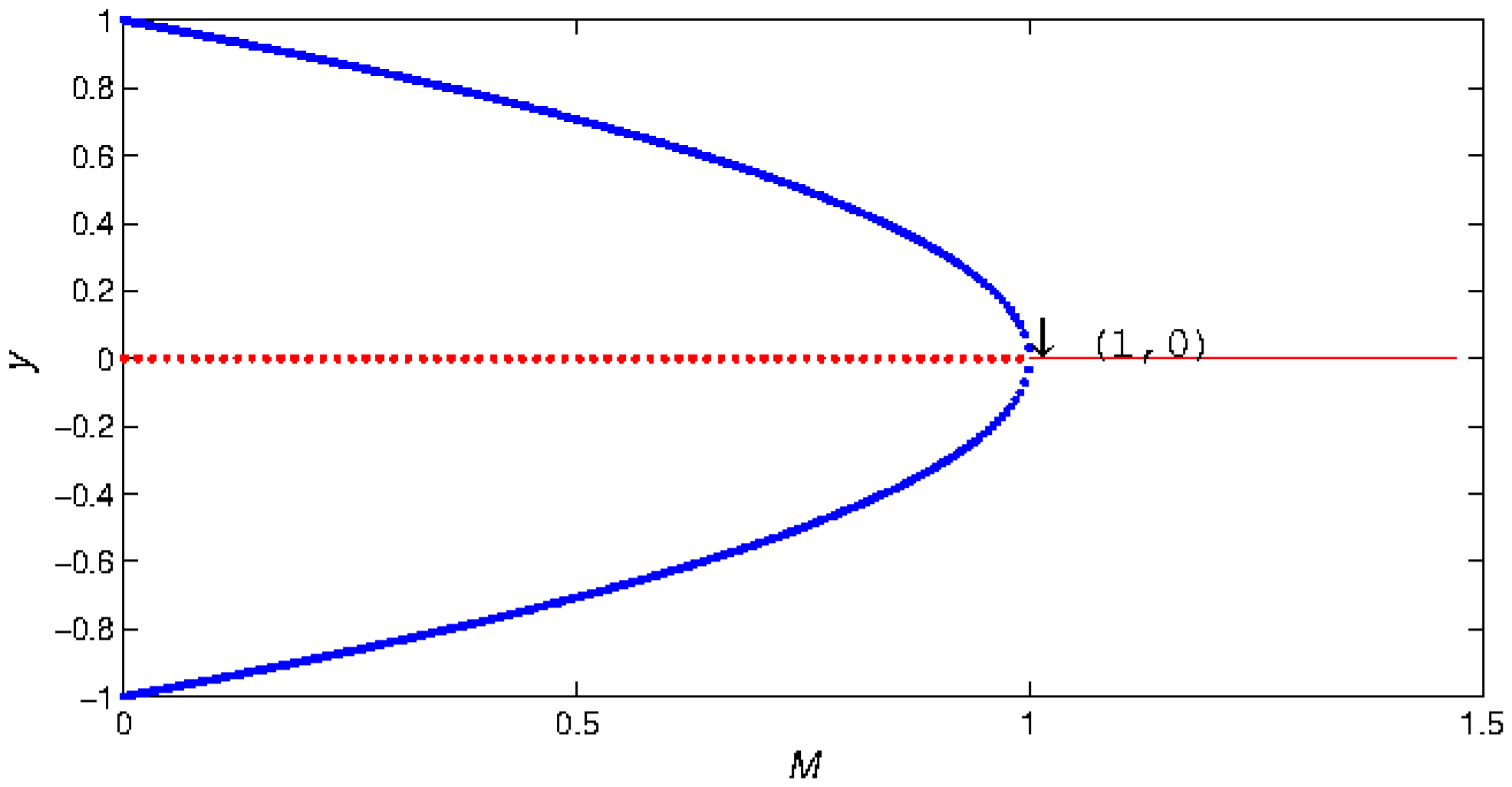
- A fold bifurcation for parameter at . In addition, with the increase of M, the number of positive fixed points of the map (5) has a 2-1-0 change. That is, when , there are and ; when , there is a unique positive fixed point , and when the positive fixed point disappears.
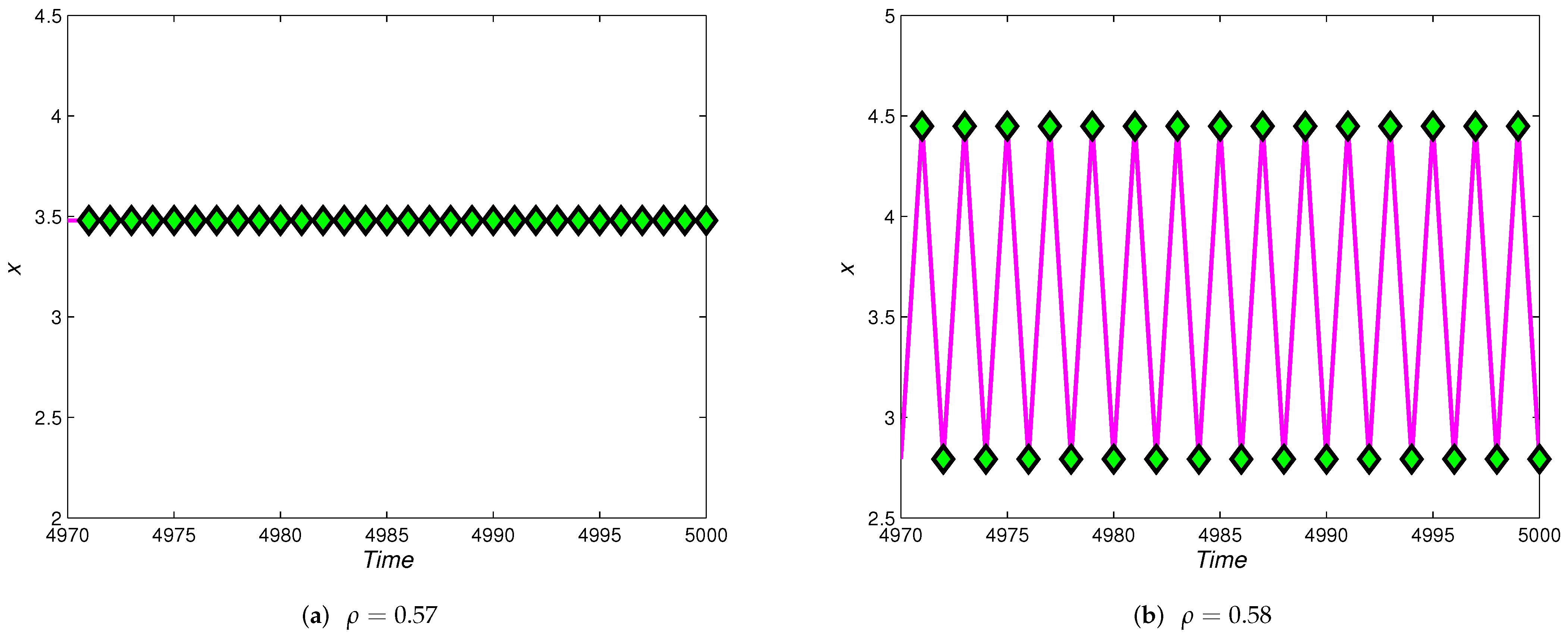
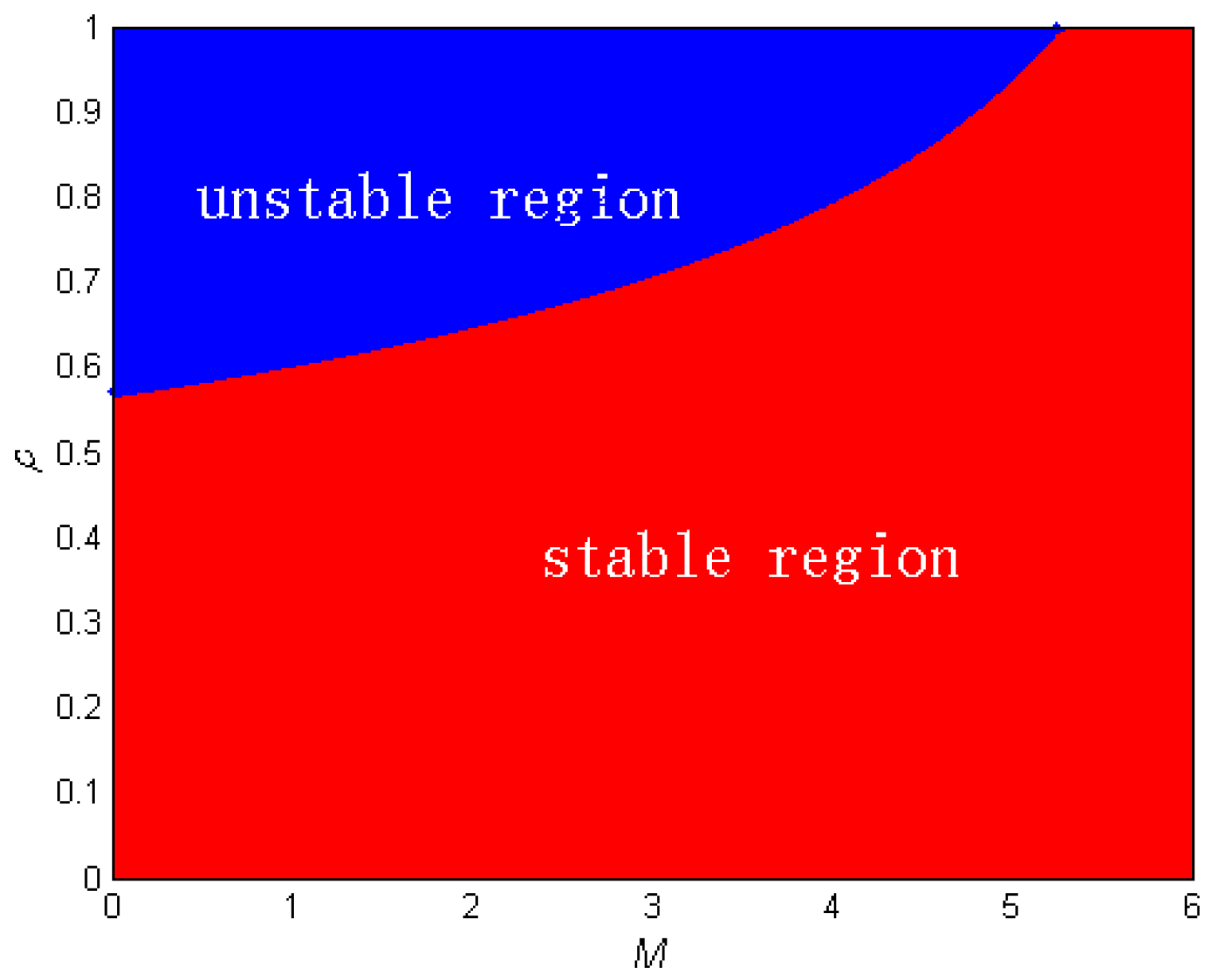
3.4. Chaos Control
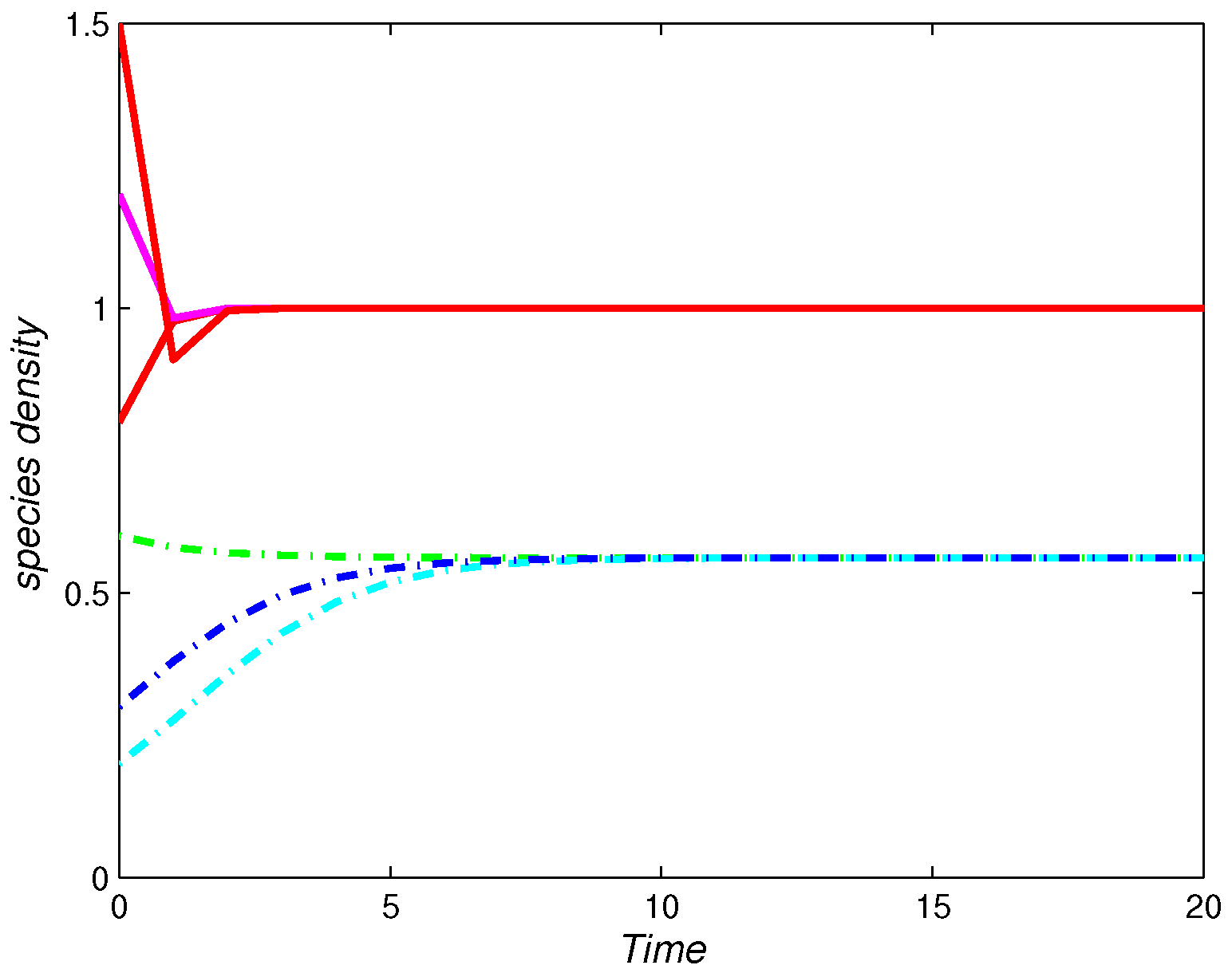
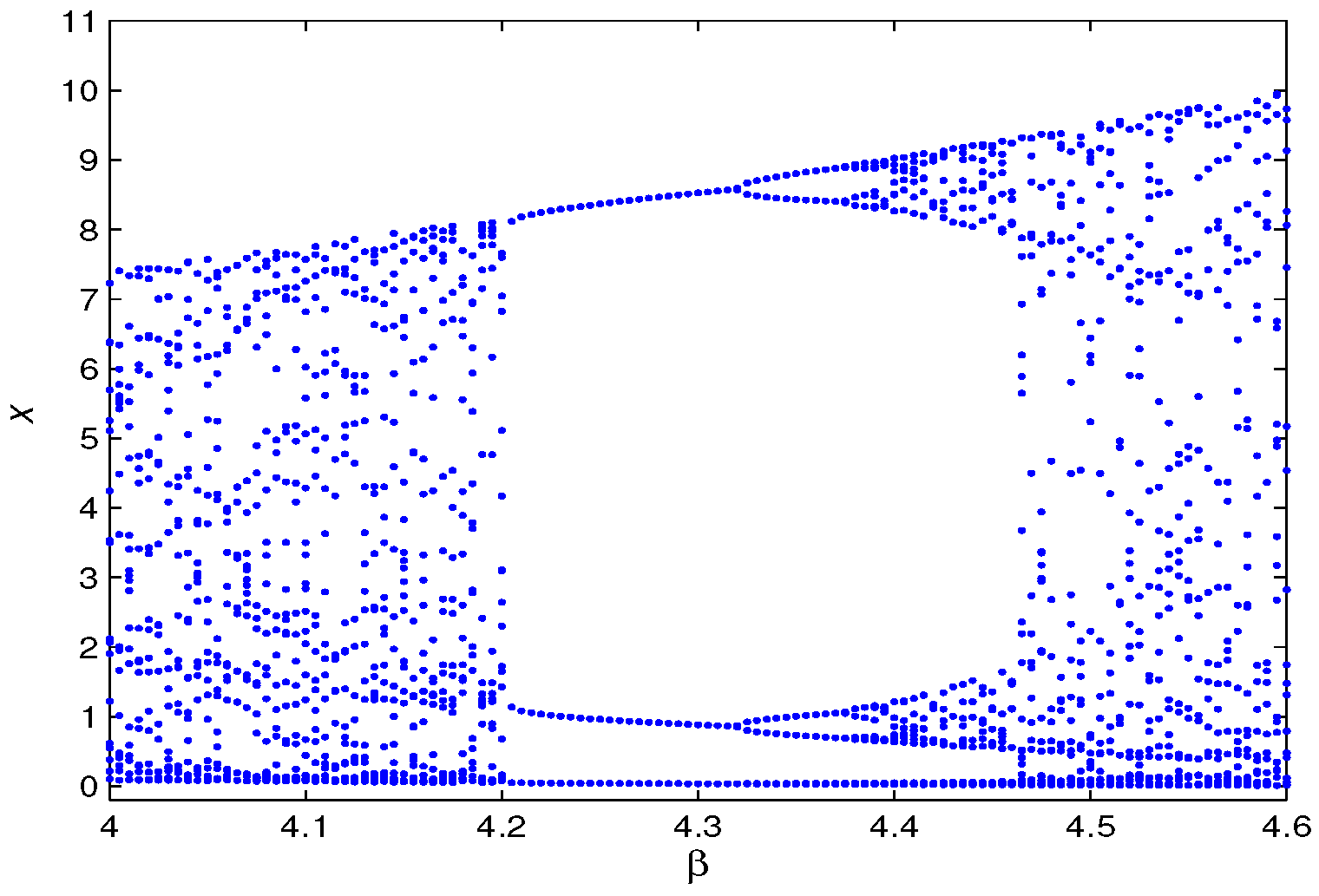
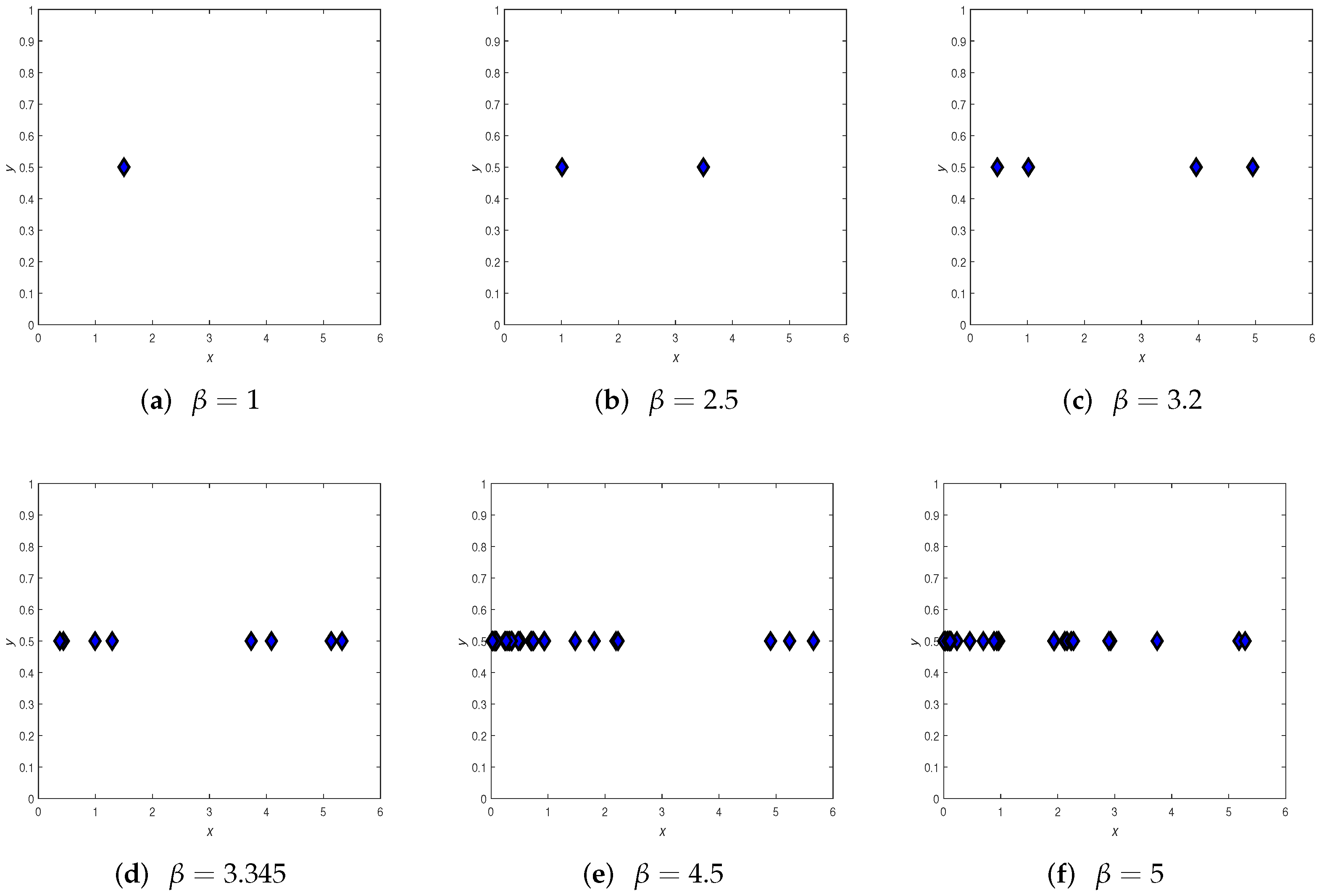
4. Numerical Simulations
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mathis, K.A.; Bronstein, J.L. Our current understanding of commensalism. Annu. Rev. Ecol. Evol. Syst. 2020, 51, 167–189. [Google Scholar] [CrossRef]
- Leung, T.L.; Poulin, R. Parasitism, commensalism, and mutualism: Exploring the many shades of symbioses. Vie Milieu 2008, 58, 107–115. [Google Scholar]
- Anderson, B.; Midgley, J.J. Density-dependent outcomes in a digestive mutualism between carnivorous Roridula plants and their associated hemipterans. Oecologia 2007, 152, 115–120. [Google Scholar] [CrossRef]
- Heard, S.B. Pitcher-plant midges and mosquitoes: A processing chain commensalism. Ecology 1994, 75, 1647–1660. [Google Scholar] [CrossRef]
- Hari, P.B.; Pattabhi, R.N.C. Discrete model of commensalism between two species. Int. J. Mod. Edu. Comput. Sci. 2012, 8, 40–46. [Google Scholar]
- Sun, G.C.; Wei, W.L. The qualitative analysis of commensal symbiosis model of two populations. Math. Theory Appl. 2003, 23, 65–68. [Google Scholar]
- Chen, F.D.; Chong, Y.B.; Lin, S.J. Global stability of a commensal symbiosis model with Holling II functional response and feedback controls. Wseas Trans. Syst. Contr. 2022, 17, 279–286. [Google Scholar] [CrossRef]
- Wu, R.X.; Li, L.; Lin, Q.F. A Holling type commensal symbiosis model involving Allee effect. Commun. Math. Biol. Neurosci. 2018, 2018, 6. [Google Scholar]
- Chen, B.G. The influence of commensalism on a Lotka–Volterra commensal symbiosis model with Michaelis–Menten type harvesting. Adv. Differ. Equ. 2019, 2019, 43. [Google Scholar] [CrossRef]
- Xu, L.L.; Lin, Q.F.; Lei, C.Q. Dynamic behavior of commensal symbiosis system with both feedback control and Allee effect. J. Shanghai Norm. Univ. 2022, 51, 391–396. [Google Scholar]
- He, X.Q.; Zhu, Z.L.; Chen, J.L.; Chen, F. Dynamical analysis of a Lotka Volterra commensalism model with additive Allee effect. Open Math. 2022, 20, 646–665. [Google Scholar] [CrossRef]
- Georgescu, P.; Maxin, D.; Zhang, H. Global stability results for models of commensalism. Int. J. Biol. 2017, 10, 1750037. [Google Scholar] [CrossRef]
- Chen, B.G. Dynamic behaviors of a commensal symbiosis model involving Allee effect and one party can not survive independently. Adv. Differ. Equ. 2018, 2018, 212. [Google Scholar] [CrossRef]
- Chen, J.H.; Wu, R.X. A commensal symbiosis model with non-monotonic functional response. Math. Biol. Neurosci. 2017, 2017, 5. [Google Scholar]
- Lin, Q.F. Dynamic behaviors of a commensal symbiosis model with non-monotonic functional response and non-selective harvesting in a partial closure. Commun. Math. Biol. Neurosci. 2018, 2018, 4. [Google Scholar]
- Li, T.T.; Lin, Q.X.; Chen, J.H. Positive periodic solution of a discrete commensal symbiosis model with Holling II functional response. Commun. Math. Biol. Neurosci. 2016, 2016, 22. [Google Scholar]
- Xie, X.D.; Miao, Z.S.; Xue, Y.L. Positive periodic solution of a discrete Lotka–Volterra commensal symbiosis model. Commun. Math. Biol. Neurosci. 2015, 2015, 2. [Google Scholar]
- Han, R.Y.; Chen, F.D. Global stability of a commensal symbiosis model with feedback controls. Commun. Math. Biol. Neurosci. 2015, 2015, 15. [Google Scholar]
- Zhou, Q.M.; Lin, S.J.; Chen, F.D.; Wu, R. Positive periodic solution of a discrete Lotka–Volterra commensal symbiosis model with Michaelis–Menten type harvesting. Wseas Trans. Math. 2022, 21, 515–523. [Google Scholar] [CrossRef]
- Chen, S.M.; Chong, Y.B.; Chen, F.D. Periodic solution of a discrete commensal symbiosis model with Hassell–Varley type functional response. Nonauton. Dyn. Syst. 2022, 9, 170–181. [Google Scholar] [CrossRef]
- Xu, L.L.; Xue, Y.L.; Lin, Q.F.; Lei, C. Global attractivity of symbiotic model of commensalism in four populations with Michaelis—Menten type harvesting in the first commensal populations. Axioms 2022, 11, 337. [Google Scholar] [CrossRef]
- Zhu, Z.L.; Wu, R.X.; Chen, F.D.; Li, Z. Dynamic behaviors of a Lotka–Volterra commensal symbiosis model with non-selective Michaelis–Menten type harvesting. IAENG Int. J. Appl. Math. 2020, 50, 1–9. [Google Scholar]
- Liu, Y.; Guan, X.Y.; Xie, X.D.; Lin, Q. On the existence and stability of positive periodic solution of a nonautonomous commensal symbiosis model with Michaelis–Menten type harvesting. Commun. Math. Biol. Neurosci. 2019, 2019, 2. [Google Scholar]
- Jawad, S. Study the dynamics of commensalism interaction with Michaels-Menten type prey harvesting. Al-Nahrain J. Sci. 2022, 25, 45–50. [Google Scholar] [CrossRef]
- Chen, F.D.; Chen, Y.M.; Li, Z.; Chen, L. Note on the persistence and stability property of a commensalism model with Michaelis—Menten harvesting and Holling type II commensalistic benefit. Appl. Math. Lett. 2022, 134, 108381. [Google Scholar] [CrossRef]
- Lei, C.Q. Dynamic behaviors of a Holling type commensal symbiosis model with the first species subject to Allee effect. Commun. Math. Biol. Neurosci. 2019, 2019, 3. [Google Scholar]
- Guan, X.Y. Stability analysis of a Lotka–Volterra commensal symbiosis model involving Allee effect. Ann. Appl. Math. 2018, 34, 364–375. [Google Scholar]
- Seval, I. Stability and period-doubling Bifurcation in a modified commensal symbiosis model with Allee effect. Erzin. Univ. J. Sci. Technol. 2022, 15, 310–324. [Google Scholar]
- Li, T.Y.; Wang, Q.R. Bifurcation analysis for two-species commensalism (amensalism) systems with distributed delays. Int. J. Bifurc. Chaos 2022, 32, 2250133. [Google Scholar] [CrossRef]
- Li, T.Y.; Wang, Q.R. Stability and Hopf bifurcation analysis for a two-species commensalism system with delay. Qual. Theory Dyn. Syst. 2021, 20, 83. [Google Scholar] [CrossRef]
- Allee, W.C. Animal Aggregations, a Study in General Sociology; University of Chicago Press: Chicago, IL, USA, 1931. [Google Scholar]
- Allee, W.C. The Social Life of Animals; William Heinemann: London, UK, 1938. [Google Scholar]
- Gonzalez-Olivares, E.; Mena-Lorca, J.; Rojas-Palma, A.; Flores, J.D. Dynamical complexities in the Leslie-Gower predator-prey model as consequences of the Allee effect on prey. Appl. Math. Model. 2011, 35, 366–381. [Google Scholar] [CrossRef]
- Sun, G.Q. Mathematical modeling of population dynamics with Allee effect. Nonlinear Dyn. 2016, 85, 1–12. [Google Scholar] [CrossRef]
- Zhang, J.H.; Chen, X.Y. Dynamic behaviors of a discrete commensal symbiosis model with Holling type functional response. IAENG Int. J. Appl. Math. 2023, 53, 277–281. [Google Scholar]
- Kundu, K.; Pal, S.; Samanta, S.; Sen, A.; Pal, N. Impact of fear effect in a discrete-time predator-prey system. Bull. Calcutta Math. Soc. 2018, 110, 245–264. [Google Scholar]
- Zhou, Q.M.; Chen, F.D.; Lin, S.J. Complex dynamics analysis of a discrete amensalism system with a cover for the first species. Axioms 2022, 11, 365. [Google Scholar] [CrossRef]
- Zhou, Q.M.; Chen, F.D. Dynamical analysis of a discrete amensalism system with the Beddington—DeAngelis functional response and Allee effect for the unaffected species. Qual. Theory Dyn. Syst. 2023, 22, 16. [Google Scholar] [CrossRef]
- Garai, S.; Pati, N.C.; Pal, N.; Layek, G.C. Organized periodic structures and coexistence of triple attractors in a predator-prey model with fear and refuge. Chaos Solitons Fractals 2022, 165, 112833. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, C.; He, Z. Codimension-one and codimension-two bifurcations of a discrete predator-prey system with strong Allee effect. Math. Comput. Sim. 2019, 162, 155–178. [Google Scholar] [CrossRef]
- Chen, Q.L.; Teng, Z.D.; Wang, F. Fold–flip and strong resonance bifurcations of a discrete-time mosquito model. Chaos Solitons Fractals 2021, 144, 110704. [Google Scholar] [CrossRef]
- Jiang, H.; Rogers, T.D. The discrete dynamics of symmetric competition in the plane. J. Math. Bio. 1987, 25, 573–596. [Google Scholar] [CrossRef]
- Liu, X.L.; Xiao, D.M. Complex dynamic behaviors of a discrete-time predator-prey system. Chaos Solitons Fractals 2007, 32, 80–94. [Google Scholar] [CrossRef]
- Kuznetsov, Y. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 1998. [Google Scholar]
- Winggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer: New York, NY, USA, 2003. [Google Scholar]
- Luo, X.S.; Chen, G.; Wang, B.H.; Fang, J.Q. Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems. Chaos Solitons Fractals 2003, 18, 775–783. [Google Scholar] [CrossRef]
- Wei, Z.; Xia, Y.H.; Zhang, T.H. Stability and bifurcation analysis of a commensal model with additive Allee effect and nonlinear growth rate. Int. J. Bifurc. Chaos 2021, 31, 2150204. [Google Scholar] [CrossRef]
- Lin, Q.F. Allee effect increasing the final density of the species subject to the Allee effect in a Lotka–Volterra commensal symbiosis model. Adv. Differ. Equ. 2018, 2018, 196. [Google Scholar] [CrossRef]
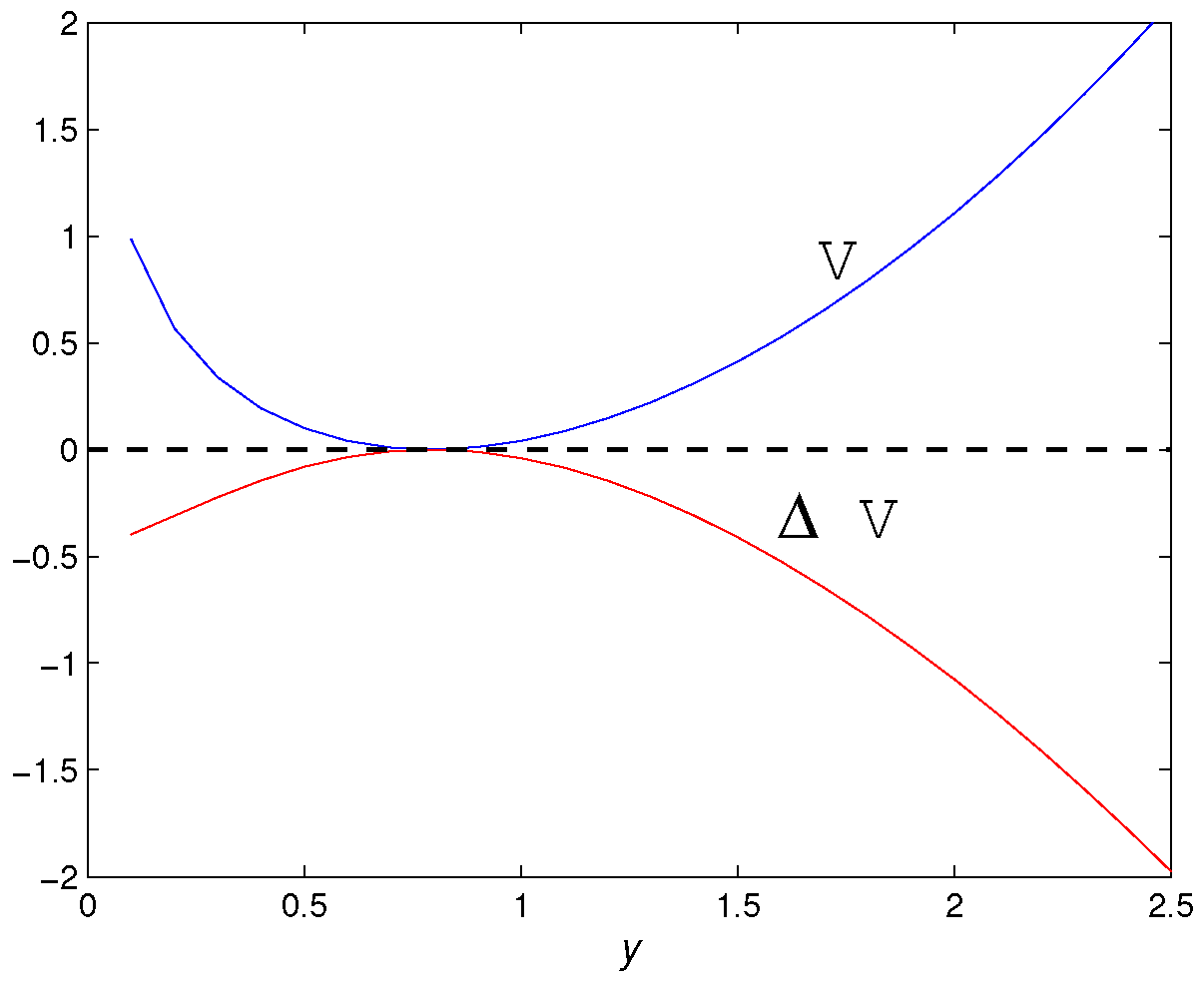
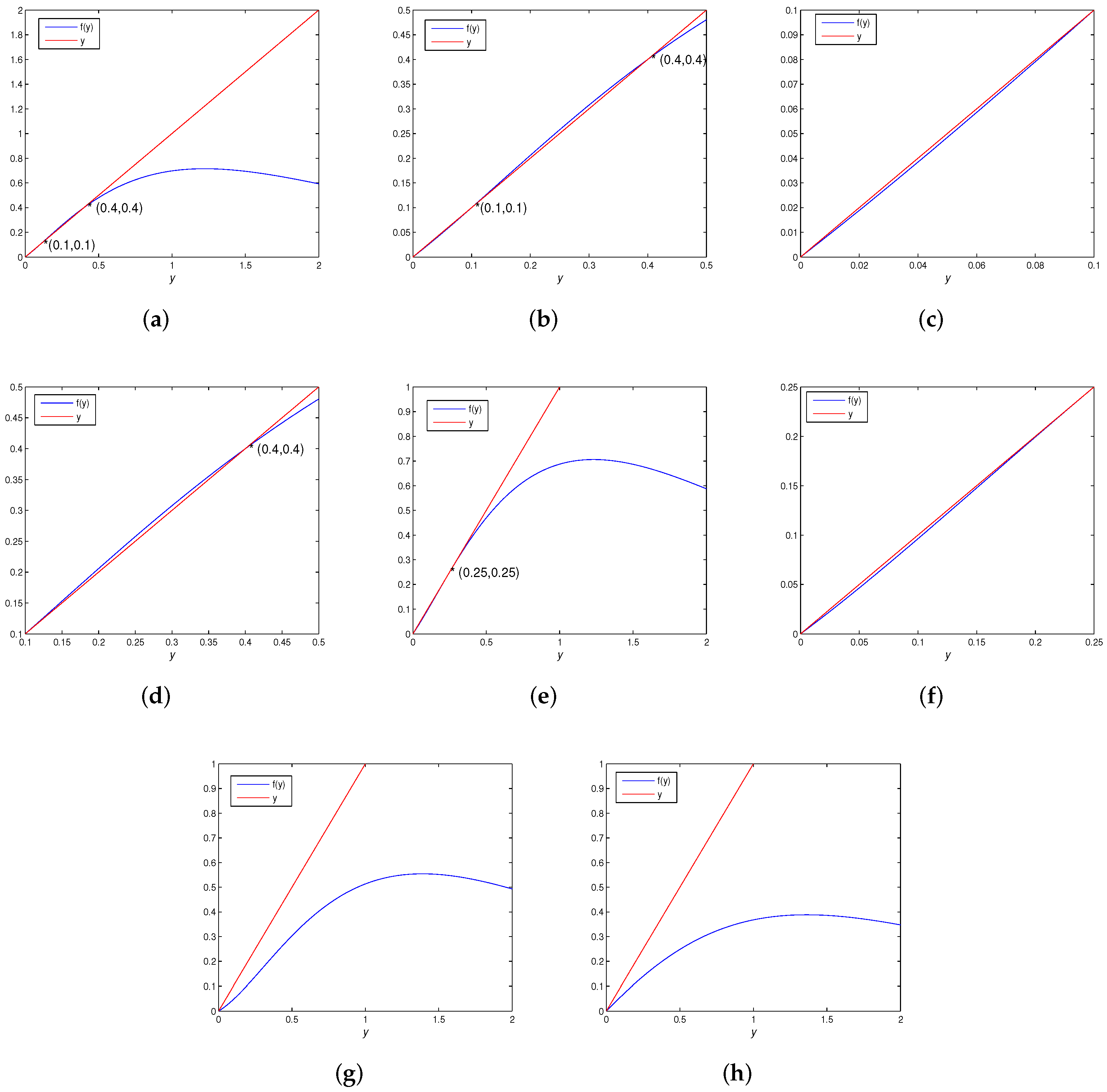



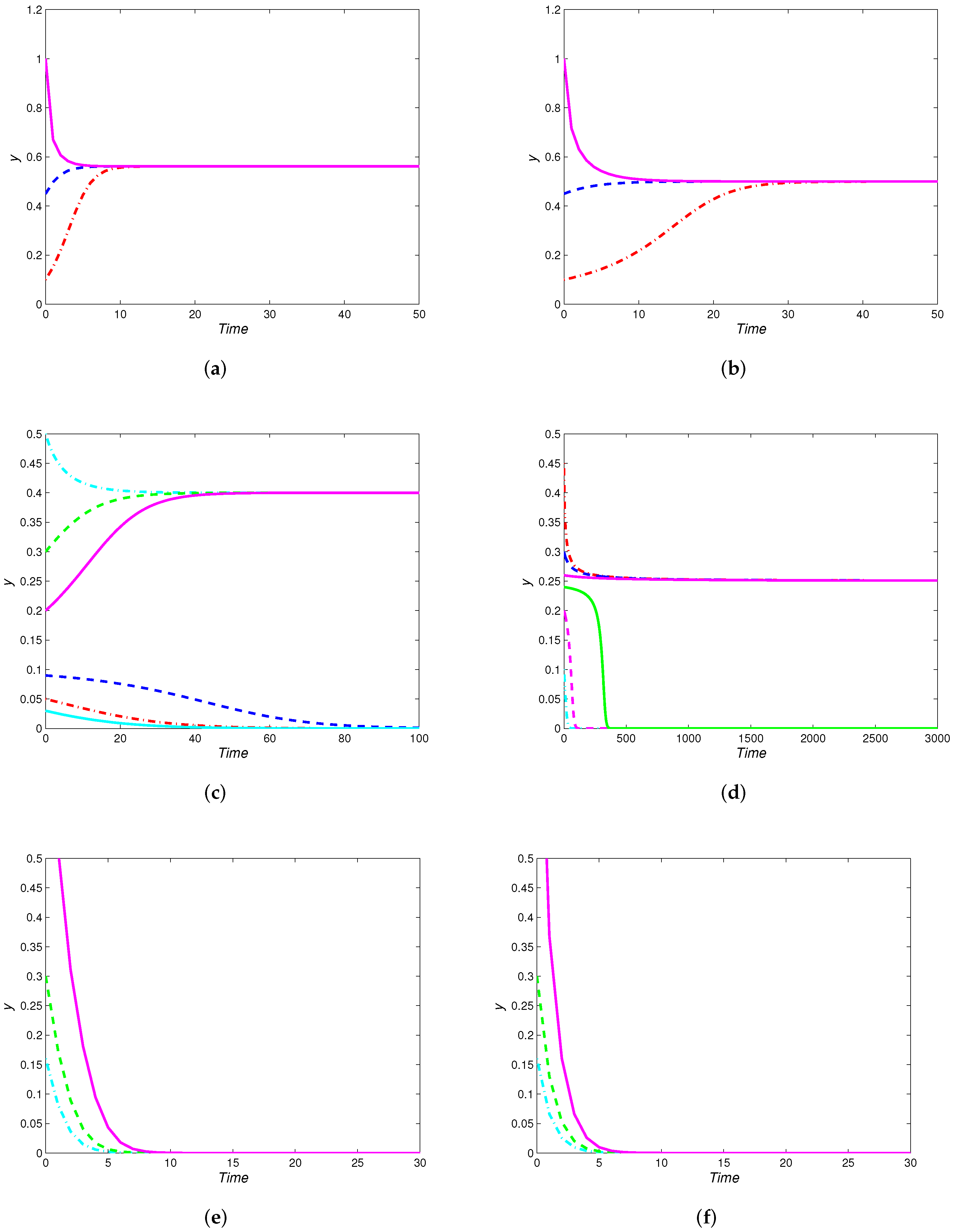

| Parameter Conditions | Existence | Stability | |
|---|---|---|---|
| 0 source, sink | |||
| 0 < A < 1 | 0 non-hyperbolic, sink | ||
| 0 | 0 non-hyperbolic | ||
| 0 < A < 1 | 0, | 0 sink, source, sink | |
| 0 | 0 sink | ||
| 0 sink, non-hyperbolic | |||
| 0 | 0 sink | ||
| 0 | 0 sink | ||
| Parameter Conditions | Existence | |
|---|---|---|
| 0 < M < A | ||
| M = A | 0 < A < 1 | |
| no other fixed points | ||
| 0 < A < 1 | ||
| no other fixed points | ||
| no other fixed points | ||
| no other fixed points | ||
| Parameter | Positive Fixed Point | Initial Value |
|---|---|---|
| no | ||
| no |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chong, Y.; Kashyap, A.J.; Chen, S.; Chen, F. Dynamics Analysis of a Discrete-Time Commensalism Model with Additive Allee for the Host Species. Axioms 2023, 12, 1031. https://doi.org/10.3390/axioms12111031
Chong Y, Kashyap AJ, Chen S, Chen F. Dynamics Analysis of a Discrete-Time Commensalism Model with Additive Allee for the Host Species. Axioms. 2023; 12(11):1031. https://doi.org/10.3390/axioms12111031
Chicago/Turabian StyleChong, Yanbo, Ankur Jyoti Kashyap, Shangming Chen, and Fengde Chen. 2023. "Dynamics Analysis of a Discrete-Time Commensalism Model with Additive Allee for the Host Species" Axioms 12, no. 11: 1031. https://doi.org/10.3390/axioms12111031





