A Strong Maximum Principle for Nonlinear Nonlocal Diffusion Equations
Abstract
:1. Introduction
- Notation
- 1.
- Norms in a single variable.
- (i)
- : those continuous functions of x on , which are continuous up to the boundary , with norm .
- (ii)
- : those Lebesgue measurable functions of x on whose p-th power has a finite Lebesgue integral, with norm . Here, .
- (iii)
- : those Lebesgue measurable functions of x on which are bounded up to a Lebesgue null set, with norm . Here, the essential supremum is the infimum of those constants , such that almost everywhere.
- 2.
- Spacetime norms. We let be bounded functions of space which are continuously differentiable in time, with norm
- 3.
- Two-point norms. We let be continuous functions of y that continuously vary in x, both up to the boundary, with norm
2. Strong Maximum Principles for Degenerate Diffusion Operators
2.1. Space-Continuous Solutions
2.2. Merely Bounded Solutions
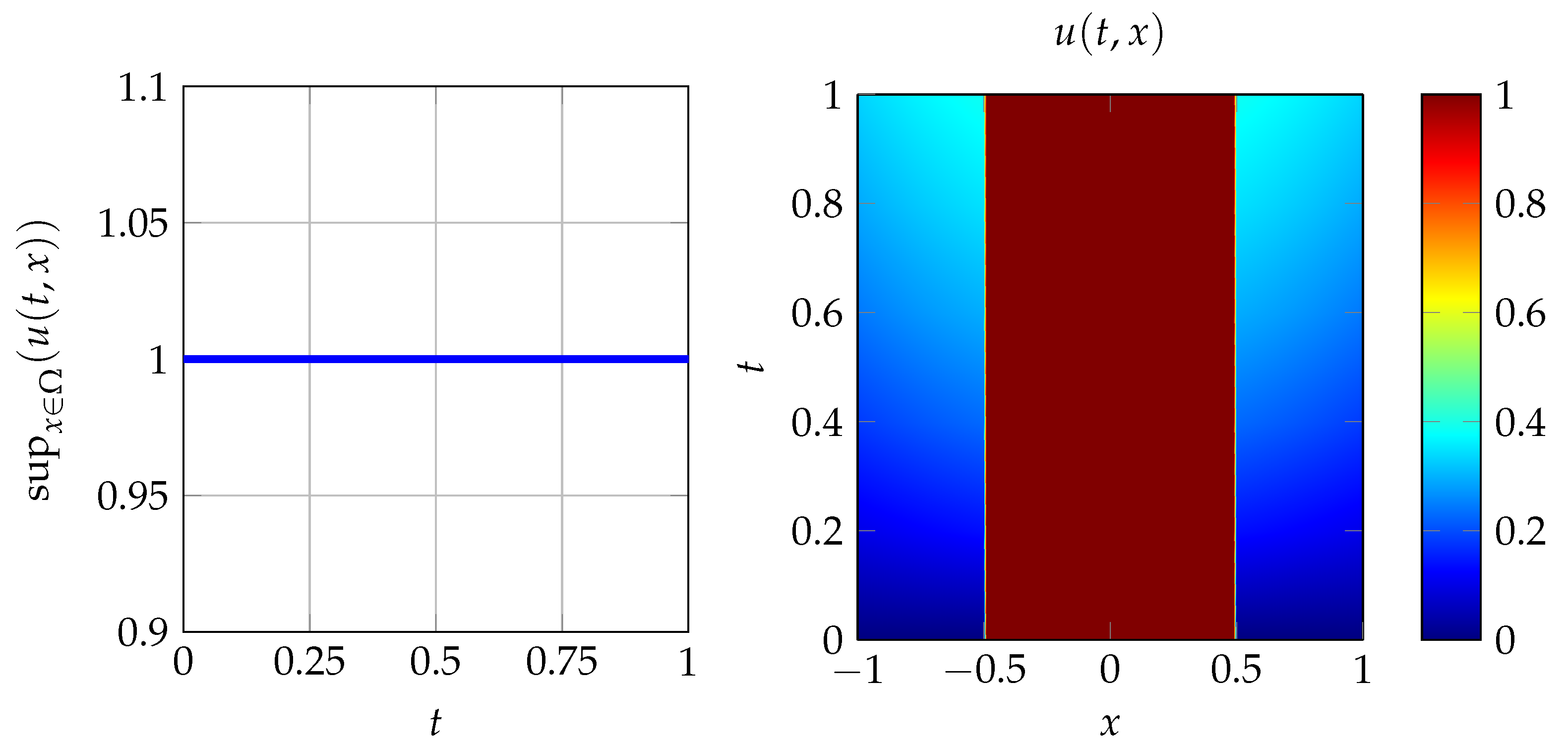
2.3. Examples of Degenerate Fluxes with Maximum Principles
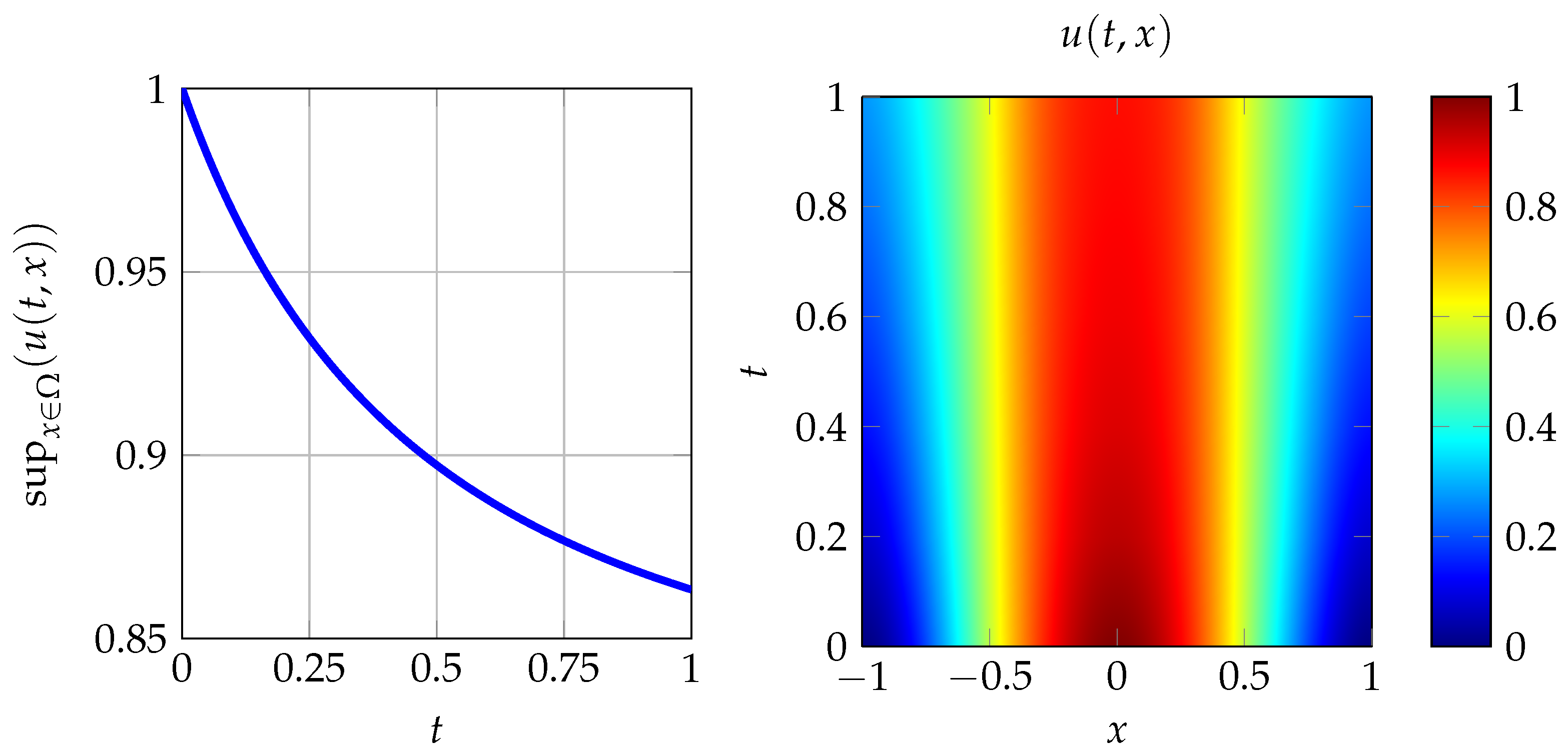
3. Counterexamples to the Strong Maximum Principle
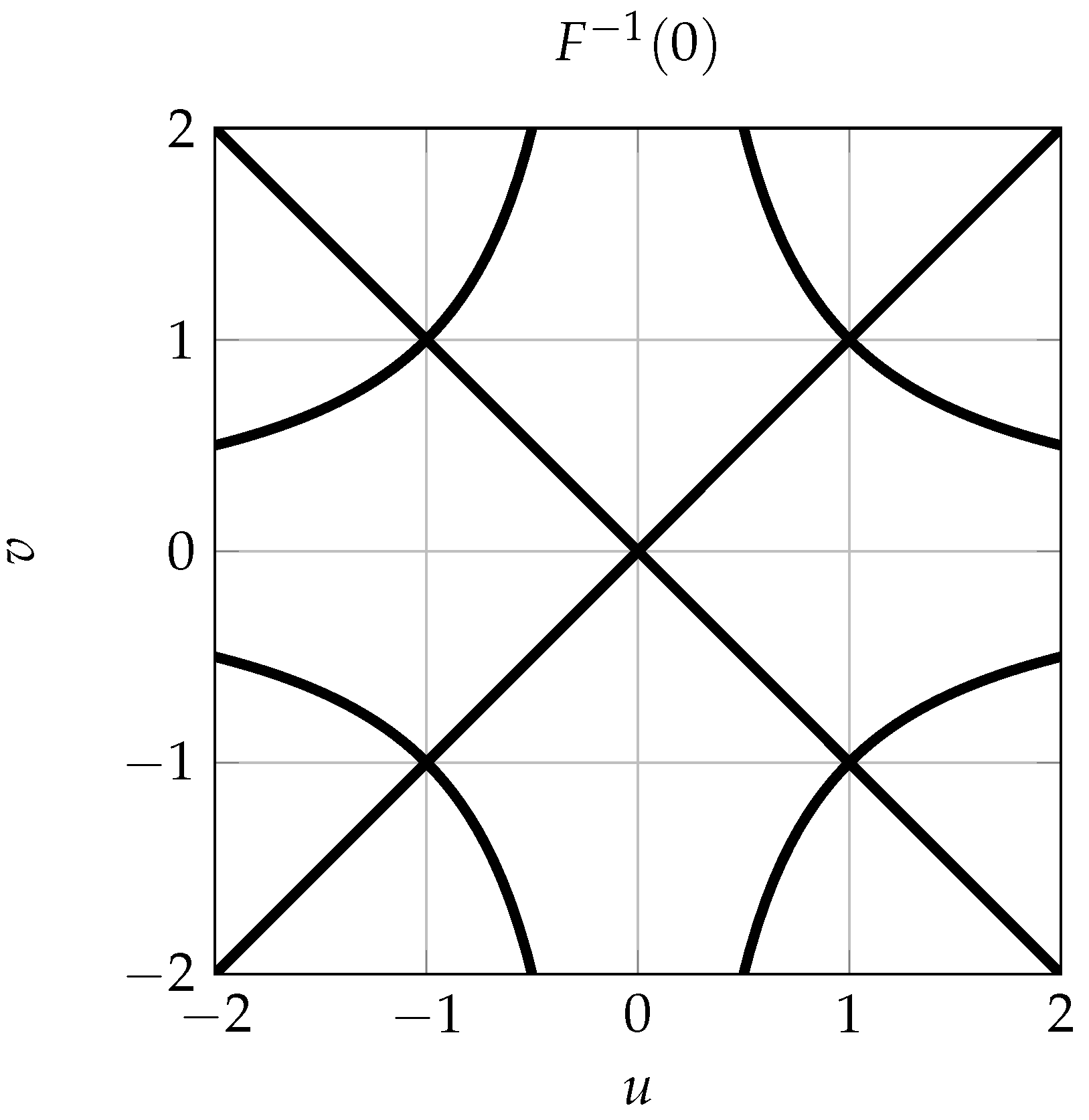
4. The Inconclusive Cases
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gilboa, G.; Osher, S. Nonlocal operators with applications to image processing. Multiscale Model. Simul. 2009, 7, 1005–1028. [Google Scholar]
- Yang, M.; Liang, J.; Zhang, J.; Gao, H.; Meng, F.; Xingdong, L.; Song, S.-J. Non-local means theory based perona–malik model for image denosing. Neurocomputing 2013, 120, 262–267. [Google Scholar]
- Zhou, M.-X.; Yan, X.; Xie, H.-B.; Zheng, H.; Xu, D.; Yang, G. Evaluation of non-local means based denoising filters for diffusion kurtosis imaging using a new phantom. PLoS ONE 2015, 10, e0116986. [Google Scholar]
- Zhang, X.; Xu, C.; Li, M.; Teng, R.K. Study of visual saliency detection via nonlocal anisotropic diffusion equation. Pattern Recognit. 2015, 48, 1315–1327. [Google Scholar]
- Tanzy, M.; Volpert, V.; Bayliss, A.; Nehrkorn, M. A Nagumo-type model for competing populations with nonlocal coupling. Math. Biosci. 2015, 263, 70–82. [Google Scholar] [PubMed]
- Carrillo, C.; Fife, P. Spatial effects in discrete generation population models. J. Math. Biol. 2005, 50, 161–188. [Google Scholar] [PubMed]
- Bernoff, A.J.; Topaz, C.M. Nonlocal aggregation models: A primer of swarm equilibria. SIAM Rev. 2013, 55, 709–747. [Google Scholar]
- Mogilner, A.; Edelstein-Keshet, L. A non-local model for a swarm. J. Math. Biol. 1999, 38, 534–570. [Google Scholar]
- Morale, D.; Capasso, V.; Oelschläger, K. An interacting particle system modelling aggregation behavior: From individuals to populations. J. Math. Biol. 2005, 50, 49–66. [Google Scholar]
- Ahmed, E.; Elgazzar, A. On fractional order differential equations model for nonlocal epidemics. Phys. Stat. Mech. Appl. 2007, 379, 607–614. [Google Scholar]
- Reluga, T.C.; Medlock, J.; Galvani, A.P. A model of spatial epidemic spread when individuals move within overlapping home ranges. Bull. Math. Biol. 2006, 68, 401–416. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Ge, J.; Lin, Z. An SEI–SI avian–human influenza model with diffusion and nonlocal delay. Appl. Math. Comput. 2014, 247, 753–761. [Google Scholar] [CrossRef]
- Benvenuti, E.; Borino, G.; Tralli, A. A thermodynamically consistent nonlocal formulation for damaging materials. Eur. J.-Mech.-A/Solids 2002, 21, 535–553. [Google Scholar] [CrossRef]
- Eringen, A. Theory of Nonlocal Elasticity and Some Applications; Technical Report, DTIC Document; DTIC: Fort Belvoir, VA, USA, 1984. [Google Scholar]
- Narendar, S. Wave dispersion in functionally graded magneto-electro-elastic nonlocal rod. Aerosp. Sci. Technol. 2016, 51, 42–51. [Google Scholar] [CrossRef]
- Salehipour, H.; Shahidi, A.; Nahvi, H. Modified nonlocal elasticity theory for functionally graded materials. Int. J. Eng. Sci. 2015, 90, 44–57. [Google Scholar] [CrossRef]
- Silling, S. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Du, Q.; Gunzburger, M.; Lehoucq, R.B.; Zhou, K. A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws. Math. Model. Methods Appl. Sci. 2013, 23, 493–540. [Google Scholar] [CrossRef]
- Du, Q.; Gunzburger, M.; Lehoucq, R.B.; Zhou, K. Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev. 2012, 54, 667–696. [Google Scholar] [CrossRef]
- Diaz, J.I. Solutions with compact support for some degenerate parabolic problems. Nonlinear Anal. 1979, 3, 831–847. [Google Scholar] [CrossRef]
- Andreu-Vaillo, F.; Mazón, J.M.; Rossi, J.D.; Toledo-Melero, J.J. Nonlocal Diffusion Problems; Volume 165 of Mathematical Surveys and, Monographs; American Mathematical Society: Providence, RI, USA; Real Sociedad Matemática Española: Madrid, Spain, 2010. [Google Scholar]
- Bobaru, F.; Duangpanya, M. The peridynamic formulation for transient heat conduction. Int. J. Heat Mass Transf. 2010, 53, 4047–4059. [Google Scholar] [CrossRef]
- Shi, Z. Nonlocal diffusion model with maximum principle. arXiv 2023, arXiv:2310.01221. [Google Scholar]
- Caffarelli, L.; Vázquez, J. Asymptotic behaviour of a porous medium equation with fractional diffusion. Discret. Contin. Dyn. Syst. 2011, 29, 1393–1404. [Google Scholar] [CrossRef]
- Li, D.; Zhang, X. On a nonlocal aggregation model with nonlinear diffusion. arXiv 2009, arXiv:0902.2017. [Google Scholar] [CrossRef]
- Bogoya, M. A nonlocal nonlinear diffusion equation in higher space dimensions. J. Math. Anal. Appl. 2008, 344, 601–615. [Google Scholar] [CrossRef]
- Coville, J.; Dupaigne, L. On a non-local equation arising in population dynamics. Proc. R. Soc. Edinb. Sect. A 2007, 137, 727–755. [Google Scholar] [CrossRef]
- Li, X.; Qiao, Z.; Wang, C. Convergence analysis for a stabilized linear semi-implicit numerical scheme for the nonlocal Cahn–Hilliard equation. Math. Comput. 2021, 90, 171–188. [Google Scholar] [CrossRef]
- Evans, L.C. Partial Differential Equations; American Math Society: Providence, RI, USA, 1998. [Google Scholar]
- Bobkov, V.; Takáč, P. A strong maximum principle for parabolic equations with the p-Laplacian. J. Math. Anal. Appl. 2014, 419, 218–230. [Google Scholar] [CrossRef]
- Pucci, P.; Serrin, J.B. The Maximum Principle; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Mincsovics, M. Discrete and continuous maximum principles for parabolic and elliptic operators. J. Comput. Appl. Math. 2010, 235, 470–477. [Google Scholar] [CrossRef]
- Gripenberg, G. On the strong maximum principle for degenerate parabolic equations. J. Differ. Equ. 2007, 242, 72–85. [Google Scholar] [CrossRef]
- Philippin, G.; Vernier-Piro, S. Discrete and continuous maximum principles for parabolic and elliptic operators. Nonlinear Anal. 2001, 47, 661–679. [Google Scholar] [CrossRef]
- Capella, A.; Dávila, J.; Dupaigne, L.; Sire, Y. Regularity of radial extremal solutions for some non-local semilinear equations. Commun. Partial. Differ. Equ. 2011, 36, 1353–1384. [Google Scholar] [CrossRef]
- Ye, H.; Liu, F.; Anh, V.; Turner, I. Maximum principle and numerical method for the multi-term time-space Riesz-Caputo fractional differential equations. Appl. Math. Comput. 2014, 227, 531–540. [Google Scholar] [CrossRef]
- García-Melián, J.; Rossi, J.D. Maximum and antimaximum principles for some nonlocal diffusion operators. Nonlin. Anal. 2009, 71, 6116–6121. [Google Scholar] [CrossRef]
- Coville, J. Remarks on the strong maximum principle for nonlocal operators. Electron. J. Differ. Equ. 2008, 2008, 1–10. [Google Scholar]
- Paredes, E. Some Results for Nonlocal Elliptic and Parabolic Nonlinear Equations. Ph.D. Thesis, Universidad de Chile, Santiago, Chile, 2014. [Google Scholar]
- Alibaud, N.; del Teso, F.; Endal, J.; Jakobsen, E.R. The Liouville theorem and linear operators satisfying the maximum principle. J. Math. Pures Appl. 2020, 142, 229–242. [Google Scholar] [CrossRef]
- Ciomaga, A. On the strong maximum principle for second order nonlinear parabolic integro-differential equations. Adv. Differ. Equ. 2012, 17, 635–671. [Google Scholar] [CrossRef]
- Jakobsen, E.R.; Karlsen, K.H. A “maximum principle for semicontinuous functions” applicable to integro-partial differential equations. NoDEA Nonlinear Differ. Equ. Appl. 2006, 13, 137–165. [Google Scholar] [CrossRef]
- Karch, G.; Kassmann, M.; Krupski, M. A framework for nonlocal, nonlinear initial value problems. SIAM J. Math. Anal. 2020, 52, 2383–2410. [Google Scholar] [CrossRef]
- Scott, W.R. Group Theory; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Burden, R.L.; Faires, D.J.; Burden, A.M. Numerical Analysis, 10th ed.; Cengage Learning: Boston, MA, USA, 2016. [Google Scholar]
- Gershgorin, S.A. Uber die abgrenzung der eigenwerte einer matrix. Izv. Akad. Nauk. SSSR Ser. Mat. 1931, 7, 749–754. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hartland, T.; Shankar, R. A Strong Maximum Principle for Nonlinear Nonlocal Diffusion Equations. Axioms 2023, 12, 1059. https://doi.org/10.3390/axioms12111059
Hartland T, Shankar R. A Strong Maximum Principle for Nonlinear Nonlocal Diffusion Equations. Axioms. 2023; 12(11):1059. https://doi.org/10.3390/axioms12111059
Chicago/Turabian StyleHartland, Tucker, and Ravi Shankar. 2023. "A Strong Maximum Principle for Nonlinear Nonlocal Diffusion Equations" Axioms 12, no. 11: 1059. https://doi.org/10.3390/axioms12111059
APA StyleHartland, T., & Shankar, R. (2023). A Strong Maximum Principle for Nonlinear Nonlocal Diffusion Equations. Axioms, 12(11), 1059. https://doi.org/10.3390/axioms12111059