On the Exact Solution of a Scalar Differential Equation via a Simple Analytical Approach
Abstract
1. Introduction
2. The Advanced Equation:
2.1. Reduced Model:
2.2. Full Model:
3. Existence and Uniqueness
4. Compact Form for the Periodic Solution of the Advanced Equation
5. Special Cases of the Advanced Equation
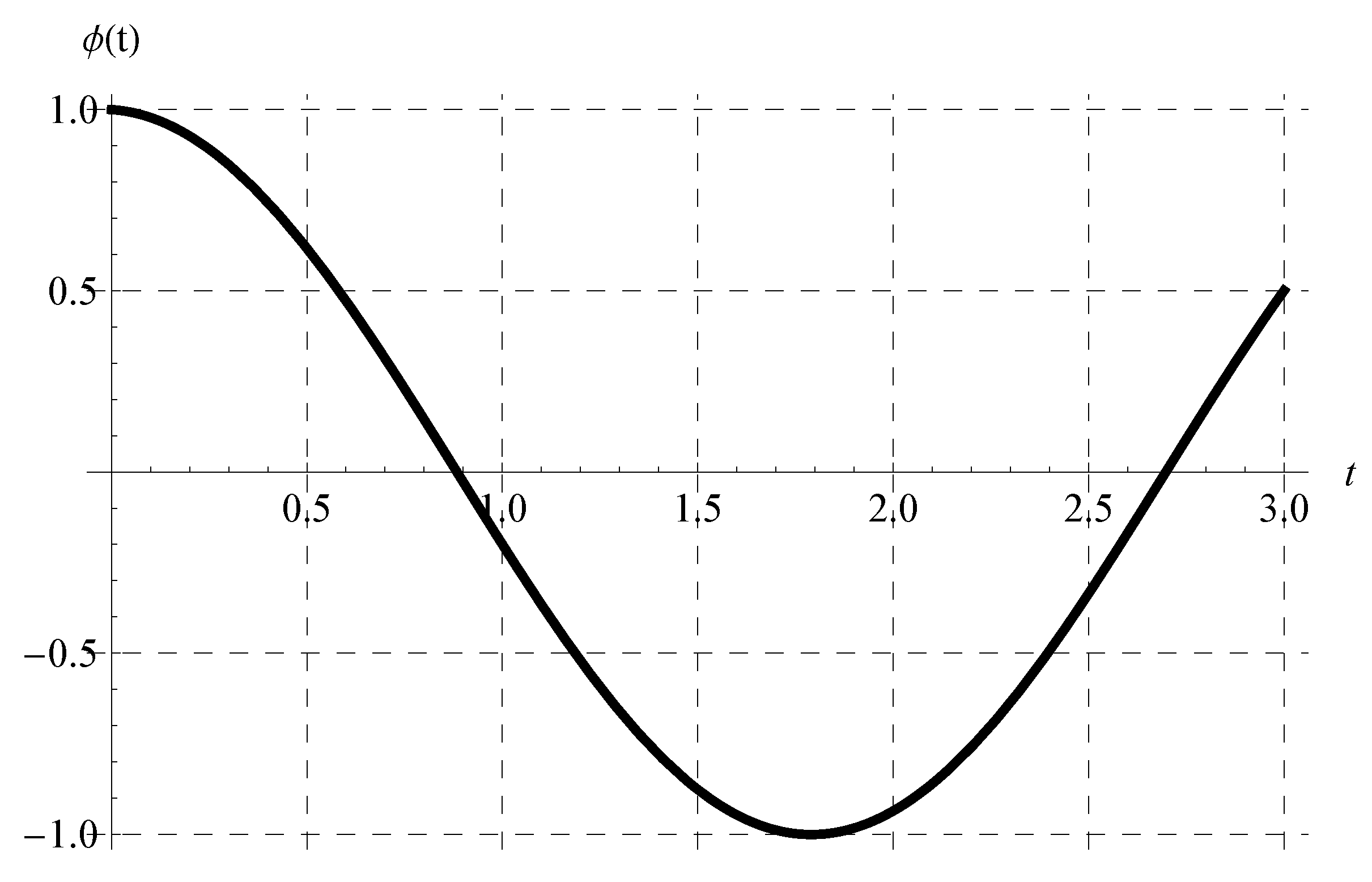
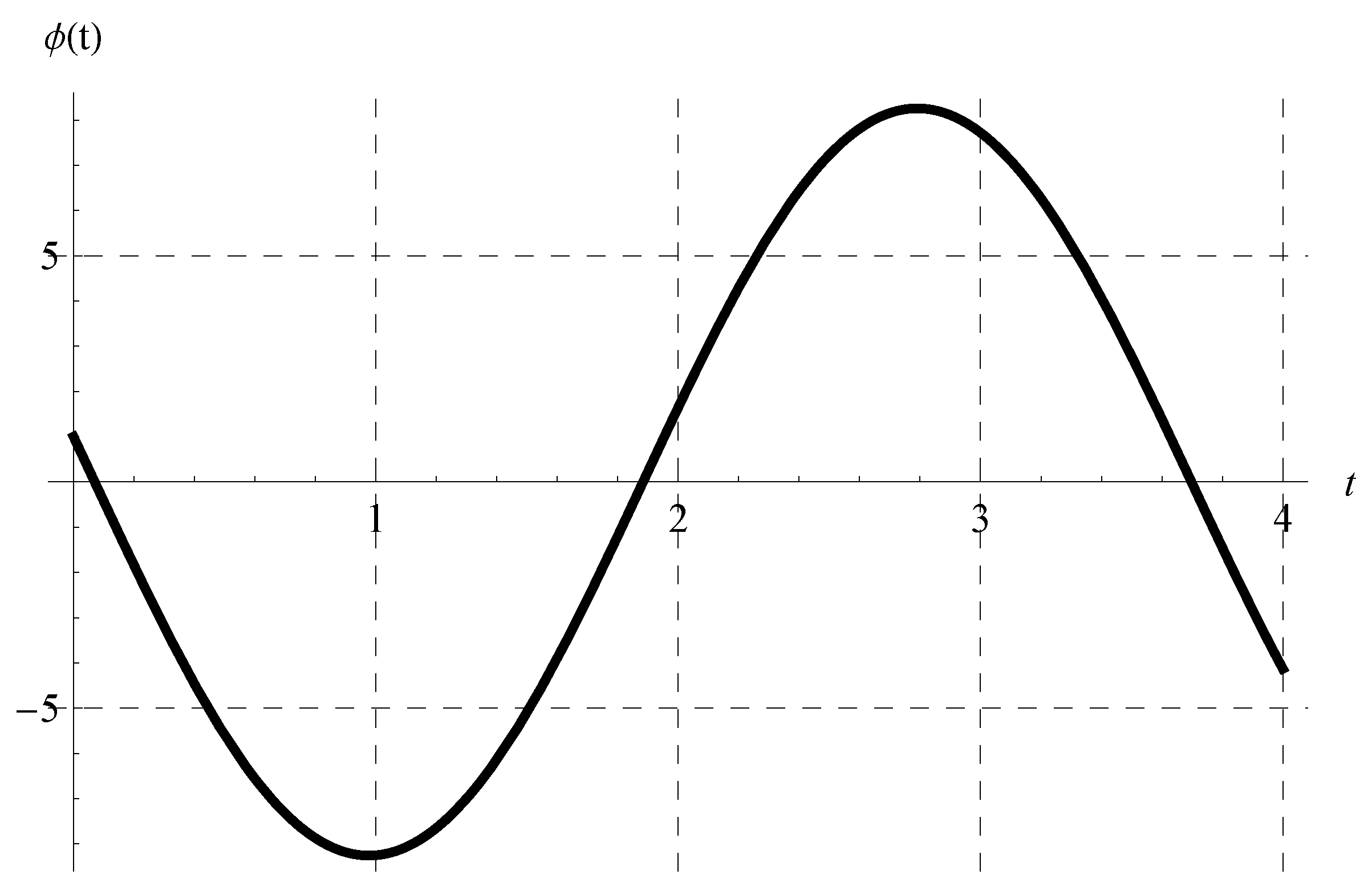
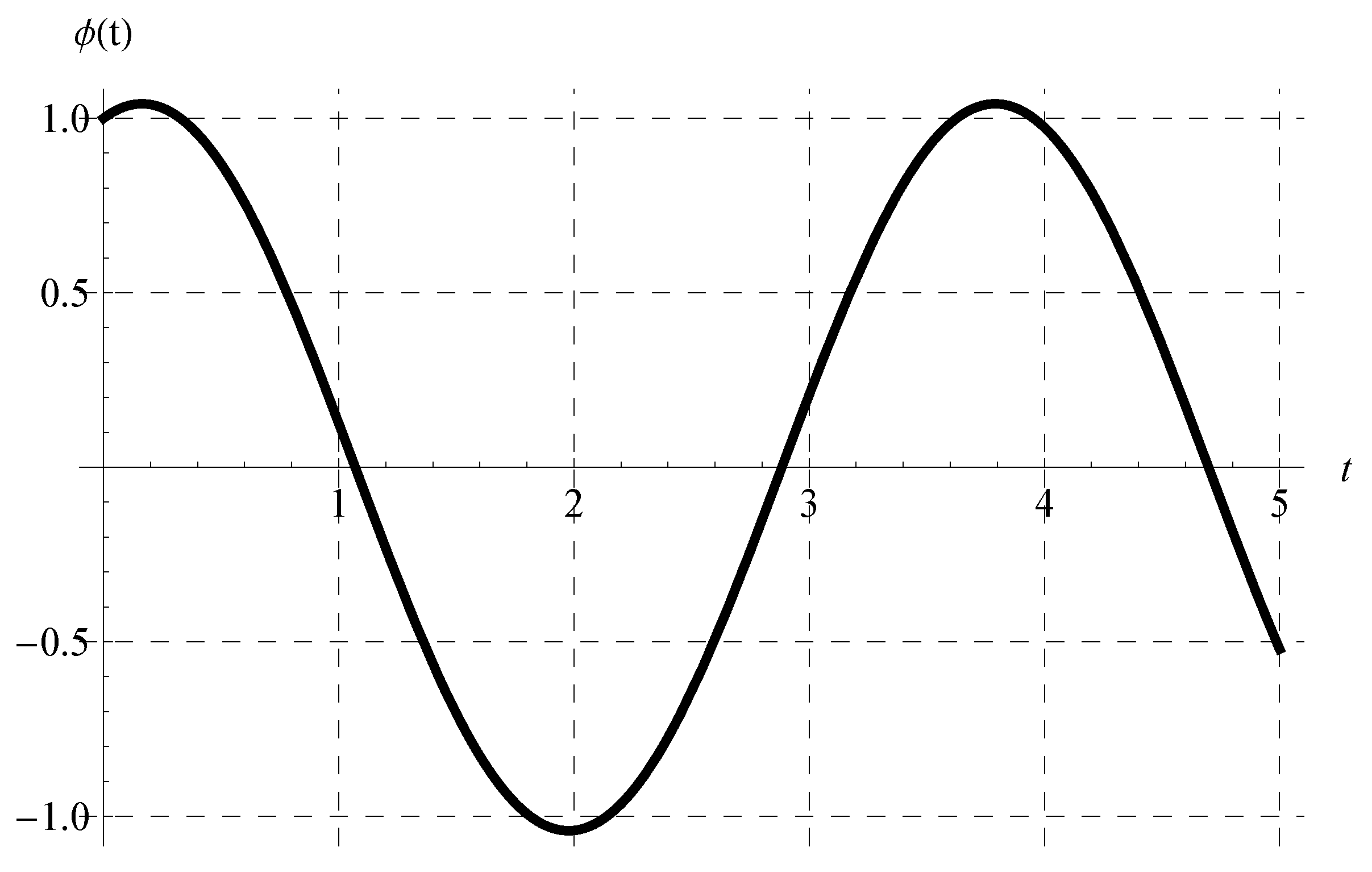
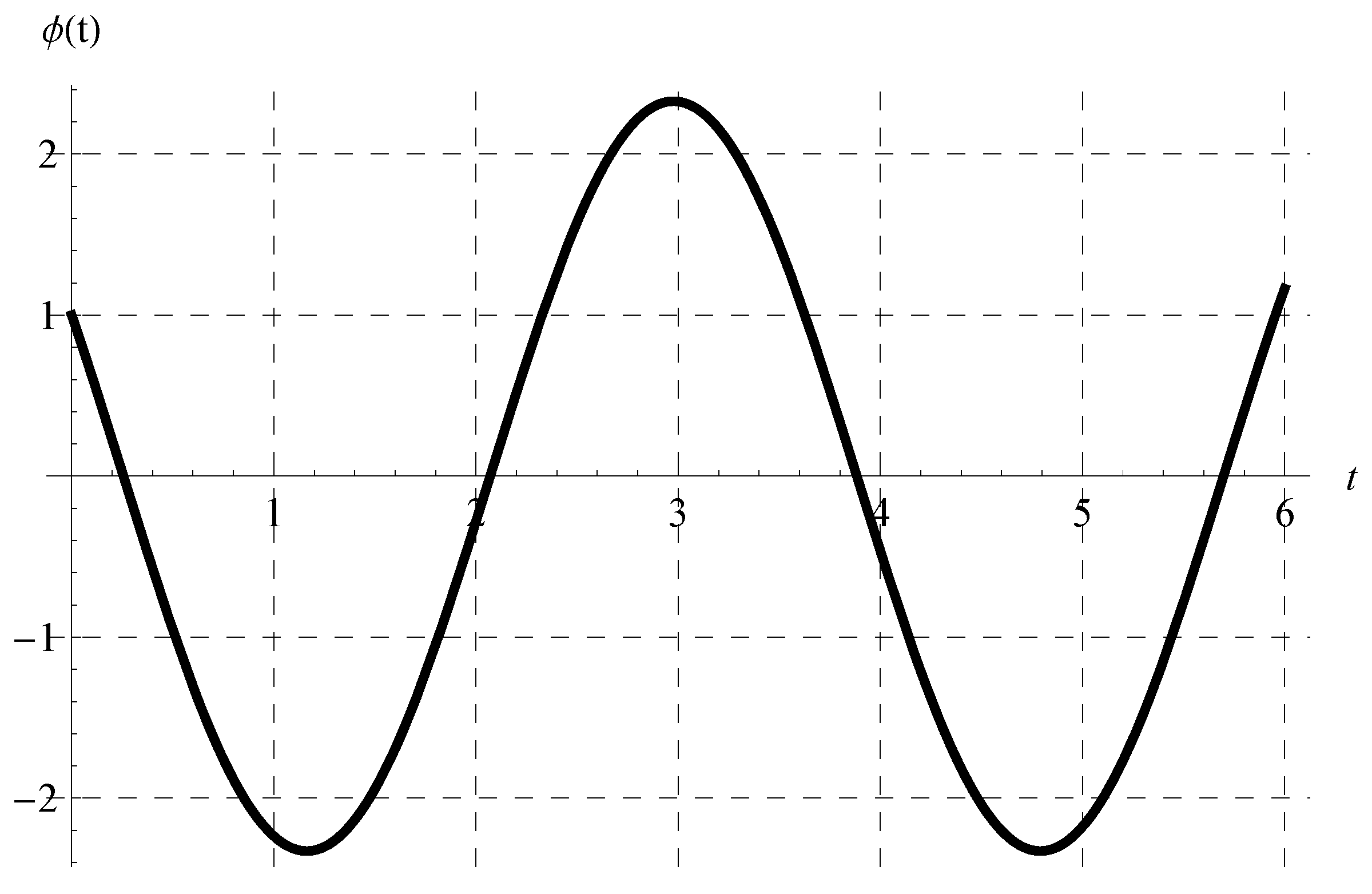
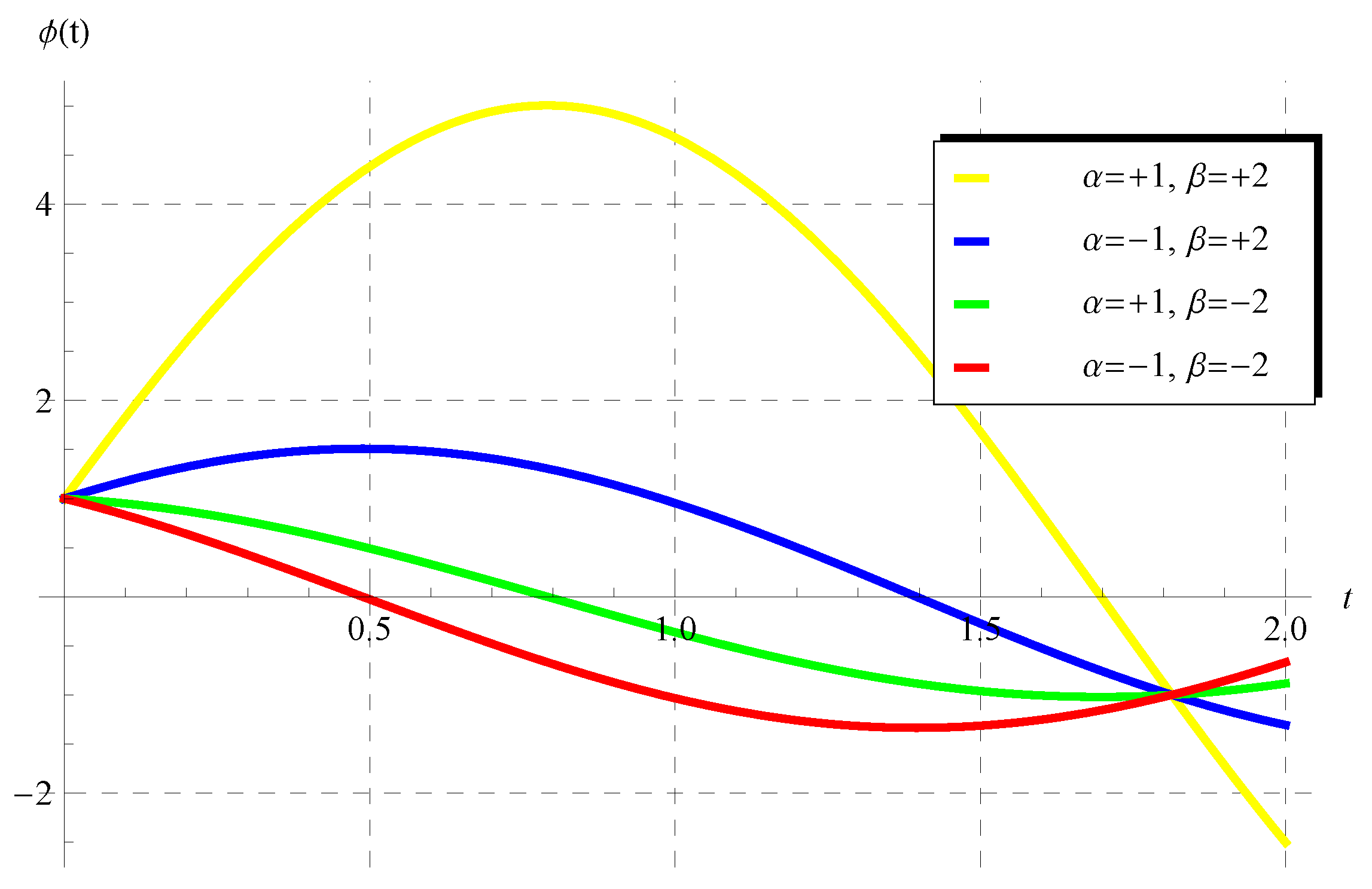
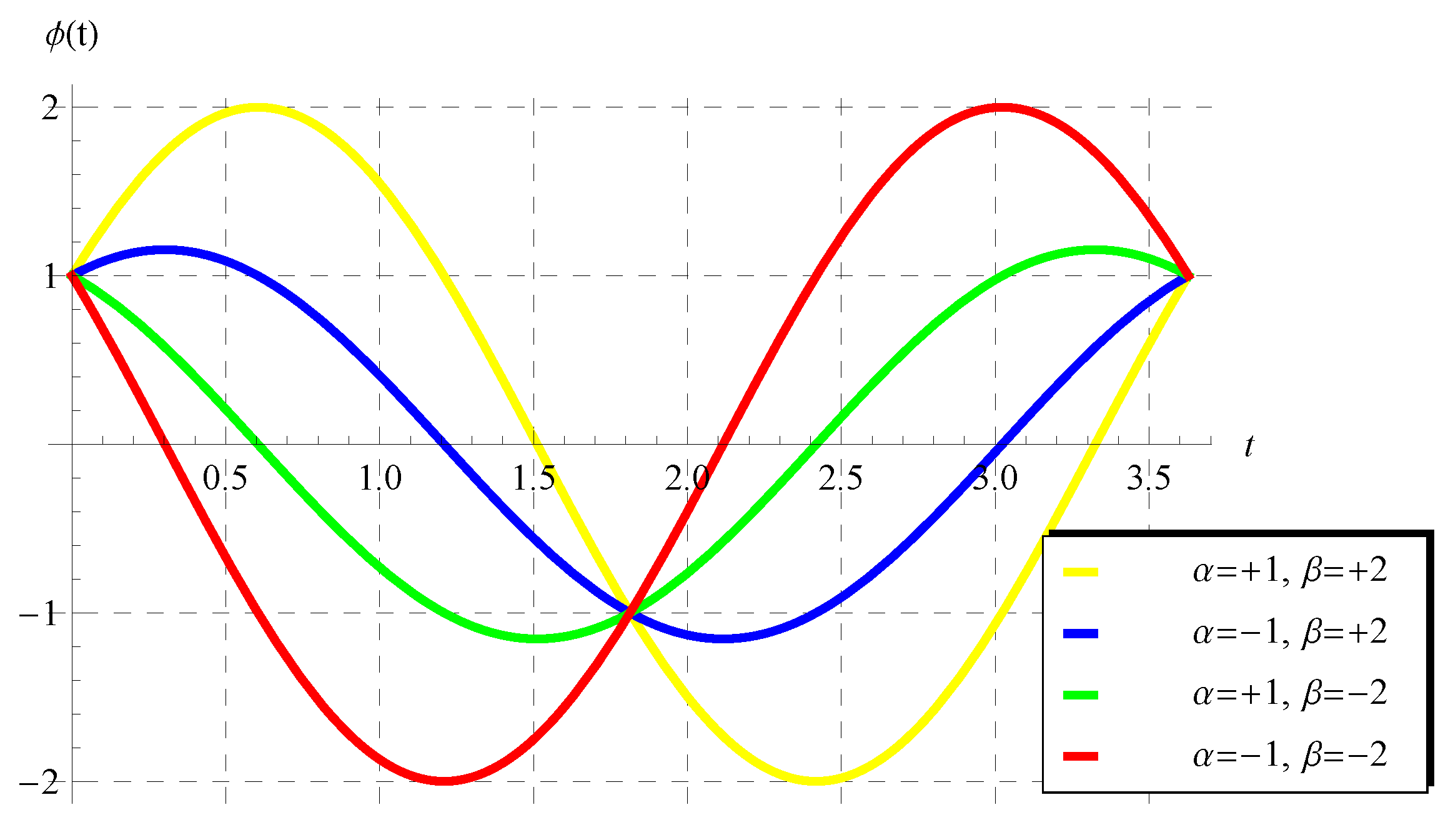
6. Characteristics of the Solution of the Advanced Equation
6.1. Behavior of the Periodic Solution
6.2. The Amplitude, Phase, and Critical Values of the Advance Parameter :
6.3. Behavior of the Polynomial Solution
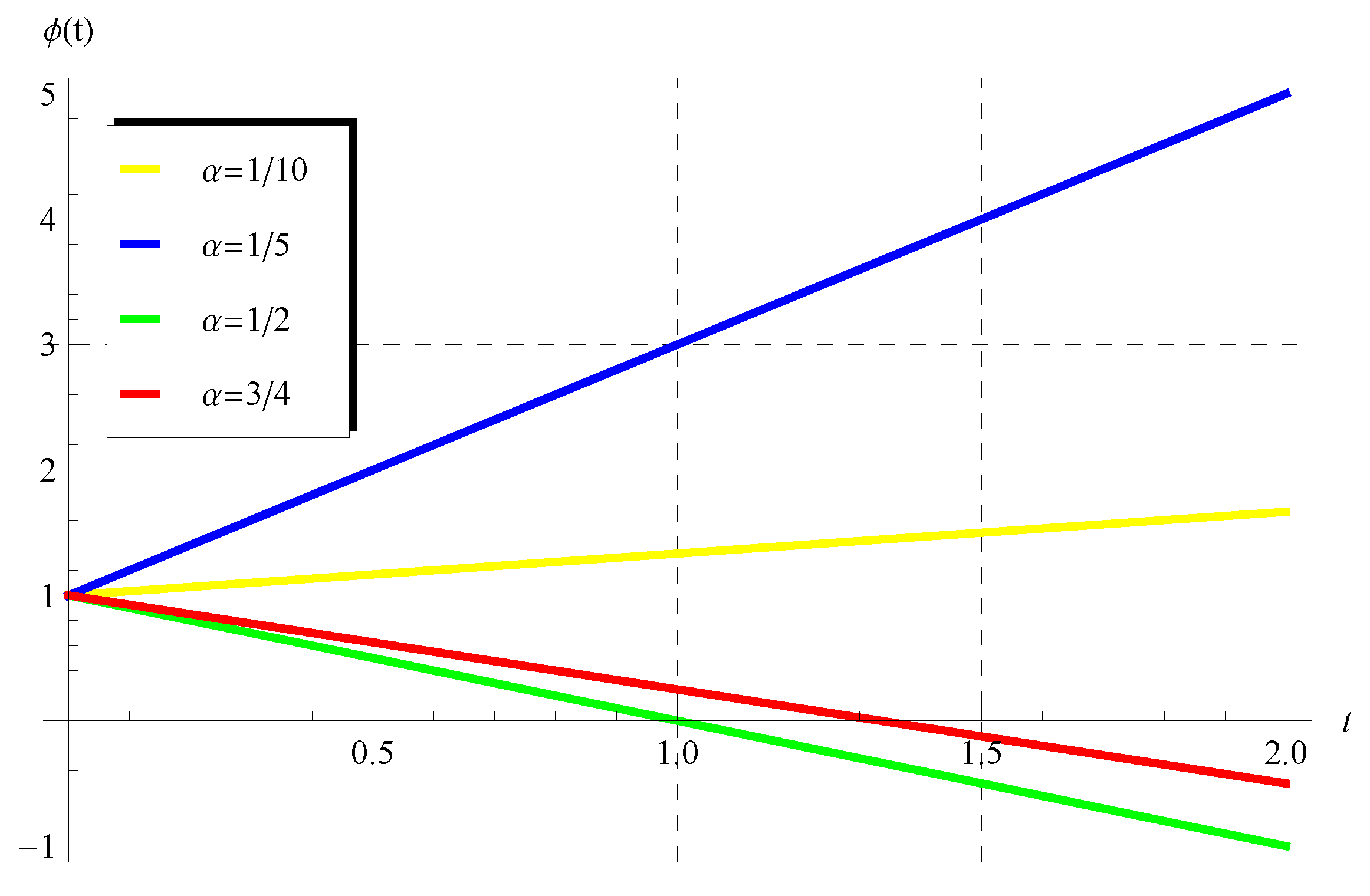
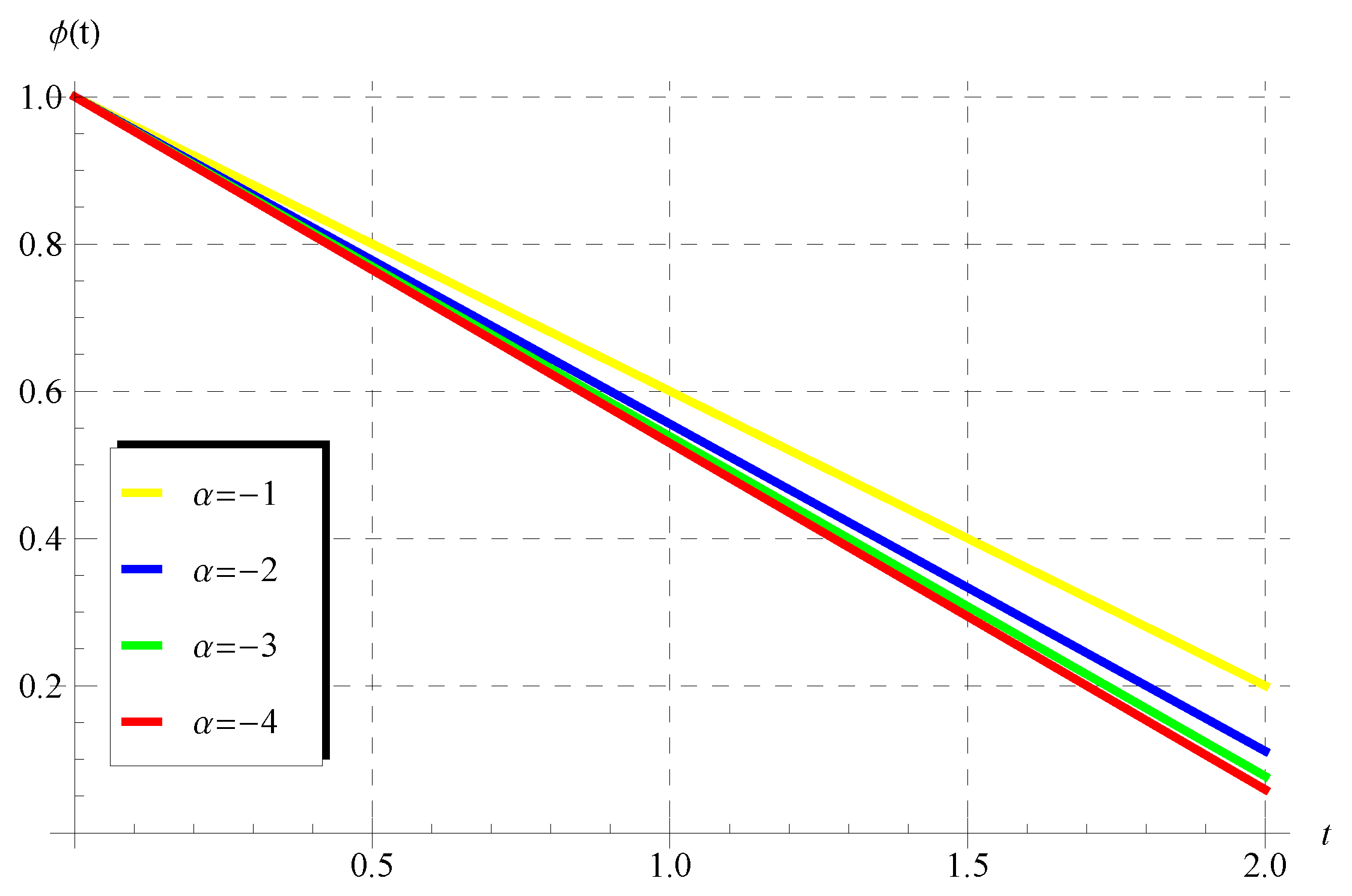
7. The Delay Equation:
7.1. The Solution in the Interval:
7.2. The Solution in the Interval of
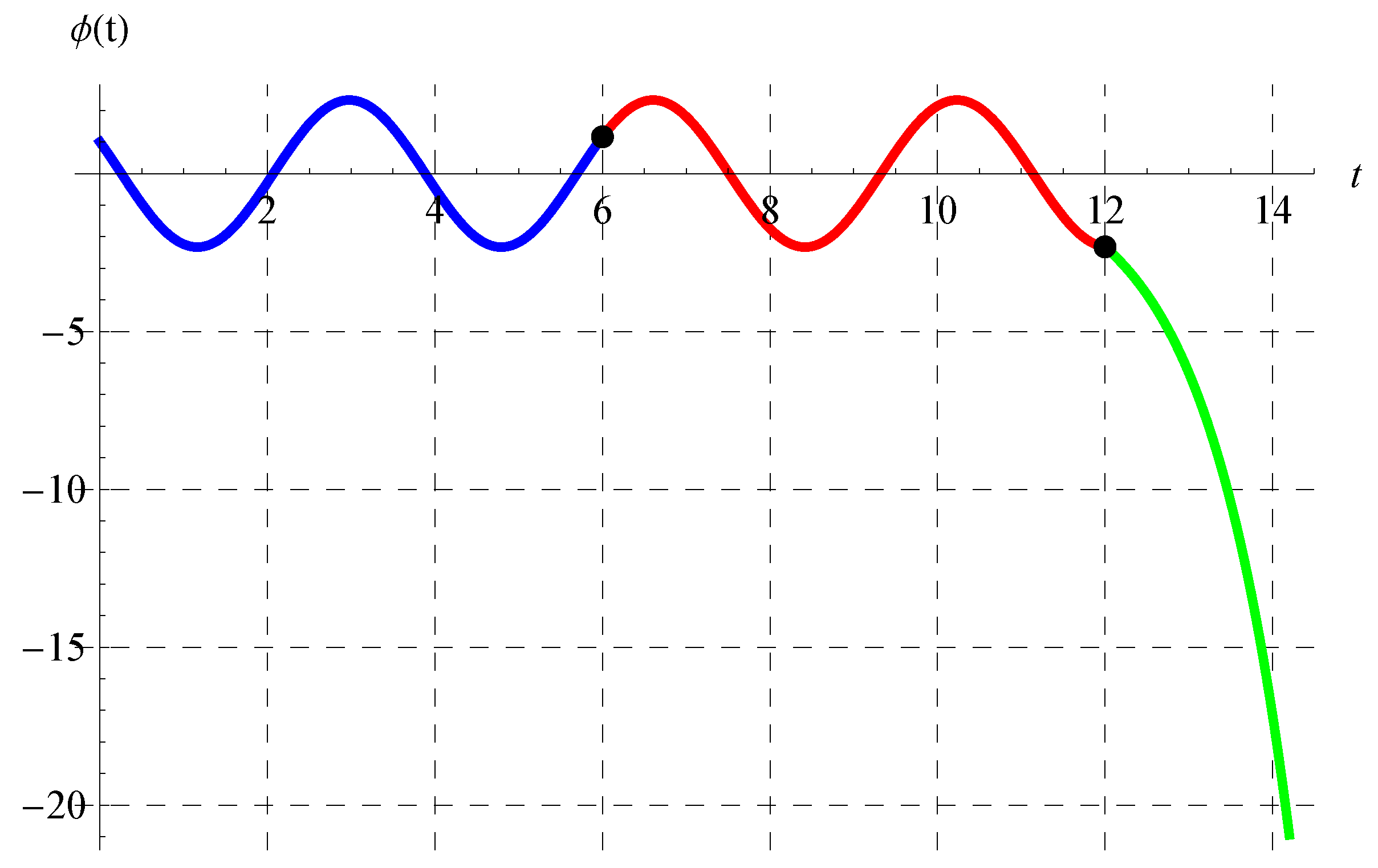
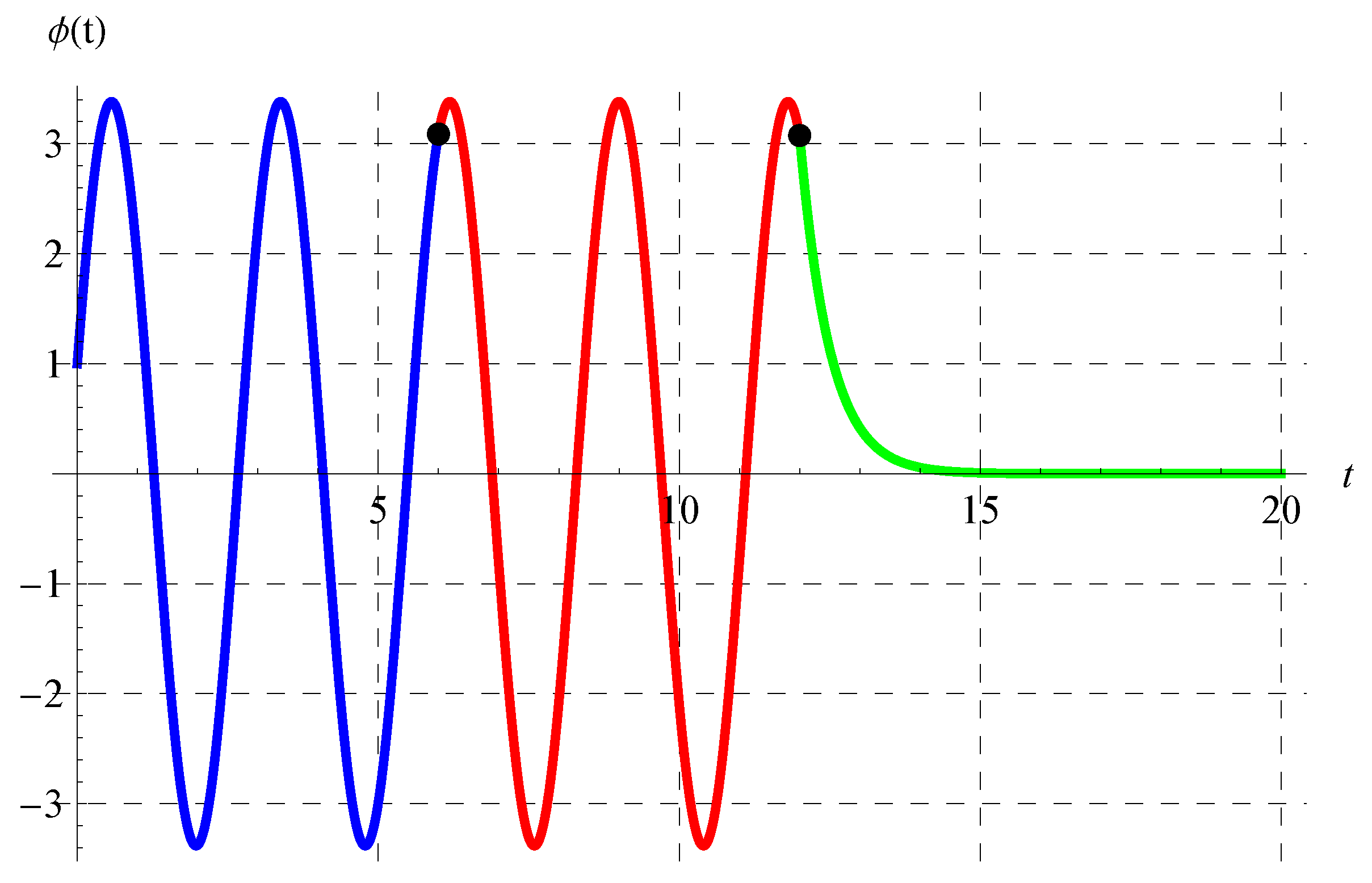
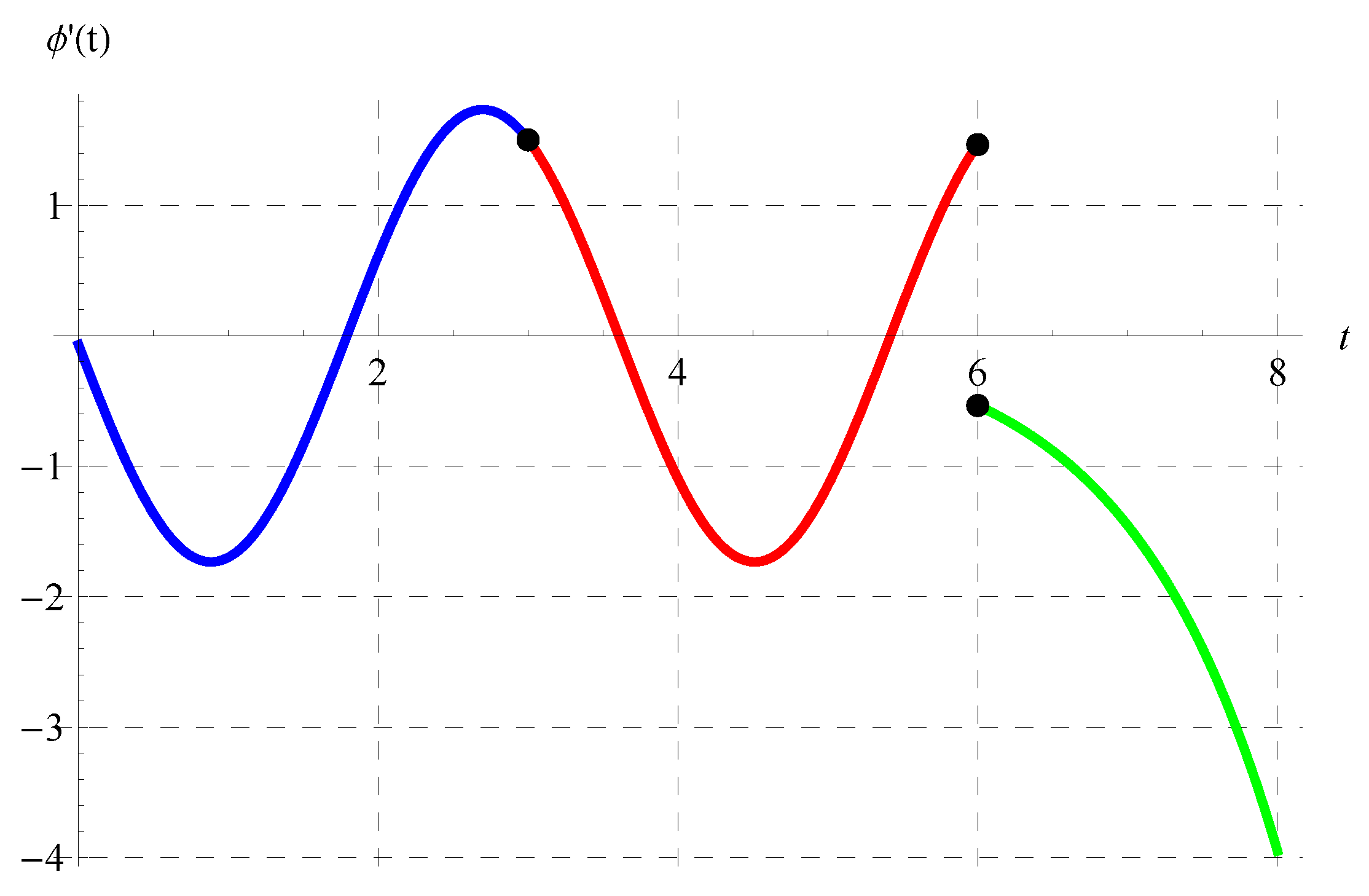
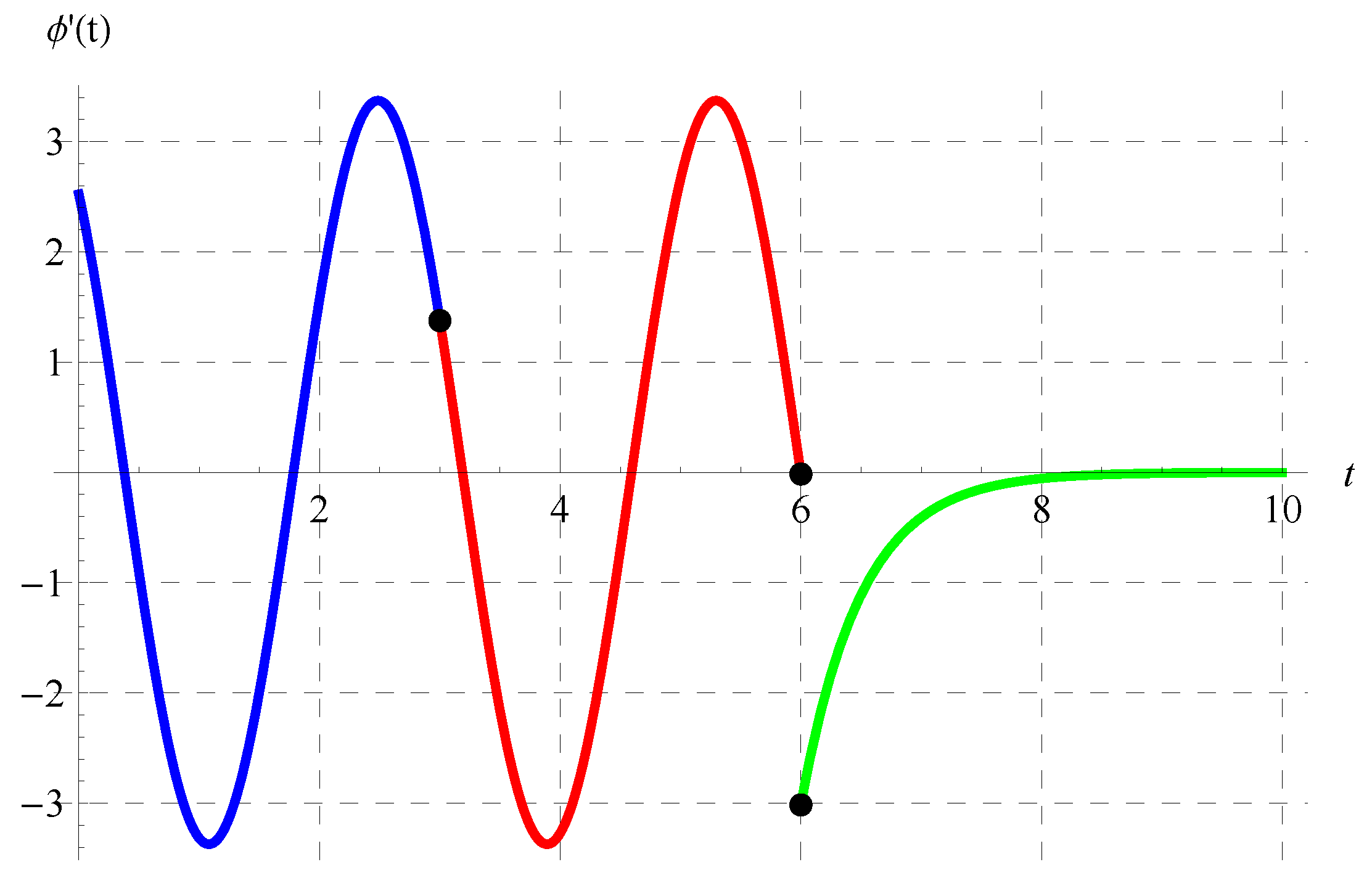
8. Properties and Behavior of the Solution in the Full Domain
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Andrews, H.I. Third paper: Calculating the behaviour of an overhead catenary system for railway electrification. Proc. Inst. Mech. Eng. 1964, 179, 809–846. [Google Scholar] [CrossRef]
- Abbott, M.R. Numerical method for calculating the dynamic behaviour of a trolley wire overhead contact system for electric railways. Comput. J. 1970, 13, 363–368. [Google Scholar] [CrossRef]
- Gilbert, G.; Davtcs, H.E.H. Pantograph motion on a nearly uniform railway overhead line. Proc. Inst. Electr. Eng. 1966, 113, 485–492. [Google Scholar] [CrossRef]
- Caine, P.M.; Scott, P.R. Single-wire railway overhead system. Proc. Inst. Electr. Eng. 1969, 116, 1217–1221. [Google Scholar] [CrossRef]
- Ockendon, J.; Tayler, A.B. The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1971, 322, 447–468. [Google Scholar]
- Fox, L.; Mayers, D.; Ockendon, J.R.; Tayler, A.B. On a functional differential equation. IMA J. Appl. Math. 1971, 8, 271–307. [Google Scholar] [CrossRef]
- Kato, T.; McLeod, J.B. The functional-differential equation y′(x)=ay(λx)+by(x). Bull. Am. Math. Soc. 1971, 77, 891–935. [Google Scholar]
- Iserles, A. On the generalized pantograph functional-differential equation. Eur. J. Appl. Math. 1993, 4, 1–38. [Google Scholar] [CrossRef]
- Ambartsumian, V.A. On the fluctuation of the brightness of the milky way. Dokl. Akad. Nauk USSR 1994, 44, 223–226. [Google Scholar]
- Patade, J.; Bhalekar, S. On analytical solution of Ambartsumian equation. Natl. Acad. Sci. Lett. 2017, 40, 291–293. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method. Mathematics 2018, 6, 331. [Google Scholar] [CrossRef]
- Khaled, S.M.; El-Zahar, E.R.; Ebaid, A. Solution of Ambartsumian delay differential equation with conformable derivative. Mathematics 2019, 7, 425. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Rathore, S. Analysis of a fractional model of the Ambartsumian equation. Eur. Phys. J. Plus 2018, 133, 133–259. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Jeaid, H.K. On the exact solution of the functional differential equation y′(t)=ay(t)+by(-t). Adv. Differ. Equ. Control Process. 2022, 26, 39–49. [Google Scholar]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Acad: Boston, MA, USA, 1994. [Google Scholar]
- Wazwaz, A.M. Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl. Math. Comput. 2005, 166, 652–663. [Google Scholar] [CrossRef]
- Duan, J.S.; Rach, R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Diblík, J.; Kúdelcíková, M. Two classes of positive solutions of first order functional differential equations of delayed type. Nonlinear Anal. Theory Methods Appl. 2012, 75, 4807–4820. [Google Scholar] [CrossRef]
- Alshaery, A.; Ebaid, A. Accurate analytical periodic solution of the elliptical Kepler equation using the Adomian decomposition method. Acta Astronaut. 2017, 140, 27–33. [Google Scholar] [CrossRef]
- Li, W.; Pang, Y. Application of Adomian decomposition method to nonlinear systems. Adv. Differ. Equ. 2020, 2020, 67. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Jeaid, H.K.; Al-Aly, H. Notes on the Perturbation Solutions of the Boundary Layer Flow of Nanofluids Past a Stretching Sheet. Appl. Math. Sci. 2013, 7, 6077–6085. [Google Scholar] [CrossRef]
- Ebaid, A. Remarks on the homotopy perturbation method for the peristaltic flow of Jeffrey fluid with nano-particles in an asymmetric channel. Comput. Math. Appl. 2014, 68, 77–85. [Google Scholar] [CrossRef]
- Ayati, Z.; Biazar, J. On the convergence of Homotopy perturbation method. J. Egypt. Math. Soc. 2015, 23, 424–428. [Google Scholar] [CrossRef]
- Khaled, S.M. The exact effects of radiation and joule heating on Magnetohydrodynamic Marangoni convection over a flat surface. Therm. Sci. 2018, 22, 63–72. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshomrani, N.A.M.; Ebaid, A.; Aldosari, F.; Aljoufi, M.D. On the Exact Solution of a Scalar Differential Equation via a Simple Analytical Approach. Axioms 2024, 13, 129. https://doi.org/10.3390/axioms13020129
Alshomrani NAM, Ebaid A, Aldosari F, Aljoufi MD. On the Exact Solution of a Scalar Differential Equation via a Simple Analytical Approach. Axioms. 2024; 13(2):129. https://doi.org/10.3390/axioms13020129
Chicago/Turabian StyleAlshomrani, Nada A. M., Abdelhalim Ebaid, Faten Aldosari, and Mona D. Aljoufi. 2024. "On the Exact Solution of a Scalar Differential Equation via a Simple Analytical Approach" Axioms 13, no. 2: 129. https://doi.org/10.3390/axioms13020129
APA StyleAlshomrani, N. A. M., Ebaid, A., Aldosari, F., & Aljoufi, M. D. (2024). On the Exact Solution of a Scalar Differential Equation via a Simple Analytical Approach. Axioms, 13(2), 129. https://doi.org/10.3390/axioms13020129







