A Simplified Approach to the Pricing of Vulnerable Options with Two Underlying Assets in an Intensity-Based Model
Abstract
:1. Introduction
2. The Model
3. The Valuation of Vulnerable Options with Two Underlying Assets
3.1. Vulnerable Exchange Option
3.2. Vulnerable Foreign Equity Option
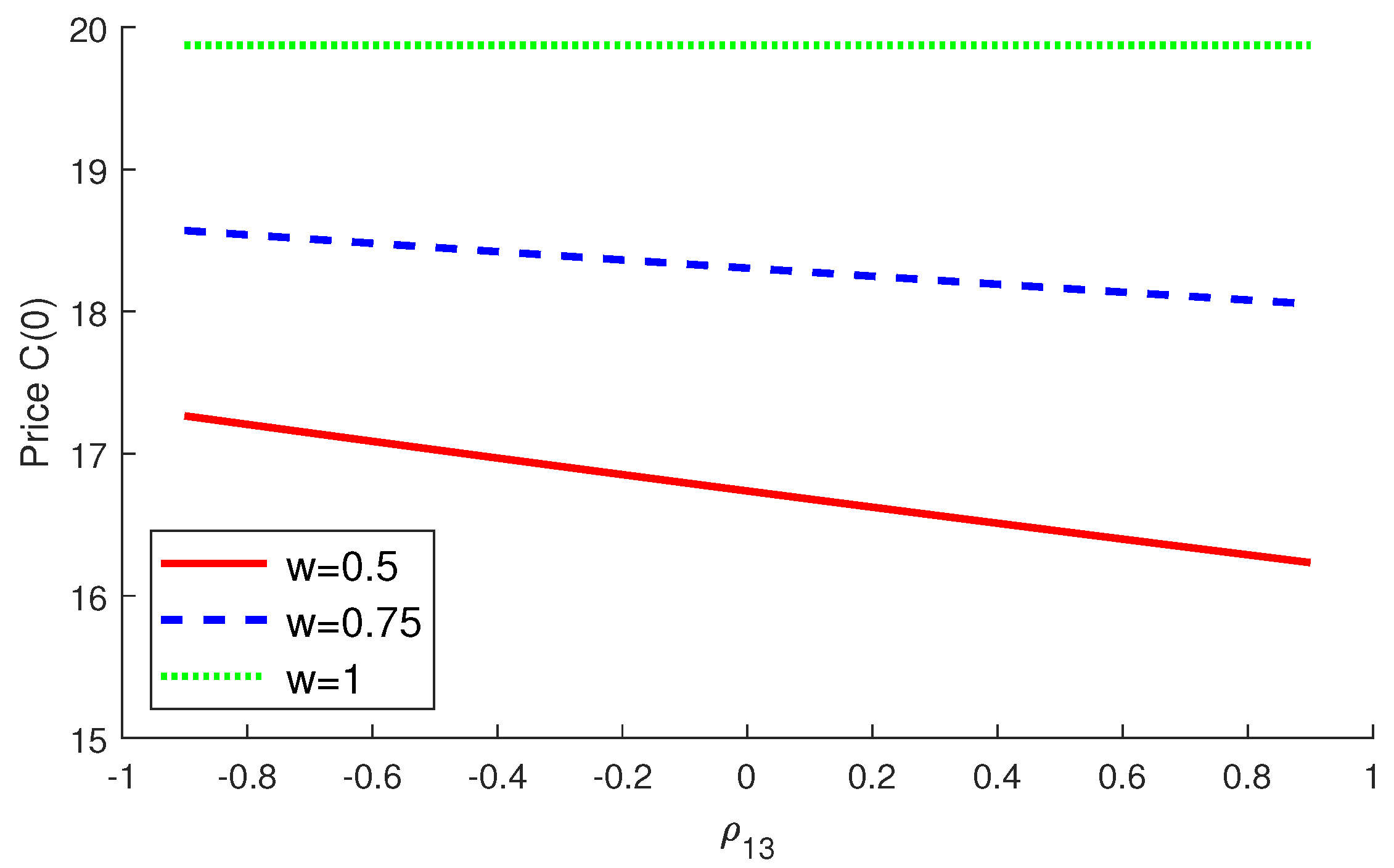
4. Numerical Experiments
4.1. Monte Carlo Simulation
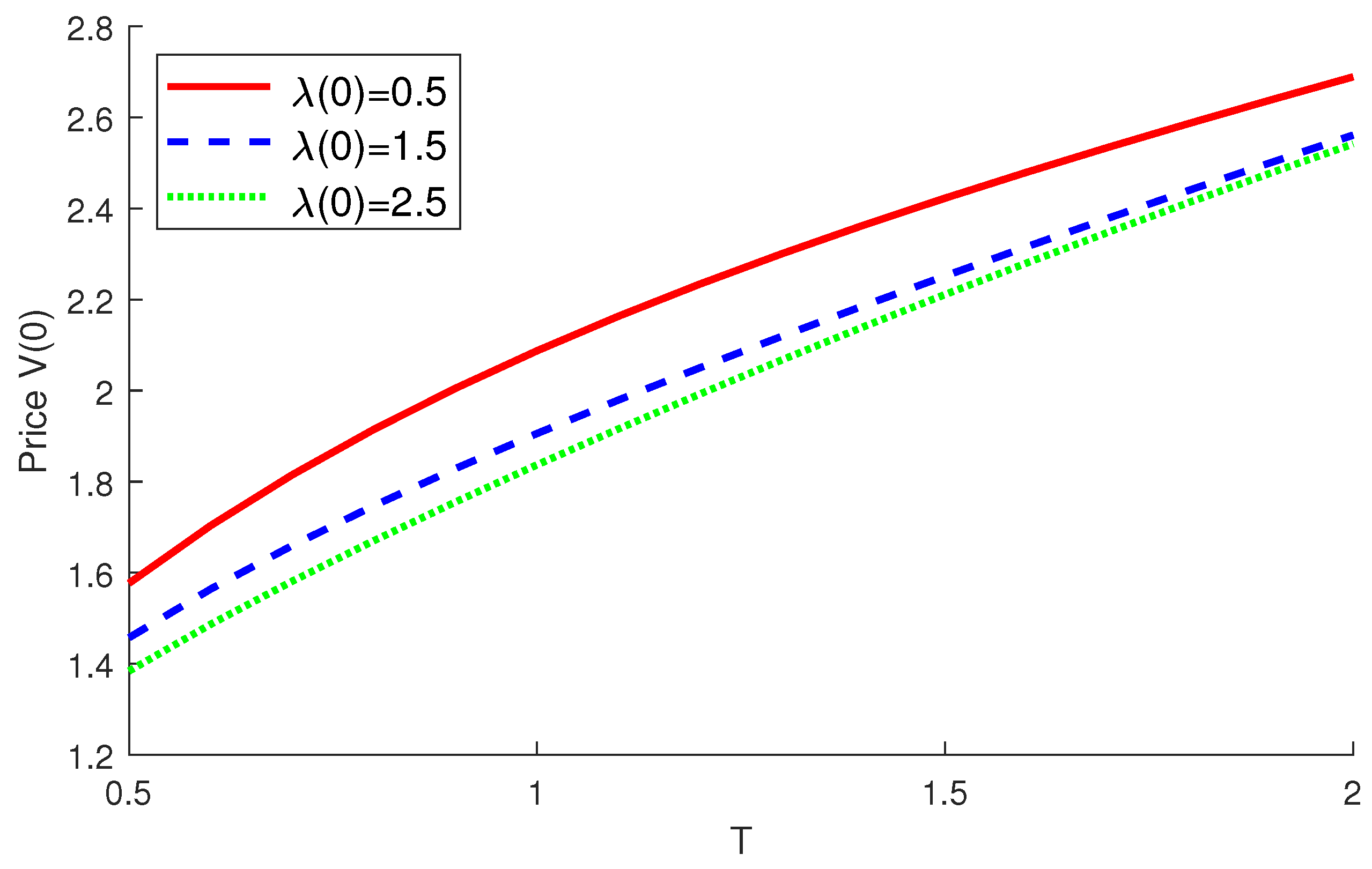
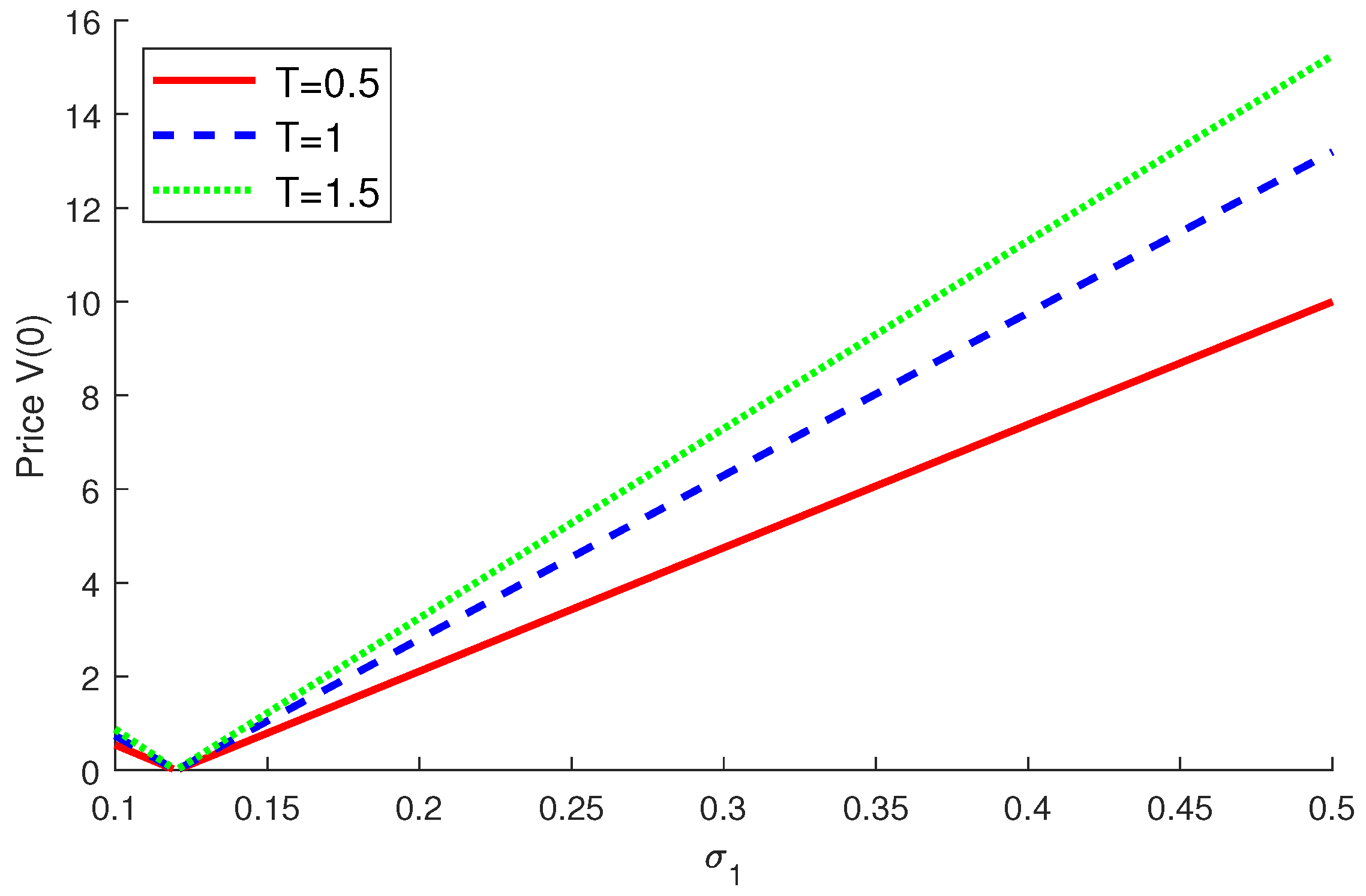
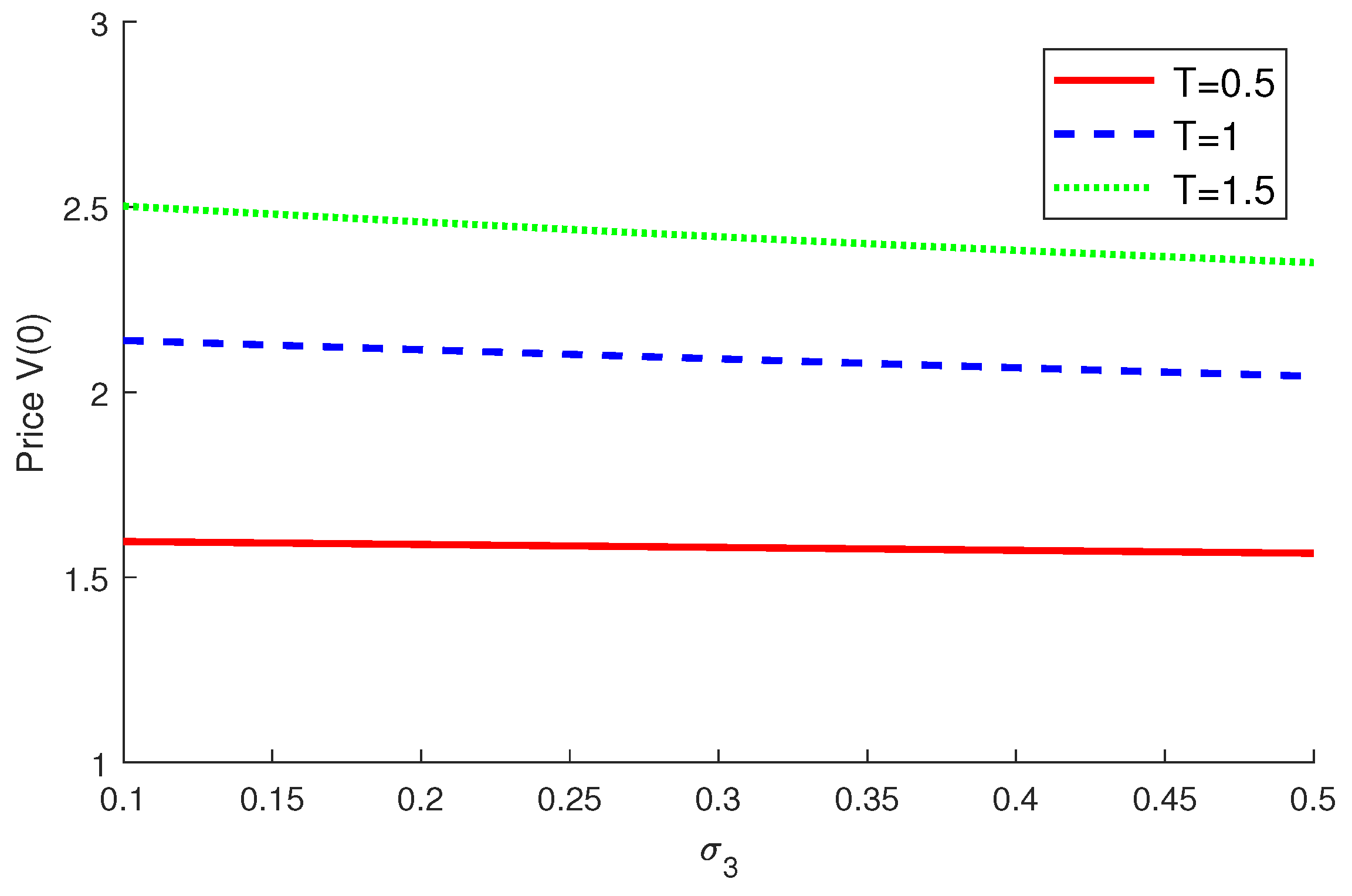
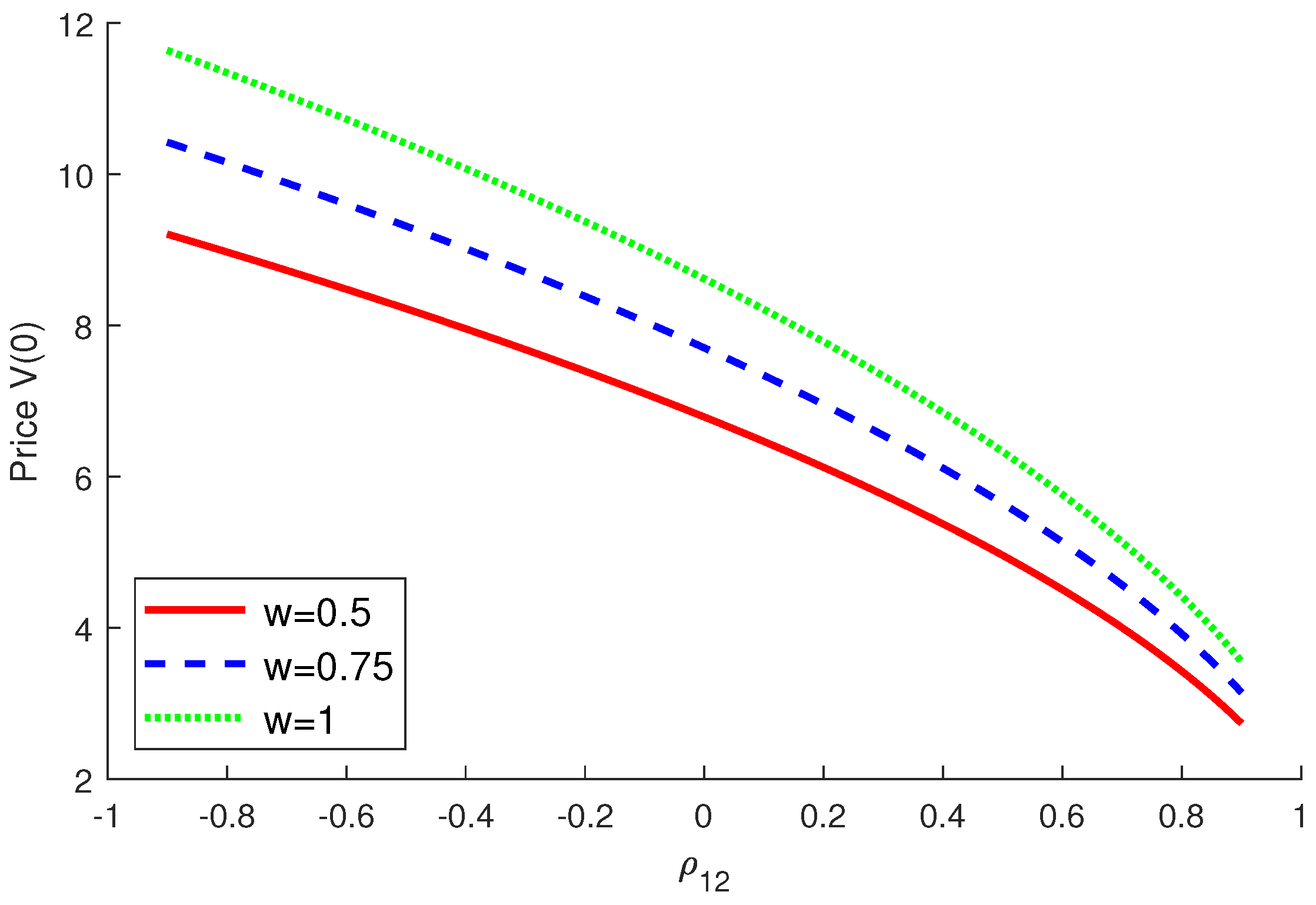
4.2. Numerical Examples
5. Concluding Remarks
Funding
Data Availability Statement
Conflicts of Interest
References
- Merton, R.C. On the pricing of corporate debt: The risk structure of interest rates. J. Financ. 1974, 29, 449–470. [Google Scholar]
- Black, F.; Cox, J.C. Valuing corporate securities: Some effects of bond indenture provisions. J. Financ. 1976, 31, 351–367. [Google Scholar] [CrossRef]
- Geske, R. The valuation of corporate liabilities as compound options. J. Financ. Quant. Anal. 1977, 12, 541–552. [Google Scholar] [CrossRef]
- Jarrow, R.; Turnbull, S. Pricing options on financial securities subject to default risk. J. Financ. 1995, 50, 53–86. [Google Scholar] [CrossRef]
- Lando, D. On Cox processes and credit risky securities. Rev. Deriv. Res. 1998, 2, 99–120. [Google Scholar] [CrossRef]
- Jarrow, R.A.; Yu, F. Counterparty risk and the pricing of defaultable securities. J. Financ. 2001, 56, 1765–1799. [Google Scholar] [CrossRef]
- Johnson, H.; Stulz, R. The pricing of options with default risk. J. Financ. 1987, 42, 267–280. [Google Scholar] [CrossRef]
- Klein, P. Pricing Black-Scholes options with correlated credit risk. J. Bank. Financ. 1996, 20, 1211–1229. [Google Scholar] [CrossRef]
- Liao, S.L.; Huang, H.H. Pricing Black–Scholes options with correlated interest rate risk and credit risk: An extension. Quant. Financ. 2005, 5, 443–457. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, G. Pricing of vulnerable options with early counterparty credit risk. N. Am. J. Econ. Financ. 2019, 47, 645–656. [Google Scholar] [CrossRef]
- Wang, X. Analytical valuation of Asian options with counterparty risk under stochastic volatility models. J. Futur. Mark. 2020, 40, 410–429. [Google Scholar] [CrossRef]
- He, W.H.; Wu, C.; Gu, J.W.; Ching, W.K.; Wong, C.W. Pricing vulnerable options under a jump-diffusion model with fast mean-reverting stochastic volatility. J. Ind. Manag. Optim. 2022, 18, 2077–2094. [Google Scholar] [CrossRef]
- Kim, D.; Choi, S.Y.; Yoon, J.H. Pricing of vulnerable options under hybrid stochastic and local volatility. Chaos Solitons Fractals 2021, 146, 110846. [Google Scholar] [CrossRef]
- Jeon, J.; Huh, J.; Kim, G. An analytical approach to the pricing of an exchange option with default risk under a stochastic volatility model. Adv. Contin. Discret. Model. 2023, 2023, 37. [Google Scholar] [CrossRef]
- Kim, G. Valuation of Exchange Option with Credit Risk in a Hybrid Model. Mathematics 2020, 8, 2091. [Google Scholar] [CrossRef]
- Wang, X. Valuing vulnerable options with two underlying assets. Appl. Econ. Lett. 2020, 27, 1699–1706. [Google Scholar] [CrossRef]
- Kim, D.; Yoon, J.H.; Kim, G. Closed-form pricing formula for foreign equity option with credit risk. Adv. Differ. Equations 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, G. Power Exchange Option with a Hybrid Credit Risk under Jump-Diffusion Model. Mathematics 2021, 10, 53. [Google Scholar] [CrossRef]
- Dong, Z.; Tang, D.; Wang, X. Pricing vulnerable basket spread options with liquidity risk. Rev. Deriv. Res. 2023, 26, 23–50. [Google Scholar] [CrossRef]
- Jamshidian, F. Valuation of credit default swaps and swaptions. Financ. Stochastics 2004, 8, 343–371. [Google Scholar] [CrossRef]
- Leung, S.Y.; Kwok, Y.K. Credit default swap valuation with counterparty risk. Kyoto Econ. Rev. 2005, 74, 25–45. [Google Scholar]
- Zhang, J.; Bi, X.; Li, R.; Zhang, S. Pricing credit derivatives under fractional stochastic interest rate models with jumps. J. Syst. Sci. Complex. 2017, 30, 645–659. [Google Scholar] [CrossRef]
- Wang, A.; Ye, Z. Total return swap valuation with counterparty risk and interest rate risk. Abstr. Appl. Anal. 2014, 12, 412890. [Google Scholar] [CrossRef]
- Wang, A. The pricing of total return swap under default contagion models with jump-diffusion interest rate risk. Indian J. Pure Appl. Math. 2020, 51, 361–373. [Google Scholar] [CrossRef]
- Fard, F.A. Analytical pricing of vulnerable options under a generalized jump–diffusion model. Insur. Math. Econ. 2015, 60, 19–28. [Google Scholar] [CrossRef]
- Wang, X. Analytical valuation of vulnerable options in a discrete-time framework. Probab. Eng. Informational Sci. 2017, 31, 100–120. [Google Scholar] [CrossRef]
- Koo, E.; Kim, G. Explicit formula for the valuation of catastrophe put option with exponential jump and default risk. Chaos Solitons Fractals 2017, 101, 1–7. [Google Scholar] [CrossRef]
- Pasricha, P.; Goel, A. Pricing vulnerable power exchange options in an intensity based framework. J. Comput. Appl. Math. 2019, 355, 106–115. [Google Scholar] [CrossRef]
- Wang, X. Analytical valuation of vulnerable European and Asian options in intensity-based models. J. Comput. Appl. Math. 2021, 393, 113412. [Google Scholar] [CrossRef]
- Margrabe, W. The value of an option to exchange one asset for another. J. Financ. 1978, 33, 177–186. [Google Scholar] [CrossRef]
- Kwok, Y.K. Mathematical Models of Financial Derivatives; Springer: Berlin, Germany, 2008. [Google Scholar]
- Kwok, Y.K.; Wong, H.Y. Currency-translated foreign equity options with path dependent features and their multi-asset extensions. Int. J. Theor. Appl. Financ. 2000, 3, 257–278. [Google Scholar] [CrossRef]
- Martzoukos, S.H. Contingent claims on foreign assets following jump-diffusion processes. Rev. Deriv. Res. 2003, 6, 27–45. [Google Scholar] [CrossRef]

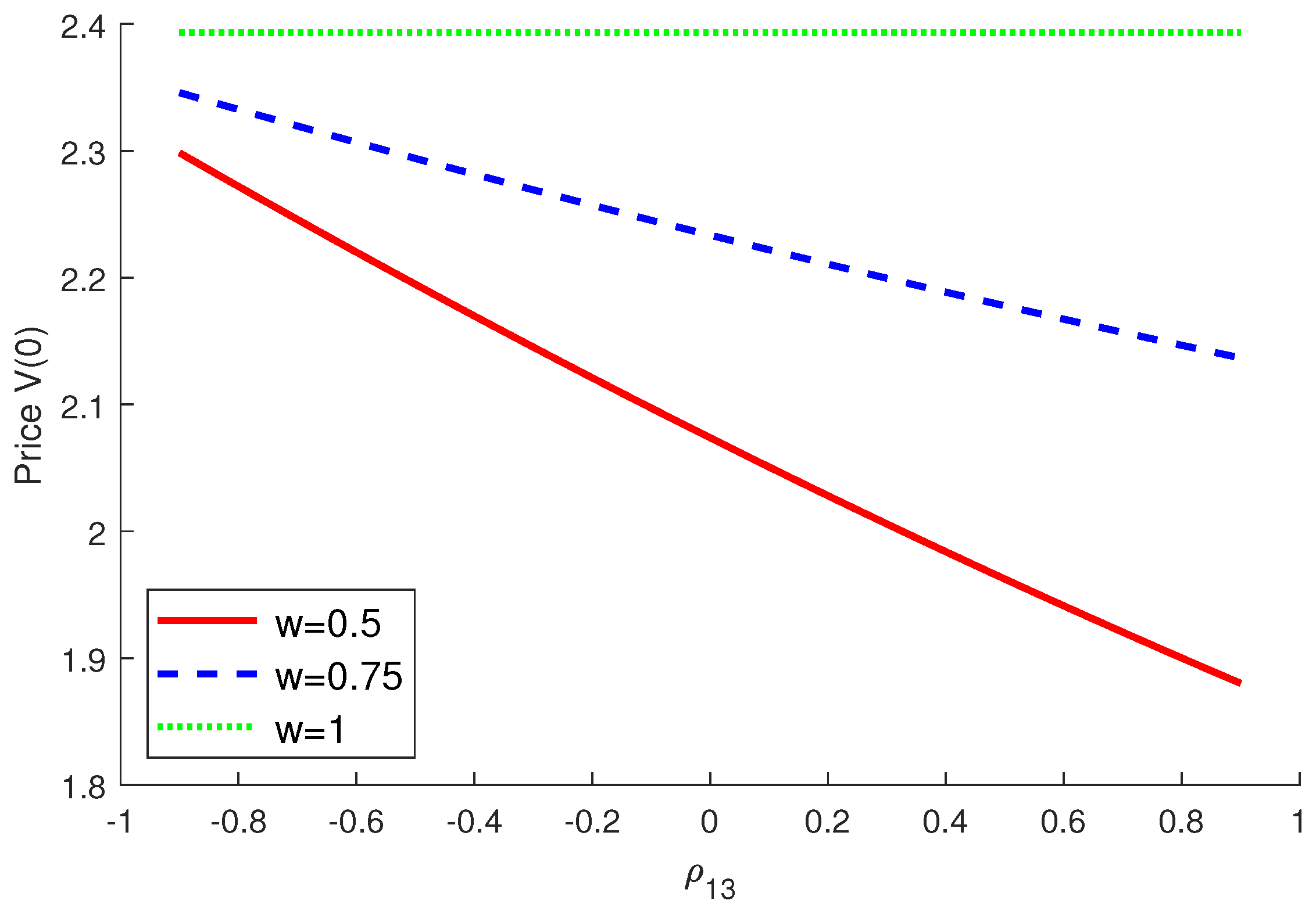
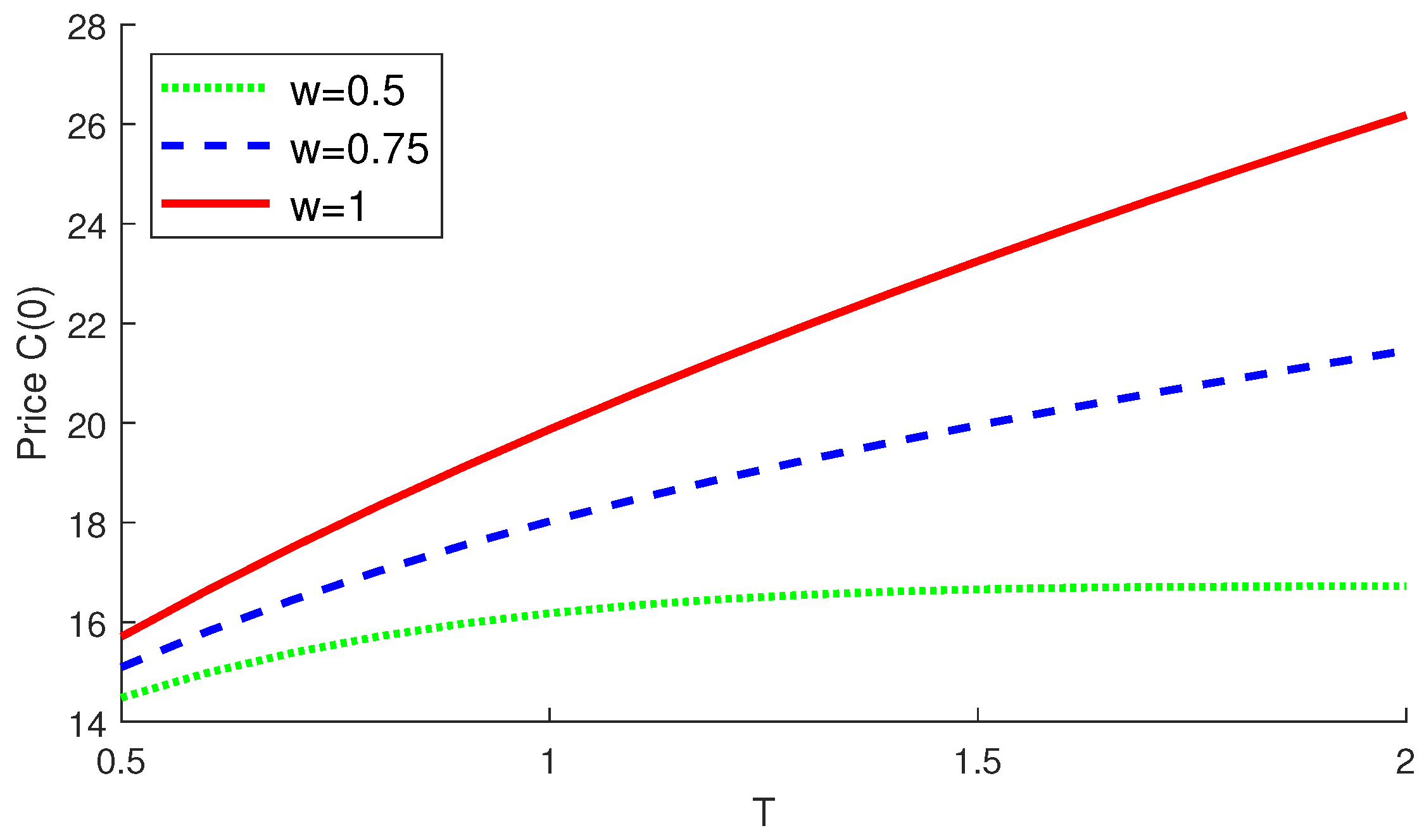
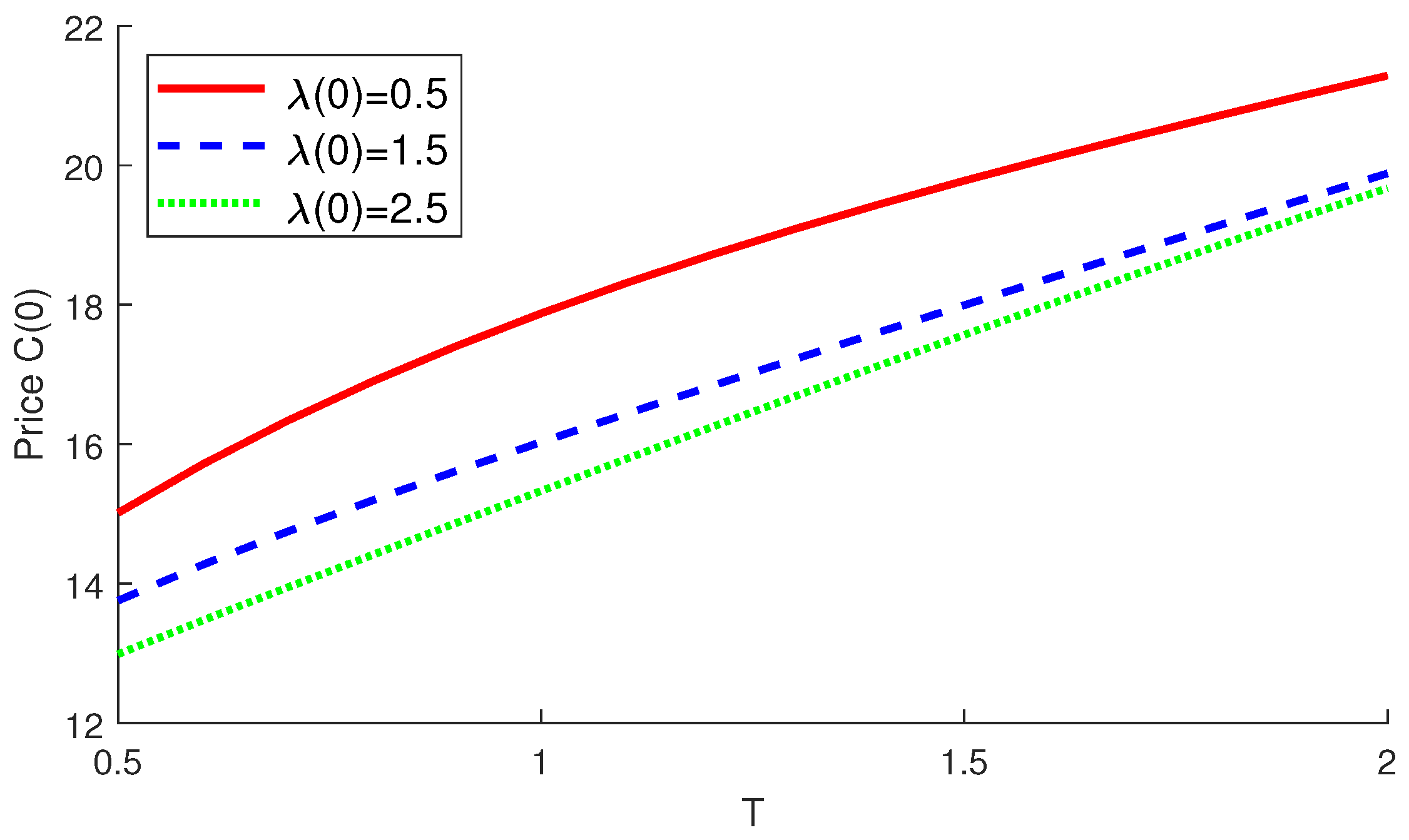


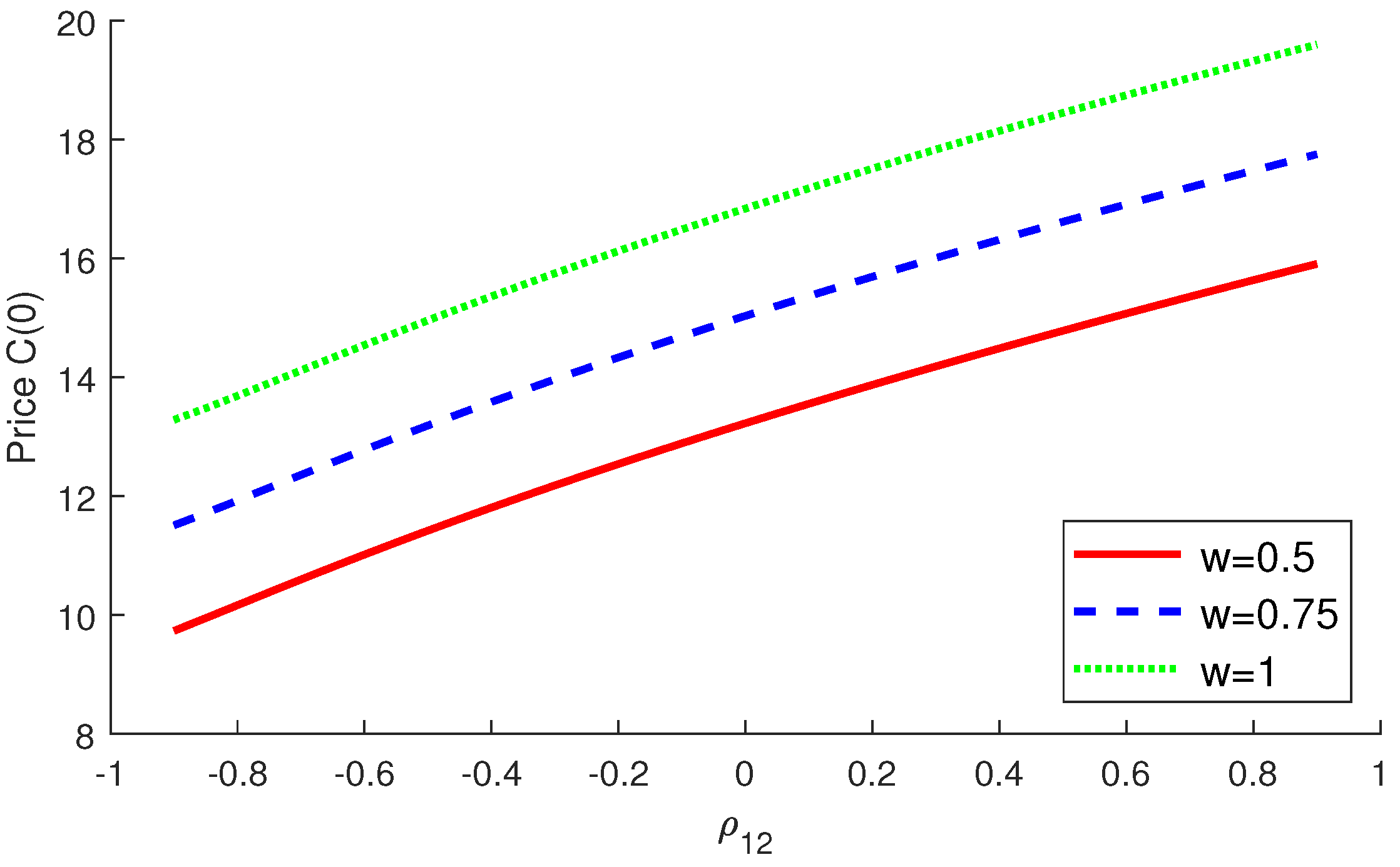
| Vulnerable Exchange Option | |||||
|---|---|---|---|---|---|
| Price | Monte Carlo | R-Err | |||
| 100 | 60 | 0.25 | 27.763 | 28.185 | 1.52 |
| 0.5 | 31.842 | 31.496 | 1.08 | ||
| 0.75 | 35.921 | 35.908 | 3.53 | ||
| 80 | 0.25 | 13.716 | 13.738 | 1.67 | |
| 0.5 | 15.811 | 15.801 | 6.01 | ||
| 0.75 | 17.905 | 17.974 | 3.89 | ||
| 100 | 0.25 | 1.519 | 1.545 | 1.71 | |
| 0.5 | 1.811 | 1.839 | 1.54 | ||
| 0.75 | 2.102 | 2.117 | 7.37 | ||
| Av. run time (s) | 0.031 | 18.1211 | |||
| Vulnerable Foreign Equity Option | |||||
|---|---|---|---|---|---|
| Price | Monte Carlo | R-Err | |||
| 100 | 60 | 0.25 | 37.211 | 37.067 | 3.87 |
| 0.5 | 42.120 | 42.454 | 7.93 | ||
| 0.75 | 47.019 | 46.960 | 1.24 | ||
| 80 | 0.25 | 24.480 | 24.418 | 2.53 | |
| 0.5 | 27.665 | 27.677 | 4.39 | ||
| 0.75 | 30.849 | 30.850 | 1.929 | ||
| 100 | 0.25 | 14.332 | 14.344 | 8.50 | |
| 0.5 | 16.179 | 16.159 | 1.21 | ||
| 0.75 | 18.028 | 17.984 | 2.41 | ||
| Av. run time (s) | 0.030 | 18.2574 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, G. A Simplified Approach to the Pricing of Vulnerable Options with Two Underlying Assets in an Intensity-Based Model. Axioms 2023, 12, 1105. https://doi.org/10.3390/axioms12121105
Kim G. A Simplified Approach to the Pricing of Vulnerable Options with Two Underlying Assets in an Intensity-Based Model. Axioms. 2023; 12(12):1105. https://doi.org/10.3390/axioms12121105
Chicago/Turabian StyleKim, Geonwoo. 2023. "A Simplified Approach to the Pricing of Vulnerable Options with Two Underlying Assets in an Intensity-Based Model" Axioms 12, no. 12: 1105. https://doi.org/10.3390/axioms12121105
APA StyleKim, G. (2023). A Simplified Approach to the Pricing of Vulnerable Options with Two Underlying Assets in an Intensity-Based Model. Axioms, 12(12), 1105. https://doi.org/10.3390/axioms12121105





