Entropy and Multi-Fractal Analysis in Complex Fractal Systems Using Graph Theory
Abstract
:1. Introduction
M-Polynomials and Fractals
2. Preliminaries
- , if ;
- and ;
- and if .
3. Results for M-Polynominal and Entropy
Entropy, Shannon Entropy, and Graph Entropy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gutman, I.; Dehmer, M.; Zhang, Y.; Ilic, A. Altenburg, Wiener, and Hosoya polynomials. In Distance in Molecular Graphs Theory; University of Kragujevac Rectorate: Kragujevac, Serbia, 2012; pp. 49–70. [Google Scholar]
- Cash, G.G. Relationship between the Hosoya polynomial and the hyper-Wiener index. Appl. Math. Lett. 2002, 15, 893–895. [Google Scholar] [CrossRef]
- Chou, C.-P.; Witek, H.A. Closed-form formulas for the Zhang-Zhang polynomials of benzenoid structures: Chevrons and generalized chevrons. MATCH Commun. Math. Comput. Chem. 2014, 72, 105–124. [Google Scholar]
- Farrell, E.J. An introduction to matching polynomials. J. Combin. Theory Ser. B 1979, 27, 75–86. [Google Scholar] [CrossRef]
- Gutman, I. Degree-based topological indices. Croat. Chem. Acta 2013, 86, 351–361. [Google Scholar] [CrossRef]
- Zhang, H.; Shiu, W.C.; Sun, P.-K. A relation between Clar covering polynomial and cube polynomial. MATCH Commun. Math. Comput. Chem. 2013, 70, 477–492. [Google Scholar]
- Zhang, H.; Zhang, F. The Clar covering polynomial of hexagonal systems I. Discrete Appl. Math. 1996, 69, 147–167. [Google Scholar] [CrossRef]
- Hassani, F.; Iranmanesh, A.; Mirzaie:, S. Schultz and modified Schultz polynomials of C100 fullerene. MATCH Commun. Math. Comput. Chem. 2013, 69, 87–92. [Google Scholar]
- Alonso-Ruiz, P.; Kelleher, D.J.; Teplyaev, A. Energy and Laplacian on Hanoi-type fractal quantum graphs. J. Phys. Math. Theor. 2016, 49, 165206. [Google Scholar] [CrossRef]
- Mograby, G.; Derevyagin, M.; Dunne, G.V.; Teplyaev, A. Spectra of perfect state transfer Hamiltonians on fractal-like graphs. J. Phys. Math. Theor. 2021, 54, 125301. [Google Scholar] [CrossRef]
- Klavzar, S.; Milutinovic, U. Graphs S(n,k) and a variant of the Tower of Hanoi problem. Czechoslov. Math. J. 1997, 47, 95104. [Google Scholar] [CrossRef]
- Gravier, S.; Kovse, M.; Parreau, A. Generalized Sierpinski graphs. In Proceedings of the Euro-Comb11, Budapest, Hungary, 29 August–2 September 2011. [Google Scholar]
- Deutsch, E.; Klavžar, S. M-polynomial and degree-based topological indices. Iran. J. Math. Chem. 2015, 6, 93–102. [Google Scholar]
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Dehmer, M.; Mowshowitz, A. A history of graph entropy measures. Inf. Sci. 2011, 181, 57–78. [Google Scholar] [CrossRef]
- Mowshowitz, A.; Dehmer, M. Entropy and the complexity of graphs revisited. Entropy 2012, 14, 559–570. [Google Scholar] [CrossRef]
- Chen, Z.; Dehmer, M.; Emmert-Streib, F.; Shi, Y. Entropy of weighted graphs with Randić weights. Entropy 2015, 17, 3710–3723. [Google Scholar] [CrossRef]
- Eagle, N.; Macy, M.; Claxton, R. Network diversity and economic development. Science 2010, 328, 1029–1031. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Gutman, I. Mathematical Aspects of Randic-Type Molecular Structure Descriptors; University of Kragujevac and Faculty of Science Kragujevac: Kragujevac, Serbia, 2006. [Google Scholar]
- Li, X.; Shi, Y.; Xu, T. Unicyclic graphs with maximum general Randic index for α>0. MATCH Commun. Math. Comput. Chem. 2006, 56, 557–570. [Google Scholar]
- Li, X.; Shi, Y.; Zhong, L. Minimum general Randic index on chemical trees with given order and number of pendent vertices. MATCH Commun. Math. Comput. Chem. 2008, 60, 539–554. [Google Scholar]
- Randic, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
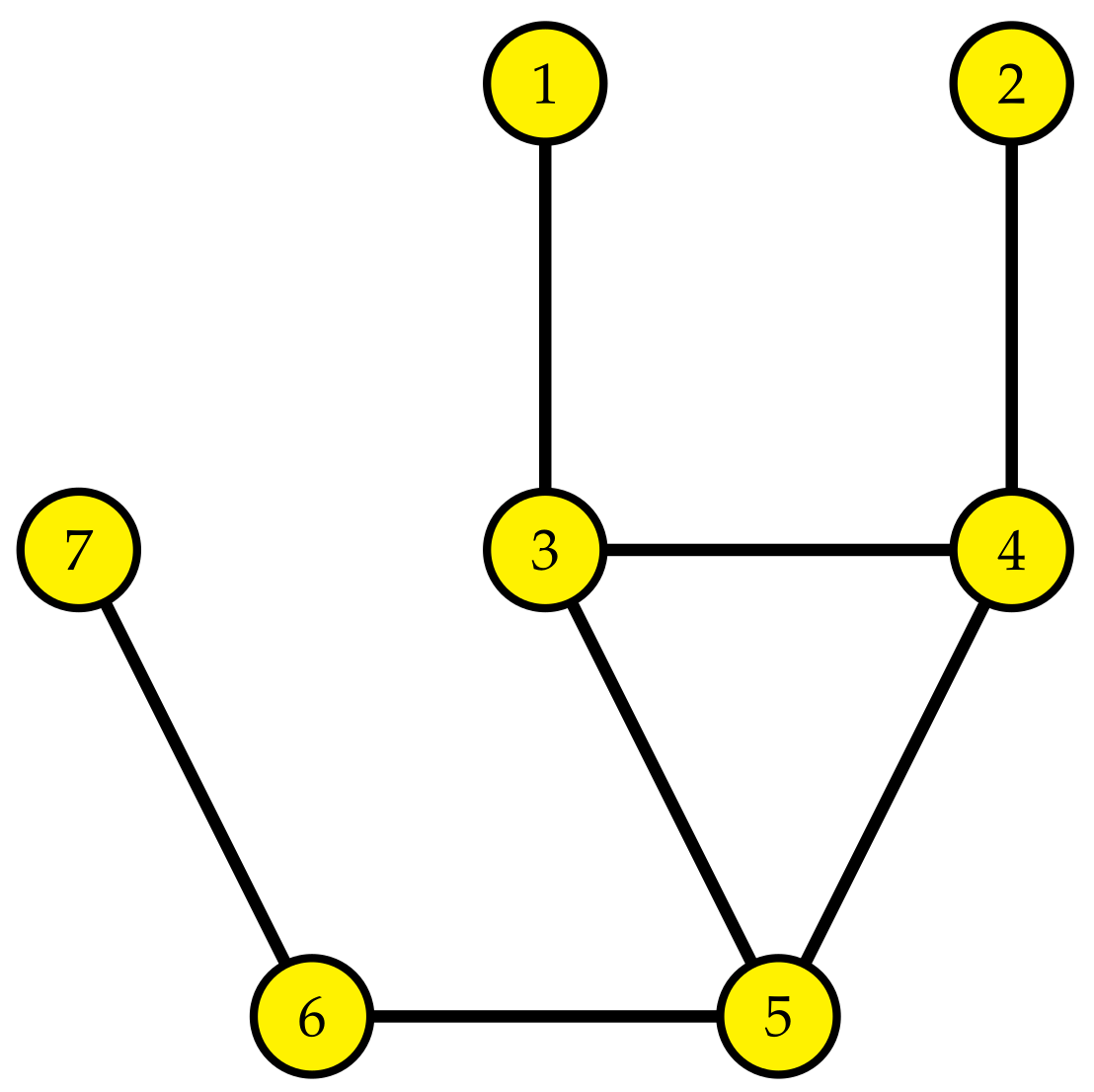
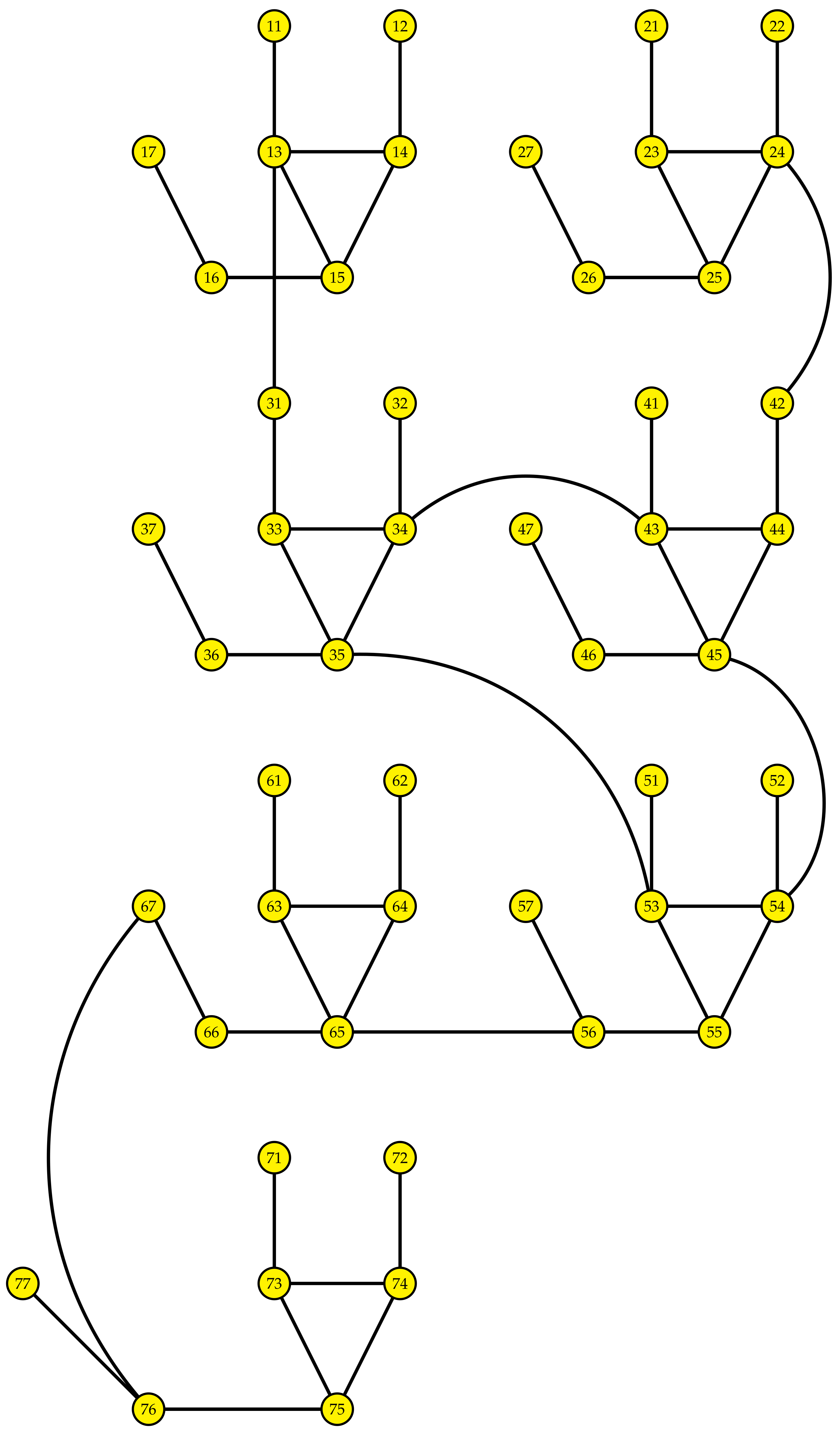
| (d,d), where, pj∈ E(G) | E | Number of Edges |
|---|---|---|
| (1, 2) | E | |
| (1, 3) | E | |
| (1, 4) | E | |
| (2, 2) | E | |
| (2, 3) | E | |
| (2, 4) | E | |
| (3, 3) | E | |
| (3, 4) | E | |
| (4, 4) | E |
| Topological Indices | Derivation from M(Sie(,t),l,q) |
|---|---|
| First Zagreb index | |
| Second Zagreb index | |
| Second modified Zagreb index | |
| General Randić index, | |
| Inverse general Randić index, | |
| Symmetric division index | |
| Harmonic index | |
| Inverse sum index | |
| Augmented Zagreb |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mufti, Z.S.; Tedjani, A.H.; Anjum, R.; Alsuraiheed, T. Entropy and Multi-Fractal Analysis in Complex Fractal Systems Using Graph Theory. Axioms 2023, 12, 1126. https://doi.org/10.3390/axioms12121126
Mufti ZS, Tedjani AH, Anjum R, Alsuraiheed T. Entropy and Multi-Fractal Analysis in Complex Fractal Systems Using Graph Theory. Axioms. 2023; 12(12):1126. https://doi.org/10.3390/axioms12121126
Chicago/Turabian StyleMufti, Zeeshan Saleem, Ali H. Tedjani, Rukhshanda Anjum, and Turki Alsuraiheed. 2023. "Entropy and Multi-Fractal Analysis in Complex Fractal Systems Using Graph Theory" Axioms 12, no. 12: 1126. https://doi.org/10.3390/axioms12121126





