Modeling Socioeconomic Determinants of Building Fires through Backward Elimination by Robust Final Prediction Error Criterion

Abstract

Fires in buildings are significant public safety hazards and can result in fatalities and substantial financial losses. Studies have shown that the socioeconomic makeup of a region can impact the occurrence of building fires. However, existing models based on the classical stepwise regression procedure have limitations. This paper proposes a more accurate predictive model of building fire rates using a set of socioeconomic variables. To improve the model’s forecasting ability, a backward elimination by robust final predictor error (RFPE) criterion is introduced. The proposed approach is applied to census and fire incident data from the South East Queensland region of Australia. A cross-validation procedure is used to assess the model’s accuracy, and comparative analyses are conducted using other elimination criteria such as p-value, Akaike’s information criterion (AIC), Bayesian information criterion (BIC), and predicted residual error sum of squares (PRESS). The results demonstrate that the RFPE criterion is a more accurate predictive model based on several goodness-of-fit measures. Overall, the RFPE equation was found to be a suitable criterion for the backward elimination procedure in the socioeconomic modeling of building fires.

1. Introduction

Building fires remain a significant concern for households, businesses, and authorities across Australia, as evidenced by the annual expenditure of over $2.5 billion on fire protection products and services [1]. Despite this significant investment, building fires claimed the lives of 51 Australians in 2020 [2] and cost the country’s economy 1.3% of its gross domestic product (GDP) [3]. These costs are a combination of losses due to injuries, property damages, environmental damages, destruction of heritage, and various costs to affected businesses. In Queensland alone, 1554 fire incidents caused damage to building structures and contents in 2020 [4], with each incident representing a significant loss to a Queenslander who may have lost a family home, a loved one, or a source of livelihood that has sustained generations of Australians. As such, continued efforts to understand and mitigate the incidence of building fires are necessary.

Studies linking socioeconomic data to building fires have been conducted in various jurisdictions using quantitative and qualitative methodologies. Lizhong, et al. [5] established the relationship between GDP per capita, education level, and fire and death rates in Jiangsu, Guangdong, and Beijing, China. It adopted partial correlation analysis to compute the correlation coefficient of every variable pairing. In Cook County, United States, geocoding and visual mapping connected poverty rates to higher ‘confined fire’ incident rates in one-family and two-family dwellings [6]. Logistic regression is also used to identify relevant socioeconomic variables through four implementations within a four-stage conceptual framework [7]. The study utilizes the census data of New South Wales residents and the corresponding variables selected to calculate indexes within the Socioeconomic Indexes for Areas (SEIFA) project.

Other methodologies have also adopted algorithms to not only assign coefficients but also select variables that build the most fitting model. For example, Chhetri, et al. [8] utilized the classical stepwise regression method and discriminant factor analysis (DFA) to select predictive determinants from variables identified in the technical papers of the Socioeconomic Indexes for Areas (SEIFA). As a result, it managed to capture variables with high t-statistics. However, its use of the classical stepwise regression method, as proposed by Efroymson [9], has been known to have several limitations. Critics have also discouraged its use of t-statistics or p-value elimination criteria and the forward selection procedure to build statistical models [10,11,12,13,14]. The limitations of the classical stepwise regression method can be summarized into five issues—overreliance on chance, overstated significance, lack of guarantee for global optimization, inconsistency-causing collinearity, and non-contingency of outliers [10,11,12,13,14]. In addition, the method has been shown to provide poorer accuracy than principal component analysis (PCA) [15]. Therefore, the methodology was improved in a study in the West Midlands, U.K., by adding PCA to discover the most predictive variables or components [16].

This paper attempts to improve the methodology in Chhetri, Corcoran, Stimson and Inbakaran [8] by using the backward elimination method and the robust final prediction error (RFPE) criterion to model the socioeconomic determinants of building fires. Such modifications to the model-building algorithm and elimination/selection criteria have the potential to produce a socioeconomic model with superior predictive accuracy. Additionally, the resulting model may make more cautious representations of individual parameters’ influence, preventing false confidence and reflecting the real world more accurately. The contribution of this paper includes the first application of the backward elimination by RFPE criterion and the comparative analysis of RFPE to other criteria applicable to the backward elimination procedure. Over and above that, the paper aims to improve the effectiveness of future fire safety regulations and programs that better protect households with the identified socioeconomic risk profile.

To evaluate the suitability of the proposed method, this paper presents a comprehensive analysis in six sections. Section 2 provides a review of the relevant literature to highlight the limitations of the conventional regression approach. Section 3 presents the proposed robust backward elimination method using the RFPE criterion. In Section 4, a case study based on data from the South East Queensland region is presented to demonstrate the effectiveness of the proposed method. The available alternative criteria to the backward elimination procedure and the comparative analysis of the proposed criterion are described in Section 5. Finally, Section 6 concludes the paper by discussing the study’s findings and outlining future research directions.

2. Related Work

Before going into the method’s ingrained limitations, the common purpose of adopting the classical regression method has to be understood. Often, researchers adopted the method of disregarding ‘insignificant’ variables to achieve parsimony, i.e., ‘simpler’ equations [10,11]. Then, the parsimonious model is inferred for the explanatory variables’ influences on the dependent variable [13,14]. Others use the resulting model for prediction and forecasting purposes [10,17].

Chhetri, Corcoran, Stimson and Inbakaran [8] conducted an ingenious study to model the socioeconomic determinants of building fires. It has resourcefully identified the Index of Socioeconomic Advantages and Disadvantages (IRSAD) by the Australian Bureau of Statistics (ABS) as a suitable pool for candidate explanatory variables. In addition, the study uses discriminant function analysis (DFA) to identify determinants of fires in different suburbs—the culturally diversified and economically disadvantaged suburbs, the predominantly traditional family suburbs, and the high-density inner suburbs with community housing. However, it uses classical stepwise regression to identify the overall socioeconomic determinants of building fires, which has been proven to have some limitations.

The limitations of the classical stepwise regression can be summarized into five issues: overreliance on chance, overstated significance, lack of guarantee for global optimization, inconsistency-causing collinearity, and non-contingency of outliers, which can be described one by one as follows:

2.1. Limitation 1: Over-Reliance on Chance

There is a high probability of the regression failing to identify actual causal variables. One of the main reasons is that the set of variables might, by chance, affect the particular training datasets. Without a validation process, the same variables might not show the same degree of influence if based on other sample datasets, such as datasets from other periods. The chance of nuisance variables getting selected, synonymously known as type I error, has been quantified by multiple studies, such as the one by Smith [11]. Apart from referencing experiments that show poor performance in small datasets [18,19], Smith [11] conducts a series of Monte Carlo simulations to show that stepwise regression can include nuisance variables 33.5% of the time while choosing from 50 candidate variables. The rate almost tripled when the method was used for 1000 candidate variables. The simulations also found that at least one valid variable was not selected 50.5% of the time when choosing from 100 candidate variables [11]. The main reason for the limitation is that the statistical tests used in stepwise regression are designed a priori, i.e., they are made to quantify a model that has been previously built or established, for example, through expert knowledge and causation studies [10]. It was never intended for model-building purposes. In turn, the method produced results that often overstated their significance.

2.2. Limitation 2: Overstated Significance

McIntyre, Montgomery, Srinivasan and Weitz [13] determine that statistical significance tests have been too liberal for any stepwise regression model since it has been ‘best-fitted’ to the dataset, biasing the data towards significance. Additionally, Smith [11] stressed that stepwise regression tends to underestimate the standard error of the coefficient estimate, leading to a narrow confidence interval, an overstated t-statistic, and understated p-values. The phenomenon also signifies the overfitting of the model to the training dataset. In practical terms, the stepwise algorithm does not pick the set of variables that determine the response variable in the population, but it picks the set of variables that ‘best’ fit the training sample dataset.

2.3. Limitation 3: Collinearity Causes Inconsistency

Stepwise regression assumes that explanatory variables are independent of each other. Therefore, there is no provision for collinearity in the stepwise regression procedure. As a result, collinearity in stepwise regression produces high variances and inaccurate coefficient estimates [20]. These effects are again attributed to the objective of finding a model that ‘best fits’ the training data. Models that contain different variables may have a similar fit in the presence of collinearity; therefore, the procedure will result in inconsistent results, i.e., the procedure becomes arbitrary [10,21]. Collinearity’s effect on the order of inclusion or elimination is one of the reasons for the varying outcomes [22,23]. With that said, these effects are more pertinent if the purpose of adopting stepwise regression is mainly inferential [24,25,26]. As a predictive model, the inconsistency is less relevant as variables compensate for each other as their coefficients are too high or too low [26]. Therefore, the resulting function may still satisfactorily predict the dependent variable but not be as reliable in estimating individual influence [26].

2.4. Limitation 4: No Guarantee of Global Optimization

Based on the limitations discussed, it is fair to question the optimality of stepwise regression’s outcome. Thompson [27], Freckleton [21], and Smith [11] discussed whether global optimization is achieved in stepwise regression, especially the forward selection algorithm. Since the algorithm selects variables one by one, the choice of the n-th variable depends on the (n − 1)th variable. Therefore, it is reasonable to conclude that the method cannot even guarantee that the n-variable model achieved is the best-fitting n-variable equation. In other words, the local optimization reached by conducting the stepwise regression does not guarantee that it is the global optima. In addition, the issue may also be exacerbated by erratic variable selection in multicollinear datasets. Even a small degree of multicollinearity has been shown to bias stepwise regression towards achieving local optimization and away from global optimization [28].

2.5. Limitation 5: Caused by Outliers

Outliers are a persistent issue in statistical analysis. They introduced bias to the most basic statistical measure, e.g., the mean value of sample data, affecting the accuracy of more advanced statistical techniques [29]. One single outlier can bias classical statistical techniques that should be optimal under normality or linearity assumptions. Firstly, population data inherently contains outliers; as the sample data gets more prominent, there is a greater likelihood of encountering outlying data points [30]. Secondly, large behavioral and social datasets are more susceptible to outliers [30,31]. Thirdly, it has been established that outliers in survey statistics of such scale are almost unpreventable, partly due to significant errors in survey responses or data entry [29,32]. Additionally, in contrast to the effect of collinearity, there is evidence that outliers affect inferential accuracy and a model’s predictive accuracy [33].

After acknowledging the limitations of classical stepwise regression, a natural progression should lead to exploring an alternative to the method. Although the criterion modification will not wholly replace causation studies or eliminate the same weaknesses, it will produce significantly more reliable and cautious inferences and predictions.

3. Backward Elimination by Robust Final Predictor Error (RFPE) Criterion

A multivariate regression equation was sought to represent the rates of building fires based on an area’s socioeconomic composition. The resulting equation is expected to take the form of Equation (1).

$$y_i={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_d{x}_{id},$$

(1)

where variable b_i represents the rate of emergency services demand at area i, x_ij ($j\in \left\{1, 2, \cdots , d\right\}$) represents socioeconomic variables respectively for demand area i, β_j ($j\in \left\{1, 2, \cdots , d\right\}$) is the regression coefficient allocated to each of the j-th socioeconomic variables, and β₀ represents the intercept.

A backward elimination was adopted to detect and eliminate insignificant socioeconomic variables based on the robust final predictor error (RFPE) criterion. The algorithm was set up to remove the single variable that improves the RFPE the most. The use of the RFPE criterion, developed by Maronna, Martin, Yohai and Salibin-Barrera [31], has the benefit of minimizing the effect of outliers. The robust technique is an improvement to Akaike’s FPE criterion, which can be significantly biased by outliers in the dataset [34]. The procedure is then adapted to the data sourcing and processing methodology in Chhetri, Corcoran, Stimson and Inbakaran [8] study on building fires in South East Queensland. The approach has been proposed and discussed by Untadi, et al. [35]. The proposed RFPE equation is presented in Equation (2) as the expected value of the function $\rho$.

$$RFP{E}_C=E\rho \left(\frac{y_0-x_{0C}^{\text{'}}\widehat{{\beta }_C}}{\sigma }\right)$$

(2)

$$\mathrm{where}\hspace{1em}\hspace{1em}\hspace{1em}\widehat{\beta }=arg\underset{\beta \in {ℝ}^q}{\min }{\displaystyle \sum }_{i=1}^n\rho \left(\frac{y_i-{\mathit{x}}_{iC}^{\prime }\mathit{\beta }}{\widehat{\sigma }}\right)$$

(3)

$$y_i={\displaystyle \sum }_{j=1}^p{x}_{ij}{\beta }_j+u_i={\mathit{x}}_i^{\prime }\mathit{\beta }+u_i$$

(4)

$$\rho \left(r\right)=r^2$$

(5)

$$x_{iC}=\left\{x_{i1}, \dots , x_{id}\right\}$$

(6)

$$C\subset \left\{1, 2, \cdots , d\right\}$$

(7)

$$i=\left\{1, 2, \cdots , n\right\}$$

(8)

where $\left(x_{ij}, y_i\right)$ is the dataset consisting of the relevant explanatory variables x_iC and response variable y_i. $\left(x_0, y_0\right)$ represents the data point that is added to measure the sensitivity of the dataset to outliers. C refers to the set of explanatory variables that are subsets of the index $\left\{1, 2, \cdots , d\right\}$. $\widehat{\beta }$ and $\widehat{\sigma }$ notated the MM-estimators of the parameters and scale, respectively. MM-estimators are a statistical estimation approach formulated by Yohai [36], which employs the Iteratively Reweighted Least Squares (IRWLS) method for optimizing the estimation procedure. The initial estimators are chosen using a strategy proposed by Pena and Yohai [37], which uses data-driven criteria to guide the selection of the starting estimates rather than a random selection method [38]. The explanatory variables and error term are i.i.d. standard normal. Adapting the estimator for Akaike’s FPE equation, the estimator for the RFPE equation was proposed as follows:

$$\widehat{RFPE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\rho \left(\frac{r_{iC}}{\widehat{\sigma }}\right)+\frac{q}{n}\frac{\widehat{A}}{\widehat{B}}$$

(9)

$$\mathrm{where}\hspace{1em}\hspace{1em}\hspace{1em}\widehat{A}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\psi {\left(\frac{r_{iC}}{\widehat{\sigma }}\right)}^2, \widehat{B}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\psi }^{\prime }\left(\frac{r_{iC}}{\widehat{\sigma }}\right)$$

(10)

$$r_{iC}=y_i-{\mathit{x}}_{iC}^{\prime }\widehat{{\mathit{\beta }}_C}$$

(11)

$$q=\left|C\right|$$

(12)

$$\psi \left(r\right)=2\left(r\right)$$

(13)

Equation (9) is then embedded in the backward elimination procedure in Algorithm 1.

Algorithm 1. Algorithm of robust backward elimination by RFPE

Let Md be the full model that contains all d explanatory variables. $$M_d\to y_i={\beta }_0+{\beta }_{1}x+\cdots +{\beta }_d{x}_{id}$$ Calculate RFPE of Md. For  k = d, d-1, …, 1: Consider all k models that contain all but one of the variables in Mk. for a total of k-1 explanatory variables. Among the k models, choose the model with the lowest RFPE and label it as Mk−1. If RFPE of Mk−1 is higher or equal to the RFPE of Mk: Terminate loop. Else Continue with the remaining body of the loop Return Mk

Firstly, the RFPE for a model that consists of all d explanatory variables and is set as M_d is calculated. Then, every variable is eliminated and returned one by one to determine which elimination improves the RFPE of model M_k−1 the most. The algorithm removes the single variable that improves the RFPE the most. The elimination iterates until the algorithm reaches an RFPE of M_k−1 that is higher or equal to the RFPE of M_k. The termination means the algorithm assumes the subsequent iteration will not improve the model fit. An implementation in South East Queensland was conducted to validate the method’s proposed adoption.

4. Case Study: South East Queensland, Australia

South East Queensland (SEQ) refers to a region that accounts for two-thirds of Queensland’s economy and where seventy percent of the state’s population resides [39]. The region is socioeconomically diverse, with no one social or economic status accounting for the majority of the population, providing sufficient complexity to ‘stress test’ the methodology [40]. In addition, the region is experiencing one of the highest population growth rates in Australia. The rate of interstate and international migration to the region has been the main driving force for the growth, potentially causing significant changes in the socioeconomic composition of suburbs in SEQ [41,42]. Hence, the region may benefit most from the method’s implementation.

The paper defines SEQ to include the Australian Bureau of Statistics (ABS)’s twelve statistical area 4 (SA4) regions—Eastern Brisbane, Northern Brisbane, Southern Brisbane, Western Brisbane, Brisbane Inner City, Gold Coast, Ipswich, Logan to Beaudesert, Northern Moreton Bay, Southern Moreton Bay, Sunshine Coast, and Toowoomba. The study’s datasets are analyzed at the statistical area 2 (SA2) level as the unit of analysis. In the 2016 Census, there were 332 SA2 areas in 12 SA4 regions in South East Queensland.

4.1. Datasets

Inspired by the methodology developed by Chhetri, Corcoran, Stimson and Inbakaran [8], the study revolves around the Australian Bureau of Statistics (ABS) technical paper for Socioeconomic Indexes for Areas (SEIFA). One of the indexes within SEIFA is the Index of Relative Socioeconomic Advantage and Disadvantage (IRSAD). In this study, the variables used to calculate IRSAD were the initial variables in the backward elimination algorithm. South East Queensland’s IRSAD is visualized in Figure 1.

Figure 1. Visualization of SEIFA scores on the map of South East Queensland [43].

The data are extracted from a 2016 Census database, “2016 Census—Counting Persons, Place of Enumeration”. It consists of tables containing aggregated values for the selected statistical areas, for example, the HIED dataset in Appendix A, Table A1. The data was accessed through the TableBuilder platform. Every variable represents a proportion of the population with a specific attribute, calculated using criteria defined for its numerator and denominator, summarized in Appendix A, Table A2.

However, such a set of explanatory variables has a predisposition to suffer from multicollinearity. It will violate the assumption of independence to which a regression model needs to conform in order to be meaningful [44]. Therefore, a stepwise elimination procedure is adopted to eliminate variables with a variation inflation factor (VIF) (Equation (14)) that are higher than a threshold of 10 [45]. The procedure is executed using the vif() function in the ‘car’ R package. As a result, five variables that are deemed multicollinear—INC_LOW, NOYEAR12, INC_HIGH, UNEMPLOYED, and OVERCROWD—are eliminated.

$$VI{F}_j=\frac{1}{R_j}$$

(14)

where R_j is the coefficient of determination of the j-th explanatory variable in a regression with all other variables.

On the other hand, the rate of building fires in South East Queensland was set as the response variable of the study. It was calculated based on the Queensland fire and emergency services (QFES) incident data points, labeled as incident types 111 (Fire: damaging structure and contents), 112 (Fire: damaging structure only), 113 (Fire: damaging contents only), and 119 (Fire: not classified above), from 2015 to 2017 [46]. The total number of incidents throughout the three years is then cumulated, multiplied by 1000, and divided by the number of persons counted at each SA2 area in Census 2016, resulting in the triannual rate of building fires for every 1000 people. The data is accessible through the Queensland government’s open data portal.

However, inconsistencies exist between QFES and ABS geographical units of data labeling. This led to QFES tagging incident locations by their state suburb (SSC), while ABS collected the relevant socioeconomic data based on its definition of SA2. The main issue brought about by the difference is that a few suburbs are located in 2–4 SA2 areas. Specifically, there are 221 suburbs out of 3263 located in more than one SA2 area. Therefore, the study has adopted a "winner takes all" approach by assuming overlapping suburbs as part of SA2, where most of the suburb residents are located (50 percent plus one). A matrix of suburbs and SA2, represented as rows and columns, respectively, was generated through the ABS TableBuilder platform and named ‘SSCSA2’. It identifies the maximum value at every row and assigns the rows a SA2—the column name at which the maximum value is located. The "winner takes all" approach is conducted through the following code segment.

SSCSA2$SA2<-colnames(x)[apply(x,1,which.max)]

It must be noted that the QFES incident data points are labeled with suburb names that contain some misspellings. For example, some identified errors include ‘Cressbrookst’ and ‘Creastmead’. Additionally, the dataset does not distinguish names used for multiple different suburbs. Therefore, the study has identified these suburb names and added parentheses, distinguishing the suburbs by following the ABS State Suburbs (SSC) naming convention and cross-referencing the postcodes of the suburbs at issue. One example is Clontarf (Moreton Bay—Qld) and Clontarf (Toowoomba—Qld).

4.2. Parameters

The results were obtained using the R software at its 2021.09.0 version on a device equipped with AMD Ryzen 5 3450U, Radeon Vega Mobile Gfx 2.10 GHz, and 5.89 GB of usable RAM. In addition, the RobStatTM package was used to execute the robust stepwise regression analysis [47]. The tuning constant for the M-scale used to compute the initial S-estimator was set to 0.5. The constant determines the breakdown point of the resulting MM-estimator. Relative convergence tolerance for the iterated weighted least square (IRWLS) iterations for the MM-estimator was set to 0.001. The tolerance level was chosen to allow convergence to occur. The desired asymptotic efficiency of the final regression M-estimator was set to 0.95. Finally, the asymptotic bias optimal family of the loss function was used in tuning the parameter for the rho function.

4.3. Results

Nine variables have initially been eliminated, leaving ten variables in the final model. A detailed model specification, which includes a coefficient β_d for every retained variable x_d (see Equation (1)), is contained in Table 1.

Table 1. y_i model for socioeconomic predictors of building fires by robust backward elimination method.

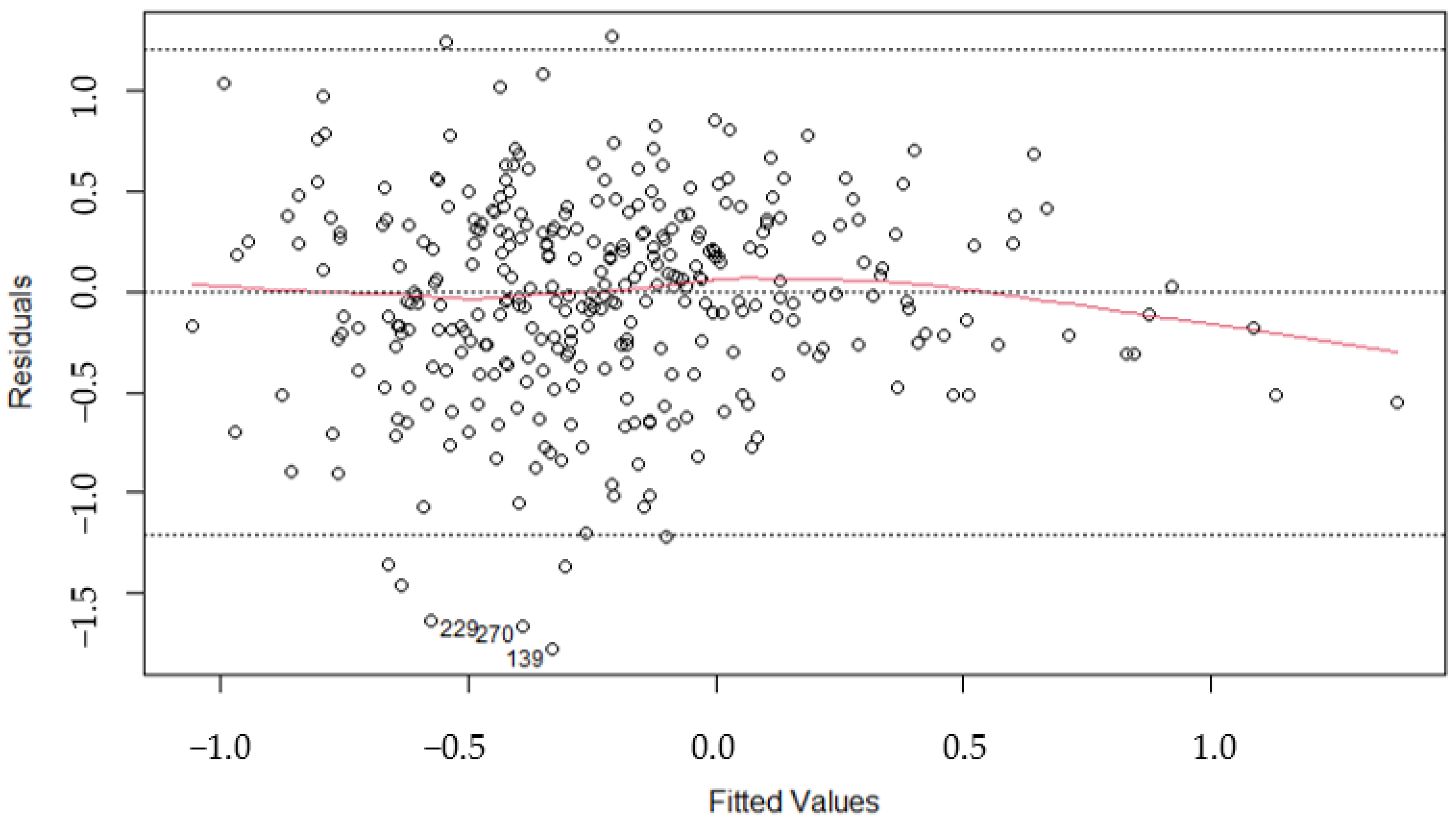
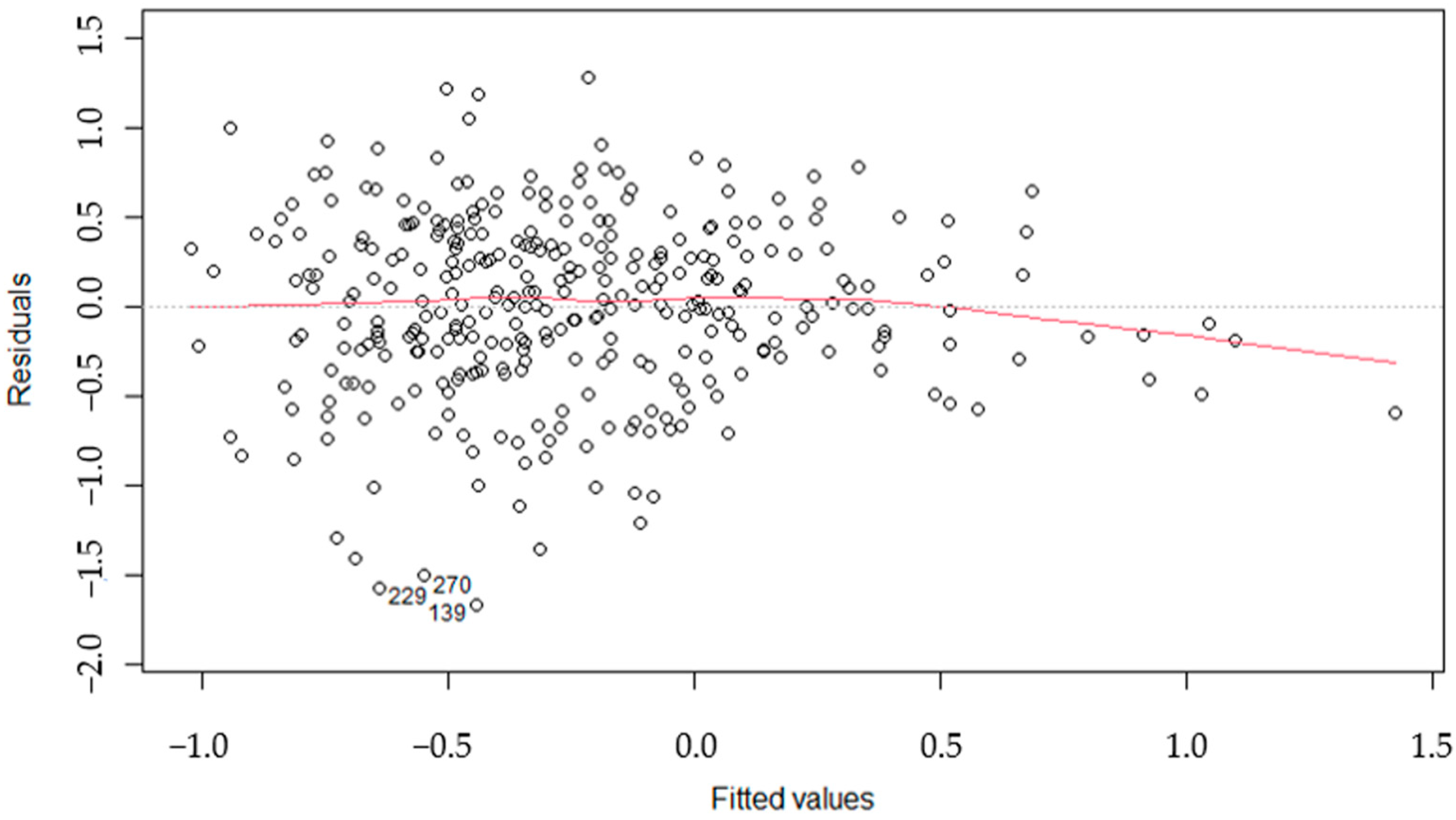
Variables	Coefficient Est.	Std. Error	VIF	t Value	F Value	(Pr > t)
(INTERCEPT)	−0.0559	0.1474	-	−0.3790	-	0.7048
CERTIFICATE	1.9462	0.5853	2.8851	3.3250	11.0567	0.0010
CHILDJOBLESS	−1.3046	0.4744	3.1884	−2.7500	7.5627	0.0063
DISABILITYU70	11.9985	3.1034	4.5289	3.8660	14.9483	0.0001
HIGHBED	−0.7390	0.1674	2.2814	−4.4150	19.4888	1.38 × 10−5
NOCAR	5.0159	0.7877	2.3775	6.3670	40.5440	6.65 × 10−10
NOEDU	13.3645	5.0603	2.1978	2.6410	6.9751	0.0087
OCC_DRIVERS	1.0718	0.5444	1.7903	1.9690	3.8757	0.0498
OCC_LABOUR	3.4219	1.0807	4.8463	3.1660	10.0263	0.0017
OCC_MANAGERS	4.7262	0.7581	1.7200	6.2340	38.8648	1.43 × 10−9
OCC_SERVICE_L	−5.9257	1.7513	2.6066	−3.3840	11.4481	0.0008

Robust residual standard error = 0.357, R-squared = 0.4154, and adj. R-squared = 0.3972. Shapiro-Wilks test on residuals: W = 0.93478, p-value = 6.832 × 10⁻¹¹. Breusch-Pagan test on residuals: BP = 22.586, df = 10, p-value = 0.01238.

The model does not satisfy the assumption of normally distributed error and equal variances of error, or homoscedasticity. A Shapiro-Wilks test on error resulted in convincing evidence to reject the null hypothesis that the error is normally distributed. A Breusch-Pagan test has also confidently rejected the null hypothesis that the error has equal variance. In light of the presented findings, various transformations—logarithmic, square root, Box Cox—are conducted on the explanatory variables and/or the response variable to find a conforming model. The logarithmic transformation to the response variable (Equation (15)) is found to be the best performing in terms of compliance with the Markov-Gauss assumptions.

$$\log \left(y_i\right)={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_d{x}_{id}$$

(15)

Subsequently, the suggested methodology is re-executed using the transformed response variable, thereby yielding outcomes that are available in Table 2.

Table 2. log(y_i) model for socioeconomic predictors of building fires by robust backward elimination method.

Variables	Coefficient Est.	Std. Error	VIF	t Value	F Value	(Pr > t)
(INTERCEPT)	−0.0961	0.2168	-	−0.4430	-	0.6579
CERTIFICATE	2.5459	0.7902	3.0107	3.2220	10.3807	0.0014
CHILDJOBLESS	−1.4660	0.6779	3.8942	−2.1630	4.6764	0.0313
DISABILITYU70	9.8059	4.4173	5.6321	2.2200	4.9278	0.0271
HIGHBED	−0.8372	0.2756	3.6520	−3.0380	9.2287	0.0026
LOWRENT	1.2476	1.4035	3.8618	0.8890	0.7902	0.3747
NOCAR	5.2416	1.1348	2.9453	4.6190	21.3329	5.61 × 10−6
NOEDU	15.0715	6.385	2.1487	2.3600	5.5716	0.0189
NONET	0.4373	1.9582	7.5825	0.2230	0.0499	0.8234
OCC_DRIVERS	1.1416	0.7837	2.1446	1.4570	2.1219	0.1462
OCC_MANAGERS	2.8106	1.1612	2.3701	2.4200	5.8581	0.0161
OCC_PROF	−1.1233	0.5293	3.4929	−2.1220	4.5043	0.0346
OCC_SERVICE_L	−11.2379	2.3258	2.8882	−4.8320	23.3456	2.11 × 10−6
ONEPARENT	1.6318	1.3821	4.3781	1.1810	1.3940	0.2386

Robust residual standard error = 0.4832, R-squared = 0.3964, and adj. R-squared = 0.3717. Shapiro-Wilks test on residuals: W = 0.98247, p-value = 0.0004502. Breusch-Pagan test on residuals: BP = 16.822, df = 13, p-value = 0.2076.

This time, six variables were initially eliminated, leaving thirteen variables in the final model. In identifying the individual parameters’ influence, caution has to be exercised as a model-building algorithm is known to overstate significance [11]. Further assessment, for example, through Monte Carlo simulations, is recommended. The model’s R-squared was calculated to be 0.4259, translating to 42.59 percent of variations explainable by the variables retained. The adjusted R-squared of 0.4024 indicates the model R-squared upon fitting to another dataset in the population. The error sufficiently satisfies the threshold set by Falk and Miller [48] for endogenous constructs such as the one obtained. A robust residual standard error (RSE) of 0.3779 meant the observed building fire rates were off from the actual regression line by approximately 0.3779 units on average. Two socioeconomic variables, NOCAR and OCC_SERVICE_L, were significant at the 0.001 level. Based on their t-statistics and F-statistics, the corresponding p-values (5.61 × 10⁻⁶ and 2.11 × 10⁻⁶, respectively) preliminarily indicated the variables’ inclusions were not due to chance. NOEDU’s highest positive coefficient increases building fire rates to the highest degree. In contrast, OCC_SERVICE_L’s lowest negative coefficient decreases building fire rates the most significantly.

The Breusch-Pagan test on the new model indicated a statistic of 0.2076. The test is unable to provide sufficient evidence to reject the null hypothesis that the error variance is equal at the 0.05 significant level. Figure 2 reinforces the indication as the plot of residuals to the fitted values forms a horizontal band around the y = 0 line.

Figure 2. Residuals—fitted values plot for the log(y) model by RFPE criterion.

However, the model still fails the Shapiro-Wilks test, as the p-value of 0.0004502 indicates sufficient evidence to reject the null hypothesis that the error is normally distributed at the 0.05 significance level. There is, however, a significant improvement in the statistic in comparison to the model prior to the transformation. The presence of skewness in the distribution of errors is observable from its Q-Q plot, as depicted in Figure 3, wherein a pronounced right tail is apparent. Despite this, several studies have proposed a relaxed normality assumption for large datasets, owing to the Central Limit Theorem. They have suggested sample size thresholds of $N>25, N\ge 15, N\ge 50$ and $\frac{N}{p}>10$ where N is the sample size and p is the number of parameters [49,50,51]. The experiment satisfied all of the thresholds with a sample size of 332.

Figure 3. Q-Q plot for the log(y) model by RFPE criterion.

A five-fold cross-validation is then conducted to assess the performance of the method’s resulting model on unseen data. The number of folds is chosen because each fold will contain approximately 55 data points, a reasonable number of observations to minimize overfitting. The root of the mean of the square of errors (RMSE) in Equation (14) and the mean of absolute value of errors (MAE) in Equation (15) are used as the basis for comparison. They measure the difference between the value predicted by the model and the value of the testing model. The presence of a square root in RMSE means the measurement has a higher penalty for large errors.

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-y_p\right)}^2}{n}}$$

(16)

$$MAE=\frac{{{\displaystyle \sum }}_{i=1}^n\left|y_i-y_p\right|}{n}$$

(17)

where y_i is the actual rate of building fires, y_p is the projected rate of building fires, and n is the number of observations/suburbs. The cross-validation procedure is showcased in Algorithm 2.

Algorithm 2. Algorithm of the five-fold cross-validation

Randomly shuffle the dataset, D. Divide D into 5 equally sized folds, D1, D2, D3, D4, and D5. For every fold: Set the current fold, Di, as the test dataset. Set the remaining dataset as the training dataset. Run the algorithm on the training dataset. Measure RMSE and MAE of the resulting model based on the training dataset. Measure RMSE and MAE of the resulting model based on the test dataset. Return RMSE and MAE data

Five sets of measurements have been obtained for each round, which have different folds as the testing dataset. They are summarized in Table 3.

Table 3. The RMSE and MAE of models produced by RFPE after 5-fold cross-validation.

Testing Dataset	Training Dataset	Measurements
		RMSE			MAE
		Train.	Test.	Diff.	Train.	Test.	Diff.
1	2, 3, 4, 5	0.476818	0.571732	−0.094914	0.371323	0.443796	−0.072473
2	1, 3, 4, 5	0.500364	0.471037	0.029327	0.388915	0.354920	0.033995
3	1, 2, 4, 5	0.491625	0.503445	−0.011820	0.378446	0.395941	−0.017495
4	1, 2, 3, 5	0.501656	0.471982	0.029674	0.392949	0.351124	0.041824
5	1, 2, 3, 4	0.500390	0.473456	0.026934	0.381941	0.387893	−0.005952
Mean Abs. Diff.		0.494171	0.498330	0.038534	0.382715	0.386735	0.034348

Table 3 shows negligible differences between the root-mean-square error (RMSE) and mean absolute error (MAE). An exception was observed in the iteration with the third fold as the testing dataset. A substantial difference was detected; however, the average difference across the five iterations is still negligibly low. This indicates the model’s equal performance on a dataset not involved in training the model, obtained through the proposed method.

5. Comparative Study

5.1. Alternative Backward Elimination Criteria

There are sizeable alternatives to backward elimination in assessing the goodness-of-fit of a model. Therefore, this paper adopts four criteria as the comparative basis for the RFPE criterion.

5.1.1. Akaike Information Criterion (AIC)

Akaike [52] proposed an indicator for a model’s quality by measuring its goodness-of-fit by estimating Kullback-Leibler divergence using the maximum likelihood principle. The Akaike’s Information Criterion (AIC) is proposed as follows [53].

$$AIC=2k-2\ln \left(L\left(\widehat{\theta }|y\right)\right)$$

(18)

where k is the number of parameters and L represents the maximum likelihood function of the parameter estimate $\widehat{\theta }$ given the data y. The criterion can be derived from the likelihood L as a function of the residual sum of squares as follows [54]:

$$AIC=n\log \left(\frac{RSS}{n}\right)+2k$$

(19)

where RSS is the residual sum of squares of the model. The stepwise AIC algorithm has been implemented in financial, medical, and epidemiological applications [55,56,57].

The AIC is the most commonly used information theoretic approach to measuring how much information is lost between a selected model and the true model. It has been widely used as an effective model selection method in many scientific fields, including ecology and phylogenetics [58,59]. Compared with the use of adjusted R-squared to evaluate the model solely on fit, AIC also considers model complexity [58].

5.1.2. Bayesian Information Criterion (BIC)

The Bayesian information criterion, also known as the Schwarz information criterion, was proposed by Gideon Schwarz [60]. Modifying Akaike’s information criterion by introducing Bayes estimators to estimate the maximum likelihood of the model’s parameters. The BIC is formulated as follows:

$$BIC=k\ln \left(n\right)-2\ln \left(L\left(\widehat{\theta }|y\right)\right)$$

(20)

Similarly to the AIC, the BIC The criterion can be derived from the likelihood L as a function of the residual sum of squares as follows:

$$BIC=n\log \left(\frac{RSS}{n}\right)+k\ln \left(n\right)$$

(21)

The strength of BIC includes its ability to find the true model if it exists within the candidates. However, it comes with a significant caveat, as the existence of a true model that reflects reality is debatable. Although BIC penalizes overfitting on larger models, it prefers a more parsimonious or lower-dimensional model. However, for its predictive ability, AIC is better because it minimizes the mean squared error of prediction/estimation [61].

5.1.3. Predicted Residual Error Sum of Squares (PRESS)

Allen [62] developed an indicator of a model’s fit through the predicted residual error sum of squares (PRESS) statistic. The differentiation of the statistic at that time was its ability to measure fit based on samples that were not used to form a model [62,63]. The statistic is a cross-validation attempt by a leave-one-out method that subtracts ${\widehat{y}}_{\left(i\right)}$ and leaves the i-th observation out, reducing the sample size to n − 1 [64]. Repeating the subtraction and omission of every data point will lead to the sum of squares of discrepancies [65,66]. PRESS is formulated as follows:

$$PRESS={\displaystyle \sum }_{i=1}^n{\left(y_i-{\widehat{y}}_{\left(i\right)}\right)}^2$$

(22)

5.2. Comparison of Robust Final Predictor Error (RFPE) Criterion to Akaike’s Information Criterion (AIC) Criterion

Eight variables have been eliminated, leaving eleven variables in the final model. A detailed model specification, which includes a coefficient β_d for every retained variable x_d (see Equation (1)), is contained in Table 4.

Table 4. Final model for socioeconomic predictors of building fires by AIC criterion.

Variables	Coefficient Est.	Std. Error	VIF	t Value	F Value	(Pr > t)
(INTERCEPT)	0.0122	0.2027	5.1767	0.0600	2.0169	0.9521
CERTIFICATE	1.4485	1.0199	3.5536	1.4200	4.8553	0.1565
CHILDJOBLESS	−1.406	0.6381	3.3722	−2.2030	4.2129	0.0283
DIPLOMA	−4.7625	2.3203	4.4612	−2.0530	8.2561	0.0409
DISABILITYU70	11.1682	3.8868	3.4764	2.8730	4.5821	0.0043
HIGHBED	−0.5626	0.2628	2.9668	−2.1410	25.8273	0.0331
NOCAR	5.7104	1.1236	1.7804	5.0820	11.7489	6.36 × 10−7
NOEDU	19.7162	5.7521	3.0316	3.4280	6.1727	0.0007
OCC_MANAGERS	3.2178	1.2952	2.7523	2.4840	9.0378	0.0135
OCC_PROF	−1.3914	0.4628	3.6245	−3.0060	12.5369	0.0029
OCC_SERVICE_L	−9.0765	2.5634	5.6759	−3.5410	4.5320	0.0005
SEPDIVORCED	4.0726	1.9131	5.1767	2.1290	2.0169	0.0340

Residual standard error = 0.5016, R-squared = 0.3916, and adj. R-squared = 0.3707. Shapiro-Wilks test on residuals: W = 0.98687, p-value = 0.00417. Breusch-Pagan test: BP = 16.481, df = 11, p-value = 0.1242.

Moreover, when identifying the influence of individual parameters, it is essential to exercise caution, as the model-building algorithm has been known to overstate the significance of the parameters [11]. Further assessment, for example, through Monte Carlo simulations, is recommended. The R-squared of the model was determined to be 0.3916, indicating that 39.16% of the variations can be explained by the retained variables. The adjusted R-squared of 0.3707 represents the R-squared value of the model fitted to another dataset from the same population. The error met the threshold criteria set by Falk and Miller [48] for endogenous constructs such as the one obtained. A robust residual standard error (RSE) of 0.5016 meant the observed building fire rates were off from the actual regression line by approximately 0.5016 units on average.

Three socioeconomic variables, namely NOCAR, NOEDU, and OCC_SERVICE_L, exhibited a significant effect at the 0.001 level. Based on their t-statistics and F-statistics, the corresponding p-values (6.36 × 10⁻⁷, 0.0007, and 0.0005, respectively) preliminarily indicated that the inclusion of these variables in the model was not due to chance. The variable NOEDU had the highest positive coefficient, and its inclusion in the model resulted in the highest increase in building fire rates. Conversely, the variable OCC_SERVICE_L had the lowest negative coefficient and had the most significant effect on decreasing building fire rates.

The Breusch-Pagan test on the new model indicated a statistic of 0.1242. Similarly to elimination by the RFPE criterion, the test is unable to provide sufficient evidence to reject the null hypothesis that the error variance is equal at the 0.05 significant level. Figure 4 reinforces the indication as the plot of residuals to the fitted values forms a horizontal band around the y = 0 line. A visual comparison to Figure 2 also does not find significant differences.

Figure 4. Residuals—fitted values plot for the log(y) model by AIC criterion.

The model’s normality assumption was tested using the Shapiro-Wilks test, which yielded a p-value of 0.00417. This result provides sufficient evidence to reject the null hypothesis that the error is normally distributed at a 0.05 significance level. The degree of skewness observed in the error distribution is more pronounced than in the model produced through the RFPE criterion in Figure 3, where the p-value was lower at 0.01238. The skewness is further evident in the Q-Q plot, as depicted in Figure 5, where a significant right tail is visible.

Figure 5. Q-Q plot for the log(y) model by AIC criterion.

The two models are comparable on RMSE and MAE. The model produced through the RFPE criterion resulted in a lower MAE but a higher RMSE than the model produced through the AIC criterion (Table 5).

Table 5. Summary of comparative measures of models produced by the AIC and RFPE methods.

Measures	RFPE	AIC
RMSE	0.494268	0.492444
MAE	0.382724	0.385877

To investigate further, we applied the same cross-validation procedure outlined in Algorithm 2 to the model generated using the AIC criterion. The results are presented in Table 6, with the most desirable outcomes highlighted in black. As RMSE penalizes models with significant errors against outliers, we can observe RFPE robustness against outliers in two ways. Firstly, the results show that the RFPE model outperformed the AIC model in terms of MAE but not RMSE. Secondly, it can be observed that the RFPE model consistently exhibited better RMSE performance in the testing dataset compared to the training dataset. Therefore, compared to the AIC, the results demonstrate RFPE and the relevant estimators’ disregard for outliers in training their model and their inability to predict extreme data points.

Table 6. Summary of comparative measures of models produced by AIC and RFPE after 5-fold cross-validation.

Elimination Criteria	Testing Dataset	Training Dataset	Measurement
			RMSE			MAE
			Train.	Test.	Diff.	Train.	Test.	Diff.
RFPE	1	2, 3, 4, 5	0.476818	0.571732	−0.094914	0.371323	0.443796	−0.072473
	2	1, 3, 4, 5	0.500364	0.471037	0.029327	0.388915	0.354920	0.033995
	3	1, 2, 4, 5	0.491625	0.503445	−0.011820	0.378446	0.395941	−0.017495
	4	1, 2, 3, 5	0.501656	0.471982	0.029674	0.392949	0.351124	0.041824
	5	1, 2, 3, 4	0.500390	0.473456	0.026934	0.381941	0.387893	−0.005952
	Mean Abs. Diff.		0.494171	0.498330	0.038534	0.382715	0.386735	0.034348
AIC	1	2, 3, 4, 5	0.475679	0.553801	−0.078122	0.373278	0.435709	−0.062431
	2	1, 3, 4, 5	0.498819	0.465867	0.032953	0.392083	0.360863	0.031220
	3	1, 2, 4, 5	0.488506	0.508005	−0.019499	0.382623	0.398990	−0.016367
	4	1, 2, 3, 5	0.500340	0.459248	0.041092	0.396239	0.344114	0.052125
	5	1, 2, 3, 4	0.498395	0.468168	0.030227	0.385111	0.388907	−0.003796
	Mean Abs. Diff.		0.492348	0.491018	0.040378	0.385867	0.385717	0.033188

5.3. Comparison of Robust Final Predictor Error (RFPE) Criterion to Other Criteria

For comparative purposes, the study has also adopted p-value, BIC, and PRESS as criteria for the backward elimination procedure. The methods are carried out using the ‘SignifReg’ R package. The criteria are consistent with their respective equations in Section 5.1. Using the entire dataset for training, the resulting model from each criterion is assessed for its goodness-of-fit, as shown in Table 7.

Table 7. Summary of comparative measures of models produced by RFPE, p-value, BIC, and PRESS criteria.

Measures	RFPE	p-Value	BIC	PRESS
RMSE	0.494268	0.533903	0.496012	0.506705
MAE	0.382724	0.415332	0.391171	0.398664

The three measures suggest that the models are comparable, although the RFPE criterion slightly outperforms the others in terms of MAE and RMSE. To further assess the models’ performance, we applied the cross-validation procedure outlined in Algorithm 2 to the four different models. The corresponding goodness-of-fit measures are presented in Table 8.

Table 8. Summary of comparative measures of models produced by RFPE, p-value, BIC, and PRESS criteria after 5-fold cross-validation.

Elimination Criteria	Testing Dataset	Training Dataset	Measurements
			RMSE			MAE
			Train.	Test.	Diff.	Train.	Test.	Diff.
RFPE	1	2, 3, 4, 5	0.476818	0.571732	−0.094914	0.371323	0.443796	−0.072473
	2	1, 3, 4, 5	0.500364	0.471037	0.029327	0.388915	0.354920	0.033995
	3	1, 2, 4, 5	0.491625	0.503445	−0.011820	0.378446	0.395941	−0.017495
	4	1, 2, 3, 5	0.501656	0.471982	0.029674	0.392949	0.351124	0.041824
	5	1, 2, 3, 4	0.500390	0.473456	0.026934	0.381941	0.387893	−0.005952
	Mean Abs. Diff.		0.494171	0.498330	0.038534	0.382715	0.386735	0.034348
p-value	1	2, 3, 4, 5	0.519079	0.588888	−0.069809	0.403196	0.463334	−0.060138
	2	1, 3, 4, 5	0.541130	0.503723	0.037407	0.420914	0.392837	0.028077
	3	1, 2, 4, 5	0.532616	0.539056	−0.006439	0.409819	0.437554	−0.027735
	4	1, 2, 3, 5	0.539241	0.511821	0.027420	0.424460	0.378545	0.045915
	5	1, 2, 3, 4	0.537111	0.521020	0.016090	0.418238	0.403838	0.014400
	Mean Abs. Diff.		0.533835	0.532902	0.031433	0.415325	0.415221	0.035253
BIC	1	2, 3, 4, 5	0.478908	0.558554	−0.079646	0.379655	0.436716	−0.057061
	2	1, 3, 4, 5	0.501584	0.472891	0.028693	0.395994	0.371731	0.024263
	3	1, 2, 4, 5	0.493470	0.506130	−0.012660	0.389651	0.397295	−0.007644
	4	1, 2, 3, 5	0.503437	0.464889	0.038548	0.400090	0.355224	0.044866
	5	1, 2, 3, 4	0.502196	0.470759	0.031437	0.390417	0.394151	−0.003734
	Mean Abs. Diff.		0.495919	0.494644	0.038197	0.391161	0.391023	0.027514
PRESS	1	2, 3, 4, 5	0.488093	0.574441	−0.086348	0.386242	0.447798	−0.061556
	2	1, 3, 4, 5	0.511723	0.485957	0.025767	0.401845	0.385843	0.016003
	3	1, 2, 4, 5	0.506614	0.507073	−0.000459	0.398344	0.399954	−0.001610
	4	1, 2, 3, 5	0.514386	0.474490	0.039896	0.409298	0.355806	0.053492
	5	1, 2, 3, 4	0.512207	0.484332	0.027875	0.397540	0.403109	−0.005568
	Mean Abs. Diff.		0.506605	0.505259	0.036069	0.398654	0.398502	0.027646

After comparing the averaged goodness-of-fit measures across the different models, the RFPE criterion exhibits a slight superiority over the averaged MAE measured on the test and train datasets. This lower MAE demonstrates the robustness of the RFPE criterion, which is less sensitive to outliers than RMSE and indicates a model that is more adaptable to extreme cases [67]. The robust nature of the RFPE criterion is further evident in the first iteration, where a test dataset with a higher incidence of outliers is observed. The RFPE criterion has produced a model with a noticeable advantage, as indicated by the lower RMSE and MAE measures, suggesting a more resilient model that provides a better fit, even for a significantly outlying dataset.

6. Conclusions

This study has identified shortcomings in current socioeconomic models of building fires and has proposed a more robust approach through backward elimination using the Robust Final Predictor Error (RFPE) criterion. The proposed method has been evaluated using datasets from the South-East Queensland region of Australia, resulting in a model that retained 13 variables out of the 24 used by the Australian Bureau of Statistics to calculate the Index of Relative Socioeconomic Advantage and Disadvantage (IRSAD). The model was deemed reasonable with an adjusted R-squared of 0.3717, a root of the mean of the square of errors (RMSE) of 0.494268, and a mean absolute value of errors (MAE) of 0.382724.

A comparative analysis revealed that the proposed RFPE-based approach outperforms other criteria such as p-value, Akaike’s Information Criterion (AIC), Bayesian Information Criterion (BIC), and predicted residual error sum of squared (PRESS) in terms of goodness-of-fit measures following cross-validation. These findings provide convincing evidence to support the use of backward elimination with the RFPE criterion for modeling the socioeconomic determinants of building fires.

Future research may involve comparing the RFPE-based approach with alternative methods such as model averaging, least absolute shrinkage and selection operator (LASSO), least absolute residuals (LAR), and principal component analysis (PCA) [16,68,69]. Monte Carlo simulations may also be used to assess the model’s reliability in identifying individual parameters and compare its performance to other modeling approaches. In the event that simulations prove unreasonable for building fire data, bootstrapping could serve as an alternative. In conclusion, this study has provided sufficient justification to adopt backward elimination with the RFPE criterion for predictive modeling of the socioeconomic determinants of building fires.