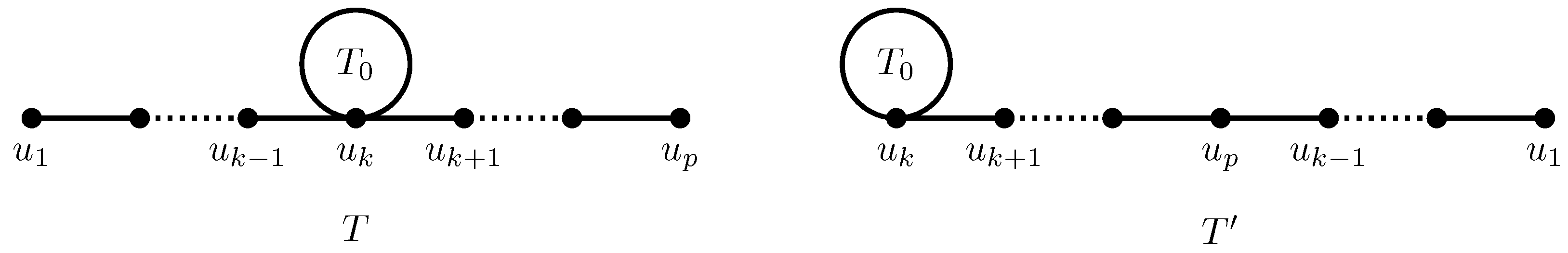Two-Matchings with Respect to the General Sum-Connectivity Index of Trees

Abstract

A vertex-degree-based topological index $\phi$ associates a real number to a graph G which is invariant under graph isomorphism. It is defined in terms of the degrees of the vertices of G and plays an important role in chemical graph theory, especially in QSPR/QSAR investigations. A subset of k edges in G with no common vertices is called a k-matching of G, and the number of such subsets is denoted by $m\left(G,k\right)$. Recently, this number was naturally extended to weighted graphs, where the weight function is induced by the topological index $\phi$. This number was denoted by $m_k\left(G,\phi \right)$ and called the k-matchings of G with respect to the topological index $\phi$. It turns out that $m_1\left(G,\phi \right)=\phi \left(G\right),$ and so for $k\ge 2,$ the k-matching numbers $m_k\left(G,\phi \right)$ can be viewed as kth order topological indices which involve both the topological index $\phi$ and the k-matching numbers. In this work, we solve the extremal value problem for the number of 2-matchings with respect to general sum-connectivity indices ${\mathcal{SC}}_{\mathit{\alpha }}$, over the set ${\mathcal{T}}_n$ of trees with n vertices, when $\alpha$ is a real number in the interval $\left[-1,0\right).$

1. Introduction

In chemical graph theory, the molecular structure of a compound is represented as a graph. In this context, atoms are represented as vertices, and chemical bonds are represented as edges connecting these vertices. One of the main goals of chemical graph theory is to analyze the molecular structure of a chemical compound through the study of its molecular graph, using graph theoretical and computation techniques [1].

A topological index, also called a molecular descriptor, is a numerical parameter of a graph which is invariant under graph isomorphism. It plays an important role in chemical graph theory, especially in the quantitative structure–property relationship (QSPR) and the quantitative structure–activity relationship (QSAR) investigations [2,3]. There are a variety of topological indices that are derived from different concepts such as entropy [4] and counting polynomials [5]. One important class of topological indices are the vertex-degree-based topological indices, which are defined in terms of the degrees of the vertices of the graph.

More precisely, let $G=(V,E)$ be a graph with vertex set $V=V\left(G\right)$ and edge set $E=E\left(G\right)$. A vertex-degree-based (VDB for short) topological index $\phi$ is defined for the graph G as

$$\phi =\phi \left(G\right)=\sum _{uv\in E}{\phi }_{d_G\left(u\right),d_G\left(v\right)},$$

where $d_G\left(u\right)$ denotes the degree of the vertex $u\in G$, and ${\phi }_{i,j}$ is an appropriate function with the property ${\phi }_{i,j}={\phi }_{j,i}$. For recent results on VDB topological indices, we refer to [6,7,8,9], where extremal value problems in significant classes of graphs are solved. A geometrical approach to VDB topological indices is considered in [10,11], and in [12], applications to COVID-19 are found.

Among the VDB topological indices, the general sum-connectivity indices are defined as

$${\mathcal{SC}}_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{\left(d_G\left(u\right)+d_G\left(v\right)\right)}^{\alpha }.$$

They were introduced by Zhou and Trinajstić [13,14] and have attracted the attention of many researchers due to their interesting mathematical properties and chemical applicability. For instance, in [15], it is shown that there is a good correlation between physico-chemical properties and the general sum-connectivity index for benzenoid hydrocarbons. Bounds for the general sum-connectivity index in different classes of graphs are found in [16,17,18,19]. In [20,21], lower bounds of the line graph are found, and extremal graphs are characterized.

Another type of topological index is the well-known Hosoya index, denoted by $Z\left(G\right)$ and introduced by Haruo Hosoya in 1971 [22] to report a good correlation of the boiling points of alkane isomers. In order to properly define it, we must recall that a set of edges $M\subseteq E\left(G\right)$ is called a matching of G if no two edges of M have a vertex in common. A matching of G with k edges is said to be a k-matching. We denote by $m(G,k)$ the number of k-matchings of G and assume that $m(G,0)=1$. Then, the Hosoya index $Z\left(G\right)$ is defined as

$$Z\left(G\right)=\sum _{k=0}^{\lfloor {\displaystyle \frac{n}{2}}\rfloor }m\left(G,k\right).$$

It is well known that if T is a tree with n vertices; then,

$$m\left(S_n,k\right)\le m\left(T,k\right)\le m\left(P_n,k\right)$$

for all $k\ge 0$, where $S_n$ is the star on n vertices, and $P_n$ is the path on n vertices (see [23] (Theorem 4.6)).

In view of its structural relationship to both the VDB topological index $\phi$ and the Hosoya topological index Z, the construction of a novel molecular descriptor was introduced in [24], called the Hosoya index of VDB-weighted graphs. It is defined as

$$Z\left(G,\phi \right)=\sum _{k\ge 0}{m}_k\left(G,\phi \right),$$

where $m_0\left(G,\phi \right)=1$, and for $k\ge 1$,

$$m_k\left(G,\phi \right)=\sum _{U\in \left\{k-\mathrm{matchings}\mathrm{of}G\right\}}\left[\prod _{uv\in U}{\phi }_{d_G\left(u\right),d_G\left(v\right)}\right].$$

It turns out that $m_1\left(G,\phi \right)=\phi \left(G\right),$ so for $k=1$, we recover the VDB topological index $\phi$, and for $k\ge 2$, the k-matching numbers $m_k\left(G,\phi \right)$ can be viewed as kth order topological indices which involve both the topological index $\phi$ and the k-matching numbers.

It is our main interest in this paper to study $m_2\left(T,\phi \right)$ when T is a tree, and $\phi ={\mathcal{SC}}_{\alpha }$ is the general sum-connectivity index. Concretely, we find the extremal values of the function $m_2\left(-,{\mathcal{SC}}_{\alpha }\right):{\mathcal{T}}_n⟶\mathbb{R}$, where ${\mathcal{T}}_n$ is the set of trees with n vertices, and $\alpha$ is a real number in the interval $\left[-1,0\right).$

2. 2-Matchings with Respect to ${\mathcal{SC}}_{\alpha }$

By $S_n$, we denote the n-vertex star. It is straightforward that for any VDB topological index $\phi$ and $T\in {\mathcal{T}}_n$ different from the star,

$$0=m_2\left(S_n,\phi \right)<m_2\left(T,\phi \right).$$

Consequently, among all trees with n vertices, $S_n$ attains the minimum number of 2-matchings with respect to any VDB topological index $\phi$.

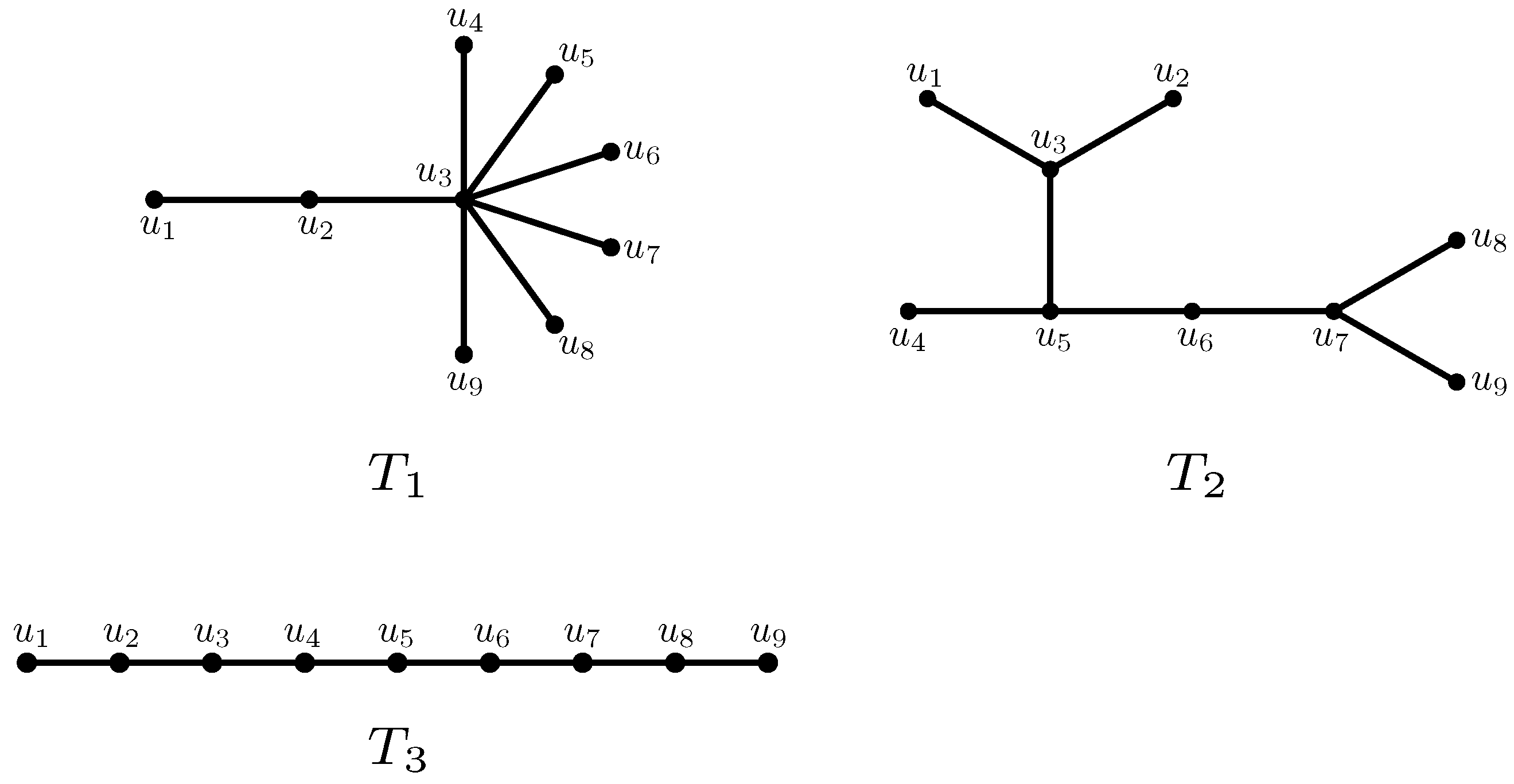
In the next example, we show how to compute the number of 2-matchings with respect to any VDB topological index $\phi$ of the trees depicted in Figure 1.

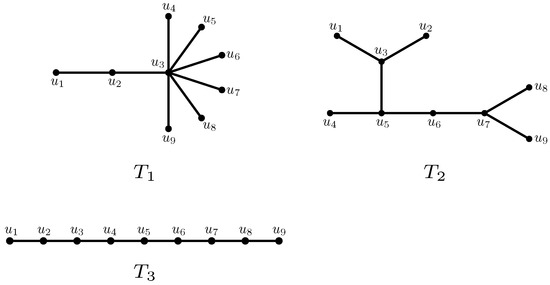
Figure 1. Trees in Example 1.

Example 1.

Consider the tree $T_1$ depicted in Figure 1, and let $M_2\left(T_1\right)$ be the set of 2-matchings of $T_1$. The elements of $M_2\left(T_1\right)$ are $\left\{u_1{u}_2,u_3{u}_4\right\}$, $\left\{u_1{u}_2,u_3{u}_5\right\}$, $\left\{u_1{u}_2,u_3{u}_6\right\}$, $\left\{u_1{u}_2,u_3{u}_7\right\}$, $\left\{u_1{u}_2,u_3{u}_8\right\}$ and $\left\{u_1{u}_2,u_3{u}_9\right\}$. Then, the number of 2-matchings of $T_1$ with respect to φ is given by

$$m_2\left(T_1,\phi \right)=\sum _{U\in M_2\left(T_1\right)}\left[\prod _{uv\in U}{\phi }_{d_{T_1}\left(u\right),d_{T_1}\left(v\right)}\right]=6{\phi }_{1,2}{\phi }_{1,7}.$$

The elements of the set $M_2\left(T_2\right)$ of 2-matchings of $T_2$ in Figure 1 are $\left\{u_1{u}_3,u_4{u}_5\right\}$, $\left\{u_1{u}_3,u_5{u}_6\right\}$, $\left\{u_1{u}_3,u_6{u}_7\right\}$, $\left\{u_1{u}_3,u_7{u}_8\right\}$, $\left\{u_1{u}_3,u_7{u}_9\right\}$, $\left\{u_2{u}_3,u_4{u}_5\right\}$, $\left\{u_2{u}_3,u_5{u}_6\right\}$, $\left\{u_2{u}_3,u_6{u}_7\right\}$, $\left\{u_2{u}_3,u_7{u}_8\right\}$, $\left\{u_2{u}_3,u_7{u}_9\right\}$, $\left\{u_3{u}_5,u_6{u}_7\right\}$, $\left\{u_3{u}_5,u_7{u}_8\right\}$, $\left\{u_3{u}_5,u_7{u}_9\right\}$, $\left\{u_4{u}_5,u_6{u}_7\right\}$, $\left\{u_4{u}_5,u_7{u}_8\right\}$, $\left\{u_4{u}_5,u_7{u}_9\right\}$, $\left\{u_5{u}_6,u_7{u}_8\right\}$ and $\left\{u_5{u}_6,u_7{u}_9\right\}$. Consequently,

$$m_2\left(T_2,\phi \right)=\sum _{U\in M_2\left(T_2\right)}\left[\prod _{uv\in U}{\phi }_{d_{T_2}\left(u\right),d_{T_2}\left(v\right)}\right]=8{\phi }_{1,3}^2+7{\phi }_{1,3}{\phi }_{2,3}+{\phi }_{3,3}{\phi }_{2,3}+2{\phi }_{3,3}{\phi }_{1,3}.$$

For the tree $T_3$ of Figure 1, the elements of $M_2\left(T_3\right)$ are $\left\{u_1{u}_2,u_3{u}_4\right\}$, $\left\{u_1{u}_2,u_4{u}_5\right\}$, $\left\{u_1{u}_2,u_5{u}_6\right\}$, $\left\{u_1{u}_2,u_6{u}_7\right\}$, $\left\{u_1{u}_2,u_7{u}_8\right\}$, $\left\{u_1{u}_2,u_8{u}_9\right\}$, $\left\{u_2{u}_3,u_4{u}_5\right\}$, $\left\{u_2{u}_3,u_5{u}_6\right\}$, $\left\{u_2{u}_3,u_6{u}_7\right\}$, $\left\{u_2{u}_3,u_7{u}_8\right\}$, $\left\{u_2{u}_3,u_8{u}_9\right\}$, $\left\{u_3{u}_4,u_5{u}_6\right\}$, $\left\{u_3{u}_4,u_6{u}_7\right\}$, $\left\{u_3{u}_4,u_7{u}_8\right\}$, $\left\{u_3{u}_4,u_8{u}_9\right\}$, $\left\{u_4{u}_5,u_6{u}_7\right\}$, $\left\{u_4{u}_5,u_7{u}_8\right\}$, $\left\{u_4{u}_5,u_8{u}_9\right\}$, $\left\{u_5{u}_6,u_7{u}_8\right\}$, $\left\{u_5{u}_6,u_8{u}_9\right\}$ and $\left\{u_6{u}_7,u_8{u}_9\right\}$. It follows that

$$m_2\left(T_3,\phi \right)=\sum _{U\in M_2\left(T_3\right)}\left[\prod _{uv\in U}{\phi }_{d_{T_3}\left(u\right),d_{T_3}\left(v\right)}\right]={\phi }_{1,2}^2+10{\phi }_{1,2}{\phi }_{2,2}+10{\phi }_{2,2}^2.$$

In this section, we consider 2-matchings with respect to ${\mathcal{SC}}_{\alpha }$, where $\alpha \in \left[-1,0\right)$, over the set of trees ${\mathcal{T}}_n$ with $n\ge 5$ vertices. In order to find the second minimum, we first analyze 2-matchings with respect to ${\mathcal{SC}}_{\alpha }$ over the set of double-star trees.

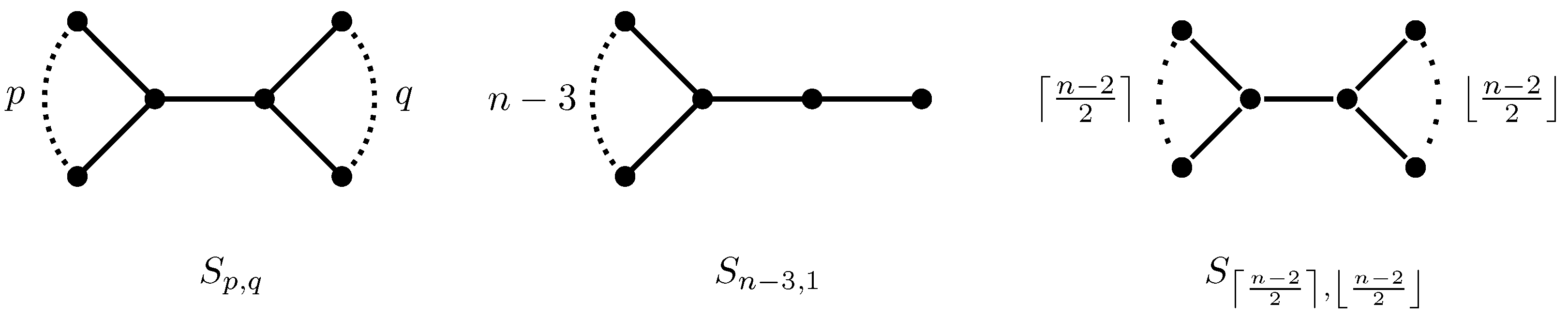
Let $p\ge q\ge 1$ and $p+q=n-2$. The double-star $S_{p,q}\in {\mathcal{T}}_n$ is a tree with exactly two vertices of degree greater than 1, one having degree $p+1$ and the other one having degree $q+1$. It is easy to see that $m_2(S_{p,q},\phi )=pq{\phi }_{p+1,1}{\phi }_{q+1,1}$.

We distinguish two extreme double-stars with respect to parameters p and q, the double star $S_{n-3,1}$ and the balanced double-star $S_{⌈{\displaystyle \frac{n-2}{2}}⌉,⌊{\displaystyle \frac{n-2}{2}}⌋}$ (see Figure 2).

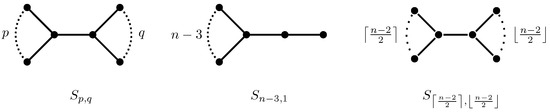
Figure 2. Double-star trees $S_{p,q}$, with $p+q=n-2$, $S_{n-3,1}$ and $S_{⌈{\displaystyle \frac{n-2}{2}}⌉,⌊{\displaystyle \frac{n-2}{2}}⌋}$.

Lemma 1.

Let $p\ge q\ge 1$ and $p+q=n-2$. If $p\ne n-3$, then

$$m_2(S_{p,q},{\mathcal{SC}}_{\alpha })>m_2(S_{n-3,1},{\mathcal{SC}}_{\alpha }).$$

Proof. 

Let $f\left(p\right)=m_2(S_{p,q},{\mathcal{SC}}_{\alpha })=p\left(n-p-2\right){(p+2)}^{\alpha }{(n-p)}^{\alpha }$ defined for $⌈{\displaystyle \frac{n-2}{2}}⌉\le p\le n-3$. The derivative

$${\displaystyle \frac{d}{dp}}f\left(p\right)={\displaystyle \frac{\left(n-2p-2\right)\left[(\alpha +1)(p+2)(n-p)-2\alpha n\right]}{{\left(p+2\right)}^{1-\alpha }{\left(n-p\right)}^{1-\alpha }}}<0,$$

since $\left(n-2p-2\right)<0$ for $⌈{\displaystyle \frac{n-2}{2}}⌉\le p\le n-3$ and $(\alpha +1)(p+2)(n-p)-2\alpha n>0$ for $\alpha \in [-1,0)$ and $⌈{\displaystyle \frac{n-2}{2}}⌉\le p\le n-3$. Consequently, $m_2(S_{p,q},{\mathcal{SC}}_{\alpha })>m_2(S_{n-3,1},{\mathcal{SC}}_{\alpha })$, and it is completed. □

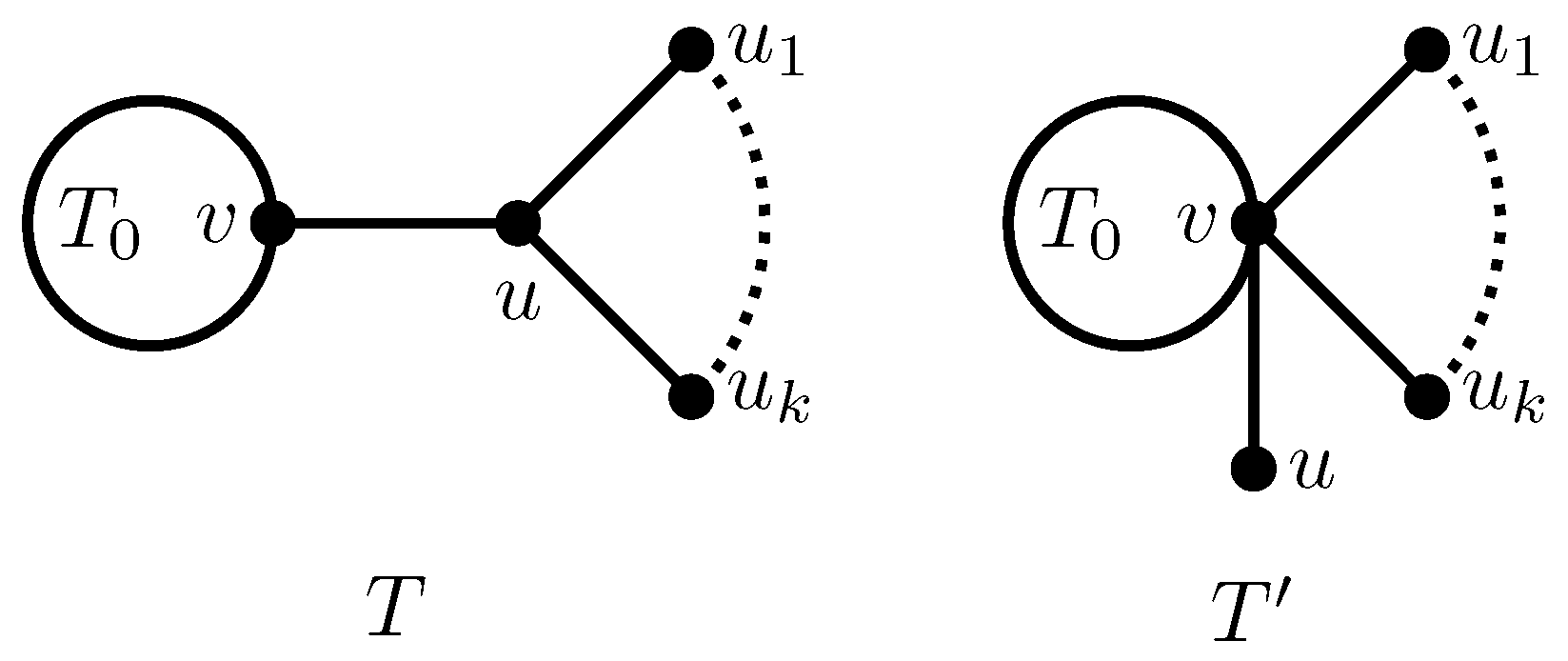
Next, we compute the variation of 2-matchings with respect to ${\mathcal{SC}}_{\alpha }$ when “Transformation A” described in [25] is performed. Let $uv\in E\left(T\right)$, $x=d_T\left(v\right)\ge 2$ and $N_T\left(u\right)=\{v,u_1,\dots ,u_k\}$ where $k\ge 1$ and $u_1,\dots ,u_k$ are leaves. Let $T^{\prime }=T-u{u}_1-\cdots .u{u}_k+v{u}_1+\cdots +v{u}_k$ and $T_0=T-u-u_1\cdots -u_k$ (see Figure 3).

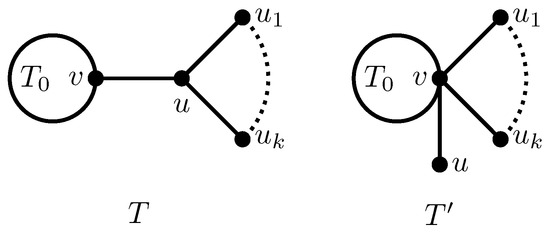
Figure 3. Trees used in “Transformation A”.

Note that $d_{T^{\prime }}\left(v\right)=x+k$. For any other vertex in $w\in V\left(T_0\right)$, we denote $y_w=d_{T_0}\left(w\right)$. Let $E_0=\{ab\in E\left(T_0\right):ab\Vert uv\}$, where $ab\Vert uv$ means that $ab$ and $uv$ are independent edges, and

$$\begin{array}{ccc}\hfill A_T& =& \sum _{e=ab\in E_0}{\left(y_a+y_b\right)}^{\alpha }\left[{\left(x+k+1\right)}^{\alpha }+k{\left(k+2\right)}^{\alpha }+\sum _{w\in N_{T_0}\left(v\right),ab\Vert wv}{\left(y_w+x\right)}^{\alpha }\right],\hfill \\ \hfill A_{T^{\prime }}& =& \sum _{e=ab\in E_0}{\left(y_a+y_b\right)}^{\alpha }\left[(k+1){\left(x+k+1\right)}^{\alpha }+\sum _{w\in N_{T_0}\left(v\right),ab\Vert wv}{\left(y_w+x+k\right)}^{\alpha }\right],\hfill \\ \hfill B_T& =& k{\left(k+2\right)}^{\alpha }\sum _{w\in N_{T_0}\left(v\right)}{\left(y_w+x\right)}^{\alpha }.\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill m_2(T,\phi )-m_2(T^{\prime },\phi )& =& A_T-A_{T^{\prime }}+B_T\hfill \\ & =& \sum _{e=ab\in E_0}{\left(y_a+y_b\right)}^{\alpha }k\left[{\left(k+2\right)}^{\alpha }-{\left(x+k+1\right)}^{\alpha }\right]\hfill \\ & & +\sum _{e=ab\in E_0}{\left(y_a+y_b\right)}^{\alpha }\sum _{w\in N_{T_0}\left(v\right),ab\Vert wv}\Delta (y_w,x,k)\hfill \\ & & +k{(k+2)}^{\alpha }\sum _{w\in N_{T_0}\left(v\right)}{\left(y_w+x\right)}^{\alpha },\hfill \end{array}$$

(1)

where $\Delta (y_w,x,k)={\left(y_w+x\right)}^{\alpha }-{\left(y_w+x+k\right)}^{\alpha }$.

Now, we can prove that the double-star $S_{n-3,1}$ attains the second minimum number of 2-matchings with respect to ${\mathcal{SC}}_{\alpha }$ over the set ${\mathcal{T}}_n$.

Theorem 1.

Let $T\in {\mathcal{T}}_n$ such that $T\not\simeq S_n$ and $T\not\simeq S_{n-3,1}$. If $-1\le \alpha <0$, then,

$$m_2(T,{\mathcal{SC}}_{\alpha })>m_2(S_{n-3,1},{\mathcal{SC}}_{\alpha })=(n-3)3^{\alpha }{\left(n-1\right)}^{\alpha }.$$

Proof. 

Assume $T\in {\mathcal{T}}_n$ is not a double-star and is of the form depicted in Figure 3; then, $T_0$ is a subtree of T different from a star with v as a central vertex. If $T^{\prime }$ is the tree obtained from T by “Transformation A”, then, $T^{\prime }$ is not a star. Since $-1\le \alpha <0$, using relation (1), we obtain

$$m_2(T,{\mathcal{SC}}_{\alpha })-m_2(T^{\prime },{\mathcal{SC}}_{\alpha })>0.$$

Applying this transformation repeatedly, we obtain a sequence of trees $T,T^{\prime },\dots ,T^{\ast }$ such that $m_2(T,{\mathcal{SC}}_{\alpha })>m_2(T^{\prime },{\mathcal{SC}}_{\alpha })>\cdots >m_2(T^{\ast },{\mathcal{SC}}_{\alpha })$, and $T^{\ast }$ is a double-star with n vertices. Now, the result follows from Lemma 1. □

Using appropriate values of $\alpha$ in the previous theorem, we obtain the results for the sum-connectivity index $\mathcal{SC}$ [13] and the harmonic index $\mathcal{H}$ [26,27].

Corollary 1.

Let $n\ge 5$ and $T\in {\mathcal{T}}_n$ such that $T\not\simeq S_n$ and $T\not\simeq S_{n-3,1}$.

1. 

$m_2\left(T,\mathcal{SC}\right)>m_2(S_{n-3,1},\mathcal{SC})={\displaystyle \frac{(n-3)}{\sqrt{3\left(n-1\right)}}}$.

2. 

$m_2\left(T,\mathcal{H}\right)>m_2(S_{n-3,1},\mathcal{H})={\displaystyle \frac{4(n-3)}{3\left(n-1\right)}}$.

Next, we show that for $-1\le \alpha <0$, the maximum number of 2-matchings with respect to ${\mathcal{SC}}_{\alpha }$ is attained in the path $P_n$, among all trees in ${\mathcal{T}}_n$. It is easy to see that

$$m_2\left(P_n,{\mathcal{SC}}_{\alpha }\right)=3^{2\alpha }+2^{2\alpha +1}{3}^{\alpha }(n-4)+2^{4\alpha -1}(n-5)(n-4).$$

Recall that a branching vertex of a tree T is a vertex of degree $k\ge 3$. If v is a branching vertex of degree k of a tree T, then T can be viewed as the coalescence of k subtrees of T at the vertex v. A branching vertex v of T is an outer branching vertex of T if all branches of T at v (except for possibly one) are paths. The concept of the outer branching vertex was introduced in [28]. In the mentioned paper, it was shown that a tree $T\in {\mathcal{T}}_n$ has no outer branching vertex if and only if $T\simeq P_n$.

Now, we compute the variation of 2-matchings with respect to ${\mathcal{SC}}_{\alpha }$ when “Transformation C” described in [25] is performed.

Let $T\in {\mathcal{T}}_n$, $T\not\simeq P_n$; then, there exists an outer branching vertex $u_k\in V\left(T\right)$ and two paths $u_1\cdots u_k$ and $u_k\cdots u_p$ (branches at $u_k$) with $1<k<p<n$. Then, T can be viewed as a coalescence at vertex $u_k$ of a subtree $T_0$ and the path $u_1\cdots u_k\cdots u_p$. We construct the tree $T^{\prime }$ as $T^{\prime }=T-u_{k-1}{u}_k+u_p{u}_{k-1}$ (see Figure 4).

Figure 4. Trees used in “Transformation C”.

Let $x=d_{T_0}\left(u_k\right)>0$; then, $d_T\left(u_k\right)=x+2$ and $d_{T^{\prime }}\left(u_k\right)=x+1$. For any other vertex in $w\in V\left(T_0\right)$, we denote $y_w=d_{T_0}\left(w\right)$. We also distinguish the subset of edges $E_0=\{ab\in E\left(T_0\right):a\ne u_k,b\ne u_k\}$.

Now, we compute the difference $\Delta m_2=m_2(T,{\mathcal{SC}}_{\alpha })-m_2(T^{\prime },{\mathcal{SC}}_{\alpha })$, where $\Delta (y_w,x)={\left(y_w+x+2\right)}^{\alpha }-{\left(y_w+x+1\right)}^{\alpha }$. By symmetry, we may assume $1<k\le ⌈{\displaystyle \frac{p}{2}}⌉$ and consider only the following three cases:

• If $k=2$ and $p=3$,

  $$\begin{array}{ccc}\hfill \Delta m_2& =& \sum _{ab\in E_0}{\left(y_a+y_b\right)}^{\alpha }\left[{\left(x+3\right)}^{\alpha }-3^{\alpha }\right]\hfill \\ & & +\sum _{w\in N_{T_0}\left(u_k\right)}\left(\sum _{ab\in E_0,ab\Vert w{u}_k}{\left(y_a+y_b\right)}^{\alpha }\right)\Delta (y_w,x)\hfill \\ & & -3^{\alpha }\sum _{w\in N_{T_0}\left(u_k\right)}{\left(y_w+x+1\right)}^{\alpha }.\hfill \end{array}$$

  (2)
• If $k=2$ and $p>3$,

  $$\begin{array}{ccc}\hfill \Delta m_2& =& \sum _{ab\in E_0}{\left(y_a+y_b\right)}^{\alpha }\left[{\left(x+4\right)}^{\alpha }-4^{\alpha }\right]\hfill \\ & & +\sum _{w\in N_{T_0}\left(u_k\right)}\left((p-3)4^{\alpha }+3^{\alpha }+\sum _{ab\in E_0,ab\Vert w{u}_k}{\left(y_a+y_b\right)}^{\alpha }\right)\Delta (y_w,x)\hfill \\ & & -4^{\alpha }\sum _{w\in N_{T_0}\left(u_k\right)}{\left(y_w+x+2\right)}^{\alpha },\hfill \end{array}$$

  (3)
• If $k>2$ and $p>k+1$,

  $$\begin{array}{ccc}\hfill \Delta m_2& =& \sum _{ab\in E_0}{\left(y_a+y_b\right)}^{\alpha }\left[2{\left(x+4\right)}^{\alpha }-{\left(x+3\right)}^{\alpha }+3^{\alpha }-2·4^{\alpha }\right]\hfill \\ & & +\sum _{w\in N_{T_0}\left(u_k\right)}\left((p-3)4^{\alpha }+3^{\alpha }+\sum _{ab\in E_0,ab\Vert w{u}_k}{\left(y_a+y_b\right)}^{\alpha }\right)\Delta (y_w,x)\hfill \\ & & +\sum _{w\in N_{T_0}\left(u_k\right)}{\left(y_w+x+2\right)}^{\alpha }(3^{\alpha }-2·4^{\alpha }).\hfill \end{array}$$

  (4)

Theorem 2.

Let $n\ge 5$ and $T\in {\mathcal{T}}_n$ such that $T\not\simeq P_n$. If $-1\le \alpha <0$, then,

$$m_2\left(T,{\mathcal{SC}}_{\alpha }\right)<m_2(P_n,{\mathcal{SC}}_{\alpha })=3^{2\alpha }+2^{2\alpha +1}{3}^{\alpha }(n-4)+2^{4\alpha -1}(n-5)(n-4).$$

Proof. 

Since $T\in {\mathcal{T}}_n$ with $T\not\simeq P_n$, then T has the form depicted in Figure 4. Let $T^{\prime }$ be a tree obtained from T by “Transformation C”. For $-1\le \alpha <0$, the expression $\Delta (y_w,x)={\left(y_w+x+2\right)}^{\alpha }-{\left(y_w+x+1\right)}^{\alpha }<0$ for any integer $x>0$. We have to consider the three cases in “Transformation C”.

For $k=2$ and $p=3$, by relation (2), $\Delta m_2<0$ if $-1\le \alpha <0$. The same occurs for $k=2$ and $p>3$. By relation (3), $\Delta m_2<0$ if $-1\le \alpha <0$.

For the case $k>2$ and $p>k+1$, by relation (4), we have to prove that

$$\begin{array}{ccc}\hfill 2{\left(x+4\right)}^{\alpha }-{\left(x+3\right)}^{\alpha }+3^{\alpha }-2·4^{\alpha }& <& 0,\hfill \\ \hfill 3^{\alpha }-2·4^{\alpha }& <& 0,\hfill \end{array}$$

for $-1\le \alpha <0$. Note that

$$3^{\alpha }-2·4^{\alpha }<2^{\alpha }-2^{2\alpha +1}=2^{\alpha }(1-2^{\alpha +1})<0.$$

Let $f\left(x\right)=2{\left(x+4\right)}^{\alpha }-{\left(x+3\right)}^{\alpha }+3^{\alpha }-2·4^{\alpha }$ defined for $x\ge 0$. The derivative

$${\displaystyle \frac{d}{dx}}f\left(x\right)=\alpha {\displaystyle \frac{2{\left(x+3\right)}^{1-\alpha }-{\left(x+4\right)}^{1-\alpha }}{{\left(x+3\right)}^{1-\alpha }{\left(x+4\right)}^{1-\alpha }}}=\alpha {\displaystyle \frac{{\left(2^{\frac{1}{1-\alpha }}\left(x+3\right)\right)}^{1-\alpha }-{\left(x+4\right)}^{1-\alpha }}{{\left(x+3\right)}^{1-\alpha }{\left(x+4\right)}^{1-\alpha }}}.$$

Note that for $-1\le \alpha <0$, $2^{{\displaystyle \frac{1}{1-\alpha }}}>\sqrt{2}>1$ and $3\left(2^{{\displaystyle \frac{1}{1-\alpha }}}\right)>3\sqrt{2}>4$. It follows that ${\displaystyle \frac{d}{dx}}f\left(x\right)<0$ for $x\ge 0$, which means that $f\left(x\right)$ is strictly decreasing for $x\ge 0$. Then, $f\left(x\right)\le f\left(0\right)=0.$ Consequently, in this case, $\Delta m_2<0$ if $-1\le \alpha <0$.

Applying this transformation repeatedly, we obtain a sequence of trees $T,T^{\prime },\dots ,T^{\ast }$ such that $m_2(T;\phi )<m_2(T^{\prime };\phi )<\cdots <m_2(T^{\ast };\phi )$ and $T^{\ast }\simeq P_n$. □

Using appropriate values of $\alpha$ in the previous theorem, we obtain the results for the sum-connectivity index $\mathcal{SC}$ and the harmonic index $\mathcal{H}$.

Corollary 2.

Let $n\ge 5$ and $T\in {\mathcal{T}}_n$ such that $T\not\simeq P_n$.

1. 

$m_2\left(T;\mathcal{SC}\right)<m_2(P_n,\mathcal{SC})={\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{\sqrt{3}}}(n-4)+{\displaystyle \frac{1}{8}}(n-5)(n-4)$.

2. 

$m_2\left(T;\mathcal{H}\right)<m_2(P_n,\mathcal{H})={\displaystyle \frac{4}{9}}+{\displaystyle \frac{2}{3}}(n-4)+{\displaystyle \frac{1}{8}}(n-5)(n-4)$.

In the following example, we show that if $\alpha$ is not in this interval, the result is not necessarily true.

Example 2.

For $\alpha =1$, we have ${\mathcal{SC}}_1=\mathcal{FZ}$, the First Zagreb index [29], defined by ${\phi }_{i,j}=i+j$. It is easy to see that

$$\begin{array}{ccc}\hfill m_2\left(S_{n-3,1},\mathcal{FZ}\right)& =& 3\left(n-3\right)\left(n-1\right)\hfill \\ \hfill m_2(P_n,\mathcal{FZ})& =& 9+24(n-4)+8(n-5)(n-4)\hfill \\ \hfill m_2(S_{⌈{\displaystyle \frac{n-2}{2}}⌉,⌊{\displaystyle \frac{n-2}{2}}⌋},\mathcal{FZ})& =& ⌈{\displaystyle \frac{n-2}{2}}⌉⌊{\displaystyle \frac{n-2}{2}}⌋\left(⌈{\displaystyle \frac{n-2}{2}}⌉+2\right)\left(⌊{\displaystyle \frac{n-2}{2}}⌋+2\right)\hfill \end{array}$$

and

$$m_2\left(S_{n-3,1},\mathcal{FZ}\right)<m_2(P_n,\mathcal{FZ})<m_2(S_{⌈{\displaystyle \frac{n-2}{2}}⌉,⌊{\displaystyle \frac{n-2}{2}}⌋},\mathcal{FZ})$$

for $n\ge 8$. Consequently, the path $P_n$ is not an extreme tree with respect to the number of 2-matchings of trees weighted with the First Zagreb index.

The same situation occurs with the Second Zagreb index $\mathcal{SZ}$ [29] defined by ${\phi }_{i,j}=ij$, as we can see in our next example.

Example 3.

It is easy to check that

$$\begin{array}{ccc}\hfill m_2\left(S_{n-3,1},\mathcal{SZ}\right)& =& 2\left(n-3\right)\left(n-2\right)\hfill \\ \hfill m_2(P_n,\mathcal{SZ})& =& 4+16(n-4)+8(n-5)(n-4)\hfill \\ \hfill m_2(S_{⌈{\displaystyle \frac{n-2}{2}}⌉,⌊{\displaystyle \frac{n-2}{2}}⌋},\mathcal{SZ})& =& ⌈{\displaystyle \frac{n-2}{2}}⌉⌊{\displaystyle \frac{n-2}{2}}⌋\left(⌈{\displaystyle \frac{n-2}{2}}⌉+1\right)\left(⌊{\displaystyle \frac{n-2}{2}}⌋+1\right)\hfill \end{array}$$

and

$$m_2\left(S_{n-3,1},\mathcal{SZ}\right)<m_2(P_n,\mathcal{SZ})<m_2(S_{⌈{\displaystyle \frac{n-2}{2}}⌉,⌊{\displaystyle \frac{n-2}{2}}⌋},\mathcal{SZ})$$

for $n\ge 8$. Hence, the path $P_n$ is not an extreme tree with respect to the number of 2-matchings of trees weighted with the Second Zagreb index.

Finally, we give an example of a VDB topological index where $S_{n-3,1}$ is not an extreme tree over ${\mathcal{T}}_n\setminus \left\{S_n\right\}$.

Example 4.

In the case of the Forgotten index $\mathcal{F}$ [30], defined by ${\phi }_{i,j}=i^2+j^2$, we have

$$\begin{array}{ccc}\hfill m_2\left(S_{n-3,1},\mathcal{F}\right)& =& 5\left(n-3\right)\left({\left(n-2\right)}^2+1\right)\hfill \\ \hfill m_2(P_n,\mathcal{F})& =& 25+80(n-4)+32(n-5)(n-4)\hfill \\ \hfill m_2(S_{⌈{\displaystyle \frac{n-2}{2}}⌉,⌊{\displaystyle \frac{n-2}{2}}⌋},\mathcal{F})& =& ⌈{\displaystyle \frac{n-2}{2}}⌉⌊{\displaystyle \frac{n-2}{2}}⌋\left({\left(⌈{\displaystyle \frac{n-2}{2}}⌉+1\right)}^2+1\right)\hfill \\ & & ·\left({\left(⌊{\displaystyle \frac{n-2}{2}}⌋+1\right)}^2+1\right)\hfill \end{array}$$

and

$$m_2(P_n,\mathcal{F})<m_2\left(S_{n-3,1},\mathcal{F}\right)<m_2(S_{⌈{\displaystyle \frac{n-2}{2}}⌉,⌊{\displaystyle \frac{n-2}{2}}⌋},\mathcal{F})$$

for $n\ge 6$. In other words, the double-star $S_{n-3,1}$ is not an extreme tree with respect to the number of 2-matchings of trees weighted with the Forgotten index.

3. Conclusions

The novel topological indices $m_k\left(G,\phi \right)$ of a graph G with respect to a VDB topological index $\phi$ described in [24] are natural extensions of VDB topological indices, which involve both the topological index $\phi$ and the k-matching numbers, perhaps two of the most important concepts of chemical graph theory. In this paper, we initiate the study of 2-matchings with respect to general sum-connectivity indices over the significant class of trees with a fixed number of vertices. The techniques used here are successful in showing that the extremal values of the function $m_2\left(-,{\mathcal{SC}}_{\alpha }\right):{\mathcal{T}}_n\setminus \left\{S_n\right\}⟶\mathbb{R}$ are attained in the path $P_n$ and the double-star $S_{n-3,1}$, when $\alpha$ is a real number in the interval $\left[-1,0\right).$ As we noted in Example 2, the result is no longer true when $\alpha \notin \left[-1,0\right)$. So, a first natural question is the following:

Problem 1.

Find the extremal values of $m_2\left(-,{\mathcal{SC}}_{\alpha }\right):{\mathcal{T}}_n\setminus \left\{S_n\right\}⟶\mathbb{R}$, when $\alpha \notin \left[-1,0\right).$

Other important types of vertex-degree-based topological indices are the general Randić indices ${\mathcal{R}}_{\alpha }$ [31,32], which are obtained from the symmetric functions ${\phi }_{i,j}={\left(ij\right)}^{\alpha },$ where $\alpha \in \mathbb{R}$. Using the same technique with some minor adaptations, we were able to show that the double-star $S_{n-3,1}$ attains the second minimal value of $m_2\left(-,{\mathcal{R}}_{\alpha }\right)$ when $\alpha \in \left[-1,0\right)$. However, we failed in showing that the path $P_n$ attains the maximal value. So, another problem is the following:

Problem 2.

Find the maximal value of $m_2\left(-,{\mathcal{R}}_{\alpha }\right):{\mathcal{T}}_n\setminus \left\{S_n\right\}⟶\mathbb{R}$, when $\alpha \in \left[-1,0\right).$

On the other hand, it would be of great interest to determine extremal values of $m_2\left(G,\phi \right)$ or, more generally, of $m_k\left(G,\phi \right)$, when G belongs to other interesting classes of graphs, for instance, chemical trees, hexagonal systems or unicyclic graphs, just to mention a few.