Algebraic and Geometric Methods for Construction of Topological Quantum Codes from Lattices

Abstract

Current work provides an algebraic and geometric technique for building topological quantum codes. From the lattice partition derived of quotient lattices ${\Lambda }^{\prime }/\Lambda$ of index m combined with geometric technique of the projections of vector basis ${\Lambda }^{\prime }$ over vector basis $\Lambda$, we reproduce surface codes found in the literature with parameter $\left[\right[2m,2,\left|a\right|+\left|b\right|\left]\right]$ for the case $\Lambda ={\mathbb{Z}}^2$ and $m=a^2+b^2$, where a and b are integers that are not null, simultaneously. We also obtain a new class of surface code with parameters $\left[\right[2m,2,\left|a\right|+\left|b\right|\left]\right]$ from the $\Lambda ={\mathcal{A}}_2$-lattice when m can be expressed as $m=a^2+ab+b^2$, where a and b are integer values. Finally, we will show how this technique can be extended to the construction of color codes with parameters $\left[\right[18m,4,6(|a|+|b|)\left]\right]$ by considering honeycomb lattices partition ${\mathcal{A}}_2/{\Lambda }^{\prime }$ of index $m=9(a^2+ab+b^2)$ where a and b are not null integers.

1. Introduction

Quantum coding theory made a significant advance with the discovery of CSS codes [1,2], leading to the development of the richer structure known as stabilizer quantum codes [3]. Since the superposition of states is essential for quantum information processing, interactions with the environment can easily destroy these superpositions, making quantum systems extremely fragile. Stabilizer codes, acting locally, can offer an alternative solution to this problem.

Kitaev [4] proposed a class of stabilizer codes associated with a square lattice, i.e., sublattices of ${\mathbb{Z}}^2$ with squares as fundamental regions. These codes depend on the topology of a surface and belong to the general class of topological quantum codes. Such codes are used to store quantum information in the non-local degrees of freedom of strongly correlated quantum systems with topological order. Because they are encoded non-locally, these quantum states are resistant to local noise that does not alter the system’s overall topology. This construction relies on an intrinsic physical mechanism that enables the topological system to self-correct local errors, which is remarkable because it does not require external detection and correction of quantum errors, unlike traditional non-topological codes. The system’s physical properties provide the mechanism for protecting the encoded quantum states. Interactions described by a Hamiltonian in certain lattices or on surfaces with non-trivial topology control this mechanism. The ground state of these Hamiltonians exhibits topological order, characterized by a robust type of ground state degeneracy that is resilient to local disturbances. This robustness is due to an energy gap in the Hamiltonian spectrum separating the ground state from excited states. Moreover, this degeneracy depends on the topology of the network where the strongly correlated system’s Hamiltonian is defined. Intuitively, topological order is a form of long-range entanglement in the ground and excited states of a quantum system. Topology may further enhance protection in ordinary-circuit quantum computing. For example, combining topological distribution and dynamical decoupling can improve error correction capabilities [5,6].

To build topological quantum codes, we can consider a tiling (tessellation) of the flat torus surface. The most significant classes of topological quantum codes are surface codes and color codes. We obtain surface codes on a flat torus by associating Pauli operators X and Z with the vertices and faces of the polygons that tessellate the torus. The encoded qubits correspond to the homologically non-trivial cycles on the torus surface.

Bombin and Martin-Delgado introduced the color codes [7]. They constructed these codes on three-valent tessellations with three-colorable faces, allowing for the coloring of each face using three different colors, resulting in distinct colors for neighboring faces. Each face of the tessellation has two Pauli operators attached, allowing for encoding twice as many qubits as surface codes, as proved in [8].

Sarvepalli and Raussendorf [9] proposed color codes with parameters $\left[[18.4^s,4,2^{s+2}]\right]$ on the flat torus obtained from honeycomb lattices, i.e., sublattices of ${\mathcal{A}}_2$, where the Voronoi regions are regular hexagons, which give rise to a three-valent tessellation. The qubits are attached to each vertex of the regular hexagons that tessellate the torus. In [10], the procedure for constructing color codes with parameters $\left[[18m^2,4,4m]\right]$ was expanded to any positive integer value of m, not only for the case where m is expressed as $m=2^s$, as obtained in [9].

Kitaev [4] proposed surface codes with parameters $\left[[2m^2,2,m]\right]$ derived from the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$ tessellation of the flat torus by $m^2$ squares (where each square represents a fundamental region of the ${\mathbb{Z}}^2$ lattice). In contrast to the proposal in [4], the authors in [7] introduced new classes of surface codes with parameters $\left[\right[m,2,d\left]\right]$. The way this structure is made is based on how the torus surface can be tiled with m polyominoes [11]. Each region is a match for a Lee sphere with radius r that is part of the ${\mathbb{Z}}^2$ lattice. The centers of these polyominoes are codewords of classic perfect codes $\mathcal{C}$ that have associated an algebraic structure of a cyclic additive group. This class of surface codes has been constructed only in cases where m can be simultaneously expressed in the forms $m=2r^2+2r+1$ and $m=a^2+b^2$ for some positive integer r and at least one pair of non-zero integers a and b.

In [12], the geometric method for making surface codes from ${\mathbb{Z}}^2$-lattices using polyominoes, which was first suggested in [7], was expanded to all situations where m can be written as $m=a^2+b^2$. Similar to the work in [7], the centers $\mathcal{C}$ of the regions that cover the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$ tessellation also have associated the algebraic structure of a cyclic group.

Recently, the study of surface codes derived from honeycomb lattices has also gained attention. These lattices were initially studied by Kitaev in [13]. The honeycomb lattice has a fundamaental role, since it is a topologically ordered system involving only two-body interactions [14], and it is also used to build new quantum memories [15].

The main goal of this work is to extend the procedure for building topological codes via square lattices ${\mathbb{Z}}^2$ to honeycomb lattices ${\mathcal{A}}_2$. If we consider the question about the construction of topological codes derived from lattices from an algebraic and geometric point of view, the following questions appear in this context:

• Is it possible to obtain surface codes with the same parameters $\left[[2m^2,2,m]\right]$ of Kitaev construction [4] from honeycomb lattices partition of index $m^2$?
• Is it possible to get surface codes from the tessellations of the torus that have regions congruent to Lee spheres with radius r and centers on the codewords of the classic perfect code $\mathcal{C}$, which come from the ${\mathcal{A}}_2$-lattices?
• Is it possible to get color codes from the tessellations of the torus that have regions congruent to Lee spheres with radius r and centers on the codewords of the classic perfect code $\mathcal{C}$, which come from the ${\mathcal{A}}_2$-lattices?

The goal is to develop fundamental tools from lattice theory to answer these questions. We can obtain the flat torus geometrically by identifying the opposite sides of the parallelogram. If the parallelogram is the fundamental region of a lattice $\Lambda$, we will denote the flat torus by $T={\mathbb{R}}^2/\Lambda$.

For instance, if we choose $\beta =\{(1,0),(0,1)\}$ as the lattice basis associated with ${\mathbb{Z}}^2$-lattice, we find a unit area square as the fundamental region associated with ${\mathbb{Z}}^2$-lattices. Because of this, considering this lattice basis gives us a parallelogram $\mathcal{P}$, and a Voronoi $\mathcal{V}$ partition that are the same up to a translation [10,16].

These partitions produce tessellations that are self-dual. Therefore, we can perform the analysis of the minimum distance of surface codes using either the parallelogram or Voronoi partition. From there, several works [4,12,17] have proposed families of surface codes derived from ${\mathbb{Z}}^2$ lattices.

If we choose $\beta =\{(1,0),({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})\}$ as the lattice basis for ${\mathcal{A}}_2$, on the other hand, we get a parallelogram whose sides are parallel to the vectors $e_1=(1,0)$ and $e_2=({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$. This is the fundamental region for the ${\mathcal{A}}_2$-lattices. As a result of choosing this lattice basis, we obtain parallelogram $\mathcal{P}$ and Voronoi $\mathcal{V}$ partitions that are not equal to a translation one each other. However, $\mathcal{P}$ and Voronoi $\mathcal{V}$ are congruent partitions on the flat torus [10,16]. As a result, in [10], new classes of surface codes and color codes were proposed, with parameters $\left[[3m^2,2,m]\right]$ and $\left[[18m^2,4,4m]\right]$, respectively.

We look at an algebraic and geometric alternative way to build topological codes on the flat torus that is related to the ${\mathbb{Z}}^2$ and ${\mathcal{A}}_2$ lattices in this work. For this purpose, we consider as the lattice basis $\gamma$ of sublattices $\Lambda$ of index $m=a^2+b^2$ in ${\mathbb{Z}}^2$:

$$\gamma =\{(a,b),(-b,a)\}.$$

(1)

We will get the same surface codes as in [4,7,12] by using the algebraic technique of lattice partition and the geometric technique of projecting a vector from the basis $\gamma$ of $\Lambda$, which is shown by Equation (1), onto the vectors $e_1=(1,0)$ and $e_2=(0,1)$ in ${\mathbb{Z}}^2$.

Classic perfect codes $\mathcal{C}$ are obtained from the ${\mathcal{A}}_2$-lattice. They are based on how the honeycomb lattice partition (${\mathbb{Z}}_m\times {\mathbb{Z}}_m$) can also be tiled by m regions, where each region is congruent to a Lee sphere of radius r. This class of classic perfect codes has been constructed only in cases where m can be simultaneously expressed in the forms $m=3r^2+3r+1$ and $m=a^2+ab+b^2$ for some positive integer r and at least one pair of non-zero integers a and b (for more details, see [18]). The centers of these m regions, which recover the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation, also form a cyclic code $\mathcal{C}$.

We consider the lattice basis $\gamma$ of sublattices $\Lambda$ of index $m=a^2+ab+b^2$ in ${\mathcal{A}}_2$:

$$\gamma =\{(a,b),(-b,a+b)\}.$$

(2)

Thus, generalizing these ideas, using lattice partition concepts and the geometric technique of projecting vectors $u=(a,b)$ and $v=(-b,a+b)$ onto vectors $(1,0)$ and $({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$, respectively, we obtain new classes of surface codes with parameters $\left[[2m^2,2,m]\right]$ and $\left[\right[2m,2,\left|a\right|+\left|b\right|\left]\right]$ on the flat torus $T={\mathbb{R}}^2/\Lambda$, where $\{u,v\}$ is the lattice basis associated with the sublattice $\Lambda$ of index $m=a^2+ab+b^2$ in ${\mathcal{A}}_2$. This answers questions (1) and (2).

Finally, we consider sublattices ${\Lambda }^{″}$ with basis ${\beta }^{″}=\{3a,3b),(3a,3a-3b)\}$ and index $9m$ on honeycomb lattices ${\mathcal{A}}_2$, where $m=1$ or $m=a^2+ab+b^2$ for at least one pair of non-zero integers a and b. We prove that ${\mathcal{A}}_2$ induces a ${\mathbb{Z}}_{3m}\times {\mathbb{Z}}_{3m}$-tessellation on each flat torus T, which is tiled by $9m$ regular hexagons. Because of this algebraic and geometric description of $T={\mathbb{R}}^2/{\Lambda }^{″}$, we get a more general process to obtain color codes with parameters ${[[18m,4,6(|a|}^2+{\left|b\right|}^2)]]$, for $m=9(a^2+ab+b^2)$. This answers question (3).

2. Lattices in ${\mathbb{R}}^{\mathit{n}}$

A lattice is a subset of ${\mathbb{R}}^n$ isomorphic to the additive group ${\mathbb{Z}}^n$. We can analyze subgroups (sublattices) and partitions (coset decompositions) induced by subgroups thanks to this algebraic structure. The Euclidean metric and volume notion of the space in which the underlying lattice is embedded are passed down to it.

Formally speaking, a lattice $\Lambda$ is a set of points $\Lambda =\{x\in {\mathbb{R}}^n:x={\sum }_{i=1}^m{\lambda }_i{u}_i\mathrm{and}{\lambda }_i\in \mathbb{Z}\}$, where $\{u_1,u_2,\dots ,u_m\}$ is a set of linearly independent vectors in ${\mathbb{R}}^n$. This set of points is known as the lattice basis. We define $\Lambda$ as a lattice in ${\mathbb{R}}^n$ with rank m. The lattice is said to have complete rank in ${\mathbb{R}}^n$ if $m=n$. We solely take into account full-rank lattices in our current work.

If $\Lambda$ is a n-dimensional lattice with basis $\{u_1,u_2,\dots ,u_n\}$, its generator matrix is given by

$$M=\left(\begin{array}{cccc}{u}_{11}& u_{12}& \cdots & u_{1n}\\ u_{21}& u_{22}& \cdots & u_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ u_{n1}& u_{n2}& \cdots & u_{nn}\end{array}\right),$$

where $u_i=(u_{i1},u_{i2},\dots ,u_{in})$, for $i=1,2,\dots ,n$. If its generator matrix has full rank, the lattice has full rank. The matrix $G=M{M}^T$ is called the Gram matrix of the lattice $\Lambda$, where $M^T$ is the transpose of M. An equivalent definition is $\Lambda =\{x=\lambda M|\lambda \in {\mathbb{Z}}^n\}$. The determinant of the lattice $\Lambda$ is defined by $Det(\Lambda )=Det(G)$.

What follows are important examples of full rank lattices in ${\mathbb{R}}^2$.

Example 1.

Let $\beta =\{e_1,e_2\}$ be a basis in ${\mathbb{R}}^2$.

1. 

Considering $e_1=(1,0)$ and $e_2=(0,1)$, we get the lattice ${\mathbb{Z}}^2$, and the generator matrix is

$$M=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right).$$

2. 

Considering $e_1=(1,0)$ and $e_2=({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$, we get the honeycomb lattice ${\mathcal{A}}_2$, and the generator matrix is given by

$$M=\left(\begin{array}{cc}1& 0\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{\sqrt{3}}{2}}\end{array}\right).$$

Given a lattice $\Lambda$, a subset ${\Lambda }^{\prime }\subset \Lambda$ is a sublattice if ${\Lambda }^{\prime }$ itself is a lattice, i.e., ${\Lambda }^{\prime }$ is an additive subgroup of $\Lambda$. The sublattice ${\Lambda }^{\prime }$ can also be characterized as

$${\Lambda }^{\prime }=\{x=\lambda BM|\lambda \in {\mathbb{Z}}^n\},$$

(3)

where M is the generator matrix associated to the lattice $\Lambda$, and B is a square matrix of integers.

Example 2.

Consider the lattice ${\mathbb{Z}}^2$ with basis $\beta =\{e_1,e_2\}$ and generating matrix M of item (1) in the Example 1

1. 

We get a family of sublattices ${\Lambda }^{\prime }=m{\mathbb{Z}}^2$ in ${\mathbb{Z}}^2$, generated by the integer basis ${\beta }^{\prime }=\{m{u}_1,m{u}_2\}$ and generating matrix $M^{\prime }=BM$, where

$$B=\left(\begin{array}{cc}m& 0\\ 0& m\end{array}\right).$$

2. 

Give a positive integer m that can be expressed as $m=a^2+b^2$, where a and b are integer values. We can also obtain a family of sublattices ${\Lambda }^{″}$ of index m in ${\mathbb{Z}}^2$ generated by the integer basis $\alpha =\{u,v\}$, where $u=(a,b)$ and $v=(-b,a)$. The generating matrix is given by $M^{″}=B^{\prime }M$, with,

$$B^{\prime }=\left(\begin{array}{cc}a& b\\ -b& a\end{array}\right).$$

Example 3.

Consider the honeycomb lattice ${\mathcal{A}}_2$ with basis $\beta =\{e_1,e_2\}$ and generating matrix M from item (2) of Example 1.

1. 

For the integer basis ${\beta }^{\prime }=\{m{u}_1,m{u}_2\}$ and generating matrix $M^{\prime }=BM$, we obtain a family of sublattices $\Lambda =m{\mathcal{A}}_2$ of index $m^2$ in ${\mathcal{A}}_2$,

$$B=\left(\begin{array}{cc}m& 0\\ 0& m\end{array}\right).$$

2. 

Give a positive integer m that can be expressed as $m=a^2+ab+b^2$, where a and b are integer values. We can also obtain a family of sublattices ${\Lambda }^{″}$ of index m in ${\mathcal{A}}_2$ generated by the integer basis $\gamma =\{u,v\}$, where $u=(a,b)$ and $v=(-b,a+b)$. The generating matrix is given by $M^{″}=B^{\prime }M$, with,

$$B^{\prime }=\left(\begin{array}{cc}a& b\\ -b& a+b\end{array}\right).$$

3. 

Give a positive integer m that can be expressed as $m=9(a^2+ab+b^2)$, where a and b are integer values. We can also obtain a family of sublattices ${\Lambda }^{″}$ of index m in ${\mathcal{A}}_2$ generated by the integer basis ${\beta }^{″}=\{u,v\}$, where $u=(3a,3b)$ and $v=(-3b,3(a+b))$. The generating matrix is given by $M^{‴}=BM$, with

$$B=\left(\begin{array}{cc}3a& 3b\\ -3b& 3(a+b)\end{array}\right).$$

2.1. Quotient Groups and Quotient Lattices

Let $\Lambda$ be an n-dimensional lattice with basis $\{u_1,\dots ,u_n\}$. The fundamental parallelepiped of $\Lambda$ is made up of all the points in ${\mathbb{R}}^n$ that are linear combinations of the basis vectors with coefficients that are between 0 and 1.

$$P=\{x=\sum _{i=1}^n{\alpha }_i{u}_i;0<{\alpha }_1,\dots ,{\alpha }_n<1\}.$$

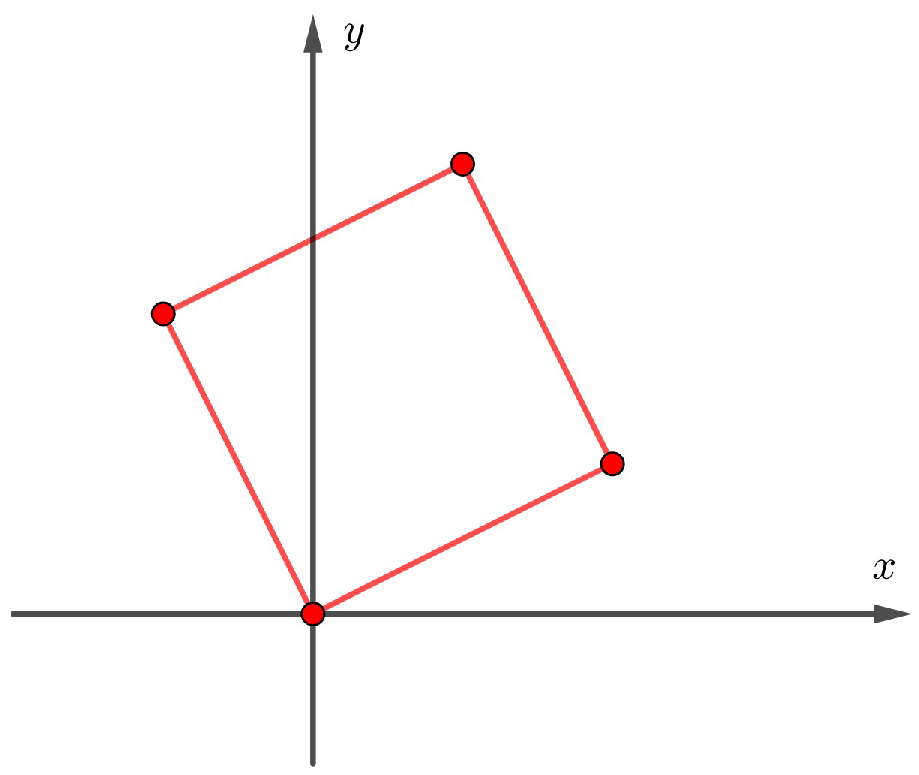
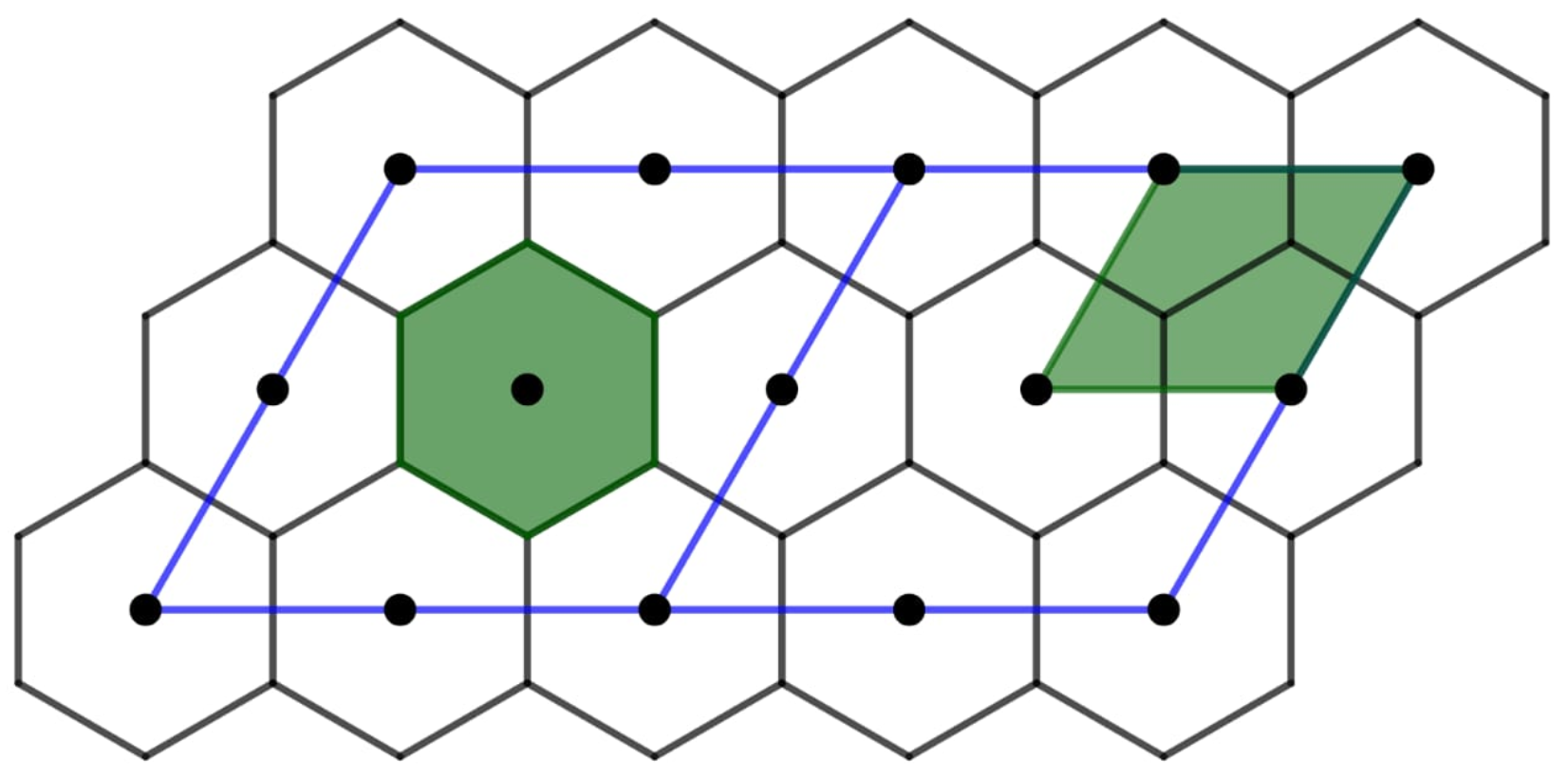
The Figure 1 and Figure 2 illustrate the fundamental regions of the sublattices ${\Lambda }^{″}$ of index 5 and 7 in ${\mathbb{Z}}^2$ and ${\mathcal{A}}_2$, respectively.

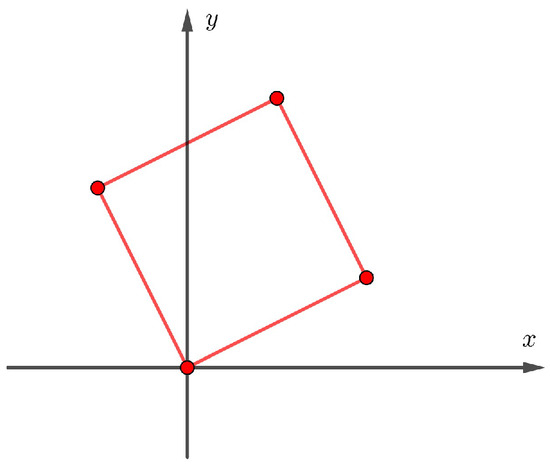
Figure 1. Fundamental region of the sublattice ${\Lambda }^{\prime }$ with index 5 in ${\mathbb{Z}}^2$ is generated by the basis $\gamma =\{u,v\}$, where $u=(2,1)$ and $v=(-1,2)$.

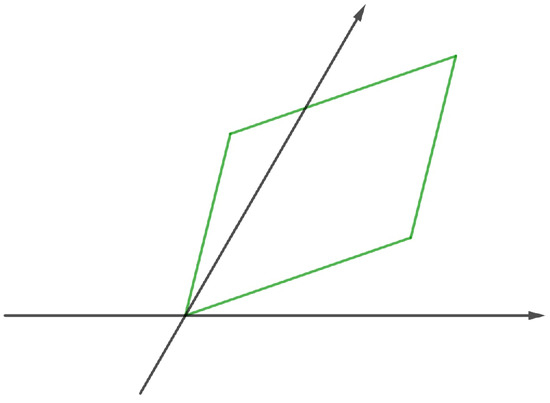
Figure 2. Fundamental region of the sublattice ${\Lambda }^{\prime }$ with index 7 in ${\mathcal{A}}_2$ is generated by the basis $\gamma =\{u,v\}$, where $u=(2,1)$ and $v=(-1,3)$.

Let ${\Lambda }^{\prime }$ be a sublattice of $\Lambda$, and suppose that the generator matrices are M and $M^{\prime }=BM$, respectively. We can prove that

$${\displaystyle |\Lambda /{\Lambda }^{\prime }|=\frac{volume(P^{\prime })}{volume(P)}=\left|det(B)\right|,}$$

(4)

where $volume(P^{\prime })$ and $volume(P)$ are the volume of the fundamental parallelepiped $P^{\prime }$, which is associated to the sublattice ${\Lambda }^{\prime }$, and the volume of the parallelepiped P, associated to the lattice $\Lambda$, respectively. The Equation (4) gives that the fundamental region of the lattice $\Lambda$ induces a partition of the fundamental region of the ${\Lambda }^{\prime }$ sublattice. The meaning is that the fundamental region of ${\Lambda }^{\prime }$ can be covered by l copies of the fundamental region of $\Lambda$, where l is the index of the sublattice ${\Lambda }^{\prime }$ in $\Lambda$, and is given by Equation (5).

The sublattice ${\Lambda }^{\prime }$ induces a partition of $\Lambda$ into cosets, and they have a structure of an additive group, denoted by $\Lambda /{\Lambda }^{\prime }$, and the cardinality is given by the Equation (5):

$$l=|\Lambda /{\Lambda }^{\prime }|=|det(B)|.$$

(5)

We also say that ${\Lambda }^{\prime }$ has index l in $\Lambda$.

Example 4.

Let $\Lambda ={\mathbb{Z}}^2$ be the lattice given by item (1) of Example 1.

1. 

The family of sublattices ${\Lambda }^{\prime }=m{\mathbb{Z}}^2$ in ${\mathbb{Z}}^2$ given by the item (1) of Example 2 has index $l=det(B)=m^2$, i.e., the quotient group $\Lambda /{\Lambda }^{\prime }$ has cardinality $m^2$.

2. 

The family of sublattices ${\Lambda }^{\prime }$ in ${\mathbb{Z}}^2$ given by the item (2) of Example 2 has index $m=det(B)=a^2+b^2$, i.e., the quotient group $\Lambda /{\Lambda }^{\prime }$ has cardinality $m=a^2+b^2$.

Example 5.

Let Λ be a honeycomb sublattice of ${\mathcal{A}}_2$ of Example 2.

1. 

The family of sublattices ${\Lambda }^{\prime }=m{\mathcal{A}}_2$ in ${\mathcal{A}}_2$ given by the item (1) of Example 3 has index $det(B)=m^2$, i.e., the quotient group $\Lambda /{\Lambda }^{\prime }$ has cardinality $m^2$.

2. 

The family of sublattices ${\Lambda }^{\prime }$ in ${\mathcal{A}}_2$ given by the item (2) of Example 3 has index $det(B)=m=a^2+ab+b^2$, i.e., the quotient group $\Lambda /{\Lambda }^{\prime }$ has cardinality $m=a^2+ab+b^2.$

3. 

The family of sublattices ${\Lambda }^{\prime }$ in ${\mathcal{A}}_2$ given by the item (3) of Example 3 has index $det(B)=9m$, i.e., the quotient group $\Lambda /{\Lambda }^{\prime }$ has cardinality $9m$, where $m=1$ or $m=a^2+ab+b^2$ for some $0\ne a,b\in \mathbb{Z}$

Remark 1.

1. 

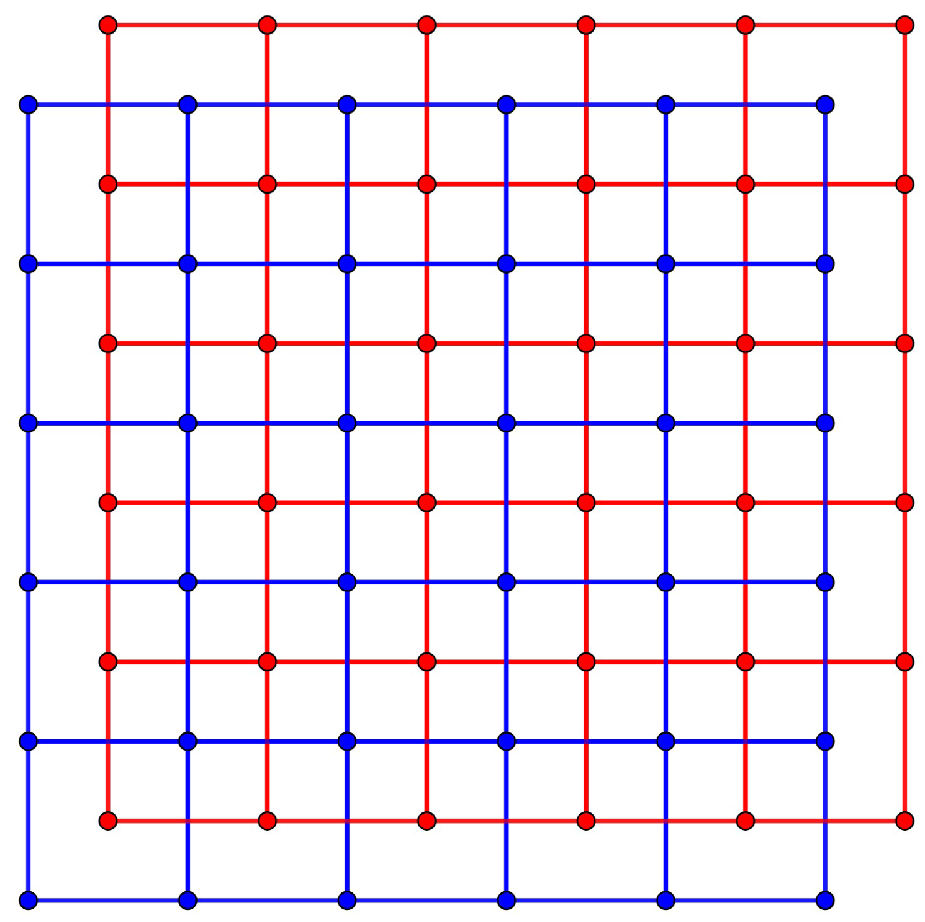
If you translate the lattice Λ of Example 2 by the vector $({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})$, you get a set of points $\tau (\Lambda )$ in ${\mathbb{R}}^2$ that have the same shape and arrangement as Λ. The action of translation Λ can result in $0\notin \tau (\Lambda )$. Therefore, $\tau (\Lambda )$ does not have a lattice structure (see Figure 3).

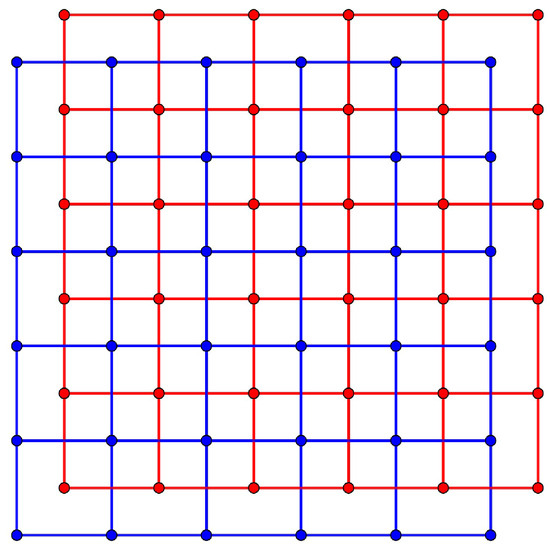Figure 3. In blue, we have the fundamental region $\mathcal{P}$ of the lattice $6{\mathbb{Z}}^2$ covered by 36 squares, and in red, the square of the fundamental region $\mathcal{P}$ translated by the vector $(1/2,1/2)$ covered by 36 squares.

2. 

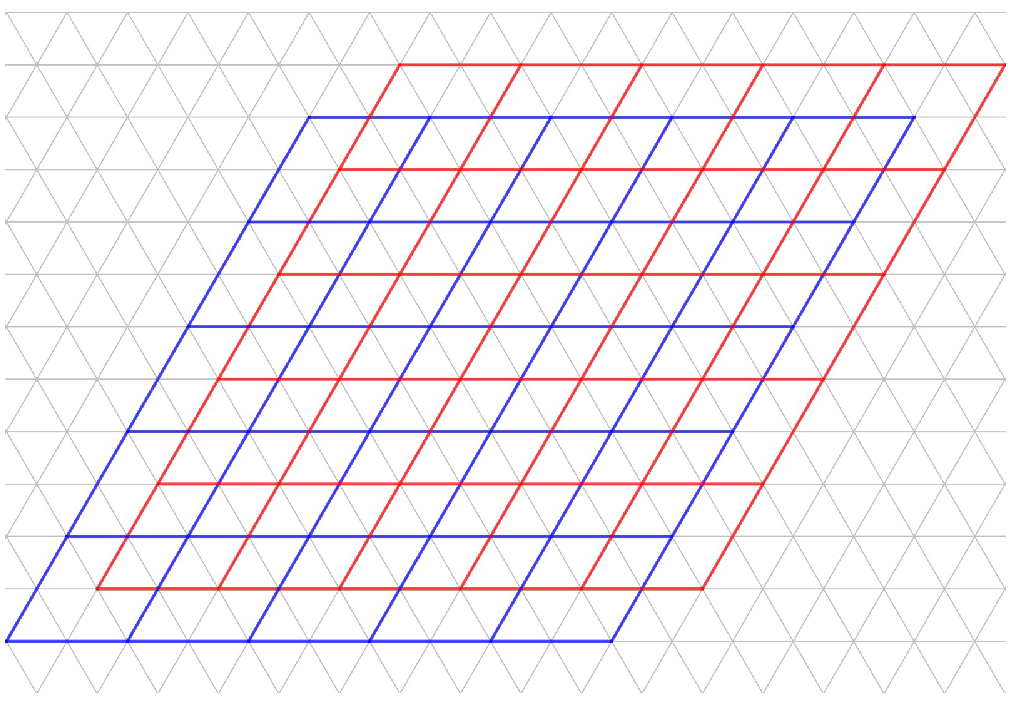
This set of points $\tau (\Lambda )$ in ${\mathbb{R}}^2$ has the same shape and arrangement as Λ. It was made by translating Λ of Example 3 by the vector $({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$. The action of translation Λ can result in $0\notin \tau (\Lambda )$ (see Figure 4). Therefore, $\tau (\Lambda )$ does not have a lattice structure. However, it will be very useful in this work to construct new classes of surface codes from the honeycomb lattice.

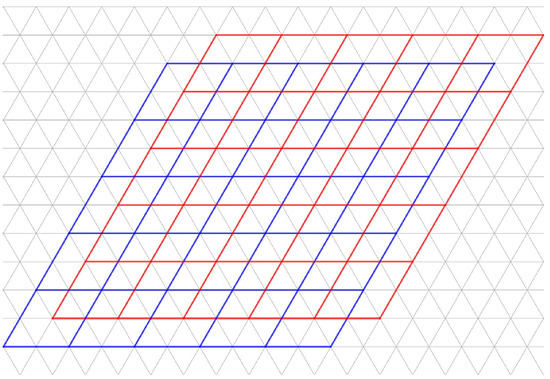Figure 4. In blue, we have the fundamental region $\mathcal{P}$ of the lattice $6{\mathcal{A}}_2$ covered by 36 parallelograms, and in red, the fundamental region $\mathcal{P}$ of the lattice $6{\mathcal{A}}_2$ translated by the vector $(1/2,\sqrt{3}/4)$ covered by 36 parallelograms.

2.2. Lattice Partitions

Parallelepiped partitions and Voronoi partitions derived from lattices $\Lambda$ in Euclidean spaces are of importance to us in our work.

Definition 1.

For a lattice Λ, a fundamental region $P_0$ is a bounded set such that it produces a partition $\mathcal{P}=\{P_{\lambda }:\lambda \in \Lambda \}$ from ${\mathbb{R}}^n$ when translated by points of the lattice Λ. Consequently,

1. 

each region $P_{\lambda }$ is obtained by translating $P_0$ by a lattice point λ, that is,

$$P_{\lambda }=P_0+\lambda =\{x:(x-\lambda )\in P_0\}.$$

2. 

the regions do not intersect, that is, $P_{\lambda }^{\circ }\cap P_{{\lambda }^{\prime }}^{\circ }\ne \varnothing$ for all $\lambda \ne {\lambda }^{\prime }\in \Lambda$, where $A^{\circ }$ denotes the interior of a set $A\subset {\mathbb{R}}^n$.

3. 

the union of all regions covers the whole space ${\mathbb{R}}^n$, i.e, ${\cup }_{\lambda \in \Lambda }{P}_{\lambda }={\mathbb{R}}^n$.

All regions belonging to the parallelogram partition $P_{\lambda }$ are congruent, which is an important geometric property.

From Definition 1, each point $x\in {\mathbb{R}}^n$ can be written uniquely as

$$x=\lambda +x_{e}where\lambda \in \Lambda and{x}_e\in P_0.$$

(6)

An approximation $x_e$ of $x\in {\mathbb{R}}^n$ satisfying (6) is found for each point $\lambda \in \Lambda$. The points $x_e\in P_0$ that satisfy (6) can be seen as the error in the approximation made by a lattice point $\lambda \in \Lambda$ to each point $x\in {\mathbb{R}}^n$. This approximation is indicated by $\lambda =Q_{\Lambda }(x)$. We refer to the quantization of x as $Q_{\Lambda }(x)$.

Using the nearest-neighbor rule, the Voronoi partition is another important partition of the space. The Euclidean norm on ${\mathbb{R}}^n$ is denoted by $\parallel .\parallel$. The distance of a point x in ${\mathbb{R}}^n$ from $\Lambda$ is given by

$$\parallel x-\Lambda \parallel =\underset{\lambda \in \Lambda }{min}\parallel x-\lambda \parallel .$$

The nearest-neighbor quantizer $Q_{\Lambda }^N$ maps x to its closest lattice point:

$$Q_{\Lambda }^N(x)=arg\underset{\lambda \in \Lambda }{min}\parallel x-\lambda \parallel .$$

Then, we define:

Definition 2.

The set ${\mathcal{V}}_{\lambda }=\{x\in {\mathbb{R}}^n:Q_{\Lambda }^N(x)=\lambda \}$ of all points that are quantized to λ, is the Voronoi region associated with a n-dimensional lattice point $\lambda \in \Lambda$.

According to the definition of $Q_{\Lambda }^N$, the resulting Voronoi regions are congruent. For each lattice $\Lambda$, let ${\mathcal{V}}_0$ be the Voronoi region associated with the lattice point $0\in \Lambda$. If we translate ${\mathcal{V}}_0$ by lattice points $\lambda \in \Lambda$, we obtain a partition $\mathcal{V}=\{{\mathcal{V}}_{\lambda }:\lambda \in \Lambda \}$ of ${\mathbb{R}}^n$. The union of all these regions give a covering of the whole space ${\mathbb{R}}^n$, where ${\mathcal{V}}_{\lambda }={\mathcal{V}}_0+\lambda =\{x\in {\mathbb{R}}^n:(x-\lambda )\in {\mathcal{V}}_0\}$. All Voroni regions belonging to the Voronoi partition $\{{\mathcal{V}}_{\lambda },\lambda \in \Lambda \}$ are congruent.

In ${\mathbb{R}}^2$, parallelepipeds are given by parallelograms, which is the case of interest in this work. Therefore, we will refer to them as partitions of parallelograms.

Proposition 1

([10,16]). The parallelogram partition and Voronoi partition of the honeycomb lattice Λ are equivalent.

3. Tessellations of the Flat Torus

For this work, we are interested in the Euclidean space ${\mathbb{R}}^2$. Here, we provide definitions and general results for the flat torus.

Definition 3.

Let G be a discrete set of isometries acting on a metric space X. If a closed set $F\subset X$, with a non-empty interior $F^{\circ }$, satisfies the following conditions, it is a fundamental region for G:

1. 

${\cup }_{T\in G}T(F)=X$;

2. 

$F^{\circ }\cap {T(F)}^{\circ }=\varnothing$, for every, $T\in G-\left\{Id\right\}$. The family $\{T(F):T\in G\}$ is called a tessellation of X.

A covering of X by copies of F under the action of a group of isometries G is called a G-tessellation, or tessellation of X associated to G.

In each of these cases, the region F in Definition 3 can be seen as the closure of the fundamental regions of the two partitions that are examined in Examples 2–4 with respect to the Euclidean norm.

The parallelogram partitions $\mathcal{P}$ of the sublattice $\Lambda$ with index $m^2$ in ${\mathbb{Z}}^2$ are also shown in Example 2. These are shown by squares, with lattice points at their points.

We can get the parallelogram partitioning $\mathcal{P}$ by translating the sublattice $\Lambda$ of index $m^2$ in ${\mathbb{Z}}^2$, as shown in Example 3, by a vector with coordinates $({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})$ in ${\mathbb{R}}^2$. This gives us another parallelogram partitioning ${\mathcal{P}}^{\prime }$ by $m^2$ square. The tessellations obtained from the parallelogram partitioning $\mathcal{P}$ and ${\mathcal{P}}^{\prime }$ are dual tessellation (illustrated by Figure 3).

The parallelogram partitioning $\mathcal{P}$ of the sublattice $\Lambda$ of index $m^2$ in ${\mathcal{A}}_2$, in Example 3, is given by parallelograms, where the vertices of the parallelograms are also lattice points.

The parallelogram partitioning $\mathcal{P}$ is linked to the sublattice $\Lambda$ of index $m^2$ in ${\mathcal{A}}_2$ in item (1) of Example 3 by a vector of coordinates $({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{4}})$ in ${\mathbb{R}}^2$, and we get ${\mathcal{P}}^{\prime }$ by $m^2$ parallelograms. The tessellations obtained from the parallelogram partitioning $\mathcal{P}$ and ${\mathcal{P}}^{\prime }$ are dual tessellations (illustrated by Figure 4).

The construction of the topological codes that we will propose on the flat torus essentially depends on covering a parallelogram $P^{\prime }$ with (smaller) congruent parallelograms. The parallelogram $P^{\prime }$ to be considered will be the fundamental region of a sublattice $\Lambda ={\mathbb{Z}}^2$ or ${\mathcal{A}}_2$. The smaller parallelogram $\mathcal{P}$ to be considered will be the fundamental region of a sublattice ${\Lambda }^{\prime }$ of $\Lambda$, in both cases of $\Lambda ={\mathbb{Z}}^2$ and $\Lambda ={\mathcal{A}}_2$.

The geometric arrangement of a fundamental region of a lattice depends on the choice of the lattice basis, which is not unique. To distinguish which basis was chosen to generate the lattice $\Lambda$, we will use the notation ${\Lambda }_{\gamma }$ when we fix $\gamma$ as the chosen basis.

Remark 2.

Different lattice basis of the same lattices in ${\mathbb{R}}^2$ reproduce different parallelogram partitions in ${\mathbb{R}}^2$.

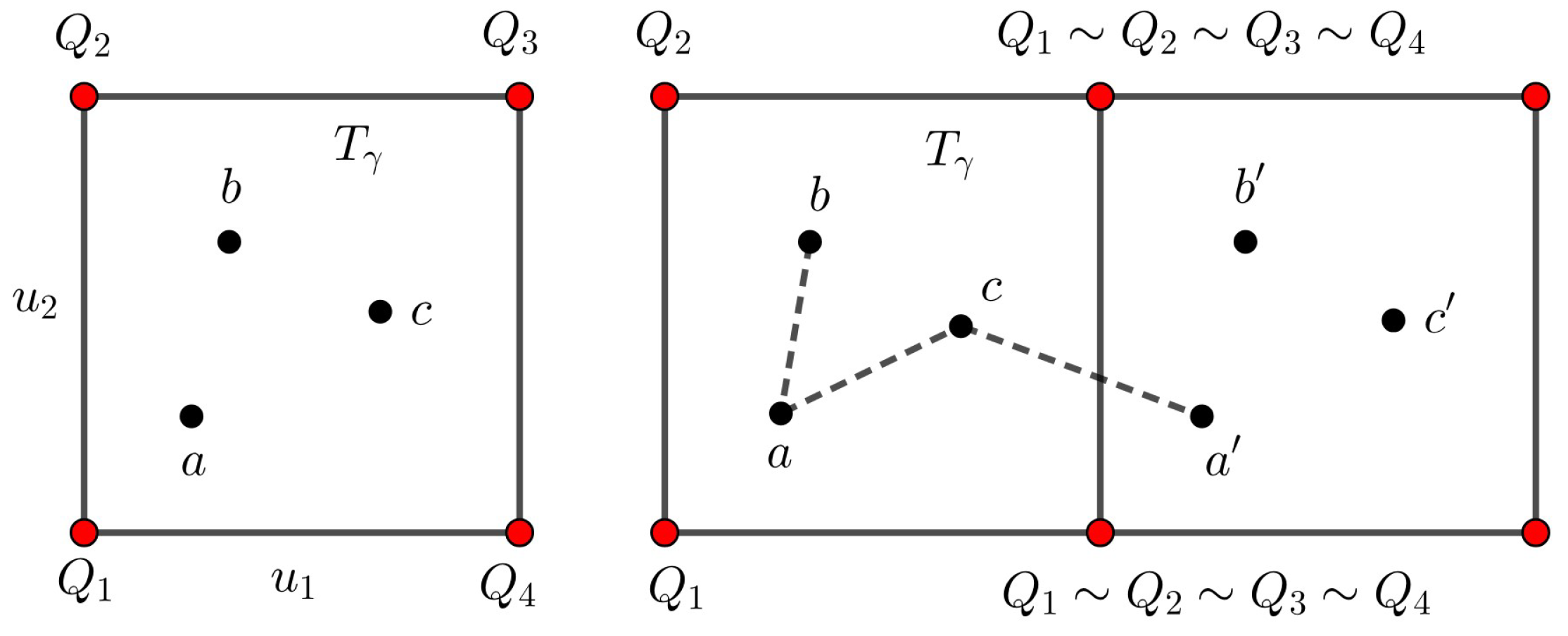
Given an n-dimensional lattice ${\Lambda }_{\beta }$ and an n-dimensional sublattice ${\Lambda }_{\gamma }$ of ${\Lambda }_{\beta }$ and a basis $\beta =\{u_1,\dots ,u_n\}$ of that lattice, the flat torus $T_{\gamma }$ is defined as the quotient space ${\mathbb{R}}^n/{\Lambda }_{\gamma }$. In the quotient, we define the map $\mu :{\mathbb{R}}^n\to {\mathbb{R}}^n$ defined as ${\mu }_{\gamma }(x)=xmod\Lambda =x-{\sum }_{i=1}^n\left[x_i\right]u_i$, where $x={\sum }_{i=1}^n{x}_i{u}_i$ and $\left[x_i\right]$ denotes the greatest integer less than or equal to x. Therefore, $x,y\in {\mathbb{R}}^n$ belongs to the same coset in $T_{\gamma }$ if and only if ${\mu }_{\gamma }(x)={\mu }_{\gamma }(y)$, i.e., $x-y={\sum }_{i=1}^n{m}_i{u}_i,m_i\in \mathbb{Z}$. The flat torus $T_{\gamma }$ can be seen as the quotient of the Euclidean space ${\mathbb{R}}^n$ by a group of translations.

For a torus $T_{\gamma }$ generated by the basis $\gamma$, we define the quotient map $\overline{{\mu }_{\gamma }}:{\mathbb{R}}^n\to T_{\gamma }$ using the fundamental region P in ${\mathbb{R}}^n$, given by the basis $\gamma$.

The Euclidean distance d in ${\mathbb{R}}^n$ induces a distance $d_{\gamma }$ on the flat torus $T_{\gamma }$. The distance measure on the flat torus between two cosets $\overline{a}$ and $\overline{b}\in {\Lambda }_{\beta }/{\Lambda }_{\gamma }$ with $a,b\in {\mathbb{R}}^n$, is (see Figure 5)

$$d_{\gamma }(\overline{a},\overline{b})=min\{d(z,y)=\parallel z-y\parallel ;z\in \overline{a},y\in \overline{b}\}.$$

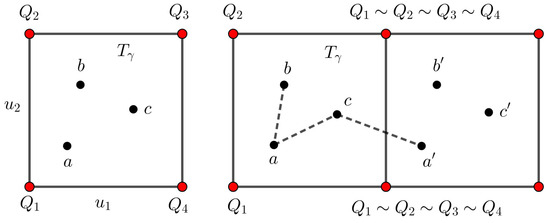
Figure 5. The distance $d_{\gamma }$ on the flat torus is viewed as the Euclidean distance d in ${\mathbb{R}}^2;d_{\gamma }(\overline{a},\overline{b})=d(a,b)$ but $d_{\gamma }(\overline{a^{\prime }},\overline{c})=d(a^{\prime },c)$.

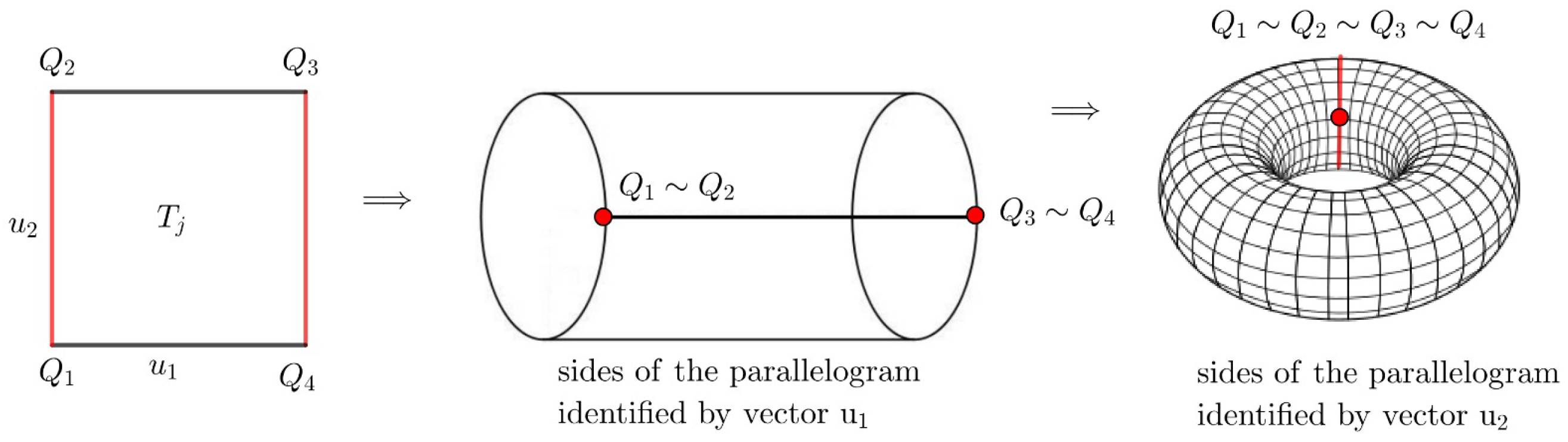
For ${\mathbb{R}}^2$, the flat torus $T_{\gamma }$ can be constructed from a parallelogram P, a fundamental region of the l parallelogram partition associated to ${\Lambda }_{\gamma }$, sublattice either from $\Lambda ={\mathbb{Z}}^2$ or from $\Lambda ={\mathcal{A}}_2$ generated by the basis $\gamma =\{u,v\}$, since we identify the opposite sides (see Figure 6).

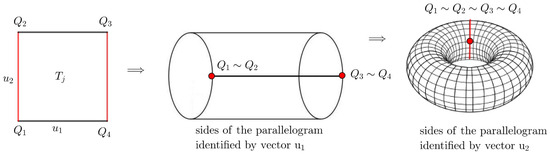
Figure 6. Edge identification to obtain the torus (sides of the parallelogram identified by vector $u_1$ and $u_2$).

With some conditions, the next result from [18] shows that it is possible to get tessellations on the flat torus $T_{\gamma }$ generated by the tessellation associated with the lattice ${\Lambda }_{\beta }$ in ${\mathbb{R}}^n$.

Proposition 2.

Let the bases of the lattices ${\Lambda }_{\gamma }$ and ${\Lambda }_{\beta }$ be $\gamma =\{u_1,\dots ,u_n\}$ and $\beta =\{v_1,\dots ,v_n\}$, respectively. Let ${\Lambda }_{\beta }$ be the tessellation of ${\mathbb{R}}^n$, with the polytope P supported on γ serving as its fundamental region. If ${\Lambda }_{\gamma }$ is a sublattice of ${\Lambda }_{\beta }$, and $\overline{{\mu }_{\gamma }}$ is the quotient map on the flat torus, we have that ${\Lambda }_{\beta }$ induces a G-tessellation on the flat torus $T_{\gamma }={\mathbb{R}}^n/{\Lambda }_{\gamma }$ with fundamental region $\overline{{\mu }_{\gamma }}(P)$, where $G={\Lambda }_{\beta }/{\Lambda }_{\gamma }$.

We will use Proposition 3 to find families of ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellations that come from $\Lambda ={\mathbb{Z}}^2$-lattices based on Proposition 2. On each flat torus $T_{\gamma }$, we also obtain families of ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellations.

Proposition 3

([10]). Assume that ${\Lambda }_{\beta }$ is any lattice of ${\mathbb{R}}^n$ with basis $\beta =\{u_1,u_2,\dots ,u_n\}$. Let ${\Lambda }_{\gamma }$ be a sublattice of index $m^n$$(m>1$) with ${\Lambda }_{\gamma }$ having basis $\gamma =\{m{u}_1,m{u}_2,\dots ,m{u}_n\}$. Thus, in each flat torus $T_{\gamma }\simeq {\mathbb{R}}^n/{\Lambda }^{\prime }$, the lattice ${\Lambda }_{\beta }$ generates a ${\mathbb{Z}}_{m^n}$-tessellation, where we have ${\Lambda }_{\beta }/{\Lambda }_{\gamma }\simeq {\mathbb{Z}}_{m^n}$ to the quotient lattice.

Corollary 1

([10]). By Proposition 3, we have that:

1. 

For the family of sublattices with basis γ and index $m^2$ in the lattice ${\Lambda }_{\beta }={\mathbb{Z}}^2$, as illustrated in item (1) of the Example 3, ${\Lambda }_{\beta }={\mathbb{Z}}^2$ induces a ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation in each flat torus $T_{\gamma }\simeq {\mathbb{R}}^2/{\Lambda }_{\gamma }$.

2. 

As stated in item (1) of Example 4, the lattice ${\Lambda }_{\beta }={\mathcal{A}}_2$ induces a ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation in each flat torus $T_{\gamma }\simeq {\mathbb{R}}^2/{\Lambda }_{\gamma }$ of the sublattice family with basis γ and index $m^2$ in the lattice ${\mathcal{A}}_2$.

Corollary 2.

By Proposition 3, we have that:

1. 

As described in item (1) of the Example 3, the lattice ${\Lambda }_{\beta }={\mathbb{Z}}^2$ induces a ${\mathbb{Z}}_m$-tessellation in each flat torus $T_{\gamma }\simeq {\mathbb{R}}^2/{\Lambda }_{\gamma }$ of sublattice family with basis γ and index m in the lattice ${\Lambda }_{\beta }={\mathbb{Z}}^2$.

2. 

As described in item (2) of the Example 3, the lattice ${\Lambda }_{\beta }={\mathcal{A}}_2$ induces a ${\mathbb{Z}}_m$-tessellation in each flat torus $T_{\gamma }\simeq {\mathbb{R}}^2/{\Lambda }_{\gamma }$ of sublattice family with basis γ and index m in the lattice ${\Lambda }_{\beta }={\mathcal{A}}_2$.

3. 

As described in item (3) of the Example 3, the lattice ${\Lambda }_{\beta }={\mathcal{A}}_2$ induces a ${\mathbb{Z}}_{9m}$-tessellation in each flat torus $T_{\gamma }\simeq {\mathbb{R}}^2/{\Lambda }_{\gamma }$ of sublattice family with basis γ and index $9m$ in the lattice ${\Lambda }_{\beta }={\mathcal{A}}_2$, where $m=1$ or $m=a^2+ab+b^2$ for some $0\ne a,b\in \mathbb{Z}$.

4. Surface Codes Derived from ${\mathbb{Z}}^{\mathbf{2}}$ and ${\mathcal{A}}_{\mathbf{2}}$ Lattices

Kitaev [4] proposed surface codes obtained from ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellations of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$, where ${\Lambda }_{\gamma }=m{\mathbb{Z}}^2$. The lattice ${\mathbb{Z}}^2$ creates a ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$ tessellation in the flat torus $T_{\gamma }$ that is made up of $m^2$ squares, as shown in item (1) of Corollary 1.

The partition of parallelograms (squares) yields this tessellation. Geometrically, the dual tessellation that goes with it is made by translating a fundamental P parallelogram partition, and it is covered by $m^2$ squares.

The qubits are in a biunivocal correspondence with the edges of the $m^2$ squares covering the flat torus $T_{\gamma }$ in the building of surface codes. The parameters for this class of codes are $\left[[2m^2,2,m]\right]$, where the code length is determined by the number of edges in the squares that tile the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation. The genus of the orientable surface g determines how many information qubits there are; since $g=1$ in the flat torus, $k=2g=2$ qubits are encoded. The distance can be found by calculating the minimal distance between edges in the smallest homologically non-trivial cycle of the flat torus’s ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation. From the parallelogram partition or the translated parallelogram partition in ${\mathbb{R}}^2$, we have $2m^2$ squares. A homologically non-trivial cycle is the path taken by the edges that cannot be contracted on a face.

We now consider the lattice points $Q_0=(0,0)$, $Q_1=(m,0)$, $Q_2=(0,m)$, and $Q_3=(m,m)\in {\Lambda }_{\gamma }$. The sides of the fundamental region $P_0$ (parallelogram) are characterized by the line segments $Q_0{Q}_1$ and $Q_0{Q}_3$. We also consider the vectors u and v of the basis $\gamma$, which are parallel to the line segments $Q_0{Q}_1$ and $Q_0{Q}_3$, respectively. Notice that in the flat torus $T_{\gamma }$, the point $Q_0$ is identified with both points $Q_1$ and $Q_3$.

When we fix $\beta =\{e_1,e_2\}$ as the lattice basis of ${\mathbb{Z}}^2$, where $e_1=(1,0)$ and $e_2=(0,1)$, we find that the shortest of these two paths corresponds to the minimal number of edges belonging to orthogonal axes in the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$ tessellations. These edges are parallel to the lattice basis vectors $e_1$ and $e_2$, respectively. Therefore, we conclude that $d=m$.

In [10], the authors obtained the surface codes $\left[[3m^2,2,m]\right]$ as a consequence of two equivalent ways of covering the fundamental region of sublattice ${\Lambda }_{\gamma }=m{\mathcal{A}}_2$ with index $m^2$ in ${\mathcal{A}}_2$: with parallelograms or regular hexagons. However, as shown in item (2) of Corollary 1, the lattice ${\mathcal{A}}_2$ creates a ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$ tessellation in the flat torus $T_{\gamma }$. This means that $T_{\gamma }$ is tiled by a $m^2$ parallelogram. This tessellation originates from the partition of parallelograms. Geometrically, its dual tessellation is obtained by translation of the $m^2$ parallelograms by the vector $({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$. Each parallelogram is congruent to fundamental region $\mathcal{P}$ of honeycomb lattices ${\mathcal{A}}_2$ when we set the lattice basis $\beta =\{(1,0),({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})\}$.

We then created a new class of surface codes where the qubits are in biunivocal correspondence with the edges of the $m^2$ parallelogram that tile the flat torus $T_{\gamma }$. The length of this code is given by the number of edges in the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation, which is $2m^2$, since each edge is shared by the vertices.

We can now look at the lattice points $Q_0=(0,0)$, $Q_1=(m,0)$, $Q_2=(0,m)$, and $Q_3=(m,m)\in {\Lambda }_{\gamma }$. The sides of the fundamental region $P_0$ (parallelogram) are made up of the line segments $Q_0{Q}_1$ and $Q_0{Q}_3$. We also consider the vectors u and v of the basis $\gamma$, which are parallel to the line segments $Q_0{Q}_1$ and $Q_0{Q}_3$, respectively. Notice that in the flat torus $T_{\gamma }$, the point $Q_0$ is associated with both points $Q_1$ and $Q_3$. When we fix $\beta =\{e_1,e_2\}$ as the lattice basis of ${\mathcal{A}}_2$, where $e_1=(1,0)$ and $e_2=({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$, we also find that the shortest of these two paths corresponds to the minimal number of edges on the line parallel to the vectors $e_1=(1,0)$ and $e_2=({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$, respectively. Thus, we conclude that $d=m$.

After these conclusions and results, we present Proposition 4.

Proposition 4.

Let $\mathcal{M}$ be the collection of all the families of ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellations of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$ given by the $m^2$ parallelogram that are congruent to fundamental region of the ${\mathcal{A}}_2$-lattice described by item (2) of Corollary 1. We then obtain a new class of codes with parameters $\left[[2m^2,2,m]\right]$.

This answers the question (1) that we asked in the introduction.

Surface Codes from ${\mathbb{Z}}_m$-Tessellation of the Flat Torus Obtained from ${\mathbb{Z}}^2$-Lattices

In [7], the proposed surface codes were based on the Lee sphere with radius r that recover the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$. Here, ${\Lambda }_{\gamma }$ was the sublattice with index $m^2$ in ${\mathbb{Z}}^2$ and was created by the basis $\gamma =\{u,v\}$, where $u=(m,0)$ and $v=(0,m)$ and m was a positive integer. The minimum distance of the code is the least number of edges to be transversed between two Lee spheres of the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation. The basic Lee sphere with radius r can be used to recover the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$. This is possible since there are non-null $r,a$ and $b\in \mathbb{Z}$ such that $m=2r^2+2r+1$ and $m=a^2+b^2$.

In [12], the authors used this method to get surface codes from the ${\mathbb{Z}}^2$-lattice by picking regions that recover the ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$, which includes cases where there is no integer solution for the equation $m=2r^2+2r+1$. From there, the authors obtained surface codes with parameters $\left[\right[2m,2,d\left]\right]$ for the cases $m=a^2+b^2$, where $d=\left|a\right|+\left|b\right|$.

Now, we begin reproducing the surface codes with parameters $\left[\right[2m,2,d\left]\right]$ for the cases $m=a^2+b^2$, where $d=\left|a\right|+\left|b\right|$. We consider $\beta =\{e_1,e_2\}$ as lattice basis of ${\mathbb{Z}}^2$ and $\gamma =\{(a,b),(-b,a)\}$ as lattice basis of sublattice ${\Lambda }_{\gamma }$ of index m in ${\mathbb{Z}}^2$, where $e_1=(1,0)$ and $e_2=(0,1)$, respectively. This class of codes is also found by ${\mathbb{Z}}_m\times {\mathbb{Z}}_m$-tessellation of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$. This is because of the lattice partition ${\mathbb{Z}}^2/{\Lambda }_{\gamma }$ and the geometric technique of projecting the lattice basis $\gamma$ onto $e_1$ and $e_2$.

Proposition 5.

Let $\mathcal{M}$ be the set of all families of ${\mathbb{Z}}_m$-tessellation of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$ tiled by m squares. Then, there are $2m$ qubits attached at the edges of these m squares.

Proof. 

The qubits are identified with the edges of the squares of the ${\mathbb{Z}}_m$-tessellation of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$. Since each square has four edges that are common to two squares, the number of qubits is given by ${\displaystyle \frac{4m}{2}}=2m$.

Similarly, we relate the ${\mathbb{Z}}_m$-tessellation of the flat torus to the qubits on the square’s edges. The number of qubits is also given by ${\displaystyle \frac{4m}{2}}=2m$. □

We also know that the homological group associated with the flat torus is isomorphic to the group ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$. From the elementary results of group theory, we conclude that the homology group has two generators. Therefore, we obtain that each code $\mathcal{C}$, constructed from each flat torus $T_{\gamma }$, encodes $k=2$ qubits. Based on Proposition 5, we obtain an algebraic procedure for obtaining surface codes from families of the flat torus $T_{\gamma }$ in Proposition 6.

Additionally, we are aware that the group ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$ is isomorphic to the homological group connected to the flat torus. From the basic group theory results, we deduce that the homology group has two generators. As a result, we derive that $k=2$ qubits are encoded by each code $\mathcal{C}$ that is built from each flat torus $T_{\gamma }$. We derive an algebraic process for obtaining surface codes from families of the flat torus $T_{\gamma }$ in Proposition 6, based on Proposition 5.

Proposition 6.

From the flat torus, $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$, where ${\Lambda }_{\gamma }$ is the sublattice of index m in ${\mathbb{Z}}^2$, generated by basis $\{(-b,a),(a,b)\}$ with $a^2+b^2=m$, we obtain a surface code with parameters $\left[\right[2m,2,d\left]\right]$, where $d=\left|a\right|+\left|b\right|$.

Proof. 

We obtain the code parameters for each flat torus $T_{\gamma }$ from Proposition 5. Then, we only need to calculate the code’s distance. The weight of the Pauli operator with the minimum weight, which preserves the code subspace and acts non-trivially on it, is by definition the minimum distance of a stabilizer code. We can see this distance as a function of the homology of the surface since we are dealing with a special kind of homological code. Accordingly, the fewest number of qubits in the support of a homologically non-trivial cycle between the tessellation and dual tessellation associated to the flat torus $T_{\gamma }$ is the minimum distance.

The homologically non-trivial cycles, which are generated from the ${\mathbb{Z}}_m$ tessellation given by m squares, are the paths determined by the edges that cannot be contracted into a face with respect to the covering of the flat torus $T_{\gamma }$. Note that nontrivial cycles on the flat torus are characterized by the possibilities of combinations of paths along the edges of the m squares with edges parallel to the vectors of the basis $\beta =\{e_1,e_2\}$, where $e_1=(1,0)$ and $e_2=(0,1)$.

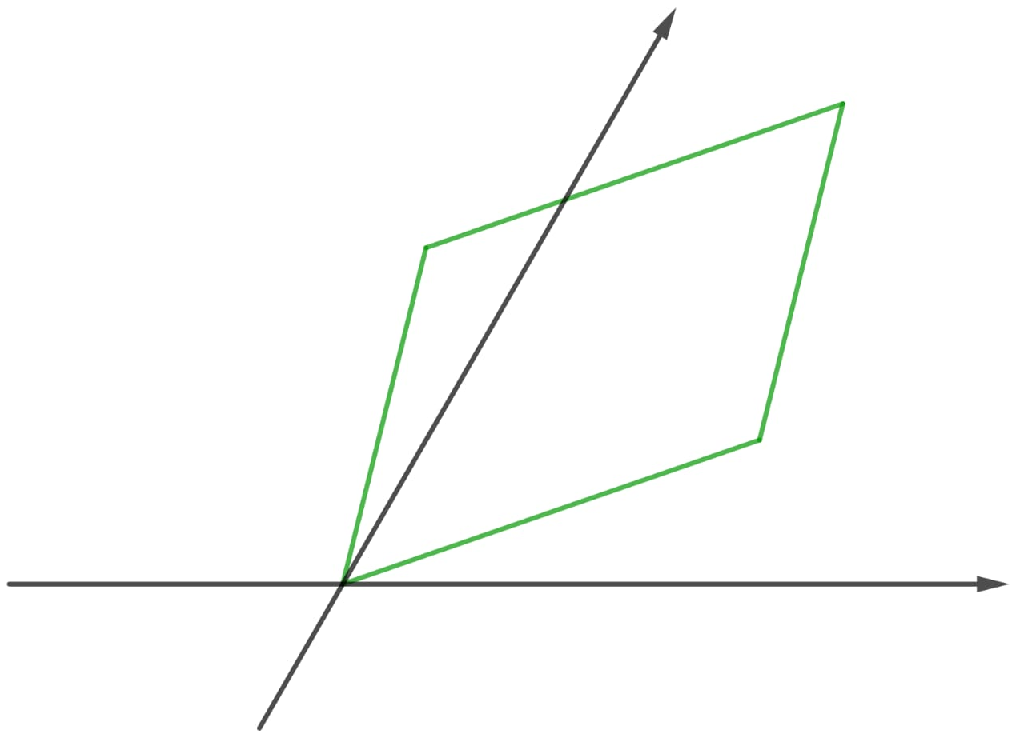
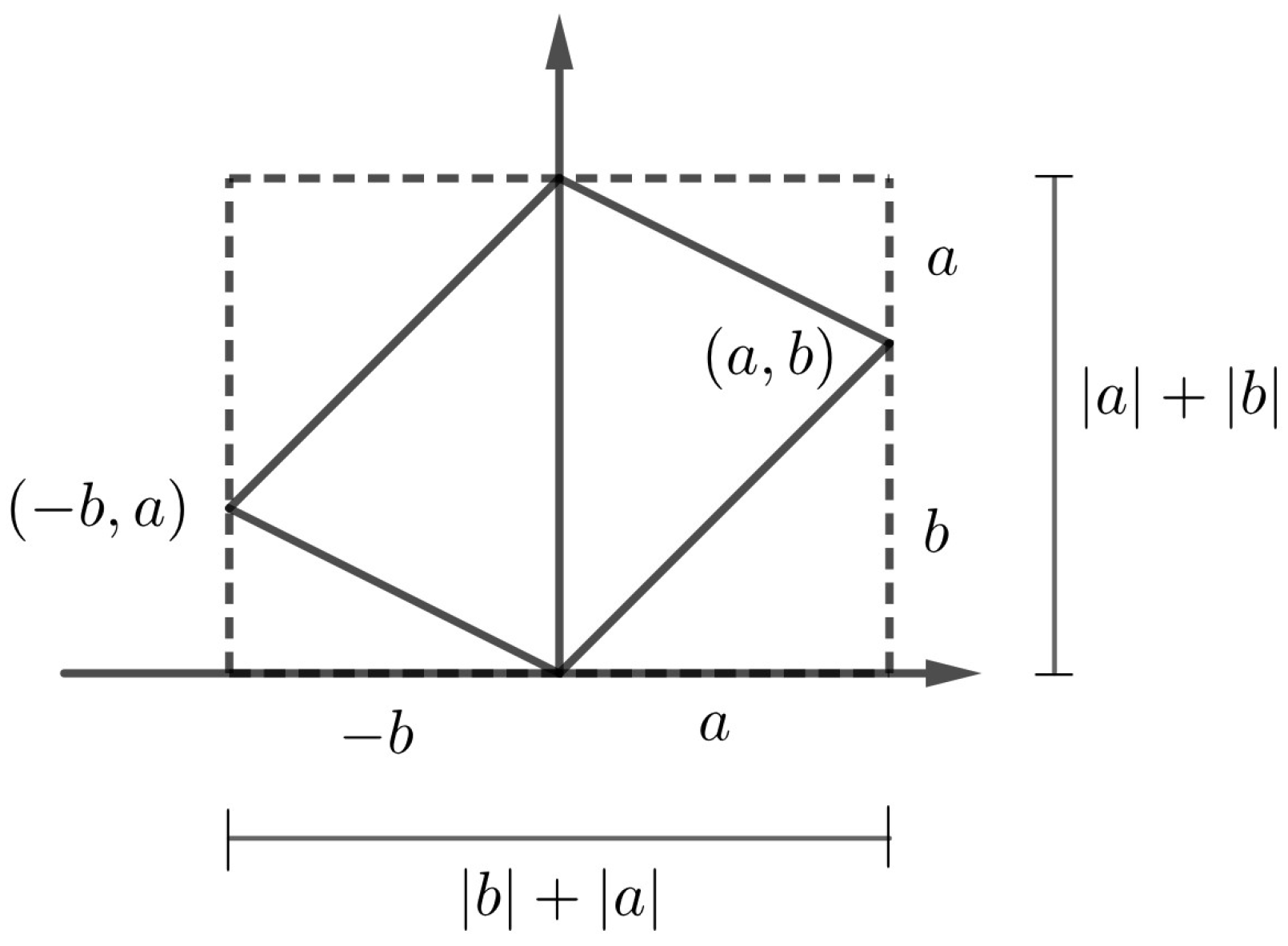
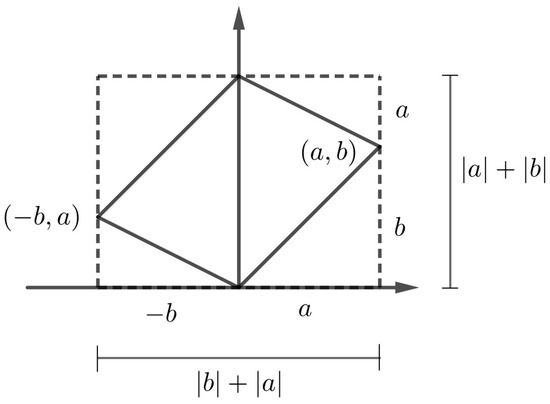
In order to obtain these minimal paths, we use the fact that the fundamental region $P^{\prime }$ of the lattice ${\Lambda }_{\gamma }$ (square) with sides of length $\left|a\right|+\left|b\right|$ parallel to the vectors u and v, is circumscribed in a square with sides parallel to the vectors $e_1$ and $e_2$ (see Figure 7). In fact, the side of length l parallel to the vector $e_1$ can be seen as the sum of the lengths of the projections of the vectors u and v onto $e_1$, given by $(-b,0)$ and $(a,0)$, respectively, that is, $l=\left|a\right|+\left|b\right|$. Similarly, the side of length l parallel to the vector $e_2$ can be seen as the length of the projection of the vector sum $u+v=(a-b,a+b)$ onto $e_2$, given by $(0,a+b)$, that is, $l=a+b$. Therefore, $d=a+b$. □

Figure 7. Projection of vector basis ${\Lambda }_{\gamma }$ over vector basis of ${\mathbb{Z}}^2$-lattice.

We now extend the method to get surface codes though ${\mathbb{Z}}_m$-tessellation of the flat torus-derived sublattices of ${\mathcal{A}}_2$ as consequence of lattice partition ${\mathcal{A}}_2/{\Lambda }_{\gamma }$, where ${\Lambda }_{\gamma }$ is a sublattice of index m in ${\mathcal{A}}_2$ and generate by basis $\gamma =\{(a,b),(-b,a+b)\}$, such that, $m=a^2+ab+b^2.$

Proposition 7.

Let $\mathcal{M}$ be the set of all families of ${\mathbb{Z}}_m$-tessellation of the flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$ with m parallelograms, that are congruent to fundamental region of ${\mathcal{A}}_2$-lattice, described by Corollary 2. Then, there are $2m$ qubits attached at edege derived from m polygons.

Proof. 

The qubits are associated with the edges of the ${\mathbb{Z}}_m$-tessellation of the parallelogram which gives origen to flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$. Since the edges of each parallelogram are shared between two parallelograms, the number of qubits is given by ${\displaystyle \frac{4m}{2}}=2m$.

Similarly, on the edges of the translated parallelogram of ${\mathbb{Z}}_m$-tessellation of the flat torus we associate the qubits. The number of qubits is also given by ${\displaystyle \frac{4m}{2}}=2m$. □

Since the homological group associated with the flat torus is isomorphic to the group ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$, from results of group theory, we obtain that the homology group has two generators. Thus, the code $\mathcal{C}$ constructed from each flat torus $T_{\gamma }$, encodes $k=2$ qubits because there are two stabilizer operators in each hexagonal face. From Proposition 5, we get an algebraic procedure for obtaining surface codes from families of the flat torus $T_{\gamma }$ in Proposition 8.

Proposition 8.

From each flat torus $T_{\gamma }={\mathbb{R}}^2/{\Lambda }_{\gamma }$, where ${\Lambda }_{\gamma }$ is the sublattice of index m in ${\mathcal{A}}_2$ generated by basis $\{(a,b),(-b,a+b)\}$ with $a^2+ab+b^2=m$, we obtain a surface code with parameters $\left[\right[2m,2,d\left]\right]$, where $d=\left|a\right|+\left|b\right|$.

Proof. 

By Proposition 7, we get the parameters of the code on each flat torus $T_{\gamma }$. We need only obtain the distance of the code.

To find nontrivial cycles on the flat torus, we can look at the different ways that the edges of the m parallelograms can be put together. These edges must be parallel to the vectors of the basis $\beta =\{e_1,e_2\}$, where $e_1=(1,0)$ and $e_2=({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$.

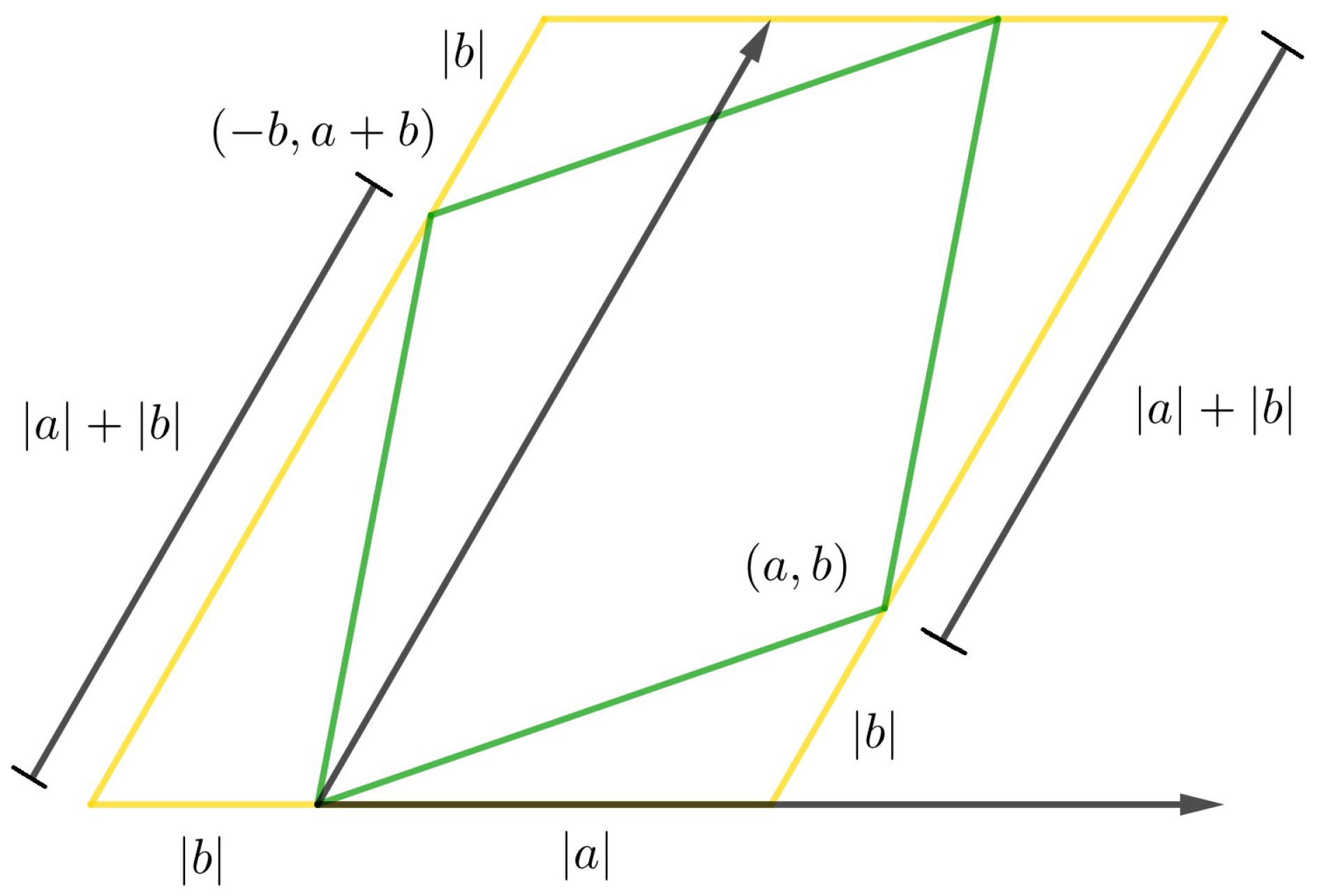
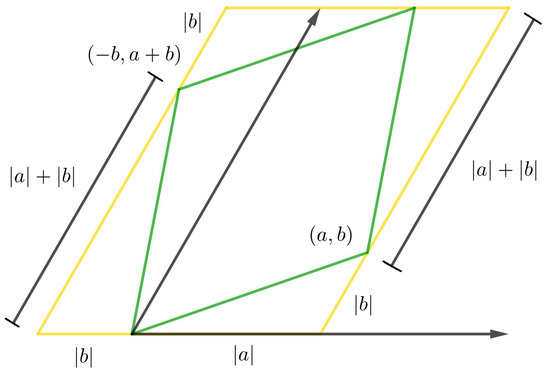
We use the fact that the basic region ${\mathcal{P}}_0$ of the lattice $\Lambda \gamma$ (parallelogram) has sides that are $\left|a\right|+\left|b\right|$ long and $\left|a\right|+2\left|b\right|$ wide, and they are parallel to the vectors u and v. This region is surrounded by a larger parallelogram whose sides are parallel to the vectors $e_1$ and $e_2$ (see Figure 8). In fact, we can see the side of length l parallel to the vector $e_1$ as the sum of the lengths of the projections of the vectors u and v onto $e_1$, represented by $(-b,0)$ and $(a,0)$, respectively, meaning $l=a+b$.

Figure 8. Projection of vector basis ${\Lambda }_{\gamma }$ over vector basis of ${\mathcal{A}}_2$-lattice.

Meanwhile, the side of length $l^{\prime }$ parallel to the vector $e_2$ can be seen as the length of the projection of the vector sum $u+v=(a-b,a+2b)$ onto $e_2$, given by $(0,a+2b)$, that is, $l^{\prime }=a+2b$. Thus, $d=minl,l^{\prime }=a+b$. □

This answers question (2) that we raseid in introduction.

5. Color Codes from Honeycomb Lattices

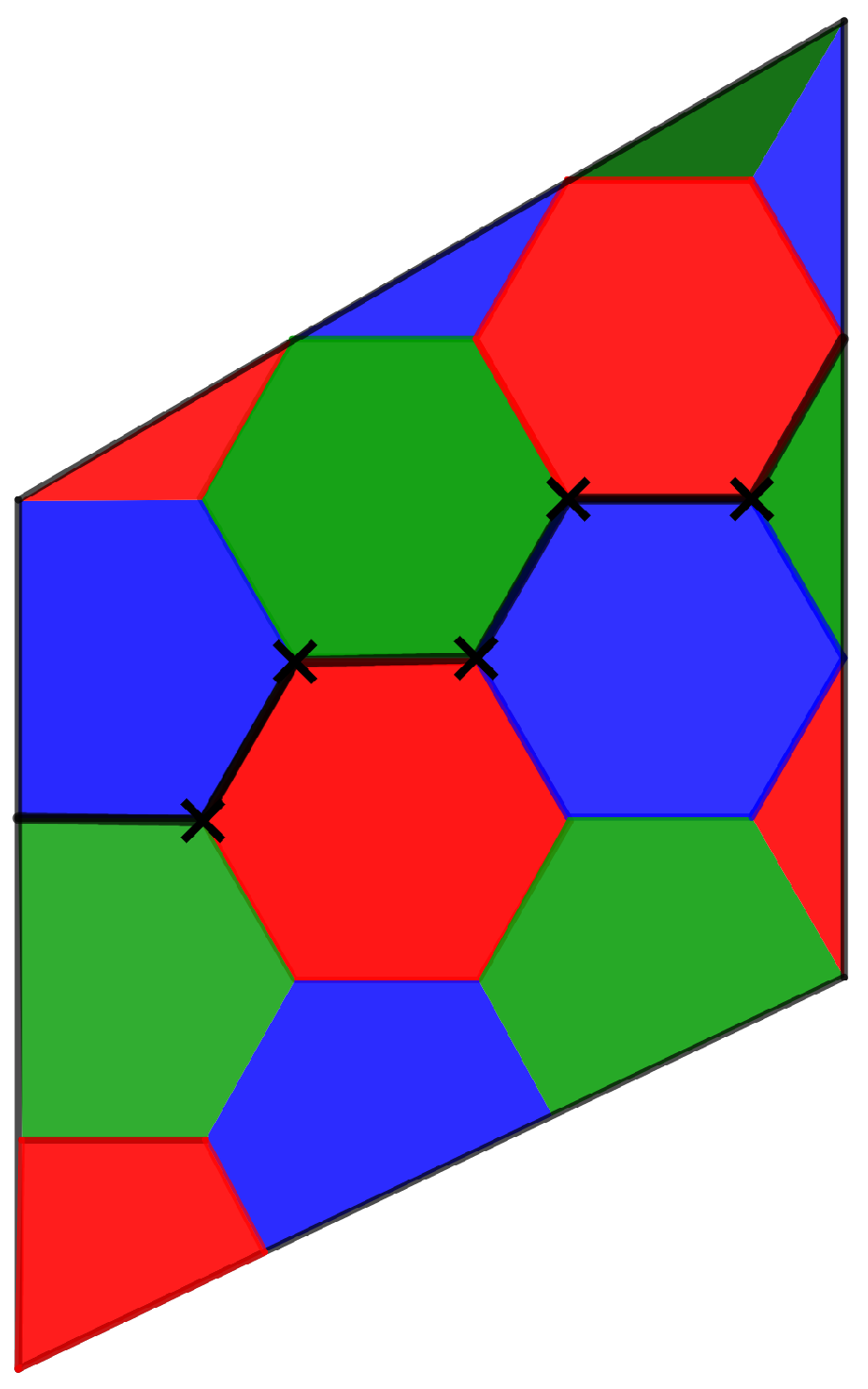
To build color codes from the flat torus, we require a three-valent tessellation with three colorable faces. These properties are presented by ${\mathbb{Z}}_{9m}$-tessellation of the flat torus $T_{{\beta }^{″}}$, where $m=a^2+ab+b^2$. Therefore, we provide an algebraic/geometric method in this section to construct quantum color codes with parameters $\left[\right[18m,4,6(|a|+|b)]]$ from tessellations ${\mathbb{Z}}_{9m}$ on the flat torus $T_{{\beta }^{″}}$.

The tessellation by regular hexagons (the lattice’s fundamental region) is depicted in Figure 9, where the lattice’s points are the hexagons’ barycentres. On the left, we observe that a parallelogram (a fundamental region of the lattice) is obtained from a regular hexagon by means of rearrangements. On the other hand, as the image on the right illustrates, the parallelogram in the bigger region is the fundamental region of the sublattice, while the smallest parallelogram represents a fundamental region of the lattice. The number of parallelograms that cover the larger one (or, conversely, the number of hexagons in the larger parallelogram) is given by the lattice’s sublattice’s index. Each smallest parallelogram has two vertices of a hexagon-based tessellation, which indexes the qubits, as seen in the right figure. The following statement, where $m=a^2+ab+b^2$, grants control over the faces in the ${\mathbb{Z}}_{9m}$-tessellations.

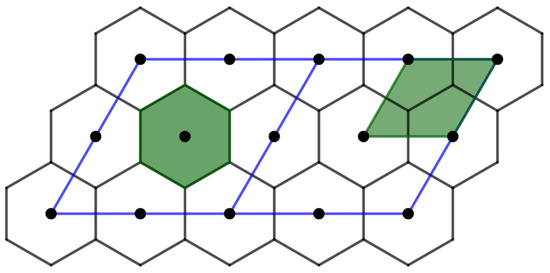
Figure 9. Equivalence between Voronoi and fundamental region associated to the honeycomb lattice.

Proposition 9.

If $\mathcal{M}$ is the set of coverings of the flat torus $T_{{\beta }^{″}}$ with $9m$ regular hexagons in each covering, then we have $18m$ qubits linked with the edges of these regular polygons.

Proof. 

The basis vectors ${\beta }^{″}$ and the basis vectors of the family of sublattices ${\Lambda }^{″}$ of the hexagonal lattice $\Lambda$ are parallel, according to Proposition 8. The ${\mathbb{Z}}_{9m}$-tessellation is 3-colorable because the length of the vectors in ${\beta }^{″}$ is three times the length of the vectors in basis $\beta$.

Because of the topology of the quotient group ${\mathcal{A}}_2/{\Lambda }^{″}$, there are $9m$ coset representatives on each flat torus $T_{{\beta }^{″}}$. As can be seen in Figure 9, in each parallelogram covering the flat torus T, there are two vertices of regular hexagons that also cover the flat torus. As a result, we conclude that each coset representative has two qubits. Thus, there are $18m$ qubits linked on each flat torus $T_{{\beta }^{″}}$.

As can be seen in Figure 9, there are two vertices of the regular hexagons that cover the flat torus T in each parallelogram that covers it. As so, we deduce that every coset representative has two qubits on it. Consequently, each flat torus $T_{{\beta }^{″}}$ has $18m$ qubits on it. □

We have that the homological group associated with the flat torus is isomorphic to the group ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$. According to group theory results, we conclude that the homology group has two generators. We obtain that each code $\mathcal{C}$, which is made up of each flat torus $T_{{\beta }^{″}}$, encodes $k=4$ qubits since each hexagonal face has two stabilizer operators.

Propositions 11 and 10, which are based on Proposition 9, provide an algebraic method for deriving color codes from families of the flat torus $T_{{\beta }^{″}}={\mathbb{R}}^2/{\Lambda }^{″}$.

Proposition 10.

The flat torus $T_{{\beta }^{″}}={\mathbb{R}}^2/{\Lambda }^{″}$ gives origen to a color code with parameters $\left[\right[18,4,6\left]\right]$, where ${\Lambda }^{″}$ is sublattice of ${\mathcal{A}}_2$ generated by basis ${\beta }^{″}=\{(3,-3),(3,0)\}$.

Proof. 

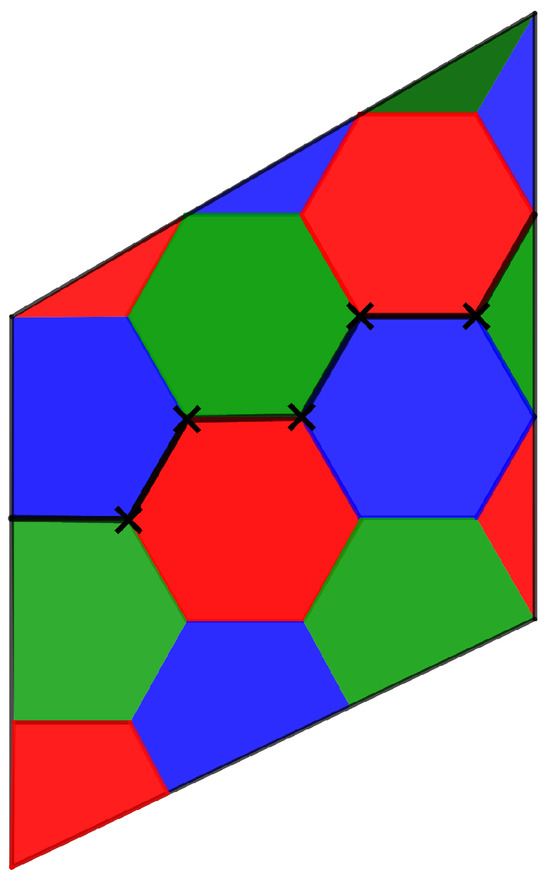
From Figure 10, we have that the code distance is $d=6$. □

Figure 10. Color code with distance 4 from ${\mathbb{Z}}_9$-tessellation of flat torus $T_{{\beta }^{″}}$.

Proposition 11.

Each flat torus $T_{{\beta }^{‴}}={\mathbb{R}}^2/{\Lambda }^{‴}$ gives origen to a color code with parameters $\left[\right[18m,4,6(|a|+|b|)\left]\right]$, where ${\Lambda }^{‴}$ is the sublattice of ${\mathcal{A}}_2$ generated by basis ${\beta }^{‴}=\{(3a,3b),(-3a,3(a+b))\}$.

Proof. 

We obtain the code’s parameters on each flat torus $T_{{\beta }^{‴}}$, where ${\beta }^{‴}=(3a,3b),-3a+(3a+3b))$ is the lattice basis associated with ${\Lambda }^{‴}$ as it was done before. Then, we only need to calculate the distance of the code.

Observe that the minimum path given by the number of edges passing through lattice points in the fundamental region of the lattice generated by the basis ${\beta }^{″}=(3,-3),(3,0)$ and parallel to the vectors $e_1=(1,0)$ and $e_2=({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$ is given by $d^{\prime }=6$. Thuw, the minimum distance of the color code obtained from the equivalent tessellation of the flat torus $T_{{\beta }^{″}}={\mathbb{R}}^2/{\Lambda }^{″}$ by hexagons, from Proposition 10, is given by $d_9=4$.

Similarly, we observe that the minimum number of edges passing through lattice points in the fundamental region of the lattice generated by $(3a,3b),(-3a,3(a+b))$ and parallel to the vectors $e_1=(1,0)$ and $e_2=({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$ is given by $d_{9m}=6(a+b)$.

In the lattice ${\Lambda }^{‴}$, when traversing the minimum path $d_{9m}=\left|a\right|+\left|b\right|$ edges in the covering of the flat torus $T_{{\beta }^{‴}}$ parallel to the vectors of the basis $e_1=(1,0)$ and $e_2=({\displaystyle \frac{1}{2}},{\displaystyle \frac{\sqrt{3}}{2}})$, to find the distance d of the color code in the equivalent covering of $T_{{\beta }^{‴}}$ by hexagons, we will use the solution to the relation ${\displaystyle \frac{d^{\prime }}{6}}={\displaystyle \frac{d}{3(a+b)}}$, that is, $d=6(|a|+|b|)$. □

This answers question (3) that we raised in the introduction.