A Fast and Accurate Numerical Method for Solving Nonlinear Fourth-Order Boundary Value Problems in the Beam Theory
Abstract
1. Introduction
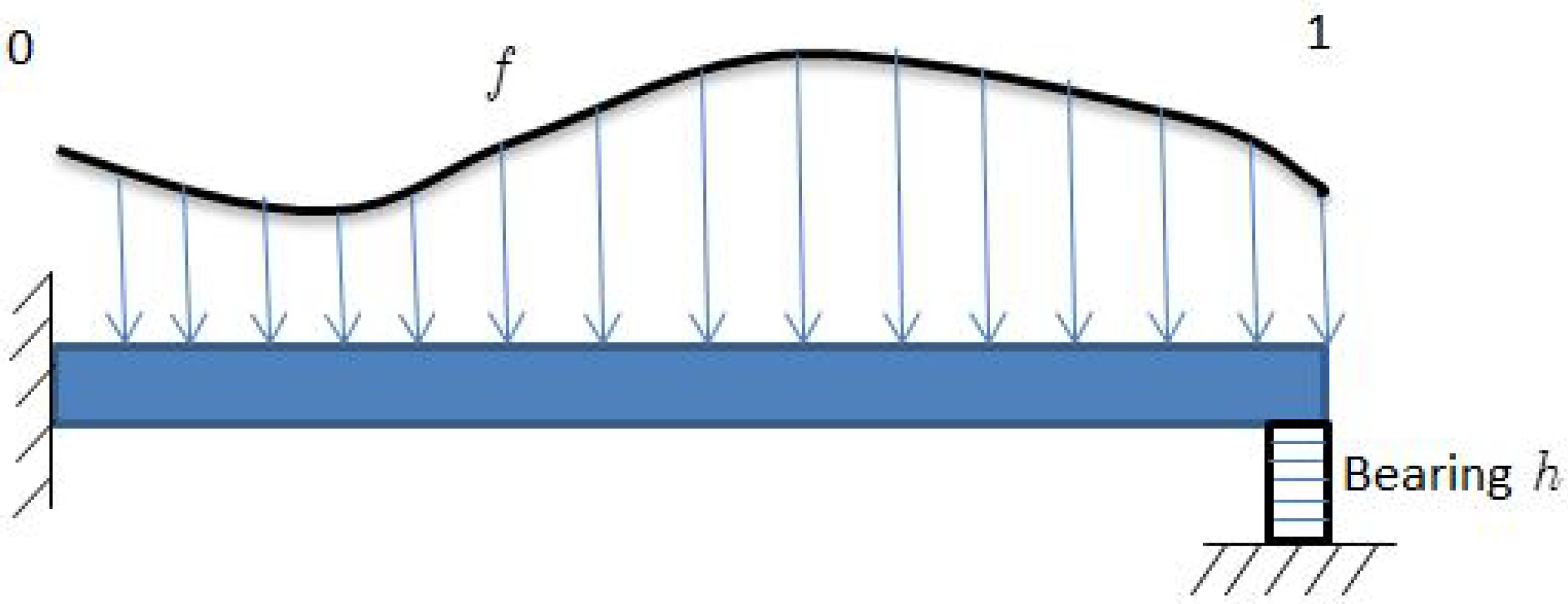
2. Problem Statement
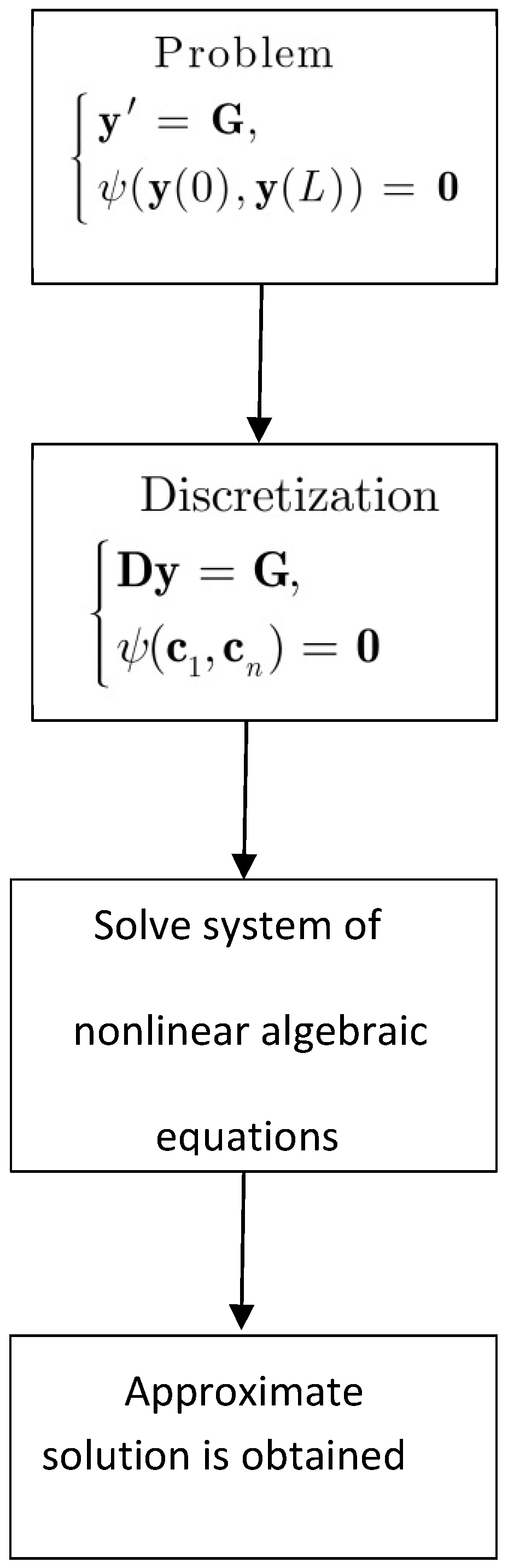
3. The Proposed Method for Solving the Boundary Value Problem in Case I
4. The Proposed Method for Solving the Boundary Value Problem in Case II
5. The Proposed Method for Solving the Boundary Value Problem in Case III
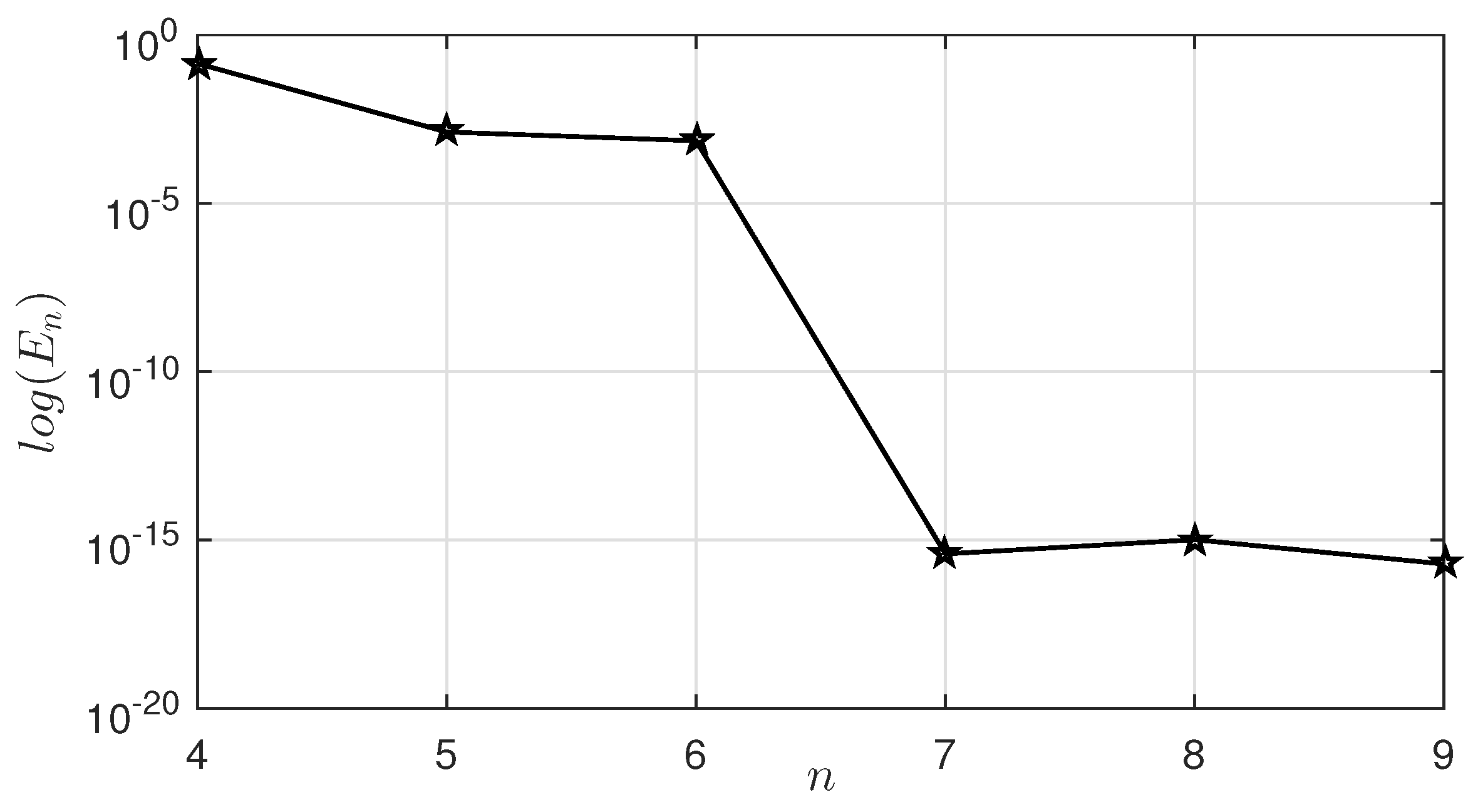
6. Convergence Analysis
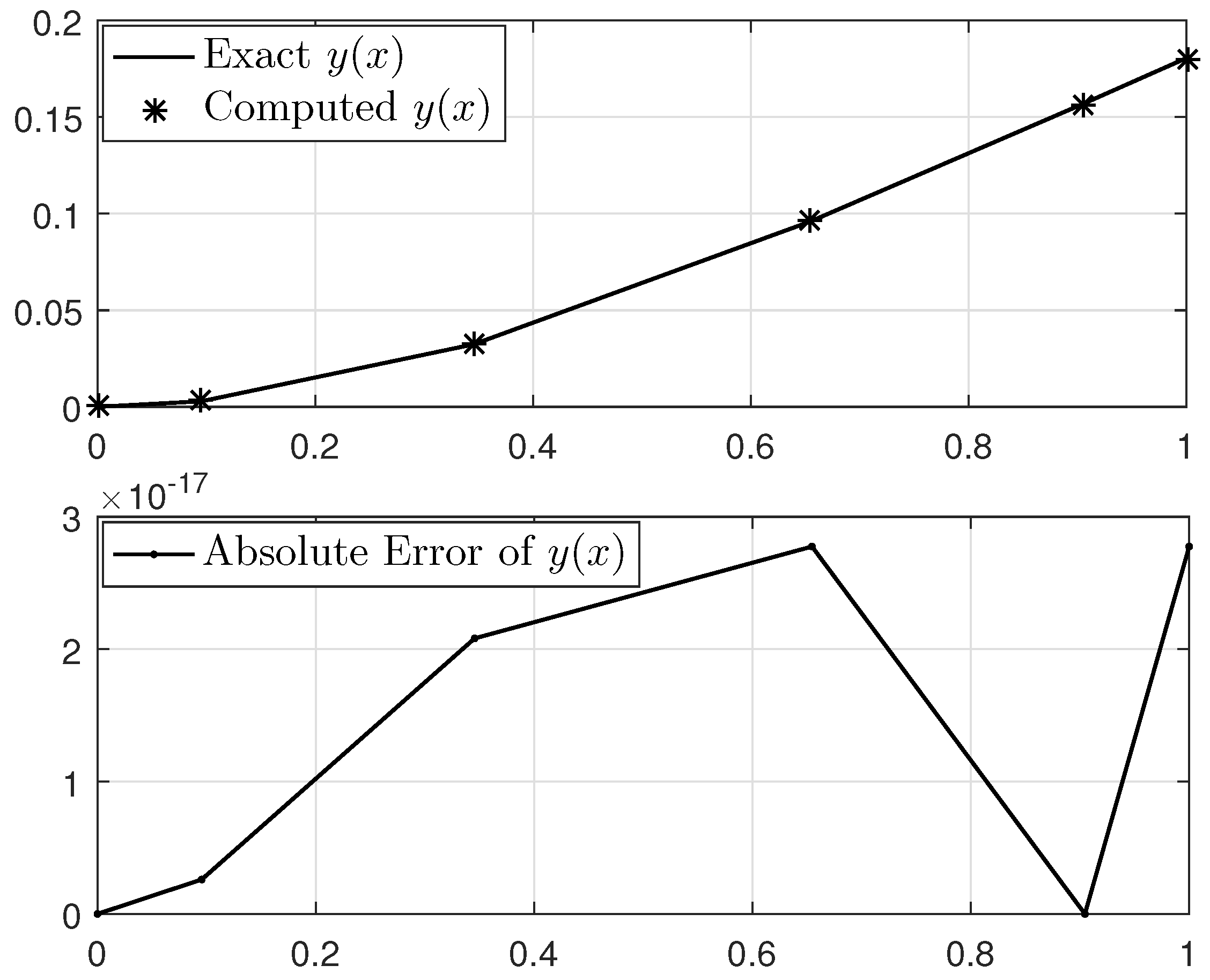
7. Numerical Illustrations
7.1. Test Example 1
7.2. Test Example 2
7.3. Test Example 3
7.4. Test Example 4
7.5. Test Example 5
7.6. Test Example 6
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gawali, A.; Sanjay, C.K. Vibration analysis of beams. World Res. J. Civ. Eng. 2011, 1, 15–29. [Google Scholar]
- Han, S.M.; Benaroya, H.; Wei, T. Dynamics of transversely vibrating beams using four engineering theories. J. Sound Vib. 1999, 225, 935–988. [Google Scholar] [CrossRef]
- Woinowsky-Krieger, S. The effect of an axial force on the vibration of hinged bars. J. Appl. Mech. 1950, 17, 35–36. [Google Scholar] [CrossRef]
- Azarnavid, B.; Parand, K.; Abbasbandy, S. An iterative kernel based method for fourth order nonlinear equation with nonlinear boundary condition. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 544–552. [Google Scholar] [CrossRef]
- Tomar, S.; Singh, M.; Ramos, H.; Wazwaz, A.M. Development of a new iterative method and its convergence analysis for nonlinear fourth-order boundary value problems arising in beam analysis. Math. Methods Appl. Sci. 2022, SI, 1–9. [Google Scholar] [CrossRef]
- Ma, T.F.; Da Silva, J. Iterative solutions for a beam equation with nonlinear boundary conditions of third order. Appl. Math. Comput. 2004, 159, 11–18. [Google Scholar] [CrossRef]
- Alves, E.; Ma, T.F.; Pelicer, M.L. Monotone positive solutions for a fourth order equation with nonlinear boundary conditions. Nonlinear Anal. Theory Methods Appl. 2009, 71, 3834–3841. [Google Scholar] [CrossRef]
- Brenner, S.C.; Gu, S.; Gudi, T.; Sung, L.y. A quadratic C0 interior penalty method for linear fourth order boundary value problems with boundary conditions of the Cahn–Hilliard type. SIAM J. Numer. Anal. 2012, 50, 2088–2110. [Google Scholar] [CrossRef]
- Geng, F. Iterative reproducing kernel method for a beam equation with third-order nonlinear boundary conditions. Math. Sci. 2012, 6, 1–4. [Google Scholar] [CrossRef]
- Shin, J. Finite-element approximation of a fourth-order differential equation. Comput. Math. Appl. 1998, 35, 95–100. [Google Scholar] [CrossRef]
- Ohm, M.R.; Lee, H.Y.; Shin, J. Error estimates of finite-element approximations for a fourth-order differential equation. Comput. Math. Appl. 2006, 52, 283–288. [Google Scholar] [CrossRef]
- Kim, J.; Shin, J. A finite element approximation of a fourth-order boundary value problem. In Proceedings of the Mathematical Optimization Theory and Applications (Proceedings of the Sixth Vietnam-Korea Joint Workshop), Hanoi, Vietnam, 25–29 February 2008; Publishing House for Science and Technology: Hanoi, Vietnam, 2008. [Google Scholar]
- Dang, Q.A.; Luan, V.T. Iterative method for solving a nonlinear fourth order boundary value problem. Comput. Math. Appl. 2010, 60, 112–121. [Google Scholar] [CrossRef]
- Dang, Q.A.; Dang, Q.L. Existence results and iterative method for a fully fourth-order nonlinear integral boundary value problem. Numer. Algorithms 2020, 85, 887–907. [Google Scholar] [CrossRef]
- Dang, Q.A.; Dang, Q.L. Existence results and numerical solution of a fourth-order nonlinear differential equation with two integral boundary conditions. Palest. J. Math. 2023, 12, 174–186. [Google Scholar]
- Zhang, X.; Ge, W. Positive solutions for a class of boundary-value problems with integral boundary conditions. Comput. Math. Appl. 2009, 58, 203–215. [Google Scholar] [CrossRef]
- Li, H.; Wang, L.; Pei, M. Solvability of a fourth-order boundary value problem with integral boundary conditions. J. Appl. Math. 2013, 782363, 1–7. [Google Scholar] [CrossRef]
- Lv, X.; Wang, L.; Pei, M. Monotone positive solution of a fourth-order BVP with integral boundary conditions. Bound. Value Probl. 2015, 2015, 172. [Google Scholar] [CrossRef]
- Benaicha, S.; Haddouchi, F. Positive solutions of a nonlinear fourth-order integral boundary value problem. Ann. West Univ. Timis.-Math. Comput. Sci. 2016, 54, 73–86. [Google Scholar] [CrossRef][Green Version]
- Heydari, M.H.; Avazzadeh, Z. Chebyshev–Gauss–Lobatto collocation method for variable-order time fractional generalized Hirota–Satsuma coupled KdV system. Eng. Comput. 2022, 38, 1835–1844. [Google Scholar] [CrossRef]
- Heydari, M.; Avazzadeh, Z. Jacobi–Gauss–Lobatto collocation approach for non-singular variable-order time fractional generalized Kuramoto–Sivashinsky equation. Eng. Comput. 2022, 38, 925–937. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.; Quarteroni, A.; Zang, T. Spectral Methods in Fluid Dynamics; Springer Series in Computational Physics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Bai, Z. The upper and lower solution method for some fourth-order boundary value problems. Nonlinear Anal. Theory Methods Appl. 2007, 67, 1704–1709. [Google Scholar] [CrossRef]
- Webb, J.; Infante, G.; Franco, D. Positive solutions of nonlinear fourth-order boundary-value problems with local and non-local boundary conditions. Proc. R. Soc. Edinb. Sect. A Math. 2008, 138, 427–446. [Google Scholar] [CrossRef]
- Li, Y. Two-parameter nonresonance condition for the existence of fourth-order boundary value problems. J. Math. Anal. Appl. 2005, 308, 121–128. [Google Scholar] [CrossRef][Green Version]
- Liu, B. Positive solutions of fourth-order two point boundary value problems. Appl. Math. Comput. 2004, 148, 407–420. [Google Scholar] [CrossRef]
- Zhang, X. Existence and iteration of monotone positive solutions for an elastic beam equation with a corner. Nonlinear Anal. Real World Appl. 2009, 10, 2097–2103. [Google Scholar] [CrossRef]
- Feireisl, E. Exponential attractors for non-autonomous systems: Long-time behaviour of vibrating beams. Math. Methods Appl. Sci. 1992, 15, 287–297. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Fornberg, B. A Practical Guide to Pseudospectral Methods; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L. Spectral Methods: Algorithms, Analysis and Applications; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Gautschi, W. Orthogonal Polynomials: Computation and Approximation; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Gheorghiu, C.I. Spectral Methods for Differential Problems; Casa Cărtii de Stiintă: Cluj-Napoca, Romania, 2007. [Google Scholar]
- Mehrpouya, M.A.; Salehi, R. A numerical scheme based on the collocation and optimization methods for accurate solution of sensitive boundary value problems. Eur. Phys. J. Plus 2021, 136, 909. [Google Scholar] [CrossRef]
- Atkinson, K. An Introduction to Numerical Analysis, 2nd ed.; Wiley: Hoboken, NJ, USA; India Pvt. Limited: Noida, India, 2008. [Google Scholar]
- Mehrpouya, M.A.; Peng, H. A robust pseudospectral method for numerical solution of nonlinear optimal control problems. Int. J. Comput. Math. 2021, 98, 1146–1165. [Google Scholar] [CrossRef]

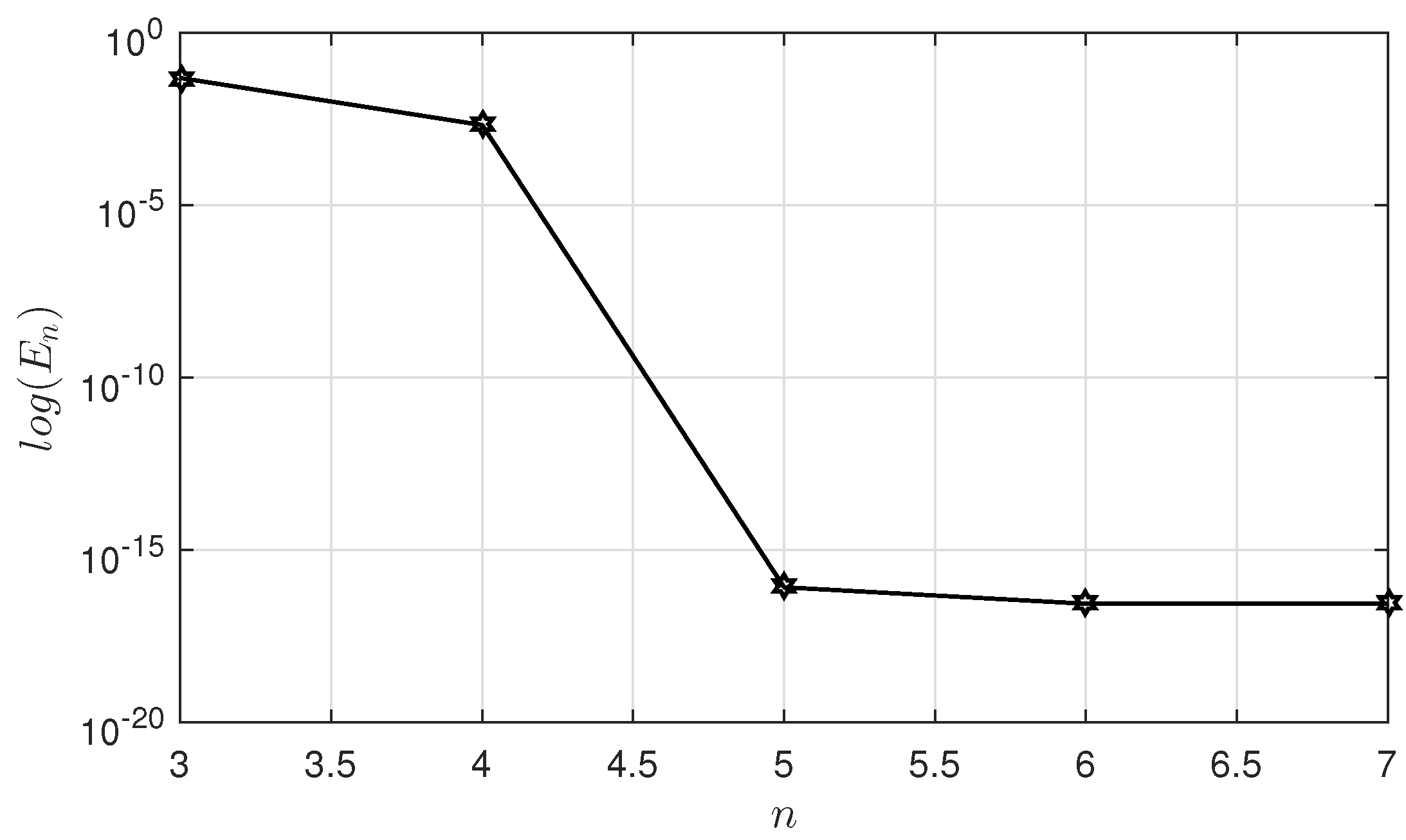

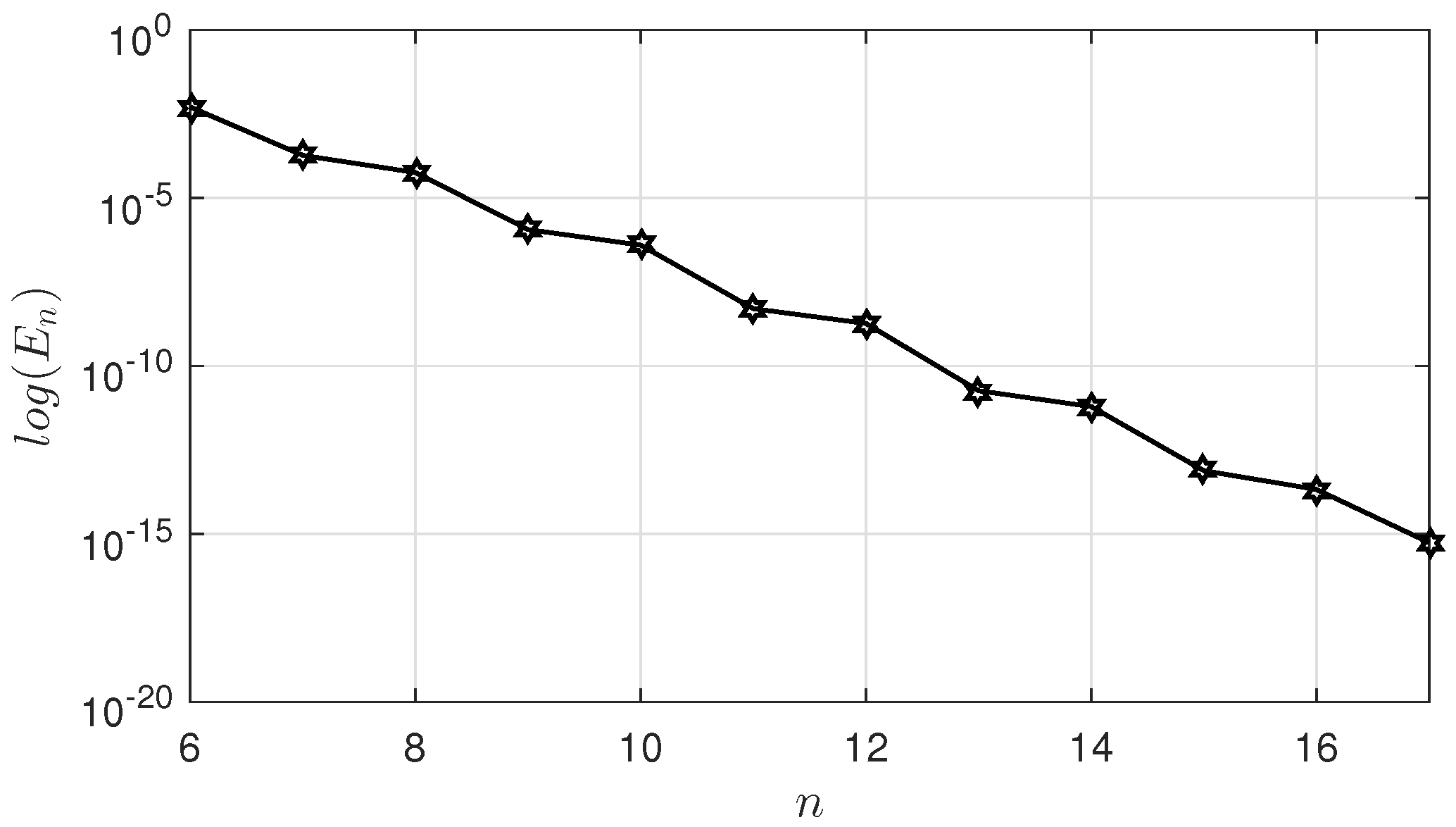

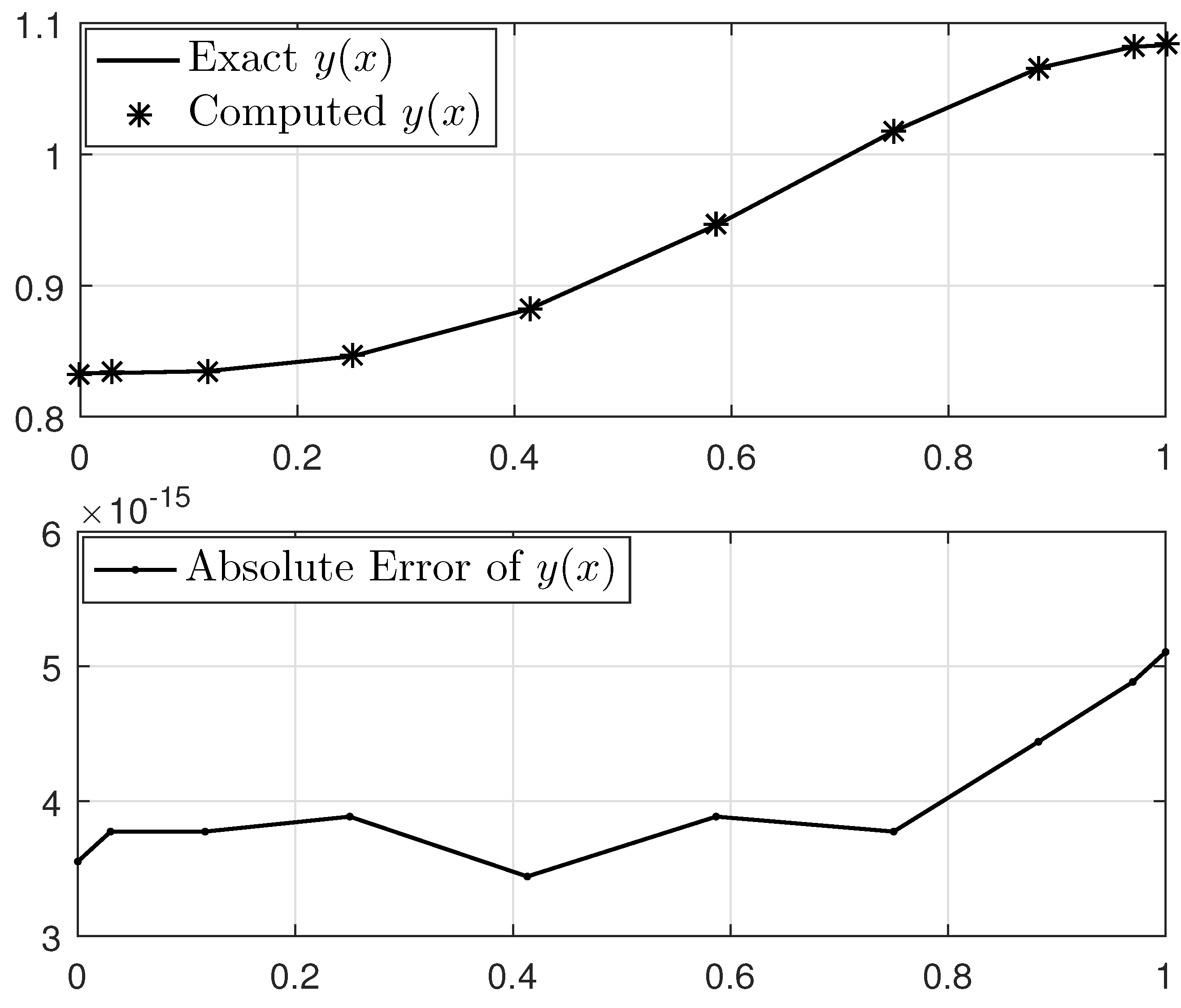
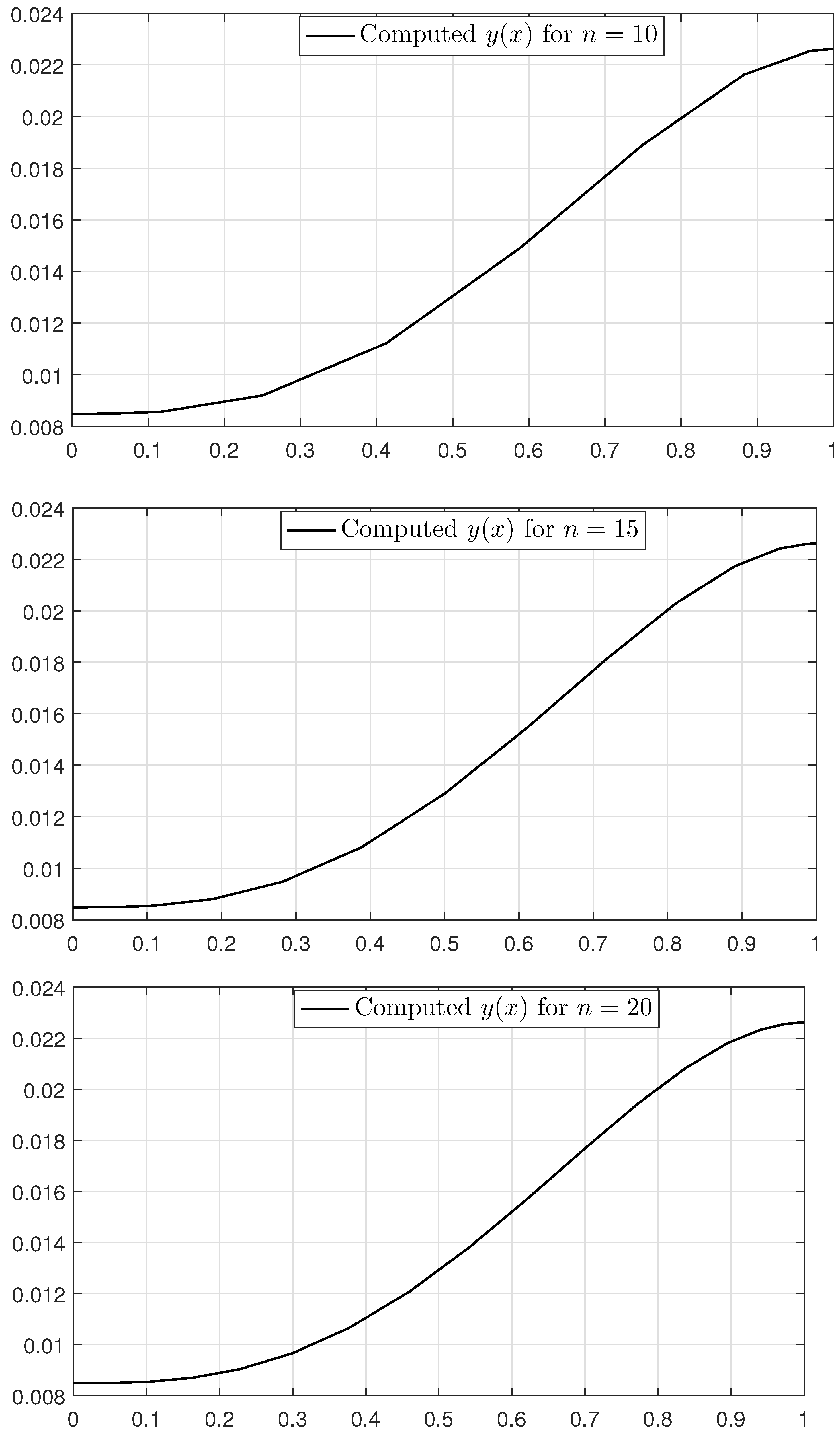
| n | CPU Time (s) | |
|---|---|---|
| 4 | 1.30 | 0.02 |
| 5 | 1.12 | 0.03 |
| 6 | 4.88 | 0.03 |
| 7 | 2.22 | 0.04 |
| 8 | 7.77 | 0.05 |
| 9 | 1.11 | 0.06 |
| The best result in [6] | 8.3914 | Not reported |
| The best result in [9] | 2.7495 | Not reported |
| n | CPU Time (s) | |
|---|---|---|
| 3 | 4.37 | 0.02 |
| 4 | 2.09 | 0.02 |
| 5 | 8.33 | 0.03 |
| 6 | 2.78 | 0.03 |
| 7 | 2.78 | 0.03 |
| The best result in [5] | The best result in [4] | The best result in [7] | The proposed method |
| 1.67 | 1.98 | 3.30 | 2.78 |
| n | CPU Time (s) | Ratio | |
|---|---|---|---|
| 6 | 5.07 | 0.05 | − |
| 8 | 5.70 | 0.09 | 15.60 |
| 10 | 3.93 | 0.11 | 22.30 |
| 12 | 1.84 | 0.13 | 29.42 |
| 14 | 6.17 | 0.14 | 36.96 |
| 16 | 2.11 | 0.21 | 42.52 |
| n | CPU Time (s) | Ratio | |
|---|---|---|---|
| 7 | 1.84 | 0.06 | − |
| 9 | 1.14 | 0.09 | 20.23 |
| 11 | 5.04 | 0.12 | 27.02 |
| 13 | 1.83 | 0.13 | 33.63 |
| 15 | 7.62 | 0.18 | 38.30 |
| 17 | 5.55 | 0.21 | 39.33 |
| The best result in [13] using 7 iterates | The best result in [10] using 29 iterates | The proposed method |
| 4.3010 | 3.0819 | 5.55 |
| x | n | CPU Time (s) | |
|---|---|---|---|
| 0 | 5 | −1.92 | 0.08 |
| 10 | −2.01 | 0.11 | |
| 15 | −8.80 | 0.18 | |
| 1 | 20 | −0.698477080299616 | 0.22 |
| 25 | −0.698477080299615 | 0.30 | |
| 30 | −0.698477080299615 | 0.37 | |
| 2 | 20 | −0.935182982105999 | 0.22 |
| 25 | −0.935182982105998 | 0.30 | |
| 30 | −0.935182982105999 | 0.37 | |
| 3 | 20 | −0.177961205799748 | 0.22 |
| 25 | −0.177961205799747 | 0.30 | |
| 30 | −0.177961205799747 | 0.37 | |
| 5 | 0 | 0.08 | |
| 10 | 1.68 | 0.11 | |
| 15 | 0 | 0.18 | |
| The best accuracy obtained in [13] for is | |||
| x | n | CPU Time (s) | |
|---|---|---|---|
| 0 | 10 | 0.008478101111174 | 0.09 |
| 15 | 0.008478101110927 | 0.15 | |
| 20 | 0.008478101110927 | 0.18 | |
| 0.25 | 10 | 0.009194450655183 | 0.09 |
| 15 | 0.009194450654920 | 0.15 | |
| 20 | 0.009194450654920 | 0.18 | |
| 0.5 | 10 | 0.012889672995238 | 0.09 |
| 15 | 0.012889672994845 | 0.15 | |
| 20 | 0.012889672994844 | 0.18 | |
| 0.75 | 10 | 0.018909279622185 | 0.09 |
| 15 | 0.018909279621708 | 0.15 | |
| 20 | 0.018909279621708 | 0.18 | |
| 1 | 10 | 0.022614795570729 | 0.09 |
| 15 | 0.022614795569874 | 0.15 | |
| 20 | 0.022614795569874 | 0.18 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrpouya, M.A.; Salehi, R.; Wong, P.J.Y. A Fast and Accurate Numerical Method for Solving Nonlinear Fourth-Order Boundary Value Problems in the Beam Theory. Axioms 2024, 13, 757. https://doi.org/10.3390/axioms13110757
Mehrpouya MA, Salehi R, Wong PJY. A Fast and Accurate Numerical Method for Solving Nonlinear Fourth-Order Boundary Value Problems in the Beam Theory. Axioms. 2024; 13(11):757. https://doi.org/10.3390/axioms13110757
Chicago/Turabian StyleMehrpouya, Mohammad Ali, Rezvan Salehi, and Patricia J. Y. Wong. 2024. "A Fast and Accurate Numerical Method for Solving Nonlinear Fourth-Order Boundary Value Problems in the Beam Theory" Axioms 13, no. 11: 757. https://doi.org/10.3390/axioms13110757
APA StyleMehrpouya, M. A., Salehi, R., & Wong, P. J. Y. (2024). A Fast and Accurate Numerical Method for Solving Nonlinear Fourth-Order Boundary Value Problems in the Beam Theory. Axioms, 13(11), 757. https://doi.org/10.3390/axioms13110757







