Dynamic Analysis and Optimal Control of a Fractional Order Fishery Model with Refuge and Protected Area
Abstract
:1. Introduction
2. Model Formulation and Methods
Model Description
3. Qualitative Analysis Results for System (1)
3.1. The Existence and Uniqueness of Solution of System (1)
3.2. Positivity and Boundedness
3.3. Existence and Stability of Equilibriums
- (1)
- ,
- (2)
- ,
- (3)
- ,
4. Optimal Control Problem
5. Examples and Numerical Simulations
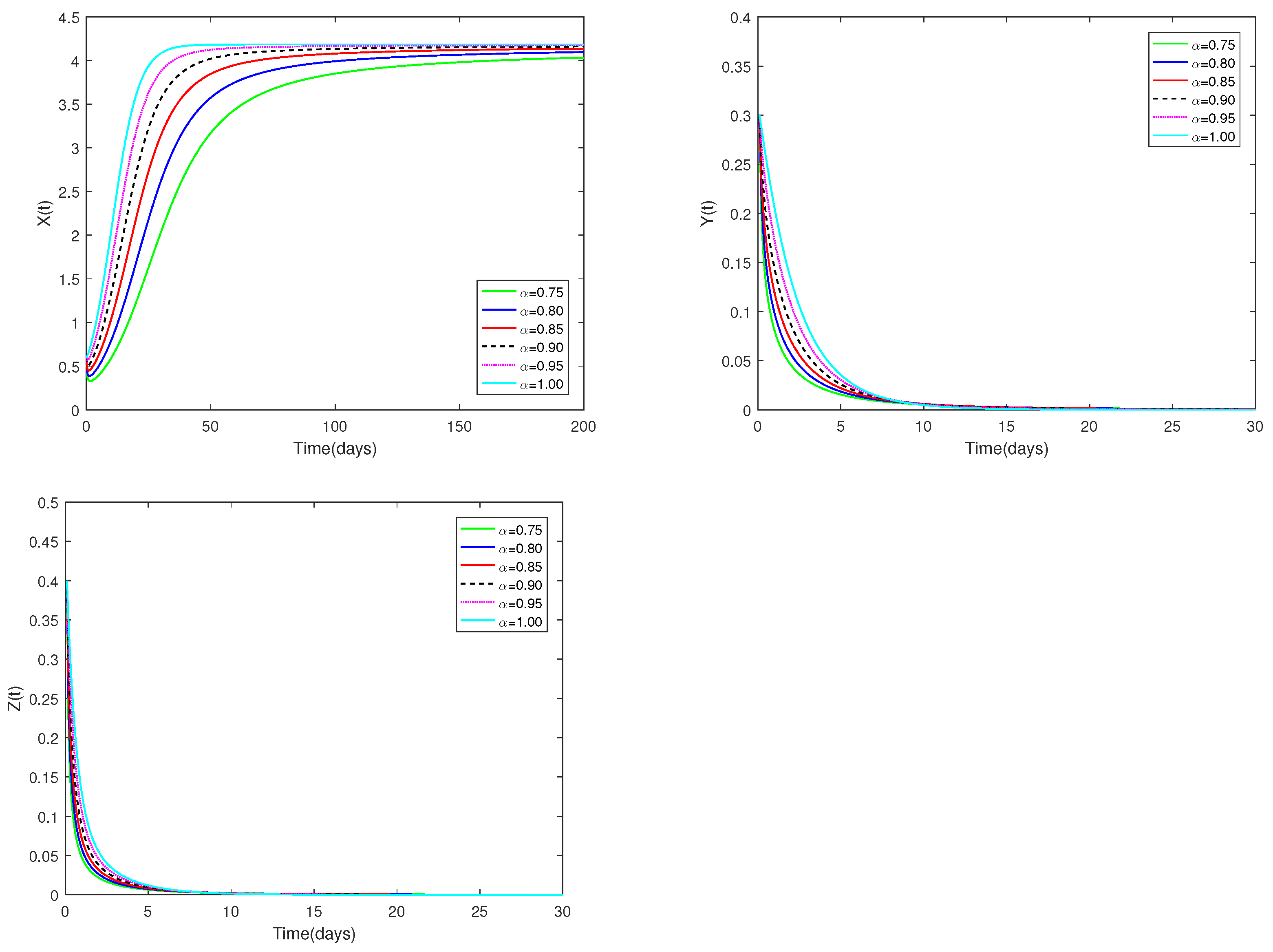
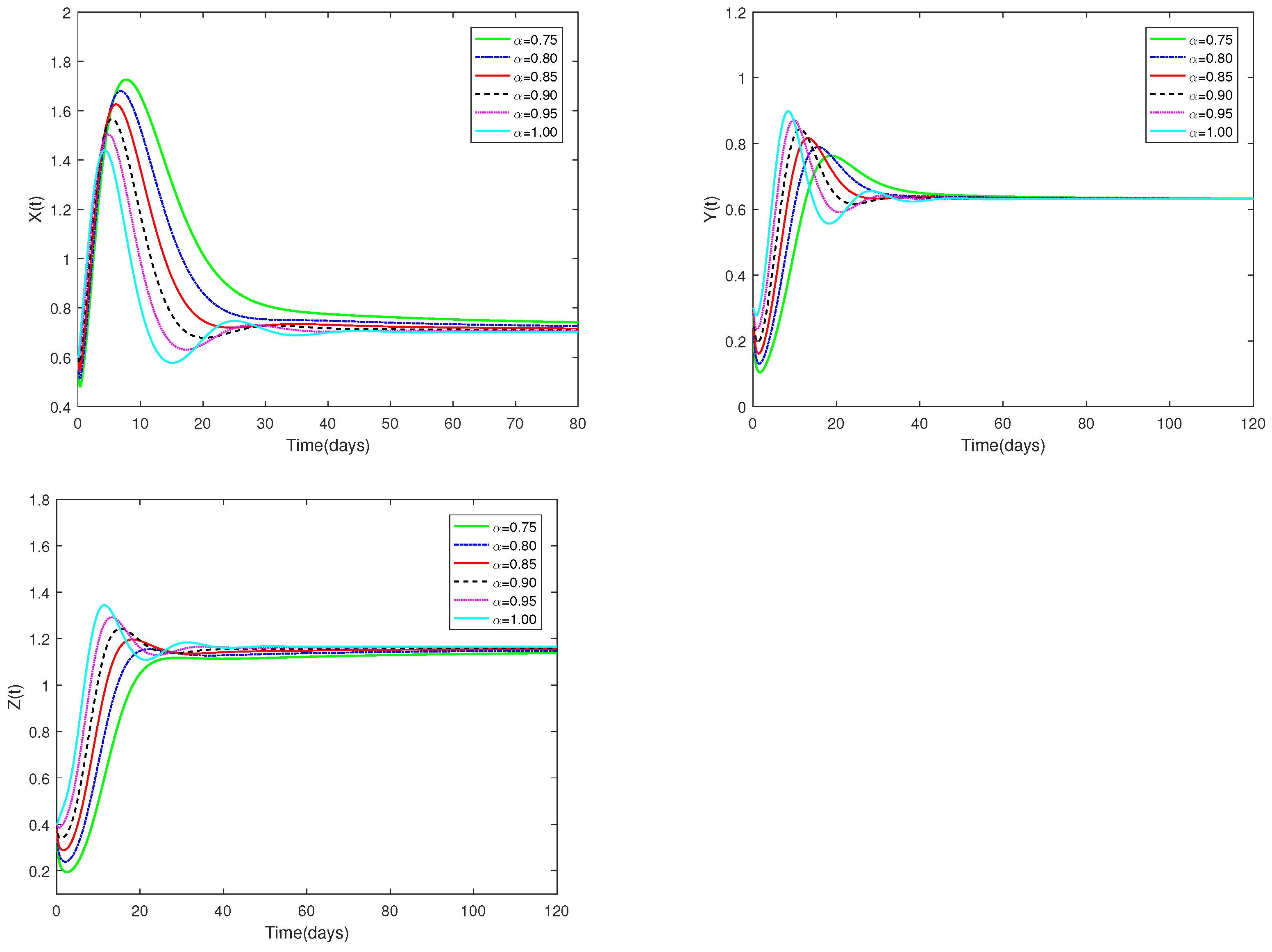
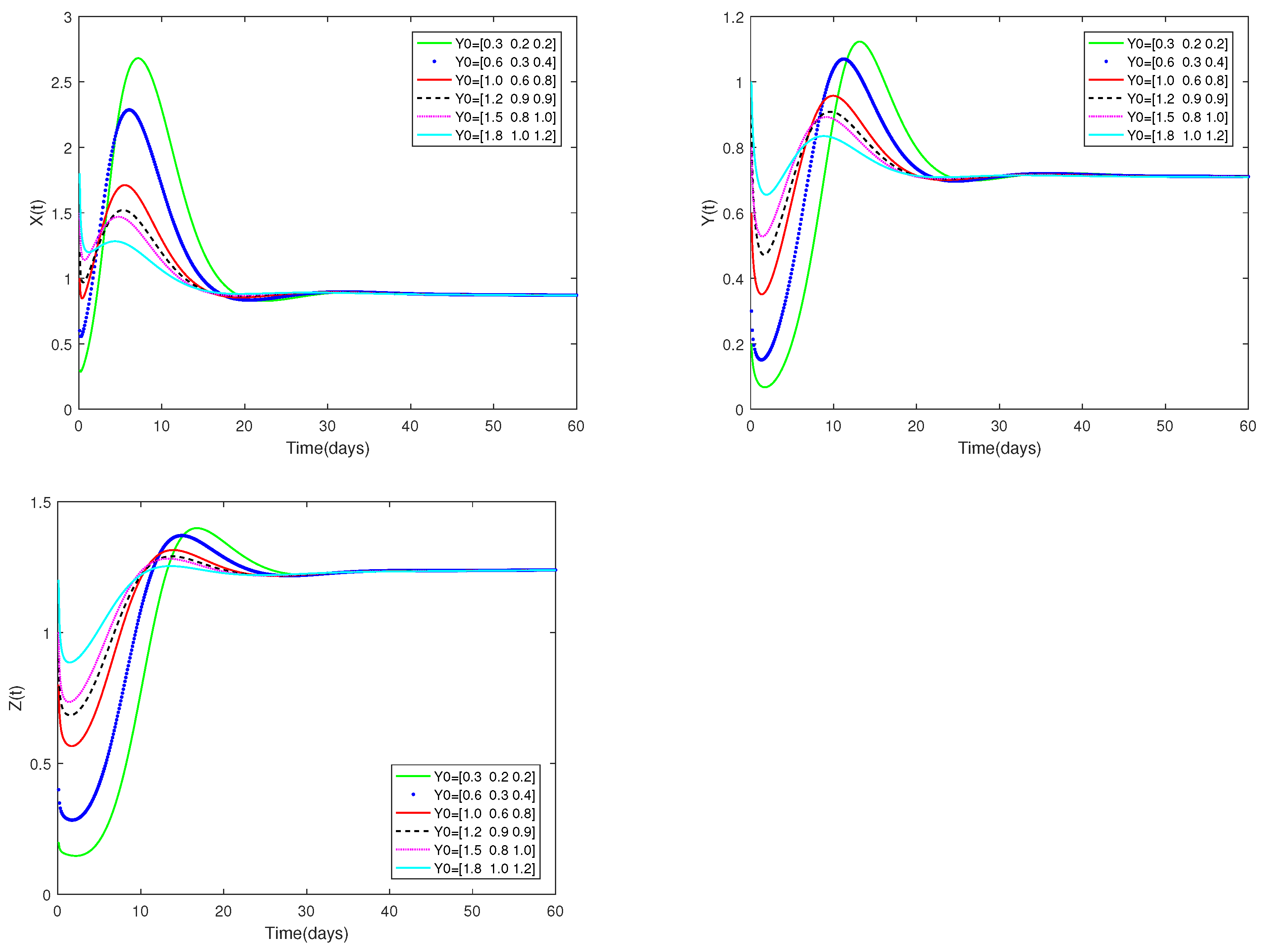
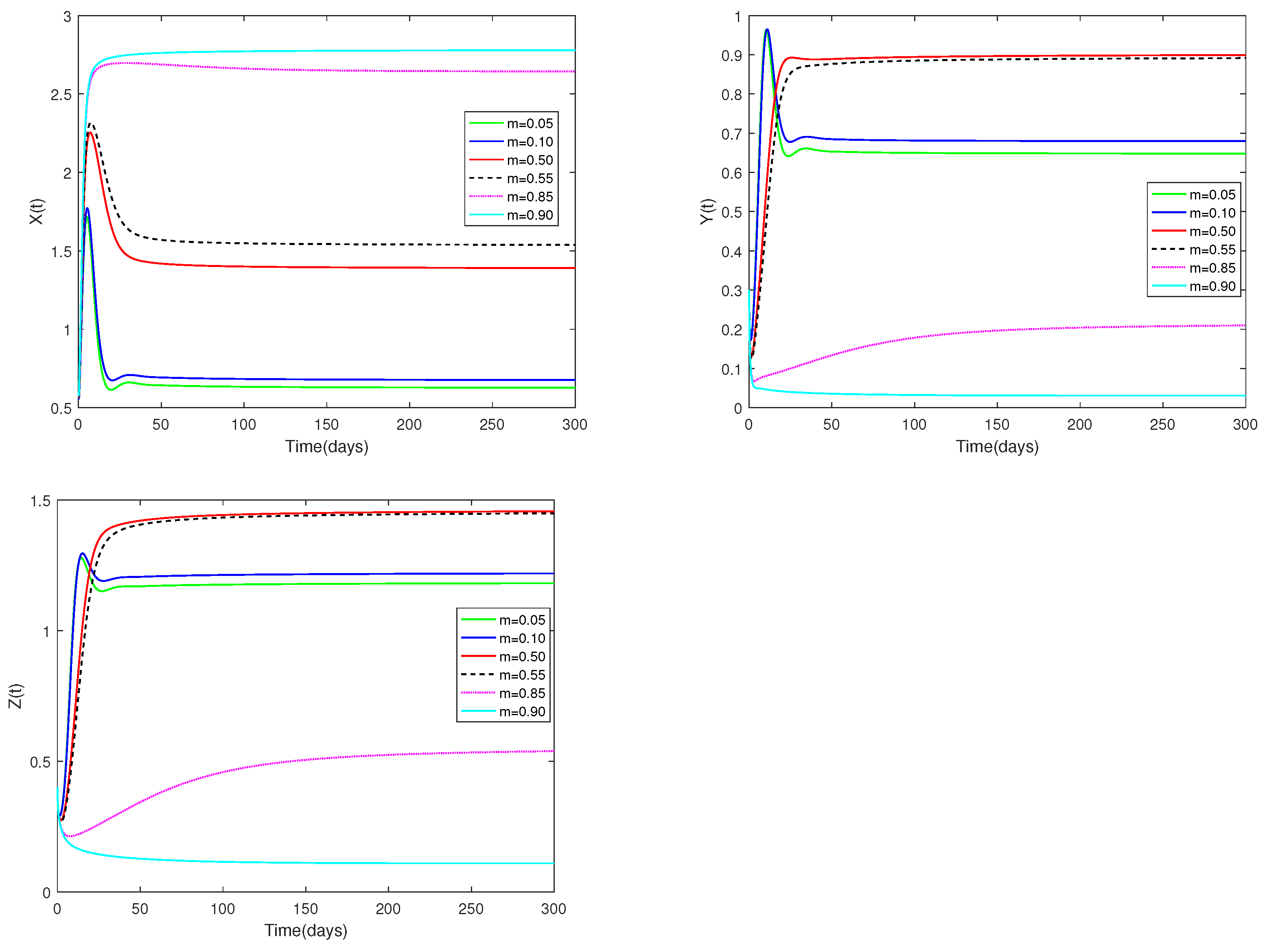
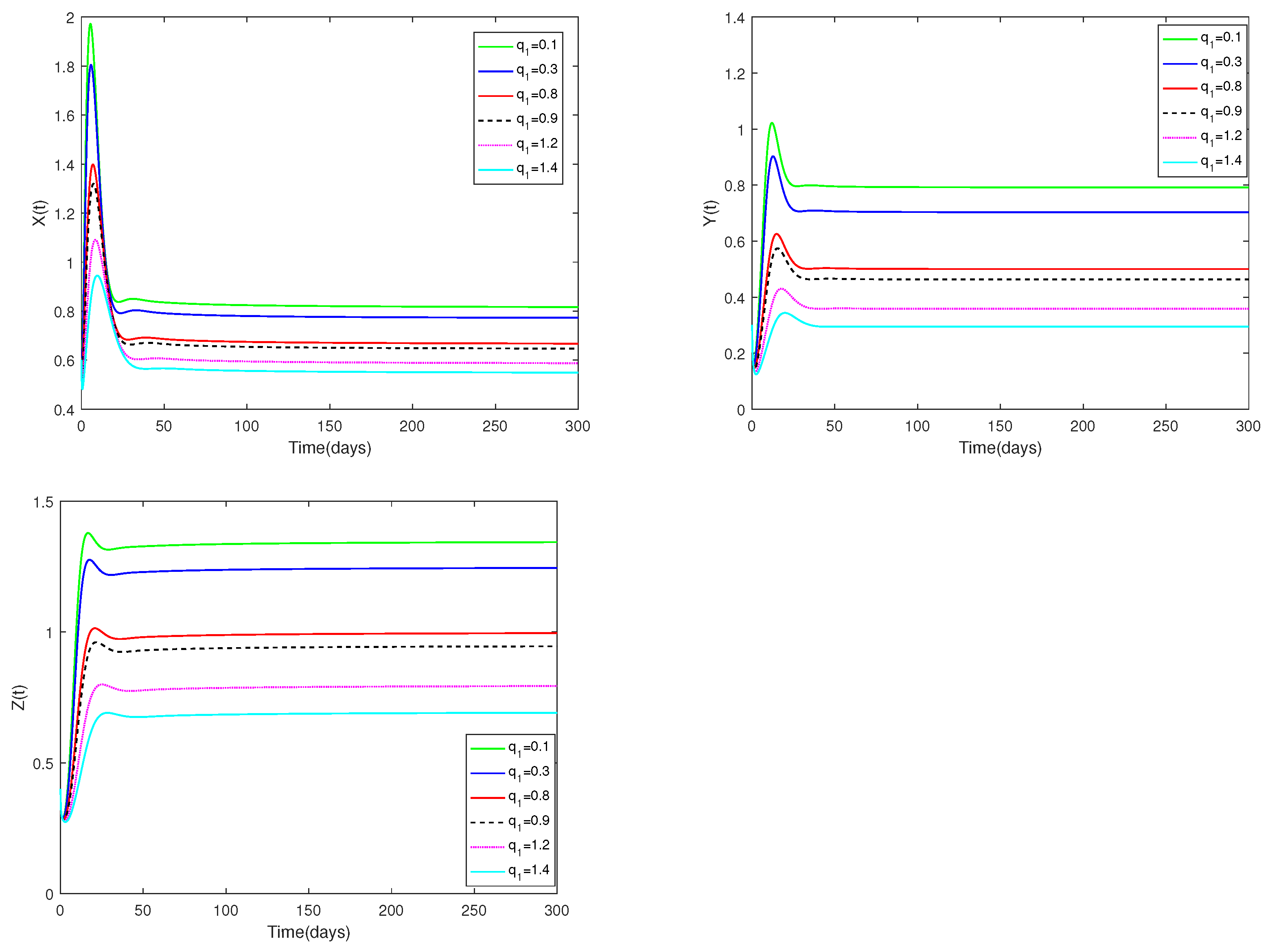
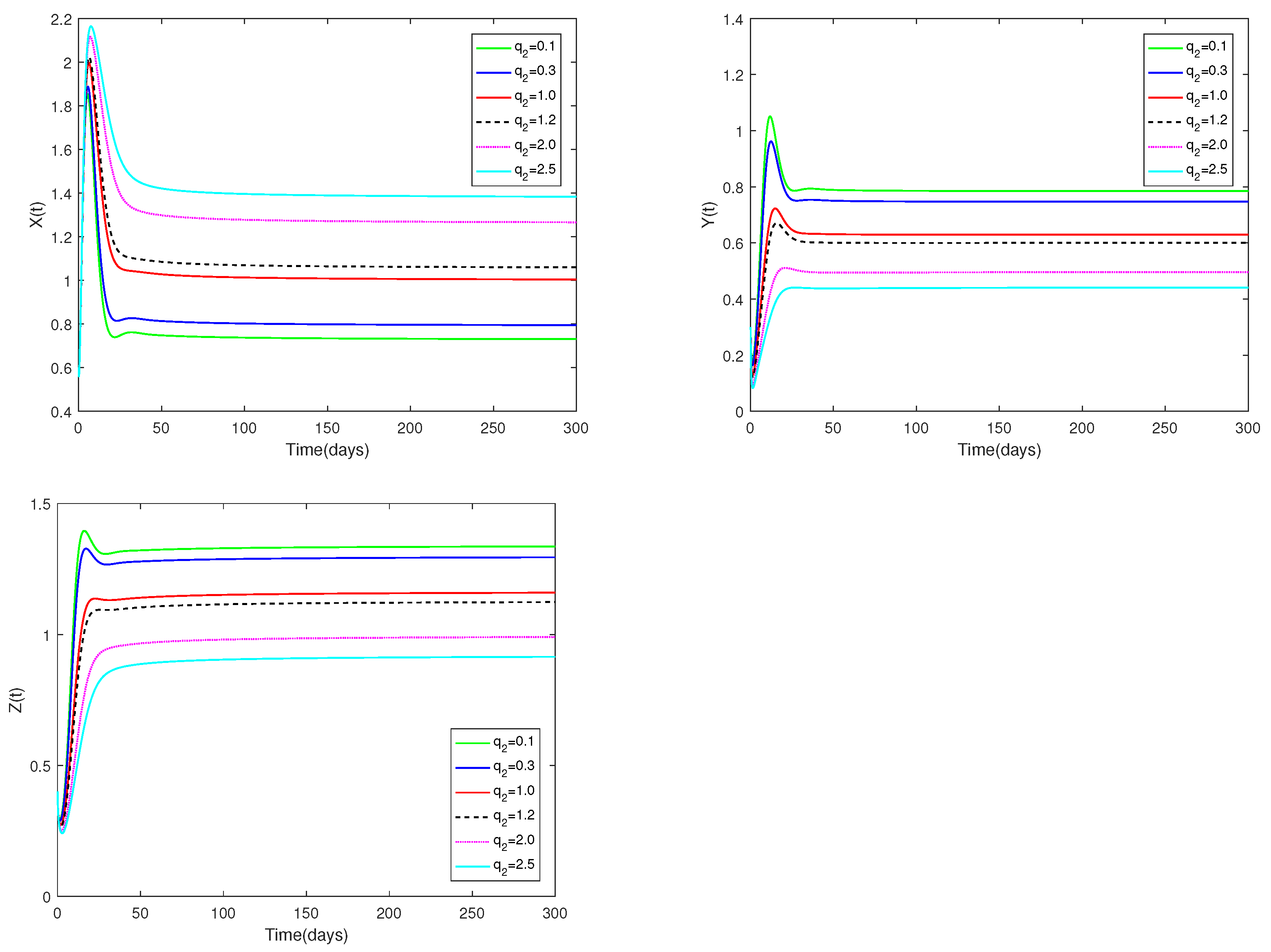
5.1. Examples and Numerical Simulation Results for System (1)
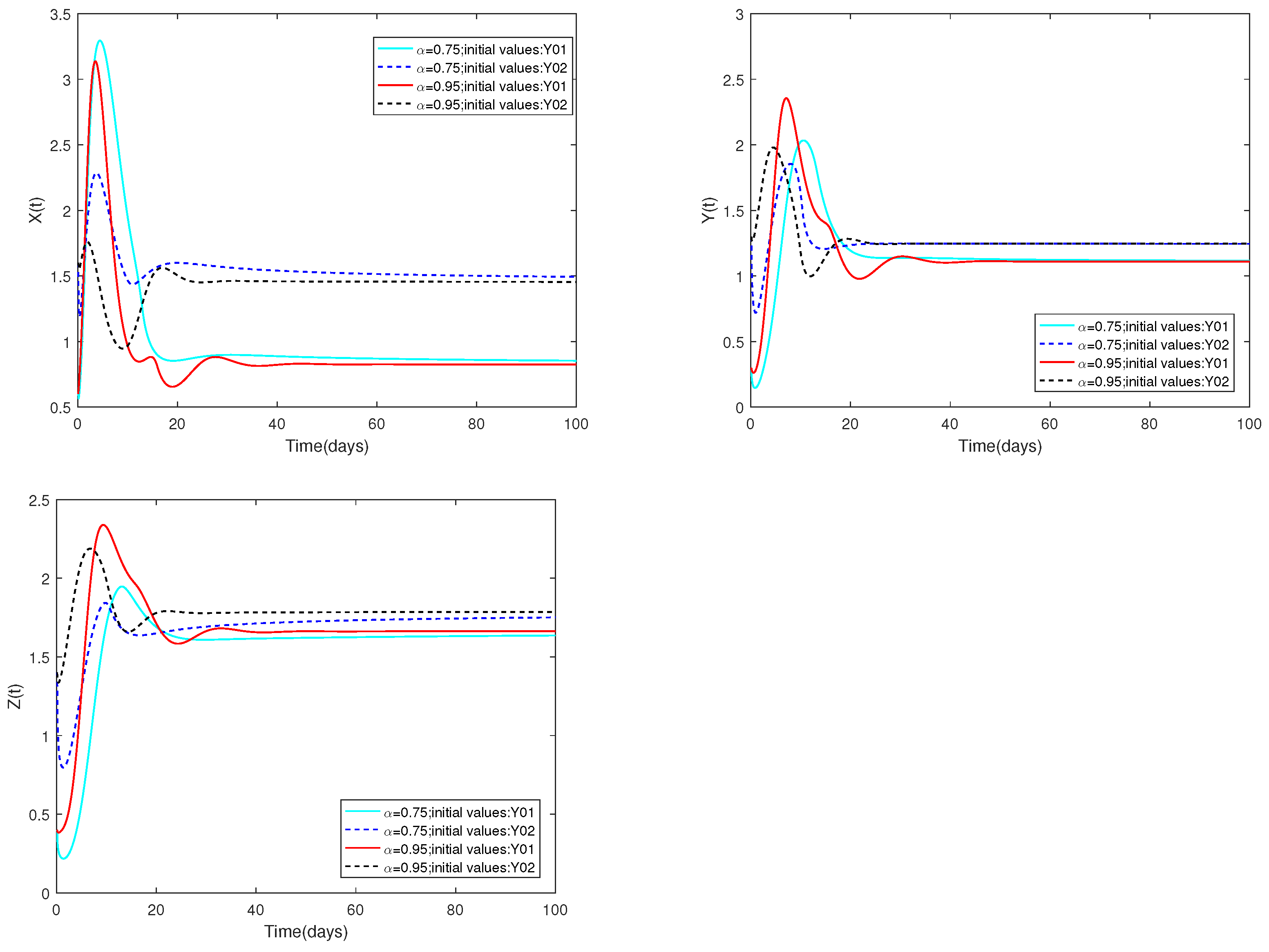
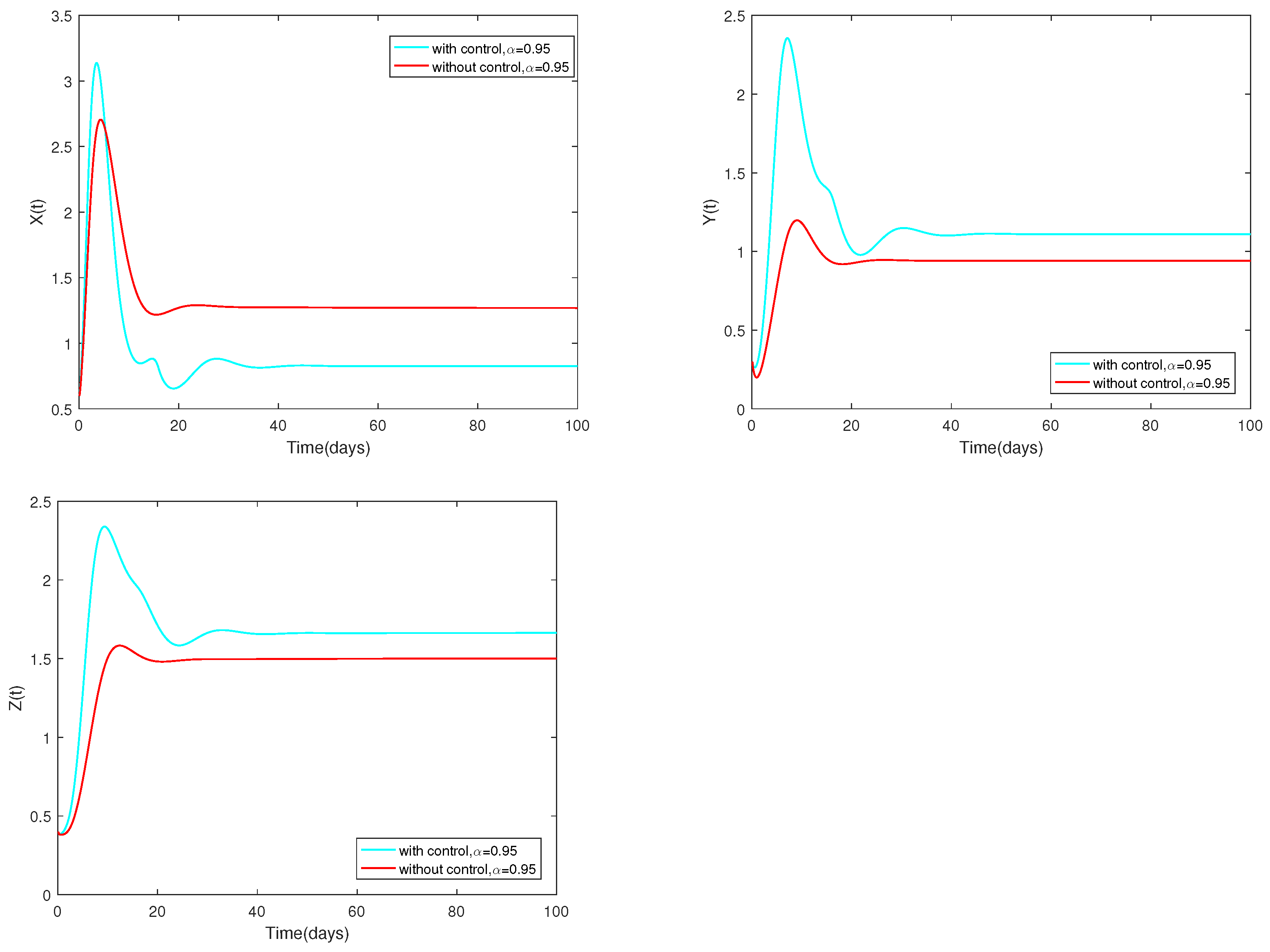
5.2. Examples and Numerical Simulation Results for Optimal Control Problem
6. Discussions and Conclusions
6.1. Discussions
6.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. (Proof of Theorem 4)
Appendix B. (Proof of Theorem 7)
References
- Liu, S.; Chen, L.; Agarwal, R. Recent progress on stage–structured population dynamics. Math. Comput. Model. 2002, 36, 1319–1360. [Google Scholar] [CrossRef]
- Swain, D.P.; Jonsen, I.D.; Simon, J.E.; Myers, R.A. Assessing threats to species at risk using stage-structured state–space models: Mortality trends in skate populations. Ecol. Appl. 2009, 19, 1347–1364. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, K.; Chakraborty, M.; Kar, T.K. Optimal control of harvest and bifurcation of a prey–predator model with stage structure. Appl. Math. Comput. 2011, 217, 8778–8792. [Google Scholar] [CrossRef]
- Chakraborty, K.; Jana, S.; Kar, T.K. Global dynamics and bifurcation in a stage structured prey–predator fishery model with harvesting. Appl. Math. Comput. 2012, 218, 9271–9290. [Google Scholar] [CrossRef]
- Holden, M.H.; Conrad, J.M. Optimal escapement in stage–structured fisheries with environmental stochasticity. Math. Biosci. 2015, 269, 76–85. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Pawelek, K.A.; Liu, S. A stage–structured predator–prey model with predation over juvenile prey. Appl. Math. Comput. 2017, 297, 115–130. [Google Scholar] [CrossRef]
- Mortoja, S.G.; Panja, P.; Mondal, S.K. Dynamics of a predator–prey model with stage–structure on both species and anti–predator behavior. Inform. Med. Unlocked 2018, 10, 50–57. [Google Scholar] [CrossRef]
- Zhao, X.; Zeng, Z. Stationary distribution of a stochastic predator–prey system with stage structure for prey. Physica A 2020, 545, 123318. [Google Scholar] [CrossRef]
- Mondal, N.; Paul, S.; Mahata, A.; ali Biswas, M.; Roy, B.; Alam, S. Study of dynamical behaviors of harvested stage–structured predator–prey fishery model with fear effect on prey under interval uncertainty. Franklin Open 2024, 6, 100060. [Google Scholar] [CrossRef]
- McNair, J.N. The effects of refuges on predator–prey interactions: A reconsideration. Theor. Popul. Biol. 1986, 29, 38–63. [Google Scholar] [CrossRef]
- Sih, A. Prey refuges and predator–prey stability. Theor. Popul. Biol. 1987, 31, 1–12. [Google Scholar] [CrossRef]
- Ruxton, G.D. Short term refuge use and stability of predator–prey models. Theor. Popul. Biol. 1995, 47, 1–17. [Google Scholar] [CrossRef]
- Křivan, V. Effects of optimal antipredator behavior of prey on predator–prey dynamics:the role of refuges. Theor. Popul. Biol. 1998, 53, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Olivares, E.G.; Jiliberto, R.R. Dynamic consequences of prey refuges in a simple model system: More prey, fewer predators and enhanced stability. Ecol. Model. 2003, 166, 135–146. [Google Scholar] [CrossRef]
- Devi, S. Effects of prey refuge on a ratio–dependent predator–prey model with stage–structure of prey population. Appl. Math. Model. 2013, 37, 4337–4349. [Google Scholar] [CrossRef]
- Sharma, S.; Samanta, G.P. A Leslie–Gower predator–prey model with disease in prey incorporating a prey refuge. Chaos Solitons Fractals 2015, 70, 69–84. [Google Scholar] [CrossRef]
- Das, M.; Maiti, A.; Samanta, G.P. Stability analysis of a prey–predator fractional order model incorporating prey refuge. Ecol. Genet. Genom. 2018, 7–8, 33–46. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, Y.; Fu, S.; Wang, W. Optimal control for the spread of infectious disease: The role of awareness programs by media and antiviral treatment. Appl. Math. Comput. 2019, 356, 328–337. [Google Scholar]
- Chakraborty, B.; Bairagi, N. Complexity in a prey–predator model with prey refuge and diffusion. Ecol. Complex. 2019, 37, 11–23. [Google Scholar] [CrossRef]
- Das, A.; Samanta, G.P. A prey–predator model with refuge for prey and additional food for predator in a fluctuating environment. Physica A 2020, 538, 122844. [Google Scholar] [CrossRef]
- Barman, D.; Roy, J.; Alrabaiah, H.; Panja, P.; Mondal, S.P.; Alam, S. Impact of predator incited fear and prey refuge in a fractional order prey predator model. Chaos Solitons Fractals 2021, 142, 110420. [Google Scholar] [CrossRef]
- Molla, H.; Sarwardi, S.; Smith, S.; Haque, M. Dynamics of adding variable prey refuge and an Allee effect to a predator–prey model. Alex. Eng. J. 2022, 61, 4175–4188. [Google Scholar] [CrossRef]
- Pandey, S.; Ghosh, U.; Das, D.; Chakraborty, S.; Sarkar, A. Rich dynamics of a delay–induced stage–structure prey-predator model with cooperative behavior in both species and the impact of prey refuge. Math. Comput. Simul. 2024, 216, 49–76. [Google Scholar] [CrossRef]
- Yang, P. Hopf bifurcation of age–structure prey–predator model with Holling type II functional response incorporating a prey refuge. Nonlinear Anal. Real World Appl. 2019, 49, 368–385. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, V.S. Bifurcations and chaos control in a discrete–time prey–predator model with Holling type II functional response and prey refuge. J. Comput. Appl. Math. 2023, 418, 114666. [Google Scholar] [CrossRef]
- Xiang, C.; Huang, J.; Wang, H. Bifurcations in Holling–Tanner model with generalist predator and prey refuge. J. Differ. Equ. 2023, 343, 495–529. [Google Scholar] [CrossRef]
- Javadi, M.; Nyamoradi, N. Dynamic analysis of a fractional order prey–predator interaction with harvesting. Appl. Math. Model. 2013, 37, 8946–8956. [Google Scholar] [CrossRef]
- Rivero, M.; Trujillo, J.J.; Vazquez, L.; Velasco, M.P. Fractional dynamics of populations. Appl. Math. Comput. 2011, 218, 1089–1095. [Google Scholar] [CrossRef]
- Ghaziani, P.K.; Alidousti, J.; Eshkaftaki, A.B. Stability and dynamics of a fractional order Leslie–Gower prey–predator model. Appl. Math. Comput. 2016, 40, 2075–2086. [Google Scholar]
- Mansal, F.; Sene, N. Analysis of fractional fishery model with reserve area in the context of time–fractional order derivative. Chaos Solitons Fractals 2020, 140, 110200. [Google Scholar] [CrossRef]
- Balci, E. Predation fear and its carry–over effect in a fractional order prey-predator model with prey refuge. Chaos Solitons Fractals 2023, 175, 114016. [Google Scholar] [CrossRef]
- Chu, C.; Liu, W.; Lv, G.; Moussaoui, A.; Auger, P. Optimal harvest for predator–prey fishery models with variable price and marine protected area. Commun. Nonlinear Sci. Numer. Simul. 2024, 134, 107992. [Google Scholar] [CrossRef]
- Liu, X.; Huang, Q. Analysis of optimal harvesting of a predator–prey model with Holling type IV functional response. Ecol. Complex. 2020, 42, 1008165. [Google Scholar] [CrossRef]
- Ibrahim, M. Optimal harvesting of a predator–prey system with marine reserve. Sci. Afr. 2021, 14, e01048. [Google Scholar] [CrossRef]
- Haukkanen, P.; Tossavainen, T. A generalization of Descartes’ rule of signs and fundamental theorem of algebra. Appl. Math. Comput. 2011, 218, 1203–1207. [Google Scholar] [CrossRef]
- Yıldız, T.A.; Arshad, S.; Baleanu, D. New observations on optimal cancer treatments for a fractional tumor growth model with and without singular kernel. Chaos Solitons Fractals 2018, 117, 226–239. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.; El-Saka, H. On some Routh–Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rssler, Chua and Chen systems. Phys. Lett. A 2006, 358, 1–4. [Google Scholar] [CrossRef]
- Pinto, C.; Carvalho, A. A latency fractional order model for HIV dynamics. J. Comput. Appl. Math. 2017, 312, 240–256. [Google Scholar] [CrossRef]
- Li, Y.; Muldowney, J.S. On Bendixson’s criterion. J. Differ. Equ. 1993, 106, 709–726. [Google Scholar] [CrossRef]
- Burler, G.; Freedman, H.I.; Waltman, P. Uniformly persistent systems. Proc. Am. Math. Soc. 1986, 96, 425–430. [Google Scholar]
- Buonomo, B.; D’Onofrio, A.; Lacitiguola, D. Global stability of an SIR epidemic model with information dependent vaccination. Math. Biosci. 2008, 216, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Martin, R.H., Jr. Logarithnic norms and projections applied to linear differential systems. J. Math. Anal. Appl. 1974, 45, 240–256. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, Y. Dynamic analysis and optimal control of a fractional order HIV/HTLV co–infection model with HIV–specific antibody immune response. AIMS Math. 2024, 9, 9455–9493. [Google Scholar] [CrossRef]
- Kamien, M.I.; Schwartz, N.L. Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management; Elsevier: New York, NY, USA, 1991. [Google Scholar]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A. Equilibrium points, stability and numerical solutions of fractional–order predator–prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; El-Mesiry, E.M.; El-Saka, H.A.A. Numerical solution for multi-term fractional (arbitrary) orders differential equations. Comput. Appl. Math. 2004, 23, 33–54. [Google Scholar] [CrossRef]


| The size of the prey | |||
| The size of the immature predator | |||
| The size of the mature predator | |||
| r | The intrinsic growth rate of prey | [0.2 0.3] | [9] |
| K | The environmental carrying capacity for prey | [9] | |
| a | The rate at which an adult predator consumes prey | [9] | |
| The conversion proportion of biomass | 0.9 | ||
| m | The coefficient of prey refuge | 0.2 | [11] |
| The rate at which an adult predator develops from an immature predator | 0.4 | ||
| The rate at which juvenile predators naturally die | [0.02 0.07] | [9] | |
| The percentage of juvenile predator deaths brought on by intraspecific competition | 0.1 | [23] | |
| The rate at which mature predators naturally die | [1.6 1.65] | [9] | |
| The percentage of adult predator deaths brought on by intraspecific competition | 0.1 | [23] | |
| The coefficient of prey and predator available for harvesting | 0.7 | [34] | |
| The effort used to harvest prey | 0.1 | [9] | |
| The effort used to harvest immature predator | 0.25 | [9] | |
| The coefficient by which prey can be captured for harvesting | 0.2 | [9] | |
| The coefficient by which immature predators can be captured for harvesting | 0.3 | [9] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Jia, X.; Shi, R. Dynamic Analysis and Optimal Control of a Fractional Order Fishery Model with Refuge and Protected Area. Axioms 2024, 13, 642. https://doi.org/10.3390/axioms13090642
Gao W, Jia X, Shi R. Dynamic Analysis and Optimal Control of a Fractional Order Fishery Model with Refuge and Protected Area. Axioms. 2024; 13(9):642. https://doi.org/10.3390/axioms13090642
Chicago/Turabian StyleGao, Wenjun, Xiu Jia, and Ruiqing Shi. 2024. "Dynamic Analysis and Optimal Control of a Fractional Order Fishery Model with Refuge and Protected Area" Axioms 13, no. 9: 642. https://doi.org/10.3390/axioms13090642
APA StyleGao, W., Jia, X., & Shi, R. (2024). Dynamic Analysis and Optimal Control of a Fractional Order Fishery Model with Refuge and Protected Area. Axioms, 13(9), 642. https://doi.org/10.3390/axioms13090642





