The Average Sentinel of the Heat Equation with an Unknown Reaction
Abstract
:1. Introduction
2. Problem Setting
3. Solving Equation (1) by the Decomposition Method
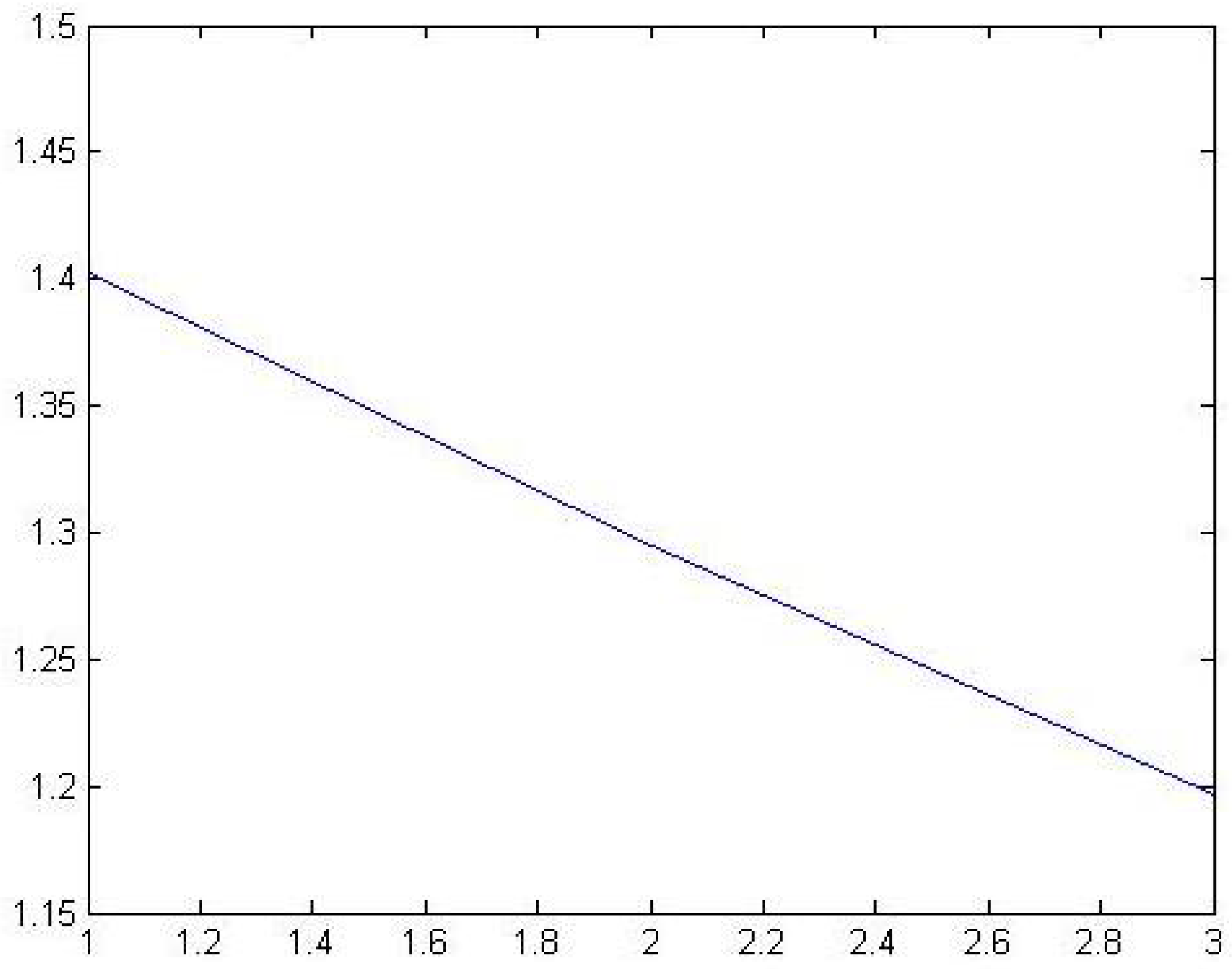
4. Gradient Method (Iterative Method (See in Figure 2))
5. Average Solution to the Heat Equation with an Unknown Parameter
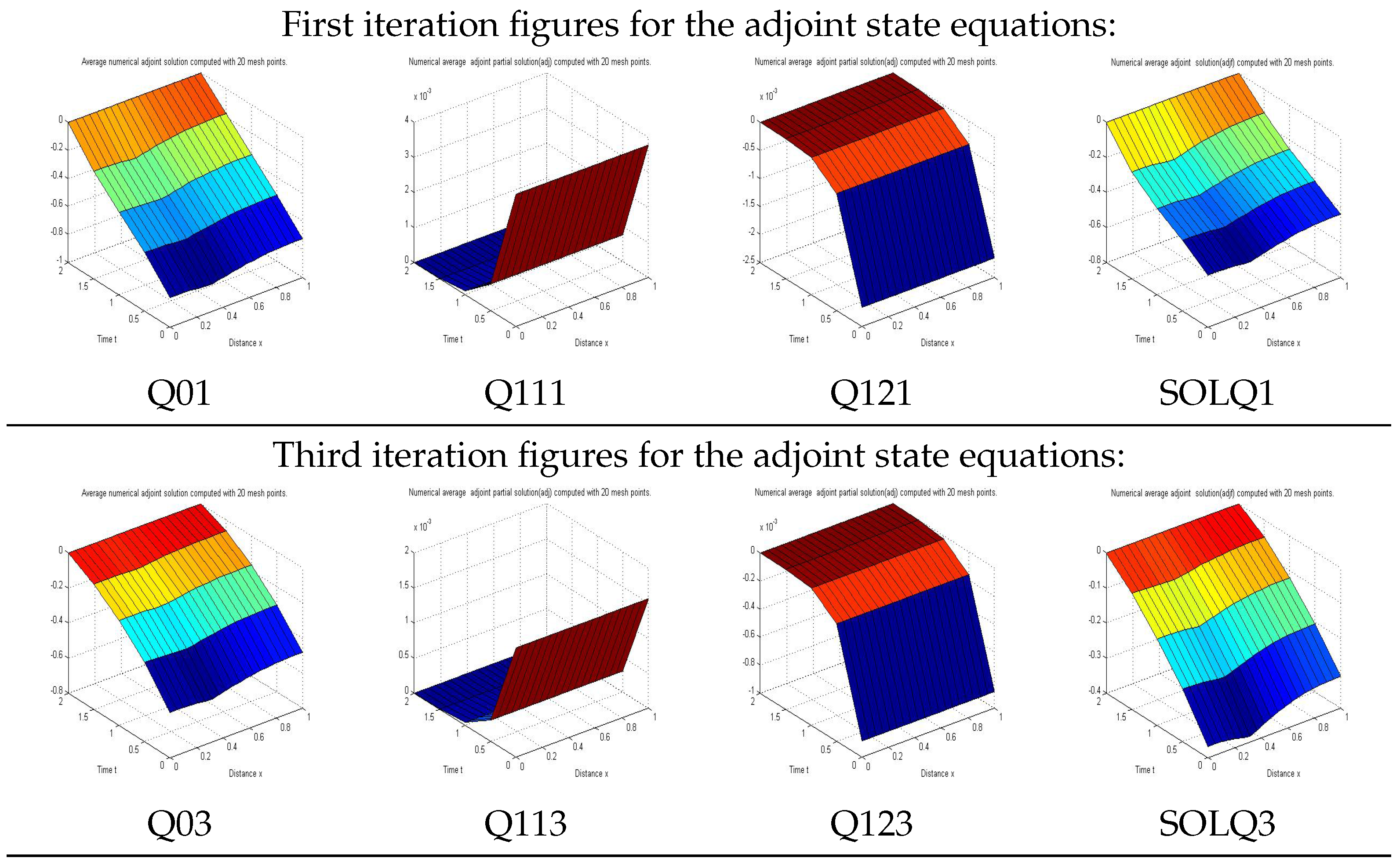
6. Numerical Application
7. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kernévez, J.P. The Sentinel Method and Its Applications to Environmental Pollution Problems; CRC Mathematical Modelling Series; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Abdelhamid, A.; Chafia, L.; Abdelhak, H. Identification problem of a fractional thermoelastic deformation system with incomplete data: A sentinel method. Nonlinear Stud. 2022, 29, 399–410. [Google Scholar]
- Elhamza, B.; Hafdallah, A. Identification of the bulk modulus coefficient in the acoustic equation from boundary observation: A sentinel method. Bound Value Probl. 2023, 2023, 23. [Google Scholar] [CrossRef]
- Zuazua, E. Averaged control. Automatica 2014, 50, 3077–3087. [Google Scholar] [CrossRef]
- Fursikov, A.V. Properties of solutions of some extremal problems connected with the Navier-Stokes system. Math. USSR-Sb. 1983, 46, 323–351. [Google Scholar] [CrossRef]
- Lions, J.L. Some notions in the analysis and control of incomplete data systems. In Proceedings of the 11th Congress on Differential Equations and Applications, Kyoto, Japan, 21–29 August 1990; pp. 43–54. [Google Scholar]
- Elhamza, B. Hafdallah: Identification of the potential coefficient in the wave equation with incomplete data: A sentinel method. Russ. Math. 2022, 2022, 113–122. [Google Scholar] [CrossRef]
- Raore, A.; Mampassi, B.; Saley, B. A Numerical Approach of the sentinel method for distributed parameter systems. Open Math. 2007, 5, 751–763. [Google Scholar] [CrossRef]
- Selatnia, H.; Berhail, A.; Ayadi, A. Average Sentinel for a Heat Equation with Incomplete Data. J. Appl. Comput. Math. 2018, 7, 2. [Google Scholar] [CrossRef]
- Fursikov, A.V.; Imanuvilov, O.Y. Controllability of Evolution Equations; Séoul National University: Seoul, Republic of Korea, 1996. [Google Scholar]
- Lions, J.L. Contrôle Optimal de Systèmes Gouvernés par des Equations aux Dérivées Partielles; Dunod: Paris, France, 1968. [Google Scholar]
- Lions, J.L.; Bensoussan, A.; Glowinski, R. Méthode de Décomposition Appliquée au Contrôle Optimal de Systèmes Distribués. In Proceedings of the 5th IFIP Conference on Optimization Techniques, Rome, Italy, 7–11 May 1973; Lecture Notes in Computer Science. Springer: Berlin, Germany, 1973; Volume 5. [Google Scholar]
- Chavent, G. Generalized sentinels de ned via least squares. Appl. Math. Optim. 1993, 31, 189–218. [Google Scholar] [CrossRef]
- Lions, J.L. Sentinelles Pour les Systémes Distribués à Données Incomplètes; Masson, RMA: Paris, France, 1992; Volume 21. [Google Scholar]
- Lions, J.L. Contrôlabilité exacte, perturbations et stabilisation de systèmes distribués. In Contrôlabilité Exacte, Recherches en Mathématiques Appliquéesl; Masson: Paris, France, 1988; Volume 8. [Google Scholar]
- Massengo, G.; Nakoulima, O. Sentinels with given sensitivity. Eur. J. Appl. Math. 2008, 19, 21–40. [Google Scholar] [CrossRef]
- Merabet, A.; Ayadi, A.; Omrane, A. Detection of pollution terms in nonlinear second order wave systems. Int. J. Parallel Emergent Distrib. Syst. 2019, 34, 13–20. [Google Scholar] [CrossRef]
- Nakoulima, O. Optimal control for distribute systems subject to null controllability. Application to discrimiting sentinels. Esaim Control Optim. Calc. Var. 2007, 13, 623–638. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selatnia, H.; Ayadi, A.; Rezzoug, I. The Average Sentinel of the Heat Equation with an Unknown Reaction. Axioms 2024, 13, 128. https://doi.org/10.3390/axioms13020128
Selatnia H, Ayadi A, Rezzoug I. The Average Sentinel of the Heat Equation with an Unknown Reaction. Axioms. 2024; 13(2):128. https://doi.org/10.3390/axioms13020128
Chicago/Turabian StyleSelatnia, Houria, Abdelhamid Ayadi, and Imad Rezzoug. 2024. "The Average Sentinel of the Heat Equation with an Unknown Reaction" Axioms 13, no. 2: 128. https://doi.org/10.3390/axioms13020128





