A New Optimal Numerical Root-Solver for Solving Systems of Nonlinear Equations Using Local, Semi-Local, and Stability Analysis
Abstract
1. Introduction
2. Existing Optimal Algorithms
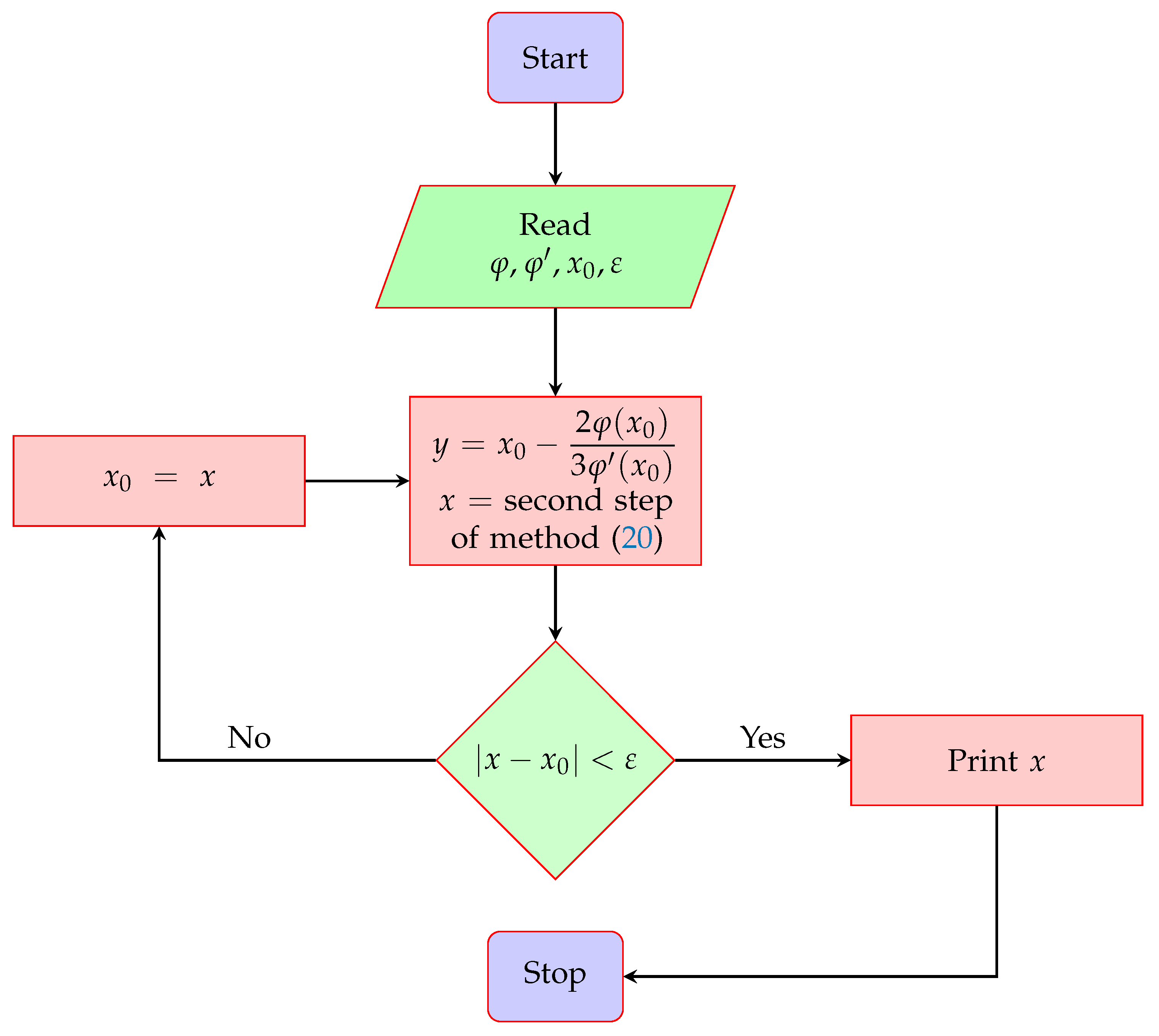
3. Construction of the Optimal Fourth-Order Numerical Solver
4. Local Convergence Analysis
4.1. Scalar Form
4.2. Vector Form
5. Convergence without Taylor Series
- (P1)
- The local convergence is carried out for functions on the real line or the finite-dimensional Euclidean space.
- (P2)
- The function must be at least five times differentiable. Let us consider a function , defined as follows:where and Then, is a solution of the equation . But the function is not continuous at Thus, the results of the previous section—being only sufficient—cannot guarantee the convergence of the sequence generated by the method to the solution . However, the method converges to if, for example, we start from . This observation indicates that the sufficient convergence conditions can be weakened.
- (P3)
- There is no a priori knowledge of the number of iterations required to reach a desired error tolerance since no computable upper bounds on are given.
- (P4)
- The separation of the solutions is not discussed.
- (P5)
- The semi-local analysis of convergence, which is considered to be more important, is not considered either.
- (P1)’
- The convergence analysis is carried out for Banach space-valued operators.
- (P2)’
- Both types of analyses use conditions only on the operators on the method (20).
- (P3)’
- The number of iterations to reach the error tolerance is known in advance since priori estimates on are provided.
- (P4)’
- The separation of the solutions is discussed.
- (P5)’
5.1. Local Analysis of Convergence
- (C1)
- There exists the smallest solution of the equation where is a continuous and non-decreasing function. Set
- (C2)
- There exists a function, , such that is defined by the following:the equation has the smallest solution in the interval denoted as .
- (C3)
- The equation where is defined byhas the smallest solution , denoted as Set and
- (C4)
- The equation where is defined by the following:has the smallest solution in denoted as Set
- (C5)
- There exists and a solution such that so that for each , Set .
- (C6)
- for each and
- (C7)
- .
- (i)
- The radius r in the condition (C7) can be replaced by
- (ii)
- Possible choices of the operator Δ can be or , provided that the operator is invertible. Other choices are possible, as long as conditions (C5) and (C6) hold.
5.2. Semi-Local Analysis of Convergence
- (H1)
- Equation has the smallest solution denoted by in the interval where is a continuous as well as a non-decreasing function. Set
- (H2)
- There exists a function , which is continuous as well as non-decreasing. We define the sequence for some and each by the following:The scalar sequence , as defined, is shown in Theorem 4 to be majorizing for the method (33). But first, a general convergence condition for it is needed.
- (H3)
- There exists , such that for each andIt follows by simple induction (46) and condition (H3) that . Thus, the real sequence is nondecreasing and bounded from above by , and as such, it is convergent to some such that .The limit is the unique least upper bound of the sequence . Notice that if is strictly increasing, we can take As in the local analysis, the functions and relate to the operators of the method (33).
- (H4)
- There exists an invertible operator such that for some ,Set Notice that for , we have Thus, and we can take
- (H5)
- for each , and
- (H6)
- (i)
- The parameter α can be switched by in the condition (C6).
- (ii)
- As in the local case, possible choices are or , provided that the operator is invertible. Other choices satisfying the conditions (C4) and (C5) are possible.
6. Stability Analysis
- and , which are super-attracting;
- , which is repelling; and
- , , and , the roots of polynomial , which are repelling.
- and ; and
- , , , and , the roots of polynomial .
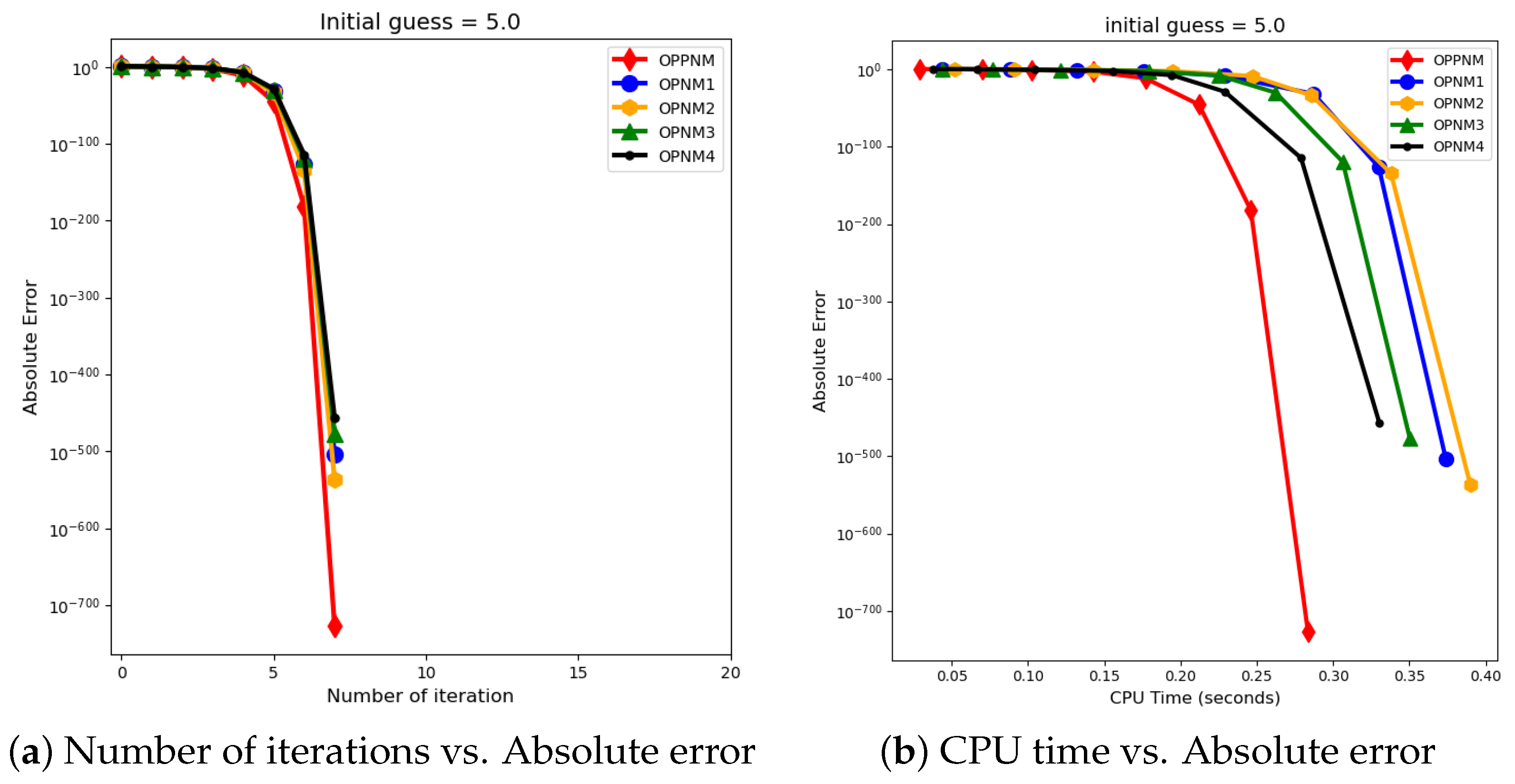
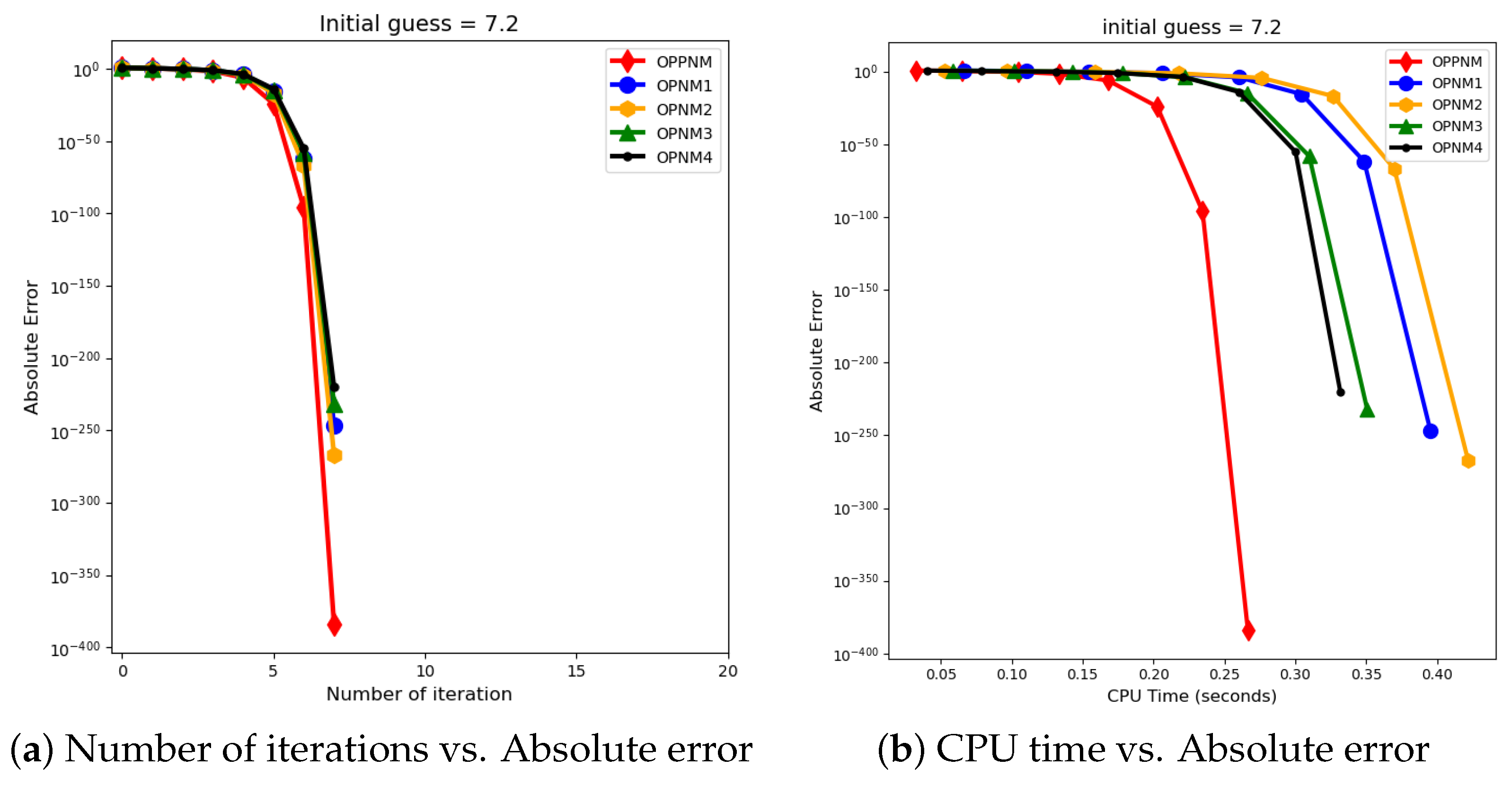
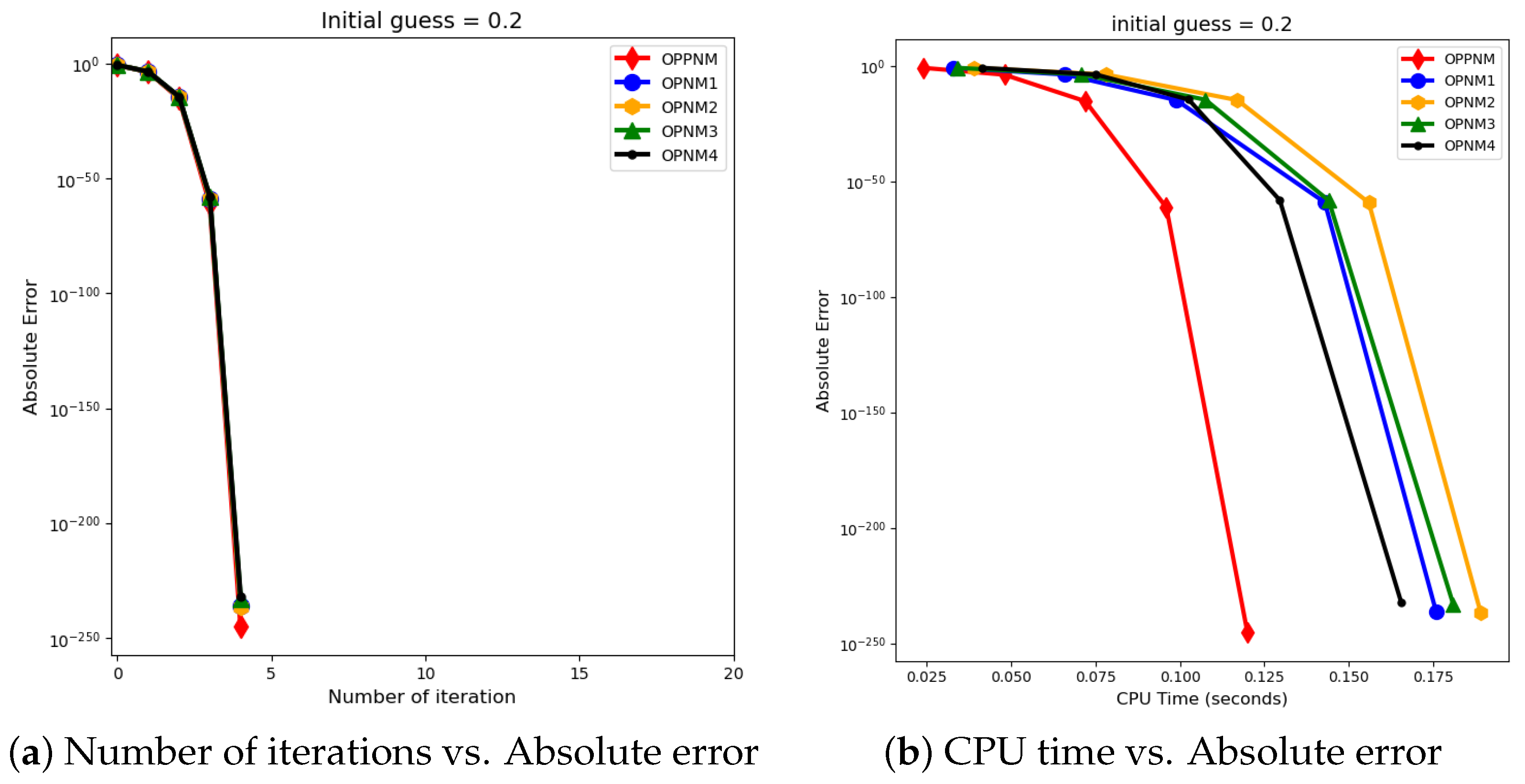
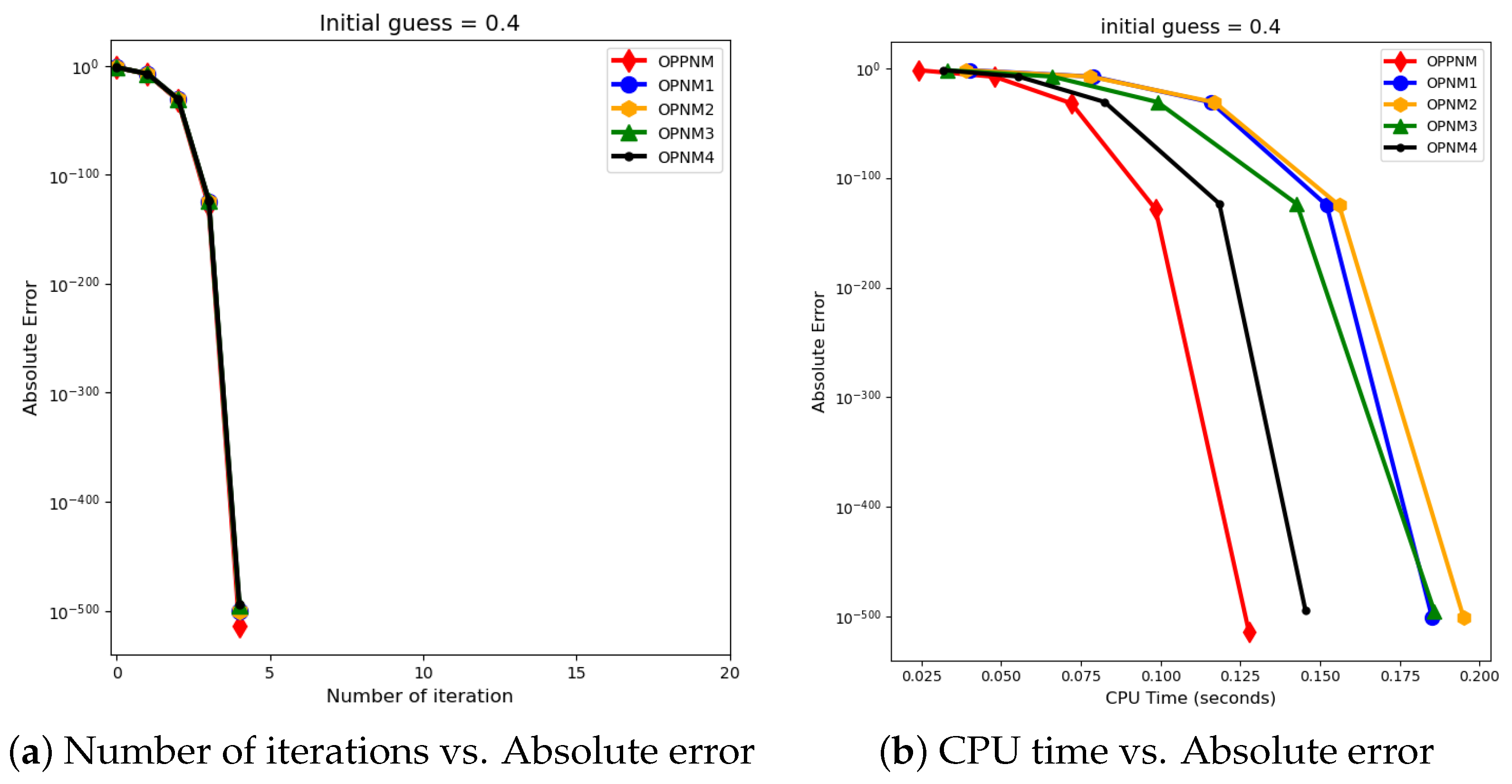
7. Numerical Results
8. Conclusions and Future Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faires, J.; Burden, R. Numerical Methods, 4th ed.; Cengage Learning: Belmont, CA, USA, 2012. [Google Scholar]
- Naseem, A.; Rehman, M.; Abdeljawad, T. A novel root-finding algorithm with engineering applications and its dynamics via computer technology. IEEE Access 2022, 10, 19677–19684. [Google Scholar] [CrossRef]
- Abro, H.A.; Shaikh, M.M. A new family of twentieth order convergent methods with applications to nonlinear systems in engineering. Mehran Univ. Res. J. Eng. Technol. 2023, 42, 165–176. [Google Scholar] [CrossRef]
- Shaikh, M.M.; Massan, S.-u.-R.; Wagan, A.I. A sixteen decimal places’ accurate Darcy friction factor database using non-linear Colebrook’s equation with a million nodes: A way forward to the soft computing techniques. Data Brief 2019, 27, 104733. [Google Scholar] [CrossRef]
- Argyros, M.I.; Argyros, I.K.; Regmi, S.; George, S. Generalized three-step numerical methods for solving equations in banach spaces. Mathematics 2022, 10, 2621. [Google Scholar] [CrossRef]
- Ramos, H.; Monteiro, M.T.T. A new approach based on the Newton’s method to solve systems of nonlinear equations. J. Comput. Appl. Math. 2017, 318, 3–13. [Google Scholar] [CrossRef]
- Ramos, H.; Vigo-Aguiar, J. The application of Newton’s method in vector form for solving nonlinear scalar equations where the classical Newton method fails. J. Comput. Appl. Math. 2015, 275, 228–237. [Google Scholar] [CrossRef]
- Abdullah, S.; Choubey, N.; Dara, S. Optimal fourth-and eighth-order iterative methods for solving nonlinear equations with basins of attraction. J. Appl. Math. Comput. 2024. [Google Scholar] [CrossRef]
- Yun, J.H. A note on three-step iterative method for nonlinear equations. Appl. Math. Comput. 2008, 202, 401–405. [Google Scholar] [CrossRef]
- Dehghan, M.; Shirilord, A. Three-step iterative methods for numerical solution of systems of nonlinear equations. Eng. Comput. 2022, 38, 1015–1028. [Google Scholar] [CrossRef]
- Soleymani, F.; Vanani, S.K.; Afghani, A. A general three-step class of optimal iterations for nonlinear equations. Math. Prob. Eng. 2011, 2011, 469512. [Google Scholar] [CrossRef]
- Darvishi, M. Some three-step iterative methods free from second order derivative for finding solutions of systems of nonlinear equations. Int. J. Pure Appl. Math. 2009, 57, 557–573. [Google Scholar]
- Kung, H.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. ACM 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Singh, A.; Jaiswal, J. Several new third-order and fourth-order iterative methods for solving nonlinear equations. Int. J. Eng. Math. 2014, 2014, 828409. [Google Scholar] [CrossRef]
- Jaiswal, J.P. Some class of third-and fourth-order iterative methods for solving nonlinear equations. J. Appl. Math. 2014, 2014, 817656. [Google Scholar] [CrossRef]
- Sharma, E.; Panday, S.; Dwivedi, M. New optimal fourth order iterative method for solving nonlinear equations. Int. J. Emerg. Technol. 2020, 11, 755–758. [Google Scholar]
- Khattri, S.K.; Abbasbandy, S. Optimal fourth order family of iterative methods. Matematički Vesnik 2011, 63, 67–72. [Google Scholar]
- Chun, C.; Lee, M.Y.; Neta, B.; Džunić, J. On optimal fourth-order iterative methods free from second derivative and their dynamics. Appl. Math. Comput. 2012, 218, 6427–6438. [Google Scholar] [CrossRef]
- Panday, S.; Sharma, A.; Thangkhenpau, G. Optimal fourth and eighth-order iterative methods for non-linear equations. J. Appl. Math. Comput. 2023, 69, 953–971. [Google Scholar] [CrossRef]
- Abro, H.A.; Shaikh, M.M. A new time-efficient and convergent nonlinear solver. Appl. Math. Comput. 2019, 355, 516–536. [Google Scholar] [CrossRef]
- Qureshi, S.; Ramos, H.; Soomro, A.K. A New Nonlinear Ninth-Order Root-Finding Method with Error Analysis and Basins of Attraction. Mathematics 2021, 9, 1996. [Google Scholar] [CrossRef]
- Argyros, I. Unified Convergence Criteria for Iterative Banach Space Valued Methods with Applications. Mathematics 2021, 9, 1942. [Google Scholar] [CrossRef]
- Argyros, I. The Theory and Applications of Iteration Methods, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Devaney, R.L. An Introduction to Chaotic Dynamical Systems; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Beardon, A.F. Iteration of Rational Functions: Complex Analytic Dynamical Systems; Springer: New York, NY, USA, 1991. [Google Scholar]
- Wang, X.; Chen, X.; Li, W. Dynamical behavior analysis of an eighth-order Sharma’s method. Intl. J. Biomath. 2023, 2023, 2350068. [Google Scholar] [CrossRef]
- Kroszczynski, K.; Kiliszek, D.; Winnicki, I. Some Properties of the Basins of Attraction of the Newton’s Method for Simple Nonlinear Geodetic Systems. Preprints 2021, 2021120151. [Google Scholar] [CrossRef]
- Campos, B.; Villalba, E.G.; Vindel, P. Dynamical and numerical analysis of classical multiple roots finding methods applied for different multiplicities. Comput. Appl. Math. 2024, 43, 230. [Google Scholar] [CrossRef]
- Campos, B.; Canela, J.; Vindel, P. Dynamics of Newton-line root finding methods. Numer. Algorithms 2023, 93, 1453–1480. [Google Scholar] [CrossRef]
- Chicharro, F.I.; Cordero, A.; Torregrosa, J.R. Drawing Dynamical and Parameters Planes of Iterative Families and Methods. Sci. World J. 2013, 2013, 708153. [Google Scholar] [CrossRef]
- Abdullah, S.; Choubey, N.; Dara, S. An efficient two-point iterative method with memory for solving non-linear equations and its dynamics. J. Appl. Math. Comput. 2024, 70, 285–315. [Google Scholar] [CrossRef]
- Verschelde, J.; Verlinden, P.; Cools, R. Homotopies exploiting Newton polytopes for solving sparse polynomial systems. SIAM J. Numer. Anal. 1994, 31, 915–930. [Google Scholar] [CrossRef]
- Grosan, C.; Abraham, A. A new approach for solving nonlinear equations systems. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2008, 38, 698–714. [Google Scholar] [CrossRef]
- Morgan, A. Solving Polynomial Systems Using Continuation for Engineering and Scientific Problems; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]



| Problem | IG | Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.5 | OPPNM | 4.58 | 1.26 | - | |||||
| OPNM1 | 4.35 | 1.46 | - | |||||||
| OPNM2 | 4.40 | 1.42 | - | |||||||
| OPNM3 | 4.33 | 1.47 | - | |||||||
| OPNM4 | 4.30 | 1.50 | - | |||||||
| 8.0 | OPPNM | 5.54 | 1.76 | - | ||||||
| OPNM1 | 5.41 | 1.85 | - | |||||||
| OPNM2 | 5.43 | 1.84 | - | |||||||
| OPNM3 | 5.39 | 1.86 | - | |||||||
| OPNM4 | 5.39 | 1.86 | - | |||||||
| 2 | 5.0 | OPPNM | 2.65 | |||||||
| OPNM1 | 2.51 | |||||||||
| OPNM2 | 2.54 | |||||||||
| OPNM3 | 2.50 | |||||||||
| OPNM4 | 2.48 | |||||||||
| 7.2 | OPPNM | 3.94 | 1.53 | |||||||
| OPNM1 | 3.68 | 1.62 | ||||||||
| OPNM2 | 3.74 | 1.61 | ||||||||
| OPNM3 | 3.66 | 1.63 | ||||||||
| OPNM4 | 3.63 | 1.64 | ||||||||
| 3 | 0.2 | OPPNM | - | - | - | |||||
| OPNM1 | - | - | - | |||||||
| OPNM2 | - | - | - | |||||||
| OPNM3 | - | - | - | |||||||
| OPNM4 | - | - | - | |||||||
| 0.4 | OPPNM | - | - | - | ||||||
| OPNM1 | - | - | - | |||||||
| OPNM2 | - | - | - | |||||||
| OPNM3 | - | - | - | |||||||
| OPNM4 | - | - | - |
| Problem | Method | |||||||
|---|---|---|---|---|---|---|---|---|
| 4 | OPPNM | - | ||||||
| OPNM1 | - | |||||||
| OPNM2 | - | |||||||
| OPNM3 | - | |||||||
| OPNM4 | - | |||||||
| 5 | OPPNM | |||||||
| OPNM1 | ||||||||
| OPNM2 | ||||||||
| OPNM3 | ||||||||
| OPNM4 | ||||||||
| 6 | OPPNM | 1.68 | ||||||
| OPNM1 | 1.63 | |||||||
| OPNM2 | 1.64 | |||||||
| OPNM3 | 1.62 | |||||||
| OPNM4 | 1.61 | |||||||
| 7 | OPPNM | |||||||
| OPNM1 | ||||||||
| OPNM2 | ||||||||
| OPNM3 | ||||||||
| OPNM4 | ||||||||
| 8 | OPPNM | |||||||
| OPNM1 | ||||||||
| OPNM2 | ||||||||
| OPNM3 | ||||||||
| OPNM4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qureshi, S.; Chicharro, F.I.; Argyros, I.K.; Soomro, A.; Alahmadi, J.; Hincal, E. A New Optimal Numerical Root-Solver for Solving Systems of Nonlinear Equations Using Local, Semi-Local, and Stability Analysis. Axioms 2024, 13, 341. https://doi.org/10.3390/axioms13060341
Qureshi S, Chicharro FI, Argyros IK, Soomro A, Alahmadi J, Hincal E. A New Optimal Numerical Root-Solver for Solving Systems of Nonlinear Equations Using Local, Semi-Local, and Stability Analysis. Axioms. 2024; 13(6):341. https://doi.org/10.3390/axioms13060341
Chicago/Turabian StyleQureshi, Sania, Francisco I. Chicharro, Ioannis K. Argyros, Amanullah Soomro, Jihan Alahmadi, and Evren Hincal. 2024. "A New Optimal Numerical Root-Solver for Solving Systems of Nonlinear Equations Using Local, Semi-Local, and Stability Analysis" Axioms 13, no. 6: 341. https://doi.org/10.3390/axioms13060341
APA StyleQureshi, S., Chicharro, F. I., Argyros, I. K., Soomro, A., Alahmadi, J., & Hincal, E. (2024). A New Optimal Numerical Root-Solver for Solving Systems of Nonlinear Equations Using Local, Semi-Local, and Stability Analysis. Axioms, 13(6), 341. https://doi.org/10.3390/axioms13060341









