Mathematical Model of the Evolution of a Simple Dynamic System with Dry Friction
Abstract
:1. Introduction
2. Materials and Methods
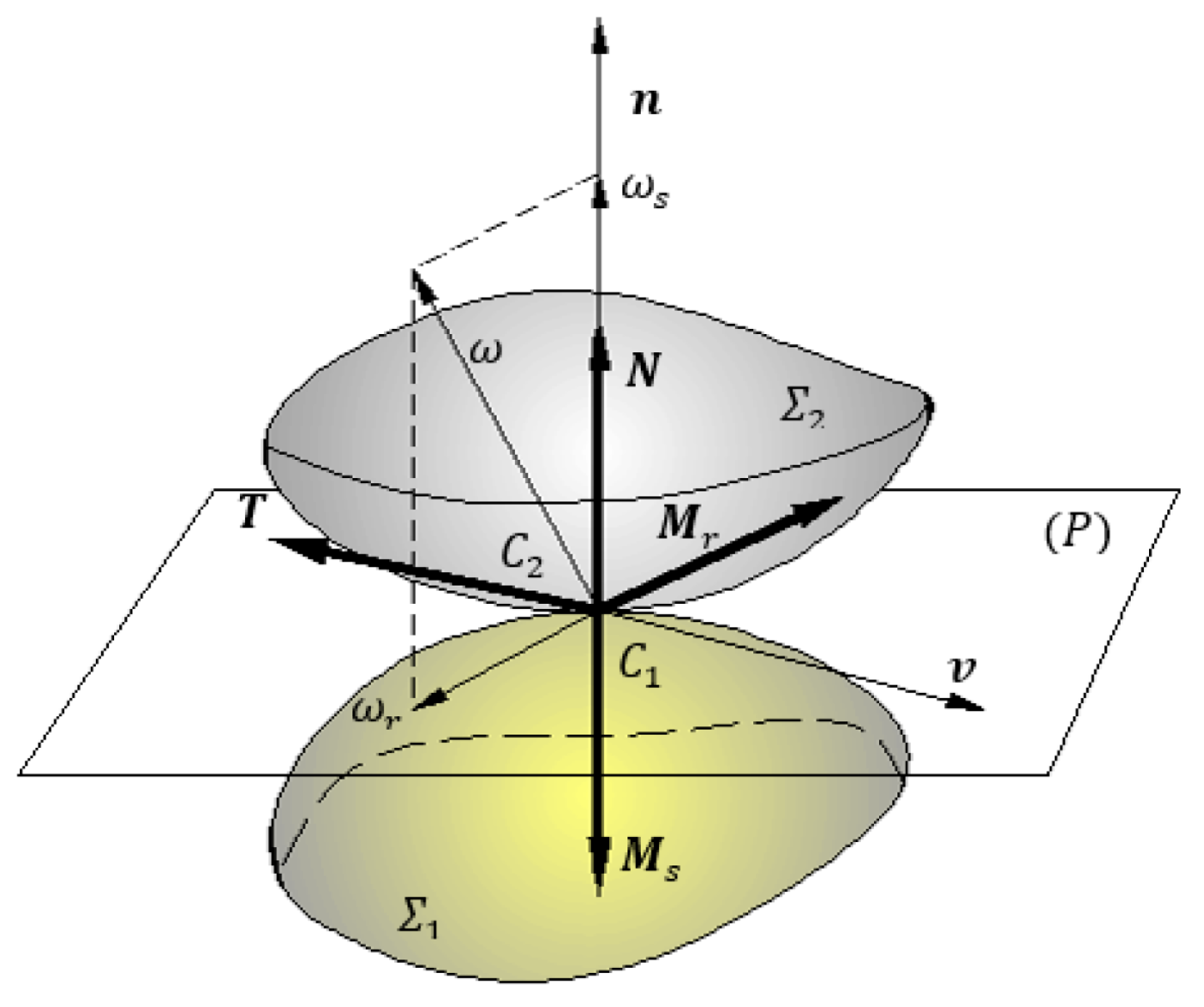
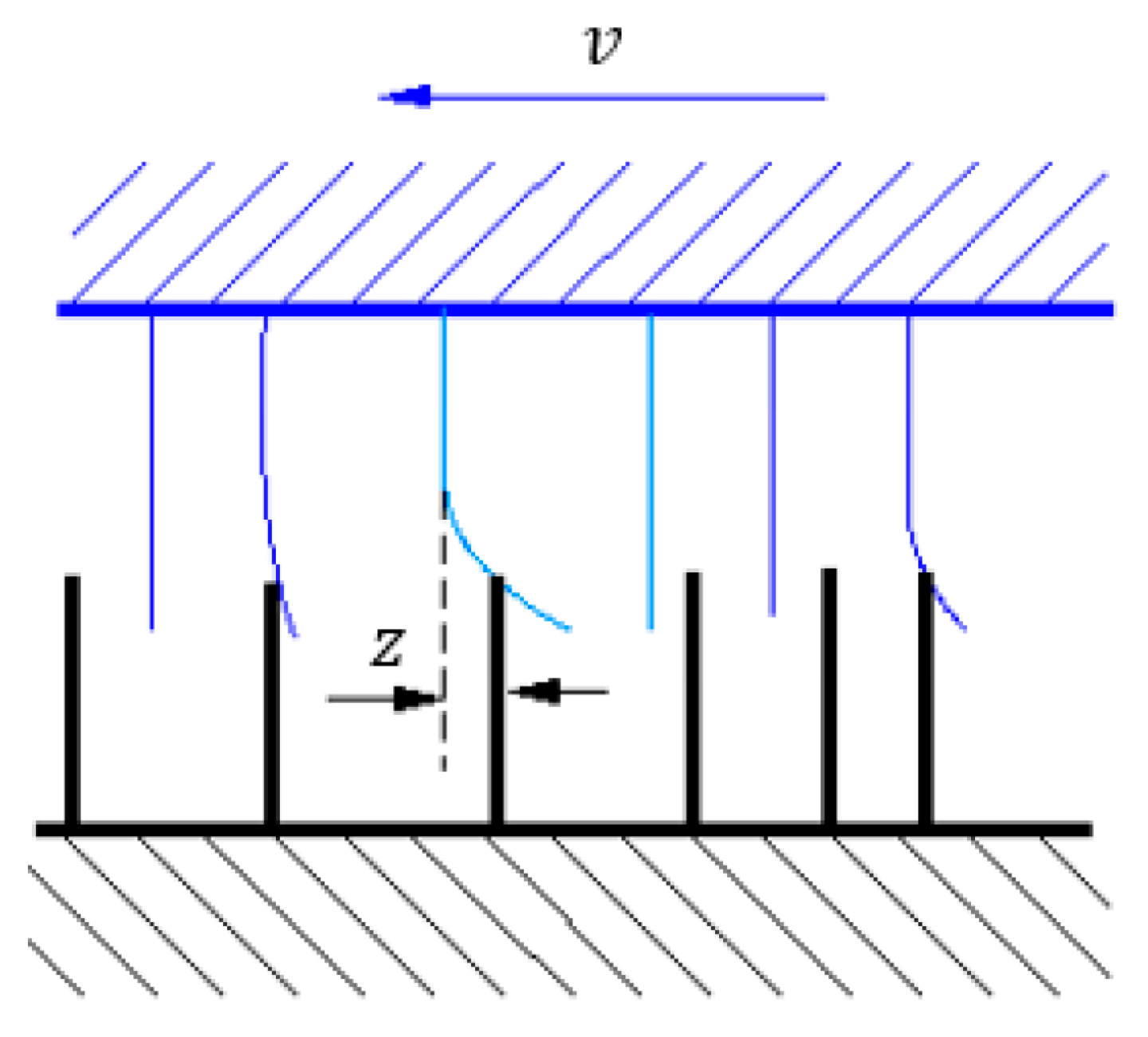
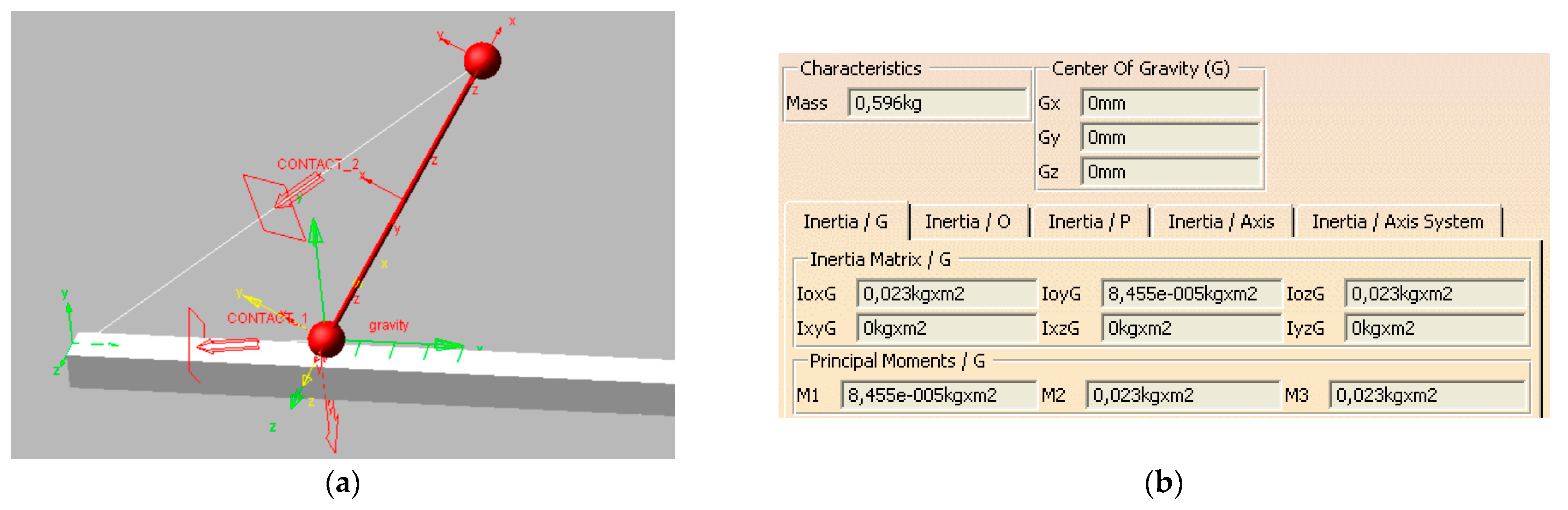
2.1. The Equations of the Dynamic Model
2.2. The Solutions of the System of Equations of Motion
2.2.1. The Study of the Motion under Pure Rolling Hypothesis
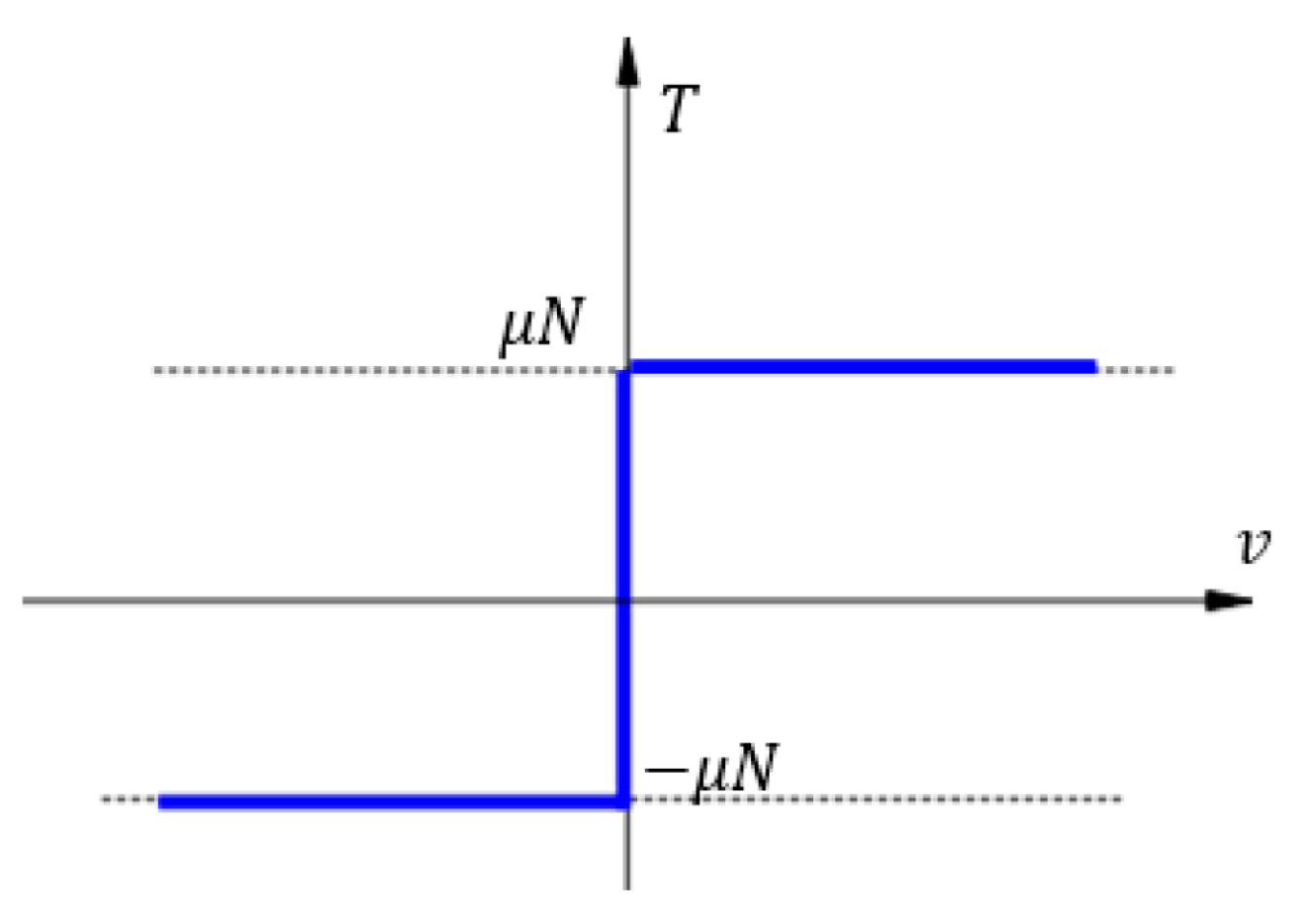
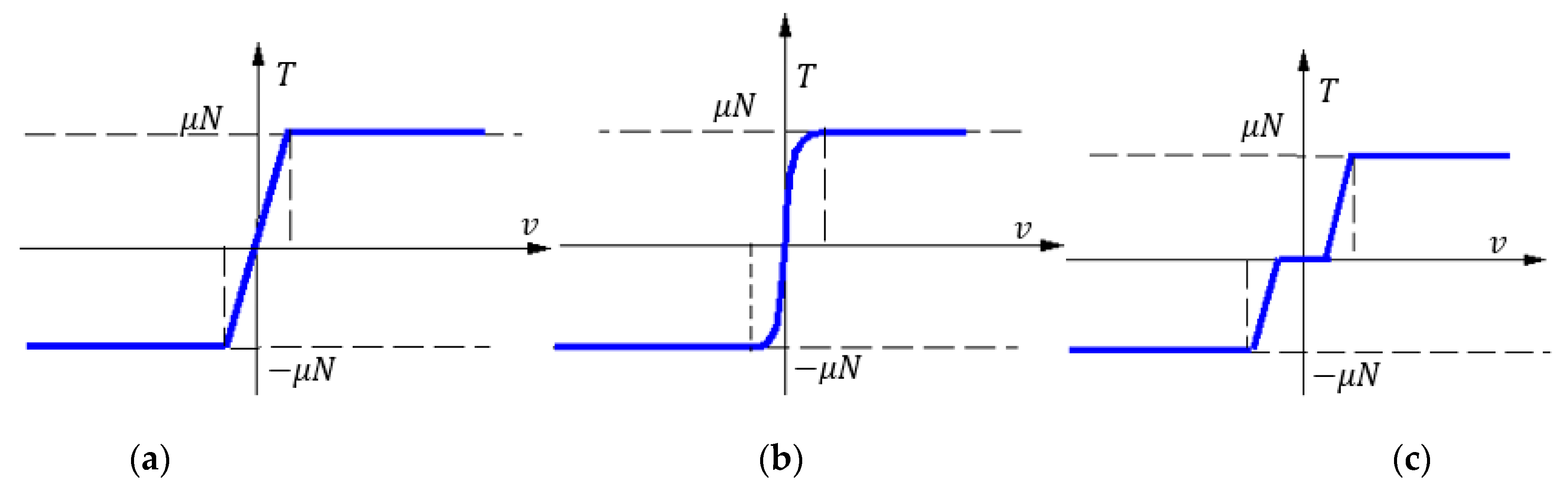
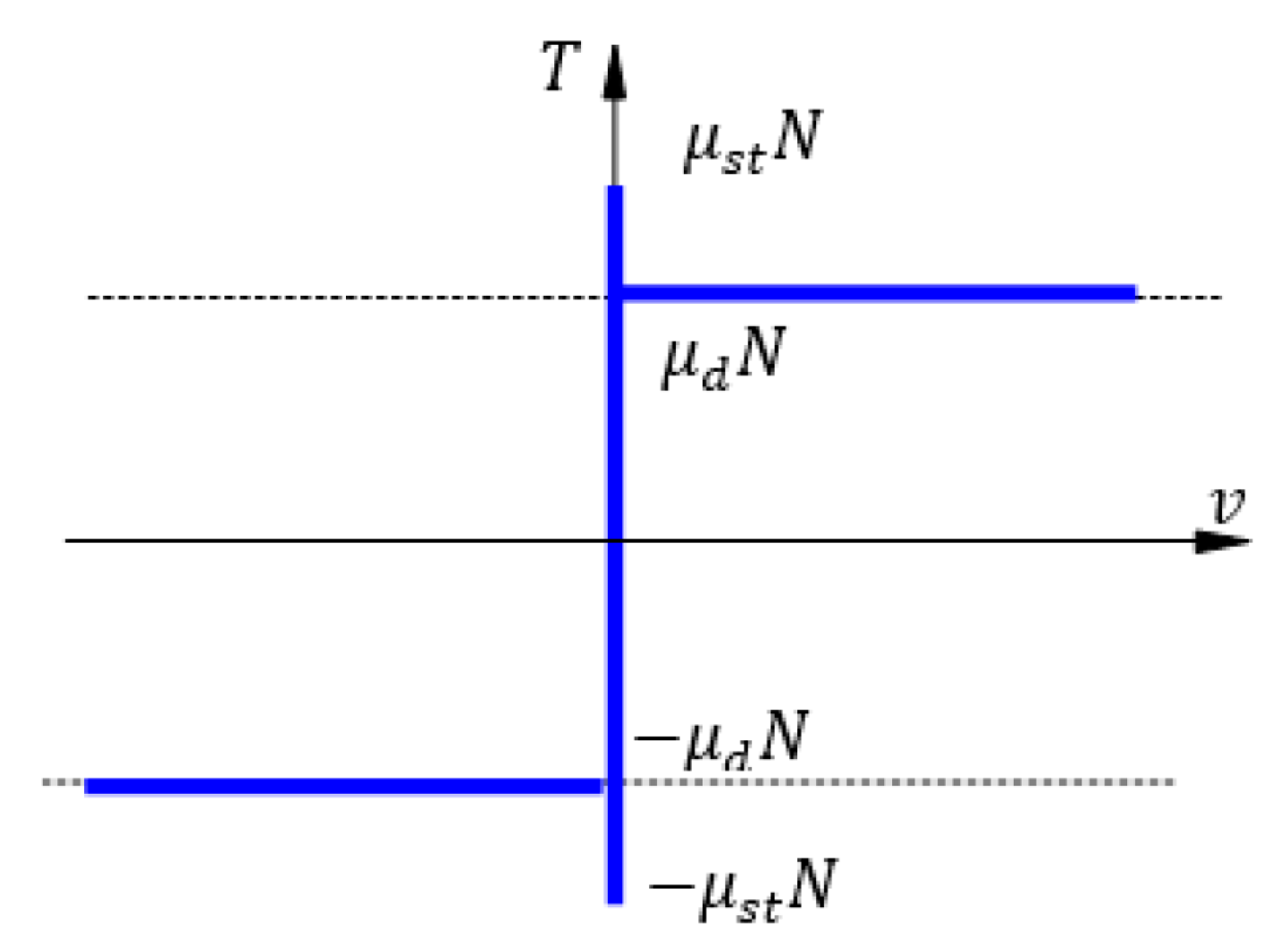
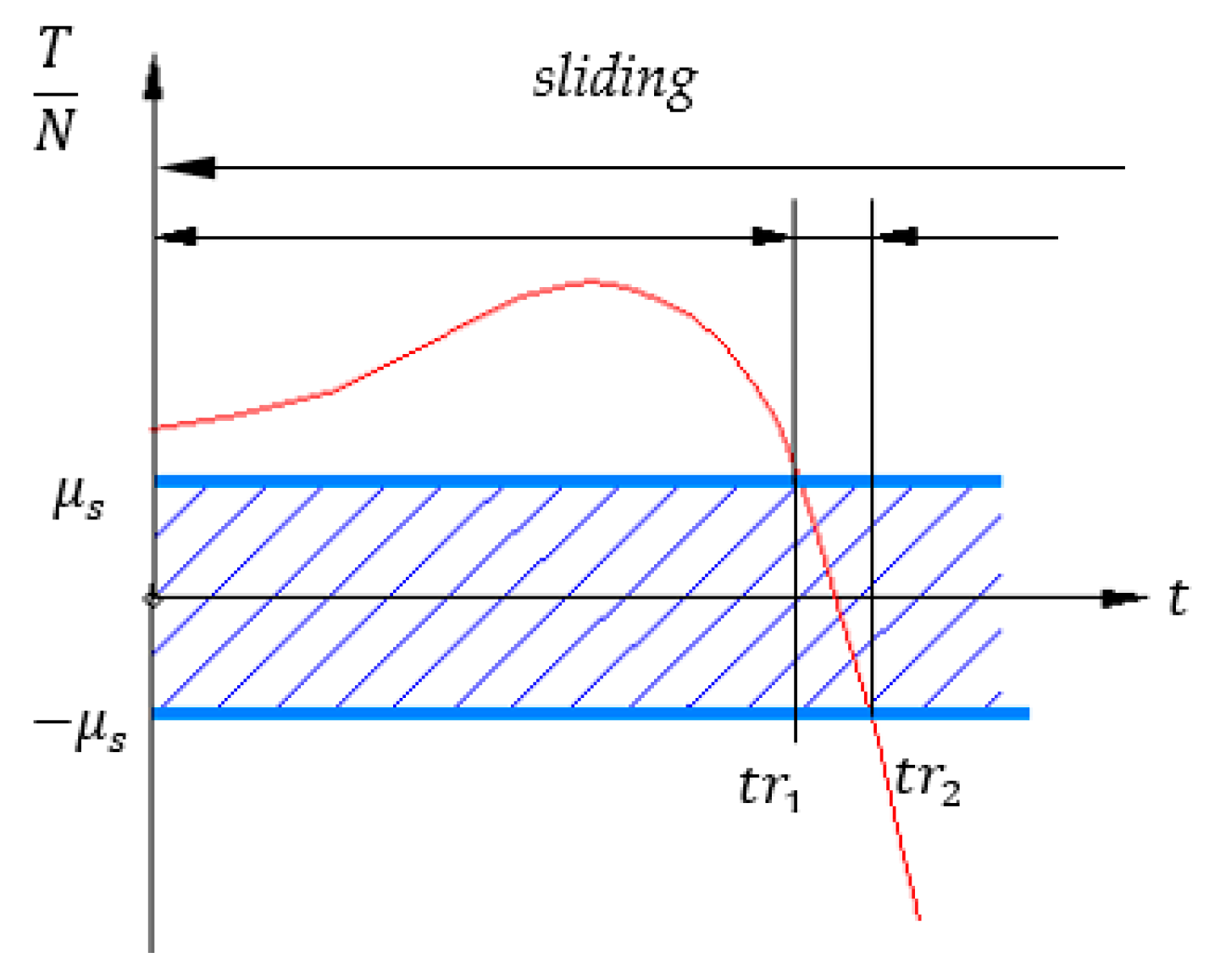
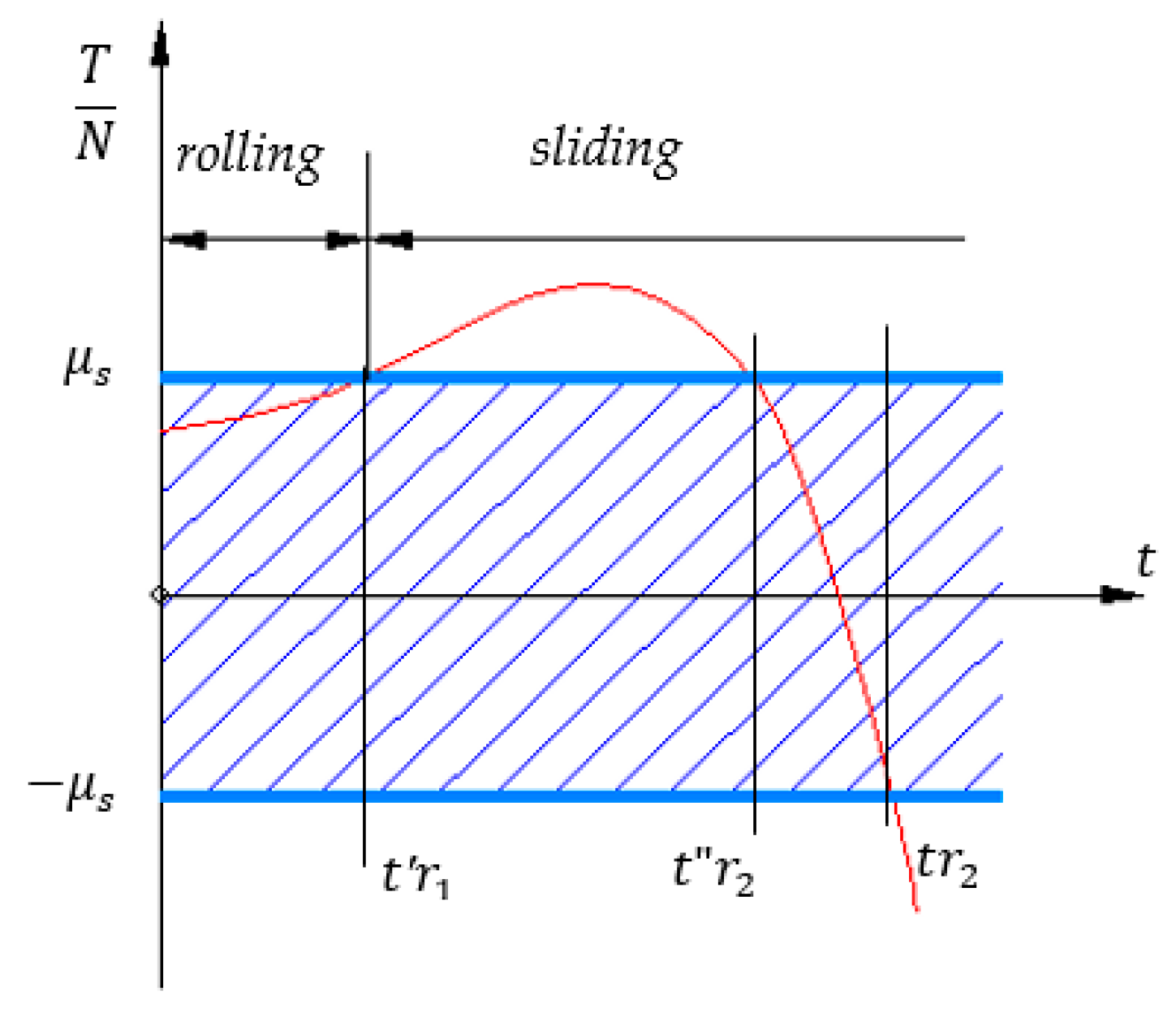
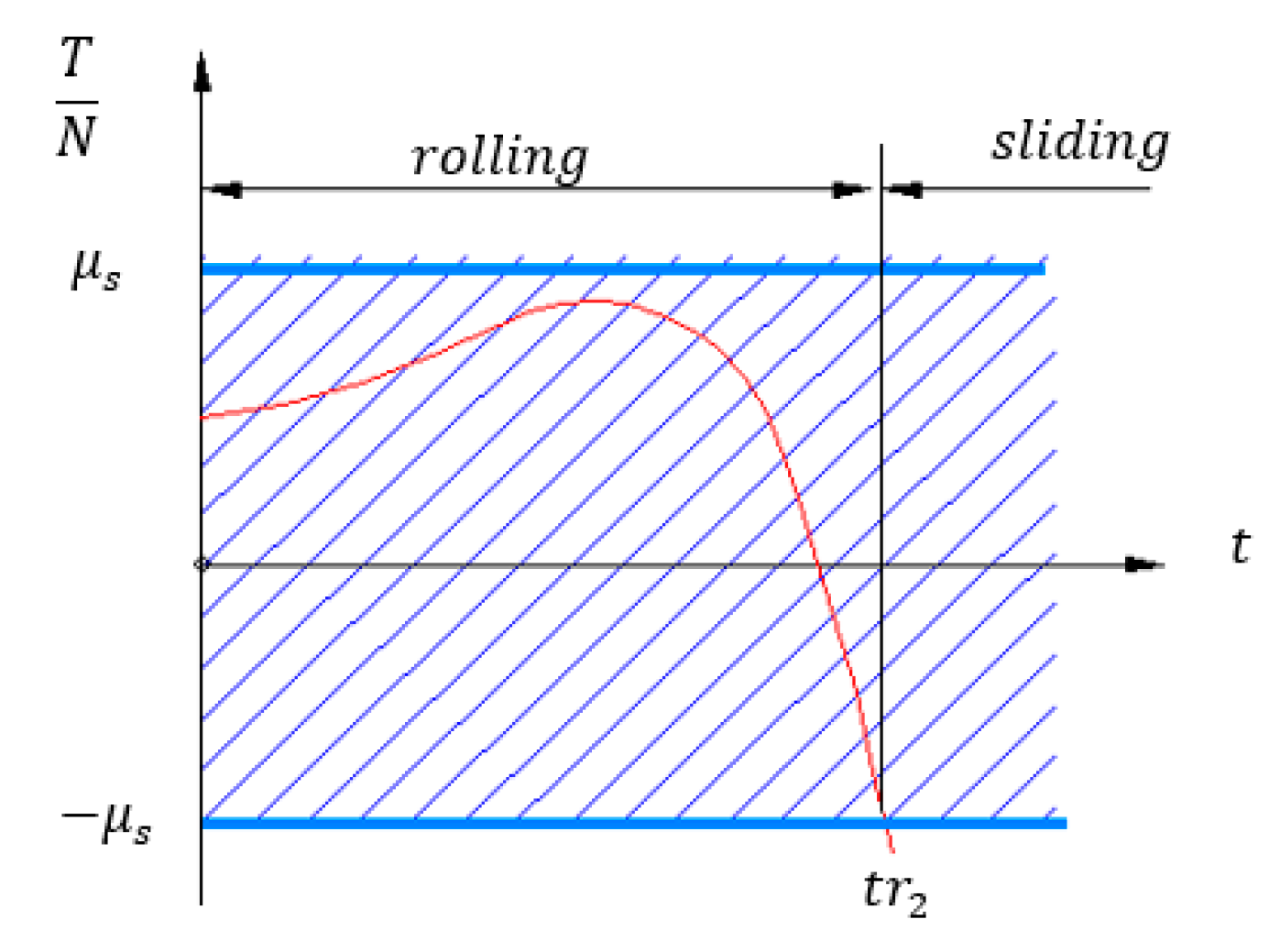
2.2.2. The Study of the Motion under Sliding Hypothesis
3. Results
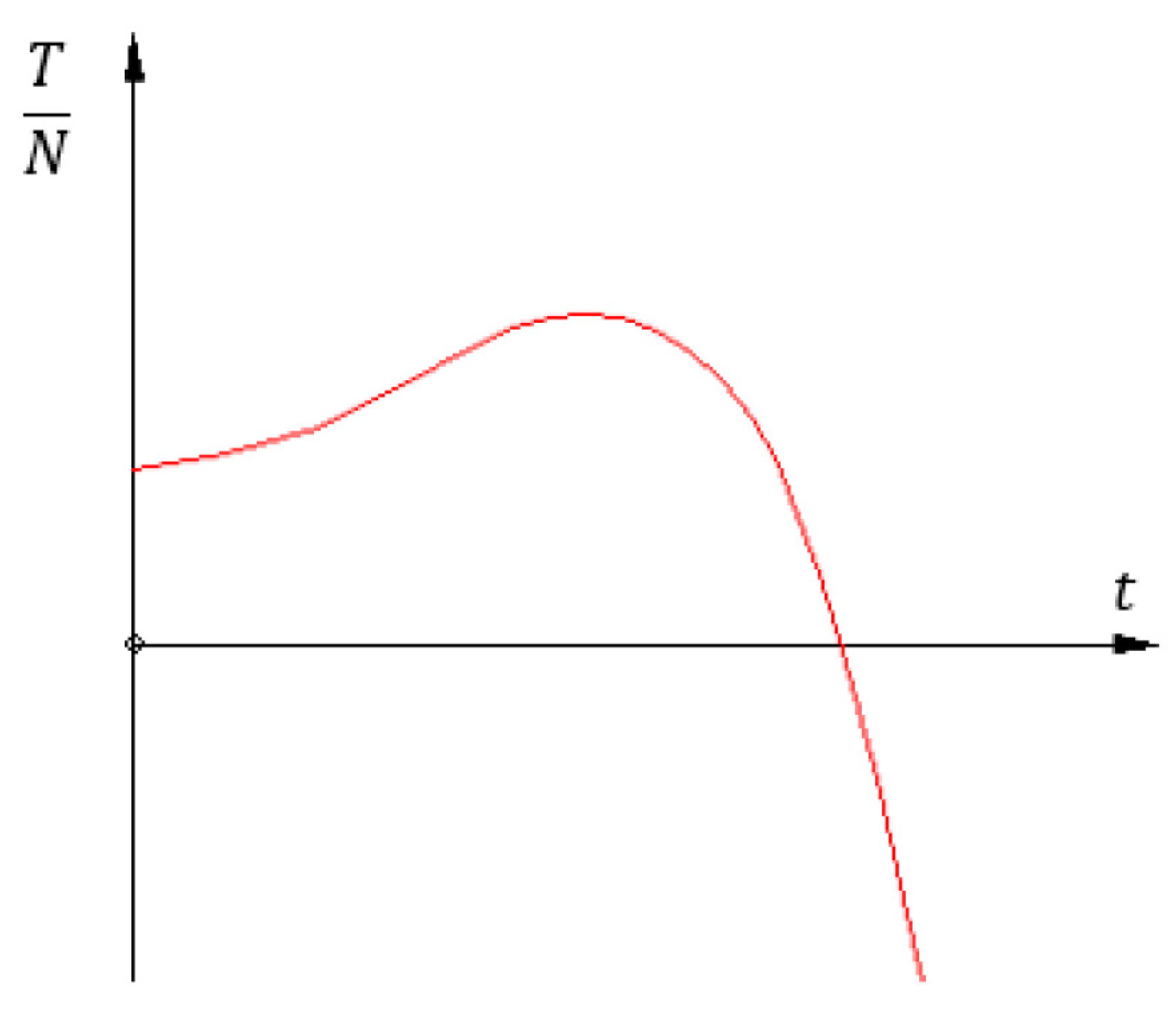
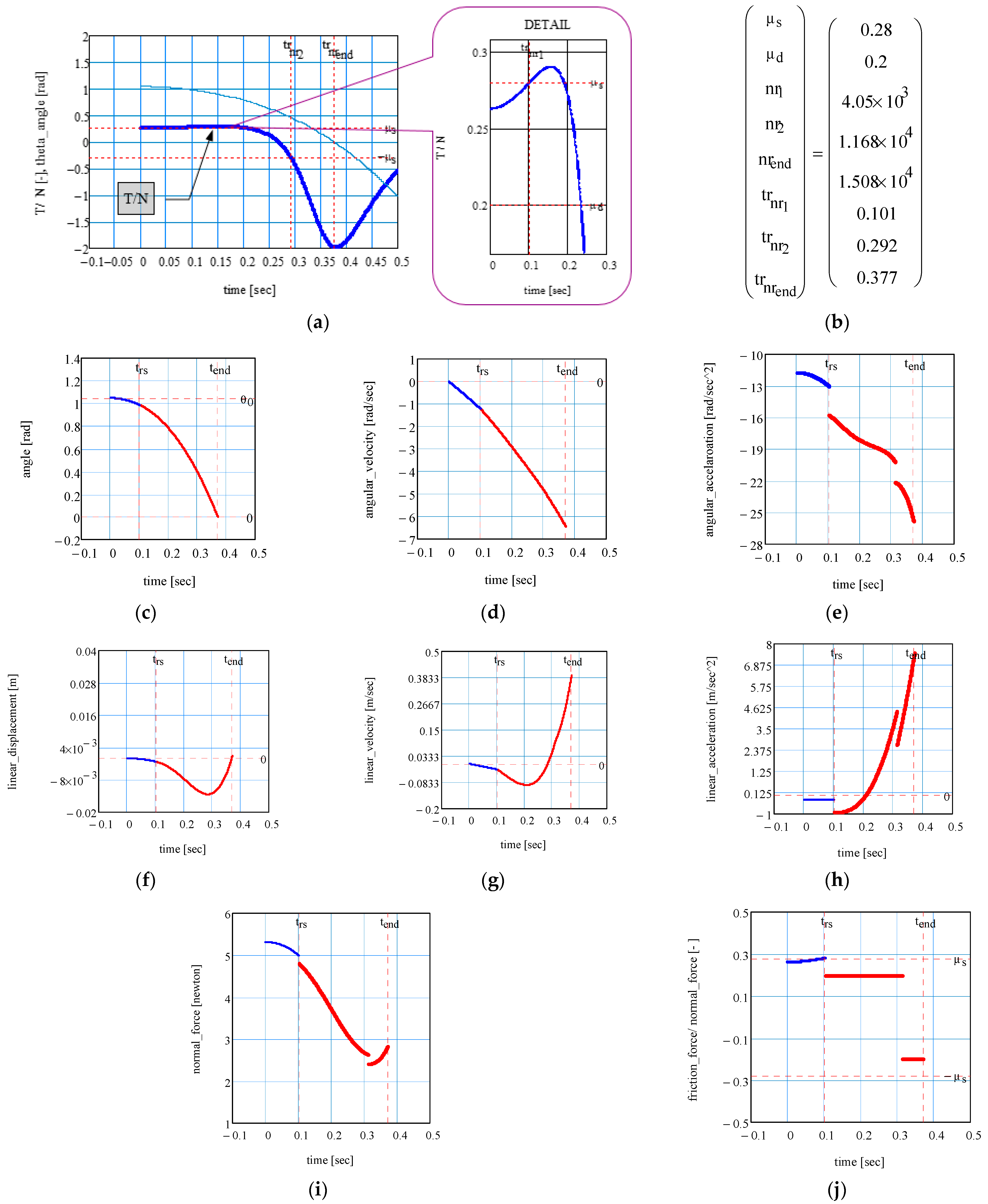
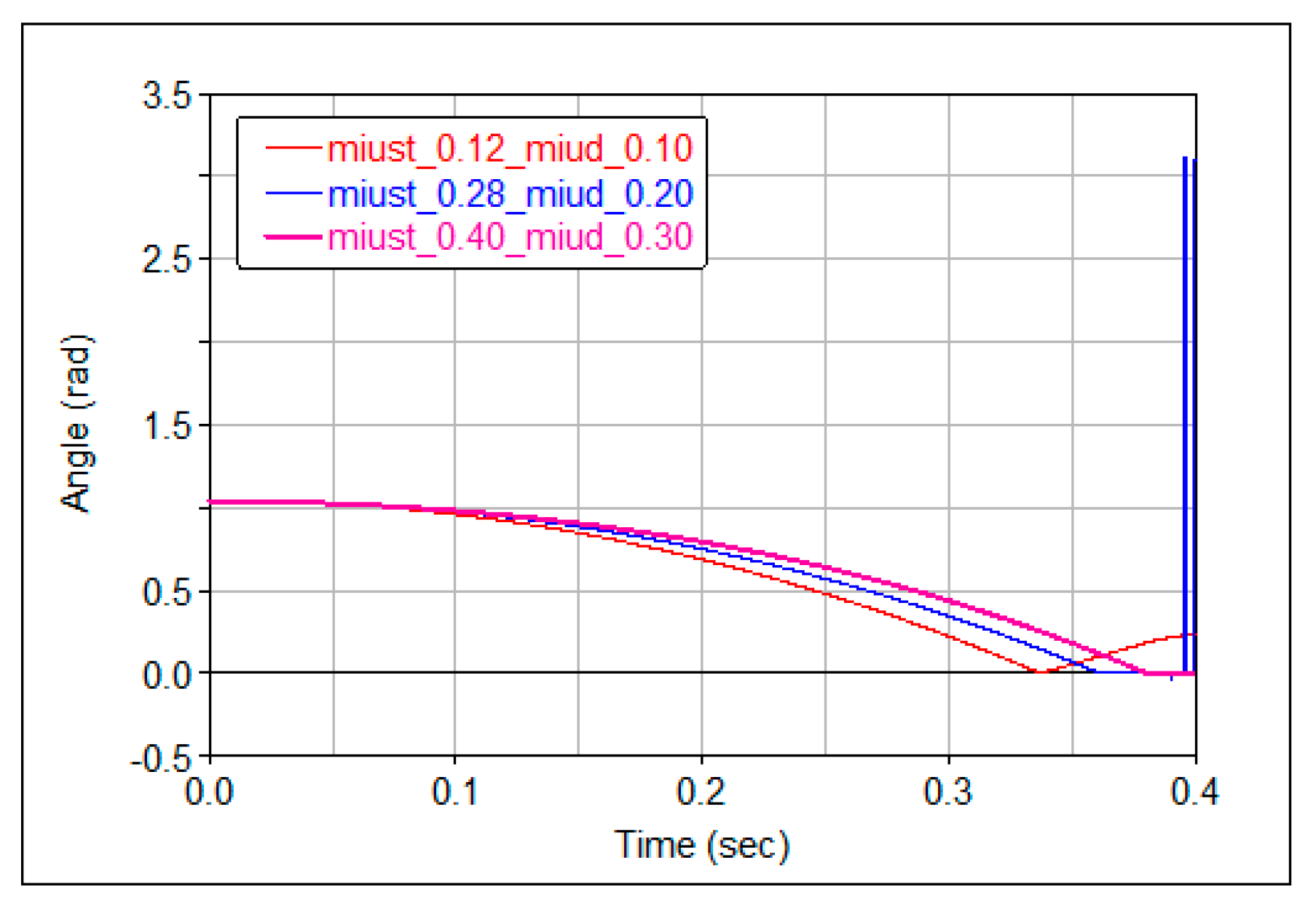
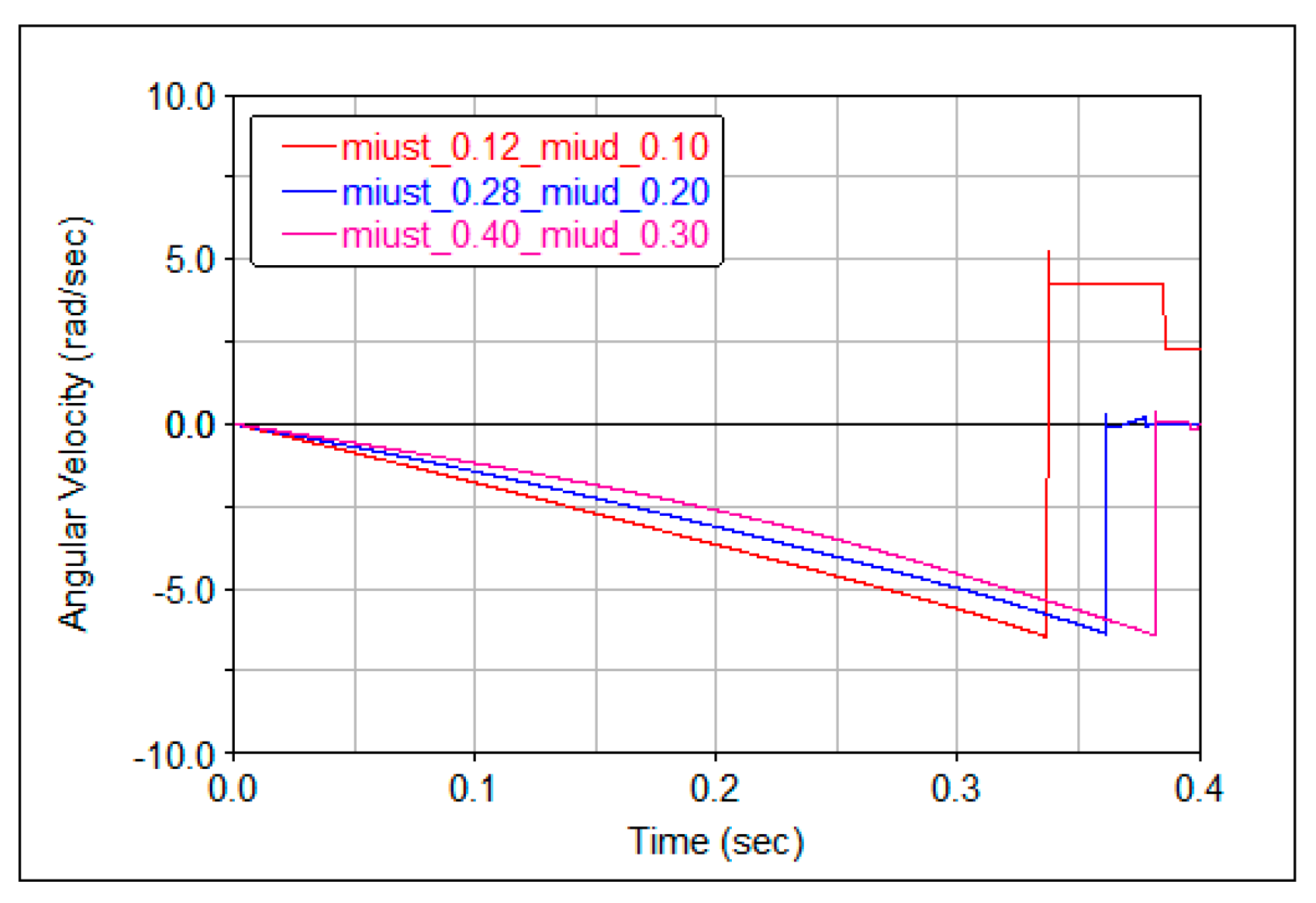
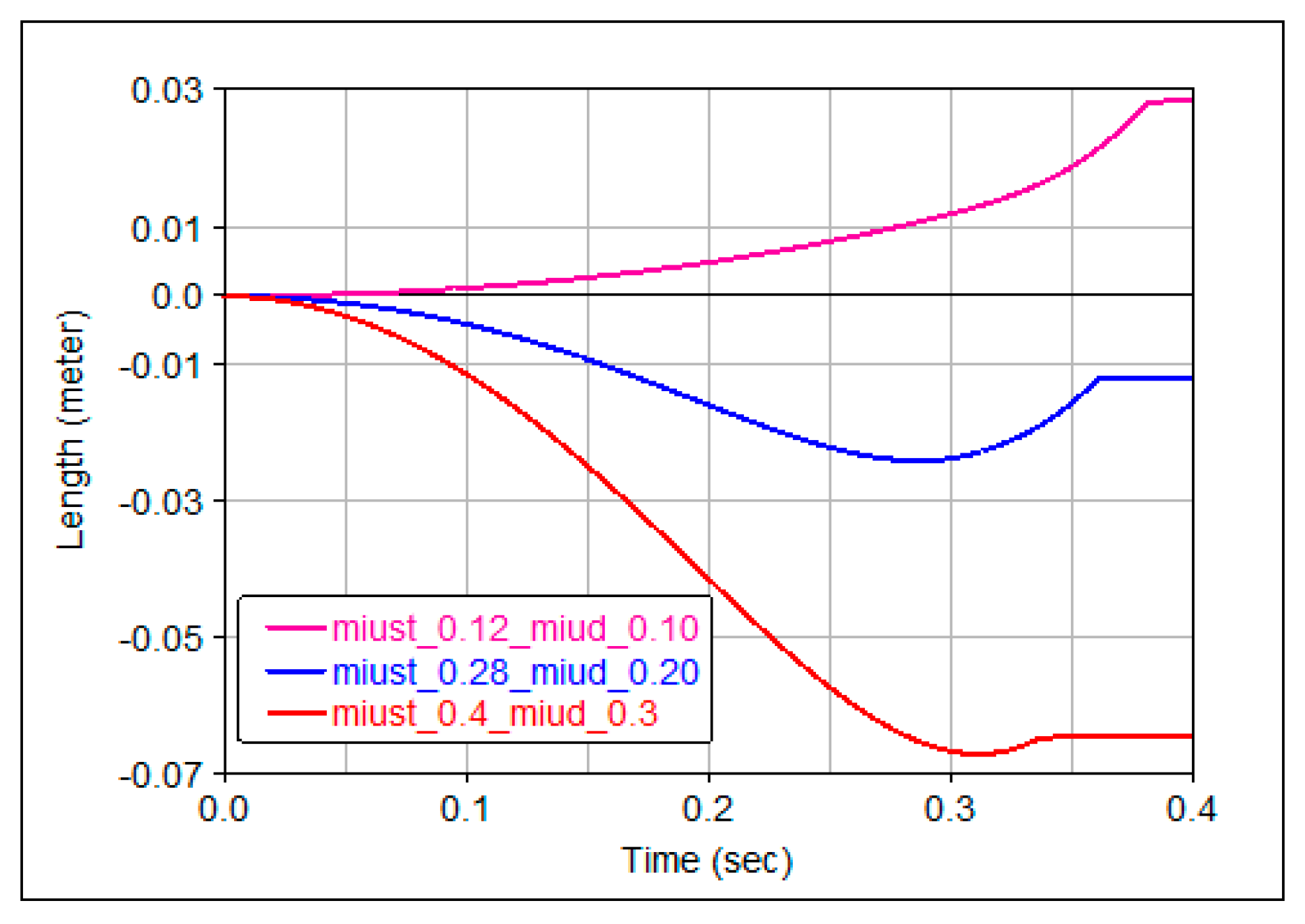
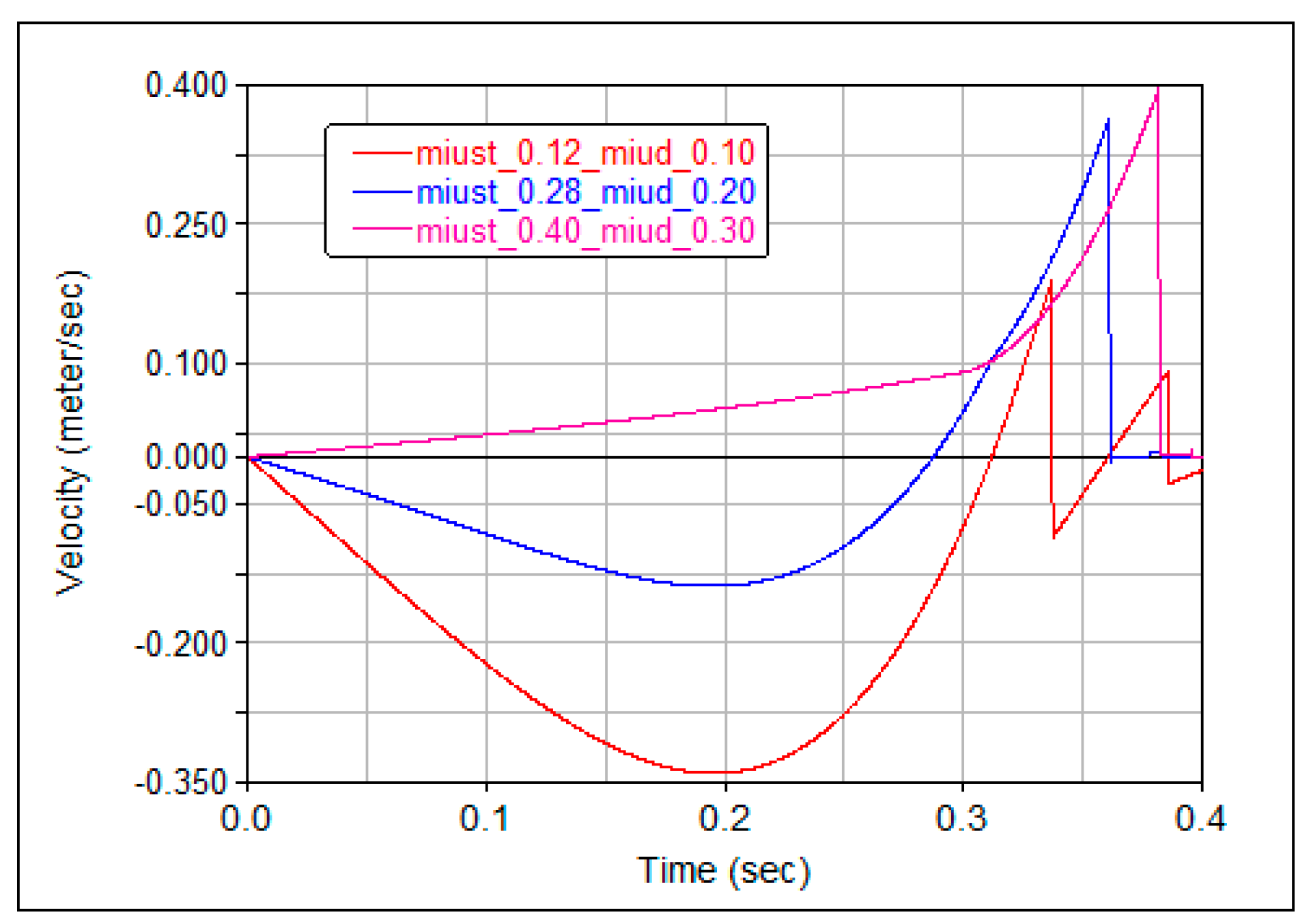
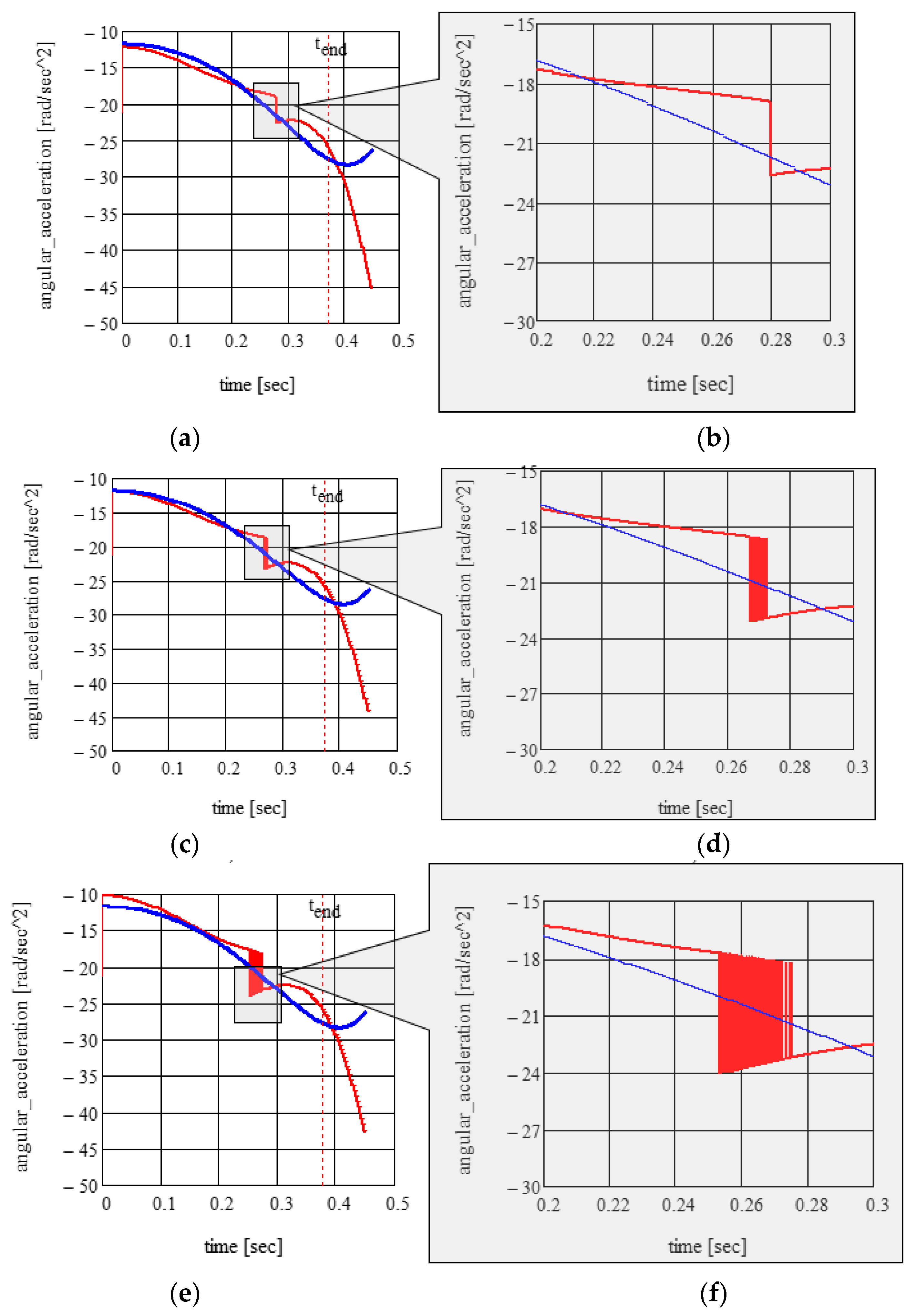
3.1. Solutions of the Equations of Motion
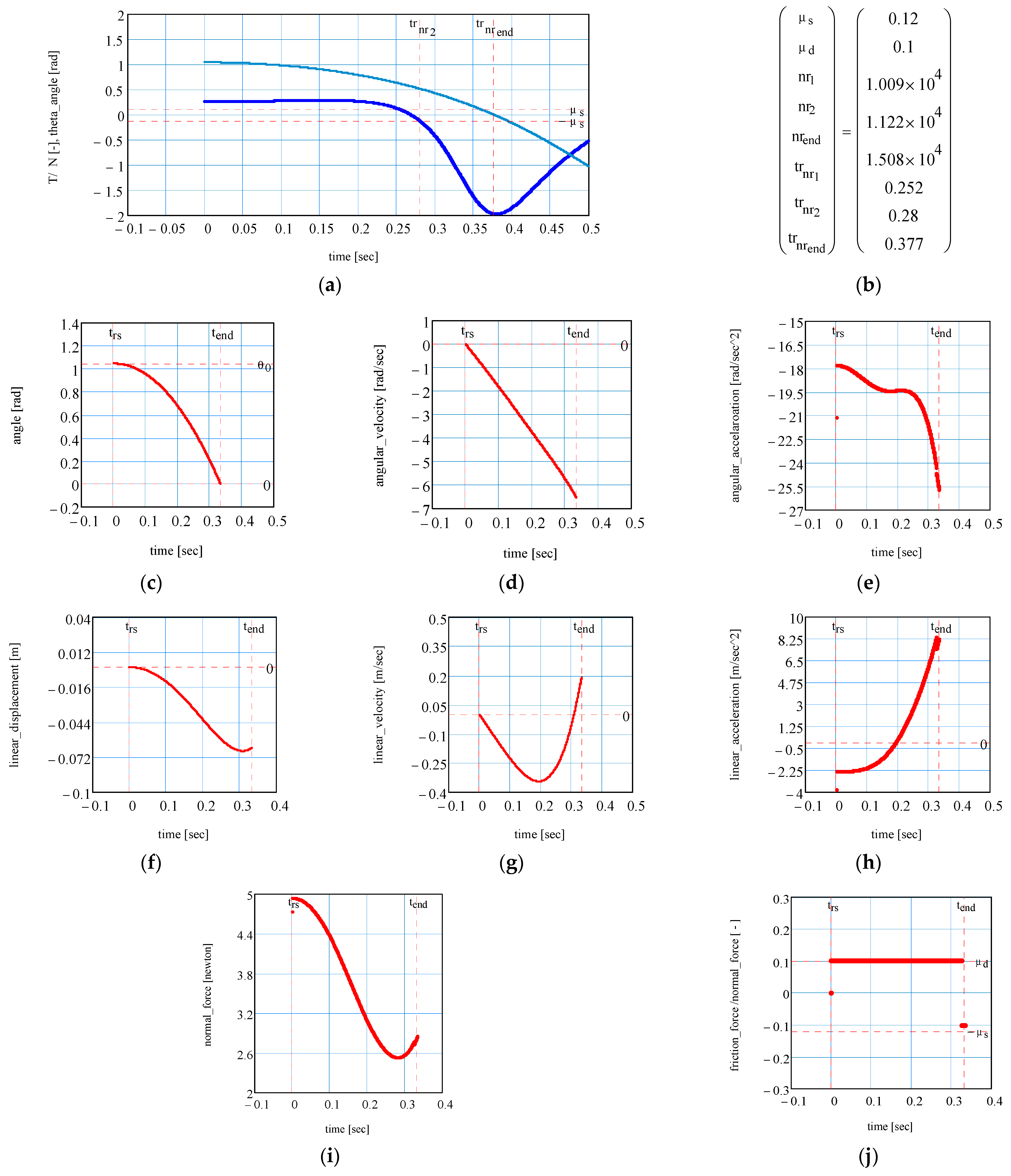
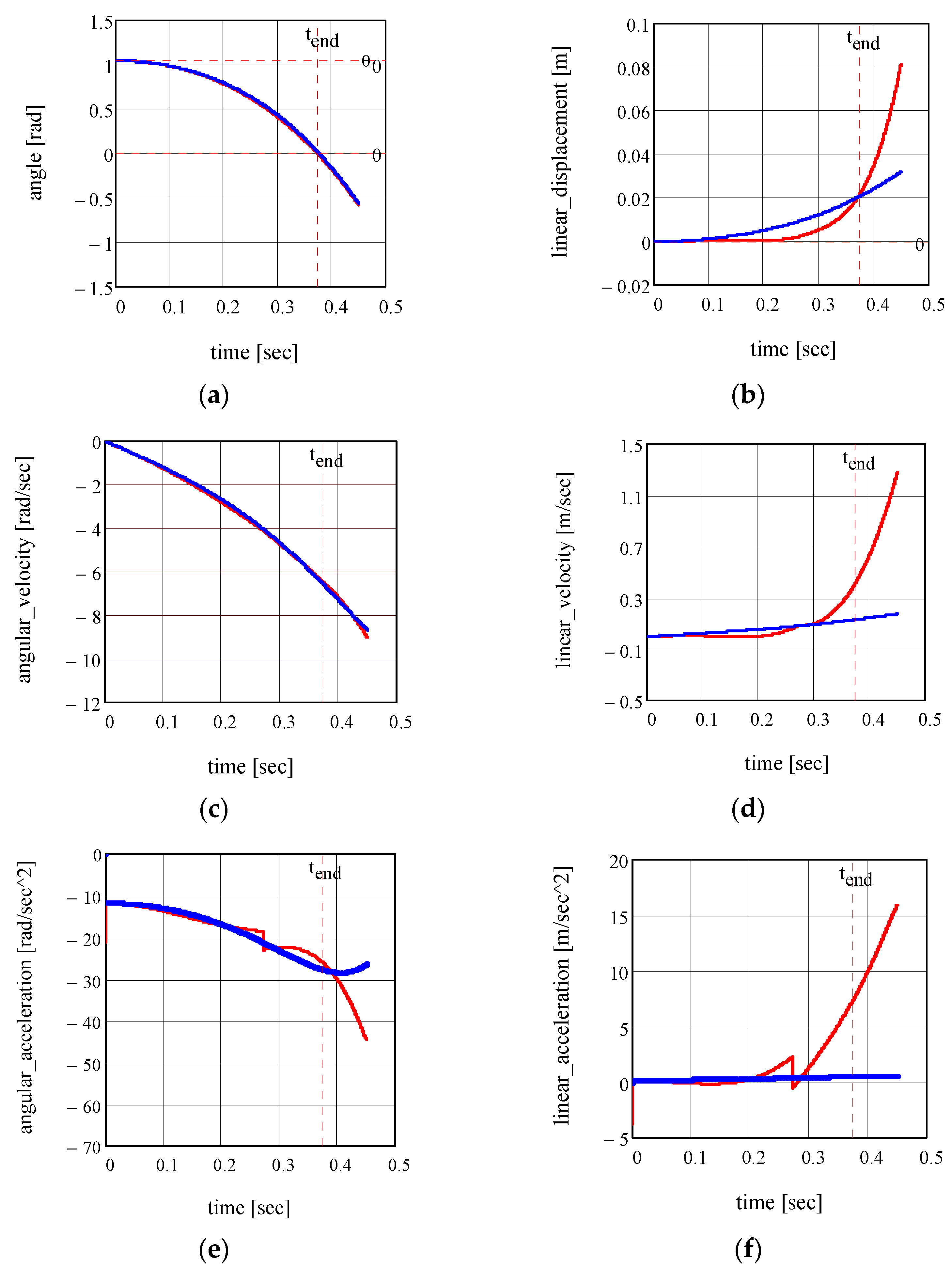
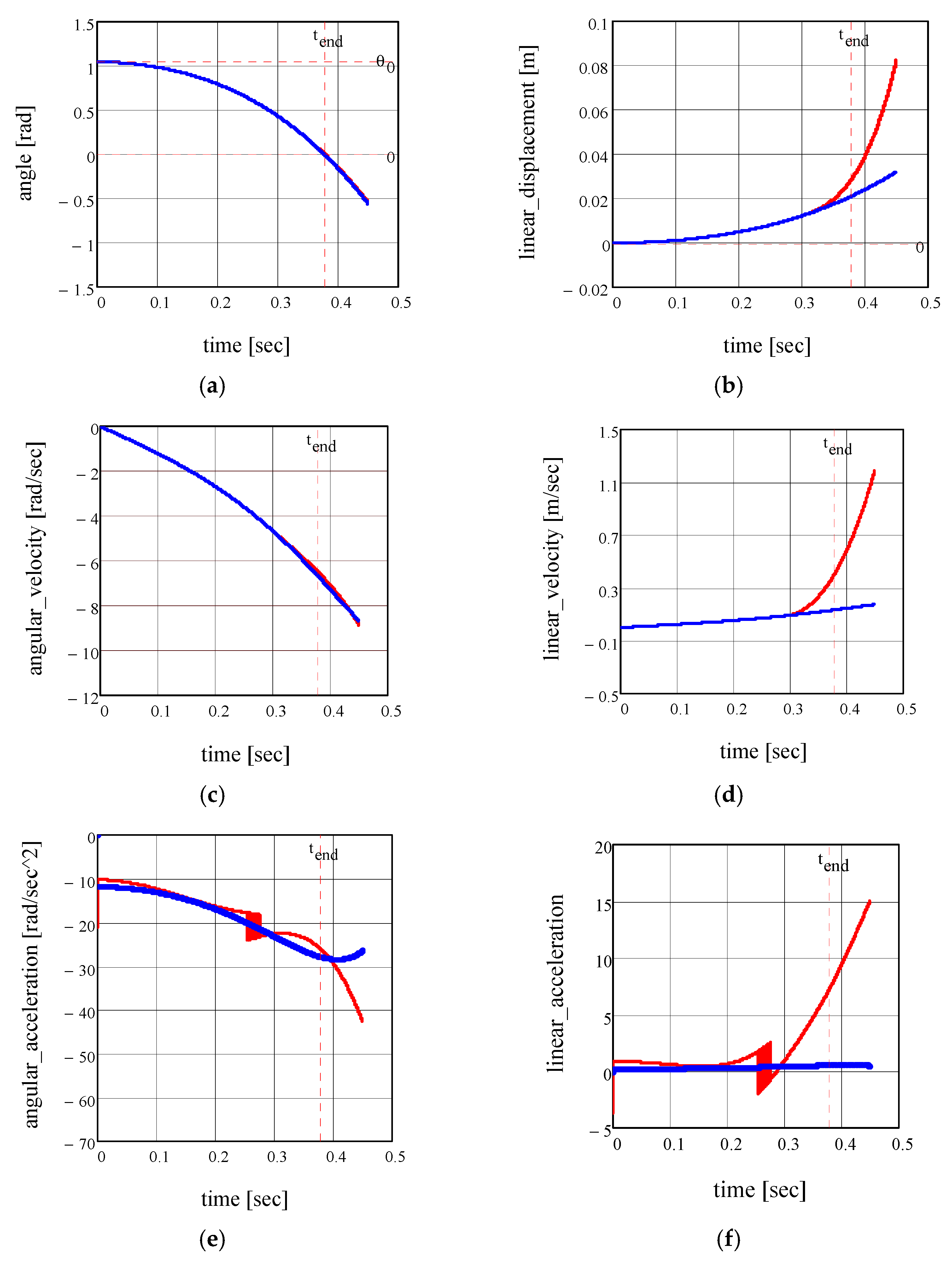
3.2. Validation of Analytical Results
- -
- For the tilt angle of the axis of the system, the variations corresponding to the two limit cases are similar;
- -
- For the motion of the centre of the lower ball, the plots for rolling and sliding are completely different.
4. Conclusions
- -
- Firstly, rolling friction—a relationship exists between the two positional parameters, and the system has in fact only one degree of freedom; the normal and the friction force are independent.
- -
- Secondly, sliding friction—when the system has two degrees of freedom but there is a relation between the normal force and the friction force stipulated by the Coulomb law.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kasdin, N.J.; Paley, D.A. Engineering Dynamics: A Comprehensive Introduction; Princeton University Press: Princeton, NJ, USA, 2011; pp. 11–38. [Google Scholar]
- Mangeron, D.; Irimiciuc, N. Mecanica Rigidelor cu Aplicaţii în Inginerie; Editura Tehnică: Bucureşti, Romania, 1978; Volume I, pp. 304–319. (In Romanian) [Google Scholar]
- Anh, L.X. Dynamics of Mechanical Systems with Coulomb Friction; Springer: Berlin/Heidelberg, Germany, 2012; pp. 11–36. [Google Scholar]
- Marques, F.; Flores, P.; Claro, J.C.P.; Lankarani, H.M. Modeling and analysis of friction including rolling effects in multibody dynamics: A review. Multibody Syst. Dyn. 2019, 45, 223–244. [Google Scholar] [CrossRef]
- Threlfall, D.C. The inclusion of Coulomb friction in mechanisms programs with particular reference to DRAM au programme DRAM. Mech. Mach. Theory 1978, 13, 475–483. [Google Scholar] [CrossRef]
- Ambrósio, J.A.C. Impact of rigid and flexible multibody systems: Deformation description and contact model. Virtual Nonlinear Multibody Syst. 2003, 103, 57–81. [Google Scholar]
- Andersson, S.; Söderberg, A.; Björklund, S. Friction models for sliding dry, boundary and mixed lubricated contacts. Tribol. Int. 2007, 40, 580–587. [Google Scholar] [CrossRef]
- Drincic, B. Mechanical Models of Friction That Exhibit Hysteresis, Stick-Slip, and the Stribeck Effect. Ph.D. Thesis, University Michigan, Ann Arbor, MI, USA, 2012; pp. 84–99. Available online: https://deepblue.lib.umich.edu/bitstream/handle/2027.42/93899/bojanad_1.pdf?sequence=1&isAllowed=y (accessed on 21 March 2024).
- Bowden, F.P.; Leben, L. The nature of sliding and the analysis of friction. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 169, 371–391. [Google Scholar] [CrossRef]
- Johannes, V.I.; Green, M.A.; Brockley, C.A. The role of the rate of application determining the static friction coefficient. Wear 1973, 24, 381–385. [Google Scholar] [CrossRef]
- Dahl, P.R. A Solid Friction Model. Technical Report; The Aerospace Corporation: El Segundo, CA, USA, 1968; pp. 12–17. [Google Scholar]
- Dahl, P.R. Solid friction damping in mechanical vibrations. AIAA J. 1976, 14, 1675–1682. [Google Scholar] [CrossRef]
- Canudas de Wit, C.; Olsson, H.; Åström, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Rill, G.; Schuderer, M. A Second-Order Dynamic Friction Model Compared to Commercial Stick–Slip Models. Modelling 2023, 4, 366–381. [Google Scholar] [CrossRef]
- Wang, H.; Cui, J.; Wu, J.; Tan, J. Dynamic Friction-Slip Model Based on Contact Theory. Machines 2022, 10, 951. [Google Scholar] [CrossRef]
- Tustin, A. The effects of backlash and of speed-dependent friction on the stability of closed-cycle control systems. J. Inst. Electr. Eng. Part I Gen. 1947, 94, 143–151. [Google Scholar] [CrossRef]
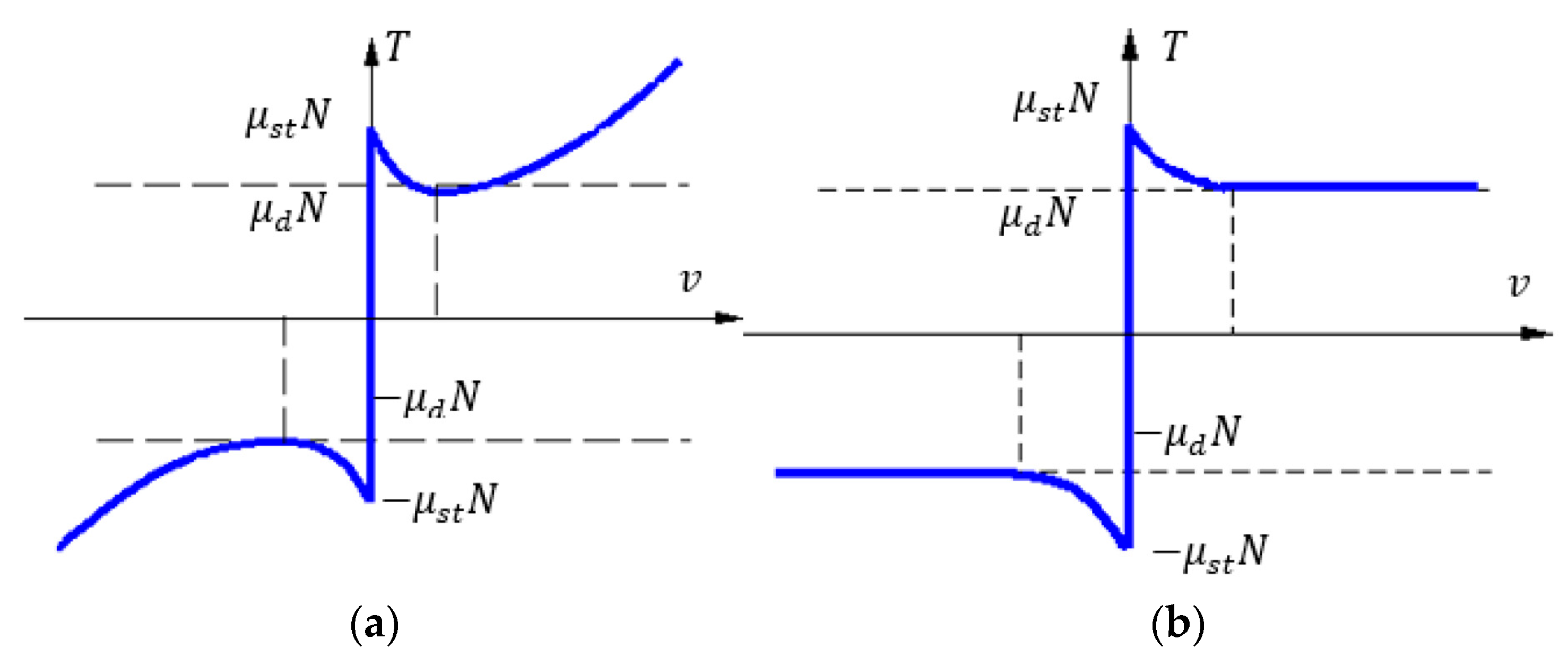
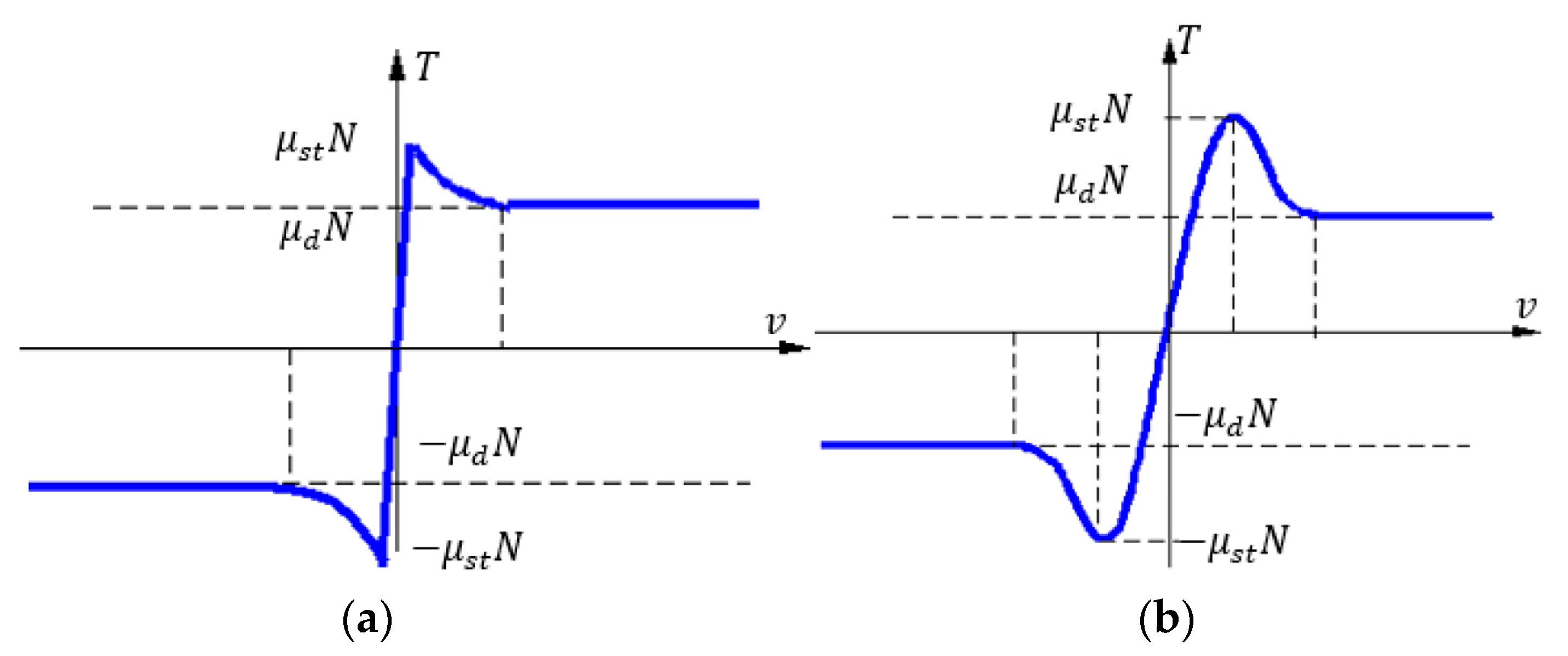
- Bo, L.C.; Pavelescu, D. the fiction-speed relation and its influence on the critical velocity of the stick-slip motion. Wear 1982, 82, 277–289. [Google Scholar]
- Armstrong-Helouvry, B. Control of Machines with Friction; Kluwer Academic Publishers: Boston, MA, USA, 1991; pp. 63–93. [Google Scholar]
- Parovik, R.; Shakirova, A.; Firstov, P. Mathematical model of the stick-slip effect for describing the “drum-beat” seismic regime during the eruption of the Kizimen volcano in Kamchatka. AIP Conf. Proc. 2022, 2467, 080015. [Google Scholar] [CrossRef]
- Shakirova, A.A.; Firstov, P.P.; Parovik, R.I. Phenomenological model of the generation of the seismic mode drumbeats earthquakes accompanying the eruption of Kizimen volcano in 2011–2012. Vestn. KRAUNC. Fiz.-Mat. Nauki. 2020, 33, 86–101. [Google Scholar] [CrossRef]
- Pennestrì, E.; Valentini, P.P.; Vita, L. Multibody dynamics simulation of planar linkages with Dahl friction. Multibody Syst. Dyn. 2007, 17, 321–347. [Google Scholar] [CrossRef]
- Pop, N.; Ungureanu, M.; Pop, A.I. An Approximation of Solutions for the Problem with Quasistatic Contact in the Case of Dry Friction. Mathematics 2021, 9, 904. [Google Scholar] [CrossRef]
- Giesbers, J. Contact Mechanics in MSC Adams—A technical evaluation of the contact models in multibody dynamics software MSC Adams. Bachelor’s Thesis, University Twente, Enschede, Holland, 2012; pp. 13–19. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alaci, S.; Ciornei, F.-C.; Lupascu, C.; Romanu, I.-C. Mathematical Model of the Evolution of a Simple Dynamic System with Dry Friction. Axioms 2024, 13, 372. https://doi.org/10.3390/axioms13060372
Alaci S, Ciornei F-C, Lupascu C, Romanu I-C. Mathematical Model of the Evolution of a Simple Dynamic System with Dry Friction. Axioms. 2024; 13(6):372. https://doi.org/10.3390/axioms13060372
Chicago/Turabian StyleAlaci, Stelian, Florina-Carmen Ciornei, Costica Lupascu, and Ionut-Cristian Romanu. 2024. "Mathematical Model of the Evolution of a Simple Dynamic System with Dry Friction" Axioms 13, no. 6: 372. https://doi.org/10.3390/axioms13060372





