Abstract
This study is motivated by the recently published papers on normal injective and normal projective hypermodules. We provide a new characterization of the normal injective and normal projective hypermodules by using the splitting of the short exact sequences of hypermodules. After presenting some of their fundamental properties, we show that if a hypermodule is normal projective, then every exact sequence ending with it is splitting. Moreover, if a hypermodule is normal injective, then every exact sequence starting with it is splitting as well. Finally, we investigate the relationships between semisimple, simple, normal injective, and normal projective hypermodules.
MSC:
20N20; 16D88
1. Introduction
Let H be a nonempty set and be the set of nonempty subsets of H. The map is referred to as hyperoperation on H. Thus, for the element , is not a single element, as the result of a classical operation, yet is a nonempty subset of the set H. Owing to this, the theory of hypercompositional structures (which are algebraic structures having at least one hyperoperation) was presented by Marty [1] as a generalization of the theory of algebraic structures while studying problems in noncommutative algebra. Following [1], Marty introduced hypergroups using the hyperoperation on a set as a first hypercompositional structure. In 1983, Krasner [2] introduced the notion of hyperring, which we now call Krasner hyperring. In that article, Krasner also defined a hypermodule over a hyperring, with the name of the Krasner hypermodule. The contribution of entire these structures is a canonical hypergroup, which has plenty applications in hypercompositional algebra. Additionally, other types of hyperrings and hypermodules were introduced by Rota [3] and Vougiouklis [4], namely, multiplicative hyperrings and generalized hyperrings. In this article, by “hypermodule”, we mean Krasner hypermodules.
Massouros studied hypermodules in detail [5], where specific hypermodules were introduced, namely, free and cyclic hypermodules. After that, Massouros investigated more properties and theorems of hypercompositional structures [6,7]. Moreover, the fundamental relationships in hypercompositional structures were studied by Vougiouklis [8]. Recently, researchers have focused on the new aspects of hypercompositional structures and have studied them from different points of view. The category of Krasner hypermodules has been studied [9,10], where researchers investigated the injectivity and projectivity properties of Krasner hypermodules.
In [11], Bordbar et al. focused on a specific type of homomorphism among hypermodules termed normal homomorphisms and, for that reason, on the normal projective; they also gave an equivalent description of these hypermodules via exact chains of Krasner hypermodules and normal epimorphism, while in [12], the supplements in Krasner R hypermodules were investigated in addition to their relationship to projective hypermodules, especially along with normal -projective hypermodules. Additionally, a novel characterization of normal injective R hypermodules via divisible R hypermodules was studied [13]. In [14], the authors contribute some consequences of normal injective hypermodules with category aspects and define torsion and torsionable elements in hypermodules.
Motivated by the injective modules and projective modules studied with help of short exact sequences in recent years (see [15,16,17,18,19]), in this study, we aimed to acquire some consequences and develop the concept of short exact sequences and their relationship with normal injective and projective hypermodules. After a brief introduction to hypermodules and homomorphisms in hypermodules, in Section 3, we define a type of short exact sequence, namely, the splitting exact sequence, and provide some examples of it. Then, we prove that the canonical hypergroup is a left hypermodule, where is a non empty family of left hypermodules. This theorem is supported by an example. Finally, we show that every exact sequence ending with a normal projective hypermodule must be split. Similarly, every exact sequence starting with a normal injective hypermodule must be split. Then, by splitting short exact sequences, we investigate the relationships between semisimple, simple, normal injective, and normal projective hypermodules as the main theorem in this study.
2. Preliminaries
This part concisely reviews the concepts and consequences pertinent to kinds of hyperrings and hypermodules. To better understand the topic, we begin with some definitions and theorems of hypercompositional algebra introduced in books [20,21] and articles [5,6,7].
Let H be a nonempty set along with a map and let be a hyperoperation on H. Then, is denoted as a hypergroupoid. Furthermore, for nonempty subsets X and Y of H, describe
We basically write and rather than and in sequence for each and any nonempty subset X of H. A hypergroupoid is denoted as a
- (1)
- Semihypergroup if + is associative;
- (2)
- Quasihypergroup if + is reproductive.
Provided that the hypergroupoid is a semihypergroup and a quasihypergroup, it is denoted as a hypergroup. A nonempty subset S of a hypergroup is termed as a subhypergroup of H if, for every , .
A hypergroup is called a canonical hypergroup if
- (1)
- + is commutative.
- (2)
- For any , there is a unique element in H, denoted by , such that .
- (3)
- If , then , where .
Observe from [22] that if is a canonical hypergroup, then for all .
(Krasner) hyperring is a triple such that
- (1)
- is a canonical hypergroup;
- (2)
- is a monoid along with a bilaterally absorbing element 0;
- (3)
- The multiplication distributes over the addition on both sides.
A hyperring is commutative provided that is commutative.
Let R and be a canonical hypergroup. M is said to be a left Krasner R hypermodule if there is a map , written , that satisfies the following conditions:
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- and .
For any and .
For simplicity, in every part of this paper, the term “hypermodule” refers to the left Krasner hypermodule. A nonempty subset N of an R hypermodule M is termed a subhypermodule of M, written as when under the same hyperoperations of M, N is an R hypermodule. It is obvious that M and are insignificant subhypermodules of M. Additionally, based on [13], every hyperring R is an R hypermodule.
For a hyperring R, assume that K becomes a subhypermodule of an R hypermodule M. Consider
Then, is an R hypermodule with the following hyperoperation
and the map is defined as and for every and . is called a quotient hypermodule of the R hypermodule M.
Given two R- = hypermodules M and N, a map is identified as an R homomorphism on the condition that
- (1)
- for all ;
- (2)
- for all and .
f is termed as a strong homomorphism each time for every . A single-valued map is called a normal homomorphism if
- (1)
- for all ;
- (2)
- for all and .
For a normal homomorphism , the set is termed as the kernel of f and is shown with . Note that .
3. Short Exact Sequences and Applications to Normal Injectivity (Projectivity)
Let be a short exact sequence of hypermodules (see [11]). denotes the short exact sequence ; that is, .
Definition 1.
Let be a short exact sequence of hypermodules. is said to be splitting if is a direct summand of N.
First, let us give the following examples.
Example 1.
For any hypermodule M, we pay attention to the short exact sequence
where is the inclusion map, and is the identity map. It is obvious that is a direct summand of M, and so is splitting.
Example 2.
Admit together with hyperoperation “+” and operation “.”:
and
| + | 0 | 1 | 2 | 3 |
| 0 | {0} | {1} | {2} | {3} |
| 1 | {1} | {0,1} | {3} | {2,3} |
| 2 | {2} | {3} | {0} | {1} |
| 3 | {3} | {2,3} | {1} | {0,1} |
| · | 0 | 1 | 2 | 3 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 2 | 2 |
| 3 | 0 | 0 | 2 | 2 |
Therefore, R is an R hypermodule. It is straightforward to see that the only proper subhypermodules of R are , , and . Therefore, the short exact sequence
is splitting.
Example 3.
Given the hyperring R with the subsequent tables:
and
Let us indicate the R hypermodule R with M. It follows that is a subhypermodule of M. For the inclusion map and the canonical projection , we take into account of the short exact sequence
Owing to the fact that N is small in M, is not a direct summand of M(see [23]). It means that is not splitting.
| + | 0 | 1 | 2 | 3 |
| 0 | ||||
| 1 | ||||
| 2 | ||||
| 3 |
| · | 0 | 1 | 2 | 3 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | 0 | 2 | 0 | 2 |
| 3 | 0 | 3 | 2 | 1 |
Example 4.
For a semisimple hypermodule M, let
be a short exact sequence of hypermodules. Since M is semisimple, it follows from [24], Theorem 9, that is a direct summand of M. From this, the short exact sequence is splitting.
Remark 1.
In classical algebra, given any two M and N modules, the trivial splitting short exact sequence is written, where is the external direct sum of these modules M and N. However, since the external direct sum of two hypermodules cannot be defined, there is no trivial splitting short exact sequence for any two given hypermodules over an arbitrary hyperring (see ([6], Theorem 16)).
Let be the set of integers and let be any canonical hypergroup. For each and , describe the set as follows:
On the set , let “+” and “·” denote the usual additive and multiplication. We identify a singleton set by n for all . Then, we can think of the triple as a hyperring, say a trivial hyperring of integers; therefore, M has the structure of a left -hypermodule together with a map via for all and .
For the trivial hyperring , let be a nonempty family of canonical hypergroups (or -hypermodules) and let be the direct product of the canonical hypergroups .
For every , let us denote and . Here, is called the ith component of . The function in case I is a countable set.
Let . Functioning by the definition of equality, if and only if for every .
Theorem 1.
Let become a nonempty family of left -hypermodules, where is the trivial hyperring. Then, the canonical hypergroup is a left hypermodule with the map .
Proof.
From [6], Theorem 16, it is sufficient to show that the axiom of the hypermodule is satisfied. Let and . Since the set contains the only element , then
Hence, the canonical hypergroup is a left hypermodule. □
We say that hypermodule is the direct product of the family . Consider the following subset of the hypermodule :
Since the empty set ∅ is finite, we have . If the union of two finite sets is finite, it can be seen that is a subhypermodule of . We say the hypermodule is an external direct sum of the family . If the index set , then is clear.
Example 5.
For the trivial hyperring , let M and K be two hypermodules. Let . Define these sets and . It follows that and are subhypermodules of N.
Next, we show that N is the internal direct sum of subhypermodules and . Let . Therefore, we can write
and so . For uniqueness, let and , where and . Therefore,
so and . Thus, and . It means that the sum is direct according to [24], Theorem 1.
For the canonical map and for the canonical projection , we have that is a direct summand of N. Hence, the short exact sequence of hypermodules
is splitting.
Now let us start by giving the lemma, which has a significant key role in our research.
Lemma 1.
Let and be normal homomorphisms of hypermodules with . Then, N has the decomposition .
Proof.
Let . Then, and so . There is an element such that . Since N is a canonical hypergroup, implies , and thus the sum is N.
If for some element , then , and so . It follows that . Hence, we obtain that . □
Corollary 1.
For hypermodules , let be the inclusion map. Provided that there is a normal homomorphism with , U is a direct summand of M.
Proof.
It follows from Lemma 1. □
Corollary 2.
If is an R-normal homomorphism such that , then .
Proof.
Assume that is an R-normal homomorphism such that . Let . From the first part of the proof of Lemma 1, there is an element such that . If condition for M, which is a canonical hypergroup, is used again, we obtain , so . From the last part of the proof of Lemma 1, we deduce that , as required. □
The following theorem characterizes the short exact sequence that is splitting.
Theorem 2.
Let be a short exact sequence of R hypermodules. In this case, the subsequent statements are equivalent:
- (1)
- There exists a normal homomorphism with .
- (2)
- splits; that is, is a direct summand of N.
- (3)
- There exists a normal homomorphism with .
Proof.
and By Lemma 1.
Let for some subhypermodule B of N. Since , the restriction function of the normal homomorphism to the B hypersubmodule is a normal monomorphism. Let . Due to the certainty of , there is an element such that . For this reason, we can to write , where and . Therefore, , and thus . It means that is a normal isomorphism.
Set . It follows that is a normal monomorphism, and . This completes the proof of .
Assume that is a direct summand of the hypermodule N. Let be the canonical projection. Now, we consider the isomorphism . Set . Now, for all ,
and thus . □
Proposition 1.
Let K be a normal projective hypermodule. Then, every exact sequence ending K is splitting.
Proof. 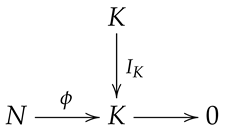 It follows from the presumption that there is a normal homomorphism with . From Theorem 2, we obtain that splits. □
It follows from the presumption that there is a normal homomorphism with . From Theorem 2, we obtain that splits. □
Let be any short exact sequence of R hypermodules. Pay attention to the subsequent diagram:
 It follows from the presumption that there is a normal homomorphism with . From Theorem 2, we obtain that splits. □
It follows from the presumption that there is a normal homomorphism with . From Theorem 2, we obtain that splits. □Proposition 2.
Let M become a normal injective hypermodule. If so every exact sequence starting M is splitting.
Proof. 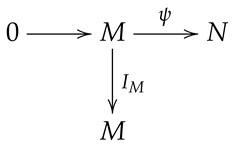 Owing to the fact that M is normal injective, there is a normal homomorphism such that . From Theorem 2, we obtain that splits. □
Owing to the fact that M is normal injective, there is a normal homomorphism such that . From Theorem 2, we obtain that splits. □
Let become any short exact sequence of R hypermodules. Take into account the subsequent diagram:
 Owing to the fact that M is normal injective, there is a normal homomorphism such that . From Theorem 2, we obtain that splits. □
Owing to the fact that M is normal injective, there is a normal homomorphism such that . From Theorem 2, we obtain that splits. □Corollary 3.
Let M be a normal injective hypermodule and N be any hypermodule containing M. Then, M is a direct summand of N.
Proof.
For the inclusion and the canonical homomorphism , we take into account the short exact sequence . Owing to fact that M is normal injective, it follows from Proposition 2 that splits. Hence, M is a direct summand of N according to Theorem 2. □
Lemma 2. 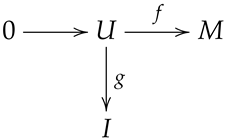 can be extended commutatively by a normal homomorphism .
can be extended commutatively by a normal homomorphism .
Let M and I be two hypermodules. If M is semisimple, then every diagram with the exact row
 can be extended commutatively by a normal homomorphism .
can be extended commutatively by a normal homomorphism .Proof.
Owing to the fact that M is a semisimple hypermodule, it follows from [24], Theorem 9, that is a direct summand of M. Therefore, we can write for some subhypermodule of M. Note that is a normal isomorphism. Set , where is the canonical projection. Now, for all ,
and thus , as required. □
Lemma 3.
Let M and P be two hypermodules. Assume that M is semisimple. Provided that is an epimorphism of hypermodules and is a normal homomorphism of hypermodules, there is a normal homomorphism together with .
Proof. 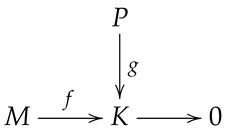 From the assumption, there exists a subhypermodule of M such that . Therefore, is isomorphism. Set , where is the inclusion. Let . Since f is a normal epimorphism, there exists an element with . Now,
Hence, we obtain that the equality . □
From the assumption, there exists a subhypermodule of M such that . Therefore, is isomorphism. Set , where is the inclusion. Let . Since f is a normal epimorphism, there exists an element with . Now,
Hence, we obtain that the equality . □
Let be a normal epimorphism and be a normal homomorphism, where K is a hypermodule. Consider the subsequent diagram:
 From the assumption, there exists a subhypermodule of M such that . Therefore, is isomorphism. Set , where is the inclusion. Let . Since f is a normal epimorphism, there exists an element with . Now,
From the assumption, there exists a subhypermodule of M such that . Therefore, is isomorphism. Set , where is the inclusion. Let . Since f is a normal epimorphism, there exists an element with . Now,
We now prove the main theorem.
Theorem 3.
Let R be a hyperring. If so, the subsequent statements are equivalent.
- (1)
- The left R hypermodule R is semisimple.
- (2)
- All left hyperideals of R are direct summands of R.
- (3)
- All R hypermodules are normal injective.
- (4)
- All R hypermodules are semisimple.
- (5)
- All R hypermodules are normal projective.
- (6)
- All semisimple R hypermodules are normal projective.
- (7)
- All simple R hypermodules are normal projective.
Proof. 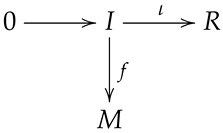 where I is any left hyperideal of R, and is the inclusion map. Since the left R hypermodule R is semisimple, it follows from Lemma 2 that there is a normal homomorphism with . By ([11], Theorem 4), we obtain that M is normal injective.
where I is any left hyperideal of R, and is the inclusion map. Since the left R hypermodule R is semisimple, it follows from Lemma 2 that there is a normal homomorphism with . By ([11], Theorem 4), we obtain that M is normal injective.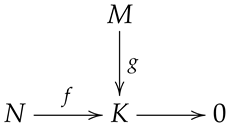 Since M is semisimple, from Lemma 3, the above diagram is commutative. It means that M is normal projective.
Since M is semisimple, from Lemma 3, the above diagram is commutative. It means that M is normal projective.
It follows from [24], Theorem 9.
Let M be any left R hypermodule. Consider the following diagram with the exact row:
 where I is any left hyperideal of R, and is the inclusion map. Since the left R hypermodule R is semisimple, it follows from Lemma 2 that there is a normal homomorphism with . By ([11], Theorem 4), we obtain that M is normal injective.
where I is any left hyperideal of R, and is the inclusion map. Since the left R hypermodule R is semisimple, it follows from Lemma 2 that there is a normal homomorphism with . By ([11], Theorem 4), we obtain that M is normal injective. Let M be any left R hypermodule and . Applying , we obtain that U is normal injective and, so, from Corollary 3, M has the decomposition , where V is a subhypermodule of M. Hence, M is semisimple according to [24], Theorem 9.
For any hypermodule M, consider the following diagram with exact row:
 Since M is semisimple, from Lemma 3, the above diagram is commutative. It means that M is normal projective.
Since M is semisimple, from Lemma 3, the above diagram is commutative. It means that M is normal projective. and are clear.
From [24], Corollary 4, it is enough to show that whenever , . Let us assume the opposite, that is, . Therefore, there is a maximal left hyperideal P of R such that P contains the essential left hyperideal I. Applying [24], Theorem 3, is a simple R hypermodule. Now, from and Proposition 1, the short exact sequence
is splitting, so there exists a minimal left hyperideal S of R such that . is a contradiction. Hence, . □
The next result follows from Theorem 3.
Corollary 4.
Let R be a hyperring. Then, the left R hypermodule R is semisimple if and only if every exact sequence of R hypermodules is splitting.
Finally, let us construct an example for Theorem 3.
Example 6.
Let . We describe “+” and “·” in the subsequent tables:
and
Then, R is a commutative hyperring together with identity element 1. It is straightforward to see that the only hyperideals of R are , , and R. Therefore, the sum is direct, so is semisimple. It follows from Theorem 3 that each left R hypermodule is normal injective (normal projective).
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | |||||||||
| 2 | 2 | |||||||||
| 3 | 3 | |||||||||
| 4 | 4 | |||||||||
| 5 | 5 | 0 | 1 | 2 | 3 | 4 | ||||
| 6 | 6 | 1 | ||||||||
| 7 | 7 | 2 | ||||||||
| 8 | 8 | 3 | ||||||||
| 9 | 9 | 4 |
| · | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 0 | 2 | 4 | 6 | 8 | 0 | 2 | 4 | 6 | 8 |
| 3 | 0 | 3 | 6 | 9 | 2 | 5 | 8 | 1 | 4 | 7 |
| 4 | 0 | 4 | 8 | 2 | 6 | 0 | 4 | 8 | 2 | 6 |
| 5 | 0 | 5 | 0 | 5 | 0 | 5 | 0 | 5 | 0 | 5 |
| 6 | 0 | 6 | 2 | 8 | 4 | 0 | 6 | 2 | 8 | 4 |
| 7 | 0 | 7 | 4 | 1 | 8 | 5 | 2 | 9 | 6 | 3 |
| 8 | 0 | 8 | 6 | 1 | 8 | 0 | 8 | 6 | 4 | 2 |
| 9 | 0 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
4. Conclusions
The concept of short exact sequences and their relationship with normal injective and projective hypermodules was developed; a type of short exact sequence, namely, the splitting exact sequence, was defined; and some examples were provided. Moreover, we proved that every exact sequence ending with a normal projective hypermodule, and every exact sequence starting with a normal injective hypermodule must be split. Finally, the relationships between semisimple, simple, normal injective, and normal projective hypermodules were investigated.
Author Contributions
Conceptualization, E.T. and B.N.T.; methodology, E.T. and B.N.T.; validation, E.T., B.N.T. and H.B.; formal analysis, E.T., B.N.T. and H.B.; investigation, E.T., B.N.T. and H.B.; data curation, H.B.; writing—original draft preparation, E.T. and B.N.T.; writing—review and editing, H.B.; visualization, E.T., B.N.T. and H.B.; supervision, H.B. All authors have read and agreed to the published version of the manuscript.
Funding
The first author gratefully acknowledges the support they received from The Scientific and Technological Research Council of Turkey (TUBITAK) through grant No. 123F236. The third author acknowledges financial support from the Slovenian Research and Innovation Agency (research core funding No. P2-0103).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Marty, F. Sur une generalization de la notion de group. In Proceedings of the 8th Congress Mathematics, Scandinaves, Stockholm, 20–26 June 2021; pp. 45–49. [Google Scholar]
- Krasner, M. A class of hyperrings and hyperfields. Int. J. Math. Sci. 1983, 6, 307–311. [Google Scholar] [CrossRef]
- Rota, R. Sugli iperanelli moltiplicativi. Rend. Mat. Appl. 1982, 2, 711–724. [Google Scholar]
- Vougiouklis, T. The fundamental relation in hyperrings. The general hyperfield. In Algebraic Hyperstructures, and Applications (Xanthi, 1990); World Scientific Publishing: Teaneck, NJ, USA, 1991; pp. 203–211. [Google Scholar]
- Massouros, C.G. Free and cyclic hypermodules. Ann. Math. Pure Appl. 1988, 159, 153–166. [Google Scholar] [CrossRef]
- Massouros, C.G.; Massouros, C. Hypercompositional Algebra, Computer Sciences and Geometry. Mathematics 2020, 8, 1338. [Google Scholar] [CrossRef]
- Massouros, C.; Massouros, C.G. An Overview of the Foundations of the Hypergroup Theory. Mathematics 2021, 9, 1054. [Google Scholar] [CrossRef]
- Vougiouklis, T. Hyperstructures and Their Representations; Hadronic Press, Inc.: Palm Harber, FL, USA, 1994. [Google Scholar]
- Ameri, R.; Shojaci, H. Projective and Injective Krasner Hypermodules. J. Algebra Its Appl. 2021, 20, 2150186. [Google Scholar] [CrossRef]
- Ameri, R. On Categories of Hypergroups and Hypermodules. J. Discret. Math. Sci.-Cryptogr. 2003, 2, 121–132. [Google Scholar] [CrossRef]
- Bordbar, H.; Cristea, I. About the Normal Projectivity and Injectivity of Krasner Hypermodules. Axioms 2021, 10, 83. [Google Scholar] [CrossRef]
- Nişancı Türkmen, B.; Bordbar, H.; Cristea, I. Supplements Related to Normal π-Projective Hypermodules. Mathematics 2022, 10, 1945. [Google Scholar] [CrossRef]
- Bordbar, H.; Cristea, I. Divisible Hypermodules. Analele Univ. Ovidius Constanta 2022, 30, 57–74. [Google Scholar] [CrossRef]
- Bordbar, H. Torsion Elements and Torsionable Hypermodules. Mathematics 2023, 11, 4525. [Google Scholar] [CrossRef]
- Durgun, Y. Projectivity relative to closed (neat) submodules. J. Algebra Appl. 2022, 21, 2250114. [Google Scholar] [CrossRef]
- Durgun, Y. Rings whose modules have maximal or minimal subprojectivity domain. J. Algebra Appl. 2015, 14, 1550083. [Google Scholar] [CrossRef]
- Durgun, Y. Subprojectivity domains of pure-projective modules. J. Algebra Appl. 2022, 19, 2050091. [Google Scholar] [CrossRef]
- Alahmadi, A.N.; Alkan, M.; López-Permouth, S. Poor modules: The opposite of injectivity. Glasg. Math. J. 2010, 52, 7–17. [Google Scholar] [CrossRef][Green Version]
- Aydoĝdu, P.; Durgun, Y. The opposite of injectivity by proper classes. Quaest. Math. 2022, 46, 1547–1570. [Google Scholar] [CrossRef]
- Corsini, P. Prolegomena of Hypergroup Theory, 2nd ed.; Aviani Editore: Tricesimo, Italy, 1993. [Google Scholar]
- Davvaz, B.; Leoreanu-Fotea, V. Hyperring Theory and Applications; International Academic Press: Palm Harbor, FL, USA, 2007. [Google Scholar]
- Massouros, C.G. Methods of constructing hyperfields. Int. J. Math. Sci. 1985, 8, 725–728. [Google Scholar] [CrossRef]
- Talaee, B. Small Subhypermodules and Their Applications. Rom. J. Math. Comput. Sci. 2013, 4, 5–14. [Google Scholar]
- Türkmen, E.; Nişancı Türkmen, B.; Bordbar, H. A Hyperstructural Approach to Semisimplicity. Axioms 2024, 13, 81. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
