Generalization of the Distance Fibonacci Sequences
Abstract
1. Introduction
2. Materials and Methods
(t,k) Generalization of Distance Fibonacci Sequences
3. Results
3.1. The Properties of
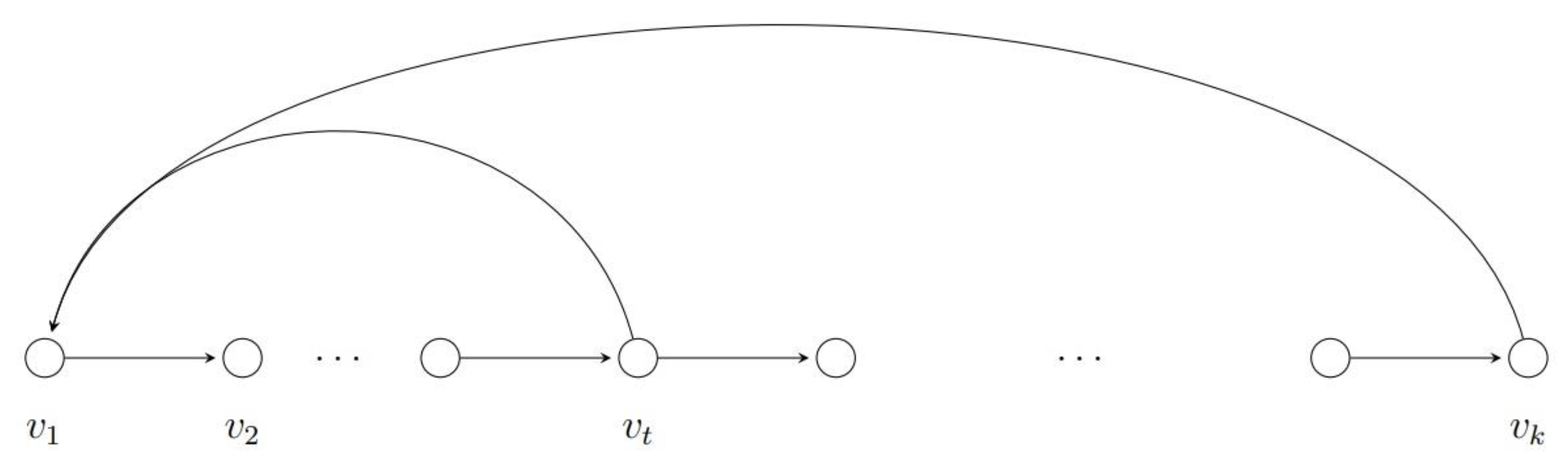
3.2. Graph Interpretation of
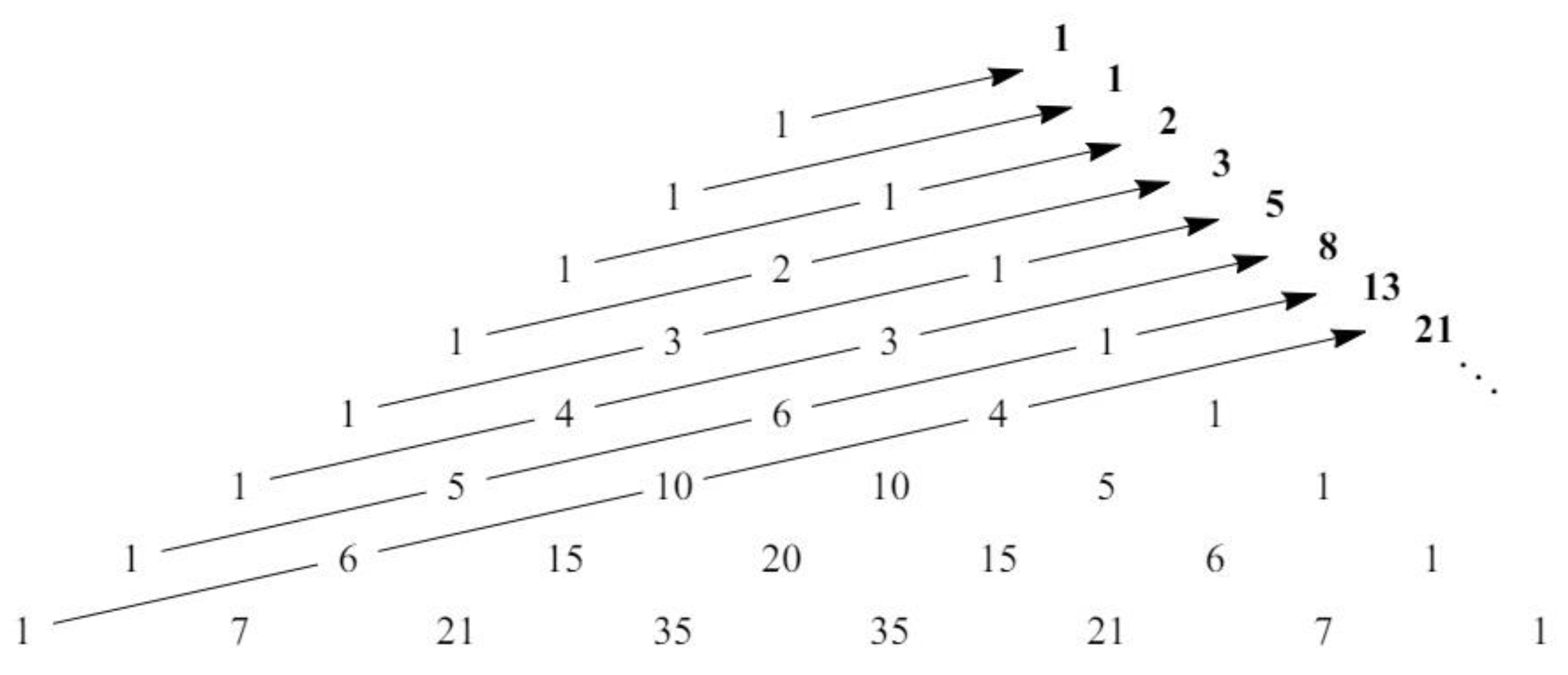
3.3. Pascal-like Triangle
3.4. Generating Functions
3.5. Matrix Generators
3.6. Connection with Pascal’s Triangle
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kiliç, E. The generalized order k-Fibonacci Pell sequence by matrix methods. J. Comput. Appl. Math. 2007, 209, 133–145. [Google Scholar] [CrossRef]
- Kiliç, E.; Taşçi, D. On the generalized Fibonacci and Pell Sequences by Hessenberg matrices. Ars. Comb. 2010, 94, 161–174. [Google Scholar]
- Koshy, T. Fibonacci and Lucas Numbers with Applications, 3rd ed.; A Wiley Interscience Publication: Waterloo, ON, Canada, 2001. [Google Scholar]
- Şen, E. Fibonacci Numbers, Golden Section and Applications. arXiv 2013, arXiv:1301.6606. [Google Scholar]
- Włoch, I.; Włoch, A. On some multinomial sums related to Fibonacci Type numbers. Tatra Mt. Math. Publ. 2020, 77, 99–108. [Google Scholar] [CrossRef]
- Feingold, A.J. A hyperbolic GCM Lie algebra and the Fibonacci numbers. Proc. Am. Math. Soc. 1980, 80, 379–385. [Google Scholar] [CrossRef]
- Souza, J.; Curado, E.M.F.; Rego-Monteiro, M.A. Generalized Heisenberg algebras and Fibonacci series. J. Phys. A Math. Gen. 2007, 39, 10415–10425. [Google Scholar] [CrossRef]
- Schork, M. Generalized Heisenberg algebras and k-generalized Fibonacci Numbers. J. Phys. A Math. Theory 2007, 40, 4207–4214. [Google Scholar] [CrossRef]
- Bednarz, U.; Włoch, A.; Wołowiec-Musiał, M. Distance Fibonacci Numbers, their interpretations and matrix generators. Comment. Math. 2013, 53, 34–46. [Google Scholar] [CrossRef]
- Kwaśnik, M.; Włoch, I. The total number of generalized stable sets and kernels in graphs. Ars Comb. 2000, 55, 139–146. [Google Scholar]
- Bród, D.; Włoch, I.; Piejko, K. Distance Fibonacci Numbers, distance Lucas numbers and their applications. Ars Comb. 2013, 161, 2695–2701. [Google Scholar]
- Stojmenovic, I. Recursive algorithms in computer science courses: Fibonacci numbers and binomial coefficients. IEEE Trans. Educ. 2000, 43, 273–276. [Google Scholar] [CrossRef]
- Atkins, J.; Geist, R. Fibonacci Numbers and computer algorithms. Coll. Math. J. 1987, 18, 328–336. [Google Scholar] [CrossRef]
- Sinha, S. The Fibonacci numbers and Its Amazing Applications. Int. J. Eng. Sci. Invent. 2017, 6, 7–14. [Google Scholar]
- Omotehinwa, T.O.; Ramon, S.O. Fibonacci Numbers and Golden Ratio in Mathematics and Science. Int. J. Comput. Inf. Technol. 2013, 2, 630–638. [Google Scholar]
- Gutman, I.; Wagner, S. Maxima and minima of the Hosoya index and the Merrifield-Simmons index. A survey of results and techniques. Acta Appl. Math. 2010, 112, 323–346. [Google Scholar]
- Prodinger, H.; Tichy, R. Fibonacci numbers of graphs. Fibonacci Q. 1982, 20, 16–21. [Google Scholar]
- Matoušová, I.; Trojovský, P. On coding by (2,q)- distance Fibonacci numbers. Mathematics 2020, 8, 2058. [Google Scholar] [CrossRef]
- Tatlow, R. The Use and Abuse of Fibonacci numbers and The Golden Section in Musicology today. Underst. Bach 2006, 1, 69–85. [Google Scholar]
- Horadam, A.F. A generalized Fibonacci sequence. Amer. Math. Mon. 1961, 68, 455–459. [Google Scholar] [CrossRef]
- Jaiswal, D.V. On a generalized Fibonacci sequence. Labdev. J. Sci. Tech. Part. A 1969, 7, 67–71. [Google Scholar]
- Falcon, S. Binomial Transform of The Generalized k-Fibonacci numbers. Commun. Math. Appl. 2019, 10, 643–651. [Google Scholar] [CrossRef]
- Falcon, S.; Plaza, A. The k-Fibonacci sequence and the Pascal 2-Triange. Chaos Solitions Fractals 2007, 33, 38–49. [Google Scholar] [CrossRef]
- Sburlati, G. Generalized Fibonacci sequences and linear congruences. Fibonacci Quart 2002, 40, 446–452. [Google Scholar]
- Bednarz, U.; Bród, D.; Włoch, A.; Włoch, I.; Wołowiec-Musiał, M. On a new type of distance Fibonacci Numbers. Discret. Appl. Math. 2013, 161, 2695–2701. [Google Scholar]
- Özkan, E.; Yılmaz, N.Ş.; Włoch, A. On F3(k,n)-numbers of the Fibonacci Type. Bol. Soc. Matemática Mex. 2021, 27, 77. [Google Scholar]
- Yilmaz, N.Ş.; Włoch, A.; Özkan, E.; Strzałka, D. On doubled and quadrupled Fibonacci type sequences. Ann. Math. Silesianae 2023, 38, 1–15. [Google Scholar]
- Diestel, R. Graph Theory; Springer: Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Soykan, Y. On Generalized Narayana Numbers. Int. J. Adv. Appl. Math. Mech. 2020, 7, 43–56. [Google Scholar]

| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | 0 | 1 | 3 | |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | 0 | 1 | 3 | 3 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 4 | 4 | 4 | 5 | 7 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yilmaz, N.Ş.; Włoch, A.; Özkan, E. Generalization of the Distance Fibonacci Sequences. Axioms 2024, 13, 420. https://doi.org/10.3390/axioms13070420
Yilmaz NŞ, Włoch A, Özkan E. Generalization of the Distance Fibonacci Sequences. Axioms. 2024; 13(7):420. https://doi.org/10.3390/axioms13070420
Chicago/Turabian StyleYilmaz, Nur Şeyma, Andrej Włoch, and Engin Özkan. 2024. "Generalization of the Distance Fibonacci Sequences" Axioms 13, no. 7: 420. https://doi.org/10.3390/axioms13070420
APA StyleYilmaz, N. Ş., Włoch, A., & Özkan, E. (2024). Generalization of the Distance Fibonacci Sequences. Axioms, 13(7), 420. https://doi.org/10.3390/axioms13070420








