Monogenity and Power Integral Bases: Recent Developments

Abstract

Monogenity is a classical area of algebraic number theory that continues to be actively researched. This paper collects the results obtained over the past few years in this area. Several of the listed results were presented at a series of online conferences titled “Monogenity and Power Integral Bases”. We also give a collection of the most important methods used in several of these papers. A list of open problems for further research is also given.

1. Introduction

Let $K=\mathbb{Q}\left(\gamma \right)$ be an algebraic number field of degree n, generated by the algebraic integer $\gamma$, with ring of integers ${\mathbb{Z}}_K$ and discriminant $D_K$. It is a classical problem of algebraic number theory, going back to R. Dedekind [1], K. Hensel [2] and H. Hasse [3] to decide if the ring ${\mathbb{Z}}_K$ can be generated by a single element $\alpha \in {\mathbb{Z}}_K$, that is, if it is mono-generated, ${\mathbb{Z}}_K=\mathbb{Z}\left[\alpha \right]$. In this case, we say that the ring ${\mathbb{Z}}_K$, or the field K, is monogenic, and the integral basis $\{1,\alpha ,\dots {\alpha }^{n-1}\}$ is called a power integral basis.

Recently, this area has been developing very rapidly. In order to create a suitable forum to present recent results on monogenity, the author started a series of online meetings “Monogenity and Power Integral Bases” (https://sway.cloud.microsoft/F2kZzeZ3bmD4dFfy?ref=Link accessed on 15 January 2021) in 2021. The purpose was to make contacts, circulate preprints and results, and support collaboration between researchers all over the world working in this area. During the time of pandemy this was the only way to contact, but later on this proved to be an easy and fast way of contacting. Therefore, up to March 2024 we already had nine meetings and we hope to continue.

The main purpose of this paper is to give an overview of the latest developments in monogenity theory, about the results that were presented at the online meetings and the results that appeared parallel. The paper is also a kind of extension of the book [4] that appeared in 2019. Most of these results are not yet contained there.

In Section 2, we collect the most important tools that were used in several works. These may be useful for further applications. Section 3 collects the most important results, and finally in Section 4 we try to indicate some possible perspectives of further research.

In favour of the reader, we collect some further concepts on monogenity.

For any primitive element $\alpha \in {\mathbb{Z}}_K$ (that is $K=\mathbb{Q}\left(\alpha \right)$), the index of $\alpha$ is defined as the module index

$$I\left(\alpha \right)=({\mathbb{Z}}_K:\mathbb{Z}\left[\alpha \right]).$$

We obviously have

$$D\left(\alpha \right)=I{\left(\alpha \right)}^2{D}_K,$$

where $D\left(\alpha \right)$ is the discriminant of $\alpha$,

$$D\left(\alpha \right)=\prod _{1\le i<j\le n}{({\alpha }^{\left(i\right)}-{\alpha }^{\left(j\right)})}^2,$$

${\alpha }^{\left(i\right)}$ denoting the conjugates of $\alpha$ corresponding to ${\gamma }^{\left(i\right)}$ ($i=1,\dots ,n$) (in the following we shall denote similarly the conjugates of any element of K). Obviously, $I\left(\alpha \right)=1$, if and only if ${\mathbb{Z}}_K=\mathbb{Z}\left[\alpha \right]$, that is, if $\{1,\alpha ,\dots {\alpha }^{n-1}\}$ is an integral basis, or in other words $\alpha$ generates a power integral basis in K.

The field index, $m\left(K\right)$, of K is defined as

$$m\left(K\right)=gcd\left\{I\left(\alpha \right)\right|\alpha \in {\mathbb{Z}}_K,K=\mathbb{Q}\left(\alpha \right)\}.$$

If K is monogenic, there are elements of index 1, and the field index is also equal to 1. The converse is not true: the field index may happen to be 1 without the field being monogenic.

If $\alpha ,\beta$ are primitive elements in ${\mathbb{Z}}_K$ and $\alpha +\beta \in \mathbb{Z}$ or $\alpha -\beta \in \mathbb{Z}$ then obviously their indices are equal. Such elements are called equivalent. It was proved by B. J. Birch and J. R. Merriman [5] and then in an effective form by K. Győry [6] that up to equivalence there are only finitely many generators of power integral bases in any number field K.

For any integral basis $(1,{\omega }_2,\dots ,{\omega }_n)$ of K set

$$L^{\left(i\right)}\left(\underline{X}\right)=X_1+{\omega }_2^{\left(i\right)}{X}_2+\dots +{\omega }_n^{\left(i\right)}{X}_n$$

($i=1,\dots ,n$). Then (see [4])

$$D\left(L\left(\underline{X}\right)\right)=\prod _{1\le i<j\le n}\left(L^{\left(i\right)}\left(\underline{X}\right)-L^{\left(j\right)}\left(\underline{X}\right)\right)=I(X_2,\dots ,X_n)D_K$$

where $I(X_2,\dots ,X_n)$ is a homogeneous polynomial of degree $n(n-1)/2$ with integer coefficients, with the property that for any primitive element $\alpha =x_1+{\omega }_2{x}_2+\dots {\omega }_n{x}_n\in {\mathbb{Z}}_K$ we have

$$I\left(\alpha \right)=|I(x_2,\dots ,x_n)|.$$

The polynomial $I(X_2,\dots ,X_n)$ is called the index form corresponding to the integral basis $(1,{\omega }_2,\dots ,{\omega }_n)$. Since equivalent algebraic integers have the same index, it is independent of $X_1$. Therefore, determining elements $\alpha \in {\mathbb{Z}}_K$ of index m is equivalent to solving the index form equation

$$I(x_2,\dots ,x_n)=m\mathrm{in}{x}_2,\dots ,x_n\in \mathbb{Z}.$$

A non-zero irreducible polynomial $f\left(x\right)\in \mathbb{Z}\left[x\right]$ is called monogenic if a root $\alpha$ of $f\left(x\right)$ generates a power integral basis in the field $K=\mathbb{Q}\left(\alpha \right)$. Obviously, if the polynomial $f\left(x\right)$ is monogenic, then K is also monogenic, but the converse is not true. The field K may happen to be monogenic without $f\left(x\right)$ being monogenic. The index of $f\left(x\right)$ is defined as $\mathrm{ind}\left(f\right)=({\mathbb{Z}}_K:\mathbb{Z}\left[\alpha \right])$.

2. Tools

2.1. Dedekind’s Criterion

Let $\overline{f\left(x\right)}={\prod }_{i=1}^r{\overline{{\varphi }_i\left(x\right)}}^{{\mathcal{l}}_i}$ modulo p be the factorization of $f\left(x\right)$ modulo p into powers of monic irreducible coprime polynomials of ${\mathbb{F}}_p\left[x\right]$.

For completeness, we recall here a well-known theorem of Dedekind:

Theorem 1

(Chapter I, Proposition 8.3 of [7]).

If p does not divide the index $I\left(\alpha \right)=({\mathbb{Z}}_K:\mathbb{Z}\left[\alpha \right])$, then

$$p{\mathbb{Z}}_K=\prod _{i=1}^r{\mathfrak{p}}_i^{{\mathcal{l}}_i},$$

where ${\mathfrak{p}}_i=p{\mathbb{Z}}_K+{\varphi }_i\left(\alpha \right){\mathbb{Z}}_K$ and the residue degree of ${\mathfrak{p}}_i$ is $f\left({\mathfrak{p}}_i\right)=deg\left({\varphi }_i\right)$.

As indicated above, it is very important to have a tool to determine prime divisors of the indices of algebraic integers. Therefore, the following well-known criterion of Dedekind is very frequently used:

Theorem 2

(Dedekind’s criterion [1], see also [8] Theorem 6.1.4, [9] p. 295).

Let $f\left(x\right)\in \mathbb{Z}\left[x\right]$ be a monic non-zero irreducible polynomial with a root α, let $K=\mathbb{Q}\left(\alpha \right)$, and let p be a prime number. Let $\overline{f\left(x\right)}={\prod }_{i=1}^r{\overline{{\varphi }_i\left(x\right)}}^{{\mathcal{l}}_i}modp$ be the factorization of $\overline{f\left(x\right)}$ in ${\mathbb{F}}_p\left[x\right]$, with monic ${\varphi }_i\in \mathbb{Z}\left[x\right]$, such that their reductions $\overline{{\varphi }_i\left(x\right)}$ are irreducible and pairwise coprime over ${\mathbb{F}}_p$. Set

$$M\left(x\right)=\frac{f\left(x\right)-{\prod }_{i=1}^r{{\varphi }_i}^{{\mathcal{l}}_i}\left(x\right)}{p}.$$

Then $M\left(x\right)\in \mathbb{Z}\left[x\right]$ and the following statements are equivalent:

1. 

p does not divide the index $I\left(\alpha \right)=({\mathbb{Z}}_K:\mathbb{Z}\left[\alpha \right])$.

2. 

For every $i=1,\cdots ,r$, either ${\mathcal{l}}_i=1$ or ${\mathcal{l}}_i\ge 2$ and $\overline{{\varphi }_i\left(x\right)}$ does not divide $\overline{M\left(x\right)}$ in ${\mathbb{F}}_p\left[x\right]$.

2.2. The Field Index

We also recall a simple but very important statement of Hensel:

Theorem 3

(K. Hensel [2] p. 280).

• The prime factors of the field index are smaller than the degree of the field.

Denote by ${\nu }_p\left(k\right)$ the highest power of the prime p dividing the integer k.

Theorem 4

(H. T. Engström [10]).

For number fields of degree $n\le 7$, ${\nu }_p\left(m\left(K\right)\right)$ is explicitly determined by the factorization of p into powers of prime ideals of $p{\mathbb{Z}}_K$.

The corresponding tables of [10] are too long to include here, but they present the explicit exponents.

2.3. Newton Polygon Method

If p divides the index $I\left(\alpha \right)=({\mathbb{Z}}_K:\mathbb{Z}\left[\alpha \right])$ then Dedekind’s Theorem 1 cannot be applied.

Using Newton polygons, an alternative method was given by Ore [11] to calculate $I\left(\alpha \right)=({\mathbb{Z}}_K:\mathbb{Z}\left[\alpha \right])$, $D_K$ and the prime ideal factorization of primes in ${\mathbb{Z}}_K$. This was further developed among others by J. Montes and E. Nart [12], Fadil, L.E. J. Montes and E. Nart [13] and L. El Fadil [14]. This theory was extended to so-called higher-order Newton polygons by J. Guardia, J. Montes and E. Nart [15]. The method is also called Montes algorithm.

Here we only give a short introduction to some basic notions and statement of this very technical method, based on the explanation used in [16]. During recent years, a huge amount of papers have applied this method.

For any prime p, let ${\nu }_p$ be the p-adic valuation of $\mathbb{Q}$. Denote by ${\mathbb{Q}}_p$ its p-adic completion and by ${\mathbb{Z}}_p$ the ring of p-adic integers. Let ${\nu }_p$ be the Gauss’s extension of ${\nu }_p$ to ${\mathbb{Q}}_p\left(x\right)$, ${\nu }_p\left(P\right)=min({\nu }_p\left(a_i\right),(i=0,\dots ,n)$ for any polynomial $P\left(x\right)={\sum }_{i=0}^n{a}_i{x}^i\in {\mathbb{Q}}_p\left[x\right]$, and extended by ${\nu }_p(P/Q)={\nu }_p\left(P\right)-{\nu }_p\left(Q\right)$ for $0\ne P,Q\in {\mathbb{Q}}_p\left[x\right]$. Let $\varphi \in {\mathbb{Z}}_p\left[x\right]$ be a monic polynomial whose reduction is irreducible in ${\mathbb{F}}_p\left[x\right]$, and let ${\mathbb{F}}_{\varphi }$ be the field ${\mathbb{F}}_p\left[x\right]/\left(\overline{\varphi }\right)$. For any monic polynomial $f\left(x\right)\in {\mathbb{Z}}_p\left[x\right]$, upon the Euclidean division by successive powers of $\varphi$, we expand $f\left(x\right)$ as follows:

$$f\left(x\right)=\sum _{i=0}^{\mathcal{l}}{a}_i\left(x\right)\varphi {\left(x\right)}^i.$$

This is called the $\varphi$-expansion of $f\left(x\right)$ ($deg\left(a_i\left(x\right)\right)<deg\left(\varphi \right),i=1,\dots ,\mathcal{l}$). The $\varphi$-Newton polygon of $f\left(x\right)$ with respect to p is the lower boundary convex envelope of the set of points $\{(i,{\nu }_p\left(a_i\left(x\right)\right)),a_i\left(x\right)\ne 0\}$ in the Euclidean plane, which we denote by $N_{\varphi }f$. The $\varphi$-Newton polygon of f is the process of joining the edges $S_1,\dots ,S_r$ ordered by increasing slopes, which can be expressed as

$${\mathbb{N}}_{\varphi }f=S_1+\cdots +S_r.$$

For every side, $S_i$, of ${\mathbb{N}}_{\varphi }f$, the length of $S_i$, denoted $\mathcal{l}\left(S_i\right)$, is the length of its projection to the x-axis. Its height, denoted by $h\left(S_i\right)$, is the length of its projection to the y-axis. Let $d\left(S_i\right)=gcd(\mathcal{l}\left(S_i\right),h\left(S_i\right))$ be the ramification degree of S. The principal $\varphi$-Newton polygon of f, denoted ${\mathbb{N}}_{\varphi }^{+}f$, is the part of the polygon ${\mathbb{N}}_{\varphi }f$, which is determined by joining all sides of negative slopes. For every side, S, of ${\mathbb{N}}_{\varphi }^{+}f$, with initial point $(s,u_s)$ and length ℓ, and for every $0\le i\le \mathcal{l}$, we attach the residue coefficient $c_i\in {\mathbb{F}}_{\varphi }$ as follows:

$${\displaystyle c_i=\left\{\begin{array}{cc}0,\hfill & \mathrm{i}\mathrm{f} (s+i,{\mathit{u}}_{\mathit{s}+\mathit{i}}) \mathrm{lies} \mathrm{strictly} \mathrm{above} S,\hfill \\ \left({\displaystyle \frac{a_{s+i}\left(x\right)}{p^{{\mathit{u}}_{\mathit{s}+\mathit{i}}}}}\right)mod(p,\varphi \left(x\right)),\hfill & \mathrm{i}\mathrm{f} (s+i,{\mathit{u}}_{\mathit{s}+\mathit{i}}) \mathrm{lies} \mathrm{on} S,\hfill \end{array}\right.}$$

where $(p,\varphi (x\left)\right)$ is the maximal ideal of ${\mathbb{Z}}_p\left[x\right]$ generated by p and $\varphi$. Let $\lambda =-h/e$ be the slope of S, where h and e are two positive coprime integers. Then $d=\mathcal{l}/e$ is the degree of S. The points with integer coordinates lying on S are exactly

$${\displaystyle (s,u_s),(s+e,u_s-h),\cdots ,(s+de,u_s-dh).}$$

Thus, if i is not a multiple of e, then $(s+i,u_{s+i})$ does not lie in S, and so $c_i=0$. The polynomial

$$f_S\left(y\right)=t_d{y}^d+t_{d-1}{y}^{d-1}+\cdots +t_{1}y+t_0\in {\mathbb{F}}_{\varphi }\left[y\right],$$

is called the residual polynomial of $f\left(x\right)$ associated to the side S, where, for every $i=0,\dots ,d$, $t_i=c_{ie}$.

Let ${\mathbb{N}}_{\varphi }^{+}f=S_1+\cdots +S_r$ be the principal $\varphi$-Newton polygon of f with respect to p. We say that f is a $\varphi$-regular polynomial with respect to p, if $f_{S_i}\left(y\right)$ is square free in ${\mathbb{F}}_{\varphi }\left[y\right]$ for every $i=1,\dots ,r$. The polynomial f is said to be p-regular if $\overline{f\left(x\right)}={\prod }_{i=1}^r{\overline{{\varphi }_i\left(x\right)}}^{{\mathcal{l}}_i}$ for some monic polynomials ${\varphi }_1,\cdots ,{\varphi }_t$ of $\mathbb{Z}\left[x\right]$, such that $\overline{{\varphi }_1},\cdots ,\overline{{\varphi }_t}$ are irreducible coprime polynomials over ${\mathbb{F}}_p$ and f is a ${\varphi }_i$-regular polynomial with respect to p for every $i=1,\dots ,t$.

Let $\varphi \in {\mathbb{Z}}_p\left[x\right]$ be a monic polynomial, such that $\overline{\varphi \left(x\right)}$ is irreducible in ${\mathbb{F}}_p\left[x\right]$. The $\varphi$-index of $f\left(x\right)$ (cf. 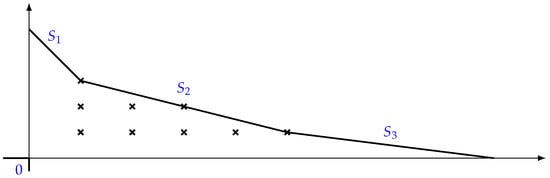[13]), denoted by ${\mathrm{ind}}_{\varphi }\left(f\right)$, is $deg\left(\varphi \right)$ times the number of points with natural integer coordinates that lie below or on the polygon ${\mathbb{N}}_{\varphi }^{+}f$, strictly above the horizontal axis and strictly beyond the vertical axis (see Figure 1).

In the example of Figure 1, $in{d}_{\varphi }\left(f\right)=9\times deg\left(\varphi \right)$.

Now assume that $\overline{f\left(x\right)}={\prod }_{i=1}^r{\overline{{\varphi }_i\left(x\right)}}^{{\mathcal{l}}_i}$ is the factorization of $\overline{f\left(x\right)}$ in ${\mathbb{F}}_p\left[x\right]$ into monic polynomials ${\varphi }_i\in \mathbb{Z}\left[x\right]$, which are irreducible and pairwise coprime in ${\mathbb{F}}_p\left[x\right]$ ($i=1,\dots ,r$).

For every $i=1,\dots ,r$, let $N_{{\varphi }_i}^{+}\left(f\right)=S_{i1}+\cdots +S_{i{r}_i}$ be the principal ${\varphi }_i$-Newton polygon of f with respect to p. For every $j=1,\dots ,r_i$, let

$$f_{S_{ij}}\left(y\right)=\prod _{k=1}^{s_{ij}}{\psi }_{ijk}^{a_{ijk}}\left(y\right)$$

be the factorization of $f_{S_{ij}}\left(y\right)$ in ${\mathbb{F}}_{{\varphi }_i}\left[y\right]$. Then we have the following index theorem of Ore.

Theorem 5

(Theorem of Ore, see Theorem 1.7 and Theorem 1.9 in [13], Theorem 3.9 in [14], pp. 323–325 in [11,12]).

1. 

We have

$${\nu }_p\left(\mathrm{ind}\left(f\right)\right)\ge \sum _{i=1}^r{\mathrm{ind}}_{{\varphi }_i}\left(f\right).$$

The equality holds if $f\left(x\right)$ is p-regular.

2. 

If $f\left(x\right)$ is p-regular, then

$$p{\mathbb{Z}}_K=\prod _{i=1}^r\prod _{j=1}^{r_i}\prod _{k=1}^{s_{ij}}{\mathfrak{p}}_{ijk}^{e_{ij}},$$

is the factorization of $p{\mathbb{Z}}_K$ into powers of prime ideals of ${\mathbb{Z}}_K$ lying above p, where $e_{ij}={\mathcal{l}}_{ij}/d_{ij}$, ${\mathcal{l}}_{ij}$ is the length of $S_{ij}$, $d_{ij}$ is the ramification degree of $S_{ij}$, and $f_{ijk}=deg\left({\varphi }_i\right)\times deg\left({\psi }_{ijk}\right)$ is the residue degree of the prime ideal ${\mathfrak{p}}_{ijk}$ over p.

2.4. Algorithmic Methods

Several of known efficient methods for the resolutions of Diophantine equations are related to Thue equations, cf. [4]. These methods are implemented, e.g., in Magma [17]. Therefore, the most efficient methods for solving index form equations also reduce the index form equation to Thue equations.

In cubic fields, the index form equation is a cubic Thue equation, see [4].

The below method of I. Gaál, A. Pethő and M. Pohst [18,19] reduces the index form equations in quartic fields to a cubic and some corresponding quartic Thue equations. This method is quite often used even nowadays, and therefore we briefly present it.

Let $K=\mathbb{Q}\left(\xi \right)$ be a quartic number field and $f\left(x\right)=x^4+a_1{x}^3+a_2{x}^2+a_{3}x+a_4\in \mathbb{Z}\left[x\right]$ the minimal polynomial of $\xi$. We represent any $\alpha \in {\mathbb{Z}}_K$ in the form

$$\alpha =\frac{a_{\alpha }+x\xi +y{\xi }^2+z{\xi }^3}{d},$$

(1)

with $a_{\alpha },x,y,z\in \mathbb{Z}$, and with a common denominator $d\in \mathbb{Z}$. Consider the solutions of the equation

$$I\left(\alpha \right)=m(\alpha \in {\mathbb{Z}}_K)$$

(2)

for $0<m\in \mathbb{Z}$. We have

Theorem 6

([18]).

Let $i_m=d^{6}m/n$, where $n=I\left(\xi \right)$. The element α of (1) is a solution of (2), if and only if there is a solution $(u,v)\in {\mathbb{Z}}^2$ of the cubic equation

$$F(u,v)=u^3-a_2{u}^{2}v+(a_1{a}_3-4a_4)u{v}^2+(4a_2{a}_4-a_3^2-a_1^2{a}_4)v^3=\pm i_m$$

(3)

such that $(x,y,z)$ satisfies

$$\begin{array}{ccc}\hfill Q_1(x,y,z)& =& x^2-xy{a}_1+y^2{a}_2+xz(a_1^2-2a_2)+yz(a_3-a_1{a}_2)\hfill \\ & & +z^2(-a_1{a}_3+a_2^2+a_4)=u,\hfill \\ \hfill Q_2(x,y,z)& =& y^2-xz-a_{1}yz+z^2{a}_2=v.\hfill \end{array}$$

(4)

Equation (3) is either trivial to solve (when F is reducible), or it is a cubic Thue equation.

For a solution $(u,v)$ of (3), we set $Q_0(x,y,z)=u{Q}_2(x,y,z)-v{Q}_1(x,y,z)$. If $\alpha$ in (1) is a solution of (2), then

$$Q_0(x,y,z)=0.$$

(5)

If $(x_0,y_0,z_0)\in {\mathbb{Z}}^3$ is a non-trivial solution of (5), with, say, $z_0\ne 0$ (such a solution can be easily found, see L. J. Mordell [20]), then we can parametrize the solutions $x,y,z$ in the form

$$x=r{x}_0+p,y=r{y}_0+q,z=r{z}_0,$$

(6)

with rational parameters $r,p,q$. Substituting these $x,y,z$ into (5), we obtain an equation of the form

$$r(c_{1}p+c_{2}q)=c_3{p}^2+c_{4}pq+c_5{q}^2,$$

with integer coefficients $c_1,\dots ,c_5$. Multiply the equations in (6) by $c_{1}p+c_{2}q$ and replace $r(c_{1}p+c_{2}q)$ by $c_3{p}^2+c_{4}pq+c_5{q}^2$. Further multiply the equations in (6) by the square of the common denominator of $p,q$ to obtain all integer relations (cf. [19]). We divide those by $gcd{(p,q)}^2$ and obtain

$$kx=c_{11}{p}^2+c_{12}pq+c_{13}{q}^2,ky=c_{21}{p}^2+c_{22}pq+c_{23}{q}^2,kz=c_{31}{p}^2+c_{32}pq+c_{33}{q}^2,$$

(7)

with integer $c_{ij}$ and integer parameters $p,q$. Here, k is an integer parameter with the property that k divides the $det\left(C\right)/d_0^2$, where C is the 3 × 3 matrix with entries $c_{ij}$ and $d_0$ is the gcd of its entries (cf. [19]). Finally, substituting the $x,y,z$ in (7) into (4) we obtain

$$F_1(p,q)=k^{2}u,F_2(p,q)=k^{2}v.$$

(8)

According to [19], at least one of the equations in Equation (8) is a quartic Thue equation over the original number field K.

3. Results

3.1. Pure Fields, Trinomials, Quadrinomials, etc.

There is no doubt that the Newton polygon method has been the most powerful tool during the last couple of years. It is frequently combined with the application of Dedekind’s criterion. While, in 2014, S. Ahmad, T. Nakahara and M. Syed [21] investigated monogenity properties of pure sextic fields using their subfield structure and relative monogenity, in 2017 T. A. Gassert [22] already used Montes algorithm to describe monogenity of pure fields. Note that this is only about the monogenity of the polynomials and not the monogenity of number fields generated by a root of the polynomial (for some corrections, see L. El Fadil [23]).

Together with Newton polygons (or instead of them), Dedekind’s criterion and Engström’s theorem are also often used. The following results often deal with polynomials of similar shape. It is important to add that, especially using Newton polygons, the whole calculation must be performed separately, even for polynomials of similar shape.

The first results investigated monogenity in pure fields (or radical extensions) generated by a root of an irreducible binomial of type $x^n-m$. Assuming that m is squarefree, conditions were given for the monogenity (or non-monogenity) of such pure fields, for $n=6,8,12,\dots$, etc. A following step was to consider general exponents like $n=2^k,2^k·3^{\mathcal{l}},\dots$, etc., and later on $n=p^k$ with a prime p. For some exponents, the more complicated case of a composite m was also investigated. Here is a list of such results, for brevity indicating only the exponents considered:

• Z. S. Aygin and K. D. Nguyen [24]: $n=3$;
• L. El Fadil [25]: $n=12$;
• L. El Fadil [26]: $n=18$;
• L. El Fadil [27]: $n=20$;
• L. El Fadil [28]: $n=24$;
• L. El Fadil [29]: $n=36$;
• Fadil, L.E. H. Ben Yakkou and J. Didi [30]: $n=42$;
• Fadil, L.E. H. Choulli and O. Kchit [31]: $n=60$;
• L. El Fadil and M. Faris [32]: $n=84$;
• H. Ben Yakkou and O. Kchit [33]: $n=3^k$;
• L. El Fadil [34]: $n=2·3^k$;
• L. El Fadil [35]: $n=6,2^k·3^{\mathcal{l}}$;
• Yakkou, H.B. A. Chillali and L. El Fadil [36]: $n=2^k·5^{\mathcal{l}}$;
• L. El Fadil [37]: $n=3^k·7^{\mathcal{l}}$;
• L. El Fadil and A. Najim [38]: $n=2^k·3^{\mathcal{l}}$;
• L. El Fadil and O. Kchit [39]: $n=2^k·7^{\mathcal{l}}$;
• L. El Fadil [40]: $n=2^k·3^{\mathcal{l}}·5^t$;
• H. Ben Yakkou and L. El Fadil [41]: $n=p^k$;
• L. El Fadil [42]: $n=6$, m composite;
• L. El Fadil and I. Gaál [16]: $n=8$, m composite.

The exponents $n\le 9$ with a squarefree m were investigated by I. Gaál and L. Remete [43], which was extended to arbitrary m by L. El Fadil and I. Gaál [16,44].

A typical statement from this list is the following:

Theorem 7

(L. El Fadil and A. Najim [38]).

Let α be a root of the irreducible polynomial $x^{2^k·3^{\mathcal{l}}}-m$ with a squarefree m. If $m\not\equiv 1(mod4)$ and $m\not\equiv \pm 1(mod9)$ then α generates a power integral basis in $K=\mathbb{Q}\left(\alpha \right)$. If $m\equiv 1(mod4)$, or $m\equiv 1(mod9)$, or $k=2$ and $m\equiv -1(mod9)$, then K is not monogenic.

A next step was to consider monogenity properties of number fields generated by a root of an irreducible trinomial of type $x^n+a{x}^m+b$. The field index is also often determined by using Engström’s theorem. In the following list, again we only indicate the type of trinomials considered:

• L. El Fadil [45]: $x^4+ax+b$;
• L. El Fadil and I. Gaál [46]: $x^4+a{x}^2+b$;
• H. Smith [47]: $x^4+ax+b,x^4+c{x}^3+d$;
• L. Jones [48] showed that there exist exactly three distinct monogenic trinomials of the form $x^4+b{x}^2+d$ with Galois $C_4$;
• Jakhar, A. S. Kaur and S. Kumar [49]: $x^5+ax+b$;
• L. El Fadil [50]: $x^5+a{x}^2+b$;
• L. El Fadil [51]: $x^5+a{x}^3+b$;
• L. El Fadil [52]: $x^6+ax+b$;
• A. Jakhar and S. Kumar [53]: $x^6+ax+b$;
• L. El Fadil [54]: $x^6+a{x}^3+b$;
• L. El Fadil and O. Kchit [55]: $x^6+a{x}^5+b$;
• A. Jakhar and S. Kaur [56]: $x^6+a{x}^m+b$;
• R. Ibarra, H. Lembeck, M. Ozaslan, H. Smith and K. E. Stange [57]: $x^n+ax+b,x^n+c{x}^{n-1}+d$ for $n=5,6$;
• L. El Fadil and O. Kchit [58]: $x^7+a{x}^3+b$;
• H. Ben Yakkou [59]: $x^7+a{x}^5+b$;
• Jakhar, A. S. Kaur and S. Kumar [60]: $x^7+ax+b$;
• H. Ben Yakkou [61]: $x^8+ax+b$;
• H. Ben Yakkou and B. Boudine [62]: $x^8+ax+b$;
• Jakhar, A. S. Kaur and S. Kumar [63]: $x^8+a{x}^m+b$;
• L. Jones [64] considered monogenic trinomials of type $x^8+a{x}^4+b$ with prescribed Galois group;
• O. Kchit [65]: $x^9+ax+b$;
• H. Ben Yakkou and P. Tiebekabe [66]: $x^9+ax+b$;
• L. El Fadil and O. Kchit [67]: $x^9+a{x}^2+b$;
• L. El Fadil and O. Kchit [68]: $x^{12}+a{x}^m+b$;
• H. Ben Yakkou [69]: $x^{2^r}+a{x}^m+b$;
• H. Ben Yakkou and L. El Fadil [70]: $x^n+ax+b,n=5,6,3^k,2^k·3^{\mathcal{l}},2^k·3^{\mathcal{l}}+1$;
• A. Jakhar and S. Kumar [71] gave explicit conditions for the non-monogenity of $x^{q^s}-ax-b$;
• A. Jakhar [72]: $x^{p^s}-a{x}^m-b$;
• B. Jhorar and S. K. Khanduja [73]: $x^n+ax+b$, showed also that $f\left(x\right)=x^n-x-1$ is monogenic, if and only if $\left|D\left(f\right)\right|=n^n-{(n-1)}^{n-1}$ is squarefree;
• H. Ben Yakkou [74]: $x^n+a{x}^m+b,n=p^k,s·p^k,2^k·3^{\mathcal{l}}$;
• L. El Fadil [75]: $x^n+a{x}^m+b,n=2^k·3^{\mathcal{l}}$;
• A. Jakhar [76]: $x^n-a{x}^m-b$;
• Jakhar, A. S. Khanduja and N. Sangwan [77]: $x^n+a{x}^m+b$;
• Jakhar, A. S. Khanduja and N. Sangwan [78] gave necessary and sufficient conditions in terms of $a,b,m,n$ for a given prime, p, to divide $I\left(\vartheta \right)$, where $\vartheta$ is a root of $x^n+a{x}^m+b$;
• L. Jones [79] considered monogenic reciprocal trinomials of type $x^{2m}+A{x}^m+1$;
• L. Jones [80] showed that there are infinitely many primes p, such that $x^6+p{x}^3+1$ is monogenic with Galois group $D_6$;
• L. Jones [81] showed that $x^n+x+1$ is monogenic, if and only if its discriminant is squarefree;
• L. Jones and T. Phillips [82] showed that $x^n+ax+b$ is monogenic infinitely often;
• L. Jones and D. White [83] found new infinite families of monogenic trinomials of type $x^n+A{x}^m+B$.

A typical statement from this list is the following:

Theorem 8

(L. Jones and D. White [83]).

Let $n\ge 2$ be an integer, with $m\ge 1$ a proper divisor of n. Let $t=n/m$ and let κ denote the squarefree kernel of m. Let A and B be positive integers with $gcd(A,B)>1$, and define

$$D:=\frac{t^t{B}^{t-1}+{(1-t)}^{t-1}{A}^t}{gcd{(A,B)}^{t-1}}.$$

If B and D are squarefree, and $gcd(A,B)=0(mod\kappa )$, then $f\left(x\right)=x^n+A{x}^m+B$ is monogenic. Moreover, $D\left(f\right)$ is not squarefree if $m\ge 2$.

The research continued into the direction considering monogenity properties of quadrinomials, quintinomials, etc., that is, polynomials with four, five, etc., terms and the number fields generated by a root of these polynomials:

• T. A. Gassert, H. Smith and K. E. Stange [84]: $x^4-6x^2-kx-3$;
• H. Ben Yakkou [85]: $x^4+a{x}^3+bx+c$;
• J. Harrington and L. Jones [86] constructed new families of quartic polynomials with various Galois groups, which are monogenic infinitely often;
• A. Jakhar and R. Kalwaniya [87]: $x^6+a{x}^m+bx+c$;
• L. Jones [64]: $x^8+a{x}^6+b{x}^4+a{x}^2+1$;
• L. Jones [88] constructed infinitely many monogenic polynomials of degree p for every odd prime p;
• L. Jones [89]: $x^p-2pt{x}^{p-1}+p^2{t}^2{x}^{p-2}+1$;
• Jakhar, A. S. Kaur and S. Kumar [90]: $x^n+a{x}^2+bx+c$;
• Jakhar, A. S. Kaur and S. Kumar [91]: $x^{p^s}-a{x}^n-b{x}^m-c$;
• A. Jakhar [92]: $x^n+a{x}^{n-1}+b{x}^{n-2}+c$;
• L. Jones [93] constructed infinite families of reciprocal monogenic polynomials with prescribed Galois group;
• L. Jones [94] showed that if $4\le n\ge m\ge 0$ and $gcd(n,m)=gcd(n,k)=1$ then $x^{n-m}{(x+k)}^m+p$ is monogenic for infinitely many primes p;
• L. Jones [95]: $x^n+A{(Bx+1)}^m$;
• L. Jones [96]: $x^n+t·g\left(x\right)$ with $n>deg\left(g\right)$, when $g\left(x\right)$ is monic and $deg\left(g\right)\in \{2,3,4\}$;
• L. Jones [97] constructed reciprocal monogenic quintinomials of type $x^{2^n}+A{x}^{3·2^{n-2}}+B{x}^{2^{n-1}}+A{x}^{2^{n-2}}+1$;
• L. Jones [98] considered infinite families of monogenic quadrinomials, quintinomials and sextinomials.

3.2. The Relative Case

In addition to the absolute case (extension of $\mathbb{Q}$), several authors considered monogenity problems in the relative case (extensions of an algebraic number field), or even similar problems in Dedekind rings. Mostly, Dedekind’s criterion is used.

• M. E. Charkani and A. Deajim [99]; (see also A. Deajim and L. El Fadil [100]): $x^p-m$ over number fields;
• M. Sahmoudi and M. E. Charkani [101] considered relative pure cyclic extensions;
• A. Soullami, M. Sahmoudi and O. Boughaleb [102]: $x^{3^n}+a{x}^{3^s}-b$ over number fields;
• O. Boughaleb, A. Soullami and M. Sahmoudi [103]: $x^{p^n}+a{x}^{p^s}-b$ over number fields;
• H. Smith [104] studied relative radical extensions;
• S. K. Khanduja and B. Jhorar [105] gave equivalent versions of Dedekind’s criterion in general rings;
• S. Arpin, S. Bozlee, L. Herr and H. Smith [106,107] studied monogenity of number rings from a modul-theoretic perspective;
• R. Sekigawa [108] constructed an infinite number of cyclic relative extensions of prime degree that are relative monogenic.

3.3. Composite Polynomials

Several authors considered monogenity of composites of polynomials, composites of binomials, etc. The authors mainly use Dedekind’s criterion.

• J. Harrington and L. Jones [109] gave conditions for the monogenity of ${(x^m-b)}^n-a$, and the composition of $x^n-a$ and $x^m-b$;
• Jakhar, A. R. Kalwaniya and P. Yadav [110] considered monogenity of ${(x^m-b)}^n-a$, and the composition of $x^n-a$ and $x^m-b$ using a refined version of the Dedekind criterion;
• J. Harrington and L. Jones [111] considered monogenity of ${\mathsf{\Phi }}_{p^a}\left({\mathsf{\Phi }}_{2^b}\left(x\right)\right)$, where ${\mathsf{\Phi }}_N\left(x\right)$ is the cyclotomic polynomial of index N;
• L. Jones [112] considered monotonically stable polynomials of type $g\left(f^n\left(x\right)\right)$;
• L. Jones [113] constructed infinite collections of monic Eisenstein polynomials $f\left(x\right)$, such that $f\left(x^{d^n}\right)$ are monogenic for all integers $n\ge 0$ and $d>1$;
• L. Jones [114] considered monogenity of $S_k\left(x^p\right)$, where $S_k\left(x\right)=x^3-k{x}^2-(k+3)x-1$ the Shanks polynomial;
• L. Jones [115] considered monogenity of $f\left(x^p\right)$, where $f\left(x\right)$ is the characteristic polynomial of an Nth order linear recurrence;
• J. Harrington and L. Jones [116] gave conditions for the monogenity of $f\left(x^{p^n}\right)$, where $f\left(x\right)=x^m+a{x}^{m-1}+b$;
• S. Kaur, S. Kumar and L. Remete [117] considered monogenity of $f\left(x^k\right)$, where $f\left(x\right)=x^d+A·h\left(x\right),degh<d$.

Let us recall a typical statement:

Theorem 9

(J. Harrington and L. Jones [111]). Let a and b be positive integers, and let p be a prime. Then the polynomial ${\mathsf{\Phi }}_{p^a}\left({\mathsf{\Phi }}_{2^b}\left(x\right)\right)$ is monogenic, where ${\mathsf{\Phi }}_N\left(x\right)$ is the cyclotomic polynomial of index N.

3.4. Connection with primes

L. Jones [118,119,120], and J. Harrington and L. Jones [121] detected relations of monogenity of power compositional polynomials with properties of primes. We present here one of these statements.

For a recurrence sequence $U_0=0,U_1=1$ and $U_n=k{U}_{n-1}+U_{n-2}$, $\left(U_n\right)$ is periodic modulo any integer. Denote by ${\pi }_k\left(m\right)$ its period length modulo m. The prime p is called a k-Wall–Sun–Sun prime, if

$$U_{{\pi }_k\left(p\right)}\equiv 0(mod{p}^2).$$

Theorem 10

(L. Jones [118]).

Let $D=k^2+4$ if $k\equiv 1(mod2)$, and $D={(k/2)}^2+1$ if $k\equiv 0(mod2)$. Suppose that $k\not\equiv 0(mod4)$ and that D is squarefree. Let h denote the class number of $\mathbb{Q}\left(\sqrt{D}\right)$. Let $s\ge 1$ be an integer, such that, for every odd prime divisor p of s, D is not a square modulo p and $gcd(p,hD)=1$. Then

$$x^{2s^n}-k{x}^{s^n}-1$$

is monogenic for all integers $n\ge 1$, if and only if no prime divisor of s is a k-Wall–Sun–Sun prime.

3.5. Number of Generators of Power Integral Bases

Some further results considered the number of non-equivalent generators of power integral bases:

• M. Kang and D. Kim [122] considered the number of monogenic orders in pure cubic fields;
• J. H. Evertse [123] considered “rationally monogenic” orders of number fields;
• S. Akhtari [124] showed that a positive proportion of cubic number fields, when ordered by their discriminant, are not monogenic;
• L. Alpöge, M. Bhargava, A. Shnidman [125] showed that, if isomorphism classes of cubic fields are ordered by absolute discriminant, then a positive proportion are not monogenic and yet have no local obstruction to being monogenic (that is, the index form equations represent $+1$ or $-1$ mod p for all primes p);
• M. Bhargava [126] proved that an order O in a quartic number field can have at most 2760 inequivalent generators of power integral bases (and at most 182 if $\left|D\right(O\left)\right|$ is sufficiently large). The problem is reduced to counting the number solutions of cubic and quartic Thue equations, somewhat analogously like described in Section 2.4, using a refined enumeration;
• S. Akhtari [127] gave another proof of Bhargava’s result [126]: she used the more direct approach of Section 2.4 and applied sharp bounds for the numbers of solutions of cubic and quartic Thue equations.

3.6. Miscellaneous

In addition to the above lists, there were several further interesting statements achieved for monogenity. We try to recall them here.

• H. H. Kim [128] showed that the number of monogenic dihedral quartic extensions with absolute discriminant $\le X$ is of size $O\left(X^{3/4}{(logX)}^3\right)$;
• N. Khan, S. Katayama, T. Nakahara and T. Uehara [129] proved that the composite of a totally real field with a cyclotomic field of odd conductor $\ge 3$ or even ≥8 has no power integral basis;
• N. Khan, T. Nakahara and H. Sekiguchi [130] proved that there are exactly three monogenic cyclic sextic fields of prime-power conductor, namely $\mathbb{Q}\left({\zeta }_7\right),\mathbb{Q}\left({\zeta }_9\right)$ and the maximal real subfield of $\mathbb{Q}\left({\zeta }_{13}\right)$;
• D. Gil-Muňoz and M. Tinková [131] considered the indices of non-monogenic simplest cubic polynomials;
• L. Jones [132] considered infinite families of monogenic Pisot (anti-Pisot) polynomials;
• A. Jakhar and S. K. Khanduja [133] gave lower bounds for the p-index of a polynomial;
• M. Castillo, [134] showed, e.g., that $\mathbb{Q}\left({\alpha }_n\right),n\ge 1$ is monogenic, where ${\alpha }_0=1$ and ${\alpha }_n=\sqrt{2+{\alpha }_{n-1}}$ for $n\ge 1$;
• T. Kashio and R. Sekigawa [135] showed that a monogenic normal cubic field is a simplest cubic field for some parameter;
• F. E. Tanoé [136] considered monogenity of biquadratic fields using a special integer basis;
• K. V. Kouakou and F. E. Tanoé [137,138], and F. E. Tanoé and V. Kouassi [139] considered monogenity of triquadratic fields;
• Aruna C. and P. Vanchinathan [140] showed that an infinite number of so-called exceptional quartic fields are monogenic.

3.7. Explicit Calculations, Algorithms

The powerful methods of Dedekind’s criterion and Newton polygons often decide about the monogenity of number fields. However, to explicitly determine all inequivalent generators of power integral bases one needs to perform calculations. These algorithms usually involve Baker-type estimates, reduction methods and enumeration algorithms, cf. [4]. There are efficient algorithms for low degree fields and some more complicated methods for higher degree fields. Since these procedures usually require considerable CPU time, if the number field is of high degree, or we need information about a large number of fields, then we turn to the so-called “fast” algorithms for determining “small” solutions. This yields a fast method to determine solutions of the index form equation with absolute values, say ≤${10}^{100}$. These algorithms determine all solutions with a high probability but do not exclude extremely large solutions (which, however, nobody has ever met).

We collect here some recent results involving explicit determination of generators of power integral bases.

• Z. Franŭsić and B. Jadrijević [141] calculated generators of relative power integral bases in a family of quartic extensions of imaginary quadratic fields;
• I. Gaál [142] showed that index form equations in composites of a totally real cubic field and a complex quadratic field can be reduced to absolute Thue equations;
• I. Gaál [143] showed that the index form equations in composites of a totally real field and a complex quadratic field can be reduced to the absolute index form equations of the totally real field;
• I. Gaál [144] considered generators of power integral bases in fields generated by monogenic trinomials of type $x^6+3x^3+3a$;
• I. Gaál [145] considered generators of power integral bases in fields generated by monogenic binomial compositions of type ${(x^3-b)}^2+1$;
• I. Gaál [146] gave an efficient method to determine all generators of power integral bases of pure sextic fields;
• I. Gaál and L. Remete [147] considered monogenity in octic fields of type $K=\mathbb{Q}\left(\sqrt[4]{a+bi}\right)$;
• I. Gaál [148] determined “small” solutions of the index form equation in $K=\mathbb{Q}\left(\sqrt[6]{m}\right)$, for $-5000<m<0$, such that $x^6-m$ is monogenic (1521 fields). Experience: $\sqrt[6]{m}$ is the only generator of power integral bases;
• I. Gaál [149] determined “small” solutions of index form equations in $K=\mathbb{Q}\left(\sqrt[8]{m}\right)$, $-5000<m<0$, such that $x^8-m$ is monogenic (2024 fields). Experience: $\sqrt[8]{m}$ is the only generator of power integral bases, except for $m=-1$;
• I. Gaál [150] extended [46] on monogenity properties of trinomials of type $x^4+a{x}^2+b$;
• I. Gaál [151] calculated generators of power integral bases in families of number fields generated by a root of monogenic quartic polynomials considered in [86].

In [150,151], the method described in Section 2.4 was used, in [141,147,149], its relative analogue, see [4,152].

Also, here we recall some typical statements:

Theorem 11

(I. Gaál [143]).

Let L be a totally real number field, $M=\mathbb{Q}\left(\sqrt{d}\right)$, $d<0$ squarefree, assume $gcd(D_L,D_M)=1$. If α generates a power integral basis in $K=LM$, then $\alpha =a+\beta \pm \omega$, where $a\in \mathbb{Z}$, β generates a power integral basis in L and $(1,\omega )$ is integral basis in M.

Theorem 12

(L. El Fadil and I. Gaál [46]).

Assume $a>1,b>1$ and $f\left(x\right)=x^4+a{x}^2+b$ is irreducible and monogenic. If a, b are not of type

$$a=\frac{u\pm 1}{v},b=\frac{u^2-1}{4v^2}$$

for some $u,v\in \mathbb{Z},v\ne 0,u\ne 1$, then up to equivalence the root α of $f\left(x\right)$ is the only generator of power integral bases in $K=\mathbb{Q}\left(\alpha \right)$.

4. Further Research

The above lists of results indicate what has already been already done and what is still missing. It would be very interesting to somehow describe monogenity properties of quartic fields and maybe quintic fields. This would require study of quintinomials and sextinomials.

What general exponents of binomials and trinomials can still be considered? Is it possible to describe in general monogenity properties of arbitrary trinomials of degree $\le 9$?

How can one extend the available algorithms to be able to calculate solutions of index form equations in higher degree fields?

All these and several other questions are to be answered. As it is seen from the above lists, in addition to some new ideas, often the application of old, forgotten methods may also help.