Generalization of the Distance Fibonacci Sequences
Abstract
:1. Introduction
2. Materials and Methods
(t,k) Generalization of Distance Fibonacci Sequences
3. Results
3.1. The Properties of
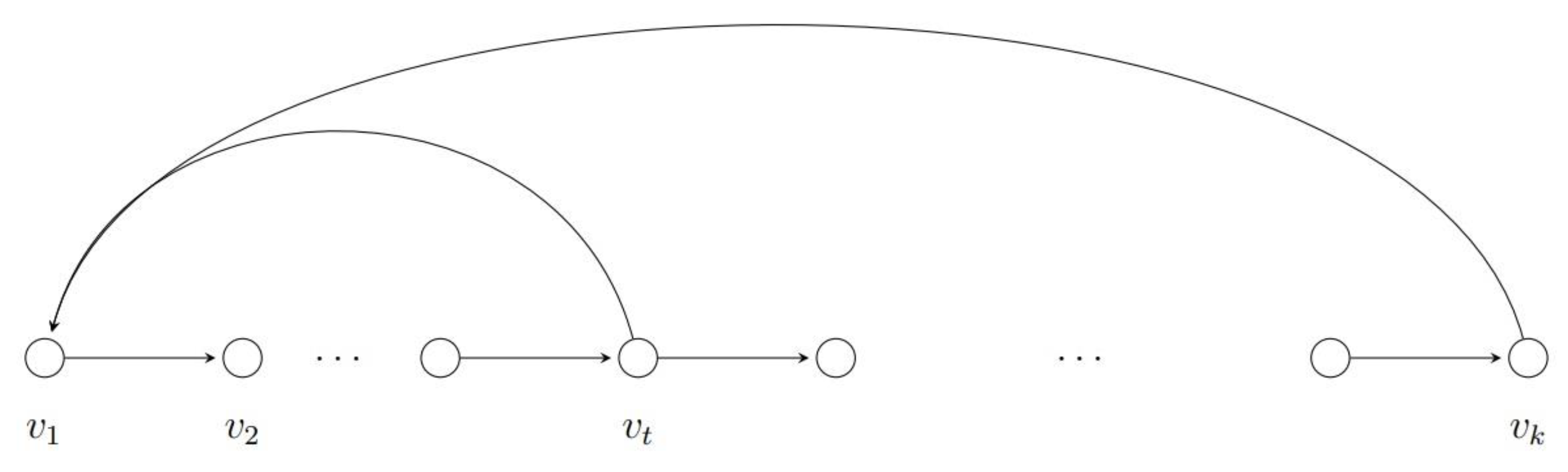
3.2. Graph Interpretation of
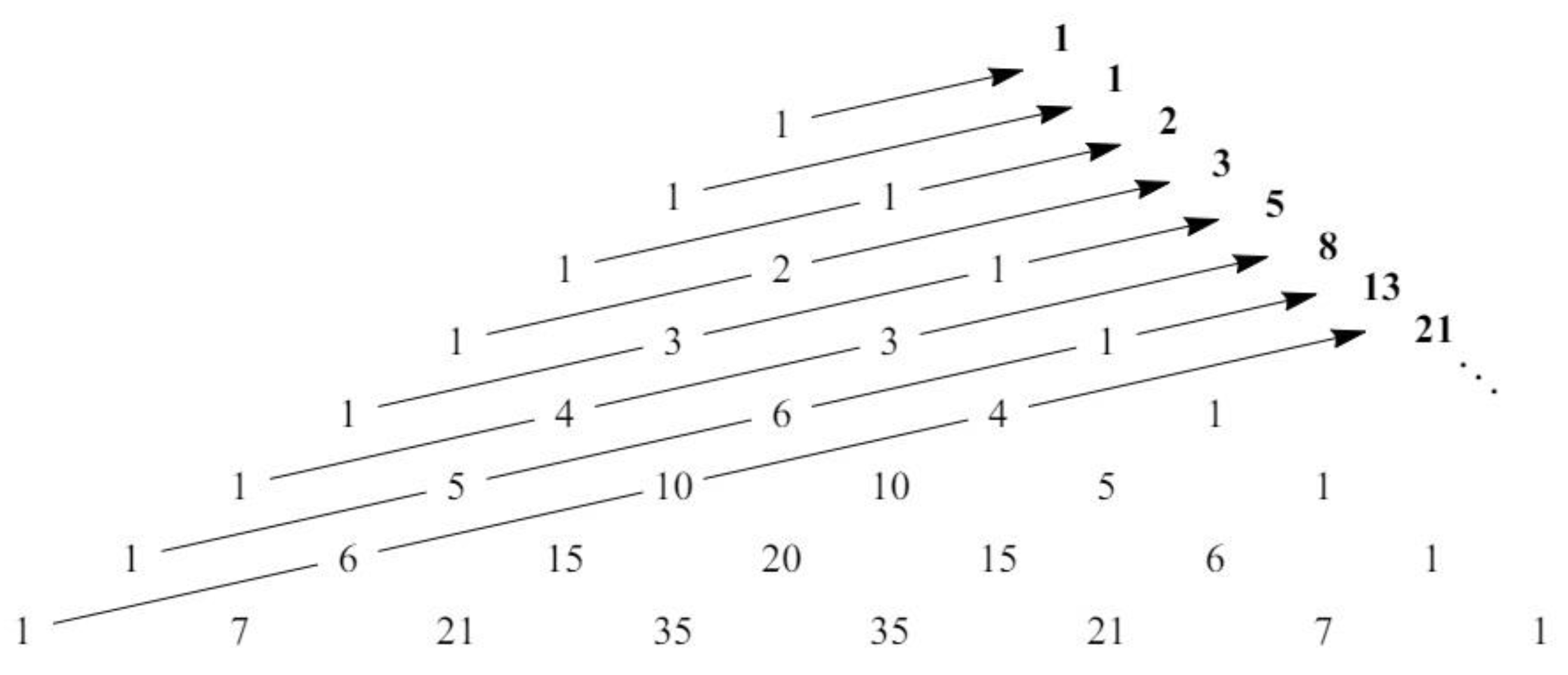
3.3. Pascal-like Triangle
3.4. Generating Functions
3.5. Matrix Generators
3.6. Connection with Pascal’s Triangle
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kiliç, E. The generalized order k-Fibonacci Pell sequence by matrix methods. J. Comput. Appl. Math. 2007, 209, 133–145. [Google Scholar] [CrossRef]
- Kiliç, E.; Taşçi, D. On the generalized Fibonacci and Pell Sequences by Hessenberg matrices. Ars. Comb. 2010, 94, 161–174. [Google Scholar]
- Koshy, T. Fibonacci and Lucas Numbers with Applications, 3rd ed.; A Wiley Interscience Publication: Waterloo, ON, Canada, 2001. [Google Scholar]
- Şen, E. Fibonacci Numbers, Golden Section and Applications. arXiv 2013, arXiv:1301.6606. [Google Scholar]
- Włoch, I.; Włoch, A. On some multinomial sums related to Fibonacci Type numbers. Tatra Mt. Math. Publ. 2020, 77, 99–108. [Google Scholar] [CrossRef]
- Feingold, A.J. A hyperbolic GCM Lie algebra and the Fibonacci numbers. Proc. Am. Math. Soc. 1980, 80, 379–385. [Google Scholar] [CrossRef]
- Souza, J.; Curado, E.M.F.; Rego-Monteiro, M.A. Generalized Heisenberg algebras and Fibonacci series. J. Phys. A Math. Gen. 2007, 39, 10415–10425. [Google Scholar] [CrossRef]
- Schork, M. Generalized Heisenberg algebras and k-generalized Fibonacci Numbers. J. Phys. A Math. Theory 2007, 40, 4207–4214. [Google Scholar] [CrossRef]
- Bednarz, U.; Włoch, A.; Wołowiec-Musiał, M. Distance Fibonacci Numbers, their interpretations and matrix generators. Comment. Math. 2013, 53, 34–46. [Google Scholar] [CrossRef]
- Kwaśnik, M.; Włoch, I. The total number of generalized stable sets and kernels in graphs. Ars Comb. 2000, 55, 139–146. [Google Scholar]
- Bród, D.; Włoch, I.; Piejko, K. Distance Fibonacci Numbers, distance Lucas numbers and their applications. Ars Comb. 2013, 161, 2695–2701. [Google Scholar]
- Stojmenovic, I. Recursive algorithms in computer science courses: Fibonacci numbers and binomial coefficients. IEEE Trans. Educ. 2000, 43, 273–276. [Google Scholar] [CrossRef]
- Atkins, J.; Geist, R. Fibonacci Numbers and computer algorithms. Coll. Math. J. 1987, 18, 328–336. [Google Scholar] [CrossRef]
- Sinha, S. The Fibonacci numbers and Its Amazing Applications. Int. J. Eng. Sci. Invent. 2017, 6, 7–14. [Google Scholar]
- Omotehinwa, T.O.; Ramon, S.O. Fibonacci Numbers and Golden Ratio in Mathematics and Science. Int. J. Comput. Inf. Technol. 2013, 2, 630–638. [Google Scholar]
- Gutman, I.; Wagner, S. Maxima and minima of the Hosoya index and the Merrifield-Simmons index. A survey of results and techniques. Acta Appl. Math. 2010, 112, 323–346. [Google Scholar]
- Prodinger, H.; Tichy, R. Fibonacci numbers of graphs. Fibonacci Q. 1982, 20, 16–21. [Google Scholar]
- Matoušová, I.; Trojovský, P. On coding by (2,q)- distance Fibonacci numbers. Mathematics 2020, 8, 2058. [Google Scholar] [CrossRef]
- Tatlow, R. The Use and Abuse of Fibonacci numbers and The Golden Section in Musicology today. Underst. Bach 2006, 1, 69–85. [Google Scholar]
- Horadam, A.F. A generalized Fibonacci sequence. Amer. Math. Mon. 1961, 68, 455–459. [Google Scholar] [CrossRef]
- Jaiswal, D.V. On a generalized Fibonacci sequence. Labdev. J. Sci. Tech. Part. A 1969, 7, 67–71. [Google Scholar]
- Falcon, S. Binomial Transform of The Generalized k-Fibonacci numbers. Commun. Math. Appl. 2019, 10, 643–651. [Google Scholar] [CrossRef]
- Falcon, S.; Plaza, A. The k-Fibonacci sequence and the Pascal 2-Triange. Chaos Solitions Fractals 2007, 33, 38–49. [Google Scholar] [CrossRef]
- Sburlati, G. Generalized Fibonacci sequences and linear congruences. Fibonacci Quart 2002, 40, 446–452. [Google Scholar]
- Bednarz, U.; Bród, D.; Włoch, A.; Włoch, I.; Wołowiec-Musiał, M. On a new type of distance Fibonacci Numbers. Discret. Appl. Math. 2013, 161, 2695–2701. [Google Scholar]
- Özkan, E.; Yılmaz, N.Ş.; Włoch, A. On F3(k,n)-numbers of the Fibonacci Type. Bol. Soc. Matemática Mex. 2021, 27, 77. [Google Scholar]
- Yilmaz, N.Ş.; Włoch, A.; Özkan, E.; Strzałka, D. On doubled and quadrupled Fibonacci type sequences. Ann. Math. Silesianae 2023, 38, 1–15. [Google Scholar]
- Diestel, R. Graph Theory; Springer: Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Soykan, Y. On Generalized Narayana Numbers. Int. J. Adv. Appl. Math. Mech. 2020, 7, 43–56. [Google Scholar]

| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | 0 | 1 | 3 | |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | 0 | 1 | 3 | 3 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 4 | 4 | 4 | 5 | 7 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yilmaz, N.Ş.; Włoch, A.; Özkan, E. Generalization of the Distance Fibonacci Sequences. Axioms 2024, 13, 420. https://doi.org/10.3390/axioms13070420
Yilmaz NŞ, Włoch A, Özkan E. Generalization of the Distance Fibonacci Sequences. Axioms. 2024; 13(7):420. https://doi.org/10.3390/axioms13070420
Chicago/Turabian StyleYilmaz, Nur Şeyma, Andrej Włoch, and Engin Özkan. 2024. "Generalization of the Distance Fibonacci Sequences" Axioms 13, no. 7: 420. https://doi.org/10.3390/axioms13070420
APA StyleYilmaz, N. Ş., Włoch, A., & Özkan, E. (2024). Generalization of the Distance Fibonacci Sequences. Axioms, 13(7), 420. https://doi.org/10.3390/axioms13070420








