The Split Equality Fixed-Point Problem and Its Applications

Abstract

It is generally known that in order to solve the split equality fixed-point problem (SEFPP), it is necessary to compute the norm of bounded and linear operators, which is a challenging task in real life. To address this issue, we studied the SEFPP involving a class of quasi-pseudocontractive mappings in Hilbert spaces and constructed novel algorithms in this regard, and we proved the algorithms’ convergences both with and without prior knowledge of the operator norm for bounded and linear mappings. Additionally, we gave applications and numerical examples of our findings. A variety of well-known discoveries revealed in the literature are generalized by the findings presented in this work.

1. Introduction

In this manuscript, we utilize the following notations: $〈.,.〉$ denotes an inner product and $∥.∥$ represents its corresponding norm. We designate $\mathbb{H}j,j=1,2,3,$ as Hilbert spaces, $\mathbb{K}j$ as nonempty, convex, and closed subsets of $\mathbb{H}j,$ and $\mathbb{D}j:\mathbb{H}j\to \mathbb{H}j,j=1,2,$ as bounded and linear mappings. The symbols ⇀ and → signify weak and strong convergences, respectively.

A mapping $\mathbb{T}:{\mathbb{H}}_1\to {\mathbb{H}}_1$ is known as a fixed point of $\mathbb{T}$(Fix($\mathbb{T}$)) if $\mathbb{T}p=p,$ for all $p\in {\mathbb{H}}_1.$ We denote the set of Fix($\mathbb{T}$) by $\{p\in Fix(\mathbb{T}):\mathbb{T}p=p\}$. $\mathbb{T}$ is known to be quasi-nonexpansive if $\parallel \mathbb{T}y-p\parallel \le \parallel y-p\parallel ,\forall y\in {\mathbb{H}}_1\mathrm{and}\mathrm{p}\in \mathrm{Fix}\left(\mathbb{T}\right).$ It is obvious that if $\mathbb{T}$ is quasi-nonexpansive then $∥\mathbb{T}y-y∥\le 2〈y-\mathbb{T}y,y-p〉.$ $\mathbb{T}$ is called demicontractive if ${\parallel p-\mathbb{T}y\parallel }^2\le$ ${\parallel p-y\parallel }^2$${+ \beta \parallel y-\mathbb{T}y\parallel }^2,$$\forall y\in {\mathbb{H}}_1,p\in Fix\left(\mathbb{T}\right)$ and $\beta \in [0,1),$ and it is called quasi-pseudocontractive if $\beta =1.$ $\mathbb{T}$ is known as $\beta -$strongly monotone if $〈\mathbb{T}y-\mathbb{T}p,y-p〉\ge \beta {\parallel \mathbb{T}y-\mathbb{T}p\parallel }^2,\forall y,p\in {\mathbb{H}}_1,\beta >0.$

Remark 1. 

The quasi-pseudocontractive mapping encompasses various types of mappings, including quasi-nonexpansive, demicontractive, and several others. For further details, please refer to [1] and the cited references therein.

The problem of finding

$$p^{*}\in {\mathbb{K}}_1\mathrm{such}\mathrm{that}{\mathbb{D}}_1{p}^{*}\in {\mathbb{K}}_2$$

(1)

is known as the “Split Feasibility Problem (SFP)”. The SFP, initially introduced by [2], has garnered significant attention from researchers due to its versatile applications in practical domains. These applications span a wide spectrum, encompassing fields such as signal processing, intensity-modulated radiation therapy, and image reconstruction, as documented in [3,4,5].

If the problem stated in (1) possesses a solution, it is evident that $p^{*}\in {\mathbb{K}}_1$ is a solution to Equation (1) if and only if it also solves

$$\begin{array}{cc}\hfill p^{*}& =P_{{\mathbb{K}}_1}\left(I-\lambda {\mathbb{D}}_1^{*}(I-P_{{\mathbb{K}}_2}){\mathbb{D}}_1\right)p^{*},\forall p^{*}\in {\mathbb{K}}_1,\hfill \end{array}$$

(2)

where $\lambda >0,$$P_{{\mathbb{K}}_j}$ are metric projections on $K_j,j=1,2,$ respectively.

To address problem (1), Byrne [6] proposed the following algorithm, known as the CQ algorithm:

$$x_{n+1}=P_{{\mathbb{K}}_1}\left(I-\lambda {\mathbb{D}}_1^{*}(I-P_{{\mathbb{K}}_2}){\mathbb{D}}_1\right)x_n,$$

(3)

where $\lambda \in (0,\frac{2}{{\mathbb{D}}_1{\mathbb{D}}_1^{*}}).$ Equation (3) involves the computation of $P_{{\mathbb{K}}_j}$ onto $K_j,j=1,2,$ and this is known to be implementable when the projections have closed-form expressions.

Related to SFP, we have the “Split Equality Problem (SEP)”. This problem was introduced by Moudafi and Al-Shemas [7] and it entails finding

$$p^{*}\in {\mathbb{K}}_1\mathrm{and}{q}^{*}\in {\mathbb{K}}_2\mathrm{such}\mathrm{that}{\mathbb{D}}_1{p}^{*}={\mathbb{D}}_2{q}^{*}.$$

(4)

By using ${\mathbb{D}}_2=I$ (identity mapping), it is easy to see that the SEP reduces to the SFP. The following algorithm was taken into consideration by Moudafi and Al-Shemas [7] to solve the SEP (4):

$$\left\{\begin{array}{c}{x}_{n+1}=P_{{\mathbb{K}}_1}\left(x_n-{\lambda }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)\right),n\ge 0;\hfill \\ y_{n+1}=P_{{\mathbb{K}}_2}\left(y_n+{\lambda }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)\right),n\ge 0;\hfill \end{array}\right.$$

(5)

where $(x_0,y_0)\in {\mathbb{H}}_1\times {\mathbb{H}}_2$ are chosen arbitrarily and $P_{{\mathbb{K}}_j},j=1,2,$ were metric projections on $K_{j}s.$ After some certain condition was imposed on ${\lambda }_n,$ they obtained a weak convergence result.

As any nonempty, closed, and convex subset of a Hilbert space can be viewed as the fixed point set of its corresponding projector, Equation (4) is consequently simplified to find

$$p^{*}\in Fix\left({\mathbb{T}}_1\right)\mathrm{and}{q}^{*}\in Fix\left({\mathbb{T}}_1\right)\mathrm{such}\mathrm{that}{\mathbb{D}}_1{\mathrm{p}}^{*}={\mathbb{D}}_2{\mathrm{q}}^{*},$$

(6)

where ${\mathbb{T}}_j:{\mathbb{K}}_j\to H_j,j=1,2,$ are nonlinear operators with $Fix\left({\mathbb{T}}_j\right)\ne \varnothing .$ Equation (6) is regarded as the “Split Equality Fixed-Point Problem (SEFPP)”.

Motivated by the result in [7], Moudafi [8] considered the algorithm below:

$$\left\{\begin{array}{c}{x}_{n+1}={\mathbb{T}}_1\left(x_n-{\lambda }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)\right),n\ge 0;\hfill \\ y_{n+1}={\mathbb{T}}_2\left(y_n+{\lambda }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)\right),n\ge 0.\hfill \end{array}\right.$$

(7)

After some conditions were imposed on the parameters and operators involved, they proved weak convergence results.

To solve (7), the inverse of a bounded and linear operator must be computed, and this is known to be no easy task. This is why Byne [6] considered an algorithm for solving the SFP without the stated inverse.

It was reported by Mohammed and Kilicman [9] that the SFP can be reduced to a convex feasibility problem (CFP) as well as a fixed-point problem (FPP). Fixed-point theory (FPT) can be considered a core area of research in nonlinear analysis due to its various applications in many areas of research, such as image processing and equilibrium problems, the study of the existence and uniqueness of solutions for the integral, and differential equations, selection, and matching problems (see Mohammed et al. [10]).

The roots of fixed-point theory can be traced back to the early developments in topology, notably through contributions from Poincaré, Lefschetz–Hopf, and Leray–Schauder. These pioneers laid the groundwork that now spans diverse areas of analysis. Topological considerations play a pivotal role in FPT, often intersecting with degree theory to tackle significant existence problems. This approach is invaluable in scenarios ranging from solving elliptic partial differential equations to identifying closed periodic orbits in dynamical systems. For more details, see Khan [11]. For further exploration, recent studies by Antón-Sancho [12] delve into the fixed points of automorphisms within vector bundle moduli spaces over compact Riemann surfaces, offering new perspectives and advancing the interdisciplinary scope of fixed-point theory.

Moudafi’s algorithm in [8] involved firmly quasi-nonexpansive mapping; this mapping includes the quasi-nonexpansive class. Very recently, Che and Li [13] considered the following algorithm for finding the solution of the SEP and proved the convergence results of the algorithm:

$$\left\{\begin{array}{c}{x}_{n+1}={\beta }_n{u}_n+(1-{\beta }_n){\mathbb{T}}_1{u}_n;\hfill \\ u_n=x_n-{\lambda }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n,n\ge 0;\hfill \\ \\ y_{n+1}={\beta }_n{v}_n+(1-{\beta }_n){\mathbb{T}}_2{v}_n;\hfill \\ v_n=y_n+{\lambda }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),n\ge 0;\hfill \end{array}\right.$$

(8)

where ${\mathbb{T}}_1$ and ${\mathbb{T}}_2$ are strictly pseudononspreading mappings.

Since quasi-pseudocontractive mapping includes firmly quasi-nonexpansive, quasi-nonexansive, directed, and demicontractive mappings, this motivated Chang et al. [1] to introduce the following algorithm for solving the SEFPP involving quasi-pseudocontractive mappings and proved the convergence result of the algorithm:

$$\left\{\begin{array}{c}{x}_{n+1}={\beta }_n{x}_n+(1-{\beta }_n)\left((1-\eta )I+\eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_1)+{\beta }_n\right)u_n;\hfill \\ u_n=x_n-{\lambda }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),n\ge 0.\hfill \\ \\ y_{n+1}={\beta }_n{y}_n+(1-{\beta }_n)\left((1-\eta )I+\eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_2)+{\beta }_n\right)u_n;\hfill \\ v_n=y_n+{\lambda }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),n\ge 0.\hfill \end{array}\right.$$

(9)

The proposed algorithm by Chang et al. [1] requires prior knowledge of operator norms. A similar result had been proved in [14]. Very recently, Mohammed et al. [10] proved the convergence of the following algorithm for the class of total quasi-asymptotically nonexpansive mappings:

$$\left\{\begin{array}{c}{x}_{n+1}=(1-{\beta }_n)u_n+{\beta }_n{\mathbb{T}}_1^n{u}_n;\hfill \\ u_n=(1-{\gamma }_n)x_n+{\gamma }_n{\mathbb{T}}_1^n{x}_n-{\lambda }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),n\ge 0;\hfill \\ \\ y_{n+1}=(1-{\beta }_n)v_n+{\beta }_n{\mathbb{T}}_2^n{v}_n;\hfill \\ v_n=(1-{\gamma }_n)y_n+{\gamma }_n{\mathbb{T}}_1^n{y}_n-{\lambda }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),n\ge 0;\hfill \end{array}\right.$$

(10)

The findings in [1,10,14] both converged weakly; in an infinite-dimensional space, weak convergence does not imply strong convergence, whereas strong and weak convergences coincide if the dimension is finite.

Based on these findings, we set out to develop new methods for solving the SEFPP for quasi-pseudocontractive mappings in Hilbert spaces and to demonstrate how the suggested methods converge. The suggested algorithms’ convergence findings will also be presented in a form that frees them from the constraints imposed by the operator norm of bounded and linear operators. At the end, we provide numerical examples that highlight our findings.

The following is how the paper is set up: The background of the study is explained in the introduction, and some fundamental findings are presented in the Section 2. The main result is discussed in Section 3, while in Section 4, applications and numerical results are discussed.

2. Preliminaries

This section offers a few fundamental findings that support the paper’s primary findings.

Definition 1. 

A mapping $\mathbb{T}:{\mathbb{H}}_1\to {\mathbb{H}}_1$ is said to be semi-compact if for any bounded sequence $\left\{x_n\right\}\subseteq {\mathbb{H}}_1$ with $\parallel x_n-\mathbb{T}{x}_n\parallel \to 0,$ then there exist $\left\{x_{n_i}\right\}\subseteq \left\{x_n\right\}$ such that $x_{n_i}\to x\in {\mathbb{H}}_1.$

Lemma 1 

(Chang et al. [14]). Suppose $\mathbb{T}:{\mathbb{H}}_1\to {\mathbb{H}}_1$ is Lipschitz with $L>0,$ and $\mathbb{U}:=(1-\eta )I+\eta \mathbb{T}\left(\right(1-\zeta )I+\zeta \mathbb{T}),$ then

a. 

$Fix\left(\mathbb{T}\right)=Fix\left(\right(1-\eta )I+\eta \mathbb{T}((1-\zeta )I+\zeta \mathbb{T})=Fix(\mathbb{U});$

b. 

$\mathbb{U}$ is demiclosed at zero only if $\mathbb{T}$ is demiclosed at zero.

c. 

$\mathbb{U}$ is Lipschitz with $L^2$

d. 

$\mathbb{U}$ is quasi-nonexpansive only if $\mathbb{T}$ is quasi-pseudocontractive.

Lemma 2 

(Opial, [15]). Suppose $\mathsf{\Omega }\subseteq \mathbb{H},$ for $\left\{x_n\right\}\subseteq \mathsf{\Omega },$ then

a. 

${\displaystyle \underset{n\to \infty }{lim}}\parallel x_n-x\parallel ,$$\forall x\in \mathsf{\Omega }$, exist;

b. 

For any weak cluster point of $x_n\subseteq \mathsf{\Omega },$ then $x_n\rightharpoonup y,$$y\in \mathsf{\Omega }.$

Lemma 3 

(Xu, [16]). Let $\left\{x_n\right\},\left\{{\gamma }_n\right\}\subseteq {\mathbb{R}}^{+}$ such that

$$x_{n+1}\le (1-{\xi }_n)x_n+{\gamma }_n,\forall n\ge 0,$$

where $\left\{{\xi }_n\right\}\subseteq (0,1),$ then

a. 

${\displaystyle \underset{n\to \infty }{lim}}{\xi }_n=0\mathrm{and}{\displaystyle \sum _n}{\xi }_n=\infty ;$

b. 

${\displaystyle \underset{n\to \infty }{lim\; sup}}\frac{{\gamma }_n}{{\xi }_n}\le 0\mathrm{or}{\displaystyle \sum _n}\left|{\gamma }_n\right|<\infty ,$ then, ${\displaystyle \underset{n\to \infty }{lim}}{x}_n=0.$

Lemma 4 

(Xu, [16]). Let $\left\{{\xi }_n\right\},$$\left\{{\eta }_n\right\}\subseteq {\mathbb{R}}^{+}$ such that ${\sum }_{n=0}^{\infty }{\eta }_n<\infty .$ If

$${\xi }_{n+1}\le (1+{\eta }_n){\xi }_{n}or{\xi }_{n+1}\le {\xi }_n+{\eta }_n,\forall n\ge 0,$$

then ${\displaystyle \underset{n\to \infty }{lim}}{\xi }_n$ exist.

3. Main Results

The sequel will use $\mathsf{\Gamma }$ to represent the solution set for (6), that is

$$\mathsf{\Gamma }:=\left\{{\mathrm{x}}^{*}\in \mathrm{Fix}\left({\mathbb{T}}_1\right)\mathrm{and}{\mathrm{y}}^{*}\in \mathrm{Fix}\left({\mathbb{T}}_2\right)\mathrm{such}\mathrm{that}{\mathbb{D}}_1{\mathrm{x}}^{*}={\mathbb{D}}_2{\mathrm{y}}^{*}\right\}.$$

(11)

The following presumptions were used to approximate (11).

Suppose that

(A1)

${\mathbb{T}}_j:{\mathbb{H}}_j\to {\mathbb{H}}_j,j=1,2,$ are two quasi-pseudocontractive operators with $Fix\left({\mathbb{T}}_j\right)\ne \varnothing ,j=1,2,$ in addition, suppose ${\mathbb{T}}_1$ is L-Lipschitz.

(A2)

${\mathbb{D}}_j:{\mathbb{H}}_j\to {\mathbb{H}}_j,j=1,2,$ are linear and bounded operators with their adjoints ${\mathbb{D}}_1^{*}$ and ${\mathbb{D}}_2^{*},$ respectively.

(A3)

$({\mathbb{T}}_j-I),j=1,2,$ are demiclosed at origin.

(A4)

Let $\mathbb{U}$ and $\mathbb{V}$ be defined below:

$$\left\{\begin{array}{c}\mathbb{U}=(1-\eta )I+\eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_1),\hfill \\ \mathbb{V}=(1-\eta )I+\eta {\mathbb{T}}_2((1-\zeta )I+\zeta {\mathbb{T}}_2),\hfill & \hfill \end{array}\right.$$

(12)

where $0<\eta <\zeta <\frac{1}{1+\sqrt{1+L^2}}.$

(A5)

Algorithm:Let ($x_n,y_n) \subseteq {\mathbb{H}}_1\times {\mathbb{H}}_2,$ be defined by

$$\left\{\begin{array}{c}{x}_{n+1}=(1-{\alpha }_n)v_n+{\alpha }_n\mathbb{U}{v}_n;\hfill \\ v_n=(1-{\tau }_n)x_n+{\tau }_n\mathbb{U}{x}_n+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n),\forall n\ge 0,\hfill \\ \\ y_{n+1}=(1-{\alpha }_n)w_n+{\alpha }_n\mathbb{V}{w}_n;\hfill \\ w_n=(1-{\tau }_n)y_n+{\tau }_n\mathbb{V}{y}_n+{\tau }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),\forall n\ge 0,\hfill & \hfill \end{array}\right.$$

(13)

where $(x_0,y_0)\in {\mathbb{H}}_1\times {\mathbb{H}}_2$ are chosen arbitrarily, $0<a<{\alpha }_n<1,$ and ${\tau }_n\in \left(0,\frac{2}{L_1+L_2}\right),$ where $L_1={\mathbb{D}}_1^{*}{\mathbb{D}}_1$ and $L_2={\mathbb{D}}_2^{*}{\mathbb{D}}_2$, respectively, ${\displaystyle \underset{n\to \infty }{lim}}{\tau }_n=0\mathrm{and}{\displaystyle \sum _n}{\tau }_n=\infty .$

Theorem 1. 

Suppose $\left(A1\right)$–$\left(A5\right)$ are held and that $\mathsf{\Gamma }\ne \varnothing .$ Then, $\left\{(x_n,y_n)\right\}$ defined by (13) converges weakly to $(x^{*},y^{*})\in \mathsf{\Gamma },$ in addition if ${\mathbb{T}}_1$ and ${\mathbb{T}}_2$ are semi-compact, then $\left\{(x_n,y_n)\right\}$ converges strongly to $(x^{*},y^{*})\in \mathsf{\Gamma }.$

Proof. 

Let $(p,q)\in \mathsf{\Gamma },$ noticing that $\mathbb{U}$ is quasi-nonexpansive (see Lemma 1), then by (13), we have

$$\begin{array}{cc}\hfill {∥x_{n+1}-p∥}^2=& {∥(1-{\alpha }_n)v_n+{\alpha }_n\mathbb{U}{v}_n-p∥}^2\hfill \\ \hfill =& {∥(1-{\alpha }_n)(v_n-p)+{\alpha }_n(\mathbb{U}{v}_n-p)∥}^2\hfill \\ \hfill =& (1-{\alpha }_n){∥v_n-p∥}^2+{\alpha }_n{∥\mathbb{U}{v}_n-p∥}^2-(1-{\alpha }_n){\alpha }_n{∥\mathbb{U}{v}_n-v_n∥}^2\hfill \\ \hfill \le & {∥v_n-p∥}^2,\mathrm{and}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {∥v_n-p∥}^2=& {∥(1-{\tau }_n)x_n+{\tau }_n\mathbb{U}{x}_n+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)-p∥}^2\hfill \\ \hfill =& {∥(1-{\tau }_n)(x_n-p)+{\tau }_n(\mathbb{U}{x}_n-P)+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)∥}^2\hfill \\ \hfill =& {∥(1-{\tau }_n)(x_n-p)+{\tau }_n(\mathbb{U}{x}_n-p)∥}^2+{\tau }_n^2{∥{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)∥}^2\hfill \\ \hfill +& 2{\tau }_n〈(1-{\tau }_n)(x_n-p)+{\tau }_n(\mathbb{U}{x}_n-p),{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)〉\hfill \\ \hfill =& (1-{\tau }_n){∥x_n-p∥}^2+{\tau }_n{∥\mathbb{U}{x}_n-p∥}^2-(1-{\tau }_n){\tau }_n{∥\mathbb{U}{x}_n-x_n∥}^2\hfill \\ \hfill +& {\tau }_n^2{∥{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)∥}^2+2{\tau }_n(1-{\tau }_n)〈x_n-p,{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)〉\hfill \\ \hfill +& 2{\tau }_n^2〈\mathbb{U}{x}_n-x_n+x_n-p,{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)〉\hfill \\ \hfill \le & {∥x_n-p∥}^2-(1-{\tau }_n){\tau }_n{∥\mathbb{U}{x}_n-x_n∥}^2\hfill \\ \hfill +& {\tau }_n^2{∥{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)∥}^2+2{\tau }_n(1-{\tau }_n)〈x_n-p,{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)〉\hfill \\ \hfill +& 2{\tau }_n^2〈\mathbb{U}{x}_n-x_n,{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)〉+2{\tau }_n^2〈x_n-p,{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)〉\hfill \\ \hfill \le & {∥x_n-p∥}^2+{\tau }_n^2{∥{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)∥}^2-(1-{\tau }_n){\tau }_n{∥\mathbb{U}{x}_n-x_n∥}^2\hfill \\ \hfill +& 2{\tau }_n〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p,{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n〉+2{\tau }_n^2〈\mathbb{U}{\mathbb{D}}_1{x}_n-{\mathbb{D}}_1{x}_n,{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n〉\hfill \\ \hfill \le & {∥x_n-p∥}^2+{\tau }_n^2{∥{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)∥}^2-(1-{\tau }_n){\tau }_n{∥\mathbb{U}{x}_n-x_n∥}^2\hfill \\ \hfill +& 2{\tau }_n〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p,{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n〉-{\tau }_n^2{∥\mathbb{U}{\mathbb{D}}_1{x}_n-{\mathbb{D}}_1{x}_n∥}^2.\hfill \end{array}$$

(15)

By (14) and (15), we have

$$\begin{array}{cc}\hfill {∥x_{n+1}-p∥}^2\le & {∥x_n-p∥}^2+{\tau }_n^2{L}_1{∥{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n∥}^2-(1-{\tau }_n){\tau }_n{∥\mathbb{U}{x}_n-x_n∥}^2\hfill \\ \hfill -& 2{\tau }_n〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p,{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n〉-{\tau }_n^2{∥\mathbb{U}{\mathbb{D}}_1{x}_n-{\mathbb{D}}_1{x}_n∥}^2.\hfill \end{array}$$

(16)

Similarly,

$$\begin{array}{cc}\hfill {∥y_{n+1}-q∥}^2\le & {∥y_n-q∥}^2+{\tau }_n^2{L}_2{∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥}^2-(1-{\tau }_n){\tau }_n{∥\mathbb{V}{y}_n-y_n∥}^2\hfill \\ \hfill +& 2{\tau }_n〈{\mathbb{D}}_2{y}_n-{\mathbb{D}}_{2}q,{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n〉-{\tau }_n^2{∥\mathbb{V}{\mathbb{D}}_2{y}_n-{\mathbb{D}}_2{y}_n∥}^2.\hfill \end{array}$$

(17)

Since ${\mathbb{D}}_{1}p={\mathbb{D}}_{2}q,$ coupled with (16) and (17), we have

$$\begin{array}{cc}\hfill {∥x_{n+1}-p∥}^2+{∥y_{n+1}-q∥}^2\le & {∥x_n-p∥}^2+{∥y_n-q∥}^2\hfill \\ \hfill -& {\tau }_n\left(2-{\tau }_n(L_1+L_2)\right){∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥}^2\hfill \\ \hfill -& (1-{\tau }_n){\tau }_n\left({∥\mathbb{U}{x}_n-x_n∥}^2+{∥\mathbb{V}{y}_n-y_n∥}^2\right)\hfill \\ \hfill -& {\tau }_n^2\left({∥\mathbb{U}{\mathbb{D}}_1{x}_n-{\mathbb{D}}_1{x}_n∥}^2+{∥\mathbb{V}{\mathbb{D}}_2{y}_n-{\mathbb{D}}_2{y}_n∥}^2\right).\hfill \end{array}$$

(18)

This implies that

$$\begin{array}{cc}\hfill s_{n+1}\le & s_n-{\tau }_n\left(2-{\tau }_n(L_1+L_2)\right){∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥}^2\hfill \\ \hfill -& (1-{\tau }_n){\tau }_n\left({∥\mathbb{U}{x}_n-x_n∥}^2+{∥\mathbb{V}{y}_n-y_n∥}^2\right)\hfill \\ \hfill -& {\tau }_n^2\left({∥\mathbb{U}{\mathbb{D}}_1{x}_n-{\mathbb{D}}_1{x}_n∥}^2+{∥\mathbb{V}{\mathbb{D}}_2{y}_n-{\mathbb{D}}_2{y}_n∥}^2\right),\hfill \end{array}$$

(19)

where $s_n:={∥x_n-p∥}^2+{∥y_n-q∥}^2.$

Thus, $s_{n+1}\le s_n,$ therefore, $s_n$ is a decreasing sequence that is bound from below by 0, hence, $s_n$ converges, therefore, we have that

$$\begin{array}{cc}\hfill {∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥}^2& \le \frac{s_n-s_{n+1}}{{\tau }_n\left(2-{\tau }_n(L_1+L_2)\right)}\hfill \\ & \le \frac{2(s_n-s_{n+1})}{\left(2-{\tau }_n(L_1+L_2)\right)(L_1+L_2)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {∥\mathbb{U}{x}_n-x_n∥}^2+{∥\mathbb{V}{y}_n-y_n∥}^2& \le \frac{s_n-s_{n+1}}{{\tau }_n\left(1-{\tau }_n\right)}\hfill \\ & \le \frac{2(s_n-s_{n+1})}{\left(1-{\tau }_n\right)(L_1+L_2)},\mathrm{and}\hfill \end{array}$$

$$\begin{array}{cc}\hfill {∥\mathbb{U}{\mathbb{D}}_1{x}_n-{\mathbb{D}}_1{x}_n∥}^2+{∥\mathbb{V}{\mathbb{D}}_2{y}_n-{\mathbb{D}}_2{y}_n∥}^2& \le \frac{s_n-s_{n+1}}{{\tau }_n^2}\hfill \\ & \le \frac{2(s_n-s_{n+1})}{L_1+L_2}.\hfill \end{array}$$

These lead to

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}}∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥=0,\end{array}$$

(20)

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}}∥\mathbb{U}{\mathbb{D}}_1{x}_n-{\mathbb{D}}_1{x}_n∥=0,{\displaystyle \underset{n\to \infty }{lim}}∥\mathbb{U}{x}_n-x_n∥=0,\mathrm{and}\hfill \\ {\displaystyle \underset{n\to \infty }{lim}}∥\mathbb{V}{\mathbb{D}}_2{y}_n-{\mathbb{D}}_2{y}_n∥=0,{\displaystyle \underset{n\to \infty }{lim}}∥\mathbb{V}{y}_n-y_n∥=0.\hfill & \hfill \end{array}$$

(21)

Since, $\mathbb{U}=(1-\eta )I-\eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_1)I$, where $0<\eta <\zeta <\frac{1}{1+\sqrt{1+L^2}}$ and ${\mathbb{T}}_1$ is Lipschitz, we have

$$\begin{array}{cc}\hfill \parallel \eta x_n-\eta {\mathbb{T}}_1{x}_n\parallel & = \parallel x_n-(1-\eta )x_n-\eta {\mathbb{T}}_1{x}_n\parallel \hfill \\ & = \parallel x_n-(1-\eta )x_n-\eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_1)x_n+\eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_1)x_n-\eta {\mathbb{T}}_1{x}_n\parallel \hfill \\ & \le \parallel x_n-(1-\eta )x_n-\eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_1)x_n\parallel \hfill \\ & + \parallel \eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_1)x_n-\eta {\mathbb{T}}_1{x}_n\parallel \hfill \\ & \le \parallel x_n-\mathbb{U}{x}_n\parallel +\eta L\parallel ((1-\zeta )I+\zeta {\mathbb{T}}_1)x_n-x_n\parallel \hfill \\ & = \parallel x_n-\mathbb{U}{x}_n\parallel +\eta \zeta L\parallel x_n-{\mathbb{T}}_1{x}_n\parallel .\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \parallel x_n-{\mathbb{T}}_1{x}_n\parallel & \le \frac{1}{(1-\zeta L)\eta }\parallel x_n-\mathbb{U}{x}_n\parallel .\hfill \end{array}$$

(22)

Similarly,

$$\begin{array}{cc}\hfill \parallel y_n-{\mathbb{T}}_2{y}_n\parallel & \le \frac{1}{(1-\zeta L)\eta }\parallel y_n-\mathbb{V}{y}_n\parallel .\hfill \end{array}$$

(23)

By (21), we see that

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}}∥{\mathbb{T}}_1{x}_n-x_n∥=0,\mathrm{and}{\displaystyle \underset{\mathrm{n}\to \infty }{lim}}∥{\mathbb{T}}_2{\mathrm{y}}_{\mathrm{n}}-{\mathrm{y}}_{\mathrm{n}}∥=0.\end{array}$$

(24)

Claim $(x_n,y_n)\rightharpoonup (x^{*},y^{*})$

Since $\left\{s_n\right\}$ converges, it follows that $(x_n,y_n)$ is bounded, which implies that there exist $(x^{*},y^{*})\in \mathsf{\Gamma }$ for which $x_n\rightharpoonup x^{*}$ and $y_n\rightharpoonup y^{*}.$

Now, $v_n=x_n-{\tau }_n(\mathbb{U}{x}_n-x_n)+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)$ and $w_n=y_n-{\tau }_n(\mathbb{V}{y}_n-y_n)+{\tau }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),$ couple with (20) and (21), we deduce that $v_n\rightharpoonup x^{*}$ and $w_n\rightharpoonup y^{*}.$

On the other hand, $x_n\rightharpoonup x^{*},$$v_n\rightharpoonup x^{*},$ and ${\displaystyle \underset{n\to \infty }{lim}}∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥=0$ together with

$$v_n=(1-{\tau }_n)x_n+{\tau }_n\mathbb{U}{x}_n+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),$$

we deduce that $x^{*}=\mathbb{U}{x}^{*}.$ Similarly, $y^{*}=\mathbb{V}{y}^{*}.$ These imply that $x^{*}={\mathbb{T}}_1{x}^{*}$ and $y^{*}={\mathbb{T}}_2{y}^{*},$ see Lemma 1.

Now that $x_n\rightharpoonup x^{*}$ and ${\displaystyle \underset{n\to \infty }{lim}}∥{\mathbb{T}}_1{x}_n-x_n∥=0$ couple with the demiclosedness of $({\mathbb{T}}_1-I)$ at origin, we have $x^{*}\in Fix\left({\mathbb{T}}_1\right).$

Similarly, $y_n\rightharpoonup y^{*}$ and ${\displaystyle \underset{n\to \infty }{lim}}∥{\mathbb{T}}_2{y}_n-y_n∥=0$ together with the demiclosedness of $({\mathbb{T}}_2-I)$ at origin, we see that $y^{*}\in Fix\left({\mathbb{T}}_2\right).$

Since $v_n\rightharpoonup x^{*},$$w_n\rightharpoonup y^{*}$ and ${\mathbb{D}}_1$ and ${\mathbb{D}}_2$ are linear mappings, we have

$${\mathbb{D}}_1{v}_n\rightharpoonup {\mathbb{D}}_1{x}^{*},\mathrm{and}{\mathbb{D}}_2{w}_n\rightharpoonup {\mathbb{D}}_2{y}^{*}.$$

This implies that

$${\mathbb{D}}_1{v}_n-{\mathbb{D}}_2{w}_n\rightharpoonup {\mathbb{D}}_1{x}^{*}-{\mathbb{D}}_2{y}^{*},$$

which implies that

$$∥{\mathbb{D}}_1{x}^{*}-{\mathbb{D}}_2{y}^{*}∥\le {\displaystyle \underset{n\to \infty }{lim\; inf}}∥{\mathbb{D}}_1{v}_n-{\mathbb{D}}_2{w}_n∥=0.$$

Therefore, ${\mathbb{D}}_1{x}^{*}={\mathbb{D}}_2{y}^{*}.$ Noticing that $(x^{*},y^{*})\in Fix\left({\mathbb{T}}_1\right)\times Fix\left({\mathbb{T}}_2\right)$, we conclude that $(x^{*},y^{*})\in \mathsf{\Gamma }.$

Thus,

(i)

${\displaystyle \underset{n\to \infty }{lim}}{s}_n$ exist, for all $(x^{*},y^{*})\in \mathsf{\Gamma },$

(ii)

$(x_n,y_n)$ belong to $\mathsf{\Gamma }.$

Hence, by Lemma 2, we see that $(x_n,y_n)\rightharpoonup (x^{*},y^{*})\in \mathsf{\Gamma }.$ Furthermore, since $(x_n,y_n)$ is bounded coupled with Equation (24) and Definition 1 we deduce that $(x_n,y_n)\to (x^{*},y^{*})\in \mathsf{\Gamma }.$ This completes the proof. □

4. The SEFPP without Prior Knowledge of Operator Norms

This section gives the convergent result of the SEFPP without prior knowledge of the operator norms of bounded and linear operators ${\mathbb{D}}_1:{\mathbb{H}}_1\to {\mathbb{H}}_2$ and ${\mathbb{D}}_2:{\mathbb{H}}_2\to {\mathbb{H}}_3,$ respectively.

Theorem 2. 

Assume $\left(A1\right)$–$\left(A4\right)$ are satisfied, $\mathsf{\Gamma }\ne \varnothing$, and let $\left\{(x_n,y_n)\right\}$ be defined by

$$\left\{\begin{array}{c}\mathbb{U}=(1-\eta )I+\eta {\mathbb{T}}_1((1-\zeta )I+\zeta {\mathbb{T}}_1);\hfill \\ x_{n+1}=(1-{\alpha }_n)v_n+{\alpha }_n\mathbb{U}{v}_n;\hfill \\ v_n=(1-{\tau }_n)x_n+{\tau }_n\mathbb{U}{x}_n+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_1{y}_n-{\mathbb{D}}_1{x}_n),\forall n\ge 0;\hfill \\ \\ \mathbb{V}=(1-\eta )I+\eta {\mathbb{T}}_2((1-\zeta )I+\zeta {\mathbb{T}}_2);\hfill \\ y_{n+1}=(1-{\alpha }_n)w_n+{\alpha }_n\mathbb{V}{w}_n;\hfill \\ w_n=(1-{\tau }_n)y_n+{\tau }_n\mathbb{V}{y}_n+{\tau }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),\forall n\ge 0;\hfill & \hfill \end{array}\right.$$

(25)

where $(x_0,y_0)\in {\mathbb{H}}_1\times {\mathbb{H}}_2$ are chosen arbitrarily and

(i) 

$0<a<{\alpha }_n<1;$

(ii) 

${\tau }_n\subseteq (0,1),$ such that $\sum {\tau }_n=\infty$ and $\sum {\tau }_n^2<\infty ;$

then, $(x_n,y_n)\rightharpoonup (x^{*},y^{*})\in \mathsf{\Gamma }.$ In addition, if ${\mathbb{T}}_1$ and ${\mathbb{T}}_2$ are semi-compact, then $\left\{(x_n,y_n)\right\}\to (x^{*},y^{*})\in \mathsf{\Gamma }.$

Proof. 

By (14), we deduce that

$$\begin{array}{cc}\hfill {∥x_{n+1}-p∥}^2\le & {∥v_n-p∥}^2\hfill \\ \hfill =& {∥x_n-{\tau }_n\left(x_n-\mathbb{U}{x}_n-{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)\right)-p∥}^2\hfill \\ \hfill =& {∥x_n-{\tau }_n{k}_n-p∥}^2,\mathrm{where}{\mathrm{k}}_{\mathrm{n}}={\mathrm{x}}_{\mathrm{n}}-\mathbb{U}{\mathrm{x}}_{\mathrm{n}}-{\mathbb{D}}_1^{*}({\mathbb{D}}_2{\mathrm{y}}_{\mathrm{n}}-{\mathbb{D}}_1{\mathrm{x}}_{\mathrm{n}})\hfill \\ \hfill =& {∥x_n-p∥}^2-2{\tau }_n〈x_n-p,k_n〉+{\tau }_n^2{∥k_n∥}^2,\hfill \end{array}$$

thus,

$$\begin{array}{cc}\hfill {∥x_{n+1}-p∥}^2\le & {∥x_n-p∥}^2-2{\tau }_n〈x_n-p,k_n〉+{\tau }_n^2{∥k_n∥}^2,\mathrm{and}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill 〈x_n-p,k_n〉=& 〈x_n-p,x_n-\mathbb{U}{x}_n-{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)〉\hfill \\ \hfill =& 〈x_n-p,x_n-\mathbb{U}{x}_n〉-〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p,{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n〉\hfill \\ \hfill \ge & \frac{1}{2}{∥x_n-\mathbb{U}{x}_n∥}^2-〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p,{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n〉,\hfill \end{array}$$

(27)

where $\mathbb{U}$ is quasi-nonexpansive.

Similarly,

$$\begin{array}{c}\hfill {∥y_{n+1}-q∥}^2\le {∥y_n-q∥}^2-2{\tau }_n〈y_n-q,r_n〉+{\tau }_n^2{∥r_n∥}^2,\end{array}$$

(28)

where ${\mathrm{r}}_{\mathrm{n}}={\mathrm{y}}_{\mathrm{n}}-\mathbb{V}{\mathrm{y}}_{\mathrm{n}}-{\mathbb{D}}_2^{*}({\mathbb{D}}_1{\mathrm{x}}_{\mathrm{n}}-{\mathbb{D}}_2{\mathrm{y}}_{\mathrm{n}}),$ and

$$\begin{array}{cc}\hfill 〈y_n-q,r_n〉\ge & \frac{1}{2}{∥y_n-\mathbb{V}{y}_n∥}^2-〈{\mathbb{D}}_2{y}_n-{\mathbb{D}}_{2}q,{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n〉,\hfill \end{array}$$

(29)

where $\mathbb{V}$ is quasi-nonexpansive. By (27) and (29), and the fact that ${\mathbb{D}}_{1}p={\mathbb{D}}_{2}q,$ we have

$$\begin{array}{cc}\hfill 〈x_n-p,k_n〉 +& 〈y_n-q,r_n〉\ge \frac{1}{2}{∥x_n-\mathbb{U}{x}_n∥}^2-〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p,{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n〉\hfill \\ \hfill +& \frac{1}{2}{∥y_n-\mathbb{V}{y}_n∥}^2-〈{\mathbb{D}}_2{y}_n-{\mathbb{D}}_{2}q,{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n〉\hfill \\ \hfill =& \frac{1}{2}\left({∥x_n-\mathbb{U}{x}_n∥}^2+{∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥}^2\right)\hfill \\ \hfill +& \frac{1}{2}\left({∥y_n-\mathbb{V}{y}_n∥}^2+{∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥}^2\right)\hfill \\ \hfill \ge & \frac{1}{2}\left({∥x_n-\mathbb{U}{x}_n∥}^2+\frac{1}{{∥{\mathbb{D}}_1∥}^2}{∥{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥}^2\right)\hfill \\ \hfill +& \frac{1}{2}\left({∥y_n-\mathbb{V}{y}_n∥}^2+\frac{1}{{∥{\mathbb{D}}_2∥}^2}{∥{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥}^2\right)\hfill \\ \hfill \ge & \frac{1}{2max\{1,{∥{\mathbb{D}}_1∥}^2\}}\left({∥x_n-\mathbb{U}{x}_n∥}^2+{∥{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥}^2\right)\hfill \\ \hfill +& \frac{1}{2max\{1,{∥{\mathbb{D}}_2∥}^2\}}\left({∥y_n-\mathbb{V}{y}_n∥}^2+{∥{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥}^2\right)\hfill \\ \hfill \ge & \frac{1}{4max\{1,{∥{\mathbb{D}}_1∥}^2,{∥{\mathbb{D}}_2∥}^2\}}({\left(∥y_n-\mathbb{V}{y}_n∥+∥{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥\right)}^2\hfill \\ \hfill +& {\left({∥x_n-\mathbb{U}{x}_n∥}^2+∥{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥\right)}^2)\hfill \\ \hfill \ge & \eta \left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right),\hfill \end{array}$$

(30)

where $\eta =\frac{1}{4max\{1,{∥{\mathbb{D}}_1∥}^2,{∥{\mathbb{D}}_2∥}^2\}},$$\parallel k_n\parallel \le ∥y_n-\mathbb{V}{y}_n∥+∥{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥$ and $\parallel r_n\parallel \le ∥x_n-\mathbb{U}{x}_n∥+∥{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥.$

By (26), (28) and (30), we have

$$\begin{array}{cc}\hfill {∥x_{n+1}-p∥}^2+{∥y_{n+1}-q∥}^2\le & {∥x_n-p∥}^2+{∥y_n-q∥}^2-2{\tau }_n〈x_n-p,k_n〉\hfill \\ \hfill -& 2{\tau }_n〈y_n-q,r_n〉+{\tau }_n^2{∥k_n∥}^2+{\tau }_n^2{∥r_n∥}^2\hfill \\ \hfill \le & {∥x_n-p∥}^2+{∥y_n-q∥}^2+{\tau }_n^2\left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right)\hfill \\ \hfill -& 2{\tau }_n\eta \left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right),\hfill \\ \hfill =& {∥x_n-p∥}^2+{∥y_n-q∥}^2-2{\tau }_n\left(\eta -\frac{{\tau }_n}{2}\right)\left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right).\hfill \end{array}$$

(31)

The fact that $\mathbb{U}$ is $L^2$-Lipschitzian, we have

$$\begin{array}{cc}\hfill ∥k_n∥=& ∥x_n-\mathbb{U}{x}_n-{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)-(p-\mathbb{U}p)+{\mathbb{D}}_1^{*}({\mathbb{D}}_{2}q-{\mathbb{D}}_{1}p)∥\hfill \\ \hfill \le & ∥x_n-p-\mathbb{U}(x_n-P)∥+∥{\mathbb{D}}_1^{*}({\mathbb{D}}_{2}q-{\mathbb{D}}_{1}p)-{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)∥\hfill \\ \hfill \le & (1+L^2)∥x_n-p∥+∥{\mathbb{D}}_1^{*}∥∥({\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p)-({\mathbb{D}}_2{y}_n-{\mathbb{D}}_{2}q)∥\hfill \\ \hfill \le & (1+L^2)∥x_n-p∥+∥{\mathbb{D}}_1^{*}∥\left(∥{\mathbb{D}}_1∥∥x_n-p∥+∥{\mathbb{D}}_2∥∥y_n-q∥\right)\hfill \\ \hfill \le & (1+L^2)∥x_n-p∥+∥{\mathbb{D}}_1^{*}∥max\left\{∥{\mathbb{D}}_1∥,∥{\mathbb{D}}_2∥\right\}\left(∥x_n-p∥+∥y_n-q∥\right).\hfill \end{array}$$

This gives

$$\begin{array}{cc}\hfill ∥k_n∥\le & (1+L^2)∥x_n-p∥+∥{\mathbb{D}}_1^{*}∥max\left\{∥{\mathbb{D}}_1∥,∥{\mathbb{D}}_2∥\right\}\left(∥x_n-p∥+∥y_n-q∥\right).\hfill \end{array}$$

(32)

Similarly,

$$\begin{array}{cc}\hfill ∥r_n∥\le & (1+L^2)∥y_n-q∥+∥{\mathbb{D}}_2^{*}∥max\left\{∥{\mathbb{D}}_1∥,∥{\mathbb{D}}_2∥\right\}\left(∥x_n-p∥+∥y_n-q∥\right).\hfill \end{array}$$

(33)

By (32) and (33), we deduce that

$$\begin{array}{cc}\hfill ∥k_n∥+∥r_n∥\le & \left(1+L^2+max(\parallel {\mathbb{D}}_1{\parallel }^2,\parallel {\mathbb{D}}_2{\parallel }^2)\right)\left\{∥x_n-p∥+∥y_n-q∥\right\}.\hfill \end{array}$$

(34)

This gives

$$\begin{array}{cc}\hfill max({∥k_n∥}^2,{∥r_n∥}^2)\le & {\phi }^2{\left\{∥x_n-p∥+∥y_n-q∥\right\}}^2\hfill \\ \hfill \le & 2{\phi }^2\left\{{∥x_n-p∥}^2+{∥y_n-q∥}^2\right\},\hfill \end{array}$$

(35)

where $\phi :=1+L^2+max(\parallel {\mathbb{D}}_1{\parallel }^2,\parallel {\mathbb{D}}_2{\parallel }^2).$

Equations (31) and (35) give

$$\begin{array}{cc}\hfill {∥x_{n+1}-p∥}^2+{∥y_{n+1}-q∥}^2\le & {∥x_n-p∥}^2+{∥y_n-q∥}^2\hfill \\ \hfill +& 2{\phi }^2{\tau }_n^2\left\{{∥x_n-p∥}^2+{∥y_n-q∥}^2\right\}.\hfill \end{array}$$

(36)

Noticing that ${\displaystyle \sum _n}{\phi }^2{\tau }_n^2<\infty ,$ by Lemma 4 we deduce that ${\displaystyle \underset{n\to \infty }{lim}}\left\{{∥x_n-p∥}^2+{∥y_n-q∥}^2\right\}$ exist. Thus, $(x_n,y_n)$ is bounded, and it is not difficult to see that $\left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right)$ is bounded.

Next, we show that ${\displaystyle \underset{n\to \infty }{lim}}∥\mathbb{U}{x}_n-x_n∥=0,$${\displaystyle \underset{n\to \infty }{lim}}∥\mathbb{V}{y}_n-y_n∥=0$ and ${\displaystyle \underset{n\to \infty }{lim}}∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥=0.$

By (31), we have

$$\begin{array}{cc}\hfill 2{\tau }_n\eta \left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right)& \le \left({∥x_n-p∥}^2-{∥x_{n+1}-p∥}^2\right)+\left({∥y_n-q∥}^2-{∥y_{n+1}-q∥}^2\right)\hfill \\ \hfill & + {\tau }_n^2\left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right),\hfill \end{array}$$

(37)

thus,

$$\begin{array}{cc}\hfill 2\eta {\displaystyle \sum _n}{\tau }_n\left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right)& \le {\displaystyle \sum _n}\left({∥x_n-p∥}^2-{∥x_{n+1}-p∥}^2+{∥y_n-q∥}^2-{∥y_{n+1}-q∥}^2\right)\hfill \\ \hfill & + {\displaystyle \sum _{n=0}}{\tau }_n^2\left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right)\hfill \\ \hfill & = {∥x_0-p∥}^2-{∥x_1-p∥}^2+{∥y_0-q∥}^2-{∥y_1-q∥}^2\hfill \\ \hfill & + {∥x_1-p∥}^2-{∥x_2-p∥}^2+{∥y_1-q∥}^2-{∥y_2-q∥}^2\hfill \\ \hfill & + {∥x_2-p∥}^2-{∥x_3-p∥}^2+{∥y_2-q∥}^2-{∥y_3-q∥}^2\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill & + {\displaystyle \sum _{n=0}}{\tau }_n^2\left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right)\hfill \\ \hfill & = {∥x_0-p∥}^2+{∥y_0-q∥}^2+{\displaystyle \sum _{n=0}}{\tau }_n^2\left(\parallel k_n{\parallel }^2+{\parallel r_n\parallel }^2\right).\hfill \end{array}$$

(38)

Since ${\displaystyle \sum _n}{\tau }_n=\infty ,$${\displaystyle \sum _n}{\tau }_n^2<\infty$ and $\left(\parallel k_n{\parallel }^2+ {\parallel r_n\parallel }^2\right)$ is bounded, thus, we deduce from (38) that

$${\displaystyle \underset{n\to \infty }{lim\; sup}}\left(\parallel k_n{\parallel }^2+ {\parallel r_n\parallel }^2\right)=0.$$

(39)

On the other hand,

$$\begin{array}{cc}\hfill ∥k_{n+1}-k_n∥& \le ∥x_{n+1}-x_n-\mathbb{U}(x_{n+1}-x_n)∥\hfill \\ \hfill & + ∥{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)-{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_{n+1}-{\mathbb{D}}_1{x}_{n+1})∥\hfill \\ \hfill & \le (1+L^2)∥x_{n+1}-x_n∥+∥{\mathbb{D}}_1^{*}∥∥({\mathbb{D}}_1{x}_{n+1}-{\mathbb{D}}_1{x}_n)-({\mathbb{D}}_2{y}_{n+1}-{\mathbb{D}}_2{y}_n)∥\hfill \\ \hfill & \le (1+L^2)∥x_{n+1}-x_n∥+∥{\mathbb{D}}_1^{*}∥\left(∥{\mathbb{D}}_1∥∥x_{n+1}-x_n∥+∥{\mathbb{D}}_2∥∥y_{n+1}-y_n∥\right)\hfill \\ \hfill & \le (1+L^2)∥x_{n+1}-x_n∥\hfill \\ \hfill & + ∥{\mathbb{D}}_1^{*}∥max\left\{∥{\mathbb{D}}_1∥,∥{\mathbb{D}}_2∥\right\}\left(∥x_{n+1}-x_n∥+∥y_{n+1}-y_n∥\right),\hfill \end{array}$$

(40)

and

$$\begin{array}{c}\hfill ∥x_{n+1}-x_n∥\le ∥{\tau }_n{k}_n∥\mathrm{and}∥{\mathrm{y}}_{\mathrm{n}+1}-{\mathrm{y}}_{\mathrm{n}}∥\le ∥{\varnothing }_{\mathrm{n}}{\mathrm{r}}_{\mathrm{n}}∥.\end{array}$$

(41)

By (40) and (41), we have that

$$\begin{array}{cc}\hfill ∥k_{n+1}-k_n∥& \le (1+L^2){\tau }_n∥k_n∥\hfill \\ \hfill & +∥{\mathbb{D}}_1^{*}∥max\left\{∥{\mathbb{D}}_1∥,∥{\mathbb{D}}_2∥\right\}{\tau }_n\left(∥k_n∥+∥r_n∥\right).\hfill \end{array}$$

(42)

Similarly,

$$\begin{array}{cc}\hfill ∥r_{n+1}-r_n∥& \le (1+L^2){\tau }_n∥r_n∥\hfill \\ \hfill & +∥{\mathbb{D}}_2^{*}∥max\left\{∥{\mathbb{D}}_1∥,∥{\mathbb{D}}_2∥\right\}{\tau }_n\left(∥r_n∥+∥k_n∥\right).\hfill \end{array}$$

(43)

By (42) and (43), we have

$$\begin{array}{cc}\hfill max\left(∥k_{n+1}-k_n∥,∥r_{n+1}-r_n∥\right)& \le (1+L^2){\tau }_n\left(∥k_n∥+∥r_n∥\right)\hfill \\ & +∥{\mathbb{D}}_1^{*}∥max\left\{{∥{\mathbb{D}}_1∥}^2,{∥{\mathbb{D}}_2∥}^2\right\}{\tau }_n\left(∥k_n∥+∥r_n∥\right)\hfill \\ & ={\tau }_n{j}_{{\mathbb{D}}_1,{\mathbb{D}}_2}\left(∥k_n∥+∥r_n∥\right),\hfill \end{array}$$

where $j_{{\mathbb{D}}_1,{\mathbb{D}}_2}=\left((1+L^2)+∥{\mathbb{D}}_1^{*}∥max\left\{{∥{\mathbb{D}}_1∥}^2,{∥{\mathbb{D}}_2∥}^2\right\}\right).$ Thus,

$$\begin{array}{cc}\hfill max\left(∥k_{n+1}-k_n∥,∥r_{n+1}-r_n∥\right)& \le {\tau }_n{j}_{{\mathbb{D}}_1,{\mathbb{D}}_2}\left(∥k_n∥+∥r_n∥\right).\hfill \end{array}$$

(44)

By (44), we deduce that

$$\begin{array}{cc}\hfill 〈k_n,k_{n+1}-k_n〉+〈r_n,r_{n+1}-r_n〉& \le \parallel k_n\parallel \parallel k_{n+1}-k_n\parallel +\parallel r_n\parallel \parallel r_{n+1}-r_n\parallel \hfill \\ \hfill & \le {\tau }_n^2{j}_{{\mathbb{D}}_1,{\mathbb{D}}_2}^2{\left(∥k_n∥+∥r_n∥\right)}^2\hfill \\ \hfill & \le 2{\tau }_n^2{j}_{{\mathbb{D}}_1,{\mathbb{D}}_2}^2\left({∥k_n∥}^2+{∥r_n∥}^2\right).\hfill \end{array}$$

(45)

On the other hand,

$$\begin{array}{cc}\hfill \parallel k_{n+1}{\parallel }^2+{\parallel r_{n+1}\parallel }^2& = \parallel k_n{\parallel }^2+〈k_n,k_{n+1}-k_n〉+{\parallel k_{n+1}-k_n\parallel }^2\hfill \\ & + \parallel r_n{\parallel }^2+〈r_n,r_{n+1}-r_n〉+{\parallel r_{n+1}-r_n\parallel }^2\hfill \\ & \le \left(1+2{\tau }_n^2{j}_{{\mathbb{D}}_1,{\mathbb{D}}_2}^2+4{\tau }_n^2{j}_{{\mathbb{D}}_1,{\mathbb{D}}_2}^2\right)\left({∥k_n∥}^2+{∥r_n∥}^2\right).\hfill \end{array}$$

(46)

Noticing that ${\displaystyle \sum _n}\left(6{\tau }_n^2{j}_{{\mathbb{D}}_1,{\mathbb{D}}_2}^2\right)<\infty ,$ thus, by Lemma 4, we deduce that

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}}\left({∥k_n∥}^2+{∥r_n∥}^2\right)\mathrm{exist},\mathrm{this}\mathrm{imply}\mathrm{that}\end{array}$$

(47)

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}}(∥k_n∥+∥r_n∥)\mathrm{exist}.\end{array}$$

(48)

Therefore, we deduce from (39) and (48) that

$$\begin{array}{cc}\hfill {\displaystyle \underset{n\to \infty }{lim}}∥k_n∥& ={\displaystyle \underset{n\to \infty }{lim}}∥x_n-\mathbb{U}{x}_n-{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)∥=0\mathrm{and}\hfill \\ \hfill {\displaystyle \underset{n\to \infty }{lim}}∥r_n∥& ={\displaystyle \underset{n\to \infty }{lim}}∥y_n-\mathbb{V}{y}_n-{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)∥=0.\hfill \end{array}$$

(49)

It is known that $\mathbb{U}$ is quasi-nonexpansive mapping if and only if $\frac{1}{2}{\parallel x_n-\mathbb{U}{x}_n\parallel }^2\le$$〈x_n-\mathbb{U}{x}_n,x_n-p〉,p\in Fix\left(\mathbb{U}\right).$ This implies that

$$\begin{array}{cc}\hfill \frac{1}{2}{\parallel x_n-\mathbb{U}{x}_n\parallel }^2& + 〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n,{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p〉\le 〈x_n-\mathbb{U}{x}_n,x_n-p〉\hfill \\ \hfill & + 〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n,{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p〉\hfill \\ \hfill & = 〈x_n-\mathbb{U}{x}_n-{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),x_n-p〉\hfill \\ \hfill & \le \parallel x_n-\mathbb{U}{x}_n-{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)\parallel \parallel x_n-p\parallel .\hfill \end{array}$$

(50)

Thus, by (49) we get

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}}∥x_n-\mathbb{U}{x}_n∥=0.\end{array}$$

(51)

Similarly,

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}}∥y_n-\mathbb{V}{y}_n∥=0,\end{array}$$

(52)

and

$$\begin{array}{cc}\hfill {∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥}^2& =〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n,{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n〉\hfill \\ & =〈{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n,{\mathbb{D}}_1{x}_n-{\mathbb{D}}_{1}p〉+〈{\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n,{\mathbb{D}}_2{y}_n-{\mathbb{D}}_{2}q〉,\hfill \\ & =〈{\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),x_n-p〉+〈{\mathbb{D}}_2^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n),y_n-q〉\hfill \\ & \le \parallel {\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)+(x_n-U{x}_n)-(x_n-\mathbb{U}{x}_n)\parallel \parallel x_n-p\parallel \parallel \hfill \\ & + \parallel {\mathbb{D}}_2^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)+(y_n-mathbbV{y}_n)-(y_n-\mathbb{V}{y}_n)\parallel \parallel y_n-q\parallel \hfill \\ & \le \parallel {\mathbb{D}}_1^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)-(x_n-\mathbb{U}{x}_n)\parallel \parallel x_n-p\parallel +\parallel (x_n-\mathbb{U}{x}_n)\parallel \parallel x_n-p\parallel \hfill \\ & + \parallel {\mathbb{D}}_2^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)-(y_n-\mathbb{V}{y}_n)\parallel \parallel y_n-q\parallel +\parallel (y_n-V{y}_n)\parallel \parallel y_n-q\parallel \hfill \end{array}$$

(53)

Thus, by (51), (52) and the fact that $\{\parallel x_n-p\parallel \}$ and $\{\parallel y_n-q\parallel \}$ are bounded, we deduce that

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}}∥{\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n∥=0.\end{array}$$

(54)

Next, we show that $(x_n,y_n)\rightharpoonup (x^{*},y^{*})\in \mathsf{\Gamma }.$ This follows directly from Section 3. This completes the proof. □

Corollary 1. 

Suppose for $j=1,2,{\mathbb{T}}_j:H_j\to H_j$ are $k_j-$ demicontractive mappings with $Fix\left({\mathbb{T}}_j\right)\ne \varnothing$ such that $({\mathbb{T}}_j-I)$ are demiclosed at zero. Let $(x_n,y_n)\in {\mathbb{H}}_1\times {\mathbb{H}}_2,$ be generated by

$$\left\{\begin{array}{c}{x}_{n+1}=(1-{\alpha }_n)v_n+{\alpha }_n{\mathbb{T}}_1{v}_n;\hfill \\ v_n=(1-{\tau }_n)x_n+{\tau }_n{\mathbb{T}}_1{x}_n+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n),\forall n\ge 0;\hfill \\ \\ y_{n+1}=(1-{\alpha }_n)w_n+{\alpha }_n{\mathbb{T}}_2{w}_n;\hfill \\ w_n=(1-{\tau }_n)y_n+{\tau }_n{\mathbb{T}}_2{y}_n+{\tau }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_1{y}_n),\forall n\ge 0;\hfill & \hfill \end{array}\right.$$

(55)

where $(x_0,y_0)\in {\mathbb{H}}_1\times {\mathbb{H}}_2,$ are chosen arbitrarily, $0<a<{\alpha }_n<1,$ and ${\tau }_n\in \left(0,\frac{2}{L_1+L_2}\right),$ where $L_1={\mathbb{D}}_1^{*}{\mathbb{D}}_1$ and $L_2={\mathbb{D}}_2^{*}{\mathbb{D}}_2,$ respectively. Then, $\left\{(x_n,y_n)\right\}$ defined by (55) converges to $(x^{*},y^{*})\in \mathsf{\Gamma }.$

Corollary 2 

(Chang et al. [14]). Suppose $\left(A1\right)$–$\left(A4\right)$ are satisfied, and that $\mathsf{\Gamma }\ne \varnothing .$ Let $\left\{(x_n,y_n)\right\}$ defined by

$$\left\{\begin{array}{c}{x}_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)\left((1-{\eta }_n)I+{\eta }_n{\mathbb{T}}_1((1-{\zeta }_n)I+{\zeta }_n{\mathbb{T}}_1)\right)v_n;\hfill \\ v_n=x_n+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n),\forall n\ge 0.\hfill \\ \\ y_{n+1}={\alpha }_n{y}_n+(1-{\alpha }_n)\left((1-{\eta }_n)I+{\eta }_n{\mathbb{T}}_2((1-{\zeta }_n)I+{\zeta }_n{\mathbb{T}}_2)\right)w_n;\hfill \\ w_n=y_n+{\tau }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),\forall n\ge 0.\hfill & \hfill \end{array}\right.$$

(56)

where $0<{\eta }_n<{\zeta }_n<\frac{1}{1+\sqrt{1+L^2}},$ $0<a<{\alpha }_n<1,$ and ${\tau }_n\in \left(0,\frac{2}{L_1+L_2}\right)$ with $L_1={\mathbb{D}}_1^{*}{\mathbb{D}}_1,$$L_2={\mathbb{D}}_2^{*}{\mathbb{D}}_2,$ and $(x_0,y_0)\in {\mathbb{H}}_1\times H_2$ are chosen arbitrarily. Then, $\left\{(x_n,y_n)\right\}$ converges to $(x^{*},y^{*})\in \mathsf{\Gamma }.$

Proof. 

Algorithm (56) is a special case of algorithm (13) by taking ${\tau }_n=1$, $V{y}_n=y_n$ and ${\beta }_n=(1-{\alpha }_n).$ Therefore, the proof of this corollary follows directly from Theorem 1. □

Corollary 3 

(Chang et al. [1]). Suppose $\left(A1\right)$–$\left(A4\right)$ are satisfied and that $\mathsf{\Gamma }\ne \varnothing .$ Let $\left\{(x_n,y_n)\right\}$ defined by

$$\left\{\begin{array}{c}U=(1-{\eta }_n)I+{\eta }_n{\mathbb{T}}_1((1-{\zeta }_n)I+{\zeta }_n{\mathbb{T}}_1);\hfill \\ x_{n+1}=x_n-{\tau }_n\left(x_n-U{x}_n+{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n)\right),\forall n\ge 0.\hfill \\ \\ V=(1-{\eta }_n)I+{\eta }_n{\mathbb{T}}_2((1-{\zeta }_n)I+{\zeta }_n{\mathbb{T}}_2);\hfill \\ y_{n+1}=y_n-{\tau }_n\left(y_n-V{y}_n+{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n)\right),\forall n\ge 0.\hfill & \hfill \end{array}\right.$$

(57)

where $0<{\eta }_n<{\zeta }_n<\frac{1}{1+\sqrt{1+L^2}},$ $0<a<{\alpha }_n<1,$ and ${\tau }_n\in \left(0,\frac{2}{L_1+L_2}\right)$ with $L_1={\mathbb{D}}_1^{*}{\mathbb{D}}_1,$ $L_2={\mathbb{D}}_2^{*}{\mathbb{D}}_2,$ and $x_0\in {\mathbb{H}}_1$ are chosen arbitrarily. Then, $\left\{(x_n,y_n)\right\}$ converges to $(x^{*},y^{*})\in \mathsf{\Gamma }.$

Proof. 

Algorithm (57) is a special case of algorithm (13) by taking ${\alpha }_n=0.$ Therefore, the proof of this corollary follows directly from Theorem 1. □

5. Applications

This section provides applications for SEFPP.

5.1. Application to the SFP

We denote the solution set of the SFP (1) by ${\mathsf{\Gamma }}_1.$

In (4), if ${\mathbb{D}}_2=I$ (identity mapping), then the SEFPP reduces to (1). Furthermore, in algorithm (13), let $y_n:={\mathbb{T}}_1{\mathbb{D}}_1{x}_n,$ we therefore deduce the following result:

Corollary 4. 

Let ${\mathbb{H}}_j,j=1,2,$${\mathbb{K}}_j,j=1,2,$${\mathbb{D}}_1,$${\mathbb{D}}_1^{*},$$\mathbb{T}$ and $(\mathbb{T}-I)$ be as in Theorem 1. Let $\left\{x_n\right\}$ be defined by

$$\left\{\begin{array}{c}{x}_{n+1}=(1-{\alpha }_n)v_n+{\alpha }_n\mathbb{U}{v}_n;\hfill \\ v_n=(1-{\tau }_n)x_n+{\tau }_n\mathbb{U}{x}_n+{\tau }_n{\mathbb{D}}^{*}(\mathbb{T}\mathbb{D}{x}_n-\mathbb{D}{x}_n);\hfill \\ \mathbb{U}=(1-\eta )I+\eta \mathbb{T}\left(\right(1-\zeta )I+\zeta \mathbb{T});\hfill \end{array}\right.$$

(58)

where $0<\eta <\zeta <\frac{1}{1+\sqrt{1+L^2}},$ $0<a<{\alpha }_n<1,$ and ${\tau }_n\in \left(0,\frac{2}{L_1}\right)$ with $L_1={\mathbb{D}}_1^{*}{\mathbb{D}}_1,$ and $x_0\in {\mathbb{H}}_1$ are chosen arbitrarily. Then, $\left\{x_n\right\}$ converges weakly to $x^{*}\in {\mathsf{\Gamma }}_1.$

5.2. Application to the Split Variational Inequality Problem (SVIP)

The SVIP was introduced by Censor et al. [17] and it entails finding

$$\begin{array}{cc}\hfill x^{*}\in {\mathbb{K}}_1\mathrm{such}\mathrm{that}& 〈{\mathbb{T}}_1\left(x^{*}\right),x-x^{*}〉\ge 0,\forall \mathrm{x}\in {\mathbb{K}}_1,\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill \mathrm{and}{\mathrm{y}}^{*}={\mathbb{D}}_1{\mathrm{x}}^{*}\in {\mathbb{K}}_2\mathrm{solves}& 〈{\mathbb{T}}_2\left(y^{*}\right),y-y^{*}〉\ge 0,\forall \mathrm{y}\in {\mathbb{K}}_2,\hfill \end{array}$$

(60)

where ${\mathbb{T}}_j:{\mathbb{H}}_j\to {\mathbb{H}}_j,j=1,2,$ are some nonlinear mappings.

Equation (59) is called the variational inequality problem (VIP), and we denote its solution set by $VI({\mathbb{K}}_1,{\mathbb{T}}_1).$ Subsequently, the solution set of the SVIP is denoted by

$${\mathsf{\Gamma }}_2=\left\{({\mathrm{x}}^{*},{\mathrm{y}}^{*})\times \mathrm{VI}({\mathbb{K}}_1,{\mathbb{T}}_1)\times \mathrm{VI}({\mathbb{K}}_2,{\mathbb{T}}_2)\in {\mathbb{K}}_1\mathrm{such}\mathrm{that}{\mathbb{D}}_1{\mathrm{x}}^{*}={\mathbb{D}}_2{\mathrm{y}}^{*}\right\}.$$

(61)

Let $g_1(y,t):{\mathbb{K}}_1\times {\mathbb{K}}_2\to \mathbb{R}$ be defined by

$$g_1(y,t)=〈{\mathbb{T}}_{1}y,t-y〉,\forall t,y\in {\mathbb{K}}_1,$$

and $g_2(x,t):{\mathbb{K}}_2\times {\mathbb{K}}_2\to \mathbb{R}$ be defined by

$$g_2(x,t)=〈{\mathbb{T}}_{2}x,t-x〉,\forall x,t\in {\mathbb{K}}_2.$$

For $\lambda >0,$ the re-solvent operators of $g_1$ and $g_2$ are denoted by $R_{\lambda ,g_1}$ and $R_{\lambda ,g_2}$, and are defined by

$$R_{\lambda ,g_1}\left(q\right)=\left\{y\in {\mathbb{K}}_1:g_1(y,t)+\frac{1}{\lambda }〈t-y,y-q〉,\forall t\in {\mathbb{K}}_1\right\},$$

(62)

and

$$R_{\lambda ,g_2}\left(p\right)=\left\{x\in {\mathbb{K}}_2:g_2(x,t)+\frac{1}{\lambda }〈t-x,x-p〉,\forall t\in {\mathbb{K}}_2\right\},$$

(63)

respectively.

It was proved in [1] that $R_{\lambda ,g_1}$ and $R_{\lambda ,g_2}$ are quasi-pseudocontractive and 1-Lipschitzian mappings with $Fix\left(R_{\lambda ,g_1}\right)=VI({\mathbb{K}}_1,g_1)\ne \varnothing$ and $Fix\left(R_{\lambda ,g_2}\right)=VI({\mathbb{K}}_2,g_2)\ne \varnothing .$ Therefore, the SVIP is equivalent to the following split equality fixed-point problem:

$$Find{x}^{*}\in Fix\left(R_{\lambda ,g_1}\right)and{y}^{*}\in Fix\left(R_{\lambda ,g_2}\right)\mathrm{such}\mathrm{that}{\mathbb{D}}_1{\mathrm{x}}^{*}={\mathbb{D}}_2{\mathrm{y}}^{*}.$$

(64)

Hence, we have the following result: Suppose that

(B1)

$R_{\lambda ,g_1}$ and $R_{\lambda ,g_2}$ be defined as in (62) and (63);

(B2)

${\mathbb{D}}_j,j=1,2$ and ${\mathbb{D}}_j^{*},j=1,2$ as in Theorem 1.

(B3)

$(R_{\lambda ,g_1}-I)$ and $(R_{\lambda ,g_2}-I)$ are demiclosed at zero.

(B4)

Let $\mathbb{U}$ and $\mathbb{V}$ be defined as follows:

$$\left\{\begin{array}{c}\mathbb{U}=(1-\eta )I+\eta R_{\lambda ,g_1}((1-\zeta )I+\zeta R_{\lambda ,g_1}),\hfill \\ \mathbb{V}=(1-\eta )I+\eta R_{\lambda ,g_2}((1-\zeta )I+\zeta R_{\lambda ,g_2}),\hfill & \hfill \end{array}\right.$$

where $0<\eta <\zeta <\frac{1}{1+\sqrt{1+L^2}}.$

(B5)

Algorithm:Let $(x_n,y_n)\in {\mathbb{H}}_1\times {\mathbb{H}}_2$ be defined by

$$\left\{\begin{array}{c}{x}_{n+1}=(1-{\alpha }_n)v_n+{\alpha }_n\mathbb{U}{v}_n;\hfill \\ v_n=(1-{\tau }_n)x_n+{\tau }_{n}U{x}_n+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n),n\ge 0.\hfill \\ \\ y_{n+1}=(1-{\alpha }_n)w_n+{\alpha }_n\mathbb{V}{w}_n;\hfill \\ w_n=(1-{\tau }_n)y_n+{\tau }_n\mathbb{V}{y}_n+{\tau }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),\forall n\ge 0.\hfill & \hfill \end{array}\right.$$

(65)

where $(x_0,y_0)\in {\mathbb{H}}_1\times {\mathbb{H}}_2$ are chosen arbitrarily, $0<a<{\alpha }_n<1,$ and ${\tau }_n\in \left(0,\frac{2}{L_1+L_2}\right),$ with $L_1={\mathbb{D}}_1^{*}{\mathbb{D}}_1$ and $L_2={\mathbb{D}}_2^{*}{D}_2,$ respectively.

Corollary 5. 

Suppose that assumptions $\left(B1\right)-\left(B5\right)$ are satisfied and that ${\mathsf{\Gamma }}_2\ne \varnothing .$ Then, the sequence $\left\{(x_n,y_n)\right\}$ generated by (65) converges to the solution of SVIP.

5.3. Application to the Split Convex Minimization Problem (SCMP)

Let $\mathbb{M}:{\mathbb{K}}_1\to \mathbb{R}$ and $\mathbb{N}:{\mathbb{K}}_2\to \mathbb{R}$ be lower semi-continuous and proper convex functions. The SCMP is formulated as follows:

$$\mathbb{M}\left(x^{*}\right)={\displaystyle \underset{x\in {\mathbb{K}}_1}{min}}\mathbb{M}\left(x\right),and\mathbb{N}\left(y^{*}\right)={\displaystyle \underset{y\in {\mathbb{K}}_2}{min}}\mathbb{N}\left(y\right)\mathrm{such}\mathrm{that}{\mathbb{D}}_1{\mathrm{x}}^{*}={\mathbb{D}}_2{\mathrm{y}}^{*}.$$

We denote the solution set of the SCMP by

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_3=& \{({\mathrm{x}}^{*},{\mathrm{y}}^{*})\in {\mathbb{K}}_1\times {\mathbb{K}}_2,\mathbb{M}\left({\mathrm{x}}^{*}\right)={\displaystyle \underset{\mathrm{x}\in {\mathbb{K}}_1}{min}}\mathbb{M}\left(\mathrm{x}\right),\mathrm{and}\mathbb{N}\left({\mathrm{y}}^{*}\right)={\displaystyle \underset{\mathrm{y}\in {\mathbb{K}}_2}{min}}\mathbb{N}\left(\mathrm{y}\right)\hfill \\ \hfill & \mathrm{such}\mathrm{that}{\mathbb{D}}_1{\mathrm{x}}^{*}={\mathbb{D}}_2{\mathrm{y}}^{*}\}.\hfill \end{array}$$

(66)

Let $h(x,y):{\mathbb{K}}_1\times {\mathbb{K}}_1\to \mathbb{R}$ and $l(r,t):{\mathbb{K}}_2\times {\mathbb{K}}_2\to \mathbb{R}$ be defined by $h(x,y)=\mathbb{M}\left(x\right)-\mathbb{N}\left(y\right)$ and $l(r,t)=\mathbb{M}\left(r\right)-\mathbb{N}\left(t\right),$ respectively. For arbitrary $\lambda >0,$ Chang et al. [1] defined the re-solvent operators of $\lambda ,$ h and l as follows:

$$R_{\lambda ,h}\left(x\right)=\left\{t\in C:f(t,y)+\frac{1}{\lambda }〈y-t,t-x〉\right\},$$

and

$$R_{\lambda ,l}\left(y\right)=\left\{t\in C:f(t,x)+\frac{1}{\lambda }〈x-t,t-y〉\right\}.$$

It was proved in [1] that $Fix\left(R_{\lambda ,h}\right)=\left\{\mathbb{M}\left(x^{*}\right)={\displaystyle \underset{x\in {\mathbb{K}}_1}{min}}\mathbb{M}\left(x\right)\right\},$ and $Fix\left(R_{\lambda ,l}\right)=\left\{\mathbb{N}\left(y^{*}\right)={\displaystyle \underset{y\in {\mathbb{K}}_2}{min}}\mathbb{N}\left(y\right)\right\}.$ Therefore, the SCMP for $\mathbb{M}$ and $\mathbb{N}$ is equivalent to the following SEFPP:

$${\mathsf{\Gamma }}_3=\{find{x}^{*}\in Fix\left(R_{\lambda ,h}\right)and{y}^{*}\in Fix\left(R_{\lambda ,l}\right)\mathrm{such}\mathrm{that}{\mathbb{D}}_1{\mathrm{x}}^{*}={\mathbb{D}}_2{\mathrm{y}}^{*}\}.$$

(67)

It was proved in [1] that $R_{\lambda ,h}$ and $R_{\lambda ,l}$ are firmly nonexpansive with $Fix\left(R_{\lambda ,h}\right)\ne \varnothing$ and $Fix\left(R_{\lambda ,k}\right)\ne \varnothing ,$ hence, we deduce the following results from Theorem 1: Suppose that

(C1)

$R_{\lambda ,h}$ and $R_{\lambda ,l}$ be defined as above;

(C2)

${\mathbb{D}}_j,j=1,2$ and ${\mathbb{D}}_j^{*},j=1,2$ as in Theorem 1;

(C3)

$(R_{\lambda ,h}-I)$ and $(R_{\lambda ,l}-I)$ are demiclosed at zero;

(C4)

Let $\mathbb{U}$ and $\mathbb{V}$ be defined as

$$\left\{\begin{array}{c}\mathbb{U}=(1-\eta )I+\eta R_{\lambda ,h}((1-\zeta )I+\zeta R_{\lambda ,h}),\hfill \\ \mathbb{V}=(1-\eta )I+\eta R_{\lambda ,l}((1-\zeta )I+\zeta R_{\lambda ,l}),\hfill & \hfill \end{array}\right.$$

(68)

where $0<\eta <\zeta <\frac{1}{1+\sqrt{1+L^2}}.$

(C5)

Algorithm: Let $(x_n,y_n)\in {\mathbb{H}}_1\times {\mathbb{H}}_2,$ be defined as

$$\left\{\begin{array}{c}{x}_{n+1}=(1-{\alpha }_n)v_n+{\alpha }_n\mathbb{U}{v}_n,\hfill \\ v_n=(1-{\tau }_n)x_n+{\tau }_n\mathbb{U}{x}_n+{\tau }_n{\mathbb{D}}_1^{*}({\mathbb{D}}_2{y}_n-{\mathbb{D}}_1{x}_n),\forall n\ge 0;\hfill \\ \\ y_{n+1}=(1-{\alpha }_n)w_n+{\alpha }_n\mathbb{V}{w}_n,\hfill \\ w_n=(1-{\tau }_n)y_n+{\tau }_n\mathbb{V}{y}_n+{\tau }_n{\mathbb{D}}_2^{*}({\mathbb{D}}_1{x}_n-{\mathbb{D}}_2{y}_n),\forall n\ge 0;\hfill & \hfill \end{array}\right.$$

(69)

where $x_0\in {\mathbb{H}}_1$ and $y_0\in {\mathbb{H}}_2$ are chosen arbitrarily, $0<a<{\alpha }_n<1,$ and ${\tau }_n\in \left(0,\frac{2}{L_1+L_2}\right),$ where $L_1={\mathbb{D}}_1^{*}{\mathbb{D}}_1$ and $L_2={\mathbb{D}}_2^{*}{\mathbb{D}}_2,$ respectively.

Corollary 6. 

Suppose that assumptions $\left(C1\right)-\left(C5\right)$ are satisfied and that ${\mathsf{\Gamma }}_3\ne \varnothing .$ Then, the sequence $\left\{(x_n,y_n)\right\}$ generated by (69) converges weakly to the solution of the SCMP.

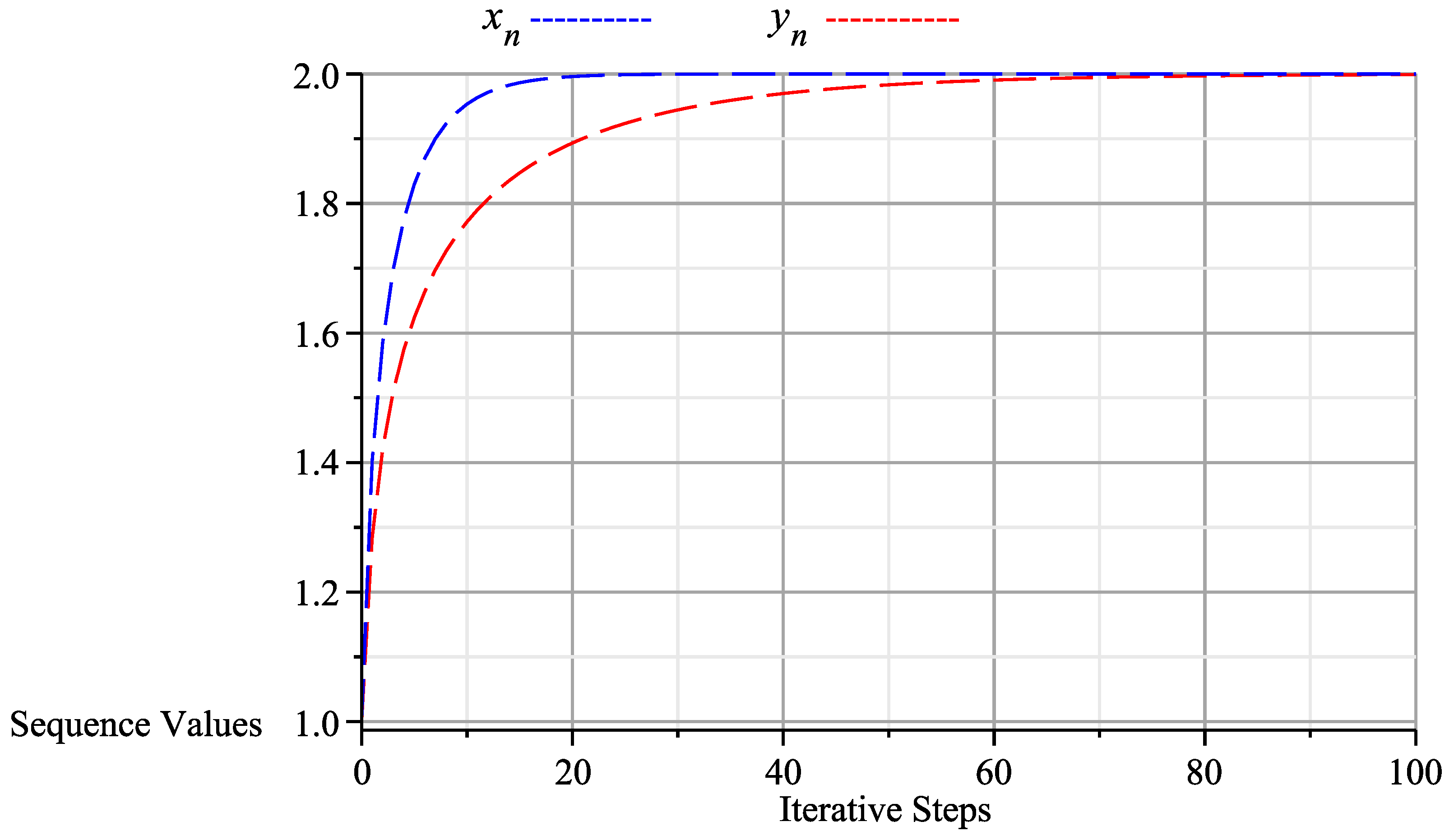
6. Numerical Examples

This section gives numerical examples that illustrate our results.

Example 1. 

In Theorem 1, let $H_1=\mathbb{R},$$C,Q\subseteq (0,\infty ),$ and let $D_{1}x=\frac{x}{2}$, $D_{2}y=\frac{y}{3},$ then $D_1=D_1^{*}=\frac{1}{2}$ and $D_2=D_2^{*}=\frac{1}{3}, respectively$. Define $T:C\to \mathbb{R}$ and $S:Q\to \mathbb{R}$ by $Tx=\frac{x+4}{2},\forall x\in C$ and $Sy=\frac{y^2+2}{y+4}$, for all $y\in Q.$ Clearly, T and S are quasi-pseudo-demicontractive mappings with Fix(T) = 4 and Fix(S) = $\frac{1}{2}$, and (I-T) and (I-S) are demiclosed at zero. In algorithm (11), let $\eta =\frac{1}{2},$ $\xi =\frac{1}{5},$${\tau }_n=\frac{1}{7},$ ${\alpha }_n=\frac{1}{6},$ clearly, these parameters satisfy the hypothesis of Theorem 1. Setting the number of iterations to 100 by using Maple, we obtain the following results in

Table 1. Numerical results of algorithm (13) starting with the initial values $x_1=1$ and $y_1=1,$ which shows that $(x_n,y_n)$ converges to (4, 1/2).

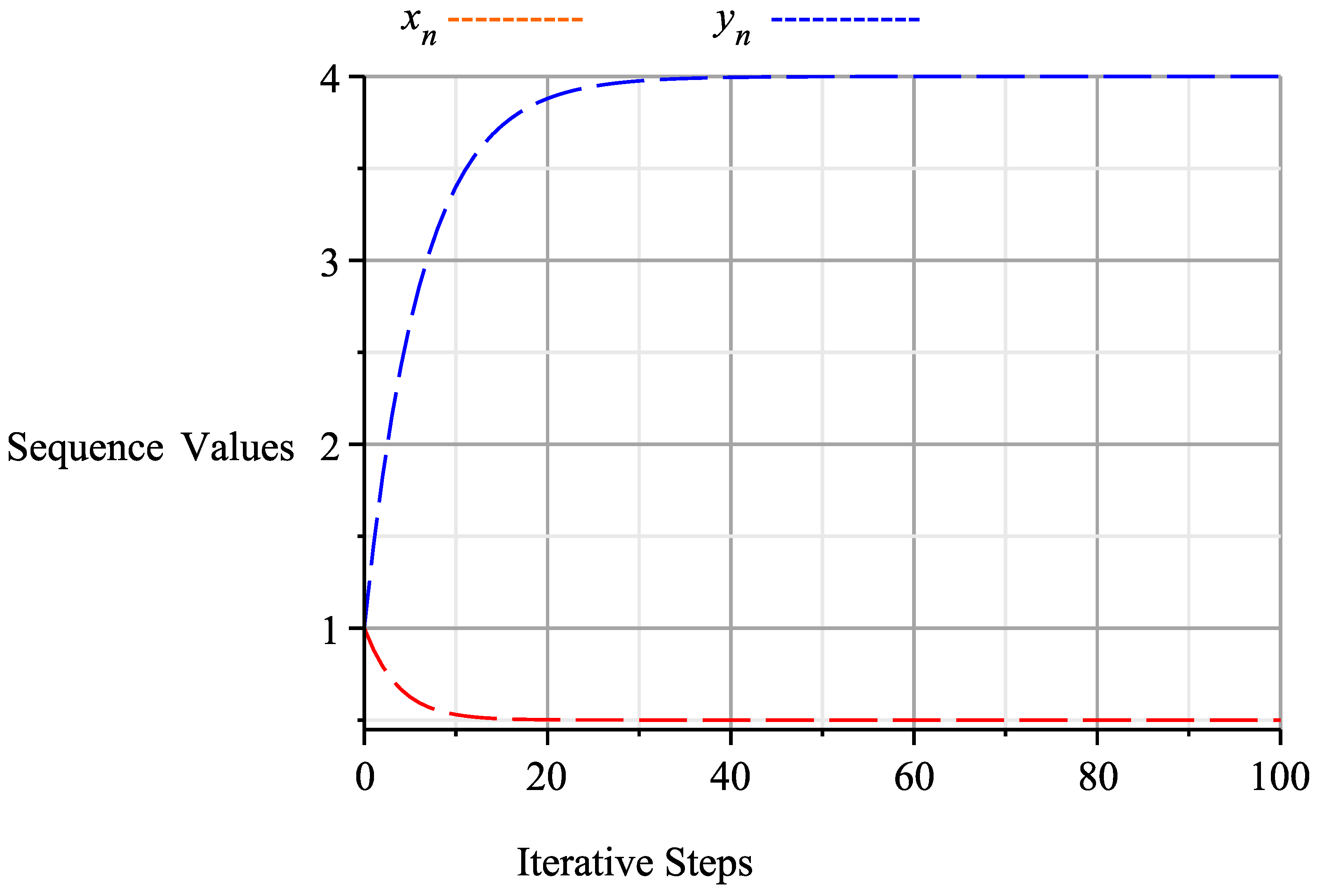
n	${\mathit{x}}_{\mathit{n}}$	${\mathit{y}}_{\mathit{n}}$
1	1.000000000	1.000000000
2	1.446428571	0.8831268924
3	1.826424319	0.7916797163
.	.	.
.	.	.
73	.	0.5000000002
74	.	0.5000000000
.	.	.
98	3.999999582	0.5000000000
99	3.999999644	0.5000000000
100	3.999999697	0.5000000000

and Figure 1:

Example 2. 

In Theorem 1, let $H_1=\mathbb{R},$$C,Q\subseteq (0,\infty ),$ and let $Ax=\frac{x}{2}$, $By=\frac{y}{3},$ then $A=A^{*}=\frac{1}{2}$ and $B=B^{*}=\frac{1}{3}, respectively$. Define $T:C\to \mathbb{R}$ and $S:Q\to \mathbb{R}$ by

$Tx=\frac{x^5+6}{x^4+2},\forall x\in C$ and $Sy=\frac{y^3+4}{y^2+y}$, for all $y\in Q.$ Clearly, T and S are quasi-pseudo-demicontractive mappings with Fix(T) = 2 and Fix(S) = 2, and (I-T) and (I-S) are demiclosed at zero. In algorithm (13), choose $\eta =\frac{1}{2},$ $\xi =\frac{1}{5},$ ${\tau }_n=\frac{1}{6},$ ${\alpha }_n=\frac{1}{7}$. Clearly, these parameters satisfy the hypothesis of Theorem (1). Setting the number of iterations to 1000 by using Maple, we obtain the following results in

Table 2. Numerical results of algorithm (13) starting with the initial values $x_1=1$ and $y_1=1,$ which shows that $(x_n,y_n)$ converges to (2,2).

n	${\mathit{x}}_{\mathit{n}}$	${\mathit{y}}_{\mathit{n}}$
1	1.000000000	1.000000000
2	1.402141502	1.283490816
3	1.584779961	1.420942750
.	.	.
.	.	.
.	.	.
80	1.999999998	.
81	1.999999999	.
.	.	.
98	1.999999999	1.998915702
99	1.999999999	1.998975310
100	1.999999999	1.999031634

and Figure 2:

7. Conclusions

It is generally known that in order to solve the split equality fixed-point problem (SEFPP), it is necessary to compute the norm of bounded and linear operators, which is a challenging task in real life. To address this issue, we studied the SEFPP involving the class of quasi-pseudocontractive mappings in Hilbert spaces and constructed novel algorithms in this regard, and we proved the algorithms’ convergences both with and without prior knowledge of the operator norm for bounded and linear mappings. Additionally, we gave applications and numerical examples of our findings as discussed in the Table 1 and Table 2 and graphs in Figure 1 and Figure 2, respectively. The discoveries highlighted in this work contribute to the generalization of various well-known findings documented in the literature. Furthermore, quasi-pseudocontractive mappings encompass various types, including quasi-nonexpansive, demicontractive, and directed mappings.

The SEFPP explored in our study is highly general; as a special example, it covers a wide range of problems, including split fixed points, split equality, and split feasibility problems. Our findings not only complement and generalize the findings in Chang et al. [1], Moudafi [7,8], and Chang et al. [14], but also offer a cohesive framework for researching further problems pertaining to the SEFPP.

Finally, strong convergence was obtained by imposing the semi-compactness condition. This compactness condition appears very strong as some mappings are not semi-compact; therefore, new research can be carried out to prove the strong convergence results without imposing the compactness condition.