Efficiency of a New Iterative Algorithm Using Fixed-Point Approach in the Settings of Uniformly Convex Banach Spaces
Abstract
:1. Introduction and Motivation
2. Preliminaries
- (a)
- If τ is enhanced with Chatterjea–Suzuki–C condition and then
- (b)
- If τ is enhanced with the condition of Chatterjea–Suzuki–C, then is closed. Moreover, if ℜ is strictly convex and ℵ is convex, then is also convex.
- (c)
- If τ is enhanced with the condition namely Chatterjea–Suzuki–C, then for any .
- (d)
- If τ is enhanced with Chatterjea–Suzuki–C condition, is weakly convergent to a, andthen provided that ℜ satisfies Opial’s condition.
Iterative Algorithms
3. Main Results
4. Application to Caputo Fractional Differential Equation
5. Numerical Simulation
- .
- τ does not satisfy condition (C).
- τ satisfies condition Chatterjea–Suzuki–C.
- Since implies that τ possesses a single fixed point, and .
- If we take and then τ does not satisfies condition (C).
- To prove the Chatterjea–Suzuki–C condition, we have 4 cases:
- (Case-1) If then, . Hence,
- (Case-2) If then, .
- (Case-3) If then, .
- (Case-4) If then, .
6. Conclusions and Further Discussions
- Compared to other schemes in the literature, our approach demonstrates superior convergence to a fixed point. This means that it reaches a stable solution more efficiently and effectively.
- Our proposed iterative scheme stands out by utilizing two scalar sequences , instead of three. This unique approach leads to better convergence in comparison with various other iterative techniques described in the literature.
- The proposed iterative scheme has been proven to be stable when it comes to initial points and sequences of scalars. This stability is demonstrated by the data presented in tabular and graphical forms, which clearly shows the consistent and reliable performance of the scheme.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tassaddiq, A.; Ahmed, W.; Zaman, S.; Raza, A.; Islam, U.; Nantomah, K. A Modified Iterative Approach for Fixed Point Problem in Hadamard Spaces. J. Funct. Spaces 2024, 1, 5583824. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Kanwal, S.; Perveen, S.; Srivastava, R. Fixed points of single-valued and multi-valued mappings in sb-metric spaces. J. Inequalities Appl. 2022, 1, 85. [Google Scholar] [CrossRef]
- Khachay, M.Y.; Ogorodnikov, Y.Y. Efficient approximation of the capacitated vehicle routing problem in a metric space of an arbitrary fixed doubling dimension. InDoklady Math. 2020, 102, 324–329. [Google Scholar] [CrossRef]
- Khamsi, M.A.; Misane, D. Fixed point theorems in logic programming. Ann. Math. Artif. Intell. 1997, 21, 231–243. [Google Scholar] [CrossRef]
- Camelo, M.; Papadimitriou, D.; Fàbrega, L.; Vilà, P. Geometric routing with word-metric spaces. IEEE Commun. Lett. 2014, 18, 2125–2128. [Google Scholar] [CrossRef]
- Tassaddiq, A. General escape criteria for the generation of fractals in extended Jungck–Noor orbit. Math. Comput. Simul. 2022, 196, 1–14. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Kalsoom, A.; Rashid, M.; Sehr, K.; Almutairi, D.K. Generating Geometric Patterns Using Complex Polynomials and Iterative Schemes. Axioms 2024, 13, 204. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Tanveer, M.; Azhar, M.; Lakhani, F.; Nazeer, W.; Afzal, Z. Escape criterion for generating fractals using Picard–Thakur hybrid iteration. Alex. Eng. J. 2024, 100, 331–339. [Google Scholar] [CrossRef]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Picard, É. Mémoire sur la théorie des équations aux dérivées partielles et la méthode des approximations successives. J. Mathématiques Pures Appliquées 1890, 6, 145–210. [Google Scholar]
- Ishikawa, S. Fixed points by a new iteration method. Proc. Am. Math. Soc. 1974, 44, 147–150. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. J. Nonlinear Convex Anal. 2007, 1, 61. [Google Scholar]
- Abbas, M.; Nazir, T. Some new faster iteration process applied to constrained minimization and feasibility problems. Mat. Vestn. 2014, 66, 223–234. [Google Scholar]
- Thakur, B.S.; Thakur, D.; Postolache, M. A new iterative scheme for numerical reckoning fixed points of Suzuki’s generalized nonexpansive mappings. Appl. Math. Comput. 2016, 275, 147–155. [Google Scholar] [CrossRef]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Konwar, N.; Srivastava, R.; Debnath, P.; Srivastava, H.M. Some new results for a class of multivalued interpolative Kannan-type contractions. Axioms 2022, 11, 76. [Google Scholar] [CrossRef]
- Debnath, P.; Srivastava, H.M. New extensions of Kannan’s and Reich’s fixed point theorems for multivalued maps using Wardowski’s technique with application to integral equations. Symmetry 2020, 12, 1090. [Google Scholar] [CrossRef]
- Debnath, P.; Mitrović, Z.D.; Srivastava, H.M. Fixed points of some asymptotically regular multivalued mappings satisfying a Kannan-type condition. Axioms 2021, 10, 24. [Google Scholar] [CrossRef]
- Suzuki, T. Fixed point theorems and convergence theorems for some generalized nonexpansive mappings. J. Math. Anal. Appl. 2008, 340, 1088–1095. [Google Scholar] [CrossRef]
- Ahmad, J.; Ullah, K.; George, R. Numerical algorithms for solutions of nonlinear problems in some distance spaces. AIMS Math. 2023, 8, 8460–8477. [Google Scholar] [CrossRef]
- Ullah, K.; Ahmad, J.; Mlaiki, N. On Noor iterative process for multi-valued nonexpansive mappings with application. Int. J. Math. Anal. 2019, 13, 293–307. [Google Scholar] [CrossRef]
- Ullah, K.; Arshad, M. Numerical reckoning fixed points for Suzuki’s generalized nonexpansive mappings via new iteration process. Filomat 2018, 32, 187–196. [Google Scholar] [CrossRef]
- Khatoon, S.; Uddin, I. Convergence analysis of modified Abbas iteration process for two G-nonexpansive mappings. Rend. Circ. Mat. Palermo Ser. 2 2021, 70, 31–44. [Google Scholar] [CrossRef]
- Wairojjana, N.; Pakkaranang, N.; Pholasa, N. Strong convergence inertial projection algorithm with self-adaptive step size rule for pseudomonotone variational inequalities in Hilbert spaces. Demonstr. Math. 2021, 54, 110–128. [Google Scholar] [CrossRef]
- Hammad, H.A.; Rehman, H.U.; Zayed, M. Applying faster algorithm for obtaining convergence, stability, and data dependence results with application to functional-integral equations. AIMS Math. 2022, 7, 19026–19056. [Google Scholar] [CrossRef]
- Hammad, H.A.; Rehman, H.U.; De la Sen, M. A novel four-step iterative scheme for approximating the fixed point with a supportive application. Inf. Sci. Lett. 2021, 10, 333–339. [Google Scholar]
- Hammad, H.A.; Rehman, H.U.; De la Sen, M. Shrinking projection methods for accelerating relaxed inertial Tseng-type algorithm with applications. Math. Probl. Eng. 2020, 2020, 7487383. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, M.; Lin, Y.; Jiang, D. An efficient technique based on least-squares method for fractional integro-differential equations. Alex. Eng. J. 2023, 64, 97–105. [Google Scholar] [CrossRef]
- Ahmad, J.; Ullah, K.; Hammad, H.A.; George, R.A. Solution of a fractional differential equation via novel fixed-point approaches in Banach spaces. AIMS Math. 2023, 8, 12657–12670. [Google Scholar] [CrossRef]
- Browder, F.E. Nonexpansive nonlinear operators in a Banach space. Proc. Natl. Acad. Sci. USA 1965, 54, 1041–1044. [Google Scholar] [CrossRef]
- Göhde, D. Zum prinzip der kontraktiven Abbildung. Math. Nach. 1965, 30, 251–258. [Google Scholar] [CrossRef]
- Senter, H.F.; Dotson, W.G. Approximating fixed points of nonexpansive mappings. Proc. Am. Math. Soc. 1974, 44, 375–380. [Google Scholar] [CrossRef]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Amer. Math. Soc. 1967, 73, 591–597. [Google Scholar] [CrossRef]
- Clarkson, J.A. Uniformly convex spaces. Trans. Am. Math. Soc. 1936, 40, 396–414. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Fixed Point Theory for Lipschitzian-Type Mappings with Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Takahashi, W. Nonlinear functional analysis. In Fixed Point Theory and its Applications; Yokohama Publishers: Yokohama, Japan, 2000. [Google Scholar]
- Schu, J. Weak and strong convergence to fixed points of asymptotically nonexpansive mappings. Bull. Aust. Math. Soc. 1991, 43, 153–159. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ali, A.; Hussain, A.; Arshad, M.U.; Al-Sulami, H.A. A certain class of θL-type non-linear operators and some related fixed point results. J. Nonlinear Var. Anal. 2022, 6, 69–87. [Google Scholar]
- Srivastava, H.M.; Deep, A.; Abbas, S.; Hazarika, B. Solvability for a class of generalized functional-integral equations by means of Petryshyn’s fixed point theorem. J. Nonlinear Convex Anal. 2021, 22, 2715–2737. [Google Scholar]
- Srivastava, H.M.; Shehata, A.; Moustafa, S.I. Some fixed point theorems for F(ψ,φ)-contractions and their application to fractional differential equations. Russ. J. Math. Phys. 2020, 27, 385–398. [Google Scholar] [CrossRef]
- Hammad, H.A.; Zayed, M. Solving a system of differential equations with infinite delay by using tripled fixed point techniques on graphs. Symmetry 2022, 14, 1388. [Google Scholar] [CrossRef]
- Karapınar, E.; Taş, K. Generalized (C)-conditions and related fixed point theorems. Comput. Math. Appl. 2011, 61, 3370–3380. [Google Scholar] [CrossRef]

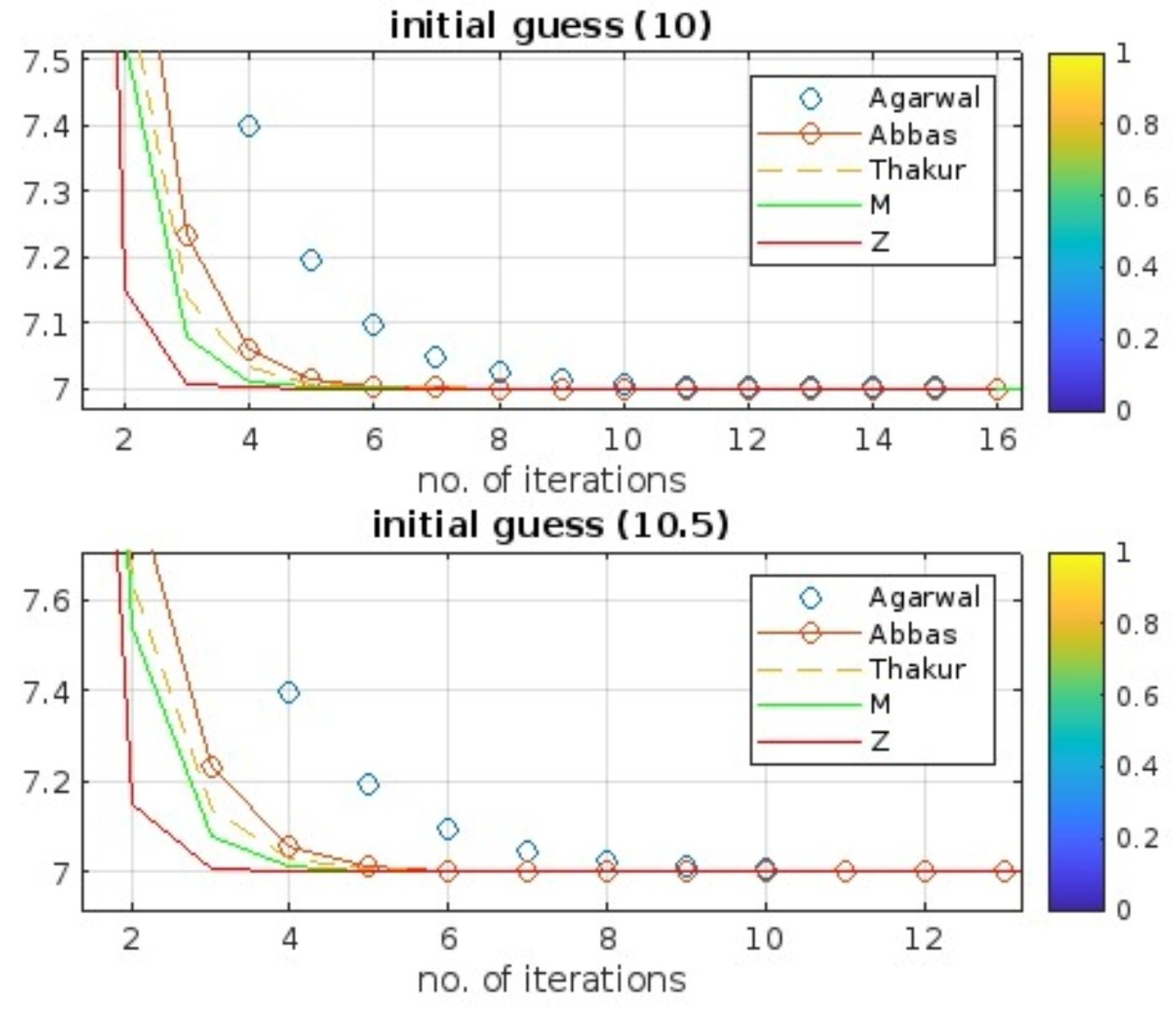
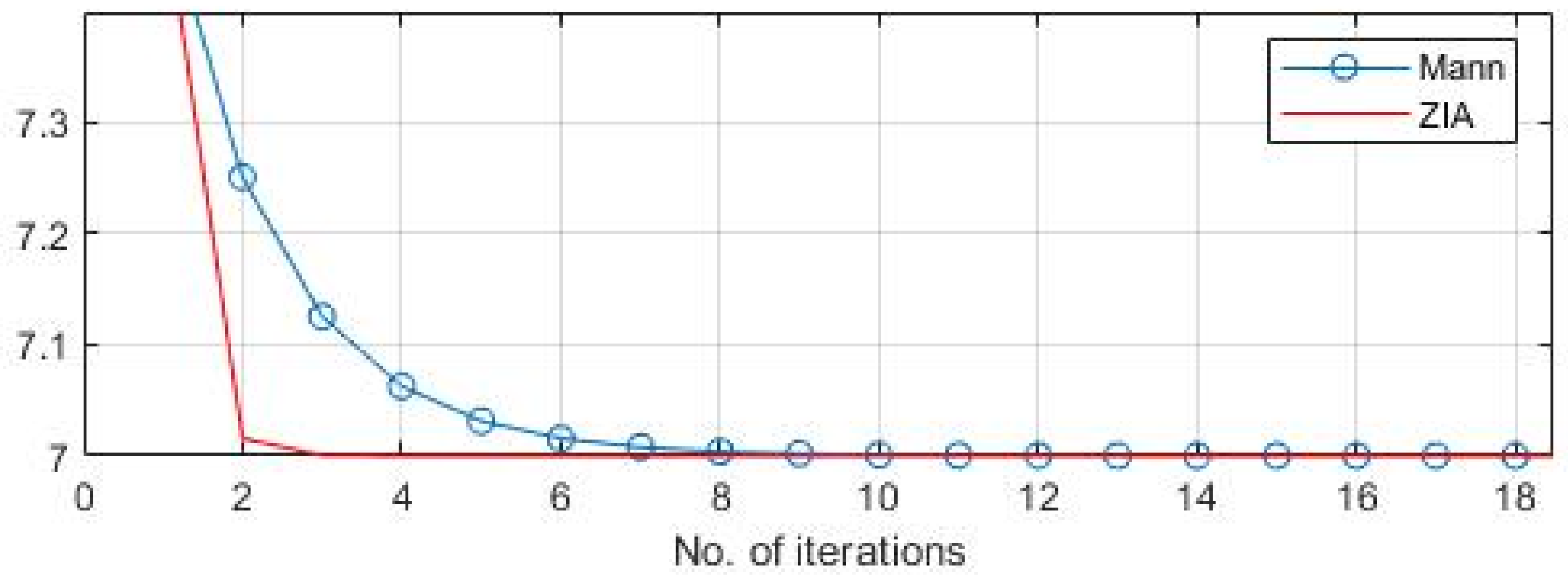
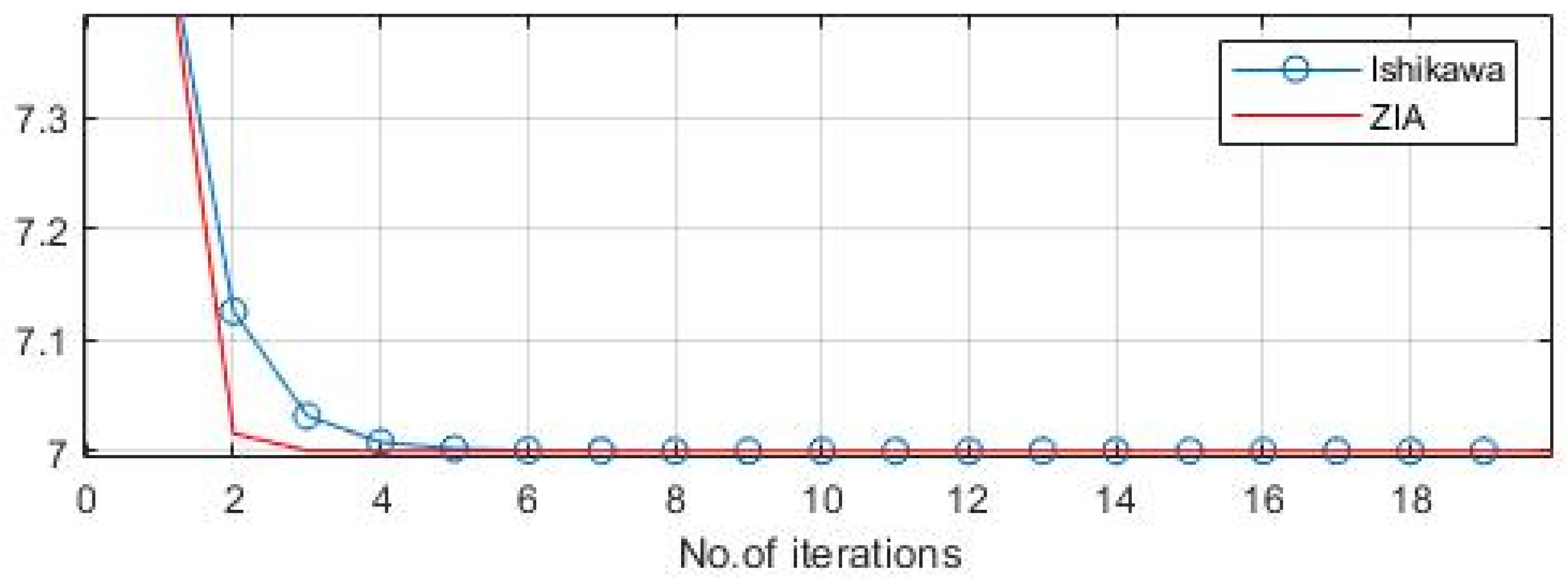
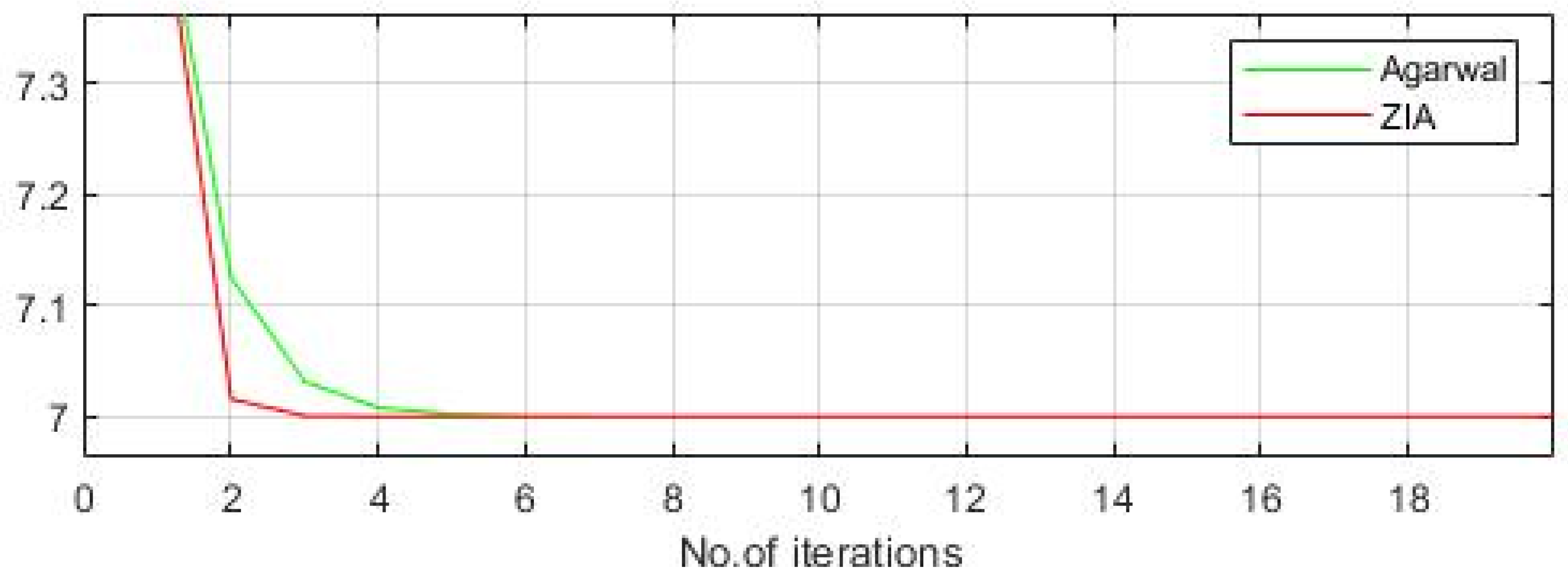

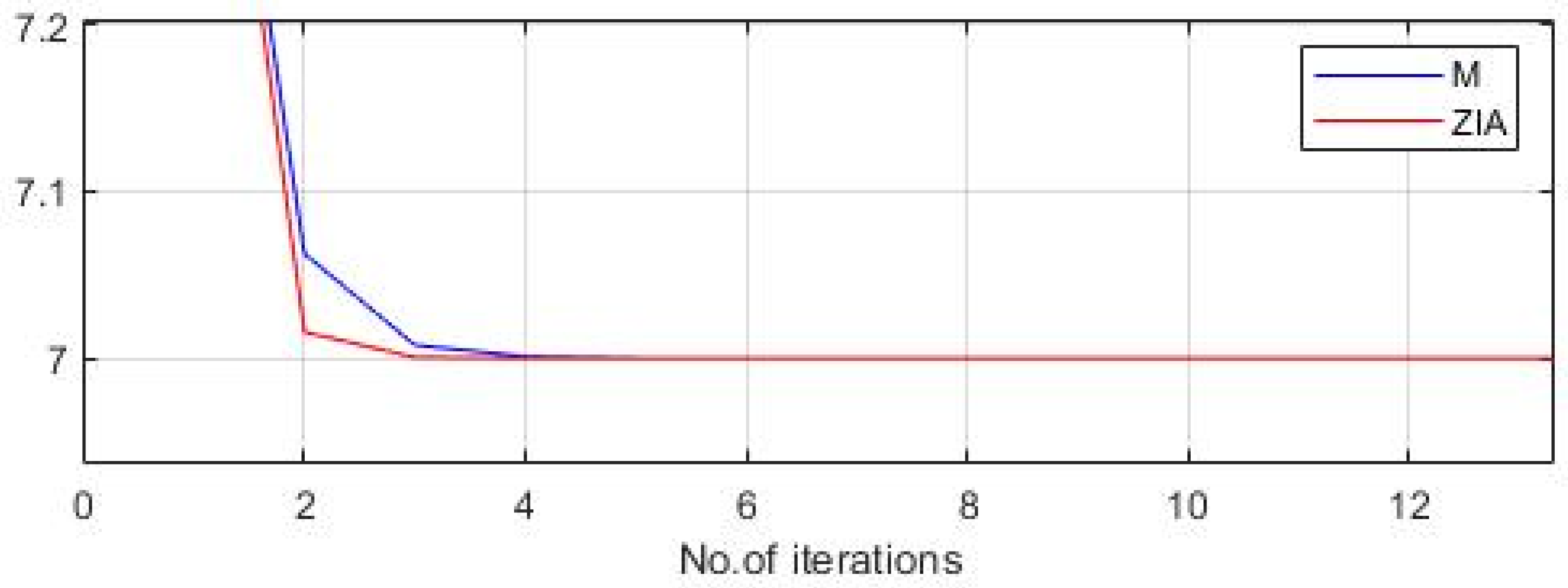
| n | Z-Iterative Algorithm | M-Iteration [22] | Abbas and Nazir [13] | Agarwal et al. [35] |
|---|---|---|---|---|
| 1 | 7.500000000000000 | 7.500000000000000 | 7.500000000000000 | 7.500000000000000 |
| 2 | 7.015655895074208 | 7.062501507040895 | 7.063055266033983 | 7.125247148819911 |
| 3 | 7.000489920215704 | 7.007812726243000 | 7.007939333106386 | 7.031354890441289 |
| 4 | 7.000015325339965 | 7.000976592259887 | 7.000998266519663 | 7.007846573196534 |
| 5 | 7.000000479276985 | 7.000122074107349 | 7.000125392389422 | 7.001963118312863 |
| 6 | 7.000000014986078 | 7.000015259267889 | 7.000015738891011 | 7.000491063737875 |
| 7 | 7.000000000468528 | 7.000001907408786 | 7.000001974395973 | 7.000122821832627 |
| 8 | 7.000000000014647 | 7.000000238426120 | 7.000000247574630 | 7.000030716651000 |
| 9 | 7.000000000000458 | 7.000000029803267 | 7.000000031033345 | 7.000007681438493 |
| 10 | 7.000000000000014 | 7.000000003725408 | 7.000000003888928 | 7.000001920828534 |
| 11 | 7.000000000000000 | 7.000000000465675 | 7.000000000487228 | 7.000000480304887 |
| 12 | 7.000000000000000 | 7.000000000058209 | 7.000000000061030 | 7.000000120096814 |
| 13 | 7.000000000000000 | 7.000000000007276 | 7.000000000007643 | 7.000000030028581 |
| 14 | 7.000000000000000 | 7.000000000000909 | 7.000000000000957 | 7.000000007508084 |
| 15 | 7.000000000000000 | 7.000000000000114 | 7.000000000000120 | 7.000000001877224 |
| 16 | 7.000000000000000 | 7.000000000000014 | 7.000000000000015 | 7.000000000469351 |
| 17 | 7.000000000000000 | 7.000000000000002 | 7.000000000000002 | 7.000000000117347 |
| 18 | 7.000000000000000 | 7.000000000000000 | 7.000000000000001 | 7.000000000029339 |
| 19 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000007335 |
| 21 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000001833 |
| 22 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000000458 |
| 23 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000000115 |
| 25 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000001833 |
| 26 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000000028 |
| 27 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000000007 |
| 28 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000000002 |
| 29 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 |
| 30 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 | 7.000000000000000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, R.; Ahmed, W.; Tassaddiq, A.; Alotaibi, N. Efficiency of a New Iterative Algorithm Using Fixed-Point Approach in the Settings of Uniformly Convex Banach Spaces. Axioms 2024, 13, 502. https://doi.org/10.3390/axioms13080502
Srivastava R, Ahmed W, Tassaddiq A, Alotaibi N. Efficiency of a New Iterative Algorithm Using Fixed-Point Approach in the Settings of Uniformly Convex Banach Spaces. Axioms. 2024; 13(8):502. https://doi.org/10.3390/axioms13080502
Chicago/Turabian StyleSrivastava, Rekha, Wakeel Ahmed, Asifa Tassaddiq, and Nouf Alotaibi. 2024. "Efficiency of a New Iterative Algorithm Using Fixed-Point Approach in the Settings of Uniformly Convex Banach Spaces" Axioms 13, no. 8: 502. https://doi.org/10.3390/axioms13080502
APA StyleSrivastava, R., Ahmed, W., Tassaddiq, A., & Alotaibi, N. (2024). Efficiency of a New Iterative Algorithm Using Fixed-Point Approach in the Settings of Uniformly Convex Banach Spaces. Axioms, 13(8), 502. https://doi.org/10.3390/axioms13080502








