The Geometry of Dynamic Time-Dependent Best–Worst Choice Pairs
Abstract
1. Introduction
2. Materials and Methods
2.1. Best–Worst Discrete Choice Experiments
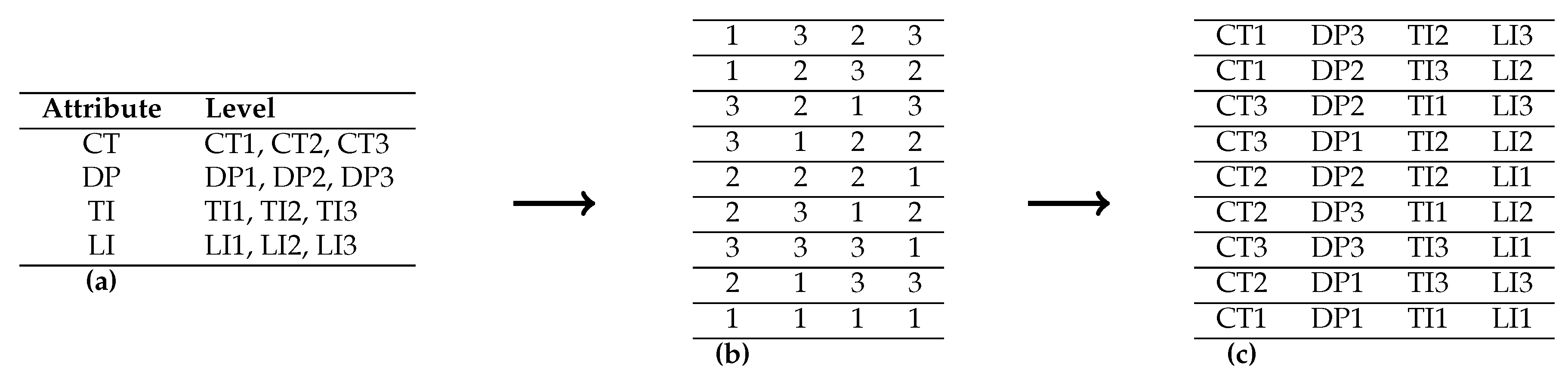
2.2. Design of Experiment
2.3. Utility Function
3. Theory of Choice Transition and Classification
3.1. Transition Probability
3.2. Network Classification Methodology
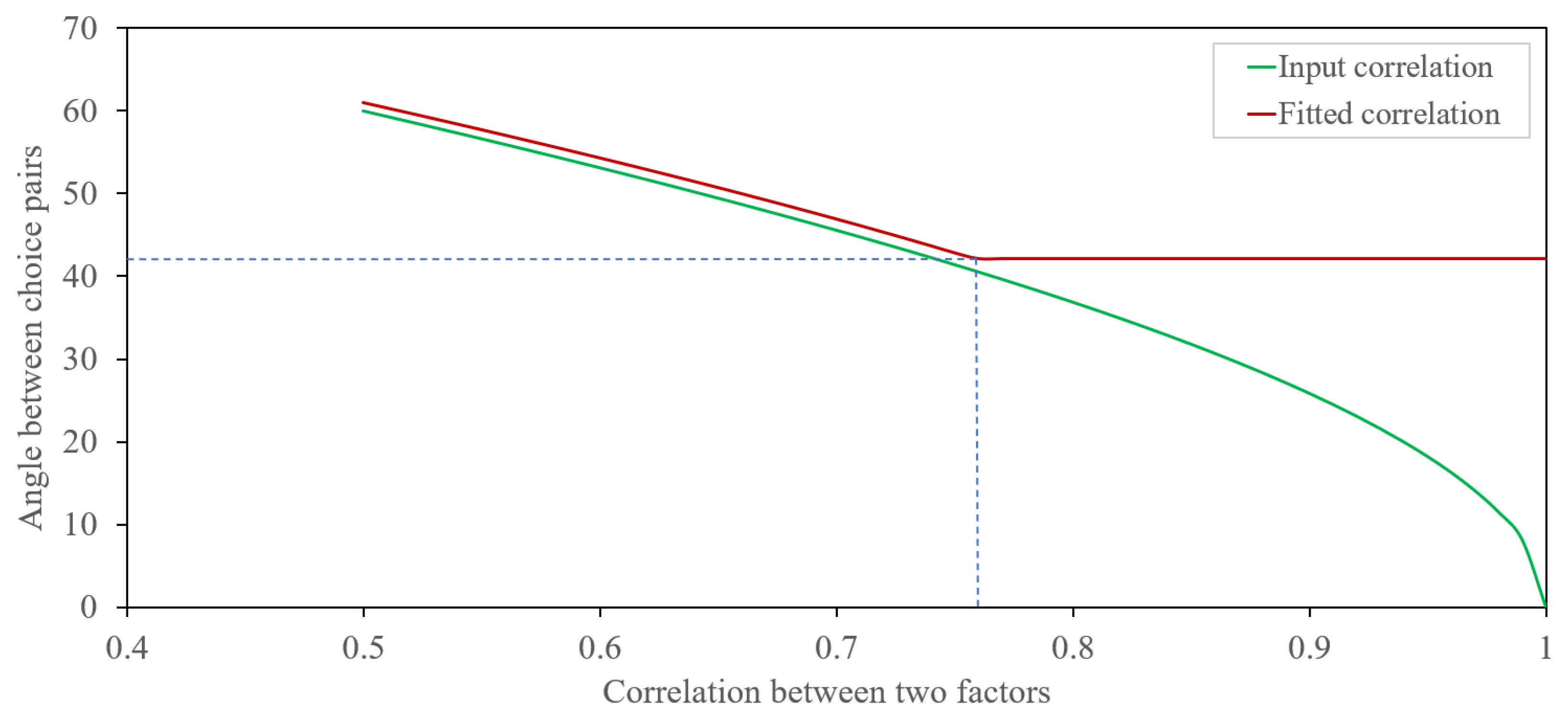
3.3. Convex Geometry Method for Classification
3.4. -Means Method for Classification
4. Results
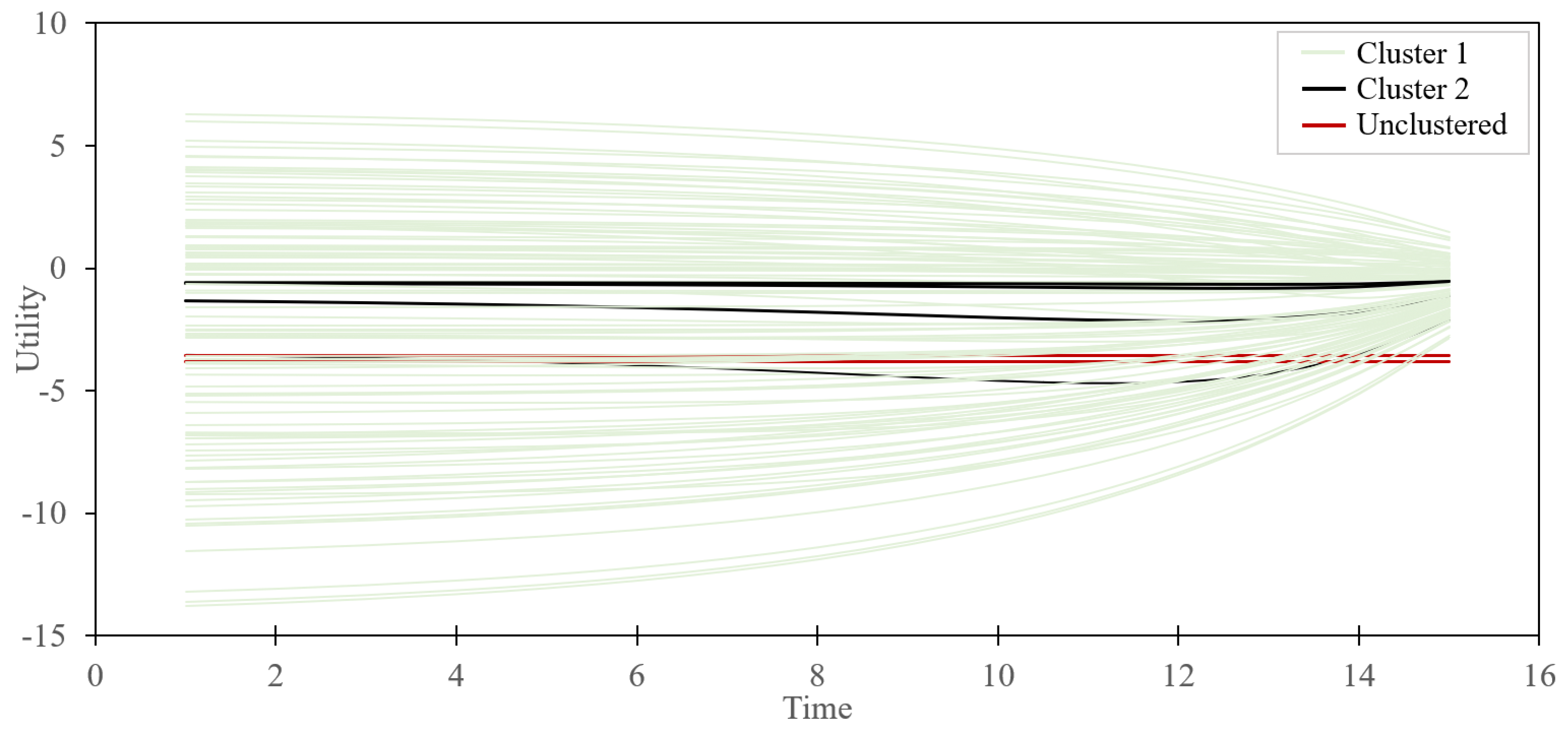
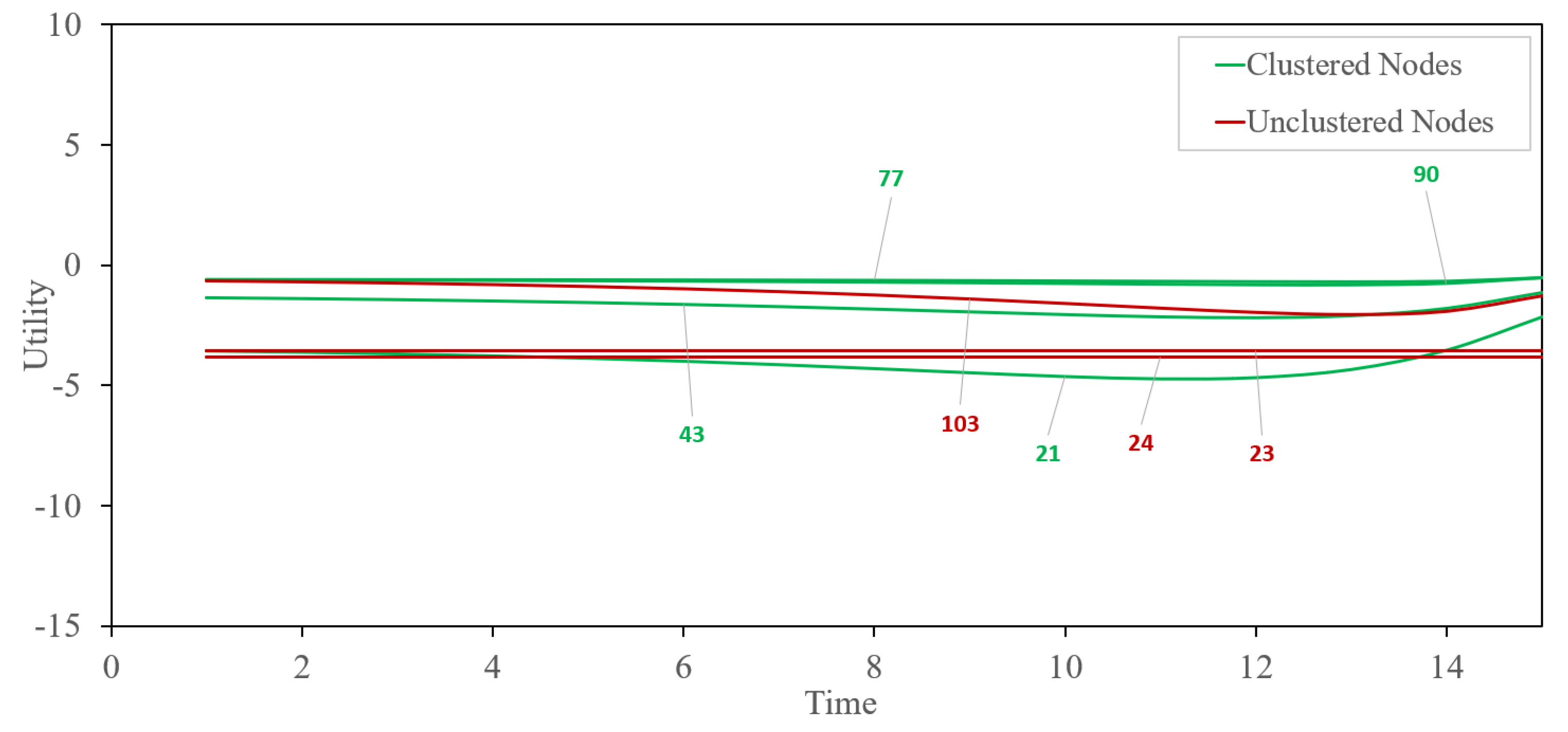
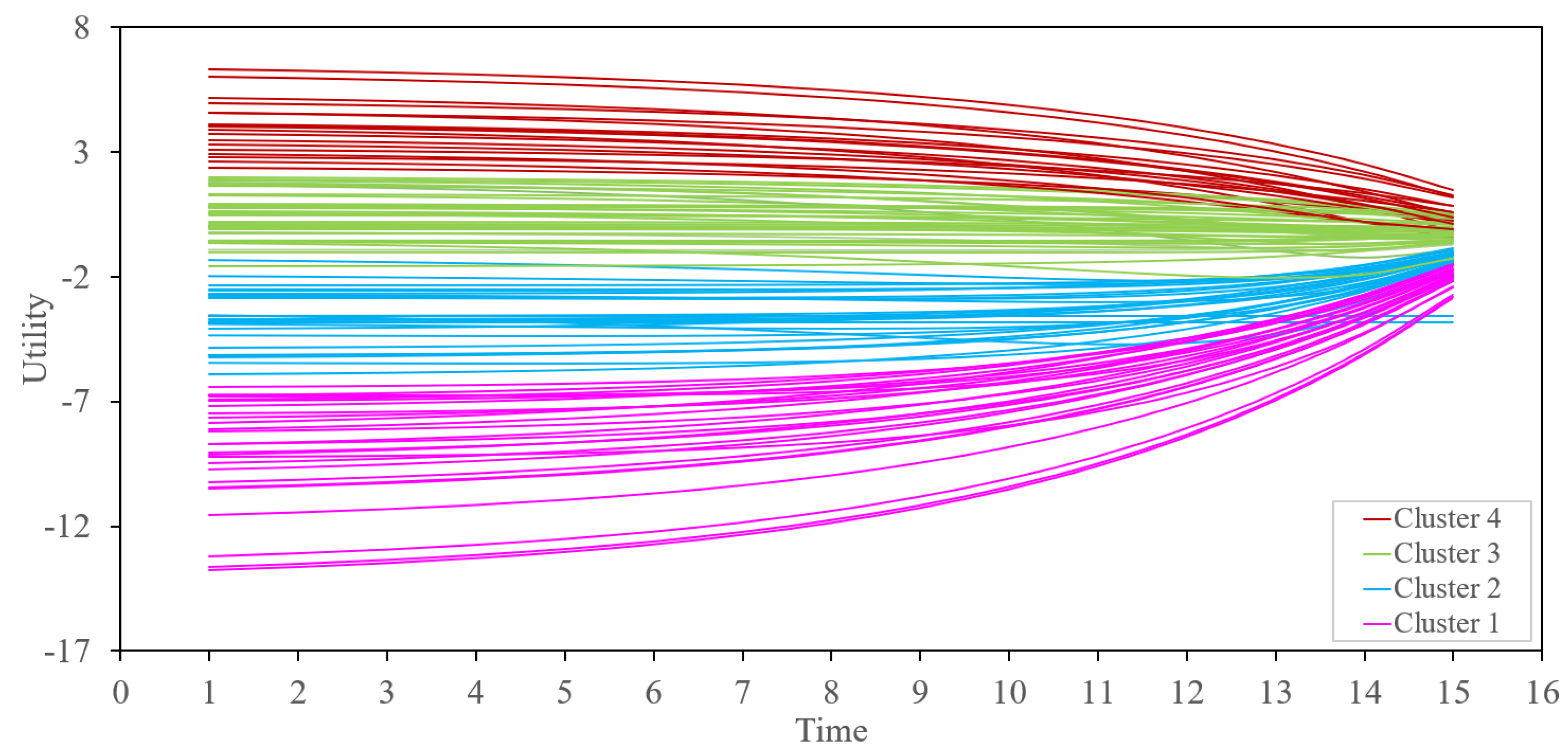
4.1. Geometry of Choice Classification
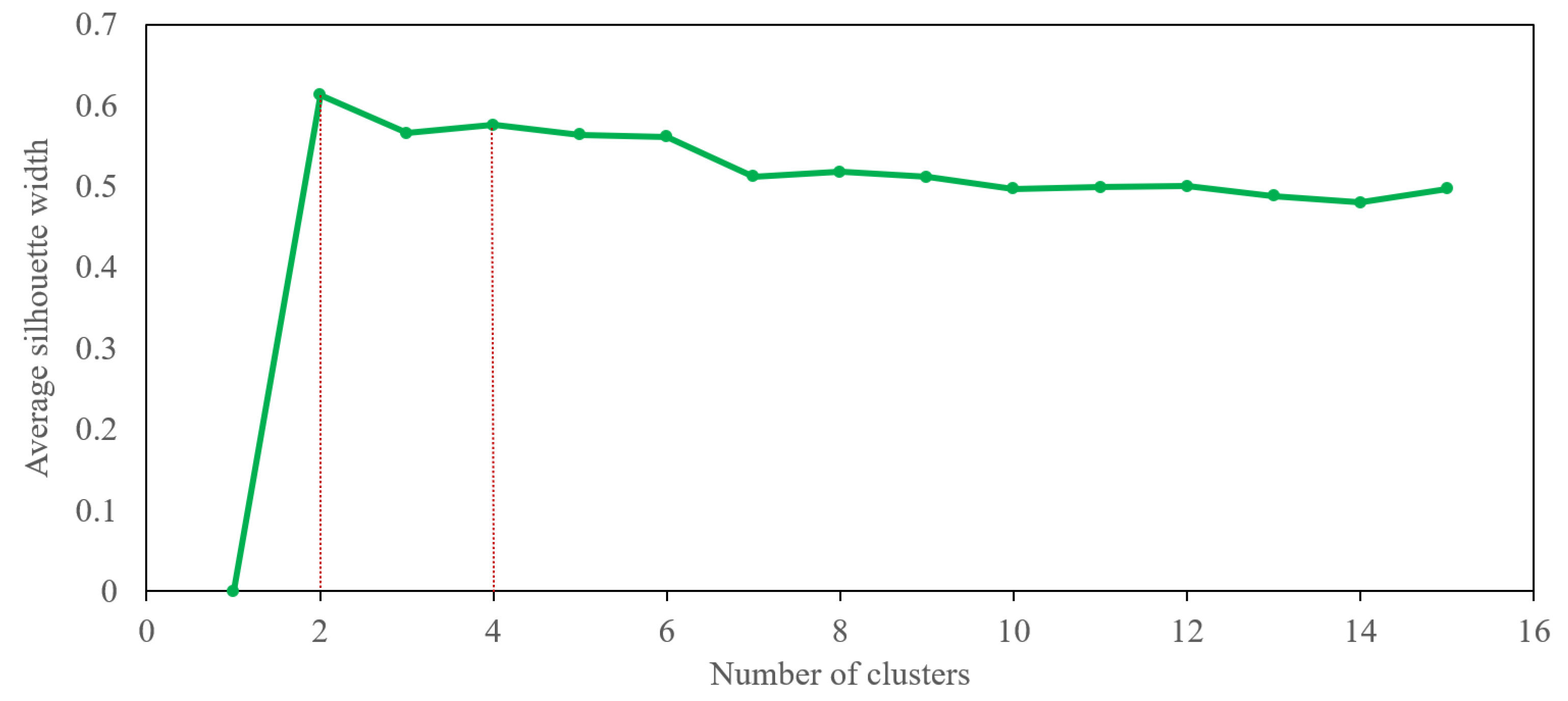
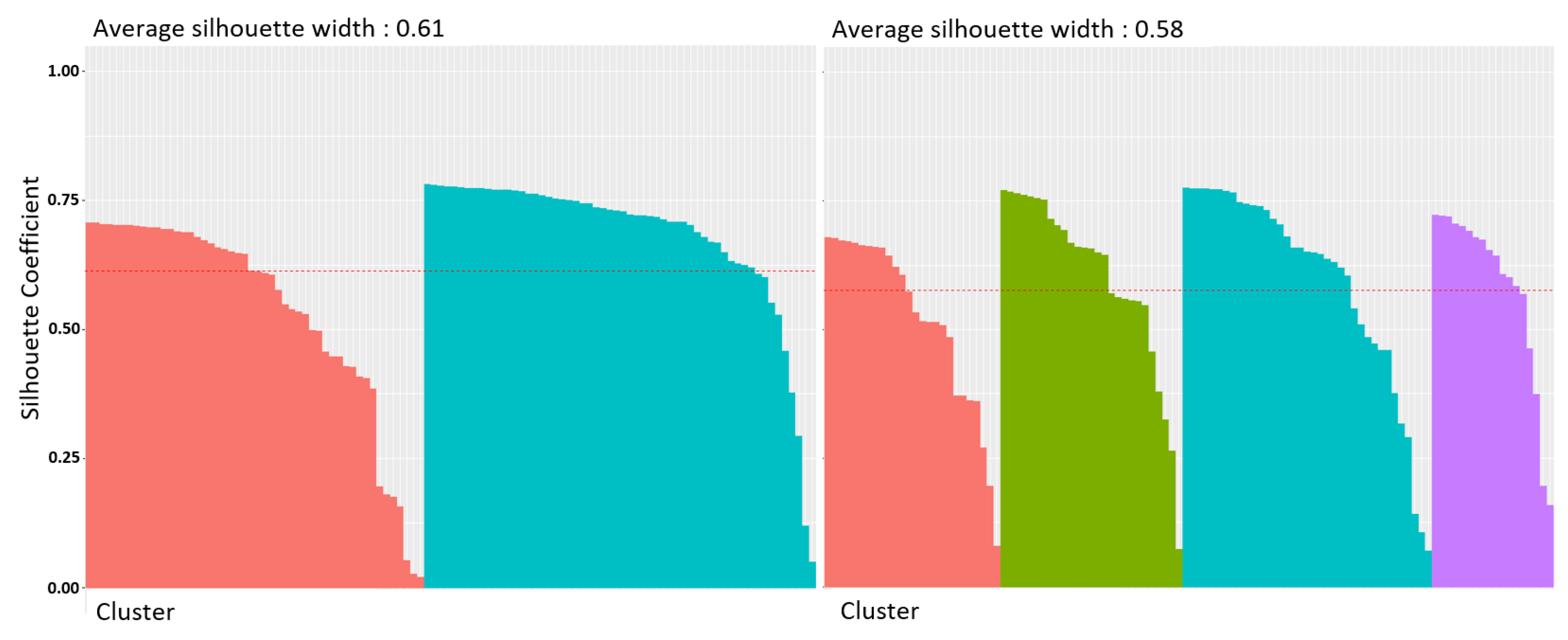
4.2. -Means Classification
5. Discussion
6. Conclusions
7. Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chambers, R.G.; Melkonyan, T.; Quiggin, J. Incomplete preferences, willingness to pay, and willingness to accept. Econ. Theory 2021, 74, 727–761. [Google Scholar] [CrossRef]
- Working, A.; Alqawba, M.; Diawara, N.; Li, L. Time Dependent Attribute-Level Best Worst Discrete Choice Modelling. Big Data Inf. Anal. 2018, 3, 55–72. [Google Scholar] [CrossRef]
- Graßhoff, U.; Großmann, H.; Holling, H.; Schwabe, R. Optimal designs for main effects in linear paired comparison models. J. Stat. Plan. Inference 2004, 126, 361–376. [Google Scholar] [CrossRef]
- Street, D.J.; Burgess, L. The Construction of Optimal Stated Choice Experiments: Theory and Methods; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Song, F.; Hess, S.; Dekker, T. A joint model for stated choice and best–worst scaling data using latent attribute importance: Application to rail-air intermodality. Transp. Transp. Sci. 2021, 17, 411–438. [Google Scholar] [CrossRef]
- Marti, J. A best–worst scaling survey of adolescents’ level of concern for health and non-health consequences of smoking. Soc. Sci. Med. 2012, 75, 87–97. [Google Scholar] [CrossRef]
- Flynn, T.N.; Louviere, J.J.; Peters, T.J.; Coast, J. Best–worst scaling: What it can do for health care research and how to do it. J. Health Econ. 2007, 26, 171–189. [Google Scholar] [CrossRef] [PubMed]
- Giergiczny, M.; Dekker, T.; Hess, S.; Chintakayala, P.K. Testing the stability of utility parameters in repeated best, repeated best-worst and one-off best-worst studies. Eur. J. Transp. Infrastruct. Res. 2017, 17. [Google Scholar] [CrossRef]
- Bech, M.; Kjaer, T.; Lauridsen, J. Does the number of choice sets matter? Results from a web survey applying a discrete choice experiment. Health Econ. 2011, 20, 273–286. [Google Scholar] [CrossRef]
- Johnson, F.R.; Lancsar, E.; Marshall, D.; Kilambi, V.; Mühlbacher, A.; Regier, D.A.; Bresnahan, B.W.; Kanninen, B.; Bridges, J.F.P. Constructing experimental designs for discrete-choice experiments: Report of the ISPOR conjoint analysis experimental design good research practices task force. Value Health 2013, 16, 3–13. [Google Scholar] [CrossRef]
- Bar, H.; Wells, M.T. On graphical models and convex geometry. Comput. Stat. Data Anal. 2023, 187, 107800. [Google Scholar] [CrossRef]
- Marley, A.A.J.; Flynn, T.N.; Louviere, J.J. Probabilistic models of set-dependent and attribute-level best–worst choice. J. Math. Psychol. 2008, 52, 281–296. [Google Scholar] [CrossRef]
- Street, D.J.; Burgess, L.; Louviere, J.J. Quick and easy choice sets: Constructing optimal and nearly optimal stated choice experiments. Int. J. Res. Mark. 2005, 22, 459–470. [Google Scholar] [CrossRef]
- Aizaki, H.; Fogarty, J. An R package and tutorial for case 2 best–worst scaling. J. Choice Model. 2019, 32, 100171. [Google Scholar] [CrossRef]
- Louviere, J.J.; Woodworth, G. Design and analysis of simulated consumer choice or allocation experiments: An approach based on aggregate data. J. Mark. Res. 1983, 20, 350–367. [Google Scholar] [CrossRef]
- Street, D.J.; Knox, S.A. Designing for attribute-level best-worst choice experiments. J. Stat. Theory Pract. 2012, 6, 363–375. [Google Scholar] [CrossRef]
- Das, A.; Singh, R. Discrete choice experiments—A unified approach. J. Stat. Plan. Inference 2020, 205, 193–202. [Google Scholar] [CrossRef]
- Thurstone, L.L. Three psychophysical laws. Psychol. Rev. 1927, 34, 424. [Google Scholar] [CrossRef]
- McFadden, D. Conditional Logit Analysis of Qualitative Choice Behavior. In Frontiers in Econometrics; Zarembka, P., Ed.; Academic Press: New York, NY, USA, 1974; pp. 105–142. [Google Scholar]
- Flynn, T.N.; Louviere, J.J.; Marley, A.A.J.; Coast, J.; Peters, T.J. Rescaling quality of life values from discrete choice experiments for use as QALYs: A cautionary tale. Popul. Health Metrics 2008, 6, 6. [Google Scholar] [CrossRef]
- Louviere, J.J.; Street, D.; Burgess, L.; Wasi, N.; Islam, T.; Marley, A.A.J. Modeling the choices of individual decision-makers by combining efficient choice experiment designs with extra preference information. J. Choice Model. 2008, 1, 128–164. [Google Scholar] [CrossRef]
- Lancsar, E.; Savage, E. Deriving welfare measures from discrete choice experiments: Inconsistency between current methods and random utility and welfare theory. Health Econ. 2004, 13, 901–907. [Google Scholar] [CrossRef]
- Berry, S.T. Estimating discrete-choice models of product differentiation. RAND J. Econ. 1994, 25, 242–262. [Google Scholar] [CrossRef]
- Rust, J. Structural estimation of Markov decision processes. Handb. Econom. 1994, 4, 3081–3143. [Google Scholar]
- Adikari, S.; Diawara, N. Utility in Time Description in Priority Best–Worst Discrete Choice Models: An Empirical Evaluation Using Flynn’s Data. Stats 2024, 7, 185–202. [Google Scholar] [CrossRef]
- Piccolo, D. On the moments of a mixture of uniform and shifted binomial random variables. Quad. Stat. 2003, 5, 85–104. [Google Scholar]
- D’Elia, A.; Piccolo, D. A mixture model for preferences data analysis. Comput. Stat. Data Anal. 2005, 49, 917–934. [Google Scholar] [CrossRef]
- Bellman, R. The theory of dynamic programming. Bull. Am. Math. Soc. 1954, 60, 503–515. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming and Lagrange multipliers. Proc. Natl. Acad. Sci. USA 1956, 42, 767–769. [Google Scholar] [CrossRef]
- Feinberg, E.A.; Shwartz, A. Markov decision models with weighted discounted criteria. Math. Oper. Res. 1994, 19, 152–168. [Google Scholar] [CrossRef]
- Cai, T.T.; Jiang, T. Limiting laws of coherence of random matrices with applications to testing covariance structure and construction of compressed sensing matrices. Ann. Stat. 2011, 39, 1496–1525. [Google Scholar] [CrossRef]
- Cai, T.T.; Jiang, T. Phase transition in limiting distributions of coherence of high-dimensional random matrices. J. Multivar. Anal. 2012, 107, 24–39. [Google Scholar]
- Cai, T.T.; Fan, J.; Jiang, T. Distributions of angles in random packing on spheres. J. Mach. Learn. Res. 2013, 14, 1837. [Google Scholar] [PubMed]
- Bar, H.; Bang, S. A mixture model to detect edges in sparse co-expression graphs with an application for comparing breast cancer subtypes. PLoS ONE 2021, 16, e0246945. [Google Scholar] [CrossRef]
- Frankl, P.; Maehara, H. Some geometric applications of the beta distribution. Ann. Inst. Stat. Math. 1990, 42, 463–474. [Google Scholar] [CrossRef]
- Absil, P.A.; Edelman, A.; Koev, P. On the largest principal angle between random subspaces. Linear Algebra Its Appl. 2006, 414, 288–294. [Google Scholar] [CrossRef]
- Cui, M. Introduction to the K-means clustering algorithm based on the elbow method. Account. Audit. Financ. 2020, 1, 5–8. [Google Scholar]
- Shahapure, K.R.; Nicholas, C. Cluster quality analysis using silhouette score. In Proceedings of the 2020 IEEE 7th International Conference on Data Science and Advanced Analytics (DSAA), Sydney, NSW, Australia, 6–9 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 747–748. [Google Scholar]
- Louviere, J.J.; Flynn, T.N.; Marley, A.A.J. Best-Worst Scaling: Theory, Methods and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Marley, A.A.J.; Islam, T.; Hawkins, G.E. A formal and empirical comparison of two score measures for best–worst scaling. J. Choice Model. 2016, 21, 15–24. [Google Scholar] [CrossRef]
- Roy, R.K. A Primer on the Taguchi Method; Society of Manufacturing Engineers: Southfield, MI, USA, 2010. [Google Scholar]
- Balbontin, C.; Ortúzar, J.d.D.; Swait, J.D. A joint best–worst scaling and stated choice model considering observed and unobserved heterogeneity: An application to residential location choice. J. Choice Model. 2015, 16, 1–14. [Google Scholar] [CrossRef]
- Dinh, D.T.; Fujinami, T.; Huynh, V.-N. Estimating the optimal number of clusters in categorical data clustering by silhouette coefficient. In Proceedings of the Knowledge and Systems Sciences: 20th International Symposium, KSS 2019, Da Nang, Vietnam, 29 November–1 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–17. [Google Scholar]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2022. [Google Scholar]



| Attribute | BW Score | Levels | Description | Analytical BW Score |
|---|---|---|---|---|
| CT (connection time) | 0.37 | conn180L (CT1) conn180T270 (CT2) conn270M (CT3) | Connection time is less than 3 h Connection time is 3 h to 4.5 h Connection time is more than 4.5 h | |
| DP (delay protection) | 0.29 | delay0 (DP1) delay1 (DP2) delay2 (DP3) | No delay protection 50% off if major leg missed due to minor leg delay Free change if major leg missed from minor leg delay | |
| TI (ticket integration) | tick1 (TI1) tick2 (TI2) tick3 (TI3) | Booked together, no easy collection, fixed-time on minor leg Booked together, easy collection, fixed-time train on minor leg Booked together, each collection, flexible train on minor leg | ||
| LI (luggage integration) | 0.16 | lugg0 (LI1) lugg1 (LI2) lugg2 (LI3) | No luggage integration, checks required on both legs Integrated luggage, checks required on both leg Integrated luggage, one security check required |
| Choice Pair | Best Attribute | Worst Attribute | Best Level | Worst Level | Utility at | Utility at | ⋯ | Utility at | Utility at | Choice Set |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | CT | TI | conn180L | tick2 | 3.098 | 3.073 | ⋯ | 1.339 | 0.825 | 1 |
| 2 | CT | DP | conn180L | delay2 | 2.802 | 2.770 | ⋯ | 1.067 | 0.605 | 1 |
| 3 | CT | LI | conn180L | lugg2 | 2.386 | 2.361 | ⋯ | 0.670 | 0.265 | 1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋯ | ⋮ | ⋮ | ⋮ |
| 12 | TI | CT | tick2 | conn180L | ⋯ | 1 | ||||
| 13 | CT | LI | conn180L | lugg1 | 6.307 | 6.252 | ⋯ | 2.506 | 1.473 | 2 |
| 14 | CT | DP | conn180L | delay1 | 6.010 | 5.954 | ⋯ | 2.217 | 1.223 | 2 |
| 15 | CT | TI | conn180L | tick3 | 5.196 | 5.140 | ⋯ | 1.416 | 0.493 | 2 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋯ | ⋮ | ⋮ | ⋮ |
| 24 | LI | CT | lugg1 | conn180L | ⋯ | 2 | ||||
| 25 | LI | DP | lugg2 | delay1 | 1.971 | 1.956 | ⋯ | 0.861 | 0.555 | 3 |
| 26 | LI | CT | lugg2 | conn270M | 1.906 | 1.890 | ⋯ | 0.788 | 0.475 | 3 |
| 27 | LI | TI | lugg2 | tick1 | 1.633 | 1.617 | ⋯ | 0.522 | 0.235 | 3 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋯ | ⋮ | ⋮ | ⋮ |
| 85 | DP | CT | delay0 | conn180T270 | 1.326 | 1.318 | ⋯ | 0.681 | 0.445 | 8 |
| 86 | DP | TI | delay0 | tick3 | 0.936 | 0.927 | ⋯ | 0.334 | 0.185 | 8 |
| 87 | LI | CT | lugg2 | conn180T270 | 0.766 | 0.757 | ⋯ | 0.202 | 0.085 | 8 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋯ | ⋮ | ⋮ | ⋮ |
| 96 | CT | DP | conn180T270 | delay0 | ⋯ | 8 | ||||
| 97 | CT | TI | conn180L | tick1 | 4.972 | 4.931 | ⋯ | 2.100 | 1.285 | 9 |
| 98 | DP | TI | delay0 | tick1 | 4.050 | 4.009 | ⋯ | 1.235 | 0.955 | 9 |
| 99 | CT | LI | conn180L | lugg0 | 4.011 | 3.970 | ⋯ | 1.155 | 0.385 | 9 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋯ | ⋮ | ⋮ | ⋮ |
| 108 | TI | CT | tick1 | conn180L | ⋯ | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adikari, S.; Diawara, N.; Bar, H. The Geometry of Dynamic Time-Dependent Best–Worst Choice Pairs. Axioms 2024, 13, 641. https://doi.org/10.3390/axioms13090641
Adikari S, Diawara N, Bar H. The Geometry of Dynamic Time-Dependent Best–Worst Choice Pairs. Axioms. 2024; 13(9):641. https://doi.org/10.3390/axioms13090641
Chicago/Turabian StyleAdikari, Sasanka, Norou Diawara, and Haim Bar. 2024. "The Geometry of Dynamic Time-Dependent Best–Worst Choice Pairs" Axioms 13, no. 9: 641. https://doi.org/10.3390/axioms13090641
APA StyleAdikari, S., Diawara, N., & Bar, H. (2024). The Geometry of Dynamic Time-Dependent Best–Worst Choice Pairs. Axioms, 13(9), 641. https://doi.org/10.3390/axioms13090641








