Generalized Bertrand Curve Pairs in Euclidean Four-Dimensional Space
Abstract
1. Introduction
2. Preliminaries
Relationship Between Space Curves via a Combescure Transformation
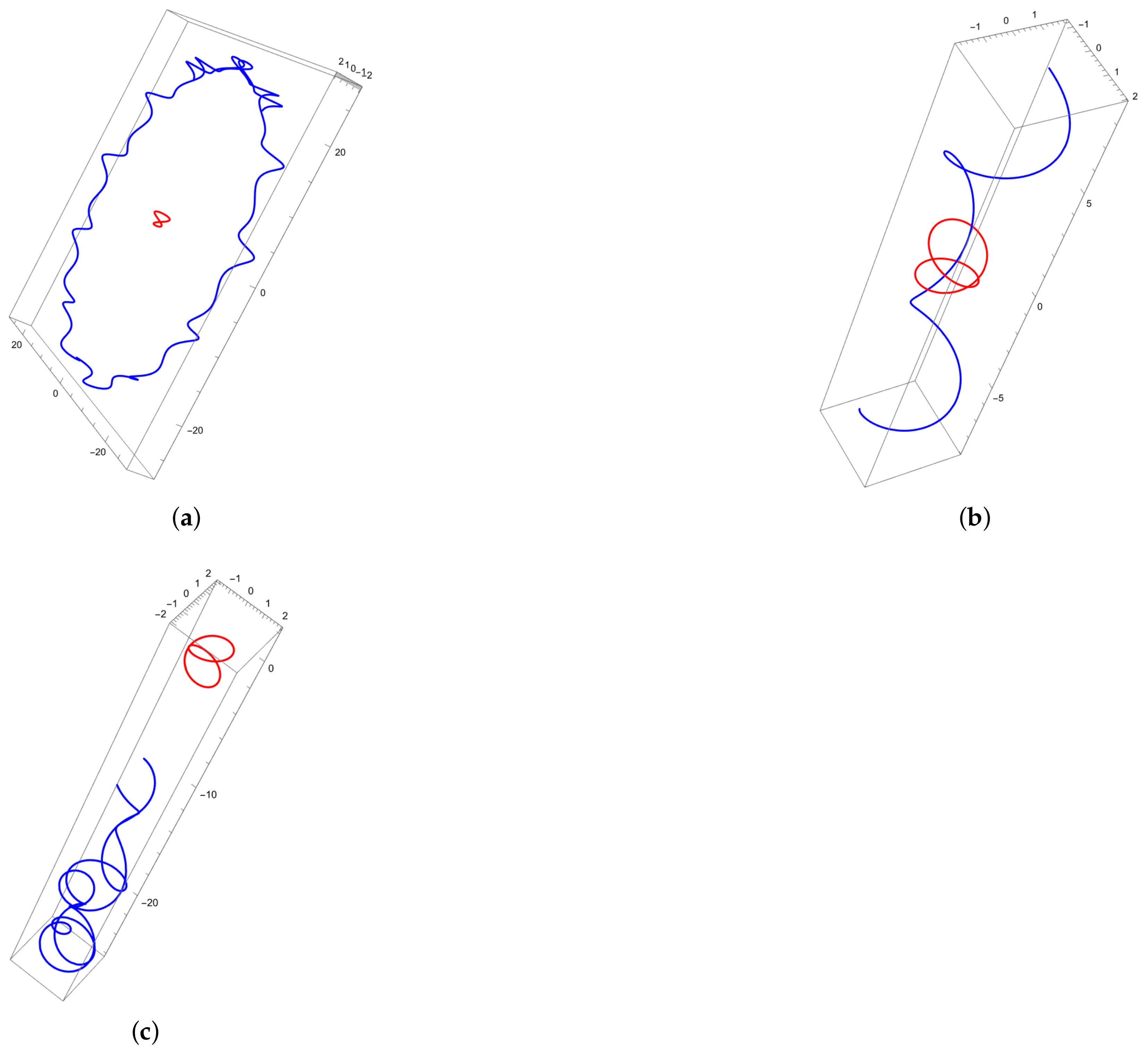
3. Bertrand Curves in Four-Dimensional Euclidean Space
- (i)
- There exist differentiable functions u, v, , and on and a constant , satisfyingor
- (ii)
- There exist differentiable functions u, v, , and on , satisfyingor
- (iii)
- There exist differentiable functions u, v, , and on , satisfyingwhere .
- 1.
- If the conditions in of Theorem 3 are satisfied, the Bertrand mate of γ is one of the following:or
- 2.
- If the conditions in of Theorem 3 are satisfied, the Bertrand mate of γ is one of the following:or
- 3.
- If the conditions in of Theorem 3 are satisfied, the Bertrand mate of γ is as follows:
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bertrand, J.M. Mémoire sur la théorie des courbes á double courbure. Comptes Rendus 1850, 15, 332–350. [Google Scholar]
- Saint Venant, B. Mémoire sur les lignes courbes non planes. J. L’Ecole Polytech. 1845, 18, 1–76. [Google Scholar]
- Lucas, P.; Ortega-Yagües, J.A. Bertrand curves in the three-dimensional sphere. J. Geom. Phys. 2012, 62, 1903–1914. [Google Scholar]
- Honda, S.I.; Takahashi, M. Bertrand and Mannheim curves of framed curves in the 3-dimensional Euclidean space. Turk. J. Math. 2020, 44, 883–899. [Google Scholar]
- Li, Y.; Eren, K.; Ersoy, S.; Savic, A. Modified Sweeping Surfaces in Euclidean 3-Space. Axioms 2024, 13, 800. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.; Eren, K.; Ersoy, S. Sweeping Surfaces of Polynomial Curves in Euclidean 3-space. An. St. Univ. Ovidius Constanta 2025, 33, 293–311. [Google Scholar]
- Moraffeh, F.; Abdel-Baky, R.A.; Alluhaibi, N. Sweeping surfaces with Darboux frame in Euclidean 3-space. Aust. J. Math. Anal. Appl. 2021, 18, 1–10. [Google Scholar]
- Cheng, Y.; Li, Y.; Badyal, P.; Singh, K.; Sharma, S. Conformal Interactions of Osculating Curves on Regular Surfaces in Euclidean 3-Space. Mathematics 2025, 13, 881. [Google Scholar] [CrossRef]
- Shaikh, A.A.; Ghosh, P.R. Rectifying and osculating curves on a smooth surface. Indian J. Pure Appl. Math. 2020, 51, 67–75. [Google Scholar]
- Isah, M.A.; Isah, I.; Hassan, T.L.; Usman, M. Some characterization of osculating curves according to Darboux frame in three-dimensional Euclidean space. Int. J. Adv. Acad. Res. 2021, 7, 47–56. [Google Scholar]
- Shaikh, A.A.; Ghosh, P.R. Rectifying curves on a smooth surface immersed in the Euclidean space. Indian J. Pure Appl. Math. 2019, 50, 883–890. [Google Scholar] [CrossRef]
- Chen, B.Y.; Dillen, F. Rectifying curve as centrode and extremal curve. Bull. Inst. Math. Acad. Sin. 2005, 33, 77–90. [Google Scholar]
- Deshmukh, S.; Chen, B.Y.; Alshammari, S.H. On rectifying curves in Euclidean 3-space. Turk. J. Math. 2018, 42, 609–620. [Google Scholar] [CrossRef]
- Pears, L.R. Bertrand curves in Riemannian space. J. London Math. Soc. 1935, 1, 180–183. [Google Scholar] [CrossRef]
- Matsuda, H.; Yorozu, S. Notes on Bertrand curves. Yokohama Math. J. 2003, 50, 41–58. [Google Scholar]
- Cheng, Y.-M.; Lin, C.-C. On the Generalized Bertrand Curves in Euclidean N-spaces. Note Mat. 2009, 29, 33–39. [Google Scholar]
- Camcı, Ç.; Uçum, A.; İlarslan, K. A New Approach to Bertrand Curves in Euclidean 3-Space. J. Geom. 2020, 111, 49. [Google Scholar] [CrossRef]
- Kuhnel, W. Differential Geometry: Curves-Surfaces-Manifolds; American Mathematical Society: Providence, RI, USA, 1999. [Google Scholar]
- Sun, J.; Zhao, Y. The Geometrical Characterizations of the Bertrand Curves of the Null Curves in Semi-Euclidean 4-Space. Mathematics 2021, 9, 3294. [Google Scholar] [CrossRef]
- Tuncer, O. Framed Bertrand and Mannheim Curves in Three-Dimensional Space Forms of Non-zero Constant Curvatures. Int. Electron. J. Geom. 2024, 17, 447–465. [Google Scholar] [CrossRef]
- Gluck, H. Higher curvatures of curves in Euclidean space. Am. Math. Mon. 1966, 73, 699–704. [Google Scholar] [CrossRef]
- Jäntschi, L. The eigenproblem translated for alignment of molecules. Symmetry 2019, 11, 1027. [Google Scholar] [CrossRef]
- Sannia, G. Combescure ed altre analoghe per le curve storte (Translated by D. H. Delphenich). Rend. Circ. Mat. Palermo 1905, 20, 83–92. [Google Scholar]
- Graustein, W.C. On two related transformations of space curves. Am. J. Math. 1917, 39, 233–240. [Google Scholar] [CrossRef]
- Sun, J.; Pei, D. Null Cartan Bertrand curves of AW (k)-type in Minkowski 4-space. Phys. Lett. A 2012, 376, 2230–2233. [Google Scholar]
- Zhu, M.; Yang, H.; Li, Y.; Abdel-Baky, R.A.; AL-Jedani, A.; Khalifa, M. Directional developable surfaces and their singularities in Euclidean 3-space. Filomat 2024, 38, 11333–11347. [Google Scholar]
- Wu, L.; Zhou, A.; Yao, K.; Pei, D. Generalized Bertrand Curves of Non-Light-like Framed Curves in Lorentz–Minkowski 3-Space. Mathematics 2024, 12, 2593. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Keçilioğlu, O.; İlarslan, K. Generalized Bertrand Curve Pairs in Euclidean Four-Dimensional Space. Axioms 2025, 14, 253. https://doi.org/10.3390/axioms14040253
Li Y, Keçilioğlu O, İlarslan K. Generalized Bertrand Curve Pairs in Euclidean Four-Dimensional Space. Axioms. 2025; 14(4):253. https://doi.org/10.3390/axioms14040253
Chicago/Turabian StyleLi, Yanlin, Osman Keçilioğlu, and Kazım İlarslan. 2025. "Generalized Bertrand Curve Pairs in Euclidean Four-Dimensional Space" Axioms 14, no. 4: 253. https://doi.org/10.3390/axioms14040253
APA StyleLi, Y., Keçilioğlu, O., & İlarslan, K. (2025). Generalized Bertrand Curve Pairs in Euclidean Four-Dimensional Space. Axioms, 14(4), 253. https://doi.org/10.3390/axioms14040253





