Circuit Design and Implementation of a Time-Varying Fractional-Order Chaotic System
Abstract
:1. Introduction
2. Variable Fractional-Order Operators
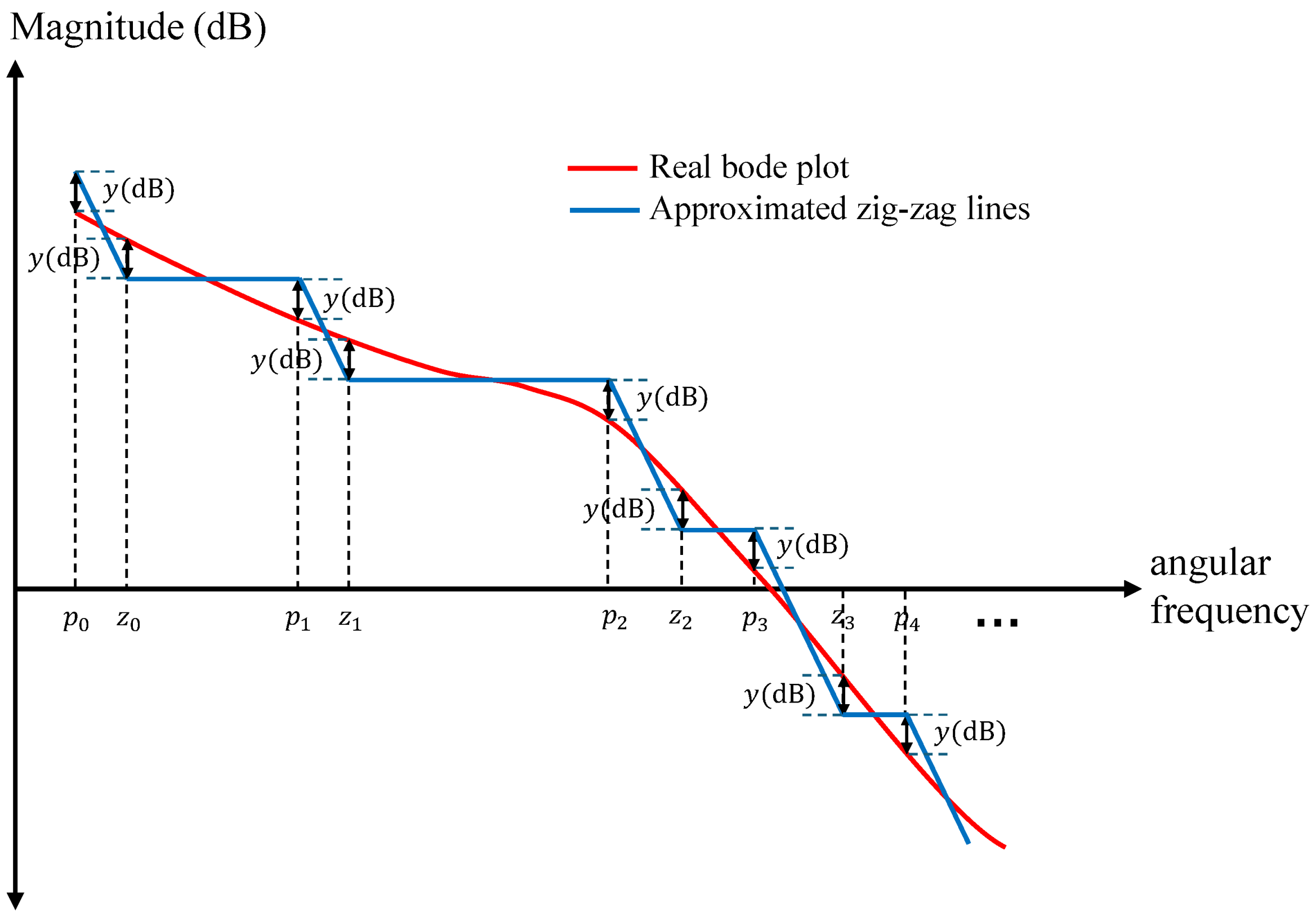
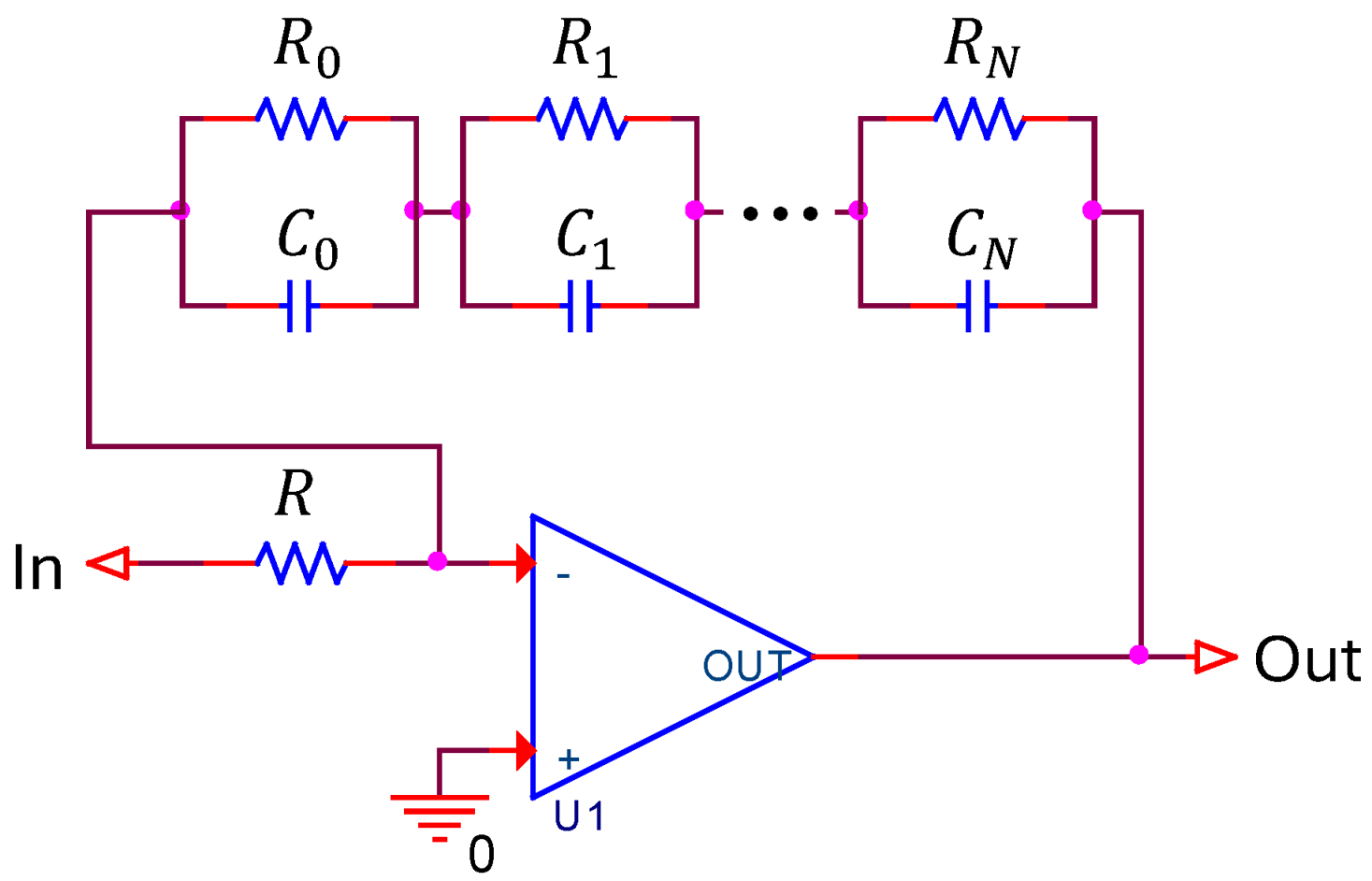
3. Circuit Design Steps for Variable Fractional-Order Integrator
| Algorithm 1 The pseudo code for calculation of pole–zero of the approximated transfer function. |
Determining the frequency range of approximation [] Setting the maximum error y while do end while |
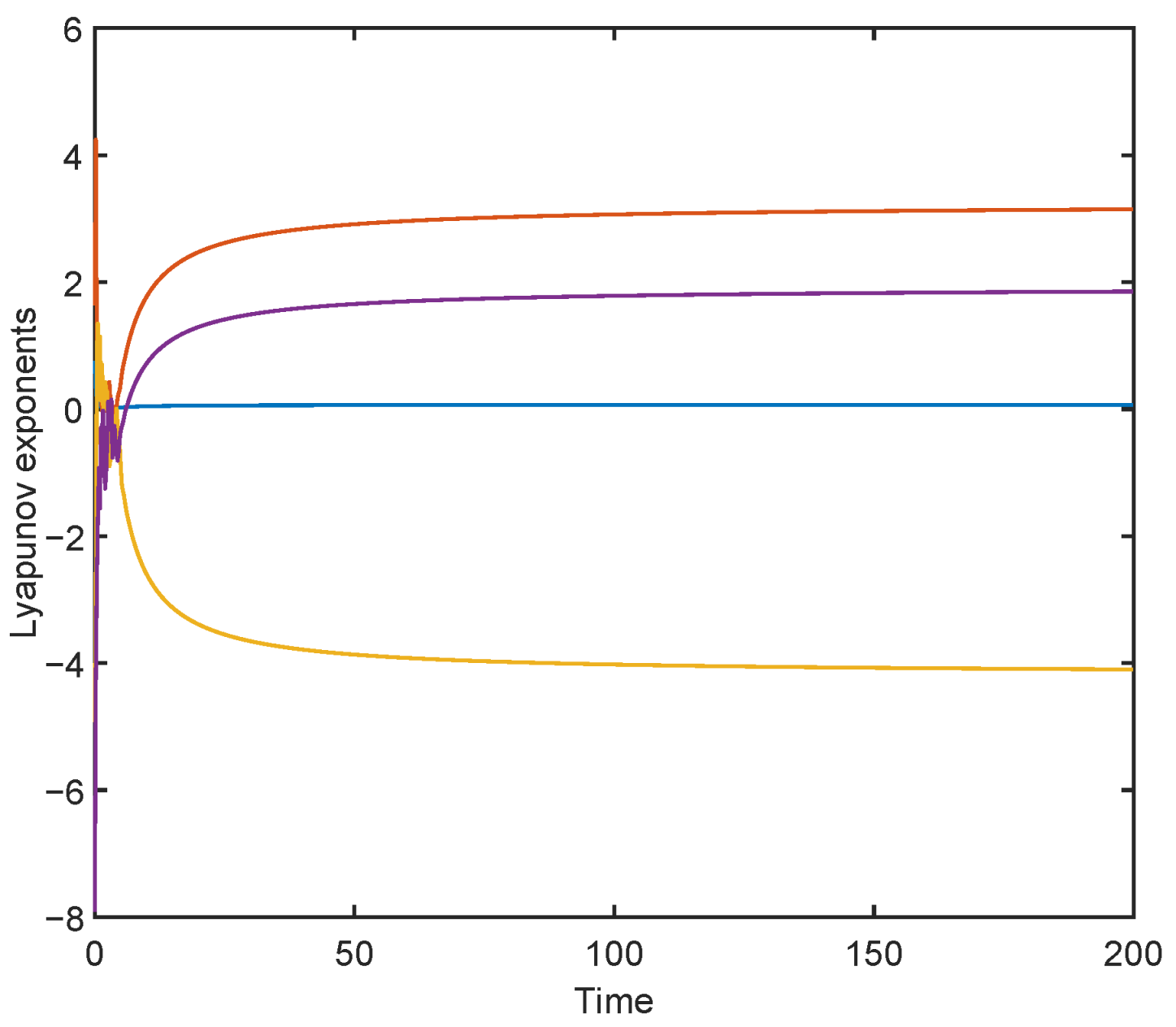
4. Variable Fractional-Order Chaotic System
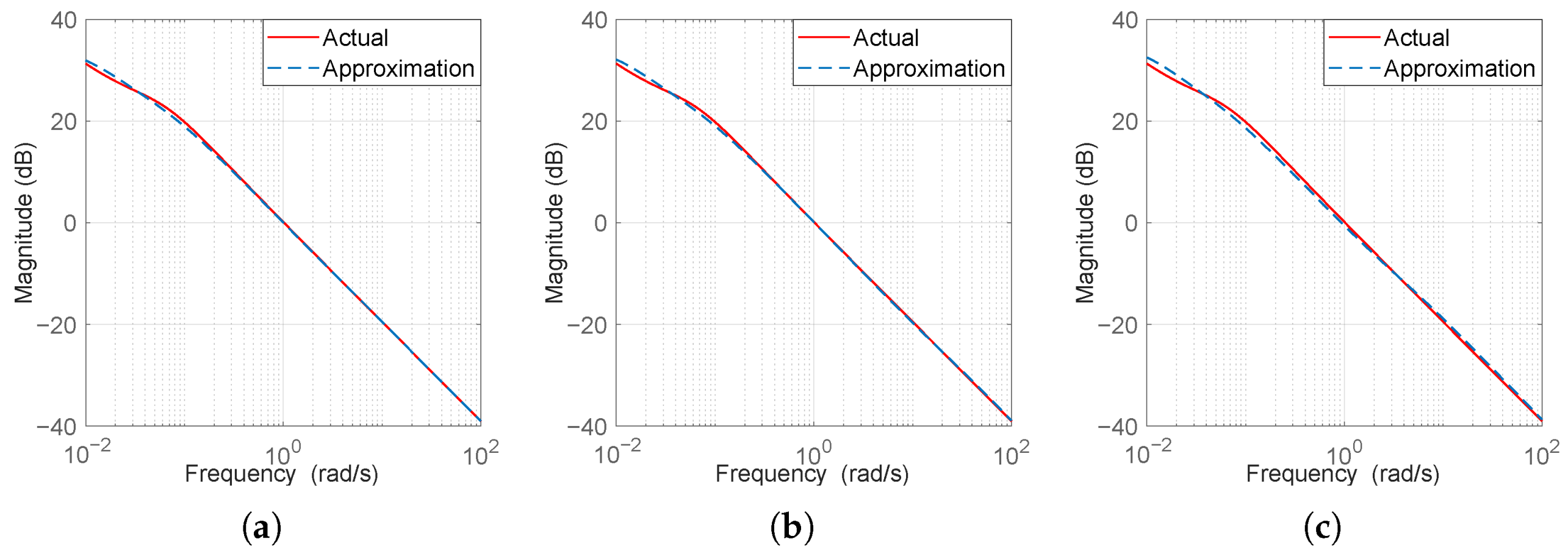
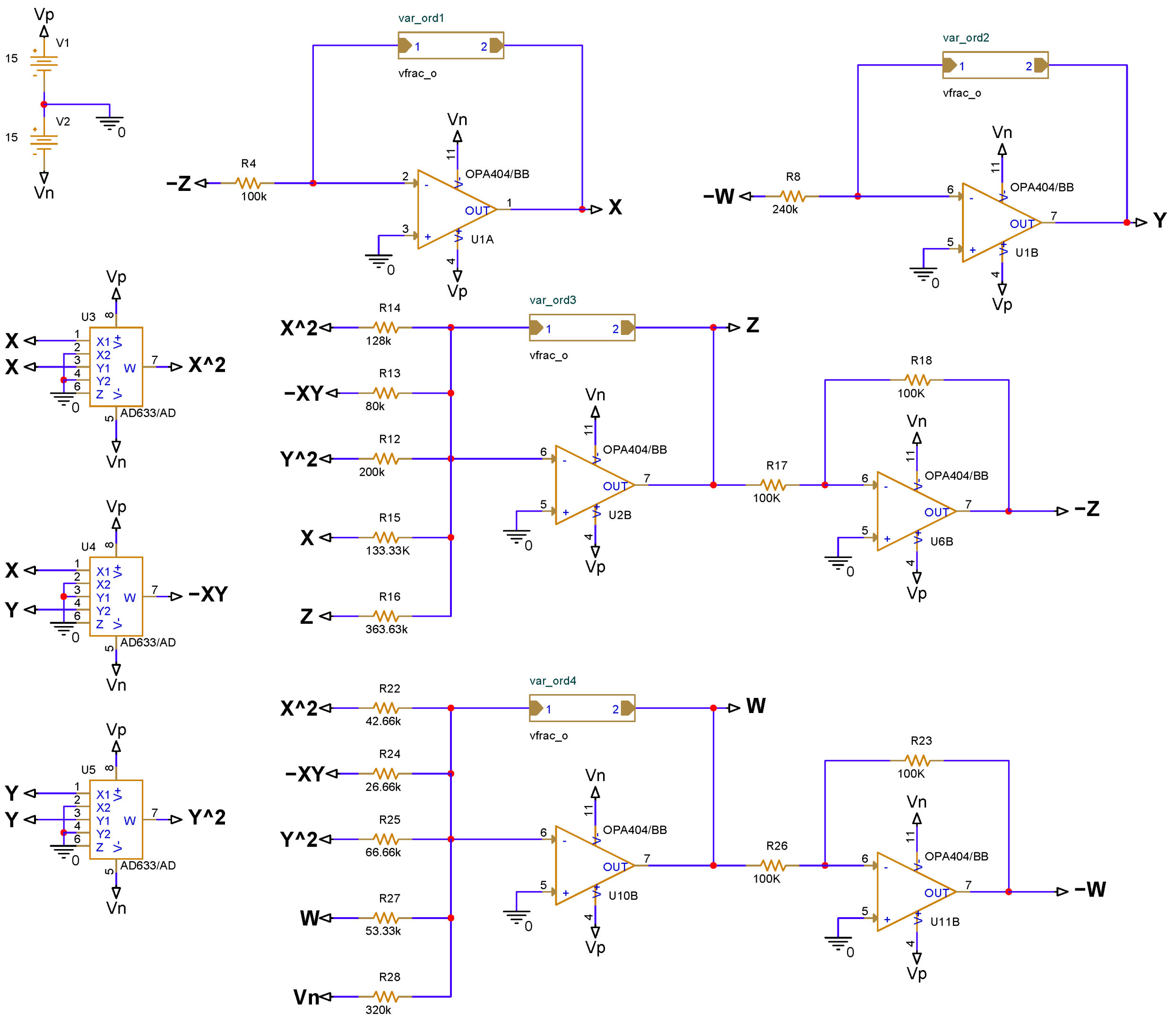
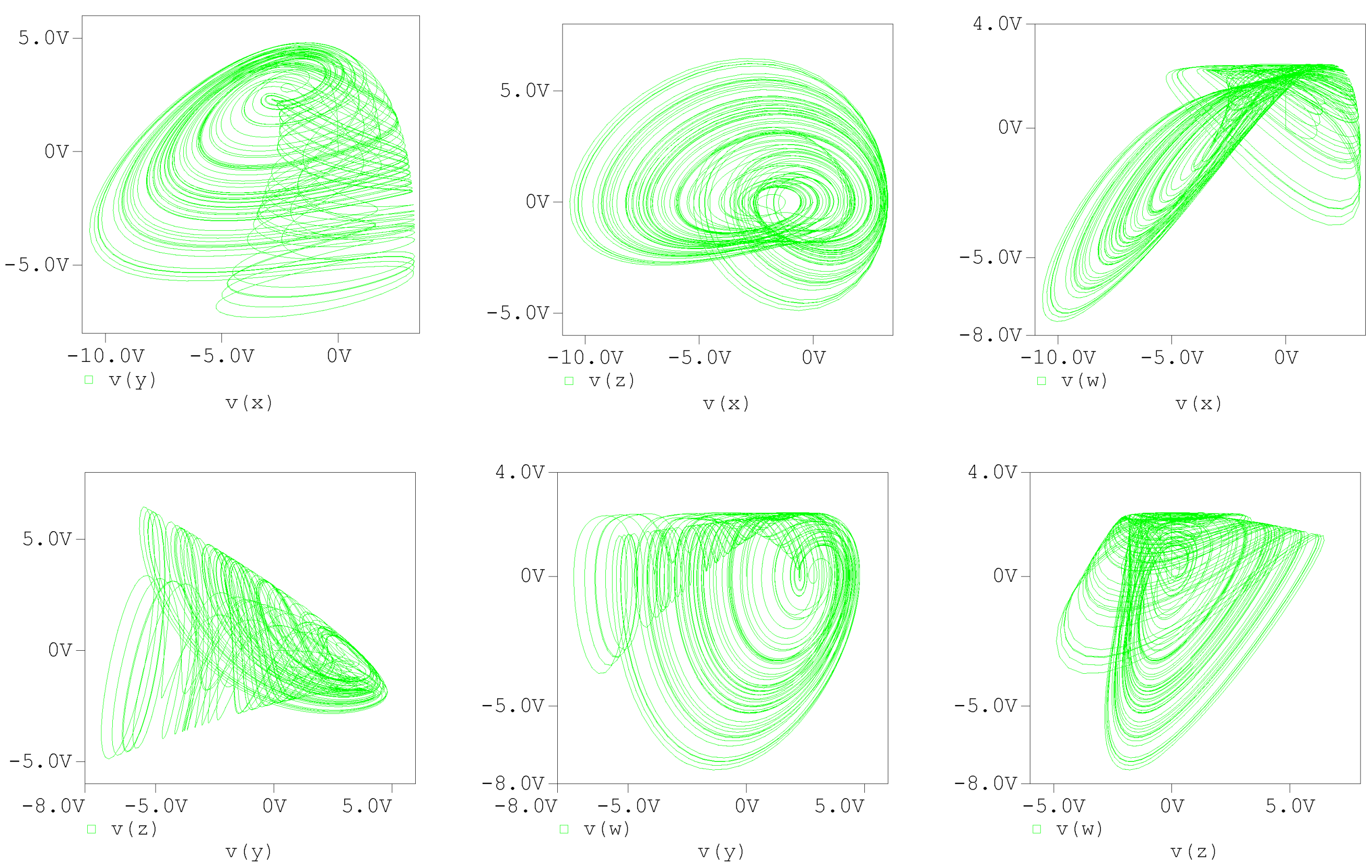
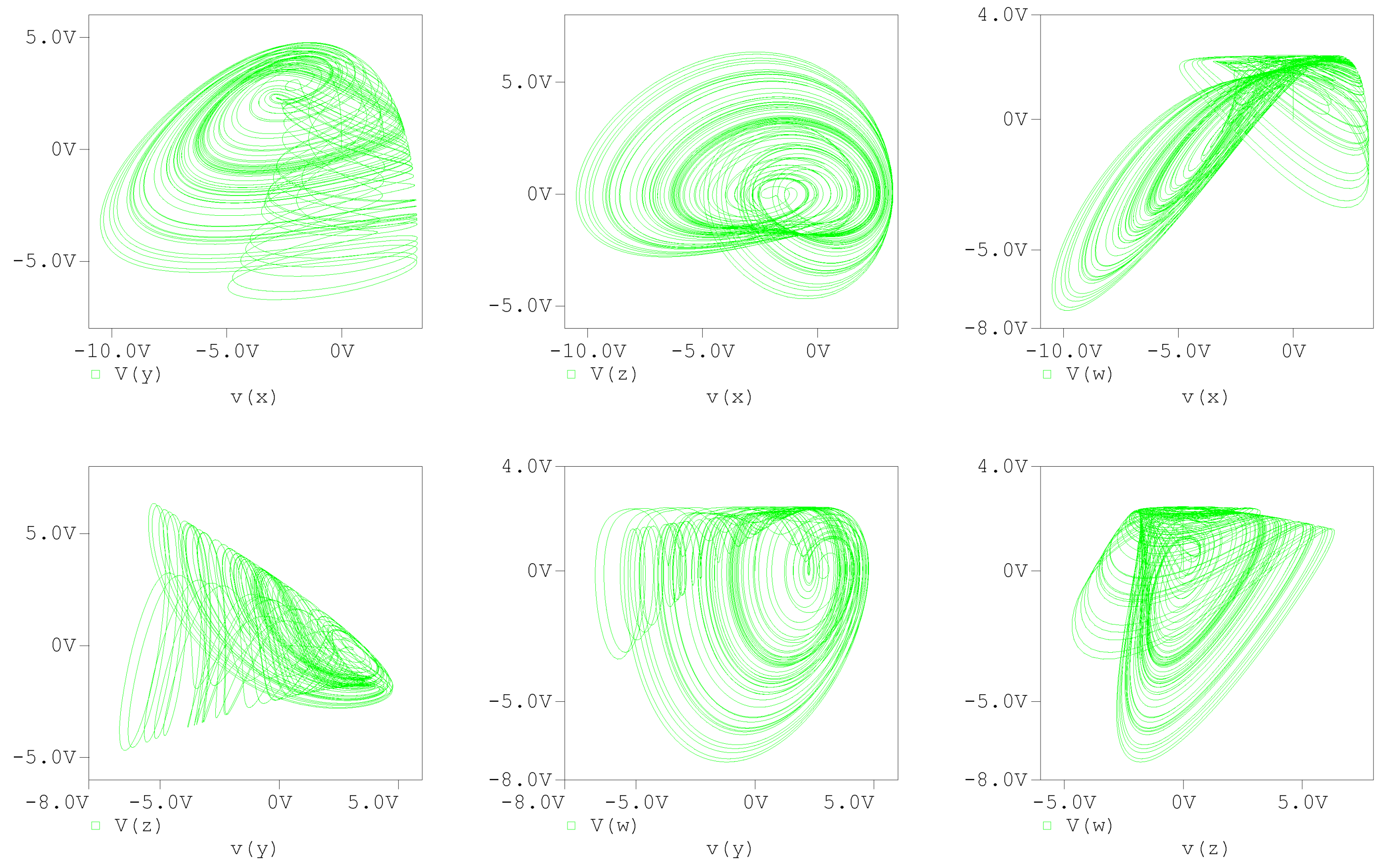
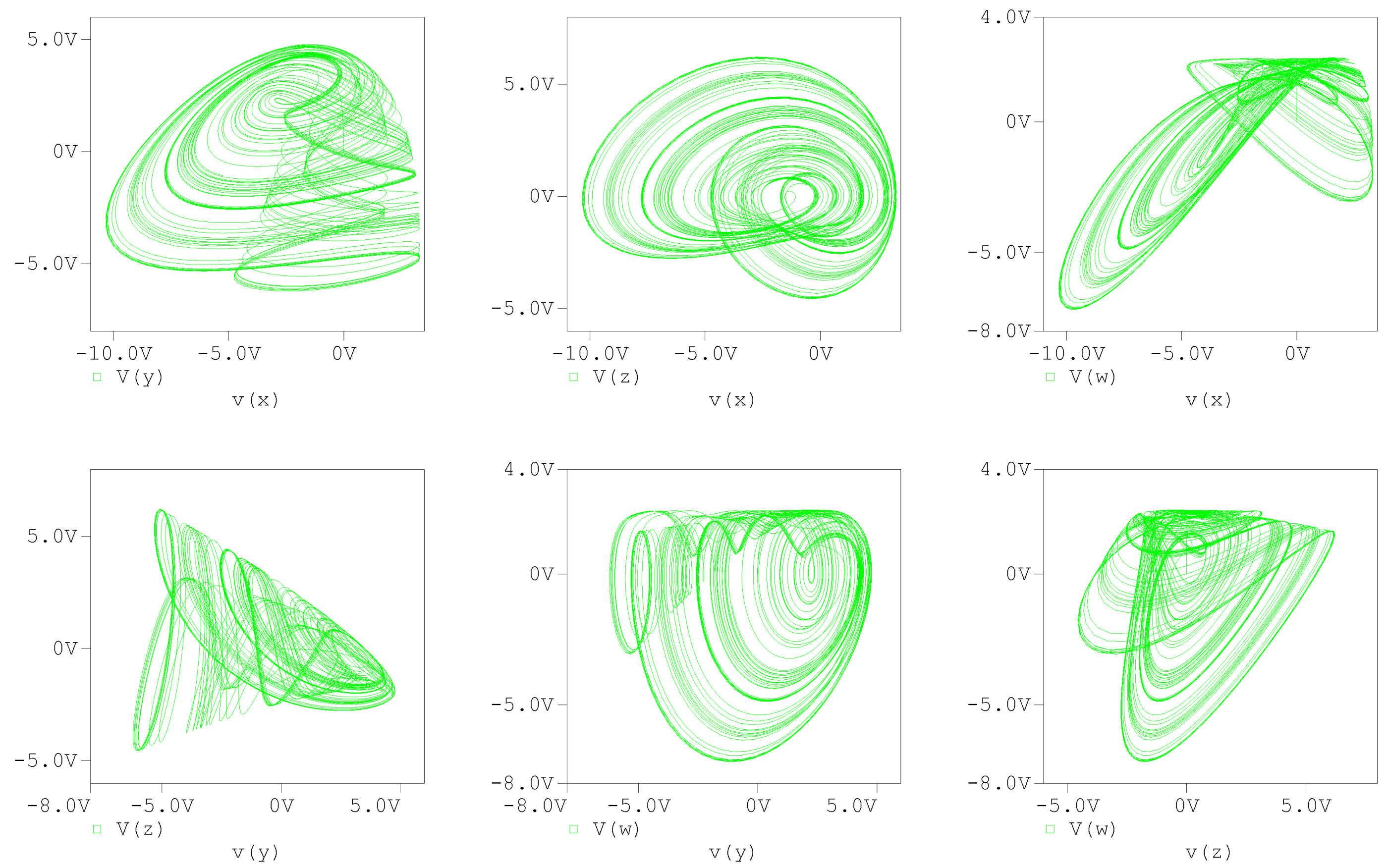
5. Circuit Implementation of Variable Fractional-Order Chaotic System
6. Discussion
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Cao, L.; Zhang, W. Double color image visual encryption based on digital chaos and compressed sensing. Int. J. Bifurc. Chaos 2023, 33, 2350044. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, L. Chaos-based image encryption: Review; application; and challenges. Mathematics 2023, 11, 2585. [Google Scholar] [CrossRef]
- Ming, H.; Hu, H.; Lv, F.; Yu, R. A high-performance hybrid random number generator based on a nondegenerate coupled chaos and its practical implementation. Nonlinear Dyn. 2023, 111, 847–869. [Google Scholar] [CrossRef]
- Alloun, Y.; Azzaz, M.S.; Kifouche, A. A new approach based on artificial neural networks and chaos for designing deterministic random number generator and its application in image encryption. Multimed. Tools Appl. 2025, 84, 5825–5860. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y.; Yang, H. Research on economic optimization of microgrid cluster based on chaos sparrow search algorithm. Comput. Intell. Neurosci. 2021, 2021, 5556780. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, J.; Zhao, C.; Li, Z.; Yan, J. Chaos Optimization Algorithms: A Survey. Int. J. Bifurc. Chaos 2024, 2450205. [Google Scholar] [CrossRef]
- Silahtar, O.; Kutlu, F.; Atan, Ö.; Castillo, O. Rendezvous and docking control of satellites using chaos synchronization method with intuitionistic fuzzy sliding mode control. In Fuzzy Logic and Neural Networks for Hybrid Intelligent System Design; Springer International Publishing: Cham, Switzerland, 2023; pp. 177–197. [Google Scholar]
- Kuz’menko, A.A. Forced sliding mode control for chaotic systems synchronization. Nonlinear Dyn. 2022, 109, 1763–1775. [Google Scholar] [CrossRef]
- Yu, F.; Qian, S.; Chen, X.; Huang, Y.; Liu, L.; Shi, C.; Cai, S.; Song, Y.; Wang, C. A new 4D four-wing memristive hyperchaotic system: Dynamical analysis; electronic circuit design; shape synchronization and secure communication. Int. J. Bifurc. Chaos 2020, 30, 2050147. [Google Scholar] [CrossRef]
- Bai, C.; Yao, J.L.; Sun, Y.Z.; Ren, H.P. Chaos Division Multi-Access Communication System. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 5814–5827. [Google Scholar] [CrossRef]
- Kyriazis, M. Applications of chaos theory to the molecular biology of aging. Exp. Gerontol. 1991, 26, 569–572. [Google Scholar] [CrossRef]
- Heltberg, M.L.; Krishna, S.; Kadanoff, L.P.; Jensen, M.H. A tale of two rhythms: Locked clocks and chaos in biology. Cell Sys. 2021, 12, 291–303. [Google Scholar] [CrossRef]
- Chu, Y.M.; Bekiros, S.; Zambrano-Serrano, E.; Orozco-López, O.; Lahmiri, S.; Jahanshahi, H.; Aly, A.A. Artificial macro-economics: A chaotic discrete-time fractional-order laboratory model. Chaos Solitons Fractals 2021, 145, 110776. [Google Scholar] [CrossRef]
- Fernández-Díaz, A. Overview and perspectives of chaos theory and its applications in economics. Mathematics 2023, 12, 92. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Iskakova, K.; Alam, M.M.; Ahmad, S.; Saifullah, S.; Akgül, A.; Yılmaz, G. Dynamical study of a novel 4D hyperchaotic system: An integer and fractional order analysis. Math. Comput. Simul. 2023, 208, 219–245. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Joshi, M.; Bhosale, S.; Vyawahare, V.A. A survey of fractional calculus applications in artificial neural networks. Artif. Intell. Rev. 2023, 56, 13897–13950. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J.H. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; Abdeljawad, T. Chaotic behavior of Bhalekar–Gejji dynamical system under Atangana–Baleanu fractal fractional operator. Fractals 2022, 30, 2240005. [Google Scholar] [CrossRef]
- Xu, C.; Farman, M.; Shehzad, A. Analysis and chaotic behavior of a fish farming model with singular and non-singular kernel. Int. J. Biomath. 2025, 18, 2350105. [Google Scholar] [CrossRef]
- Xua, C.; Liaob, M.; Farman, M.; Shehzade, A. Hydrogenolysis of glycerol by heterogeneous catalysis: A fractional order kinetic model with analysis. MATCH Commun. Math. Comput. Chem. 2024, 91, 635–664. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Chen, W.; Reeves, D.M. Use of a variable-index fractional-derivative model to capture transient dispersion in heterogeneous media. J. Contam. Hydrol. 2014, 157, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A review on variable-order fractional differential equations: Mathematical foundations; physical models; numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sajjadi, S.S.; Bekiros, S.; Aly, A.A. On the development of variable-order fractional hyperchaotic economic system with a nonlinear model predictive controller. Chaos Solitons Fractals 2021, 144, 110698. [Google Scholar] [CrossRef]
- Macias, M.; Sierociuk, D.; Malesza, W. Realization of the Fractional Variable-Order Model with Symmetric Property. In Proceedings of the Conference on Non-Integer Order Calculus and Its Applications, Białystok, Poland, 20–21 September 2018; pp. 43–54. [Google Scholar]
- Malesza, W.; Macias, M.; Sierociuk, D. Analytical solution of fractional variable order differential equations. J. Comput. Appl. Math. 2019, 348, 214–236. [Google Scholar] [CrossRef]
- Jia, H.Y.; Chen, Z.Q.; Qi, G.Y. Chaotic characteristics analysis and circuit implementation for a fractional-order system. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 845–853. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Sambas, A.; Kacar, S.; Cavusoglu, U. A new finance chaotic system; its electronic circuit realization; passivity based synchronization and an application to voice encryption. Nonlinear Eng. 2019, 8, 193–205. [Google Scholar] [CrossRef]
- Zhou, C.; Li, Z.; Xie, F. Coexisting attractors; crisis route to chaos in a novel 4D fractional-order system and variable-order circuit implementation. Eur. Phys. J. Plus 2019, 134, 73. [Google Scholar] [CrossRef]
- Yao, J.; Wang, K.; Huang, P.; Chen, L.; Machado, J.T. Analysis and implementation of fractional-order chaotic system with standard components. J. Adv. Res. 2020, 25, 97–109. [Google Scholar] [CrossRef]
- Arıcıoğlu, B.; Kaçar, S. Circuit implementation and PRNG applications of time delayed Lorenz System. Chaos Theory Appl. 2022, 4, 4–9. [Google Scholar] [CrossRef]
- Kaçar, S. Digital circuit implementation and PRNG-based data security application of variable-order fractional Hopfield neural network under electromagnetic radiation using Grünwald-Letnikov method. Eur. Phys. J. Spec. Top. 2022, 231, 1969–1981. [Google Scholar] [CrossRef]
- Emiroglu, S.; Akgül, A.; Adıyaman, Y.; Gümüş, T.E.; Uyaroglu, Y.; Yalçın, M.A. A new hyperchaotic system from T chaotic system: Dynamical analysis, circuit implementation, control and synchronization. Circuit World 2022, 48, 265–277. [Google Scholar] [CrossRef]
- Charef, A.; Sun, H.H.; Tsao, Y.Y.; Onaral, B. Fractal system as represented by singularity function. IEEE Trans. Autom. Control 1992, 37, 1465–1470. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Chen, H.; Holland, F.; Stynes, M. An analysis of the Grünwald–Letnikov scheme for initial-value problems with weakly singular solutions. Appl. Numer. Math. 2019, 139, 52–61. [Google Scholar] [CrossRef]
- Liouville, J. Mémoire Sur quelques Questions de Géometrie et de Mécanique, et sur un nouveau genre de Calcul pour résoudre ces Questions. J. L’École Polytech. 1832, 13, 1–69. [Google Scholar]
- Riemann, B. Versuch einer allgemeinen Auffassung der Integration und Differentiation. Gesammelte Werke 1876, 62, 52–61. [Google Scholar]
- Grünwald, A.K. Uber “begrente” Derivationen und deren Anwedung. Z. Angew. Math. Phys. 1867, 12, 441–480. [Google Scholar]
- Letnikov, A.V. Theory of differentiation with an arbtraly indicator. Matem Sb. 1868, 3, 1–68. [Google Scholar]
- Tarasov, V.E. Lattice model of fractional gradient and integral elasticity: Long-range interaction of Grünwald–Letnikov–Riesz type. Mech. Mater. 2014, 70, 106–114. [Google Scholar] [CrossRef]
- Sierociuk, D.; Malesza, W.; Macias, M. On the recursive fractional variable-order derivative: Equivalent switching strategy, duality, and analog modeling. Circuits Syst. Signal Process. 2015, 34, 1077–1113. [Google Scholar] [CrossRef]
- Sierociuk, D.; Malesza, W.; Macias, M. Derivation, interpretation, and analog modelling of fractional variable order derivative definition. Appl. Math. Model. 2015, 39, 3876–3888. [Google Scholar] [CrossRef]
- Ahmad, W.M.; Sprott, J.C. Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 2003, 16, 339–351. [Google Scholar] [CrossRef]
- Kacar, S.; Wei, Z.; Akgul, A.; Aricioglu, B. A novel 4D chaotic system based on two degrees of freedom nonlinear mechanical system. Z. Naturforschung A 2018, 73, 595–607. [Google Scholar] [CrossRef]
- Moysis, L. Bifurcation Diagram for the Lorenz System (Local Maxima). 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/158081-bifurcation-diagram-for-the-lorenz-system-local-maxima (accessed on 11 April 2025).
- Li, H.; Shen, Y.; Han, Y.; Dong, J.; Li, J. Determining Lyapunov exponents of fractional-order systems: A general method based on memory principle. Chaos Solitons Fractals 2023, 168, 113167. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 460, 603–611. [Google Scholar] [CrossRef]
- Cui, Q.; Xu, C.; Xu, Y.; Ou, W.; Pang, Y.; Liu, Z.; Shen, J.; Baber, M.Z.; Maharajan, C.; Ghosh, U. Bifurcation and Controller Design of 5D BAM Neural Networks with Time Delay. Int. J. Numer. Model. Electron. Netw. Devices Fields 2024, 37, e3316. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, C.; Xu, Y.; Lin, J.; Pang, Y.; Liu, Z.; Shen, J. Mathematical exploration on control of bifurcation for a 3D predator-prey model with delay. AIMS Math. 2024, 9, 29883–29915. [Google Scholar] [CrossRef]
- Berkal, M.; Almatrafi, M.B. Bifurcation and stability of two-dimensional activator–inhibitor model with fractional-order derivative. Fractal Fract. 2023, 7, 344. [Google Scholar] [CrossRef]
- Berkal, M.; Navarro, J.F.; Hamada, M.Y.; Semmar, B. Qualitative behavior for a discretized conformable fractional-order predator–prey model. J. Appl. Math. Comput. 2025, 1–23. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Marin, M.; Ellahi, R.; Fudulu, I.M. Insight into the dynamics of EMHD hybrid nanofluid (ZnO/CuO-SA) flow through a pipe for geothermal energy applications. J. Therm. Anal. Calorim. 2023, 148, 14261–14273. [Google Scholar] [CrossRef]
- Yadav, A.K.; Carrera, E.; Marin, M.; Othman, M.I.A. Reflection of hygrothermal waves in a Nonlocal Theory of coupled thermo-elasticity. Mech. Adv. Mater. Struct. 2024, 31, 1083–1096. [Google Scholar] [CrossRef]







| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0.010 | 0.029 | 0.039 | 0.050 | 0.066 | 0.094 | 3.908 | 78.446 | 1345.376 | |
| 0.025 | 0.033 | 0.044 | 0.060 | 0.086 | 3.642 | 73.082 | 1253.360 | - |
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| (F) | 2.30 | 21.87 | 12.02 | 7.89 | 6.28 | 6.57 | 13.57 | 12.67 | 11.74 |
| () | 43.46 | 1.56 | 2.15 | 2.51 | 2.40 | 1.63 | 0.02 | 0.001 | 0.0001 |
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| (F) | 5.75 | 54.68 | 30.06 | 19.73 | 15.71 | 16.41 | 33.92 | 31.68 | 29.36 |
| (k) | 17,385.20 | 623.47 | 860.50 | 1004.83 | 960.70 | 651.44 | 7.55 | 0.60 | 0.03 |
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| (nF) | 2.30 | 21.87 | 12.02 | 7.89 | 6.28 | 6.57 | 13.57 | 12.67 | 11.74 |
| (k) | 17,385.20 | 623.47 | 860.50 | 1004.83 | 960.70 | 651.44 | 7.55 | 0.60 | 0.03 |
| n | 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|---|
| dB | (nF) | 2.21 | 9.01 | 4.61 | 4.23 | 7.85 | 6.97 |
| (k) | 18,089.12 | 1253.39 | 15,871.7 | 1062.10 | 2.42 | 0.02 | |
| dB | (nF) | 1.98 | 2.41 | 4.06 | 3.22 | - | - |
| (k) | 20,179.28 | 3093.95 | 24.80 | 0.002 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arıcıoğlu, B. Circuit Design and Implementation of a Time-Varying Fractional-Order Chaotic System. Axioms 2025, 14, 310. https://doi.org/10.3390/axioms14040310
Arıcıoğlu B. Circuit Design and Implementation of a Time-Varying Fractional-Order Chaotic System. Axioms. 2025; 14(4):310. https://doi.org/10.3390/axioms14040310
Chicago/Turabian StyleArıcıoğlu, Burak. 2025. "Circuit Design and Implementation of a Time-Varying Fractional-Order Chaotic System" Axioms 14, no. 4: 310. https://doi.org/10.3390/axioms14040310
APA StyleArıcıoğlu, B. (2025). Circuit Design and Implementation of a Time-Varying Fractional-Order Chaotic System. Axioms, 14(4), 310. https://doi.org/10.3390/axioms14040310








