Initial Value Problem For Nonlinear Fractional Differential Equations With ψ-Caputo Derivative Via Monotone Iterative Technique

Abstract

In this article, we discuss the existence and uniqueness of extremal solutions for nonlinear initial value problems of fractional differential equations involving the $\psi$-Caputo derivative. Moreover, some uniqueness results are obtained. Our results rely on the standard tools of functional analysis. More precisely we apply the monotone iterative technique combined with the method of upper and lower solutions to establish sufficient conditions for existence as well as the uniqueness of extremal solutions to the initial value problem. An illustrative example is presented to point out the applicability of our main results.

1. Introduction

Fractional differential equations have been applied in many fields of engineering, physics, biology, and chemistry see [1,2,3,4]. Moreover, to get a couple of developments about the theory of fractional differential equations, one can allude to the monographs of Abbas et al. [5,6,7], Kilbas et al. [8], Miller and Ross [9], Podlubny [10], and Zhou [11,12], as well as to the papers by Agarwal, et al. [13], Benchohra, et al. [14,15,16], and the references therein. In the recent past, Almeida in [17] presented a new fractional differentiation operator called by $\psi$-Caputo fractional operator. For more details see [18,19,20,21,22,23], and the references given therein.

At the present day, different kinds of fixed point theorems are widely used as fundamental tools in order to prove the existence and uniqueness of solutions for various classes of nonlinear fractional differential equations for details, we refer the reader to a series of papers [24,25,26,27,28,29,30] and the references therein, but here we focus on those using the monotone iterative technique, coupled with the method of upper and lower solutions. This method is a very useful tool for proving the existence and approximation of solutions to many applied problems of nonlinear differential equations and integral equations (see [31,32,33,34,35,36,37,38,39,40,41,42]). However, as far as we know, there is no work yet reported on the existence of extremal solutions for the Cauchy problem with $\psi$-Caputo fractional derivative. Motivated by this fact, in this paper we deal with the existence and uniqueness of extremal solutions for the following initial value problem of fractional differential equations involving the $\psi$-Caputo derivative:

$$\left\{\begin{array}{c}{}^{c}D_{a^{+}}^{\alpha ;\psi }x\left(t\right)=f(t,x\left(t\right)),t\in \mathrm{J}:=[a,b],\hfill \\ x\left(a\right)=a^{\ast },\hfill \end{array}\right.$$

(1)

where ${}^c{D}_{a^{+}}^{\alpha ;\psi }$ is the $\psi$-Caputo fractional derivative of order $\alpha \in (0,1],f:[a,b]\times \mathbb{R}⟶\mathbb{R}$ is a given continuous function and $a^{\ast }\in \mathbb{R}.$

The rest of the paper is organized as follows: in Section 2, we give some necessary definitions and lemmas. The main results are given in Section 3. Finally, an example is presented to illustrate the applicability of the results developed.

2. Preliminaries

In this section, we introduce some notations and definitions of fractional calculus and present preliminary results needed in our proofs later.

We begin by defining $\psi$-Riemann-Liouville fractional integrals and derivatives. In what follows,

Definition 1

([8,17]). For $\alpha >0$, the left-sided ψ-Riemann-Liouville fractional integral of order α for an integrable function $x:\mathrm{J}⟶\mathbb{R}$ with respect to another function $\psi :\mathrm{J}⟶\mathbb{R}$ that is an increasing differentiable function such that ${\psi }^{\prime }\left(t\right)\ne 0$, for all $t\in \mathrm{J}$ is defined as follows

$$I_{a^{+}}^{\alpha ;\psi }x\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}x\left(s\right)\mathrm{ds},$$

(2)

where Γ is the classical Euler Gamma function.

Definition 2

([17]). Let $n\in \mathbb{N}$ and let $\psi ,x\in C^n(\mathrm{J},\mathbb{R})$ be two functions such that ψ is increasing and ${\psi }^{\prime }\left(t\right)\ne 0$, for all $t\in \mathrm{J}$. The left-sided ψ-Riemann–Liouville fractional derivative of a function x of order α is defined by

$$\begin{array}{ccc}{D}_{a^{+}}^{\alpha ;\psi }x\left(t\right)\hfill & =& {\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}\right)}^n{I}_{a^{+}}^{n-\alpha ;\psi }x\left(t\right)\hfill \\ & =& \frac{1}{\Gamma (n-\alpha )}{\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}\right)}^n{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{n-\alpha -1}x\left(s\right)\mathrm{ds},\hfill \end{array}$$

where $n=\left[\alpha \right]+1$.

Definition 3

([17]). Let $n\in \mathbb{N}$ and let $\psi ,x\in C^n(\mathrm{J},\mathbb{R})$ be two functions such that ψ is increasing and ${\psi }^{\prime }\left(t\right)\ne 0$, for all $t\in \mathrm{J}$. The left-sided ψ-Caputo fractional derivative of x of order α is defined by

$$\begin{array}{ccc}{}^c{D}_{a^{+}}^{\alpha ;\psi }x\left(t\right)\hfill & =& I_{a^{+}}^{n-\alpha ;\psi }{\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{n}x\left(t\right),\hfill \end{array}$$

where $n=\left[\alpha \right]+1$ for $\alpha \notin \mathbb{N}$, $n=\alpha$ for $\alpha \in \mathbb{N}$.

To simplify notation, we will use the abbreviated symbol

$$x_{\psi }^{\left[n\right]}\left(t\right)={\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{n}x\left(t\right).$$

From the definition, it is clear that

$${}^c{D}_{a^{+}}^{\alpha ;\psi }x\left(t\right)=\left\{\begin{array}{ccc}{\int }_a^t\frac{{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{n-\alpha -1}}{\Gamma (n-\alpha )}{x}_{\psi }^{\left[n\right]}\left(s\right)\mathrm{ds}& ,& if\alpha \notin \mathbb{N},\\ x_{\psi }^{\left[n\right]}\left(t\right)& ,& if\alpha \in \mathbb{N}.\end{array}\right.$$

(3)

We note that if $x\in C^n(\mathrm{J},\mathbb{R})$ the $\psi$-Caputo fractional derivative of order $\alpha$ of x is determined as

$${}^{c}D_{a^{+}}^{\alpha ;\psi }x\left(t\right)=D_{a^{+}}^{\alpha ;\psi }\left[x\left(t\right)-\sum _{k=0}^{n-1}\frac{x_{\psi }^{\left[k\right]}\left(a\right)}{k!}{(\psi \left(t\right)-\psi \left(a\right))}^k\right].$$

(see, for instance, [17], Theorem 3).

Lemma 1

([20]). Let $\alpha ,\beta >0,$ and $x\in L^1(\mathrm{J},\mathbb{R})$. Then

$$I_{a^{+}}^{\alpha ;\psi }{I}_{a^{+}}^{\beta ;\psi }x\left(t\right)=I_{a^{+}}^{\alpha +\beta ;\psi }x\left(t\right),a.e.t\in \mathrm{J}.$$

In particular, if $x\in C(\mathrm{J},\mathbb{R})$, then $I_{a^{+}}^{\alpha ;\psi }{I}_{a^{+}}^{\beta ;\psi }x\left(t\right)=I_{a^{+}}^{\alpha +\beta ;\psi }x\left(t\right),$ $t\in \mathrm{J}.$

Lemma 2

([20]). Let $\alpha >0,$ The following holds:

If $x\in C(\mathrm{J},\mathbb{R})$ then

$${}^c{D}_{a^{+}}^{\alpha ;\psi }{I}_{a^{+}}^{\alpha ;\psi }x\left(t\right)=x\left(t\right),t\in \mathrm{J}.$$

If $x\in C^n(\mathrm{J},\mathbb{R}),$ $n-1<\alpha <n$. Then

$$I_{a^{+}}^{\alpha ;\psi }{}^c{D}_{a^{+}}^{\alpha ;\psi }x\left(t\right)=x\left(t\right)-\sum _{k=0}^{n-1}\frac{x_{\psi }^{\left[k\right]}\left(a\right)}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k,t\in \mathrm{J}.$$

Lemma 3

([8,20]). Let $t>a,\alpha \ge 0,$ and $\beta >0.$ Then

• $I_{a^{+}}^{\alpha ;\psi }{(\psi \left(t\right)-\psi \left(a\right))}^{\beta -1}=\frac{\Gamma \left(\beta \right)}{\Gamma (\beta +\alpha )}{(\psi \left(t\right)-\psi \left(a\right))}^{\beta +\alpha -1},$
• ${}^c{D}_{a^{+}}^{\alpha ;\psi }{(\psi \left(t\right)-\psi \left(a\right))}^{\beta -1}=\frac{\Gamma \left(\beta \right)}{\Gamma (\beta -\alpha )}{(\psi \left(t\right)-\psi \left(a\right))}^{\beta -\alpha -1},$
• ${}^c{D}_{a^{+}}^{\alpha ;\psi }{(\psi \left(t\right)-\psi \left(a\right))}^k=0,forallk\in \{0,\cdots ,n-1\},n\in \mathbb{N}.$

Definition 4

([43]). The one-parameter Mittag–Leffler function ${\mathbb{E}}_{\alpha }(·)$, is defined as:

$${\mathbb{E}}_{\alpha }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\alpha k+1)},(z\in \mathbb{R},\alpha >0).$$

Definition 5

([43]). The Two-parameter Mittag–Leffler function ${\mathbb{E}}_{\alpha ,\beta }(·)$, is defined as:

$$\begin{array}{c}{\mathbb{E}}_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\alpha k+\beta )},\alpha ,\beta >0andz\in \mathbb{R}.\hfill \end{array}$$

(4)

Theorem 1

(Weissinger’s fixed point theorem [44]). Assume $(E,d)$ to be a non empty complete metric space and let ${\beta }_j\ge 0$ for every $j\in \mathbb{N}$ such that ${\sum }_{j=0}^{n-1}{\beta }_j$ converges. Furthermore, let the mapping $\mathbb{T}:E\to E$ satisfy the inequality

$$d({\mathbb{T}}^{j}u,{\mathbb{T}}^{j}v)\le {\beta }_{j}d(u,v),$$

for every $j\in \mathbb{N}$ and every $u,v\in E$. Then, $\mathbb{T}$ has a unique fixed point $u^{\ast }$. Moreover, for any $v_0\in E$, the sequence ${\left\{{\mathbb{T}}^j{v}_0\right\}}_{j=1}^{\infty }$ converges to this fixed point $u^{\ast }$.

3. Main Results

Let us recall the definition and lemma of a solution for problem (1). First of all, we define what we mean by a solution for the boundary value problem (1).

Definition 6.

A function $x\in C(\mathrm{J},\mathbb{R})$ is said to be a solution of Equation (1) if x satisfies the equation ${}^c{D}_{a^{+}}^{\alpha ;\psi }x\left(t\right)=f(t,x\left(t\right))$, for each $t\in \mathrm{J}$ and the condition

$$x\left(a\right)=a^{\ast }.$$

For the existence of solutions for problem (1) we need the following lemma for a general linear equation of $\alpha >0$, that generalizes expression (3.1.34) in [8].

Lemma 4.

For a given $h\in C(\mathrm{J},\mathbb{R})$ and $\alpha \in (n-1,n]$, with $n\in \mathbb{N}$, the linear fractional initial value problem

$$\left\{\begin{array}{c}{}^c{D}_{a^{+}}^{\alpha ;\psi }x\left(t\right)+rx\left(t\right)=h\left(t\right),t\in \mathrm{J}:=[a,b],\hfill \\ x_{\psi }^{\left[k\right]}\left(a\right)=a_k,k=0,\dots ,n-1,\hfill \end{array}\right.$$

(5)

has a unique solution given by

$$\begin{array}{c}\begin{array}{ccc}x\left(t\right)\hfill & =\hfill & \sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }x\left(t\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)\hfill \\ & =\hfill & \sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k-\frac{r}{\Gamma \left(\alpha \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}x\left(s\right)\mathrm{ds}\hfill \\ & & +\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}h\left(s\right)\mathrm{ds}.\hfill \end{array}\hfill \end{array}$$

(6)

Moreover, the explicit solution of the Volterra integral Equation (6) can be represented by

$$\begin{array}{c}\begin{array}{cc}x\left(t\right)=\hfill & \sum _{k=0}^{n-1}{a}_k{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k{\mathbb{E}}_{\alpha ,k+1}\left(-r{(\psi \left(t\right)-\psi \left(a\right))}^{\alpha }\right)\hfill \\ & +{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}{\mathbb{E}}_{\alpha ,\alpha }\left(-r{(\psi \left(t\right)-\psi \left(a\right))}^{\alpha }\right)h\left(s\right)\mathrm{ds},\hfill \end{array}\hfill \end{array}$$

(7)

where ${\mathbb{E}}_{\alpha ,\beta }(·)$ is the two-parametric Mittag–Leffer function defined in (4).

Proof. 

Since $\alpha \in (n-1,n]$, from Lemma 2 we know that the Cauchy problem (5) is equivalent to the following Volterra integral equation

$$\begin{array}{ccc}x\left(t\right)\hfill & =\hfill & \sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }x\left(t\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)\hfill \\ & =\hfill & \sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k-\frac{r}{\Gamma \left(\alpha \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}x\left(s\right)\mathrm{ds}\hfill \\ & & +\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}h\left(s\right)\mathrm{ds}.\hfill \end{array}$$

Note that the above equation can be written in the following form

$$x\left(t\right)=\mathcal{T}x\left(t\right),$$

where the operator $\mathcal{T}$ is defined by

$$\mathcal{T}x\left(t\right)=\sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }x\left(t\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right).$$

Let $n\in \mathbb{N}$ and $x,y\in C(\mathrm{J},\mathbb{R})$. Then, we have

$$\begin{array}{ccc}|{\mathcal{T}}^n\left(x\right)\left(t\right)-{\mathcal{T}}^n\left(y\right)\left(t\right)|\hfill & =& \left|-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\left({\mathcal{T}}^{n-1}x\left(t\right)-{\mathcal{T}}^{n-1}y\left(t\right)\right)\right|\hfill \\ & =& \left|-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\left(-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\left({\mathcal{T}}^{n-2}x\left(t\right)-{\mathcal{T}}^{n-2}y\left(t\right)\right)\right)\right|\hfill \\ & ⋮& \\ & =& \left|{(-r)}^n{\mathcal{I}}_{a^{+}}^{n\alpha ;\psi }(x\left(t\right)-y\left(t\right))\right|\hfill \\ & \le & \frac{{\left(r{(\psi \left(b\right)-\psi \left(a\right))}^{\alpha }\right)}^n}{\Gamma (n\alpha +1)}\parallel x-y\parallel .\hfill \end{array}$$

Hence, we have

$$\parallel {\mathcal{T}}^n\left(x\right)-{\mathcal{T}}^n\left(y\right)\parallel \le \frac{r^n{(\psi \left(b\right)-\psi \left(a\right))}^{n\alpha }}{\Gamma (n\alpha +1)}\parallel x-y\parallel .$$

It’s well known that

$$\sum _{n=0}^{\infty }\frac{r^n{(\psi \left(b\right)-\psi \left(a\right))}^{n\alpha }}{\Gamma (n\alpha +1)}={\mathbb{E}}_{\alpha }\left(r{(\psi \left(b\right)-\psi \left(a\right))}^{\alpha }\right),$$

it follows that the mapping ${\mathcal{T}}^n$ is a contraction. Hence, by Weissinger’s fixed point theorem, $\mathcal{T}$ has a unique fixed point. That is (5) has a unique solution.

Now we apply the method of successive approximations to prove that the integral Equation (6) can be expressed by

$$\begin{array}{cc}x\left(t\right)\hfill & =\sum _{k=0}^{n-1}{a}_k{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k{\mathbb{E}}_{\alpha ,k+1}\left(-r{(\psi \left(t\right)-\psi \left(a\right))}^{\alpha }\right)\hfill \\ & +{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}{\mathbb{E}}_{\alpha ,\alpha }\left(-r{(\psi \left(t\right)-\psi \left(a\right))}^{\alpha -1}\right)h\left(s\right)\mathrm{ds}.\hfill \end{array}$$

For this, we set

$$\begin{array}{c}\left\{\begin{array}{cc}{x}_0\left(t\right)=\hfill & {\displaystyle \sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k}\hfill \\ x_m\left(t\right)=\hfill & x_0\left(t\right)-\frac{r}{\Gamma \left(\alpha \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}{x}_{m-1}\left(s\right)\mathrm{ds}\hfill \\ & +\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}h\left(s\right)\mathrm{ds}.\hfill \end{array}\right.\hfill \end{array}$$

(8)

It follows from Equation (8) and Lemma 3 that

$$\begin{array}{cc}{x}_1\left(t\right)\hfill & =x_0\left(t\right)-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{x}_0\left(t\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)\hfill \\ & {\displaystyle =\sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k-r\sum _{k=0}^{n-1}\frac{a_k}{\Gamma (\alpha +k+1)}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^{\alpha +k}+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right).}\hfill \end{array}$$

(9)

Similarly, Equations (8) and (9) and Lemmas 1 and 3 yield

$$\begin{array}{ccc}{x}_2\left(t\right)\hfill & =\hfill & x_0\left(t\right)-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{x}_1\left(t\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)\hfill \\ & =\hfill & {\displaystyle \sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k-r{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\left({\displaystyle \sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k}\right.}\hfill \\ & & \left.{\displaystyle -r\sum _{k=0}^{n-1}\frac{a_k}{\Gamma (\alpha +k+1)}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^{\alpha +k}+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)}\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)\hfill \\ & =\hfill & {\displaystyle \sum _{k=0}^{n-1}\frac{a_k}{k!}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k-r\sum _{k=0}^{n-1}\frac{a_k}{\Gamma (\alpha +k+1)}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^{\alpha +k}}\hfill \\ & & +r^2\sum _{k=0}^{n-1}\frac{a_k}{\Gamma (2\alpha +k+1)}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^{2\alpha +k}-r{\mathcal{I}}_{a^{+}}^{2\alpha ;\psi }h\left(t\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)\hfill \\ & =\hfill & \sum _{l=0}^2\sum _{k=0}^{n-1}\frac{{(-r)}^l{a}_k}{\Gamma (l\alpha +k+1)}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^{l\alpha +k}+{\int }_a^t{\psi }^{\prime }\left(s\right)\sum _{l=0}^1\frac{{(-r)}^{l-1}{(\psi \left(t\right)-\psi \left(s\right))}^{l\alpha +\alpha -1}}{\Gamma (l\alpha +\alpha )}h\left(s\right)\mathrm{ds}.\hfill \end{array}$$

Continuing this process, we derive the following relation

$$\begin{array}{cc}{x}_m\left(t\right)=\hfill & \sum _{l=0}^m\sum _{k=0}^{n-1}\frac{{(-r)}^l{a}_k}{\Gamma (l\alpha +k+1)}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^{l\alpha +k}+{\int }_a^t{\psi }^{\prime }\left(s\right)\sum _{l=0}^{m-1}\frac{{(-r)}^{l-1}{(\psi \left(t\right)-\psi \left(s\right))}^{l\alpha +\alpha -1}}{\Gamma (l\alpha +\alpha )}h\left(s\right)\mathrm{ds}.\hfill \end{array}$$

Taking the limit as $n\to \infty$, we obtain the following explicit solution $x\left(t\right)$ to the integral Equation (6):

$$\begin{array}{ccc}x\left(t\right)\hfill & =\hfill & \sum _{l=0}^{\infty }\sum _{k=0}^{n-1}\frac{{(-r)}^l{a}_k}{\Gamma (l\alpha +k+1)}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^{l\alpha +k}+{\int }_a^t{\psi }^{\prime }\left(s\right)\sum _{l=0}^{\infty }\frac{{(-r)}^{l-1}{(\psi \left(t\right)-\psi \left(s\right))}^{l\alpha +\alpha -1}}{\Gamma (l\alpha +\alpha )}h\left(s\right)\mathrm{ds}\hfill \\ & =\hfill & \sum _{k=0}^{n-1}{a}_k{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^k\sum _{l=0}^{\infty }\frac{{(-r)}^l}{\Gamma (l\alpha +k+1)}{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^{l\alpha }\hfill \\ & & +{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}\sum _{l=0}^{\infty }\frac{{(-r)}^{l-1}{(\psi \left(t\right)-\psi \left(s\right))}^{l\alpha }}{\Gamma (l\alpha +\alpha )}h\left(s\right)\mathrm{ds}.\hfill \end{array}$$

Taking into account (4), we get

$$\begin{array}{cc}x\left(t\right)\hfill & =\sum _{k=0}^{n-1}{a}_k{\left[\psi \left(t\right)-\psi \left(a\right)\right]}^k{\mathbb{E}}_{\alpha ,k+1}\left(-r{(\psi \left(t\right)-\psi \left(a\right))}^{\alpha }\right)\hfill \\ & +{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}{\mathbb{E}}_{\alpha ,\alpha }\left(-r{(\psi \left(t\right)-\psi \left(s\right))}^{\alpha }\right)h\left(s\right)\mathrm{ds}.\hfill \end{array}$$

Then the proof is completed. □

Lemma 5

(Comparison result). Let $\alpha \in (0,1]$ be fixed and $r\in \mathbb{R}$. If $\rho \in C(\mathrm{J},\mathbb{R})$ satisfies the following inequalities

$$\begin{array}{c}\left\{\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }\rho \left(t\right)\ge -r\rho \left(t\right),\hfill & t\in [a,b],\hfill \\ \rho \left(a\right)\ge 0,\hfill \end{array}\right.\hfill \end{array}$$

(10)

then $\rho \left(t\right)\ge 0$ for all $t\in \mathrm{J}$.

Proof. 

Using the integral representation (7) and the fact that, ${\mathbb{E}}_{\alpha ,1}\left(z\right)\ge 0$ and ${\mathbb{E}}_{\alpha ,\alpha }\left(z\right)\ge 0$ for all $\alpha \in (0,1]$ and $z\in \mathbb{R}$, (see [45]) it suffices to take $h\left(t\right)={}^c\mathcal{D}_{a^{+}}^{\alpha ;\psi }\rho \left(t\right)+r\rho \left(t\right)\ge 0$ with initial conditions $\rho \left(a\right)=a^{\ast }\ge 0$. □

Definition 7.

A function $x_0\in C(\mathrm{J},\mathbb{R})$ is said to be a lower solution of the problem (1), if it satisfies

$$\begin{array}{c}\left\{\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }{x}_0\left(t\right)\le f(t,x_0),\hfill & t\in (a,b],\hfill \\ x_0\left(a\right)\le a^{\ast }.\hfill \end{array}\right.\hfill \end{array}$$

(11)

Definition 8.

A function $y_0\in C(\mathrm{J},\mathbb{R})$ is called an upper solution of problem (1), if it satisfies

$$\begin{array}{c}\left\{\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }{y}_0\left(t\right)\ge f(t,y_0),\hfill & t\in (a,b],\hfill \\ y_0\left(a\right)\ge a^{\ast }.\hfill \end{array}\right.\hfill \end{array}$$

(12)

Theorem 2.

Let the function $f\in C(\mathrm{J}\times \mathbb{R},\mathbb{R})$. In addition assume that:

(H₁)

There exist $x_0$, $y_0\in C(\mathrm{J},\mathbb{R})$ such that $x_0$ and $y_0$ are lower and upper solutions of problem (1), respectively, with $x_0\left(t\right)\le y_0\left(t\right),t\in \mathrm{J}$.

(H₂)

There exists a constant $r\in \mathbb{R}$ such that

$$f(t,y)-f(t,x)\ge -r(y-x)\mathit{for}{x}_0\le x\le y\le y_0.$$

Then there exist monotone iterative sequences $\left\{x_n\right\}$ and $\left\{y_n\right\}$, which converge uniformly on the interval $\mathrm{J}$ to the extremal solutions of (1) in the sector $[x_0,y_0]$, where

$$[x_0,y_0]=\{z\in C(\mathrm{J},\mathbb{R}):x_0\left(t\right)\le z\left(t\right)\le y_0\left(t\right),t\in \mathrm{J}\}.$$

Proof. 

First, for any $x_0\left(t\right),y_0\left(t\right)\in C(\mathrm{J},\mathbb{R})$, we consider the following linear initial value problems of fractional order:

$$\begin{array}{c}\left\{\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }{x}_{n+1}\left(t\right)=f(t,x_n\left(t\right))-r(x_{n+1}\left(t\right)-x_n\left(t\right)),\hfill & t\in \mathrm{J},\hfill \\ x_{n+1}\left(a\right)=a^{\ast },\hfill \end{array}\right.\hfill \end{array}$$

(13)

and

$$\begin{array}{c}\left\{\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }{y}_{n+1}\left(t\right)=f(t,y_n\left(t\right))-r(y_{n+1}\left(t\right)-y_n\left(t\right)),\hfill & t\in \mathrm{J},\hfill \\ y_{n+1}\left(a\right)=a^{\ast }.\hfill \end{array}\right.\hfill \end{array}$$

(14)

By Lemma 4, we know that (13) and (14) have unique solutions in $C(\mathrm{J},\mathbb{R})$ which are defined as follows:

$$\begin{array}{c}\begin{array}{cc}\hfill & x_{n+1}\left(t\right)=a^{\ast }{\mathbb{E}}_{\alpha ,1}\left(-r{(\psi \left(t\right)-\psi \left(a\right))}^{\alpha }\right)\hfill \\ \hfill & +{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}{\mathbb{E}}_{\alpha ,\alpha }\left(-r{(\psi \left(t\right)-\psi \left(s\right))}^{\alpha }\right)\left(f(s,x_n\left(s\right))+r{x}_n\left(s\right)\right)\mathrm{ds},t\in \mathrm{J},\hfill \end{array}\hfill \end{array}$$

(15)

$$\begin{array}{c}\begin{array}{cc}\hfill & y_{n+1}\left(t\right)=a^{\ast }{\mathbb{E}}_{\alpha ,\alpha }\left(-r{(\psi \left(t\right)-\psi \left(a\right))}^{\alpha }\right)\hfill \\ \hfill & +{\int }_a^t{\psi }^{\prime }\left(s\right){(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}{\mathbb{E}}_{\alpha ,\alpha }\left(-r{(\psi \left(t\right)-\psi \left(s\right))}^{\alpha }\right)\left(f(s,y_n\left(s\right))+r{y}_n\left(s\right)\right)\mathrm{ds},t\in \mathrm{J}.\hfill \end{array}\hfill \end{array}$$

(16)

We will divide the proof into three steps.

• Step 1: We show that the sequences $x_n\left(t\right),y_n\left(t\right)(n\ge 1)$ are lower and upper solutions of problem (1), respectively and the following relation holds

  $$\begin{array}{c}{x}_0\left(t\right)\le x_1\left(t\right)\le \cdots \le x_n\left(t\right)\le \cdots \le y_n\left(t\right)\le \cdots \le y_1\left(t\right)\le y_0\left(t\right),t\in \mathrm{J}.\hfill \end{array}$$

  (17)

First, we prove that

$$\begin{array}{c}{x}_0\left(t\right)\le x_1\left(t\right)\le y_1\left(t\right)\le y_0\left(t\right),t\in \mathrm{J}.\hfill \end{array}$$

(18)

Set $\rho \left(t\right)=x_1\left(t\right)-x_0\left(t\right)$. From (13) and Definition 7, we obtain

$$\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }\rho \left(t\right)\hfill & ={}^{c}D_{a^{+}}^{\alpha ;\psi }{x}_1\left(t\right)-{}^{c}D_{a^{+}}^{\alpha ;\psi }{x}_0\left(t\right)\hfill \\ & \ge f\left(t,x_0\left(t\right)\right)-r(x_1\left(t\right)-x_0\left(t\right))-f\left(t,x_0\left(t\right)\right)\hfill \\ & =-r\rho \left(t\right).\hfill \end{array}$$

Again, since

$$\rho \left(a\right)=x_1\left(a\right)-x_0\left(a\right)=a^{\ast }-x_0\left(a\right)\ge 0.$$

By Lemma 5, $\rho \left(t\right)\ge 0$, for $t\in \mathrm{J}$. That is, $x_0\left(t\right)\le x_1\left(t\right)$. Similarly, we can show that $y_1\left(t\right)\le y_0\left(t\right),t\in \mathrm{J}$.

Now, let $\rho \left(t\right)=y_1\left(t\right)-x_1\left(t\right)$. From (13), (14) and $\left(H2\right)$, we get

$$\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }\rho \left(t\right)\hfill & ={}^{c}D_{a^{+}}^{\alpha ;\psi }{y}_1\left(t\right)-{}^{c}D_{a^{+}}^{\alpha ;\psi }{x}_1\left(t\right)\hfill \\ & =f\left(t,y_0\left(t\right)\right)-r\left(y_1\left(t\right)-y_0\left(t\right)\right)-f\left(t,x_0\left(t\right)\right)+r\left(x_1\left(t\right)-x_0\left(t\right)\right)\hfill \\ & =f\left(t,y_0\left(t\right)\right)-f\left(t,x_0\left(t\right)\right)-r\left(y_1\left(t\right)-y_0\left(t\right)\right)+r\left(x_1\left(t\right)-x_0\left(t\right)\right)\hfill \\ & \ge -r\left(y_0\left(t\right)-x_0\left(t\right)\right)-r\left(y_1\left(t\right)-y_0\left(t\right)\right)+r\left(x_1\left(t\right)-x_0\left(t\right)\right)\hfill \\ & =-r\rho \left(t\right).\hfill \end{array}$$

Since, $\rho \left(a\right)=x_1\left(a\right)-y_1\left(a\right)=a^{\ast }-a^{\ast }=0$. By Lemma 5, we get $x_1\left(t\right)\le y_1\left(t\right),t\in \mathrm{J}$.

Secondly, we show that $x_1\left(t\right),y_1\left(t\right)$ are lower and upper solutions of problem (1), respectively. Since $x_0$ and $y_0$ are lower and upper solutions of problem (1), by $\left(H_2\right)$, it follows that

$$\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }{x}_1\left(t\right)\hfill & =f\left(t,x_0\left(t\right)\right)-r\left(x_1\left(t\right)-x_0\left(t\right)\right)\le f\left(t,x_1\left(t\right)\right),\hfill \end{array}$$

also $x_1\left(a\right)=a^{\ast }.$ Therefore, $x_1\left(t\right)$ is a lower solution of problem (1). Similarly, it can be obtained that $y_1\left(t\right)$ is an upper solution of problem (1).

By the above arguments and mathematical induction, we can show that the sequences $x_n\left(t\right),y_n\left(t\right),(n\ge 1)$ are lower and upper solutions of problem (1), respectively and the following relation holds

$$\begin{array}{c}{x}_0\left(t\right)\le x_1\left(t\right)\le \cdots \le x_n\left(t\right)\le \cdots \le y_n\left(t\right)\le \cdots \le y_1\left(t\right)\le y_0\left(t\right),t\in \mathrm{J}.\hfill \end{array}$$

• Step 2: The sequences $\left\{x_n\left(t\right)\right\}$, $\left\{y_n\left(t\right)\right\}$ converge uniformly to their limit functions $x^{\ast }\left(t\right),y^{\ast }\left(t\right)$, respectively.

Note that the sequence $\left\{x_n\left(t\right)\right\}$ is monotone nondecreasing and is bounded from above by $y_0\left(t\right)$. Since the sequence $\left\{y_n\left(t\right)\right\}$ is monotone nonincreasing and is bounded from below by $x_0\left(t\right)$, therefore the pointwise limits exist and these limits are denoted by $x^{\ast }$ and $y^{\ast }$. Moreover, since $\left\{x_n\left(t\right)\right\}$, $\left\{y_n\left(t\right)\right\}$ are sequences of continuous functions defined on the compact set $[a,b]$, hence by Dini’s theorem [46], the convergence is uniform. This is

$$\begin{array}{c}\underset{n\to \infty }{lim}{x}_n\left(t\right)=x^{\ast }\left(t\right)\mathrm{and}\underset{n\to \infty }{lim}{y}_n\left(t\right)=y^{\ast }\left(t\right),\hfill \end{array}$$

uniformly on $t\in \mathrm{J}$ and the limit functions $x^{\ast }$, $y^{\ast }$ satisfy problem (1). Furthermore, $x^{\ast }$ and $y^{\ast }$ satisfy the relation

$$x_0\le x_1\le \cdots \le x_n\le x^{\ast }\le y^{\ast }\le \cdots \le y_n\le \cdots \le y_1\le y_0.$$

• Step 3: We prove that $x^{\ast }$ and $y^{\ast }$ are extremal solutions of problem (1) in $[x_0,y_0]$.

Let $z\in [x_0,y_0]$ be any solution of (1). We assume that the following relation holds for some $n\in \mathbb{N}$:

$$\begin{array}{c}{x}_n\left(t\right)\le z\left(t\right)\le y_n\left(t\right),t\in \mathrm{J}.\hfill \end{array}$$

(19)

Let $\rho \left(t\right)=z\left(t\right)-x_{n+1}\left(t\right)$. We have

$$\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }\rho \left(t\right)\hfill & ={}^{c}D_{a^{+}}^{\alpha ;\psi }z\left(t\right)-{}^{c}D_{a^{+}}^{\alpha ;\psi }{x}_{n+1}\left(t\right)\hfill \\ & =f\left(t,z\left(t\right)\right)-f\left(t,x_n\left(t\right)\right)+r\left(x_{n+1}\left(t\right)-x_n\left(t\right)\right)\hfill \\ & \ge -r\left(z\left(t\right)-x_n\left(t\right)\right)+r\left(x_{n+1}\left(t\right)-x_n\left(t\right)\right)\hfill \\ & =-r\rho \left(t\right).\hfill \end{array}$$

Furthermore, $\rho \left(a\right)=z\left(a\right)-x_{n+1}\left(a\right)=a^{\ast }-a^{\ast }=0$. By Lemma 5, we obtain $\rho \left(t\right)\ge 0,t\in \mathrm{J}$, which means

$$x_{n+1}\left(t\right)\le z\left(t\right),t\in \mathrm{J}.$$

Using the same method, we can show that

$$z\left(t\right)\le y_{n+1}\left(t\right),t\in \mathrm{J}.$$

Hence, we have

$$x_{n+1}\left(t\right)\le z\left(t\right)\le y_{n+1}\left(t\right),t\in \mathrm{J}.$$

Therefore, (19) holds on $\mathrm{J}$ for all $n\in \mathbb{N}$. Taking the limit as $n\to \infty$ on both sides of (19), we get

$$x^{\ast }\le z\le y^{\ast }.$$

Therefore $x^{\ast }$, $y^{\ast }$ are the extremal solutions of (1) in $[x_0,y_0]$. This completes the proof. □

Now, we shall prove the uniqueness of the solution of the system (1) by monotone iterative technique.

Theorem 3.

Suppose that (H1) and (H2) are satisfied. Furthermore, we impose that:

(H3) 

There exists a constant $r^{\ast }\ge -r$ such that

$$f(t,y)-f(t,x)\le r^{\ast }(y-x),$$

for every $x_0\le x\le y\le y_0,t\in \mathrm{J}$. Then problem (1) has a unique solution between $x_0$ and $y_0$.

Proof. 

From the Theorem 2, we know that $x^{\ast }\left(t\right)$ and $y^{\ast }\left(t\right)$ are the extremal solutions of the IVP (1) and $x^{\ast }\left(t\right)\le y^{\ast }\left(t\right),t\in \mathrm{J}$. It is sufficient to prove $x^{\ast }\left(t\right)\ge y^{\ast }\left(t\right),t\in \mathrm{J}$. In fact, let $\rho \left(t\right)=x^{\ast }\left(t\right)-y^{\ast }\left(t\right),t\in \mathrm{J}$, in view of (H3), we have

$$\begin{array}{cc}{}^{c}D_{a^{+}}^{\alpha ;\psi }\rho \left(t\right)\hfill & ={}^{c}D_{a^{+}}^{\alpha ;\psi }{x}^{\ast }\left(t\right)-{}^{c}D_{a^{+}}^{\alpha ;\psi }{y}^{\ast }\left(t\right)\hfill \\ & =f\left(t,x^{\ast }\left(t\right)\right)-f\left(t,y^{\ast }\left(t\right)\right)\hfill \\ & \ge r^{\ast }\left(x^{\ast }\left(t\right)-y^{\ast }\left(t\right)\right)\hfill \\ & =r^{\ast }\rho \left(t\right).\hfill \end{array}$$

Furthermore, $\rho \left(a\right)=x^{\ast }\left(a\right)-y^{\ast }\left(a\right)=a^{\ast }-a^{\ast }=0$. From Lemma 5, it follows that $\rho \left(t\right)\ge 0,t\in \mathrm{J}.$ Hence, we obtain

$$x^{\ast }\left(t\right)\ge y^{\ast }\left(t\right),t\in \mathrm{J}.$$

Therefore, $x^{\ast }\equiv y^{\ast }$ is the unique solution of the Cauchy problem (1) in $[x_0,y_0]$. This ends the proof of Theorem 3. □

As a direct consequence of the previous result, we arrive at the following one

Corollary 1.

Suppose that (H1) is satisfied and that $f\in C(E,\mathbb{R})$, is differentiable with respect to x and $\partial f/\partial x\in C(E,\mathbb{R})$, with

$$E=\{(t,x)\in {\mathbb{R}}^2,suchthat{x}_0\left(t\right)\le x\le y_0\left(t\right)\}.$$

Then problem (1) has a unique solution between $x_0$ and $y_0$.

Proof. 

The proof follows immediately from the fact that E is a compact set and, as a consequence, $\partial f/\partial x$ is bounded in E. □

4. An Example

Example 1.

Consider the following problem:

$$\left\{\begin{array}{c}{}^{c}D_{0^{+}}^{\frac{1}{2}}x\left(t\right)=1-x^2\left(t\right)+2t,t\in \mathrm{J}:=[0,1],\hfill \\ x\left(0\right)=1\hfill \end{array}\right.$$

(20)

Note that, this problem is a particular case of IVP (1), where

$$\begin{array}{cc}\alpha \hfill & =\frac{1}{2},a=0,b=1,a^{\ast }=1,\psi \left(t\right)=t,\hfill \end{array}$$

and $f:\mathrm{J}\times \mathbb{R}⟶\mathbb{R}$ given by

$$f(t,x)=1-x^2+2t,fort\in \mathrm{J},x\in \mathbb{R}.$$

Taking $x_0\left(t\right)\equiv 0$ and $y_0\left(t\right)=1+t$, it is not difficult to verify that $x_0,y_0$ are lower and upper solutions of (20), respectively, and $x_0\le y_0$. So $\left(H_1\right)$ of Theorem 2 holds

On the other hand, it is clear that the function f is continuous and satisfies

$$\begin{array}{c}\left|\frac{f(t,x)}{\partial x}(t,x)\right|=|-2x|\le 4forallt\in [0,1]and0\le x\le t+1.\hfill \end{array}$$

Hence, by Corollary 1, the initial value problem (20) has a unique solution $u^{\ast }$ and there exist monotone iterative sequences $\left\{x_n\right\}$ and $\left\{y_n\right\}$ converging uniformly to $u^{\ast }$. Furthermore, we have the following iterative sequences

$$\begin{array}{cc}{x}_{n+1}\left(t\right)\hfill & ={\mathbb{E}}_{\frac{1}{2},1}\left(-4\sqrt{t}\right)+{\int }_0^t{(t-s)}^{-1/2}{\mathbb{E}}_{\frac{1}{2},\frac{1}{2}}\left(-4\sqrt{t-s}\right)\left(1-x_n^2\left(s\right)+2s+4x_n\left(s\right)\right)\mathrm{ds},t\in \mathrm{J},\hfill \\ y_{n+1}\left(t\right)\hfill & =E_{\frac{1}{2},1}\left(-4\sqrt{t}\right)+{\int }_0^t{(t-s)}^{-1/2}{\mathbb{E}}_{\frac{1}{2},\frac{1}{2}}\left(-4\sqrt{t-s}\right)\left(1-y_n^2\left(s\right)+2s+4y_n\left(s\right)\right)\mathrm{ds},t\in \mathrm{J}.\hfill \end{array}$$

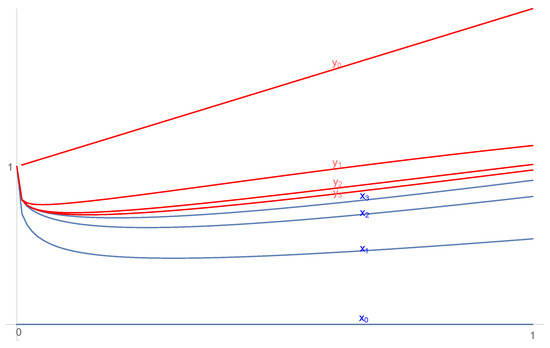
We notice that the sequences are obtained by solving a recurrence formula of the type $v_{n+1}=A{v}_n$, with A a suitable integral operator and $v_0$ given. So, by a simple numerical procedure, it is not difficult to represent some iterates of the recurrence sequence. We plot in Figure 1 the four first iterates of each sequence. We point out that the unique solution is lying within $x_3$ and $y_3$ which gives us a good approximation of such a solution.

Figure 1. First four iterates for problem (20).

5. Conclusions

In previous sections, we have presented the existence and uniqueness of extremal solutions to a Cauchy problem with $\psi$-Caputo fractional derivative. Moreover, some uniqueness results are obtained. The proof of the existence results is based on the monotone iterative technique combined with the method of upper and lower solutions. Moreover, an example is presented to illustrate the validity of our main results. Our results are not only new in the given configuration but also correspond to some new situations associated with the specific values of the parameters involved in the given problem.