Degeneration Effects of Thin-Film Sensors after Critical Load Conditions of Machine Components
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sensor Manufacturing
2.1.1. Sensor Design
2.1.2. Sputter Deposition
2.1.3. Sample Preparation
2.2. Measurement Details
3. Results
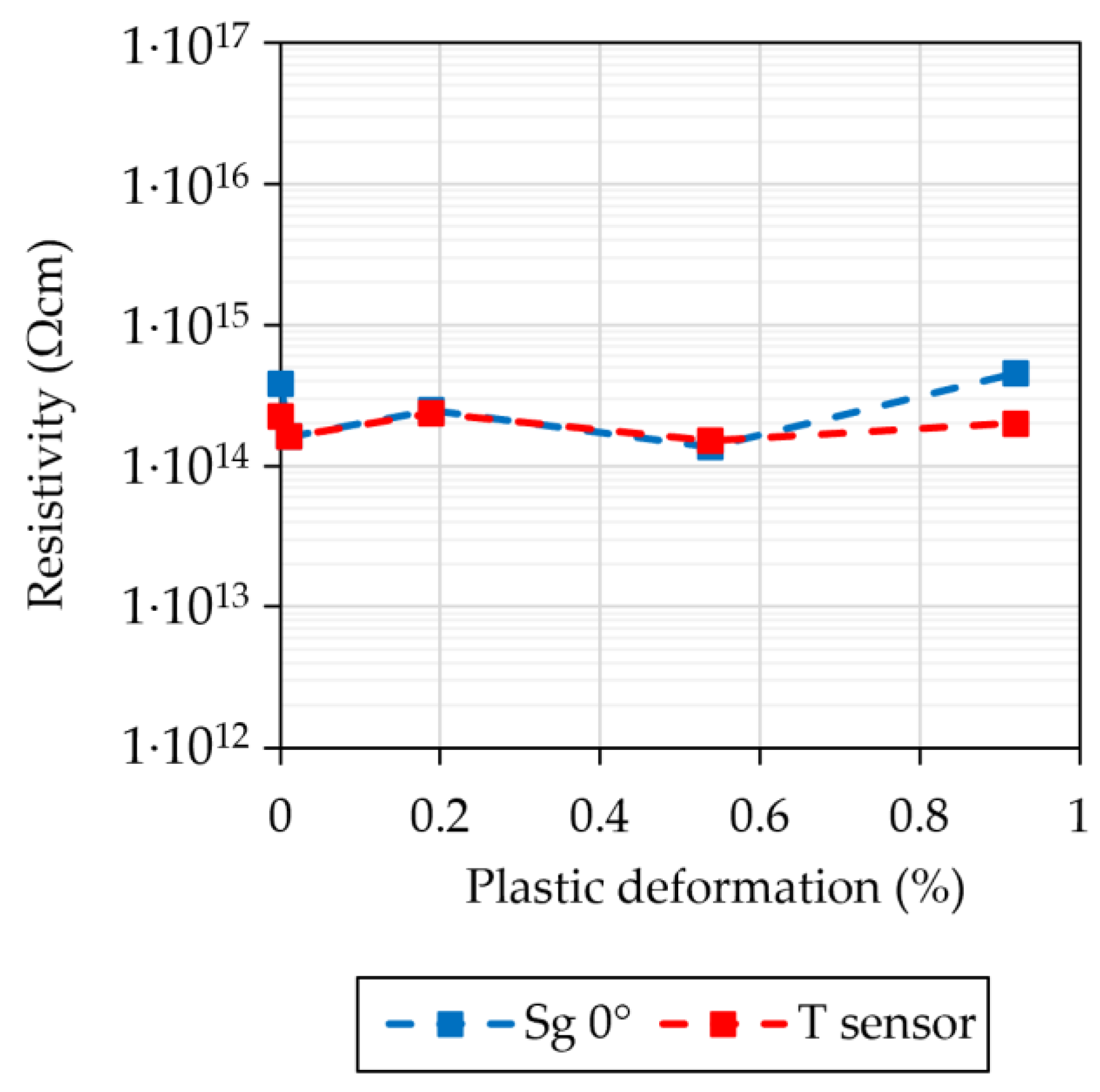
3.1. Influence of Plastic Deformation on the Insulation Resistivity
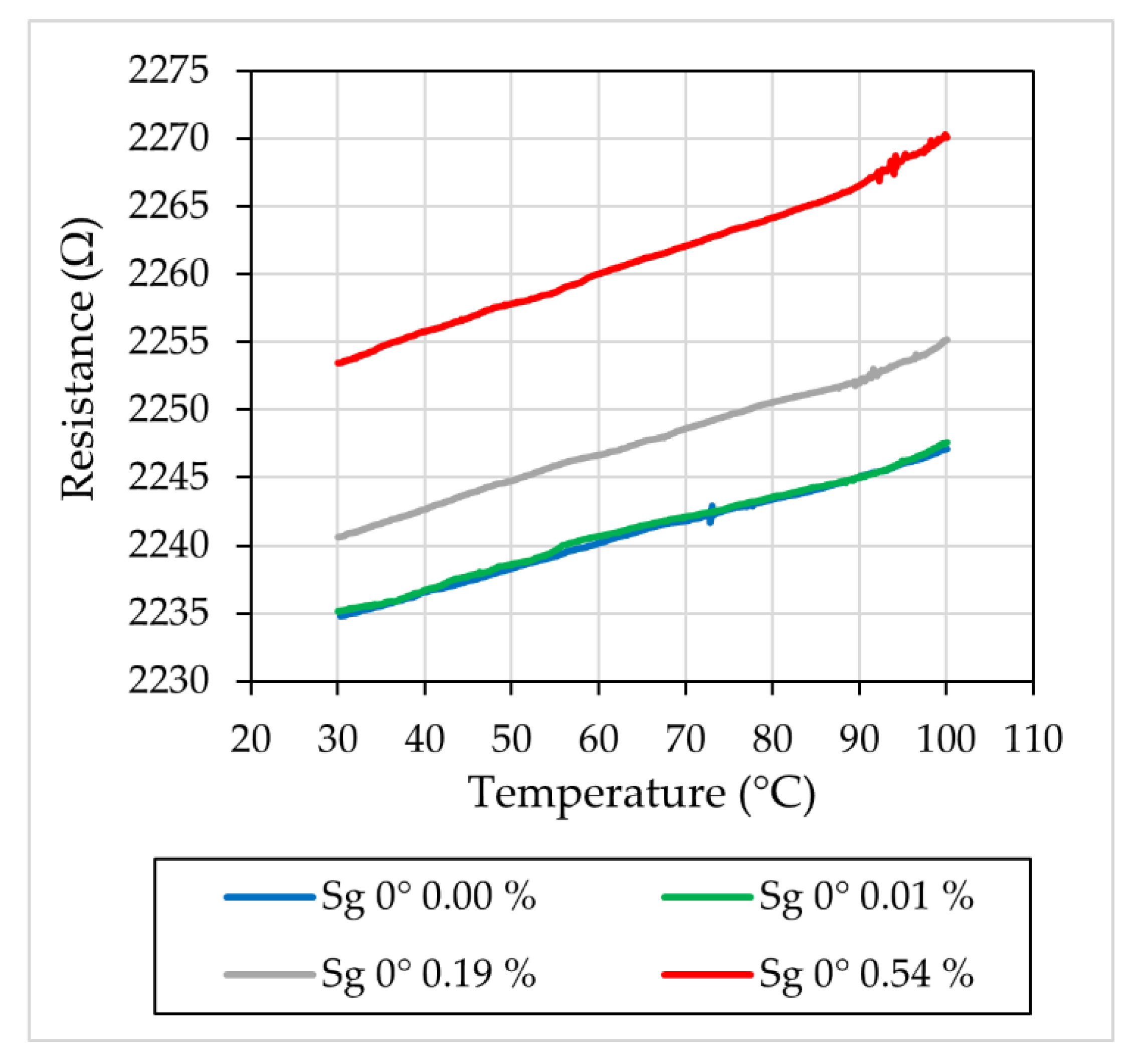
3.2. Influence of Plastic Deformation on the Initial Resistance
3.3. Influence of Plastic Deformation on the Strain Sensitivity (k-Factor)
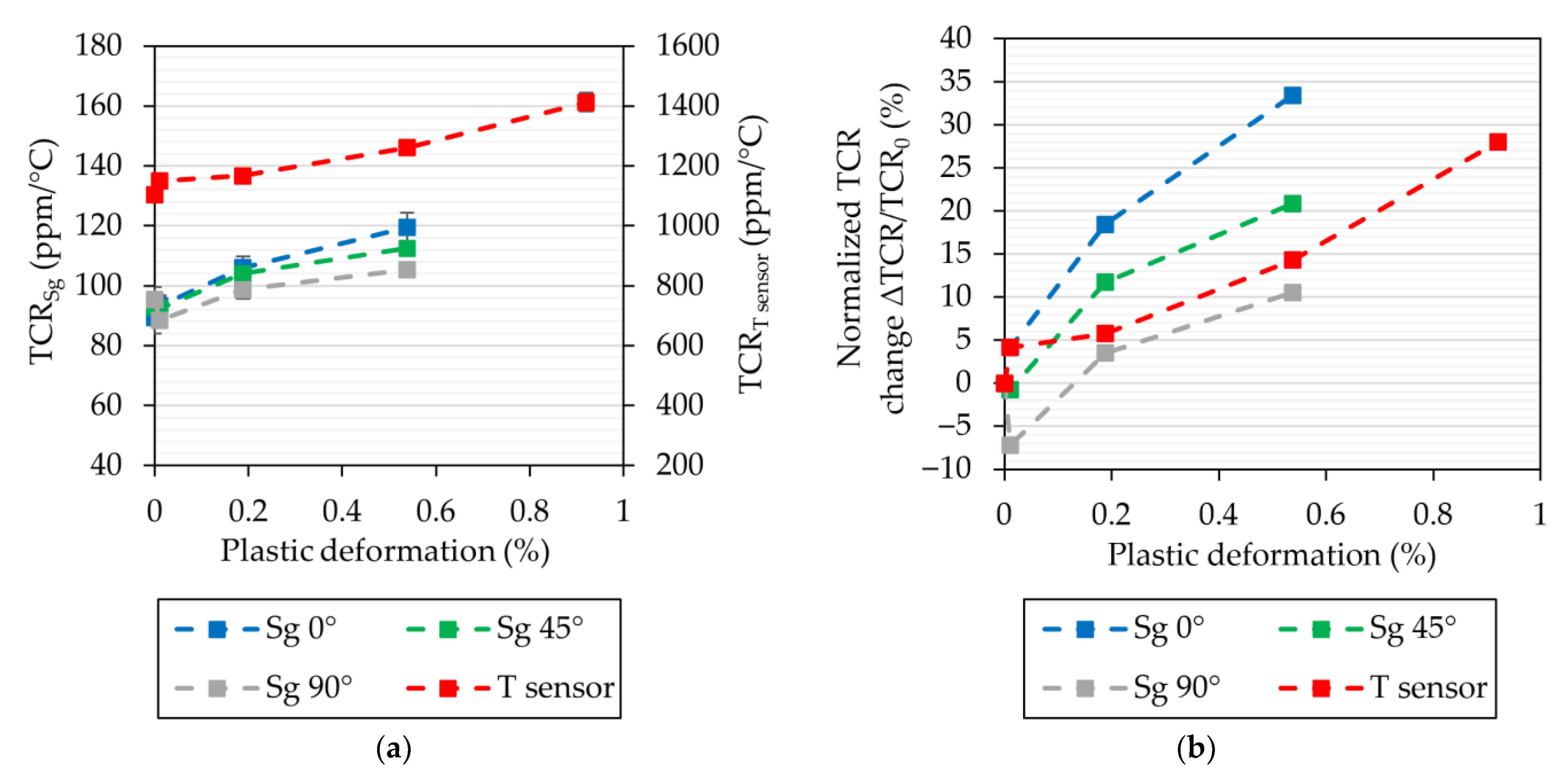
3.4. Influence of Plastic Deformation on the Temperature Coefficient of Resistance (TCR)
4. Discussion
4.1. Insulation Resistivity
4.2. Initial Resistance
4.3. K-Factor
4.4. Temperature Coefficient of Resistance (TCR)
4.5. Condition Monitoring
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sediako, D.; Stroh, J.; Kianfar, S. Residual Stress in Automotive Powertrains: Methods and Analyses. Mater. Sci. Forum 2021, 1016, 1291–1298. [Google Scholar] [CrossRef]
- Zhao, D.; Rasool, S.; Forde, M.; Weafer, B.; Archer, E.; McIlhagger, A.; McLaughlin, J. Development of an embedded thin-film strain-gauge-based SHM network into 3D-woven composite structure for wind turbine blades. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Portland, OR, USA, 25–29 March 2017; Volume 10171, pp. 1–9. [Google Scholar] [CrossRef]
- Tegtmeier, F.L. Strain gauge based microsensor for stress analysis in building structures. Measurement 2008, 41, 1144–1151. [Google Scholar] [CrossRef]
- Chen, X.F.; Wang, S.B.; Qiao, B.J.; Chen, Q. Basic research on machinery fault diagnostics: Past, present, and future trends. Front. Mech. Eng. 2018, 13, 264–291. [Google Scholar] [CrossRef]
- Gao, R.X.; Holm-Hansen, B.T.; Wang, C. Design of a mechatronic bearing through sensor integration. In Proceedings of the Photonics East, Sensors and Controls for Intelligent Machining, Agile Manufacturing and Mechatronics, Boston, MA, USA, 1–6 November 1998; Volume 3518, pp. 244–250. [Google Scholar] [CrossRef]
- Holm-Hansen, R.X. Vibration Analysis of a Sensor-Integrated Ball Bearing. J. Vib. Acoust. 2000, 122, 384–392. [Google Scholar] [CrossRef]
- Marble, S.; Tow, D. Bearing health monitoring and life extension in satellite momentum/reaction wheels. In Proceedings of the 2006 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2006; pp. 1–7. [Google Scholar] [CrossRef]
- Frosini, L.; Harlisca, C.; Szabo, L. Induction Machine Bearing Fault Detection by Means of Statistical Processing of the Stray Flux Measurement. IEEE Trans. Ind. Electron. 2014, 62, 1846–1854. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, X.; Zhang, C.-A.; Liu, W. An Ensemble Convolutional Neural Networks for Bearing Fault Diagnosis Using Multi-Sensor Data. Sensors 2019, 19, 5300. [Google Scholar] [CrossRef] [PubMed]
- Heikebrügge, S.; Ottermann, R.; Breidenstein, B.; Dencker, F.; Wurz, M.C. Residual stresses from incremental hole drilling using directly deposited thin film strain gauges. Exp. Mech. 2022, 62, 701–713. [Google Scholar] [CrossRef]
- Ottermann, R.; Klaas, D.; Dencker, F.; Hoheisel, D.; Rottengatter, P.; Kruspe, T.; Wurz, M.C. Direct Deposition of Thin-Film Strain Gauges with a New Coating System for Elevated Temperatures. In Proceedings of the IEEE Sensors, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Klaas, D.; Ottermann, R.; Dencker, F.; Wurz, M.C. Development, Characterisation and High-Temperature Suitability of Thin-Film Strain Gauges Directly Deposited with a New Sputter Coating System. Sensors 2020, 20, 3294. [Google Scholar] [CrossRef] [PubMed]
- Keil, S. Dehnungsmessstreifen, 2nd ed.; Springer Verlag GmbH: Wiesbaden, Germany, 2017; ISBN 9783658136123. [Google Scholar]
- Ottermann, R.; Klaas, D.; Dencker, F.; Hoheisel, D.; Jung, S.; Wienke, A.; Duesing, J.F.; Koch, J.; Wurz, M.C. Directly Deposited Thin-Film Strain Gauges on Curved Metallic Surfaces. In Proceedings of the IEEE Sensors, Sydney, Australia, 31 October–4 November 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Biehl, S.; Luethje, H.; Bandorf, R.; Sick, J.-H. Multifunctional thin film sensors based on amorphous diamond-like carbon for use in tribological applications. Thin Solid Films 2006, 515, 1171–1175. [Google Scholar] [CrossRef]
- Emmrich, S.; Plogmeyer, M.; Bartel, D.; Herrmann, C. Development of a Thin-Film Sensor for In Situ Measurement of the Temperature Rise in Rolling Contacts with Fluid Film and Mixed Lubrication. Sensors 2021, 21, 6787. [Google Scholar] [CrossRef] [PubMed]
- ASTM International. ASTM E837-20: Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method; ASTM: West Conshohocken, PA, USA, 2020; Available online: https://www.astm.org/e0837-20.html (accessed on 20 August 2022).
- ICS: 77.040.10; Deutsches Institut für Normung e.V. Standard DIN 50125: Testing of Metallic Materials-Tensile Test Pieces. Beuth Verlag GmbH: Düsseldorf, Germany, 2004. [CrossRef]
- ICS 17.040.40; Deutsches Institut für Normung e.V. Standard Geometrical product specifications (GPS)-Filtration-Part 21: Linear profile filters: Gaussian filters (ISO 16610-21:2011). Beuth Verlag GmbH: Düsseldorf, Germany, 2013. [CrossRef]
- Bartzsch, H.; Gloeß, D.; Boecher, B.; Frach, P.; Goedicke, K. Properties of SiO2 and Al2O3 films for electrical insulation applications deposited by reactive pulse magnetron sputtering. Surf. Coat. Technol. 2003, 174–175, 774–778. [Google Scholar] [CrossRef]
- Voigt, M.; Sokolowski, M. Electrical properties of thin rf sputtered aluminum oxide films. Mater. Sci. Eng. B 2004, 109, 99–103. [Google Scholar] [CrossRef]
- Waechter, M. Tabellenbuch der Chemie, 1st ed.; Wiley-VCH: Weinheim, Germany, 2012; ISBN 978-3-527-32960-1. [Google Scholar]
- Schmid, U. The impact of thermal annealing and adhesion film thickness on the resistivity and the agglomeration behavior of titanium/platinum thin films. J. Appl. Phys. 2008, 103, 054902. [Google Scholar] [CrossRef]
- Fricke, S.; Friedberger, A.; Mueller, G.; Seidel, H.; Schmid, U. Strain gauge factor and TCR of sputter deposited Pt thin film up to 850 °C. In Proceedings of the IEEE Sensors, Lecce, Italy, 26–29 October 2008; pp. 1531–1535. [Google Scholar] [CrossRef]
- Gordillo, G.; Mesa, F.; Calderon, C. Electrical and Morphological Properties of Low Resistivity Mo thin Films Prepared by Magnetron Sputtering. Braz. J. Phys. 2006, 36, 982–985. [Google Scholar] [CrossRef]
- Barbalas, D.; Legros, A.; Rimal, G.; Oh, S.; Armitage, N.P. Disorder-enhanced effective masses and deviations from Matthiessen’s rule in PdCoO2 thin films. arXiv 2022, arXiv:2205.05006, 1–10. [Google Scholar] [CrossRef]
- Isabellenhuette. Isotan Cu55Ni44Mn1 Data Sheet. 2021, pp. 1–4. Available online: https://www.isabellenhuette.de/fileadmin/Daten/Praezisionslegierungen/Datenblaetter_Widerstand/ISOTAN.pdf (accessed on 19 August 2022).
- AZO Materials. Platinum (Pt)–Properties, Applications–Data Sheet. 2013, pp. 1–3. Available online: https://www.azom.com/article.aspx?ArticleID=9235 (accessed on 19 August 2022).
- Hottinger Baldwin Messtechnik GmbH. Strain gages–Datasheet–Order No. 1-XY71-3/350, Foil Lot A421/17, Production Batch 812088898. Available online: https://www.hbm.com/en/2122/strain-gauge-datasheets/ (accessed on 20 August 2022).
- Duemke, A.; Lampe, K.; Machon, W.; Milde, H.; Moussaoui, M.; Scheurmann, M.; Vehreschild, K.; Zantis, F.-P. Friedrich-Tabellenbuch Elektrotechnik/Elektronik, 10th ed.; Bildungsverlag EINS: Koeln, Germany, 2007; ISBN 978-3-427-53030-5. [Google Scholar]
- ICS: 17.200.20; Deutsches Institut für Normung e. V. Standard DIN EN 60751:2009-05: Industrial platinum resistance thermometers and platinum temperature sensors (IEC 60751:2008). Beuth Verlag GmbH: Düsseldorf, Germany, 2009. [CrossRef]
- Dembo, R.S.; Eisenstat, S.C.; Steihaug, T. Inexact Newton Methods. SIAM J. Numer. Anal. 1982, 19, 400–408. [Google Scholar] [CrossRef]
- Klaas, D.; Becker, J.; Wurz, M.C.; Schlosser, J.; Kunze, M. New coating system for direct-deposition of sensors on components of arbitrary size. In Proceedings of the IEEE Sensors, Orlando, FA, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar] [CrossRef]






| Material | T Sensor [10−4 Ωcm] | Sg 0° [10−4 Ωcm] | Sg 45° [10−4 Ωcm] | Sg 90° [10−4 Ωcm] | Average [10−4 Ωcm] | Std. dev. [10−4 Ωcm] | Bulk [10−4 Ωcm] | Thin-Film [10−4 Ωcm] |
|---|---|---|---|---|---|---|---|---|
| Constantan | - | 1.34 | 1.36 | 1.33 | 1.34 | 0.013 | 0.49 [22] | 1.10 [11] |
| Platinum | 0.30 | - | - | - | - | - | 0.11 [22] | 0.18 [23] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ottermann, R.; Steppeler, T.; Dencker, F.; Wurz, M.C. Degeneration Effects of Thin-Film Sensors after Critical Load Conditions of Machine Components. Machines 2022, 10, 870. https://doi.org/10.3390/machines10100870
Ottermann R, Steppeler T, Dencker F, Wurz MC. Degeneration Effects of Thin-Film Sensors after Critical Load Conditions of Machine Components. Machines. 2022; 10(10):870. https://doi.org/10.3390/machines10100870
Chicago/Turabian StyleOttermann, Rico, Tobias Steppeler, Folke Dencker, and Marc Christopher Wurz. 2022. "Degeneration Effects of Thin-Film Sensors after Critical Load Conditions of Machine Components" Machines 10, no. 10: 870. https://doi.org/10.3390/machines10100870
APA StyleOttermann, R., Steppeler, T., Dencker, F., & Wurz, M. C. (2022). Degeneration Effects of Thin-Film Sensors after Critical Load Conditions of Machine Components. Machines, 10(10), 870. https://doi.org/10.3390/machines10100870






