Investigation of the Voltage-Induced Damage Progression on the Raceway Surfaces of Thrust Ball Bearings
Abstract
:1. Introduction
- They describe if a corrugation progression is likely, but they do not provide information about the point in time when a damage occurs or the rapidity of its progression.
- They do not quantify the bearing damage.
- The bearing current is a quantity difficult to measure in real e-motor applications. Therefore, these two values of damage progression and damage value respective to the bearing current are difficult to obtain.
- The scale is ordinal, meaning it cannot be assumed that the differences between two different grades are equal. This leads to several obstacles like the inability to apply basic calculus operators like plus or minus, which makes calculations based on this scale impossible.
- There is no objective quantification of the different scale grades. The grade of a specific bearing surface depends on the person evaluating it.
- Requirement 1: At least a moderate correlation of of the Spearman Rank correlation coefficient has to exist between a suitable surface property and the subjective evaluation.
- Requirement 2: A suitable surface property should allow for the distinction between corrugations and crater surfaces. Hence, the probability that the corrugation and grey frosting surfaces are equally distributed should be in a Wilcoxon rank-sum test [26].
- Requirement 3: The variation of the suitable surface property should be lower than the variation of the subjective surface evaluation.
- Requirement 4: The variation of the suitable surface property should be independent from the value of the surface property. The surface property and its variation should have a Spearman rank correlation coefficient of .
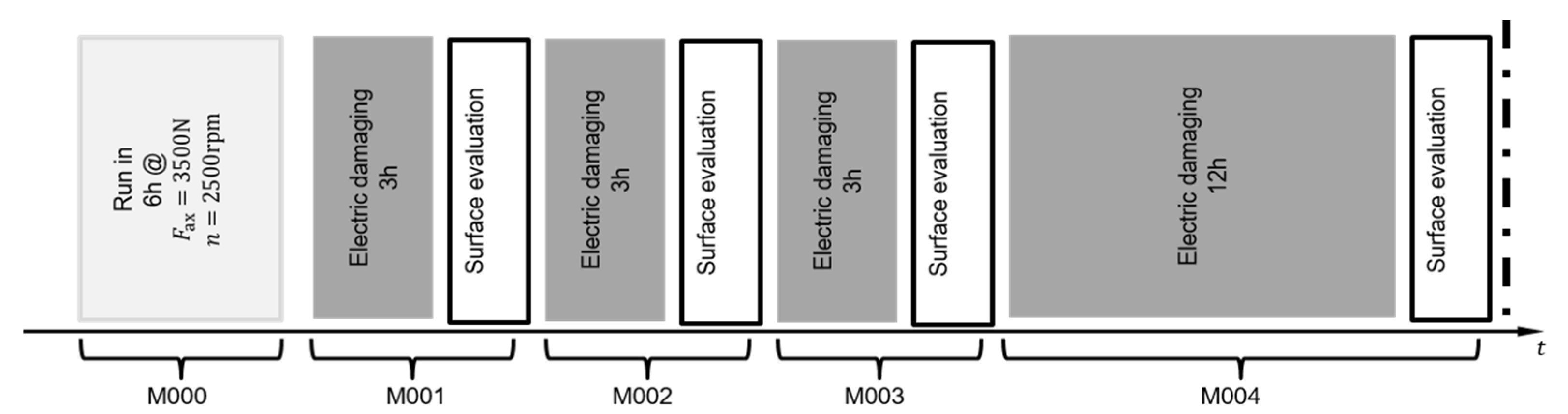
2. Materials and Methods
3. Results
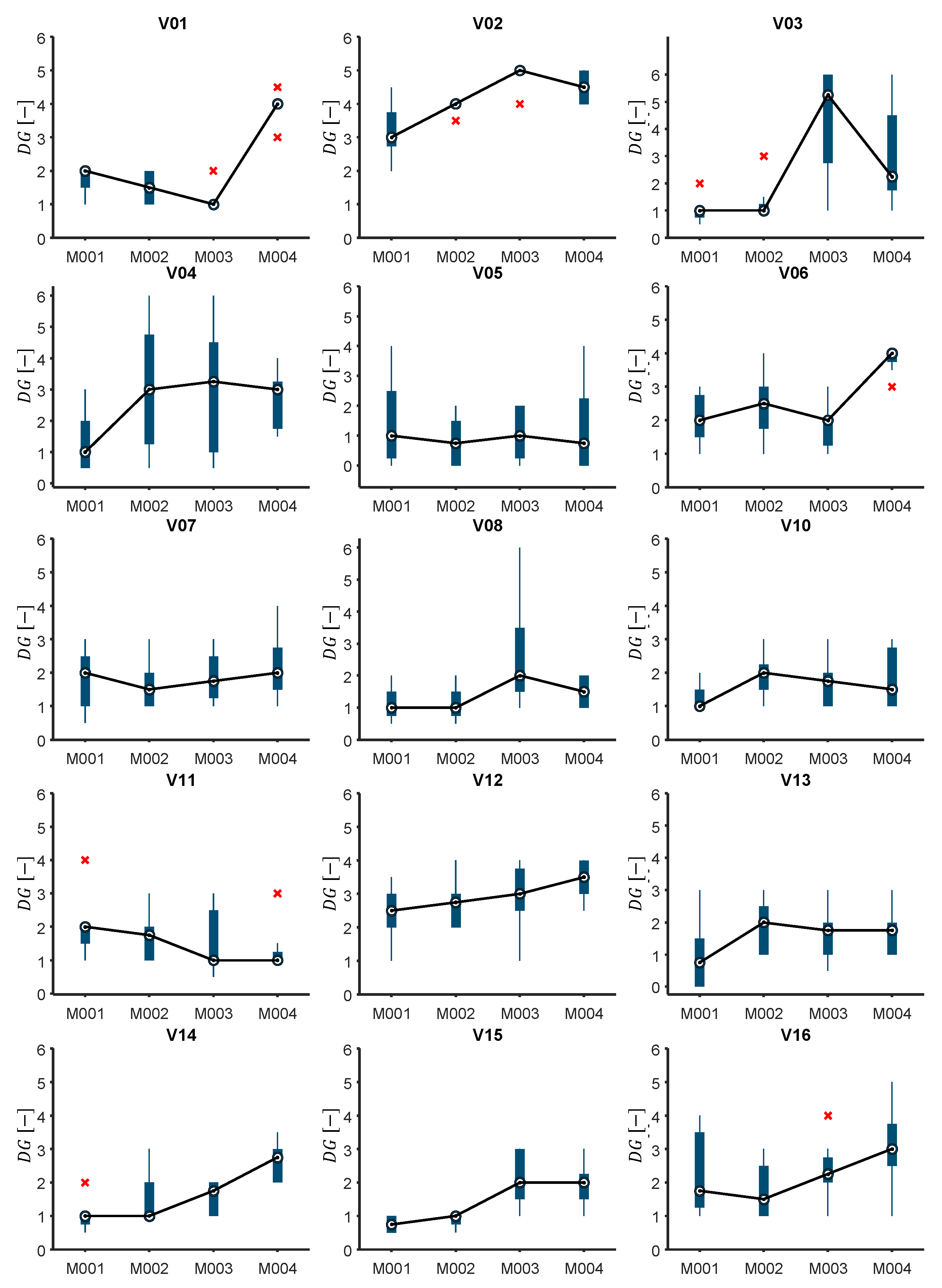
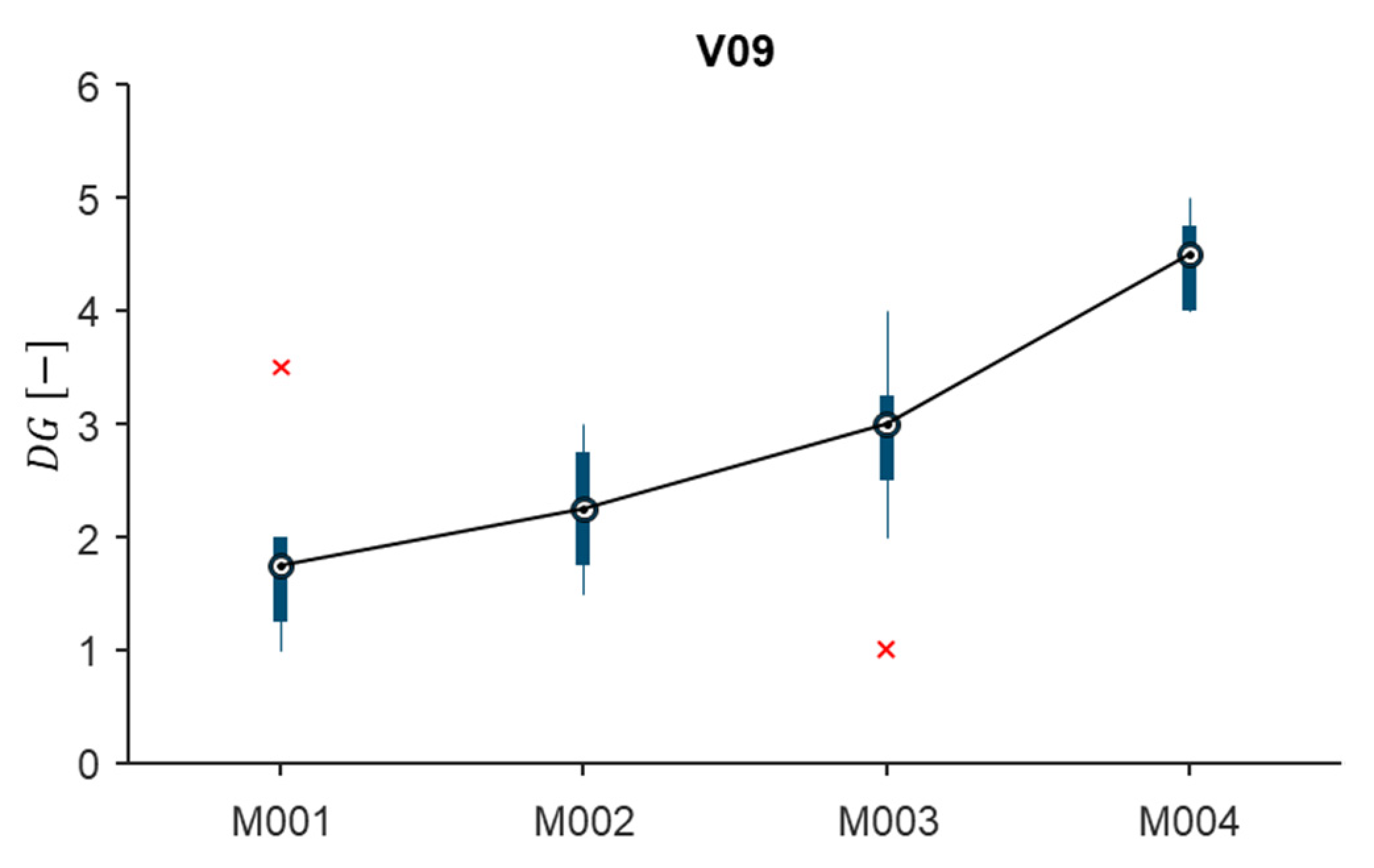
3.1. Degree of Damage Assessment Study
3.2. Testing Surface Property Requirements
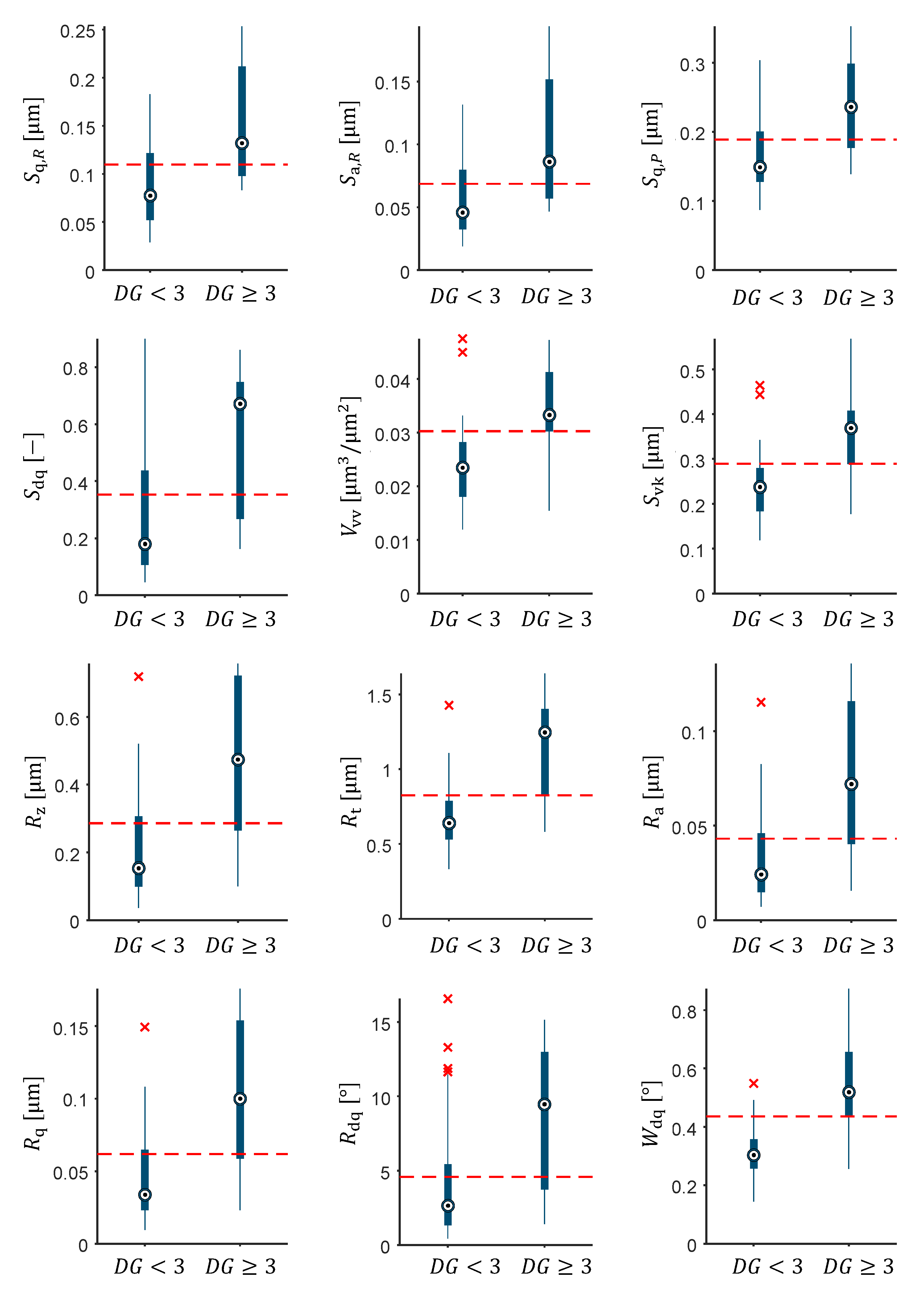
3.2.1. Correlation with the Damage Grade
3.2.2. Identification of Corrugation
3.2.3. Investigation of the Variation of the Surface Properties
3.2.4. Investigation of the Correlation between the Magnitude and Variation of the Surface Property
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Test Nr. | Axial Load (kN) | Rotation Speed (rpm) | Voltage (V) | Frequency (f) | Signal Form (-) |
|---|---|---|---|---|---|
| V01 | 3.5 | 2500 | 5 | 20 | Sine |
| V02 | 1 | 2500 | 5 | 5 | Sine |
| V03 | 1 | 500 | 2.5 | 5 | Sine |
| V04 | 3.5 | 500 | 2.5 | 20 | Sine |
| V05 | 1 | 2500 | 5 | 20 | Square |
| V06 | 3.5 | 2500 | 5 | 5 | Square |
| V07 | 3.5 | 500 | 2.5 | 5 | Square |
| V08 | 1 | 500 | 2.5 | 20 | Square |
| V09 | 1 | 2500 | 2.5 | 5 | Square |
| V10 | 3.5 | 500 | 5 | 20 | Square |
| V11 | 1 | 500 | 5 | 20 | Sine |
| V12 | 1 | 500 | 5 | 5 | Square |
| V13 | 3.5 | 2500 | 2.5 | 20 | Square |
| V14 | 3.5 | 2500 | 2.5 | 5 | Sine |
| V15 | 1 | 2500 | 2.5 | 20 | Sine |
| V16 | 3.5 | 500 | 5 | 5 | Sine |
References
- Muetze, A. Thousands of hits: On inverter-induced bearing currents, related work and the literature. e & i Elektrotechnik und Informationstechnik 2011, 128, 82–388. [Google Scholar] [CrossRef]
- Prashad, H. Tribology in Electrical Environments; Elsevier: Amsterdam, The Netherlands, 2006; Volume 49, pp. 1–494. [Google Scholar]
- Boyanton, H.E.; Hodges, G. Bearing fluting. IEEE Ind. Appl. Mag. 2002, 8, 53–57. [Google Scholar] [CrossRef]
- Busse, D.; Erdman, J.; Kerkman, R.J.; Schlegel, D.; Skibinski, G. System electrical parameters and their effects on bearing currents. IEEE Trans. Ind. Appl. 1997, 33, 577–584. [Google Scholar] [CrossRef]
- Gennaro, M.D.; Scheuermann, P.; Wellerdieck, T.; Ravello, V.; Pellegrino, G.; Trancho, E. The H2020 project FITGEN: Preliminary results and design guidelines of an integrated e-axle for the third-generation electric vehicles. In Proceedings of the 8th Transport Research Arena TRA 2020, Helsinki, Finland, 27–30 April 2020. [Google Scholar]
- Beyer, M.; Brown, G.; Gahagan, M.; Higuchi, T.; Hunt, G.; Huston, M.; Jayne, D.; McFadden, C.; Newcomb, T.; Patterson, S.; et al. Lubricant Concepts for Electrified Vehicle Transmissions and Axles. Tribol. Online 2019, 14, 428–437. [Google Scholar] [CrossRef]
- Graf, S.; Sauer, B. Simulative Untersuchungen des Einflusses elektromechanischer Belastungen an einem Axiallager auf die Glättung der Oberflächen und den Traganteil im Kugel-Laufbahnkontakt. Forsc. Ing. 2022, 86, 145–159. [Google Scholar] [CrossRef]
- Schiferl, R.F.; Melfi, M.J. Bearing current remediation options. IEEE Ind. Appl. Mag. 2004, 10, 40–50. [Google Scholar] [CrossRef]
- Lin, F.; Chau, K.T.; Chan, C.; Liu, C. Fault Diagnosis of Power Components in Electric Vehicles. J. Asian Electr. Veh. 2013, 11, 1659–1666. [Google Scholar] [CrossRef]
- Mütze, A. Bearing Currents in Inverter Fed AC-Motors. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2004. [Google Scholar]
- He, F.; Xie, G.; Luo, J. Electrical bearing failures in electric vehicles. Friction 2020, 8, 4–28. [Google Scholar] [CrossRef]
- Schneider, V.; Behrendt, C.; Höltje, P.; Cornel, D.; Becker-Dombrowsky, F.M.; Puchtler, S.; Gutiérrez Guzmán, F.; Ponick, B.; Jacobs, G.; Kirchner, E. Electrical Bearing Damage, A Problem in the Nano- and Macro-Range. Lubricants 2022, 10, 194. [Google Scholar] [CrossRef]
- Wittek, E.; Kriese, M.; Tischmacher, H.; Gattermann, S.; Ponick, B.; Poll, G. Capacitances and lubricant film thicknesses of motor bearings under different operating conditions. In Proceedings of the XIX International Conference on Electrical Machines—ICEM, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Loos, J.; Bergmann, I.; Goss, M. Influence of Currents from Electrostatic Charges on WEC Formation in Rolling Bearings. Tribol. Trans. 2016, 59, 865–875. [Google Scholar] [CrossRef]
- Schirra, T.; Martin, G.; Vogel, S.; Kirchner, E. Ball Bearings as Sensors for Systematical Combination of Load and Failure Monitoring. In Proceedings of the DESIGN 2018 15th International Design Conference, Dubrovnik, Croatia, 21–24 May 2018; pp. 3011–3022. [Google Scholar] [CrossRef]
- Martin, G.; Becker, F.; Kirchner, E. A novel method for diagnosing rolling bearing surface damage by electric impedance analysis. Tribol. Int. 2021, 170, 107503. [Google Scholar] [CrossRef]
- Tischmacher, H. Bearing Wear Condition Identification on Converter-fed Motors. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Amalfi, Italy, 20–22 June 2018. [Google Scholar] [CrossRef]
- Bechev, D.; Gonda, A.; Capan, R.; Sauer, B. Untersuchung der Oberflächenmutationen und der Riffelbildung bei spannungsbeaufschlagten Wälzlagern. In VDI-Tagung Gleit-und Wälzlagerungen; VDI Verlag: Düsseldorf, Germany, 2019; pp. 301–312. [Google Scholar]
- Graf, S.; Sauer, B. Surface Mutation of the Bearing Raceway caused by electrical Current Passage in Mixed Friction Operation. Bear. World J. 2020, 5, 137–147. [Google Scholar]
- Zika, T.; Gebeshuber, I.C.; Buschbeck, F.; Preisinger, G.; Gröschl, M. Surface analysis on rolling bearings after exposure to defined electric stress. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 787–797. [Google Scholar] [CrossRef]
- Gemeinder, Y. Lagerimpedanz und Lagerschädigung bei Stromdurchgang in Umrichtergespeisten Elektrischen Maschinen. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2016. [Google Scholar]
- Forschungsvereinigungs Antriebstechnik. Schädlicher Stromdurchgang 1—Untersuchung des Schädigungsmechanismus und der zulässigen Lagerstrombelastung von Wälzlagern in E-Motoren und Generatoren Verursacht Durch Parasitäre Hochfrequente Lagerströme; Forschungsvorhaben Nr. 650 I Heft 1127; Forschungsvereinigungs Antriebstechnik: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Forschungsvereinigungs Antriebstechnik. Schädlicher Stromdurchgang 2—Methodik zur Praxisnahen Charakterisierung von Elektrischen Schmierstoffeigenschaften zur Verbesserung der Rechnerischen Vorhersage von Lagerströmen; Forschungsvorhaben Nr. 650 II Heft 1387; Forschungsvereinigungs Antriebstechnik: Frankfurt am Main, Germany, 2020. [Google Scholar]
- DIN EN ISO 4287:2010-07; Geometrische Produktspezifikation (GPS)—Oberflächenbeschaffenheit: Tastschnittverfahren—Benennungen, Definitionen und Kenngrößen der Oberflächenbeschaffenheit. ISO: Geneva, Switzerland, 2010.
- ISO 25178-2:2012; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface texture Parameters. ISO: Geneva, Switzerland, 2012.
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80. [Google Scholar] [CrossRef]
- Schirra, T.; Martin, G.; Puchtler, S.; Kirchner, E. Electric impedance of rolling bearings—Consideration of unloaded rolling elements. Tribol. Int. 2021, 158, 106927. [Google Scholar] [CrossRef]
- Harder, A.; Kirchner, E. Voltage Induced Damage Progression on the Raceway Surfaces of Thrust Ball Bearings, Part I: Surface Measurements; TUdatalib: Darmstadt, Germany, 2022. [Google Scholar] [CrossRef]
- Fahrmeir, L. Statistik: Der Weg zur Datenanalyse; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 13 978-3662503713. [Google Scholar]


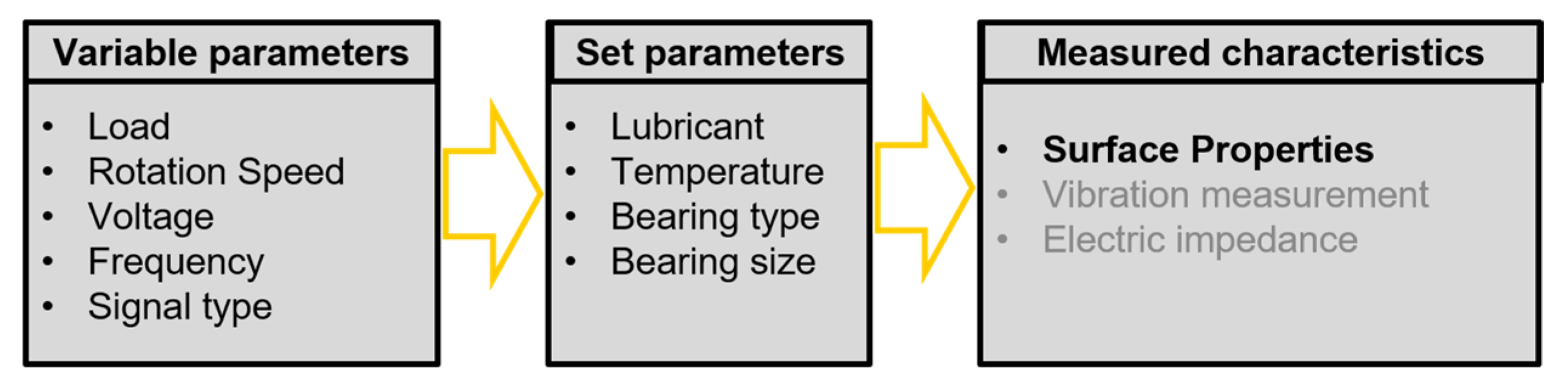
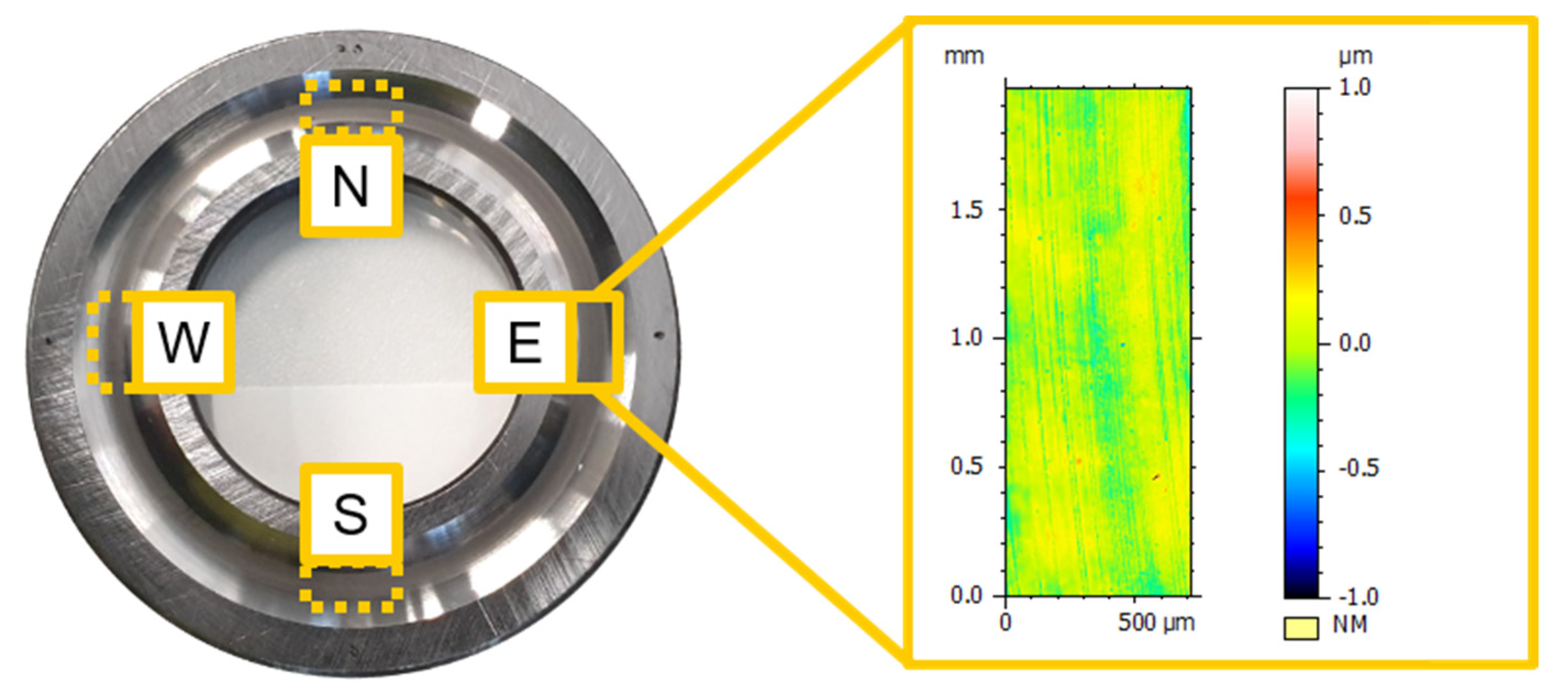





| Factor | Unit | - | + |
|---|---|---|---|
| Axial Load | kN | 1 | 3.5 |
| Rotation Speed | rpm | 500 | 2500 |
| Voltage | V | 2.5 | 5 |
| Frequency | Hz | 5000 | 20,000 |
| Signal Form | - | Square Wave | Sine Wave |
| Parameter | Value |
|---|---|
| Lubricant | FVA3 reference oil |
| Oil Temperature T | 40 °C |
| Bearing Type | Thrust ball bearing |
| Bearing Size | 51,305 |
| Variable | Parameter | Variable | Parameter |
|---|---|---|---|
| Maximum Profile Height | Material Volume | ||
| Total Profile Height | Void Volume | ||
| Arithmetic Mean of Profile Ordinate | Material Volume of peaks | ||
| Quadratic Mean of Profile Ordinate | Material Volume at the core | ||
| Skewness of Profile | Void Volume at the core | ||
| Steepness of Profile | Void Volume at the valleys | ||
| Median Groove Width of Profile Elements | Core height | ||
| Quadratic Mean of Profile Pitch | Average peak height above the core | ||
| Material Fraction of Profile | Average valley depth below the core | ||
| Height Difference between two Intersection Lines |
| Surface Property | Comparison to Literature | |
|---|---|---|
| No comparable data | ||
| No contradiction | ||
| Deviation; no contradiction [15,19] | ||
| No comparable data | ||
| No comparable data | ||
| Deviation; no contradiction [14,15,19] | ||
| Deviation; no contradiction [17,18] | ||
| Confirmed [16,19] | ||
| No contradiction [17,18,19] | ||
| No contradiction [16,17,18,19] | ||
| No comparable data | ||
| No comparable data |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harder, A.; Zaiat, A.; Becker-Dombrowsky, F.M.; Puchtler, S.; Kirchner, E. Investigation of the Voltage-Induced Damage Progression on the Raceway Surfaces of Thrust Ball Bearings. Machines 2022, 10, 832. https://doi.org/10.3390/machines10100832
Harder A, Zaiat A, Becker-Dombrowsky FM, Puchtler S, Kirchner E. Investigation of the Voltage-Induced Damage Progression on the Raceway Surfaces of Thrust Ball Bearings. Machines. 2022; 10(10):832. https://doi.org/10.3390/machines10100832
Chicago/Turabian StyleHarder, André, Anatoly Zaiat, Florian Michael Becker-Dombrowsky, Steffen Puchtler, and Eckhard Kirchner. 2022. "Investigation of the Voltage-Induced Damage Progression on the Raceway Surfaces of Thrust Ball Bearings" Machines 10, no. 10: 832. https://doi.org/10.3390/machines10100832
APA StyleHarder, A., Zaiat, A., Becker-Dombrowsky, F. M., Puchtler, S., & Kirchner, E. (2022). Investigation of the Voltage-Induced Damage Progression on the Raceway Surfaces of Thrust Ball Bearings. Machines, 10(10), 832. https://doi.org/10.3390/machines10100832







