A Study on Dimensional Accuracy of a Vehicle Hood-Catch Considering Material Shrinkage of Polyamide 6 and Length-to-Volume Ratio Characteristic of a Shape
Abstract
:1. Introduction
2. Theoretical Background
2.1. Characteristics of PA6
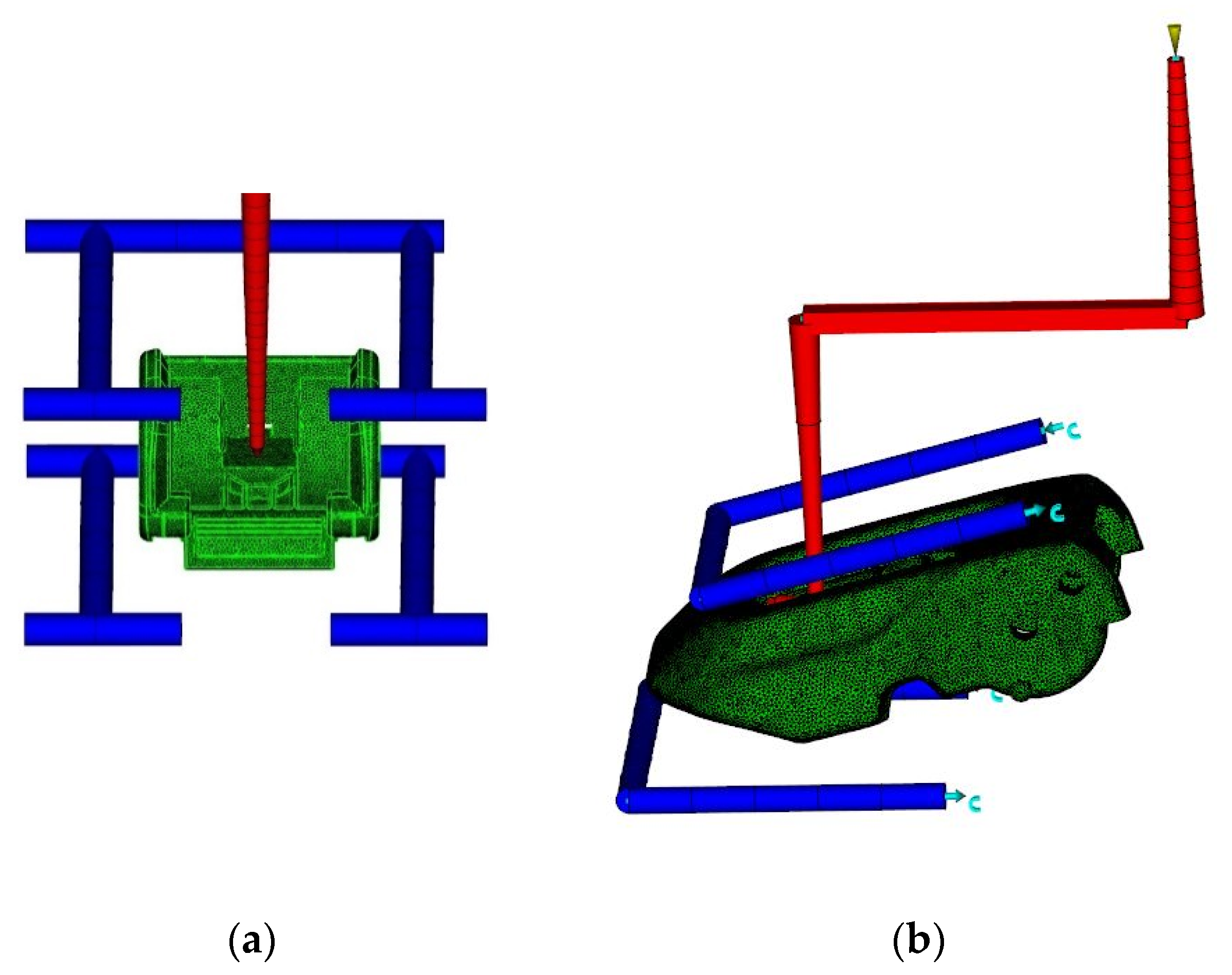
2.2. Hood-Catch Modeling and Injection Molding Process Conditions
2.3. Experimental Factors and Preparation of Table of Orthogonal Arrays
2.4. Shrinkage Ratio Selection Considering Both Material and Shape Characteristics and Part Modeling
3. Analysis Results
3.1. Analysis of Nominal Dimension Parts for Process Condition Selection
3.1.1. Injection Flow Analysis Applying Experiments Design
3.1.2. Setting Process Conditions by S/N Ratio Analysis
3.2. Analysis Results of Applying 0.2% Shrinkage
3.2.1. Pivot Sub-Assembly
3.2.2. Open Lever
3.3. Analysis Results of Applying 0.5% Shrinkage
3.3.1. Pivot Sub-Assembly
3.3.2. Open Lever
3.4. Analysis of Results for Injection Molding Analysis
4. Verification of Injection Molding Analysis Results
5. Conclusions
- (1)
- Dimensions 1, 2, and 3 are selected as the key, main sections of the joints between the pivot sub-assembly and open lever to secure the dimensional accuracy of hood-catch.
- (2)
- The shrinkage-rate constant with PA6 material and part shape characteristics for the pivot sub-assembly and open lever were calculated to be 0.19% and 0.48%, respectively. Therefore, the shrinkage-rate constant was selected as the approximate values of 0.2% and 0.5% for parts modeling.
- (3)
- To determine process conditions for securing the accuracy of key dimensions, melt temperature, coolant temperature, and cooling were selected as control factors in DOE, and the injection flow analysis was accordingly performed. As a result of comparing the S/N ratio specialized at reaching the specific value, the pivot sub-assembly process conditions were shown to be melt temperature 250 °C, coolant temperature 30 °C, cooling time 26 s; for the open lever, they were shown to be melt temperature 280 °C, coolant temperature 30 °C, cooling time 16 s.
- (4)
- In consideration of the proposed 0.2% and 0.5% shrinkage rate, the injection flow analysis of the pivot sub-assembly and the open lever was performed using Moldflow. As a result of the analysis, in the case of the pivot sub-assembly, the target values of the key dimensions 1, 2, and 3 were satisfied with both shrinkage rates. Therefore, the application of the 0.2% shrinkage rate was suitable for minimizing material usage.
- (5)
- In the case of the open lever, when applying the 0.2% shrinkage rate, key dimensions 1 and 2 did not satisfy the target values; however, when applying the 0.5% shrinkage rate, the target values were satisfied except for key dimension 2. Dimension 2 was determined to require additional dimensional correction because the warp caused by the orthogonal rib reinforcement was large, and the corresponding analysis results satisfied all key dimensions’ target values. Therefore, the application of the 0.5% shrinkage rate was suitable except for the specificity caused by the orthogonal rib reinforcement.
- (6)
- To verify the research results, the key dimensions of the actual injection molded product, applying the suggested shrinkage rate, were compared with the analysis results. In the case of the pivot sub-assembly, the results showed dimension 1 = 47.620 mm, dimension 2 = 6.117 mm, and dimension 3 = 55.837 mm, and the reliability was more than 99.77% with an 0.05~0.23% error range. In the case of the open lever, the results showed dimension 1 = 47.500 mm, dimension 2 = 22.202 mm, and dimension 3 = 5.901 mm, and the reliability was more than 98.29% with an 0.8~1.71% error range.
- (7)
- Consequently, it is reasonable to consider not only the material shrinkage rate but also the part shape shrinkage rate depending on the length-to-volume ratio; according to the results of the study, the shrinkage rates of the pivot sub-assembly and open lever with MF 25%/GF 15% reinforced PA6, with length-to-volume ratios of 1.24 × 10−3 and 3.10 × 10−3 for each, is suggested as 0.2% and 0.5%. To generalize the theory, further research should be performed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- U.S. Department of Transportation. Available online: https://datahub.transportation.gov/dataset/NHTSA-Recalls-by-Manufacturer/mu99-t4jn (accessed on 1 August 2022).
- Choi, B.J.; Kang, I.J.; Jeon, Y.H.; Hong, M.S. Deformation Analysis for Injection Molding of Lower Stiffener in Automobile Bumper. J. Korean Soc. Manuf. Technol. Eng. 2018, 27, 564–569. [Google Scholar]
- Lee, J.H.; Lee, S.B. Determined Car Door Latch Injection Molding Process Conditions through the Finite Elements Analysis. J. Korea Acad. Ind. Coop. Soc. 2016, 17, 499–508. [Google Scholar]
- Park, K.; Ahn, J.H.; Choi, S.R. Optimal Design for Injection Molding Processes using Design of Experiments and Finite Element Analysis. Proc. Korean Soc. Technol. Plast. 2001, 19043, 150–153. [Google Scholar]
- Lee, J.H.; Kim, J.S. A Study on the Experimental Verification and Prediction of Mold Deformation at Injection Stage during Injection Molding through Simulation Analysis. Mech. Technol. 2020, 22, 1061–1074. [Google Scholar]
- Chen, C.P.; Chuang, M.T.; Hsiao, Y.H.; Yang, Y.K.; Tsai, C.H. Simulation and experimental study in determining injection molding process parameters for thin-shell plastic parts via design of experiments analysis. Expert Syst. Appl. 2009, 36, 10752–10759. [Google Scholar] [CrossRef]
- Oh, J.Y.; Huh, Y.J. A Study on Optimization of Injection-molded System Using CAE and Design of Experiment. J. Korea Acad. Ind. Coop. Soc. 2006, 7, 271–277. [Google Scholar]
- Carpenter, B.; Patil, S.; Hoffman, R.; Lilly, B.; Castro, J. Effect of machine compliance on mold deflection during injection and packing of thermoplastic parts. Polym. Eng. Sci. 2006, 46, 844–852. [Google Scholar] [CrossRef]
- Lin, W.C.; Fan, F.Y.; Huang, C.F.; Shen, Y.K.; Wang, H. Analysis of the warpage phenomenon of micro-sized parts with precision injection molding by experiment, numerical simulation, and grey theory. Polymers 2022, 14, 1845. [Google Scholar] [CrossRef] [PubMed]
- Seow, L.W.; Lam, Y.C. Optimizing flow in plastic injection molding. J. Mater. Process. Technol. 1997, 72, 333–341. [Google Scholar] [CrossRef]
- Ginghtong, T.; Nakpathomkun, N.; Pechyen, C. Effect of injection parameters on mechanical and physical properties of super ultra-thin wall propylene packaging by Taguchi method. Results Phys. 2018, 9, 987–995. [Google Scholar] [CrossRef]
- Lee, S.C.; Kim, J.W.; Yoon, S.I. Injection Molding Analysis for Development of Torque Roll Engine Mount Module using Composite Materials. In Proceedings of the KAIS Spring Conference, Jeongseon, Korea, 22–23 May 2015. [Google Scholar]
- Jeong, H.J.; Kim, S.H.; Cho, S.W.; Jeong, S.W.; Kwon, I.J. A Study on the Optimization of Injection Molding Process for Automotive Parts Using Nanocarbon Reinforced Composite Materials. In Proceedings of the KSME Conference, Daejeon, Korea, 28–30 April 2021. [Google Scholar]
- Choi, M.J.; Cho, J.M.; Choi, Y.H.; Choi, M.H.; Lee, C.S.; Sung, H.K.; Lee, K.S.; Park, K.H.; Hwang, S.J. Development of Paint-free Metallic Plastic Material for Automotive Parts. Korean Chem. Eng. Res. 2022, 60, 295–299. [Google Scholar]
- Fernandez, E.; Edeleva, M.; Fiorio, R.; Cardon, L.; D’hooge, D.R. Increasing the Sustainability of the Hybrid Mold Technique through Combined Insert Polymeric Material and Additive Manufacturing Method Design. Sustainability 2022, 14, 877. [Google Scholar] [CrossRef]
- Yu, S.H.; Kim, M.S.; Yoon, H.S.; Park, J.S.; Jeon, S.M.; Sim, J.H. A Study on the Mechanical Properties and Performance Prediction Simulation of PA6/GF Composite Materials with Injection Molding Pressure. Text. Color. Finish. 2022, 34, 46–57. [Google Scholar]
- Bula, K.; Korzeniewski, B. Polyamide 6-Aluminum Assembly Enhanced by Laser Microstructuring. Polymers 2022, 14, 288. [Google Scholar] [CrossRef]
- Rochardjo, H.S.; Budiyantoro, C. Manufacturing and analysis of overmolded hybrid fiber polyamide 6 composite. Polymers 2021, 13, 3820. [Google Scholar] [CrossRef]
- Myalski, J.; Godzierz, M.; Olesik, P. Effect of carbon fillers on the wear resistance of pa6 thermoplastic composites. Polymers 2020, 12, 2264. [Google Scholar] [CrossRef] [PubMed]
- Sathees Kumar, S.; Kanagaraj, G. Investigation on mechanical and tribological behaviors of PA6 and graphite-reinforced PA6 polymer composites. Arab. J. Sci. Eng. 2016, 41, 4347–4357. [Google Scholar]
- Güllü, A.; Özdemir, A.; Özdemir, E. Experimental investigation of the effect of glass fibres on the mechanical properties of polypropylene (PP) and polyamide 6 (PA6) plastics. Mater. Des. 2006, 27, 316–323. [Google Scholar] [CrossRef]
- AUTODESK Moldflow-Plastic Injection and Compression Mold Simulation for Design and Manufacturing. Available online: https://www.autodesk.com/products/moldflow/overview (accessed on 6 August 2022).
- Yang, W.P.; Tarng, Y.S. Design optimization of cutting parameters for turning operations based on the Taguchi method. J. Mater. Process. Technol. 1998, 84, 122–129. [Google Scholar]
- Jou, Y.T.; Lin, W.T.; Lee, W.C.; Yeh, T.M. Integrating the Taguchi method and response surface methodology for process parameter optimization of the injection molding. Appl. Math. Inf. Sci. 2014, 8, 1277. [Google Scholar]
- Hakimian, E.; Sulong, A.B. Analysis of warpage and shrinkage properties of injection-molded micro gears polymer composites using numerical simulations assisted by the Taguchi method. Mater. Des. 2012, 42, 62–71. [Google Scholar] [CrossRef]
- Lee, S.B.; Cho, H.S.; Lyu, M.Y. Processability and Mechanical Characteristics of Glass Fiber and Carbon Fiber Reinforced PA6 for Reinforcement Content. Elastomers Compos. 2015, 50, 184–188. [Google Scholar] [CrossRef] [Green Version]
- Lee, M. The effects of warpage in injection molded part for various rib design and resins. J. Korea Soc. Mech. Technol. 2012, 14, 59–65. [Google Scholar] [CrossRef]
- Lee, M.; Lyu, M.Y. A study on the warpage in injection molded part for various rib design. J. Korea Soc. Die Mold Eng. 2008, 2, 54–61. [Google Scholar]


















| Fiber | Mineral Fiber | Glass Fiber |
|---|---|---|
| Proportion ratio [%] | 25 | 15 |
| Property | Value |
|---|---|
| Water absorption [%] | 1.3 |
| Tensile strength at break [MPa] | 130 |
| Elongation at break [%] | 2.5 |
| Izod impact, Notched [J/cm] | 0.530 |
| Part | Description | Target |
|---|---|---|
| Pivot sub-assembly [mm] | Dimension 1 | 47.90.5 |
| Dimension 2 | ||
| Dimension 3 | ||
| Open lever [mm] | Dimension 1 | 47.40.3 |
| Dimension 2 | ||
| Dimension 3 |
| Part | Factor | Description | Value |
|---|---|---|---|
| Pivot sub-assembly [mm] | A | Gate height | 3.3 |
| B | Gate first diameter | 3 | |
| C | Gate second diameter (Sprue first diameter) | 4 | |
| D | Sprue second diameter | 6.8 | |
| E | Sprue height | 52 | |
| Open lever [mm] | F | Gate first width | 2 |
| G | Gate second width (Runner first diameter) | 3 | |
| H | Gate height | 1 | |
| I | Gate depth | 2.4 | |
| J, K | Runner second diameter | 5 | |
| L | Sprue first diameter | 6 | |
| M | Sprue second diameter | 4 | |
| N | Sprue height | 70 |
| Description | Value |
|---|---|
| Maximum machine injection stroke | 176 mm |
| Maximum machine injection rate | 304 cm3/s |
| Machine screw diameter | 44 mm |
| Maximum injection pressure | 220 MPa |
| Maximum machine clamp force | 150 ton |
| Part | Description | Value | |
|---|---|---|---|
| Pivot sub-assembly | Mold temperature | 60 °C | |
| Melt temperature | 270 °C | ||
| Injection time | 10 s | ||
| Packing pressure | Step 1 | 95 MPa for 5 s | |
| Step 2 | 75 MPa for 6 s | ||
| Coolant temperature | 20 °C | ||
| Cooling time | 26 s | ||
| Open lever | Mold temperature | 60 °C | |
| Melt temperature | 295 °C | ||
| Injection time | 6 s | ||
| Packing pressure | Step 1 | 54 MPa for 4 s | |
| Step 2 | 32 MPa for 1.5 s | ||
| Coolant temperature | 20 °C | ||
| Cooling time [s] | 16 s | ||
| Part | Dimension 1 | Dimension 2 | Dimension 3 |
|---|---|---|---|
| Pivot sub-assembly [mm] | 47.32 | 6.17 | 55.52 |
| Open lever [mm] | 46.55 | 21.60 | 5.85 |
| Factor | Variables | Level | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| A | Melt temperature [°C] | 250 | 260 | 270 |
| B | Coolant temperature [°C] | 20 | 25 | 30 |
| C | Cooling time [s] | 22 | 26 | 30 |
| Factor | Variables | Level | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| A | Melt temperature [°C] | 270 | 280 | 290 |
| B | Coolant temperature [°C] | 20 | 25 | 30 |
| C | Cooling time [s] | 12 | 16 | 20 |
| Simulation No. | A | B | C |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 |
| 3 | 1 | 3 | 3 |
| 4 | 2 | 1 | 2 |
| 5 | 2 | 2 | 3 |
| 6 | 2 | 3 | 1 |
| 7 | 3 | 1 | 3 |
| 8 | 3 | 2 | 1 |
| 9 | 3 | 3 | 2 |
| Part | Description | Target | 0.2% Applied | 0.5% Applied |
|---|---|---|---|---|
| Pivot sub-assembly [mm] | Dimension 1 | 47.90.5 | 48.01 | 48.14 |
| Dimension 2 | 6.09 | 6.07 | ||
| Dimension 3 | 56.12 | 56.28 | ||
| Open lever [mm] | Dimension 1 | 47.40.3 | 47.50 | 47.63 |
| Dimension 2 | 21.94 | 22.01 | ||
| Dimension 3 | 5.79 | 5.77 |
| Case No. | Pivot Sub-Assembly [mm] | Open Lever [mm] | ||||
|---|---|---|---|---|---|---|
| Dimension 1 | Dimension 2 | Dimension 3 | Dimension 1 | Dimension 2 | Dimension 3 | |
| 1 | 47.32 | 6.13 | 55.57 | 46.55 | 21.59 | 5.85 |
| 2 | 47.33 | 6.12 | 55.58 | 46.59 | 21.61 | 5.85 |
| 3 | 47.34 | 6.13 | 55.59 | 46.62 | 21.62 | 5.85 |
| 4 | 47.31 | 6.13 | 55.56 | 46.57 | 21.60 | 5.84 |
| 5 | 47.32 | 6.13 | 55.58 | 46.60 | 21.61 | 5.84 |
| 6 | 47.32 | 6.13 | 55.58 | 46.60 | 21.61 | 5.85 |
| 7 | 47.32 | 6.13 | 55.57 | 46.56 | 21.60 | 5.85 |
| 8 | 47.32 | 6.13 | 55.58 | 46.57 | 21.60 | 5.85 |
| 9 | 47.33 | 6.12 | 55.59 | 46.61 | 21.62 | 5.84 |
| Case No. | Dimension 1 [mm] | S/N Ratio |
|---|---|---|
| 1 | 47.32 | 7.742 |
| 2 | 47.33 | 7.893 |
| 3 | 47.34 | 8.047 |
| 4 | 47.31 | 7.593 |
| 5 | 47.32 | 7.742 |
| 6 | 47.32 | 7.742 |
| 7 | 47.32 | 7.742 |
| 8 | 47.32 | 7.893 |
| 9 | 47.33 | 7.893 |
| Case No. | Dimension 2 [mm] | S/N Ratio |
|---|---|---|
| 1 | 6.13 | 33.468 |
| 2 | 6.12 | 36.990 |
| 3 | 6.13 | 33.468 |
| 4 | 6.13 | 33.468 |
| 5 | 6.13 | 33.468 |
| 6 | 6.13 | 33.468 |
| 7 | 6.13 | 33.468 |
| 8 | 6.13 | 33.468 |
| 9 | 6.12 | 36.990 |
| Case No. | Dimension 3 [mm] | S/N Ratio |
|---|---|---|
| 1 | 55.57 | 10.341 |
| 2 | 55.58 | 10.545 |
| 3 | 55.59 | 10.755 |
| 4 | 55.56 | 10.141 |
| 5 | 55.58 | 10.545 |
| 6 | 55.58 | 10.545 |
| 7 | 55.57 | 10.341 |
| 8 | 55.58 | 10.545 |
| 9 | 55.59 | 10.755 |
| Description | Melt Temperature | Coolant Temperature | Cooling Time | ||
|---|---|---|---|---|---|
| Dimension 1 | Level | 1 | 7.894 | 7.692 | 7.792 |
| 2 | 7.692 | 7.842 | 7.793 | ||
| 3 | 7.842 | 7.894 | 7.843 | ||
| Delta | 0.201 | 0.201 | 0.051 | ||
| Rank | 1.5 | 1.5 | 3 | ||
| Dimension 2 | Level | 1 | 34.64 | 33.47 | 33.47 |
| 2 | 33.47 | 34.64 | 35.82 | ||
| 3 | 34.64 | 34.64 | 33.47 | ||
| Delta | 1.17 | 1.17 | 2.35 | ||
| Rank | 2.5 | 2.5 | 1 | ||
| Dimension 3 | Level | 1 | 10.55 | 10.27 | 10.48 |
| 2 | 10.41 | 10.55 | 10.48 | ||
| 3 | 10.55 | 10.68 | 10.55 | ||
| Delta | 0.14 | 0.41 | 0.07 | ||
| Rank | 2 | 1 | 3 | ||
| Case No. | Dimension 1 [mm] | S/N Ratio |
|---|---|---|
| 1 | 46.55 | 4.422 |
| 2 | 46.59 | 4.841 |
| 3 | 46.62 | 5.168 |
| 4 | 46.57 | 4.629 |
| 5 | 46.60 | 4.949 |
| 6 | 46.60 | 4.949 |
| 7 | 46.56 | 4.525 |
| 8 | 46.57 | 4.629 |
| 9 | 46.61 | 5.058 |
| Case No. | Dimension 2 [mm] | S/N Ratio |
|---|---|---|
| 1 | 21.59 | 13.183 |
| 2 | 21.61 | 13.762 |
| 3 | 21.62 | 14.067 |
| 4 | 21.60 | 13.468 |
| 5 | 21.61 | 13.762 |
| 6 | 21.61 | 13.762 |
| 7 | 21.60 | 13.478 |
| 8 | 21.60 | 13.478 |
| 9 | 21.62 | 14.067 |
| Case No. | Dimension 3 [mm] | S/N Ratio |
|---|---|---|
| 1 | 5.85 | 29.309 |
| 2 | 5.85 | 29.309 |
| 3 | 5.85 | 29.309 |
| 4 | 5.84 | 30.9691 |
| 5 | 5.84 | 30.9691 |
| 6 | 5.85 | 29.309 |
| 7 | 5.85 | 29.309 |
| 8 | 5.85 | 29.309 |
| 9 | 5.84 | 30.9691 |
| Description | Melt Temperature | Coolant Temperature | Cooling Time | ||
|---|---|---|---|---|---|
| Dimension 1 | Level | 1 | 4.810 | 4.525 | 4.666 |
| 2 | 4.842 | 4.806 | 4.842 | ||
| 3 | 4.737 | 5.058 | 4.881 | ||
| Delta | 0.105 | 0.533 | 0.214 | ||
| Rank | 3 | 1 | 2 | ||
| Dimension 2 | Level | 1 | 13.67 | 13.37 | 13.47 |
| 2 | 13.66 | 13.66 | 13.77 | ||
| 3 | 13.67 | 13.97 | 13.77 | ||
| Delta | 0.01 | 0.59 | 0.29 | ||
| Rank | 3 | 1 | 2 | ||
| Dimension 3 | Level | 1 | 29.03 | 29.68 | 29.03 |
| 2 | 30.32 | 29.68 | 30.32 | ||
| 3 | 29.68 | 29.68 | 29.68 | ||
| Delta | 1.29 | 0.00 | 1.29 | ||
| Rank | 1.5 | 3 | 1.5 | ||
| Description | Dimension 1 | Dimension 2 | Dimension 3 |
|---|---|---|---|
| Value [mm] | 47.73 | 6.11 | 55.81 |
| Description | Dimension 1 | Dimension 2 | Dimension 3 |
|---|---|---|---|
| Value [mm] | 46.85 | 21.67 | 5.83 |
| Description | Dimension 1 | Dimension 2 | Dimension 3 |
|---|---|---|---|
| Value [mm] | 47.77 | 6.10 | 55.93 |
| Description | Dimension 1 | Dimension 2 | Dimension 3 |
|---|---|---|---|
| Value [mm] | 47.10 | 21.72 | 5.80 |
| Description | Dimension 1 | Dimension 2 | Dimension 3 |
|---|---|---|---|
| Value [mm] | 47.12 | 22.01 | 5.80 |
| Description | Simulation | CPK Data of Actual Product | Error Rate [%] | |
|---|---|---|---|---|
| Average | Standard Deviation | |||
| Dimension 1 [mm] | 47.73 | 47.620 | 0.0105 | 0.23 |
| Dimension 2 [mm] | 6.11 | 6.117 | 0.0080 | 0.11 |
| Dimension 3 [mm] | 55.81 | 55.837 | 0.0088 | 0.05 |
| Description | Simulation | CPK Data of Actual Product | Error Rate [%] | |
|---|---|---|---|---|
| Average | Standard Deviation | |||
| Dimension 1 [mm] | 47.12 | 47.500 | 0.0147 | 0.8 |
| Dimension 2 [mm] | 22.01 | 22.202 | 0.0150 | 0.86 |
| Dimension 3 [mm] | 5.80 | 5.901 | 0.0079 | 1.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-L.; Kim, W.-J.; Lee, S.-B. A Study on Dimensional Accuracy of a Vehicle Hood-Catch Considering Material Shrinkage of Polyamide 6 and Length-to-Volume Ratio Characteristic of a Shape. Machines 2022, 10, 934. https://doi.org/10.3390/machines10100934
Lee S-L, Kim W-J, Lee S-B. A Study on Dimensional Accuracy of a Vehicle Hood-Catch Considering Material Shrinkage of Polyamide 6 and Length-to-Volume Ratio Characteristic of a Shape. Machines. 2022; 10(10):934. https://doi.org/10.3390/machines10100934
Chicago/Turabian StyleLee, Soo-Lim, Won-Jin Kim, and Seon-Bong Lee. 2022. "A Study on Dimensional Accuracy of a Vehicle Hood-Catch Considering Material Shrinkage of Polyamide 6 and Length-to-Volume Ratio Characteristic of a Shape" Machines 10, no. 10: 934. https://doi.org/10.3390/machines10100934
APA StyleLee, S.-L., Kim, W.-J., & Lee, S.-B. (2022). A Study on Dimensional Accuracy of a Vehicle Hood-Catch Considering Material Shrinkage of Polyamide 6 and Length-to-Volume Ratio Characteristic of a Shape. Machines, 10(10), 934. https://doi.org/10.3390/machines10100934







