Unbalance Prediction of Low Pressure Rotor Based on Mechanism and Data Fusion

Abstract

The assembly, as the core part of low-pressure rotor manufacturing, is of great importance to ensure its unbalance. Low-voltage rotor assembly is a multi-process process influenced by the quality of part machining, assembly process, and assembly quality, resulting in unbalance that is difficult to predict during the assembly process. The unbalance measurement in the assembly process is important for the subsequent process optimization. Therefore, in order to achieve the prediction of unbalance measurement in the assembly process, this paper proposes an unbalance measurement prediction method based on mechanism and data fusion. Firstly, through research and analysis, the influencing factors of unbalance are determined, the low-pressure rotor blade sequencing mechanism model is established, and the blade sequencing optimization is realized by using reinforcement learning. Then, since the unbalance is formed after all the processes are completed and the subsequent work steps in the assembly process have not been carried out yet, the actual process parameters cannot be obtained, the semi-physical simulation method is used to combine the actual data of the assembled work steps with the theoretical data of the unassembled work steps to build a prediction model of the unbalance based on the BRNN (bidirectional recurrent neural network) network to achieve the prediction of the unbalance measurement in the assembly process. Finally, the model was validated using actual assembly process data, which proved the feasibility and effectiveness of the method.

1. Introduction

The low-pressure rotor of an aero-engine has an impact on the vibration response of the whole machine when it is rotating at high speed. Too much unbalance will make the low-pressure rotor rotate at high speed when the unbalance force rises, thus causing the whole machine to vibrate, and even lead to the blade touching to grind, and then affect the reliability and service life of the aero-engine operation [1,2,3,4]. Depending on statistics, about 60% of aero-engine vibrations are caused by rotor unbalance [5]. Therefore, it is very important to control the unbalance of the low-pressure rotor.

The low-pressure rotor is composed of a disk and blades. It is a typical multistage disk structure. The unbalance is the result of the superposition of unbalance vectors distributed on every single piece [6]. The changing and coupled assembly processes lead to the following difficulties in predicting low-pressure rotor unbalance during assembly:

• Unbalance is associated across processes. The assembly process of low-pressure rotors is divided into three processes: three-disc assembly, second-stage blade assembly, and first and third-stage blade assembly. The participating parts in each process are different, and the factors that affect the imbalance are also different. The unbalanced amount of the current process is not only related to the influencing factors of the process but also related to the unbalance of the previous process, which has a certain cumulative effect;
• Effect of blade assembly sequence on imbalance. The blade is an important part of the low-pressure rotor. The imbalance of the blade group will affect the imbalance of the rotor;
• Many factors are influencing unbalance and they are coupled with each other. The unbalance is related to the quality of parts processing, the assembly process, and the assembly quality, and involves numerous influencing factors, which are dynamically changing and coupled with each other. It is difficult to establish the relationship model between influencing factors and unbalance through a mechanism under the synergistic action of multiple factors;
• Assembly steps of low-pressure rotors are interrelated. Unbalance is formed after all the steps of a process are completed. The subsequent steps in the assembly process have not yet been carried out, the actual process parameters of the subsequent assembly steps cannot be obtained, and the prediction of unbalance in the assembly process cannot be realized. Additionally, the work steps are carried out step by step according to the process planning, with a certain time sequence relationship, and the assembly result of each work step not only has an impact on the unbalance of the process but also influences each other between the work steps. This requires that the unbalance prediction model can consider the influence of subsequent working steps on unbalancing while mining the temporal correlation.

In view of the above difficulties in predicting low-pressure rotor unbalance, this paper proposes a low-pressure rotor unbalance prediction method based on the fusion of mechanism and data drive, taking the low-pressure rotor of an engine model as the research object. Firstly, the blade assembly sequence optimization model is established through the mechanism analysis method to realize the blade assembly sequence optimization. Then, on the basis of determining the blade assembly sequence through the mechanism model, the actual assembly data of the assembled blade is combined with the design data of the unassembled blade to build a semi-physical simulation model based on the bidirectional recurrent neural network BRNN for predicting the unbalance in the assembly process while assembling, which provides data support for the subsequent optimization of unbalance.

2. Literature Review

2.1. Prediction Methods of Rotor Unbalance

Yue Chen et al. [7] proposed an unbalance optimization method for multistage rotors in the assembly process. A multistage rotor assembly error propagation model was established considering the alignment process and the distribution of screw holes in adjacent rotors. Based on the geometric parameters of the rotor in discrete stages, the change of the coordinate value of any point in each rotor before and after assembly is predicted. Liu Yongmeng et al. [8] propose a method to minimize stage-by-stage initial unbalance in the aero engine assembly of multistage rotors based on the connective assembly model. The process of the mass eccentric deviation propagation in the assembly is analyzed. The initial unbalance of the final assembly is improved by properly selecting the assembly orientations of multistage rotors. Chen Yue et al. [9] proposed an optimization method for aero-engine multistage rotor assembly, which predicted assembly coaxiality and unbalance at each stage in the assembly process and gave the best assembly direction.. Yang Yi et al. [10] proposed a method to predict the corresponding unbalance of the gear rotor system. Gohari M et al. [11] investigated the application of vibration signals in the prediction of rotor imbalance parameters, including unbalanced position and unbalanced magnitude values. Abbasi A et al. [12] proposed a hybrid algorithm detailing the salp group algorithm and the Nelder-Mead algorithm for determining the magnitude and phase of imbalance in rotor-bearing systems with rotational imbalance. Choudhury T et al. [13] applied a method based on force and displacement minimization to determine the unbalance position, magnitude, and phase of a large flexible rotor.

The above studies have realized the prediction of inequality to a certain extent. Unbalance prediction based on the stack model is mainly to compute the offset of the centroid of each disk to obtain the unbalance of the rotor as a whole. However, this method only examines the characteristics of parts and ignores the influencing factors in the assembly process, so the prediction result has a large error. Deep learning can consider multiple elements or even all elements in the assembly process. Using actual assembly process data can bring us closer to the actual assembly process. Therefore, this paper tries to use the deep learning method to mine the relationship between the influencing factors and the imbalance in the assembly process and realize the prediction of the imbalance.

2.2. Application of Semi-Physical Simulation Technology in The Assembly Field

Yi Tang et al. [14] proposed a real-time semi-physical co-simulation platform scheme to develop control centers and hardware devices based on the grid simulation developed by Real Time Laboratory (RT-LAB) and the communication network simulation developed by OPNET to achieve real-world control behavior instead of digital simulation. Jamshidi, J. et al. [15] integrated the measurement system into the assembly process and formed Measurement Assisted Assembly (MAA) technology, which provides guidance to the assembly process through continuous measurement of size and realizes the assembly size precision control technology. K. Cheng et al. [16] propose a semi-physical simulation method for industrial software testing and evaluation based on digital twin-driven technology. By building a semi-physical simulation model of SMS, the reliability and robustness of software systems are quickly verified by running industrial software in various manufacturing scenarios. Bao Jinsong et al. [17] proposed a hardware-in-kind virtual assembly model based on a fat model, which guided product preassembly, assembly analysis, and manufacturing decisions by combining the CAD model with point cloud data. Zhao Bin [18] established a semi-physical simulation model of aero-engine vibration by combining a finite element model with experimental data to decrease the error of engine vibration analysis because of the complex structure of the aero-engine and the substantial error of vibration simulation analysis.

The above research shows that the semi-physical simulation technology can think of the context information in the assembly process and combine the theoretical data with the measured data. In the process of the rotor assembly, unbalance is formed only after the completion of a specified procedure. In the assembly process, the subsequent work steps have not been carried out, so the actual process parameters and assembly quality of the ensuing work steps cannot be obtained, so theoretical data should be used instead. Therefore, this paper intends to use the idea of semi-physical simulation to establish a prediction model for the unbalance of low-voltage rotors.

2.3. Application of BRNN Neural Network

Wennian Yu et al. [19] proposed a sensor-based data-driven scheme that takes advantage of BRNN neural networks to correlate historical and future information, combined with similarity-based curve matching techniques to estimate the RUL of the system. Alvaro Peris et al. [20] introduced bidirectional recurrent neural networks to capture forward and backward temporal relationships in video input frames. Cheng Z. Heng et al. [21] used BRNN networks in the video snapshot compression imaging problem to improve the quality of reconstructed video by taking advantage of BRNN networks in time correlation to reconstruct subsequent frames of video in a sequential manner. Xianlong Tang et al. [22] proposed a multilayer bidirectional recurrent neural network-based model for predicting short-term electricity load and validated it on two data sets. The experimental results show that the proposed method outperforms the competition winner in terms of prediction accuracy on the EUTN competition data.

In summary, the BRNN (bidirectional recurrent neural network) neural network can correlate not only historical information but also future information to achieve a two-way correlation in time sequence. During the assembly process of the rotor, the assembly result of the previous process will have an impact on the assembly process and assembly quality of the next process. The assembly result of the next process will also change the assembly result of the previous process, and the assembly process of the rotor has a two-way timing correlation. Therefore, BRNN can build the prediction model of the rotor’s unbalance to achieve the prediction of unbalance.

3. Influence Factors of Low-Pressure Rotor Unbalance

The low-pressure rotor is a three-stage disk structure. Each stage is composed of a disk and a certain number of blades. Different assembly processes are involved in the assembly of the parts and the process is not consistent, making the influence factors of each process different, so the influence factors of each process are analyzed separately.

3.1. Factors Affecting Unbalance of the Disc Assembly Process

3.1.1. Disk Processing Quality Influencing Factors

Due to the inevitable errors in the machining process, there will be an uneven mass distribution of the discs at all levels in the molding process, making the initial unbalance of the discs at all levels. The initial unbalance of the disc is an important factor affecting the unbalance of the disc assembly process.

When the two disks are bolted together, the shape and position errors lead to uneven force in all parts of the connecting surface after assembly [2]. The form and position errors of all levels of disks are transmitted and accumulated along with the connecting surface of the joint, making all levels of disks produce eccentricity and deflection. The distribution of unbalance in the process is affected by adding another unbalance to the initial unbalance of the disk. Therefore, the shape and position error at the joint of the disk is the factor affecting the unbalance of the process [23].

The surface roughness of the column and section at the disk connection stop will also affect the final unbalance. The surface roughness of the cylinder and end face will change the contact stiffness at the connecting surface of the disk. The part surface is composed of many peaks and valleys, and the contact between the mating surfaces is actually the contact of the peaks. The contact of the bump affects the contact stiffness of the mating part. The smaller the roughness value, the less the contact of the bump, the smaller the clearance of the mating surface, the better the contact stiffness of the part, and the smaller the deformation [24,25].

Based on the above analysis of the factors affecting the machining quality of the unbalance of the disk assembly process, the formal expression of the factors affecting the machining quality of the unbalance of this process is as follows:

$$proQu{a}_1=\left(iu{b}_i,p{d}_i,per{p}_i,a{s}_i,at{r}_i,cs{r}_i,ts{r}_i,rc{y}_i,rs{r}_i,rp{h}_i,rh{s}_i\right)$$

(1)

In the formula $proQu{a}_1$ is the influencing factor of unbalanced processing quality in the disk assembly process; $iu{b}_i$,$p{d}_i$,$per{p}_i$,$a{s}_i$,$at{r}_i$,$cs{r}_i$,$ts{r}_i$,$rc{y}_i$,$rs{r}_i$,$rp{h}_i$,$rh{s}_i$ are the initial unbalance of the level i disk, the parallelism, runout, and surface roughness of the end face of the disk connection.

3.1.2. Disk Assembly Process Influencing Factors

The mounting angle between the two discs affects the transmission of the deviation, which in turn affects the mass eccentricity of the discs [26]. The assembly process influences that affect unbalance in this process include the mounting angle between the discs, expressed formally as follows:

$$assTe{c}_1=\left(ip{h}_i\right)$$

(2)

In the formula,$assTe{c}_1$ is the set of factors influencing the unbalanced amount of the disk installation process;$ip{h}_i$ is the installation phase of the grade$i$disk.

3.1.3. Disk Assembly Quality Influencing Factors

Due to the manufacturing error of the single-stage disk, it makes the coaxiality error of the disk at all levels after the completion of assembly, and the existence of coaxiality error leads to the deviation of the disk inertia axis and rotation axis, which changes the eccentricity of the unbalanced mass [27]. In addition, the roughness between the contact surfaces can lead to inconsistent preload on the bolts, which can further distort the disk connection surfaces and affect the rotor’s mass eccentricity. Therefore, the coaxiality between the discs of each level is the influencing factor for the unbalance of the disc assembly process, which is expressed formally as follows:

$$assQu{a}_1=\left(dca\right)$$

(3)

In the formula,$assQu{a}_1$ is the set of factors affecting the assembly quality of the unbalance of the disk assembly process;$dca$ is the coaxiality between two disks.

3.2. Influencing Factors of Unbalanced Amount of Blade Assembly Process

3.2.1. Factors Affecting the Processing Quality of the Blade Installation Process

Due to the processing error making the blade weight moment deviation, different weight moments will appear in different blade group sorting ways. Different sorting methods of blade groups will produce different unbalance of blade groups. Therefore, the weight moment of the blade and the unbalance of the blade set are the main influencing factors on the unbalance of the low-pressure rotor. The formal expression of the factors influencing the processing quality of the unbalance of the process is as follows:

$$proQu{a}_{2,3}=\left(\overrightarrow{UB},w{d}_i^j,pu{b}_i\right)$$

(4)

In the formula,$proQu{a}_{2,3}$ is the unbalance of the blade installation process of grade $i$; $\overrightarrow{ UB}$ is the unbalance after the assembly of the previous process.$w{d}_i^j$ is the weight moment of the jth blade of the $i$ disk; $pu{b}_i$ is the unbalance of grade $i$ blade group.

3.2.2. Factors Influencing the Assembly Process of Blade Mounting Process

Different blade installation positions will have different blade unbalance. Therefore, the installation position of the blade is an influential factor affecting the amount of unbalance, expressed formally as follows.

$$assTe{c}_{2,3}=\left(bs{e}_i^j\right)$$

(5)

In the formula,$assTe{c}_{2,3}$ is the influencing factor of the assembly process of blade mounting process unbalance;$bs{e}_i^j$ is the jth blade installation position of grade i disk.

3.2.3. Factors Influencing Assembly Quality of Blade Mounting Process

In the process of the blade assembly, the clearance fit between blade and disk will affect the overall eccentricity of the rotor. Therefore, the assembly gap between blade and disk is the influencing factor of unbalance.

$$assQu{a}_{2,3}=\left(pc{l}_i^j\right)$$

(6)

In the formula,$assQu{a}_{2,3}$ is the influencing factor of assembly quality of blade mounting process unbalance; $pc{l}_i^j$ is the assembly clearance of the jth blade of the grade $i$ disk.

4. Overall Method Description

For the rotor unbalance prediction problem, this paper proposes a semi-physical simulation model framework for unbalance prediction based on the fusion of mechanism and data drive. Firstly, the blade assembly sequence optimization model is established through the mechanism analysis method to realize the blade assembly sequence optimization. Then, based on the bidirectional recurrent neural network BRNN, a semi-physical simulation model for rotor unbalance prediction is constructed. The actual data of the assembled part is fused with the theoretical design data of the unassembled part to achieve the prediction of rotor unbalance. The framework includes ranking optimization of blades, data enhancement based on adversarial self-encoder AAE (adversarial auto-encoder), and semi-physical simulation of unbalance prediction based on BRNN (bidirectional recurrent neural network). The semi-physical method of low-pressure rotor imbalance prediction is shown in Figure 1 below.

Blade sequencing is based on the establishment of a blade sequencing optimization mechanism model, using reinforcement learning to optimize the blade sequencing so that the sum of blade group unbalance and disc initial unbalance is minimized, so as to obtain the optimal blade sequencing.

Data augmentation based on the AAE method is to learn the distribution of the original data by combining the generative adversarial network and the self-encoder. New sample data are generated based on the distribution of the original data to provide data support for the training imbalance prediction model.

The semi-physical simulation of imbalance prediction based on BRNN (bidirectional recurrent neural network) is divided into two parts: data fusion and imbalance prediction.

Data fusion is used to fuse theoretical data with actual data in order to construct inputs for the imbalance prediction model. Since the part to be assembled has been determined before assembly, the processing quality factors of each step are the actual value $x_{pqr}^t$ when predicting the imbalance amount. When the assembly of the tth working step is completed. The assembly process $x_{atr}^t$and assembly quality $x_{aqr}^t$ before this working step are actual values. The assembly process $x_{atv}^t$and assembly quality $x_{aqv}^t$ of the later steps are theoretical values. The data after fusion is$X^t=\left(X_r^1,X_r^2,\cdots ,X_r^t,\cdots ,X_v^N\right)$. The data $X_r^1$ to $X_r^t$ before the tth working step are all actual data, $X_r^t=\left(x_{pqr}^t,x_{atr}^t,x_{aqr}^t\right)$. $X_v^{t+1}$ to $X_v^N$ are the theoretical values,$X_v^{t+1}=\left(x_{pqv}^t,x_{atv}^t,x_{aqv}^t\right)$.

The imbalance prediction is to input the fused data $X^t$ into the model to realize the prediction of the imbalance $\overrightarrow{UB}$ of the process step.

5. Blade Sorting Mechanism Model

The blade assembly sequence is the main factor affecting rotor unbalance. Existing methods usually divide the disc into several areas and control the difference in blade quality between the areas so that the imbalance of the blade group is small. In this process, the initial imbalance of the disk is not considered. Although the imbalance of the blade group is small, the overall imbalance after assembly still does not meet the requirements. Therefore, in this paper, based on the establishment of the blade sorting optimization mechanism model, reinforcement learning [28] is used to optimize the blade sorting so that the sum of the unbalance of the blade sorting and the initial unbalance of the disk is minimized and the optimal blade sorting order is obtained.

The blade affects the unbalance of the rotor through the mass moment. The blade mass moment is composed of the mass and the distance from the center of mass to the blade tenon [29]. The theoretical mass of blade i is $m_i$, The theoretical radius of the rotation vector is ${\overrightarrow{r}}_i$. The theoretical mass moment is as follows:

$${\overrightarrow{M}}_{li}=m_i\times {\overrightarrow{r}}_i$$

(7)

The mass moment of the blade is decomposed orthogonally, as shown in Figure 2 below. Under ideal conditions, the vector sum of the mass moments of all blades with respect to the axis of rotation is zero. The centroid of the blade group coincides with the origin. Due to the machining error of the blade, the centroid of the blade group is deviated, which leads to unbalance.

$$M_x={\displaystyle \sum }_1^n{M}_{i}cos {\alpha }_i{M}_y={\displaystyle \sum }_1^n{M}_{i}sin {\alpha }_i$$

(8)

Since the number of blades in each stage of the low-pressure rotor is fixed, so${\alpha }_i=\frac{360°}{n}*i\left(i=1,2,3\dots n\right)$. In the formula, n is the number of blades, and i is the ith blade. After the mass moments of the blade set are orthogonally decomposed, the amount of unbalance of the blade set can be determined.

$$M_n=\sqrt{M_x^2+M_y^2}=\sqrt{{\left({\displaystyle \sum }_1^n{M}_{i}cos{\alpha }_i\right)}^2+{\left({\displaystyle \sum }_1^n{M}_{i}sin{\alpha }_i\right)}^2}$$

(9)

The initial unbalance of the disk is called ${\overrightarrow{M}}_d$. By optimizing the blade sequence, the sum of the blade mass moments ${\overrightarrow{M}}_n$ and the initial unbalance ${\overrightarrow{M}}_d$ of the disk cancel each other as much as possible, to minimize the initial unbalance of the rotor.

$$min({\overrightarrow{M}}_n+{\overrightarrow{M}}_d)$$

(10)

There are n blades in the low-pressure rotor, and there are n! ways to arrange the blades. The calculation is large, and the exhaustive method is difficult to complete. In this paper, reinforcement learning is used to optimize the blade ordering, and the optimal blade ordering result is obtained to ensure that the unbalance of the rotor after blade assembly meets the requirements.

6. Imbalance Data Enhancement Based on AAE Model

The low-voltage rotor is a single-piece small batch production mode, and the assembly data volume is small. While the existing deep learning model requires a large sample size, small sample data is difficult to ensure the accuracy and generalization ability of the prediction model. To achieve an accurate prediction of inequality, it is necessary to enhance the existing small sample data and expand the existing data set. An adversarial auto-encoder (AAE) is a generation network that can learn the distribution of original samples and generate new sample data without the guidance of human experience. Therefore, AAE is selected as the data enhancement model in this paper. The problem of low accuracy and poor generalization of the prediction model caused by the small amount of assembly data is solved by generating new sample data.

6.1. Imbalance Data Enhancement Network Design Based on AAE Model

The AAE model is composed of an autoencoder and an adversarial network. The basic structure is shown in Figure 3 below. The AAE model matches the implicit coding of the encoder with the prior distribution by training on the target. In the application, the sampled data in the prior distribution is used as the input, and the decoder completed by training is used as the generating model to generate new data with the same distribution as the original data set.

In the above figure $x$ represents the actual sample. $z$represents the implicit encoding of the autoencoder. $p\left(z\right)$ is the preset prior distribution. Each batch training of the AAE model is divided into two stages: sample reconstruction and regularization. In the sample reconstruction stage, the autoencoder updates the encoder and decoder to reduce the input reconstruction error. In the regularization stage, the adversarial network updates its discriminant network to distinguish real samples from generated samples and updates its generative network to confuse the discriminant network. When the training is completed, the decoder of the autoencoder can be used as a generative model to realize sample enhancement [30].

The design of the AAE model includes the setting of model layers, input dimension, hidden coding dimension, prior distribution, and other parameters. The input dimension of the AAE model is the number of influencing factors included in the process. The optimal model depth and the number of neurons in each layer were obtained through multiple-model training. In the AAE model, prior distribution $p\left(z\right)$ can be preset arbitrarily. Most of the influencing factors studied in this paper, including form and position tolerance, assembly process, and assembly quality, conform to the Gaussian distribution. Therefore, the Gaussian distribution is selected as the prior distribution $p\left(z\right)$ required for the model. In addition, the sampling data $z^{\prime }$ of $p\left(z\right)$ in the model training stage needs to be input into the discriminator at the same time as the encoder’s implicit code $z$ for antagonistic training. In the application phase, the preset $z^{\prime }$ is used as the input of the decoder to generate new data samples. Therefore, the dimension must be the same as the dimension of the encoder’s implicit code $z^{\prime }$.

6.2. Implementation of Imbalanced Data Enhancement Network Based on AAE Model

This article uses the Python-based machine learning open-source platform TensorFlow to achieve unbalanced data enhancement. The following

Table 1. Training process of AAE model.

Steps	Specific Content
Input	Input sequence $\mathrm{X}=\left\{X_1,X_2,\dots ,X_L\right\}$ composed of key influencing factors and unbalanced data of an assembly process
Output	Decoder weights $W^T$ and bias $b^T$
The first stage: sample reconstruction stage
Step 1.1	Set the algorithm parameters, including batch size, learning rate, random initialization of encoder, decoder, and discriminator weight $W$, and bias$b$;
Step 1.2	The normalized feature sequence was obtained by z-Score normalization for the input sequence X;
Step 1.3	The standard sequence after standardization is input into AE to obtain the implicit coding and the reconstructed sequence; $z=f\left(WX+b\right),X^{\prime }=g\left(W^{T}z+b^T\right)$;
Step 1.4	The mean square error function is used as the loss function to calculate the error between the input data and the reconstructed data; $L_A=\frac{1}{m}{\displaystyle {\displaystyle \sum }_{i=1}^m}\frac{1}{2}||X-X^{\prime }{||}^2$
Step 1.5	Gradient descent algorithm was used to update AE model parameters. $W=W-\eta \frac{\partial L_A\left(W,b\right)}{\partial W},\mathrm{b}=\mathrm{b}-\eta \frac{\partial L_A\left(W,b\right)}{\partial b}$
The second stage: regularization stage
Step 2.1	The encoder output z and some random input $z^{\prime }$ are input to the discriminator for classification;
Step 2.2	The cross-entropy function is used as the loss function to calculate the error between discriminator and encoder; $L_D=-\frac{1}{m}{\displaystyle {\displaystyle \sum }_{k=1}^m}\left[\log \left(D\left(z^{\prime }\right)\right)+\log \left(1-D\left(z\right)\right)\right],L_E=-\frac{1}{m}{\displaystyle {\displaystyle \sum }_{k=1}^m}\log \left(D\left(z\right)\right)$
Step 2.3	Discriminator parameters are reversely optimized according to errors; $W^{\prime }=W^{\prime }-\eta \frac{\partial L_D\left(W^{\prime },b^{\prime }\right)}{\partial W^{\prime }}, b^{\prime }=b^{\prime }-\eta \frac{\partial L_D\left(W^{\prime },b^{\prime }\right)}{\partial b^{\prime }}$
Step 2.4	The encoder parameters are reversely optimized according to the error. $W=W-\eta \frac{\partial L_E\left(W,b\right)}{\partial W},\mathrm{b}=\mathrm{b}-\eta \frac{\partial L_E\left(W,b\right)}{\partial b}$
Step 3	Repeat the above steps until the loss functions $L_A,L_D$ and $L_E$ converge;
Step 4	After network training, weight $W^T$ and bias $b^T$ of decoder are output.

is a detailed introduction to AAE model training.

For each assembly process of a low-voltage rotor, the decoder weight $W^T$ and bias $b^T$ of the data generation model for each assembly process are obtained through the training of the above steps. Then, the data is sampled from the predefined a priori distribution and input to the decoder to obtain new sample data for each assembly process, so as to expand the data of each assembly process of the low-voltage rotor and lay the foundation for establishing the prediction of process unbalance.

7. Prediction of Inequality Based on BRNN

In the assembly process of a low-voltage rotor, the assembly result of the front installation process will affect the assembly process and assembly quality of the rear installation process. The assembly result of the following installation process will change the assembly result of the previous installation process, and the assembly process has a bi-directional temporal correlation. The relationship between process unbalance and its influencing factors is complex and the mechanism of action is not clear, so the mapping relationship between process unbalance and its influencing factors cannot be established by a mathematical formula. BRNN [31] is a recurrent neural network. In addition to constructing nonlinear and complex mapping relationships, its special LSTM (Long-Short Term Memory) unit can not only associate historical information but also associate future information to realize bidirectional association in time sequence. Therefore, this paper adopts the BRNN network to establish the unbalance prediction model of the low-voltage rotor and realize the unbalance prediction of each process.

7.1. Parameter Design of Unbalanced Prediction Model Based on BRNN Network

Due to the different meanings and changes of each influencing factor, it is difficult to directly take each key influencing factor as the input of the prediction model. In this paper, the influencing factors are divided into the following two types of influencing factors: those that change with the process and those that change with the work step according to the changes of the influencing factors. Influencing factors that change with the process are factors that do not change in a given assembly process, such as the initial unbalance of the disk and its mounting angle at each level in the disk assembly process. The influence factor that changes with the work step is the factor that changes with the assembly work step repeatedly in a certain assembly process, for example, the weight moment of the blade at each level and its installation position in the blade assembly process. The input of the unbalance prediction model of each assembly process is a combination of the influencing factors that change with the process and the influencing factors that change with the work step. The input dimension is the number of influencing factors of the corresponding assembly process.

Each assembly process is composed of a number of assembly steps and has a certain degree of repeatability. The repeatability of assembly steps makes it possible to predict the unbalance of each process by using the BRNN network. Therefore, the number of repeated work steps in each assembly process is taken as the time step of BRNN when constructing the prediction model of the unbalance of each process.

Although this paper uses the AAE model to enhance the unbalance data of each process, the generated data still has some errors. To reduce the effect of data errors, the number of neurons contained in each LSTM unit is set to a lesser value.

To sum up, the input neurons of the BRNN unbalance prediction model are LSTM units. The number of units contained in each LSTM unit is determined according to different processes. The time step of the model is the number of working steps included in each process. The dimension of the time window is the number of influencing factors that change with the working procedure and working step.

7.2. Realization of Unbalance Prediction Model Based on BRNN Network

This paper uses TensorFlow, an open-source machine learning algorithm library based on Python, to build a prediction model of inequality based on the BRNN network. The training steps of the model are shown Figure 4 and

Table 2. Training steps of unbalance prediction model based on the BRNN network.

Steps	Specific Content
Input	The work step sequence $X_i^t=\left\{X_i^1,X_i^2,\cdots ,X_i^N\right\}$ of an assembly process i and the corresponding actual unbalance $U{B}_i$;
Output	BRNN network weight $W$ and bias b;
Step 1	Setting network hyperparameters, including setting network learning rate, batch size, initializing network weight $W$, and bias$b$;
Step 2	The input of each time step is formed by combining the influencing factors that vary with the working procedure and working step;
Step 3	Network forward prediction unbalance $U_i^t$; $h_t=f\left(W_1{X}_i^t+W_2{h}_{t-1}\right),h_t^{’}=f\left(W_3{X}_i^t+W_4{h}_{t-1}^{’}\right),U_i^t=g\left(W_5{h}_t+W_6{h}_t^{’}\right)$
Step 4	Calculate the root mean square error L of the actual unbalance $U{B}_i$ and the predicted value $U_i$; $L=\frac{1}{m}{\displaystyle {\displaystyle \sum }_{i=1}^m}\frac{1}{2}||U{B}_i-U_i^t||{}^2$
Step 5	Adam algorithm is used to optimize and update the weight W and bias b according to L;
Step 6	Repeat the above step3~step5 until L convergence;
Step 7	Save the network weight W and bias b.

.

8. Case Study

8.1. Example Verification of Blade Sorting Mechanism Model

This paper studies a model of an aero-engine low-pressure rotor with three sets of blades. When assembling, the second-stage blades are assembled first, and then the overall unbalance of the rotor is measured. Then, the first-stage blades or the third-stage blades are assembled, and the overall unbalance is measured after the three sets of blades are assembled. It can be seen that the second-stage blades are a relatively important part of the low-pressure rotor. Therefore, this paper takes the second-stage blade arrangement as an example for verification. The constructed model is used to optimize the blade arrangement. The data for second-stage blades are shown in the following

Table 3. Second-level blade data.

Blade Number	Mass Moment	Blade Number	Mass Moment	Blade Number	Mass Moment	Blade Number	Mass Moment
1	69,960	16	69,740	31	69,860	46	69,720
2	67,600	17	68,140	32	68,100	47	68,180
3	69,720	18	69,620	33	69,700	48	69,580
4	68,260	19	68,300	34	68,260	49	68,320
5	69,540	20	69,240	35	69,480	50	69,460
6	68,400	21	68,500	36	68,420	51	68,560
7	69,340	22	69,300	37	69,340	52	69,260
8	69,600	23	68,660	38	68,640	53	68,680
9	69,480	24	69,200	39	69,200	54	69,200
10	68,700	25	68,800	40	68,700	55	68,800
11	69,180	26	69,100	41	69,100	56	69,080
12	68,840	27	68,880	42	68,840	57	68,900
13	69,060	28	69,040	43	69,040	58	69,020
14	68,920	29	68,940	44	68,940	59	68,960
15	69,020	30	68,980	45	69,000	60	68,980

.

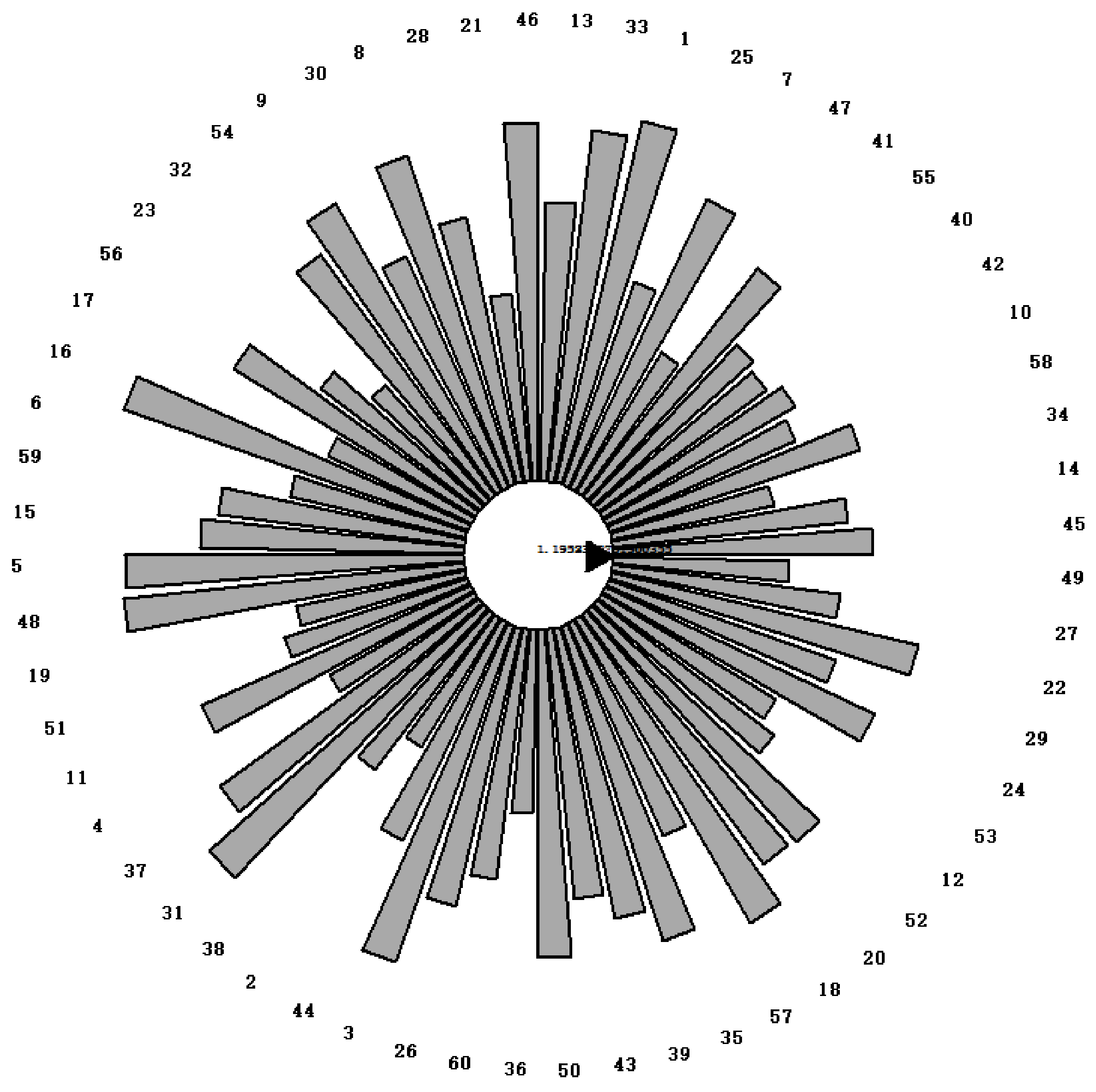
The blade ordering model was constructed to optimize the blade ordering, and the results of the ordering graph were as follows: Figure 5 and

Table 4. Order table of secondary blades.

Serial Number	Blades Sequence	Mass Moment	Serial Number	Blades Sequence	Mass Moment
1	47	68,180	31	25	68,800
2	49	68,320	32	54	69,200
3	53	68,680	33	22	69,300
4	35	69,480	34	3	69,720
5	56	69,080	35	19	68,300
6	50	69,460	36	51	68,560
7	31	69,860	37	1	69,960
8	16	69,740	38	33	69,700
9	27	68,880	39	7	69,340
10	9	69,480	40	41	69,100
11	24	69,200	41	14	68,920
12	6	68,400	42	45	69,000
13	42	68,840	43	44	68,940
14	23	68,660	44	43	69,040
15	48	69,580	45	15	69,020
16	29	68,940	46	37	69,340
17	59	68,960	47	17	68,140
18	26	69,100	48	36	68,420
19	34	68,260	49	39	69,200
20	10	68,700	50	46	69,720
21	40	68,700	51	12	68,840
22	18	69,620	52	30	68,980
23	8	69,600	53	20	69,240
24	58	69,020	54	2	67,600
25	32	68,100	55	52	69,260
26	28	69,040	56	60	68,980
27	11	69180	57	5	69,540
28	38	68,640	58	21	68,500
29	55	68,800	59	57	68,900
30	4	68,260	60	13	69,060

.

The result of the blade sorting determines the overall assembly unbalance of the rotor. In order to verify the optimization effect of the method in this paper, several methods mentioned in the literature [32,33], simulated annealing algorithm SA, and particle swarm optimization algorithm PSO were used to sort the blades, and the results of unbalance and mass moment difference of the diagonal position of the blades were obtained, as shown in

Table 5. Comparison of sorting method results.

Sorting Method	Weight Sorted [32]	Work-Shop [32]	Sorting-1 4 Skip [32]	Sorting-2 7 Skip [32]
Unbalance	10,563.27	2162.00	3452.83	2241.50
Mass moment difference	1820	1200	2060	580
Sorting method	Sorting-3 [33]	Sorting-4 [33]	Sorting-5 [33]
Unbalance	1126.86	947.02	807.56
Mass moment difference	340	580	340
Sorting method	SA	PSO	Q-learning
Unbalance	15.18	22.59	4.95
Mass moment difference	680	1340	1400

.

As can be seen from Table 5, the Weight Sorted and Sorting-1 (4 skip) methods have a serious excess of unbalance in the blade arrangement process, and the diagonal mass moment difference is too large. Work-shop, Sorting-2 (7 skip), Sorting-3, Sorting-4, and Sorting-5 have relatively small unbalance under the condition that the diagonal mass moment difference meets the requirements, but the unbalance is still greater than 100 $g\ast mm$, and the result is still not ideal. Next is a comparison of the three intelligent algorithms (SA, PSO, and GA) with traditional sorting methods. It can be seen from the table that the diagonal mass moment differences optimized by the intelligent algorithm all meet the requirements, and the calculated unbalance value is far less than that of the traditional sorting method.

In order to further explore the performance of each intelligent algorithm, MEAN, and root MEAN square error (RMSE) were used to evaluate the accuracy and robustness of each intelligent algorithm. The smaller the values of MEAN and RMSE, the higher the accuracy and the better the robustness of the algorithm.

From

Table 6. Intelligent algorithm comparison.

Algorithm	SA	PSO	Q-Learning
MEAN	20.26	18.11	9.24
RMSE	12.36	11.80	3.33

, the MEAN and RMSE values of Q-learning are the smallest, with 9.24 and 3.33, respectively. The optimization effect and robustness of Q-learning are more suitable for the solution of aero-engine rotor blade sequencing optimization problems compared with SA and PSO algorithms. Additionally, the reinforcement learning algorithm can make the blade sorting model converge to the optimal value rapidly as the model is continuously trained.

8.2. Example Validation of The Model with Enhanced Inequality Data

Taking the second-stage blade assembly process as an example, the actual data of the second-stage blade assembly process were input into the AAE model as the original samples. The weight of each part is optimized and updated by the Adma optimization algorithm. The model reconstruction error, discrimination error, and generation error are reduced. The variation trend of the above errors with the number of iterations of the training process is shown in Figure 6 below.

According to Figure 6 above, the reconstruction error of the autoencoder converges to 0.19 after 100 iterations. The discrimination error of the discriminator converges to 1.49 after 300 iterations. The generator error converges to 0.8 after 400 iterations. The decrease in reconstruction error indicates that the auto-encoder has a higher degree of feature fitting and that the decoder can reconstruct the original data well. The increase in discriminator error and the decrease in generator error indicate that the difference between the generated data and the real data decreases with the increase in training times. When the curve converges, it indicates that the model has reached equilibrium.

After the AAE model training is completed, 1000 groups of new data samples are generated using prior distribution as input and the decoder as the generation model. There are 183 columns in the sample. A partial sample is shown in

Table 7. AAE generates model results.

	Disk Unbalance	Unbalance of Blade Group	Blade 1 Weight Moment	Blade 1 Installation Position	Blade 1 Assembly Clearance	Blade 60 Weight Moment	Blade 60 Installation Position	Blade 60 Assembly Clearance	Unbalance Assembly Process
1	1154.34	3200	65,754.01	41	0.09	65,514.17	56	0.11	654.575
2	1182.16	3349.41	65,510.354	11	0.1	65,496.28	49	0.20	993.479
3	1458.55	3114.59	67,65467.	48	0.16	65,532.05	39	0.18	805.35
4	1423.65	3395.08	65,564.01	36	0.15	65,587.37	18	0.15	620.321
5	1193.25	3212.92	65,487.86	19	0.18	65,538.48	29	0.5	741.677
6	1167.26	3184.96	65,792.56	26	0.04	65,571.05	17	0.17	885.119
7	1167.262	3237.32	65,716.85	12	0.11	65,518.22	19	0.13	915.048
8	1207.559	3215.63	65,546.92	15	0.05	65,650.04	3	0.08	695.812

.

In total, 1000 groups of sample data generated by the AAE model were input into the BRNN network for training. After training, 20 groups of original data were input into the trained model to observe the error between the actual value and the predicted value of unbalance. The loss function curve and prediction results of the training process are shown in Figure 7 below.

The trained BRNN network converges to 0.14 after 150 iterations. The prediction results show that the constructed prediction network can predict the unbalance of the assembly process better and the prediction effect is better. At the same time, it shows that the sample data generated by the model is distributed with the original data, which has a certain validity. The data generated based on the AAE model is only used for the training of the unbalance prediction model. In practice, data augmentation is not required and will not affect the runtime of the unbalance prediction model.

8.3. Example Verification of Unbalance Prediction Model

Take the second-stage blade assembly process as an example; there are 60 blades in this process, so the time step of the process prediction model is 60. The input of each time step is the initial unbalance of the disk, the unbalance of the secondary blade group, the weight moment of the blade, the installation position of the blade, and the blade assembly gap. In order to facilitate data reading and training, the generated $1000\times 183$ data storage format is changed to a $\mathrm{60,000}\times 5$ data format. Every 60 lines is a group of assembly data, and one line is a time step data. One set of data is as follows:

$$\left\{\begin{array}{c}{X}_1^2=\left(\begin{array}{ccccc}1154.34& 967.09& 41& 65754.01& 0.09\end{array}\right)\\ X_2^2=\left(\begin{array}{ccccc}1154.34& 967.09& 16& 65617.62& 0.16\end{array}\right)\\ \cdots \hfill \\ X_{60}^2=\left(\begin{array}{ccccc}1154.34& 967.09& 56& 65514.17& 0.11\end{array}\right)\end{array}\right.$$

(11)

In order to evaluate the established unbalance prediction model, this paper compares the prediction results of the BRNN network with those of the LSTM network and BP neural network. The root mean square error (RMSE), mean absolute error (MAE), and R² are also selected as evaluation metrics to compare the accuracy and robustness of each algorithm. The comparison with the LSTM network method is performed to verify the advantages of the BRNN network in the problem of bidirectional timing correlation of rotor assembly, and the comparison with the BP [34] network method is performed to compare with other methods from the literature.

In this paper, k-fold cross-validation is used for validation. The 1000 sets of data were sequentially divided into 5 copies of 200 sets each, and 4 of them were taken for training and 1 for testing each time. The loss function curves and test sample prediction curves for the training process of each model are shown in the following Figure 8.

The prediction results of 10 randomly selected groups of prediction models are shown in

Table 8. Model prediction results.

	BP	LSTM	BRNN	True Value	BP Relative Error (%)	LSTM Relative Error (%)	BRNN Relative Error (%)
1	713.72	704.44	849.67	786.21	9.22	10.4	8.07
2	736.24	842.07	768.54	805.67	8.62	4.52	4.61
3	702.53	811.34	756.49	794.59	11.59	2.11	4.79
4	684.28	669.66	86.39	762.82	10.3	12.21	8.33
5	838.43	818.91	803.16	771.69	8.65	6.12	4.08
6	893.24	776.84	753.87	835.18	6.96	6.99	9.74
7	762.13	785.93	793.46	843.54	9.65	6.83	5.94
8	866.42	724.68	726.81	782.94	10.66	7.44	7.42
9	883.41	861.79	847.66	812.37	8.74	6.08	4.34
10	727.33	749.24	839.65	792.54	8.23	5.46	5.94

below.

As can be seen from Table 8, the maximum relative error of the BP neural network model is 11.59%, the minimum relative error is 6.96%, and the average relative error is 9.26%. The maximum relative error of the LSTM neural network is 12.21%, the minimum relative error is 2.11%, and the average relative error is 6.82%. The maximum relative error of the BRNN neural network is 9.74%, the minimum relative error is 4.08%, and the average relative error is 6.33%. In summary, the prediction results of the BRNN neural network are relatively balanced and the average relative error is minimal, which proves the effectiveness and accuracy of the proposed method.

Evaluated from the metrics of the prediction models, the RMSE, MAE, and R² values of each prediction model are shown in

Table 9. Evaluation results of different models.

Model	RMSE	MAE	R2
BRNN network	11.798	9.6718	0.664
LSTM network	14.939	11.704	0.462
BP network	19.163	15.442	0.114

.

From the above loss function curves, we can see that the BRNN network converges to 0.12 after 150 iterations, the LSTM converges to 0.16 after 200 iterations, and the BP network converges to 0.18 after 250 iterations, indicating that the BRNN network can fit better and faster. By comparing the RMSE, MAE, and R² of each model in Table 9 above, it can be seen that the BRNN network has the smallest RMSE and MAE and the largest R², and the BRNN network proposed in this paper has better effectiveness and accuracy in the prediction of the unbalance.

After the above training and validation processes, the unbalance prediction model for the second stage blade assembly process is obtained. In order to validate the prediction model of unbalance using semi-physical ideas, the original data set is used as the test set, and it is tested by fusing the actual data with the theoretical data to form $50\times 60$ sets of data. The theoretical values of the initial unbalance of the disk, the unbalance of the secondary blade set, the blade weight moment, and the assembly clearance are shown in the following

Table 10. Theoretical values of key influencing factors of secondary blade assembly process.

Influencing Factors	Theoretical Value	Influencing Factors	Theoretical Value
Disk initial unbalance measurement	1300 g.mm	Blade weight moment	65,500 g.mm
Imbalance of secondary blade set	800 g.mm	Assembly clearance	0.12 mm

.

Among the above influencing factors, the initial unbalance of the disk and the unbalance of the secondary blade set are influencing factors that change with the process. Blade weight moment and mounting position are determined before blade assembly. The only undetermined influencing factor is the assembly clearance between the blade and the disk. Therefore, the theoretical data for this process is only the assembly gap. After the first step is completed, the actual data is fused with the theoretical data to form one of the data sets as follows. Each subsequent step replaces the corresponding process data in the input. Input the above data into the model to predict inequality, and some specific prediction results are shown in the following

Table 11. Semiphysical simulation model prediction results.

Sample Number	Actual Value	Predictive Value	Relative Error (%)
1	828.33	871.23	5.18
5	805.94	866.34	7.49
10	811.45	702.68	13.40
20	783.13	801.56	2.35
25	791.22	806.31	1.91
30	803.84	730.69	9.1
35	788.27	832.68	5.6
40	797.23	876.49	9.94
45	792.04	755.82	4.57
50	836.79	801.45	4.22

:

$$\left\{\begin{array}{c}{X}_1^2=\left(\begin{array}{ccccc}1435.36& 1066.14& 32& 67340& 0.14\end{array}\right)\\ X_2^2=\left(\begin{array}{ccccc}1435.36& 1066.14& 5& 68860& 0.12\end{array}\right)\\ \cdots \hfill \\ X_{60}^2=\left(\begin{array}{ccccc}1435.36& 1066.14& 6& 66960& 0.12\end{array}\right)\end{array}\right.$$

(12)

The above prediction results show that the unbalance prediction model of the two-stage blade assembly process can realize the unbalance prediction in the assembly process. The maximum relative error is 13.4%, and the minimum relative error is 2.35%. Based on the above case verification, the proposed semi-physical simulation method of mechanism and data-driven fusion for low-voltage rotor unbalance prediction is effective, which can realize the unbalance prediction in the assembly process. The accuracy of the unbalance prediction model is affected by the blade sequencing results and the model training data, and the above example validation results also demonstrate again the effectiveness of the AAE-based generated data and the blade sequencing mechanism model.

9. Conclusions

In order to solve the problem of multiple assemblies and trials caused by the over-uniformity and low success rate of one-time assembly, this paper proposes a mechanism and data-driven fusion of a low-pressure rotor unbalance prediction method. Firstly, a blade sequencing mechanism model is established, and reinforcement learning is used to achieve blade sequencing optimization. Secondly, the actual data of the assembled blades are combined with the theoretical data of the blades that have not been assembled, and a semi-physical simulation framework of unbalance prediction with a BRNN network as the core is constructed to realize the imbalance prediction during the assembly process. Finally, the effectiveness of the method is demonstrated by comparing it with the BP neural network method and the LSTM neural network method. The method can be extended to other rotary multi-stage equipment assembly areas, such as turbine assembly. However, in this paper, the construction of the prediction model is completed by the samples generated by the AAE model, and there will be a gap between the generated samples and the actual samples. With the accumulation of real data, how to conduct incremental learning of the model is the next research direction.