Fault Feature Enhanced Extraction and Fault Diagnosis Method of Vibrating Screen Bearings
Abstract
:1. Introduction
2. Improved Singular Value Decomposition Based on Singular Value’s Unilateral Ascent Rate Method (SSVD) for Pre-Denoising
2.1. Signal Reconstruction Principle Based on Singular Value’s Unilateral Ascent Rate Method
2.2. Simulation
3. Variational Mode Decomposition Improved by Revised Whale Optimization Algorithm (RWOA-VMD) for Fault FEATURE Enhancement
3.1. Whale Optimization Algorithm (WOA)
3.2. Revised Whale Optimization Algorithm (RWOA)
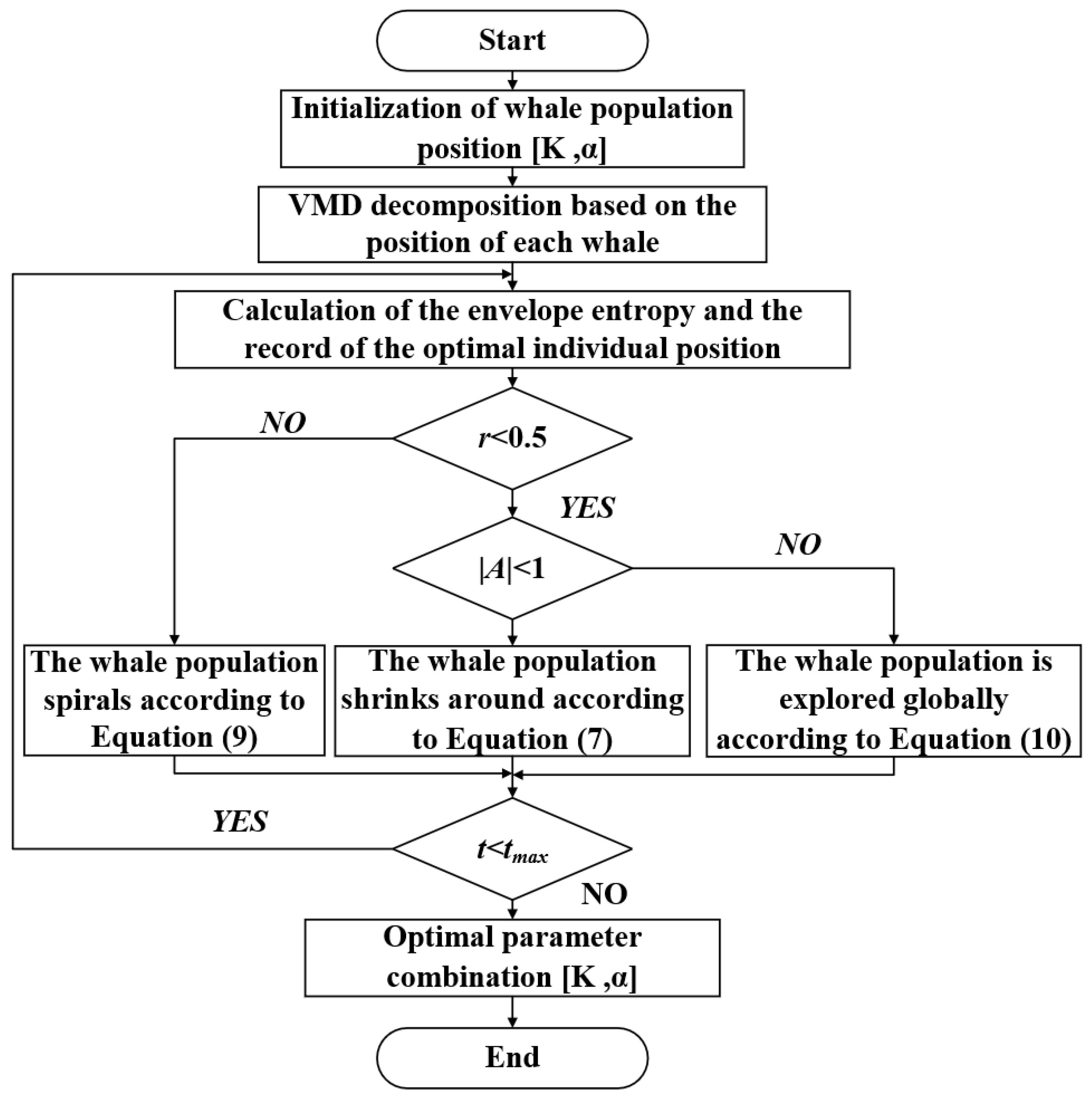
3.3. Variational Mode Decomposition Improved by Revised Whale Optimization Algorithm (RWOA-VMD)
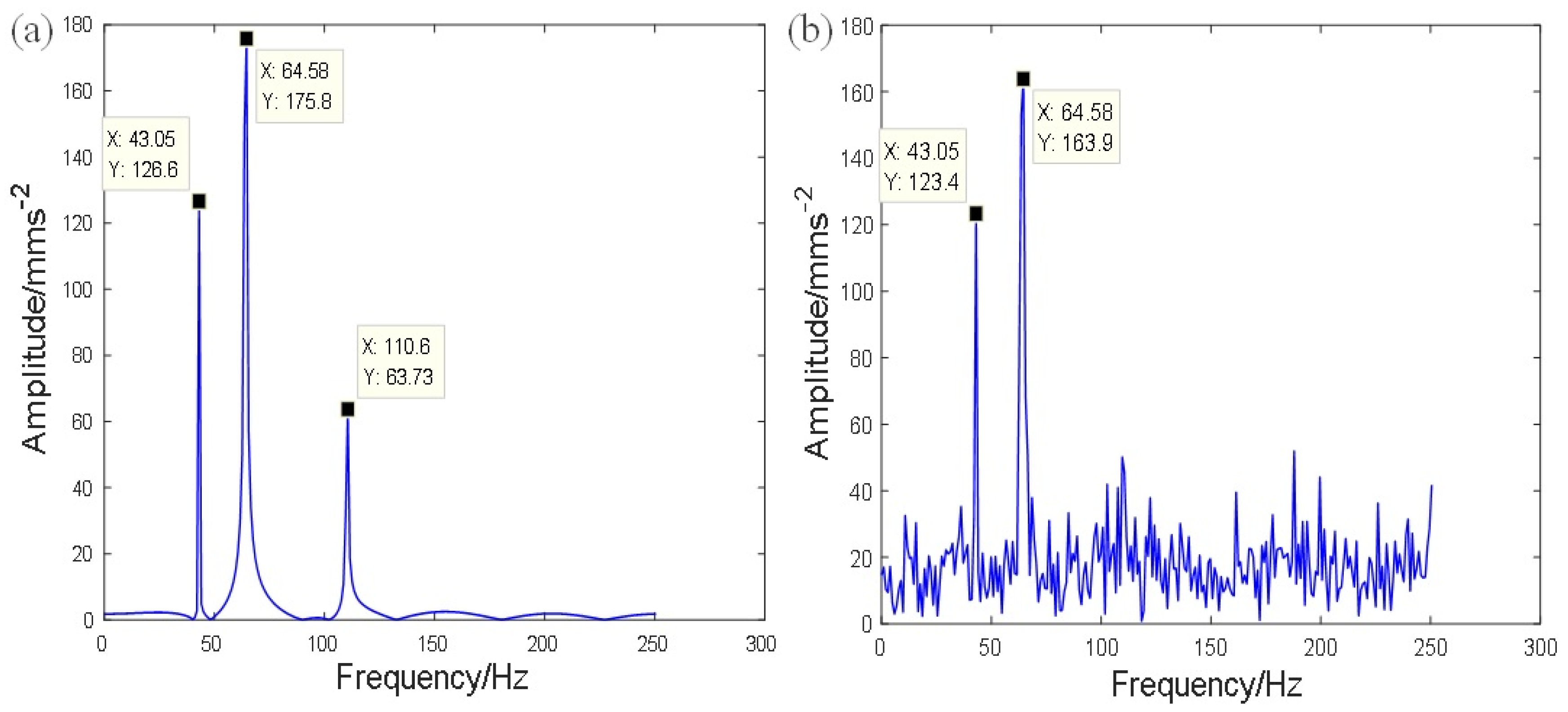
3.4. Experimental Validation of RWOA-VMD
4. A Novel Feature Enhancement Method for Vibrating Screen Exciter Bearing FAILURE
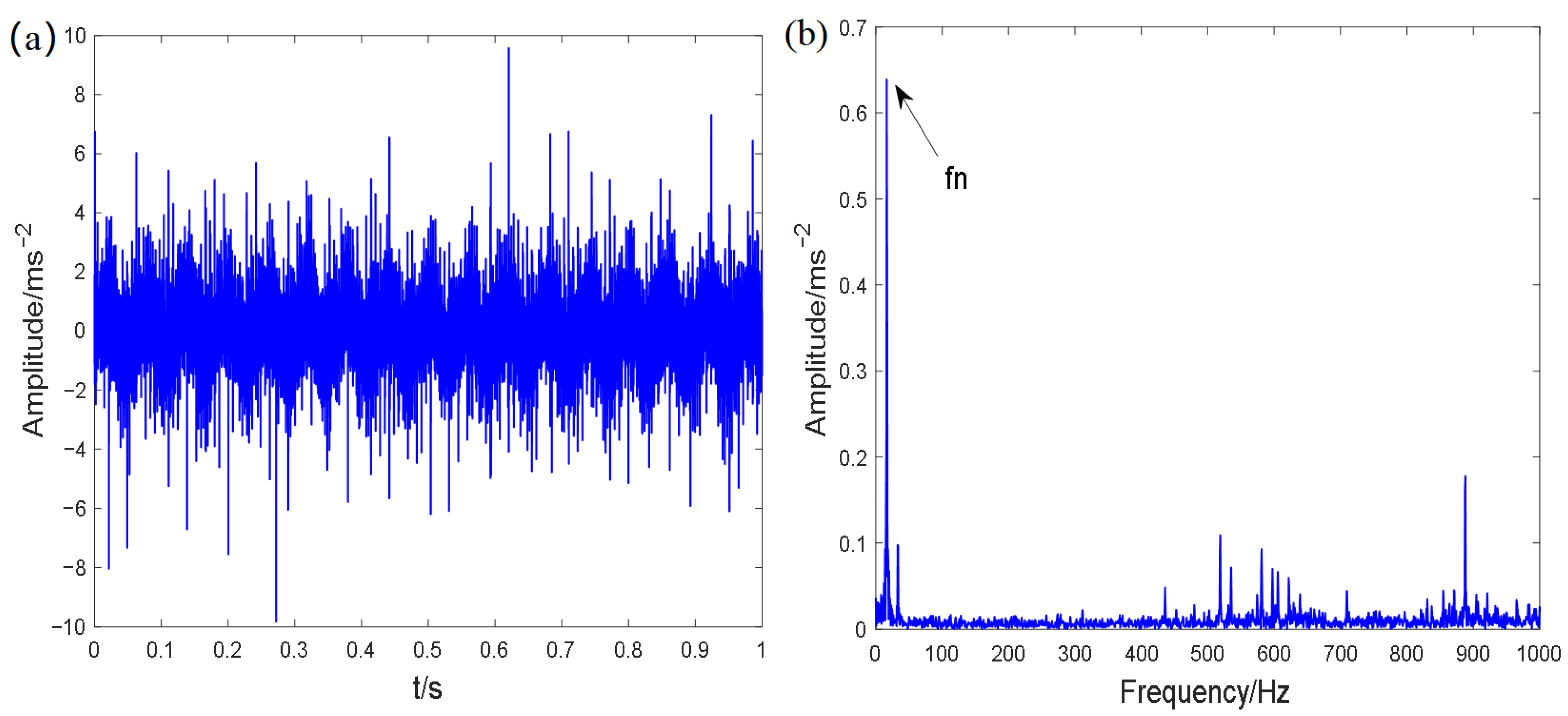
4.1. Experimental Arrangement
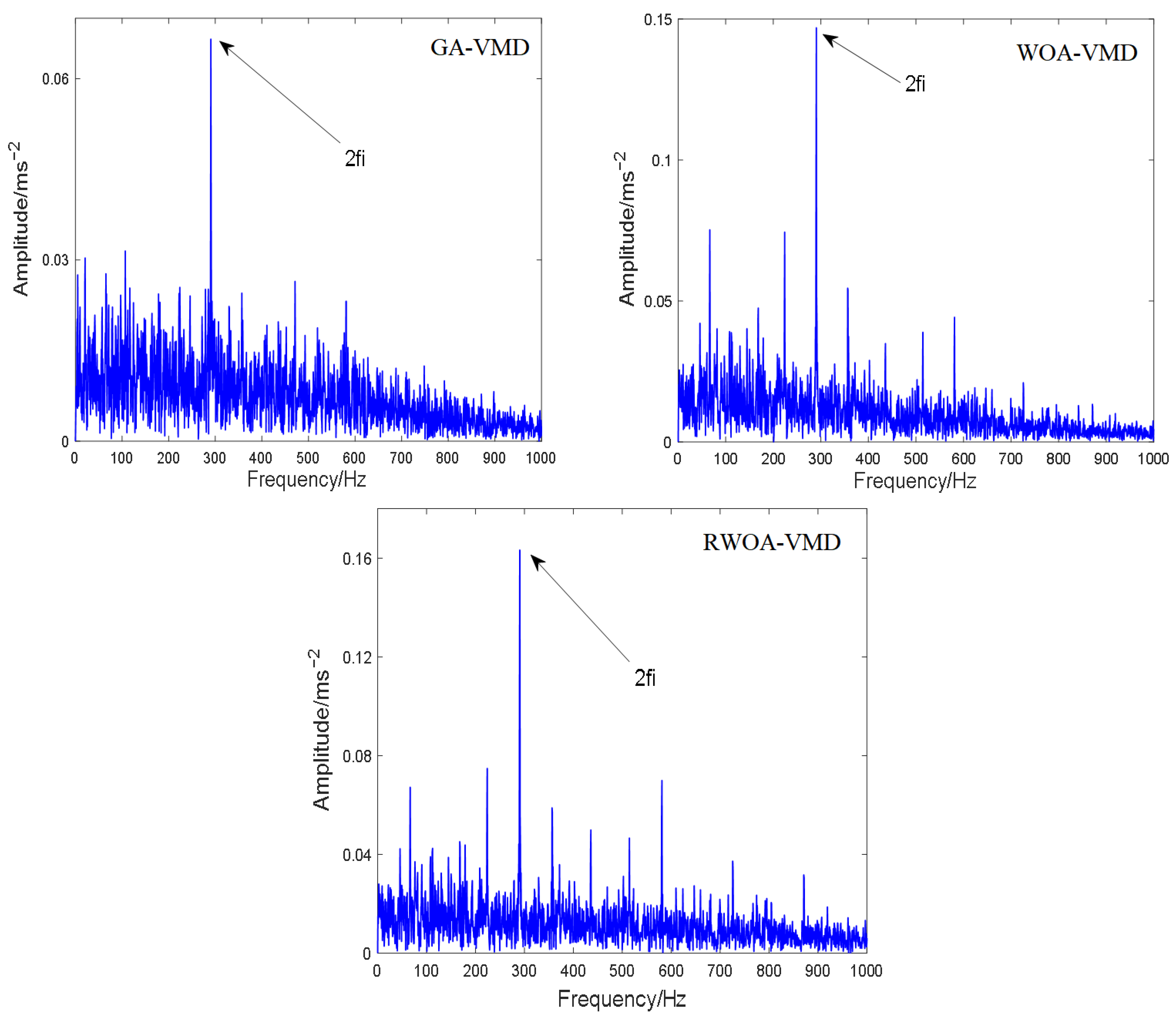
4.2. Signal Processing Method Combining SSVD and RWOA-VMD
5. Early Fault Diagnosis Method of Vibrating Screen Exciter Bearing Based on AO-SVM Method
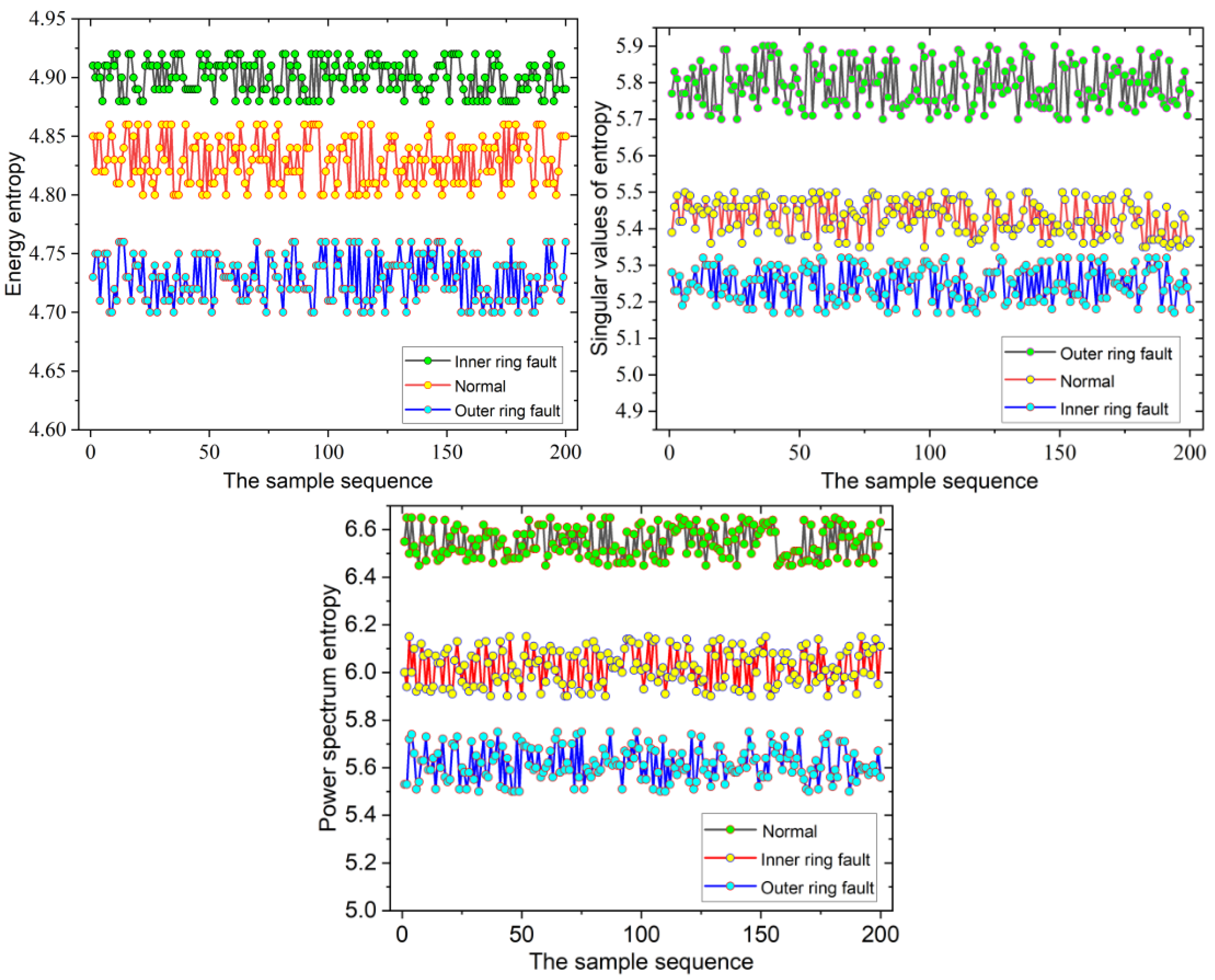
5.1. Fault Feature Extraction of Vibrating Screen Bearing
5.2. Support Vector Machine Optimized by Aquila Optimizer Algorithm (AO-SVM)
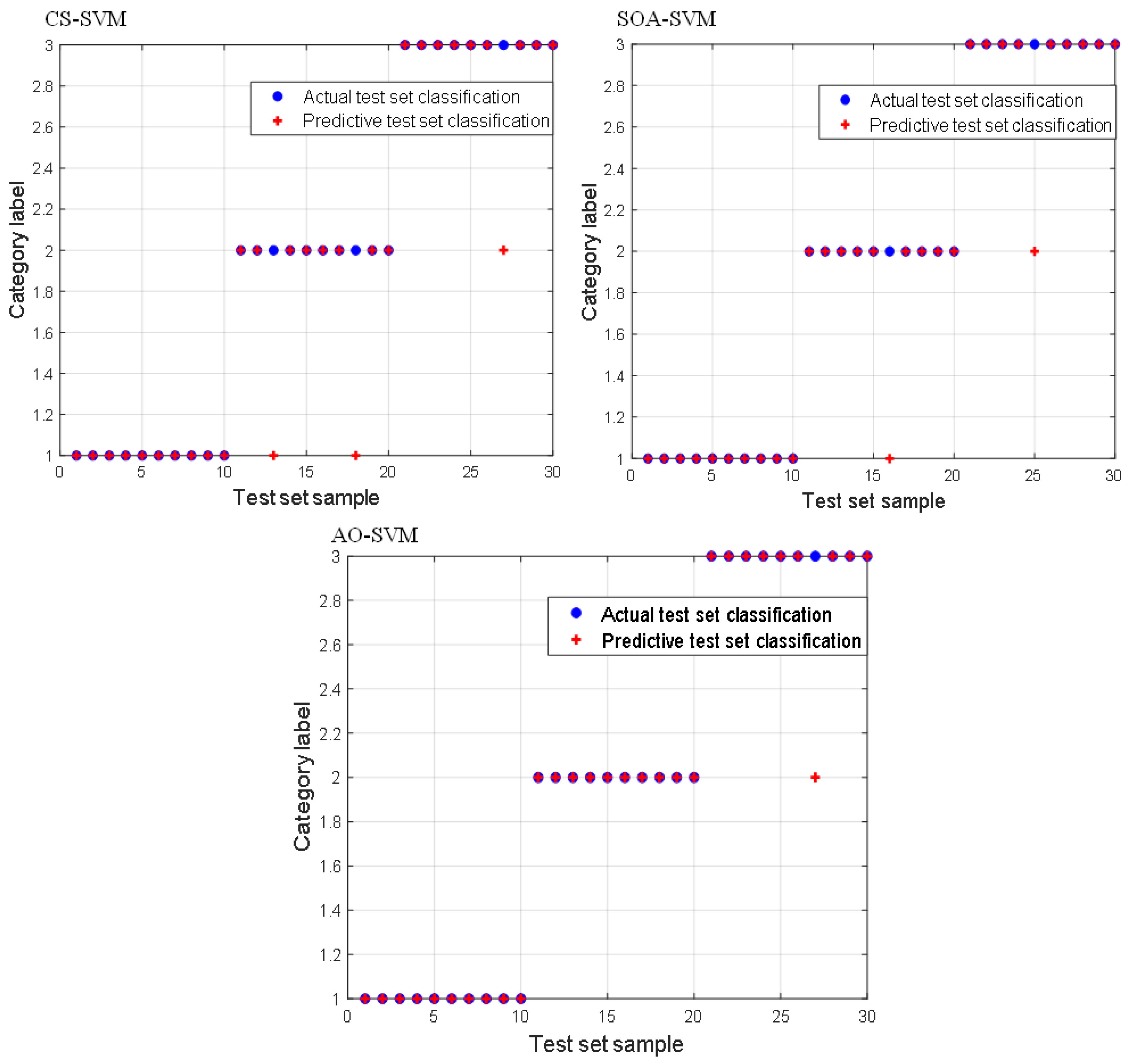
5.3. Application Comparison of Different SVM Optimization Algorithms
6. Conclusions
- Considering the strong background noise of the early fault signal of bearings, an improved SVD based on singular value’s unilateral ascent method, i.e., SSVD, for pre-denoising is proposed.
- In view of the weak fault characteristics of the early fault signal of bearings, a fault feature enhancement method, i.e., variational modal decomposition improved by revised whale algorithm optimization (RWOA-VMD), is proposed.
- Considering that the early fault characteristics of the vibrating screen bearings are much weaker than those of the traditional rotating machinery, it is impossible to effectively extract fault features by separately using SSVD or RWOA-VMD; and then, the joint application of SSVD and RWOA-VMD can achieve remarkable application effects.
- In order to intelligently realize the early fault diagnosis of the bearing of vibrating screen bearings, a multi-modal feature matrix consisting of the energy entropy, singular value entropy, and power spectrum entropy, is constructed.
- By improving the support vector machine using the Aquila optimizer algorithm, the early fault diagnosis of vibrating screen bearings is accurately realized.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lv, G. Present Situation and Development Trend of Vibrating Screen Equipment. Coal Min. Mach. 2021, 42, 41–43. [Google Scholar]
- Vashisht, R.; Peng, Q. Crack detection in the rotor ball bearing system using switching control strategy and Short Time Fourier Transform. J. Sound Vib. 2018, 432, 502–529. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Wang, H.; Zhang, J. Periodic impulses extraction based on improved adaptive VMD and sparse code shrinkage denoising and its application in rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2019, 126, 568–589. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. Modified EEMD algorithm and its applications. J. Vib. Shock 2013, 32, 21–26+46. [Google Scholar]
- Kedadouche, M.; Thomas, M.; Tahan, A. A comparative study between Empirical Wavelet Transforms and Empirical Mode Decomposition Methods: Application to bearing defect diagnosis. Mech. Syst. Signal Process. 2016, 11, 88–107. [Google Scholar] [CrossRef]
- Li, Q.; Liao, X.; Zhang, Q.; Cui, D. Feature Extraction and Classification of Bearings Based on EWT and Multi-Scale Entropy. Bearing 2016, 1, 48–52. [Google Scholar]
- Chen, J.; Pan, J.; Li, Z.; Zi, Y.; Chen, X. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals. Renew. Energy 2016, 89, 80–92. [Google Scholar] [CrossRef]
- Yan, B.; Nie, S.; Tang, B.; Liu, Z. Research on Bearing Fault Diagnosis Based on Order Analysis and EWT. Modul. Mach. Tool Autom. Manuf. Tech. 2018, 7, 51–54. [Google Scholar]
- Zhu, W.; Feng, Z. Fault diagnosis of planetary gearbox based on improved empirical wavelet transform. Chin. J. Sci. Instrum. 2016, 37, 2193–2201. [Google Scholar]
- Amezquitasanchez, J.; Adeli, H. A new music-empirical wavelet transform methodology for time-frequency analysis of noisy nonlinear and non-stationary signals. Digit. Signal Process. 2015, 45, 55–68. [Google Scholar] [CrossRef]
- Wang, D.; Tsui, K.; Qin, Y. Optimization of segmentation fragments in empirical wavelet transform and its applications to extracting industrial bearing fault features. Measurement 2019, 133, 328–340. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Z.; Li, W. An improved VMD with empirical mode decomposition and its application in incipient fault detection of rolling bearing. IEEE Access 2016, 6, 44483–44493. [Google Scholar] [CrossRef]
- Shi, P.; Yang, W. Precise feature extraction from wind turbine condition monitoring signals by using optimised variational mode decomposition. Renew. Power Gener. IET 2017, 11, 245–252. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Wang, C.; Hu, Z.; Kong, F. Adaptive variational mode decomposition based on artificial fish swarm algorithm for fault diagnosis of rolling bearings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 45–52. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Yan, X. Novel particle swarm optimization-based variational mode decomposition method for the fault diagnosis of complex rotating machinery. IEEE-ASME Trans. Mechatron. 2017, 23, 68–79. [Google Scholar] [CrossRef]
- Wang, Z.; He, G.; Du, W.; Zhou, J.; Han, X.; Wang, J.; He, H.; Guo, X.; Wang, J.; Kou, Y. Application of parameter optimized variational mode decomposition method in fault diagnosis of gearbox. IEEE Access 2019, 7, 44871–44882. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, W.; Chen, H.; Zhang, B.; Shao, J.; Teng, W. Enhanced fault diagnosis using broad learning for traction systems in high-speed trains. IEEE Trans. Power Electron. 2021, 36, 7461–7469. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B. A review of fault detection and diagnosis for the traction system in high-speed trains. IEEE Trans. Intell. Transp. Syst. 2020, 21, 450–465. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Ding, S.; Huang, B. Data-driven fault diagnosis for traction systems in high-speed trains: A survey, challenges, and perspectives. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1700–1716. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Lu, N. A multi-mode incipient sensor fault detection and diagnosis method for electrical traction systems. Int. J. Control Autom. Syst. 2018, 16, 1783–1793. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Zhang, T.; Lu, N. Data-driven and deep learning-based detection and diagnosis of incipient faults with application to electrical traction systems. Neurocomputing 2020, 396, 429–437. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, Z. Application of Variational Modal Decomposition and K-L Divergence to Bearing Fault Diagnosis of Vibrating Screens. Noise Vib. Control 2017, 36, 306–308. [Google Scholar]
- Cai, Z.; Xu, Y.; Duan, Z. An alternative demodulation method using envelope-derivative operator for bearing fault diagnosis of the vibrating screen. J. Vib. Control JVC 2018, 24, 3249–3261. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, W.; Ming, A.; Li, Z.; Chu, F. A Novel Fault Diagnosis Method Based on Improved Empirical Wavelet Transform and Maximum Correlated Kurtosis Deconvolution for Rolling Element Bearing. J. Mech. Eng. 2019, 55, 136–146. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Elaziz, M.A.; Ewees, A.A.; Al-qaness, M.A.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 1–59. [Google Scholar] [CrossRef]
- Abualigah, L. Aquila Optimizer: A meta-heuristic optimization algorithm, MATLAB Central File Exchange. Retrieved 1 November 2022. Available online: https://www.mathworks.com/matlabcentral/fileexchange/89386-aquila-optimizer-a-meta-heuristic-optimization-algorithm (accessed on 1 June 2022).



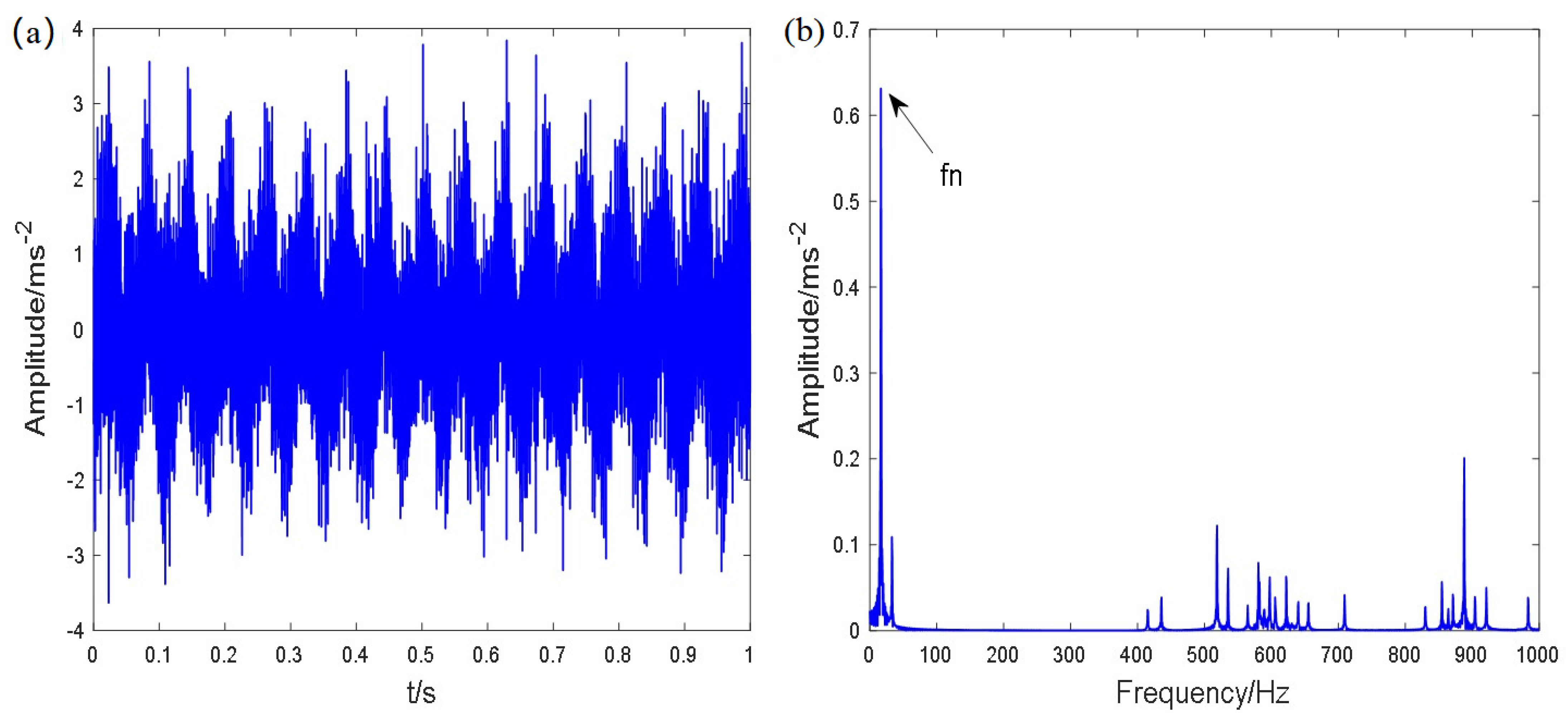



| Bearing Specification | Inner Diameter/mm | Outside Diameter/mm | Diameter/mm | Knot Diameter/mm | Number of Rollers | Contact Angle (°) |
|---|---|---|---|---|---|---|
| 1308 | 40 | 90 | 12.5 | 65 | 15 | 30 |
| Location | Width | Depth | Length | Length |
|---|---|---|---|---|
| Inner ring | 1 | 0.2 | Bearing width/2 | Bearing width/2 |
| Outer ring | 0.7 | 0.2 | Bearing width/2 | Bearing width/2 |
| Location | Rotation Speed/r/min | Rotation Frequency fn/Hz | Sampling FREQUENCY fs/Hz | Failure Frequency/Hz |
| Inner ring | 910 | 15.17 | 20,000 | 104.92 (fo) |
| Outer ring | 910 | 15.17 | 20,000 | 146.86 (fi) |
| SVM Model | Penalty Parameters C | Kernel Function Width g | Accuracy (%) |
|---|---|---|---|
| CS-SVM | 76.9775 | 56.3112 | 90.0000 |
| SOA-SVM | 61.4716 | 98.3154 | 93.3333 |
| AO-SVM | 46.2141 | 22.6567 | 96.6667 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Yang, H.; Yuan, L.; Lu, Y.; Cao, C.; Wu, G. Fault Feature Enhanced Extraction and Fault Diagnosis Method of Vibrating Screen Bearings. Machines 2022, 10, 1007. https://doi.org/10.3390/machines10111007
Cheng X, Yang H, Yuan L, Lu Y, Cao C, Wu G. Fault Feature Enhanced Extraction and Fault Diagnosis Method of Vibrating Screen Bearings. Machines. 2022; 10(11):1007. https://doi.org/10.3390/machines10111007
Chicago/Turabian StyleCheng, Xiaohan, Hui Yang, Long Yuan, Yuxin Lu, Congjie Cao, and Guangqiang Wu. 2022. "Fault Feature Enhanced Extraction and Fault Diagnosis Method of Vibrating Screen Bearings" Machines 10, no. 11: 1007. https://doi.org/10.3390/machines10111007
APA StyleCheng, X., Yang, H., Yuan, L., Lu, Y., Cao, C., & Wu, G. (2022). Fault Feature Enhanced Extraction and Fault Diagnosis Method of Vibrating Screen Bearings. Machines, 10(11), 1007. https://doi.org/10.3390/machines10111007






