The Effect of Manufacturing Errors on the Performance of a Gas-Dynamic Bearing Gyroscope
Abstract
:1. Introduction
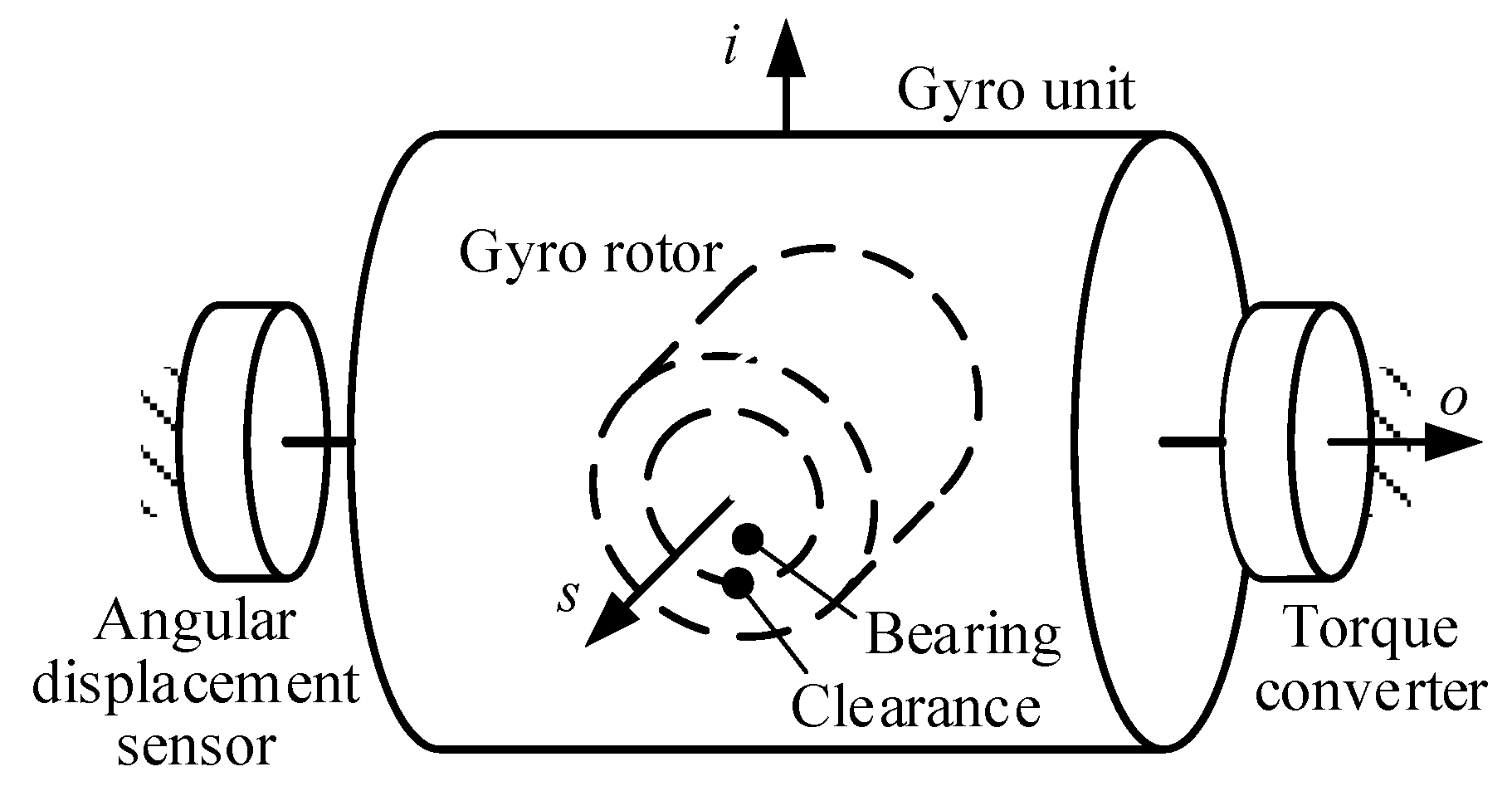
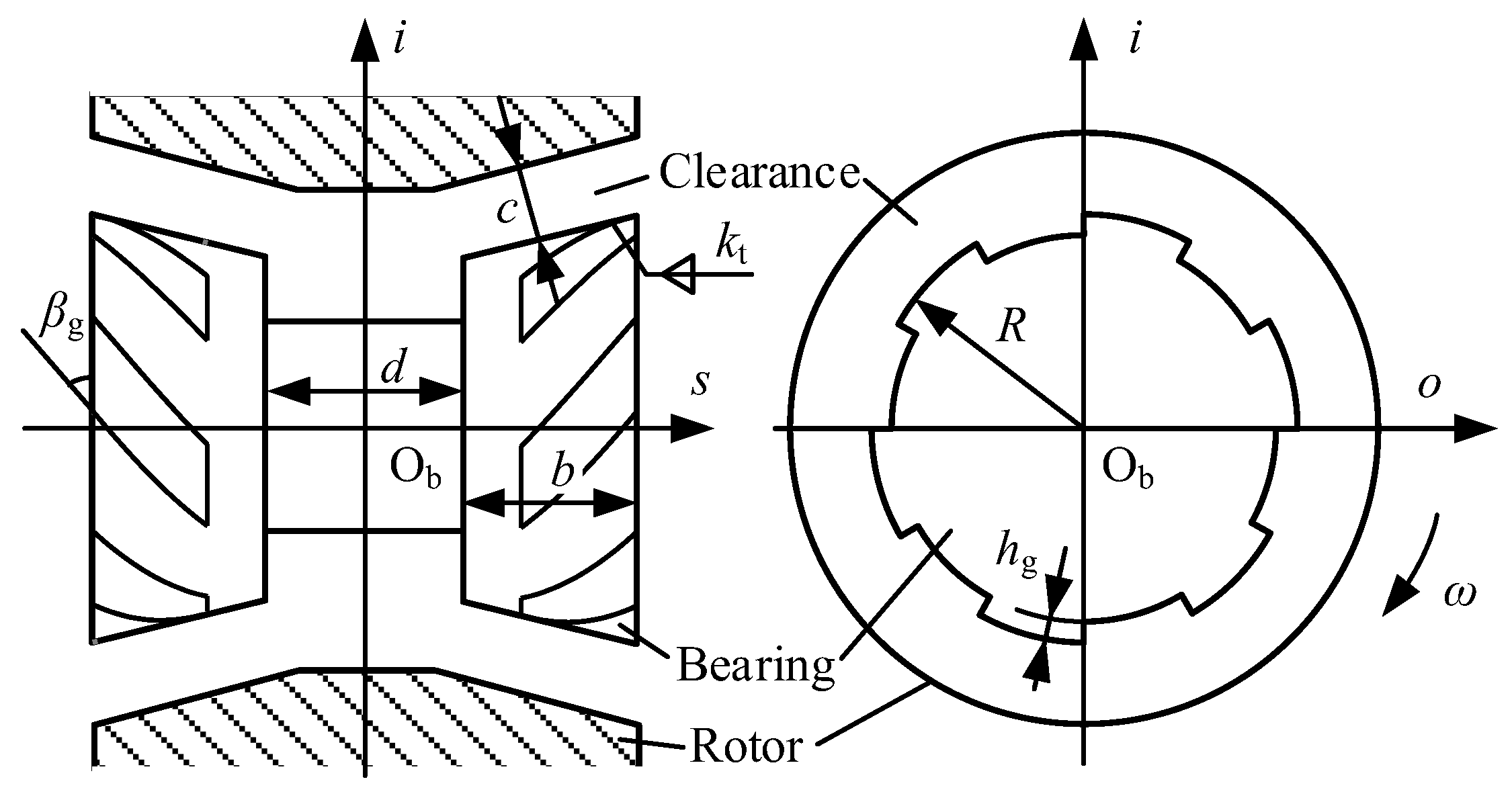
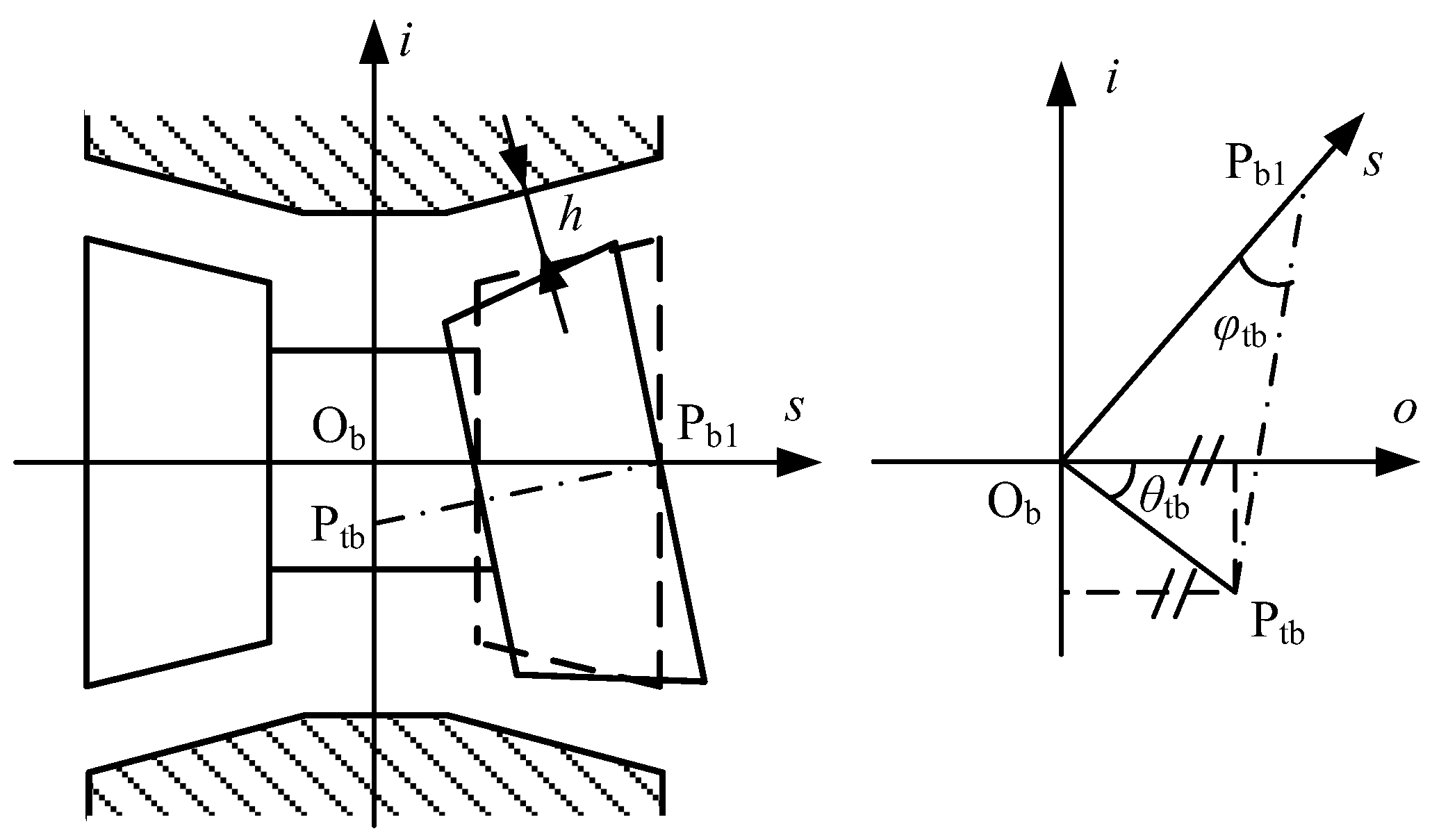
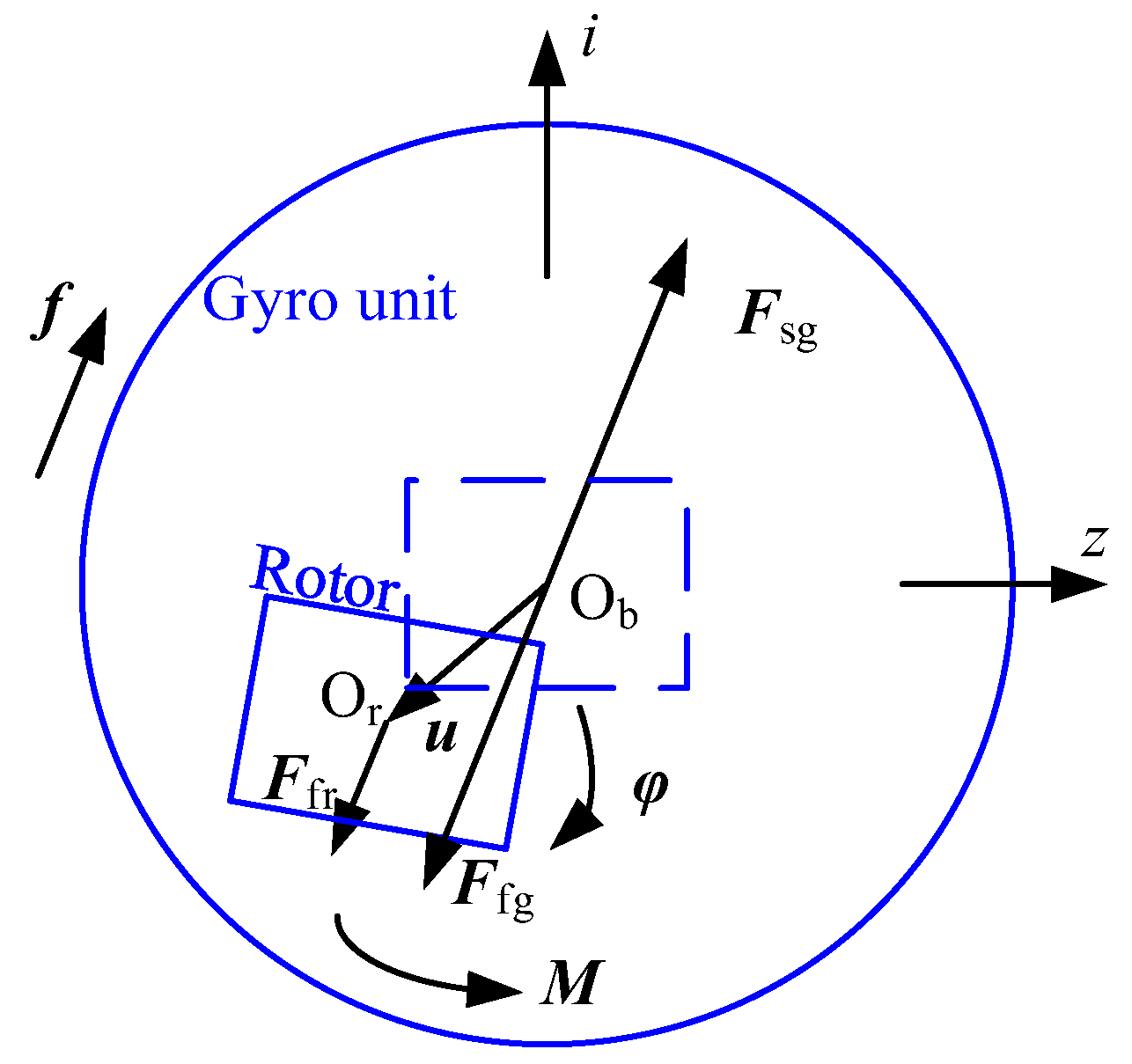
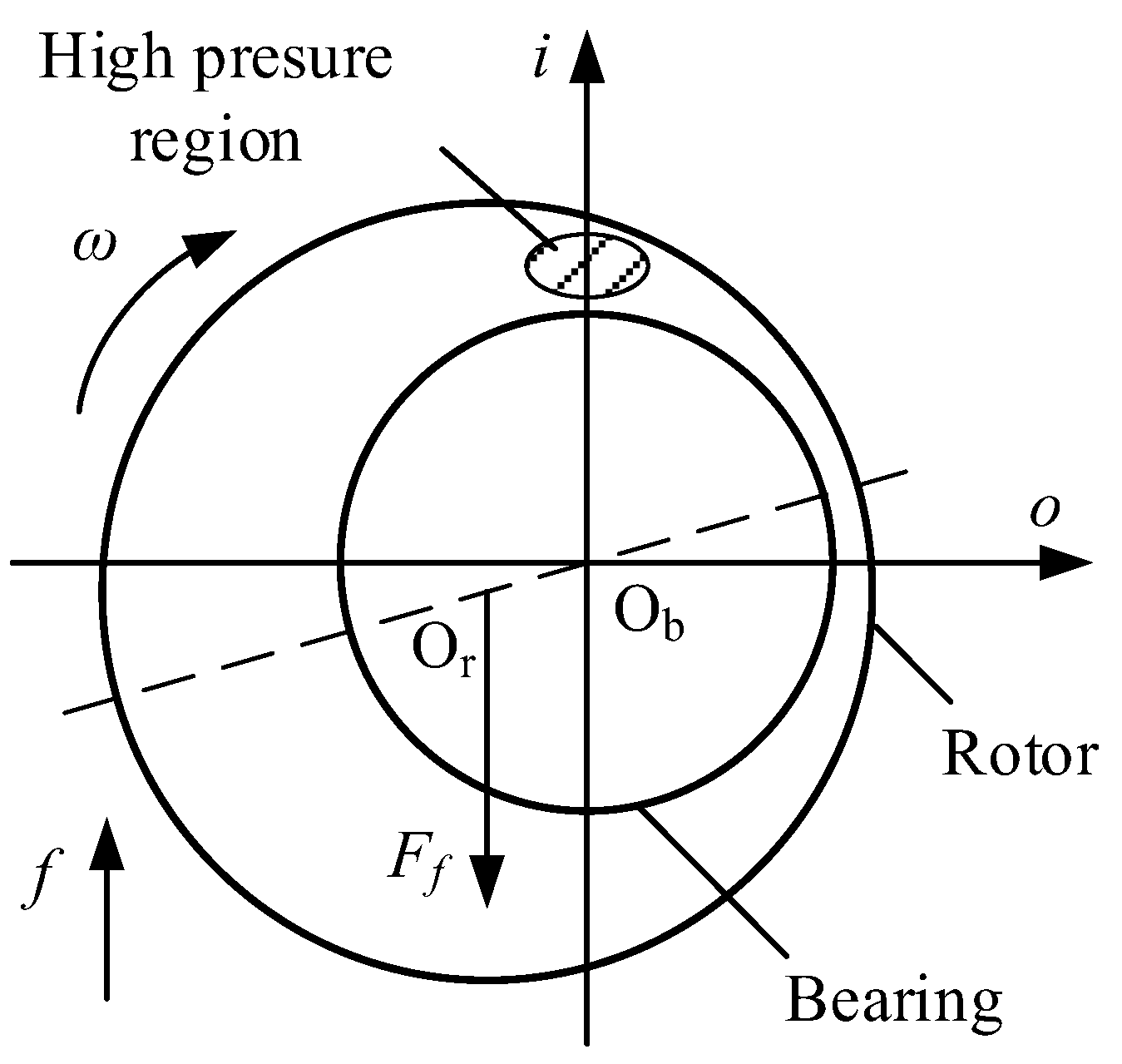
2. Mechanical Model of the Gyroscope
3. Mathematical Model of the Manufacturing Errors
3.1. Taper Error
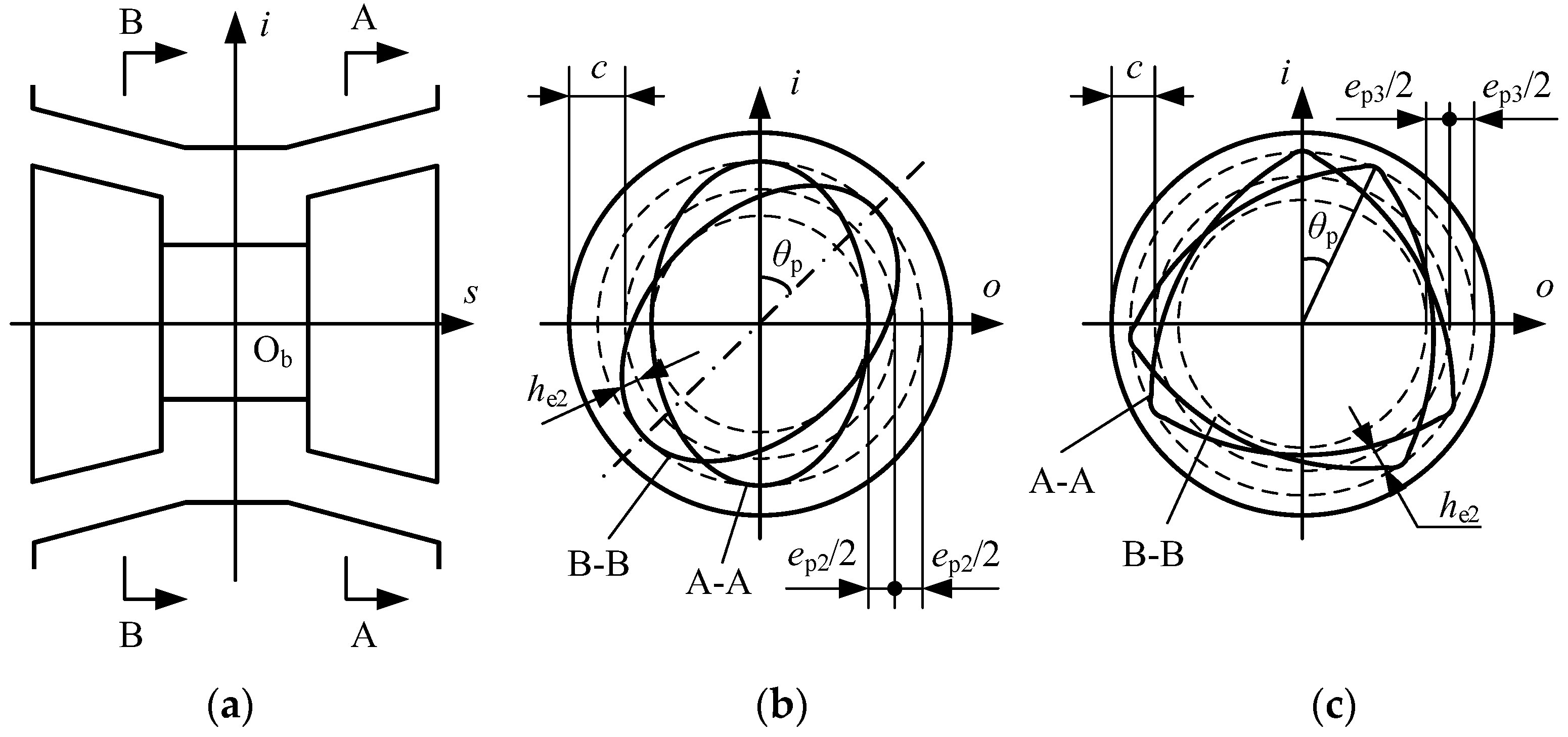
3.2. Oval Error and Trigone Error
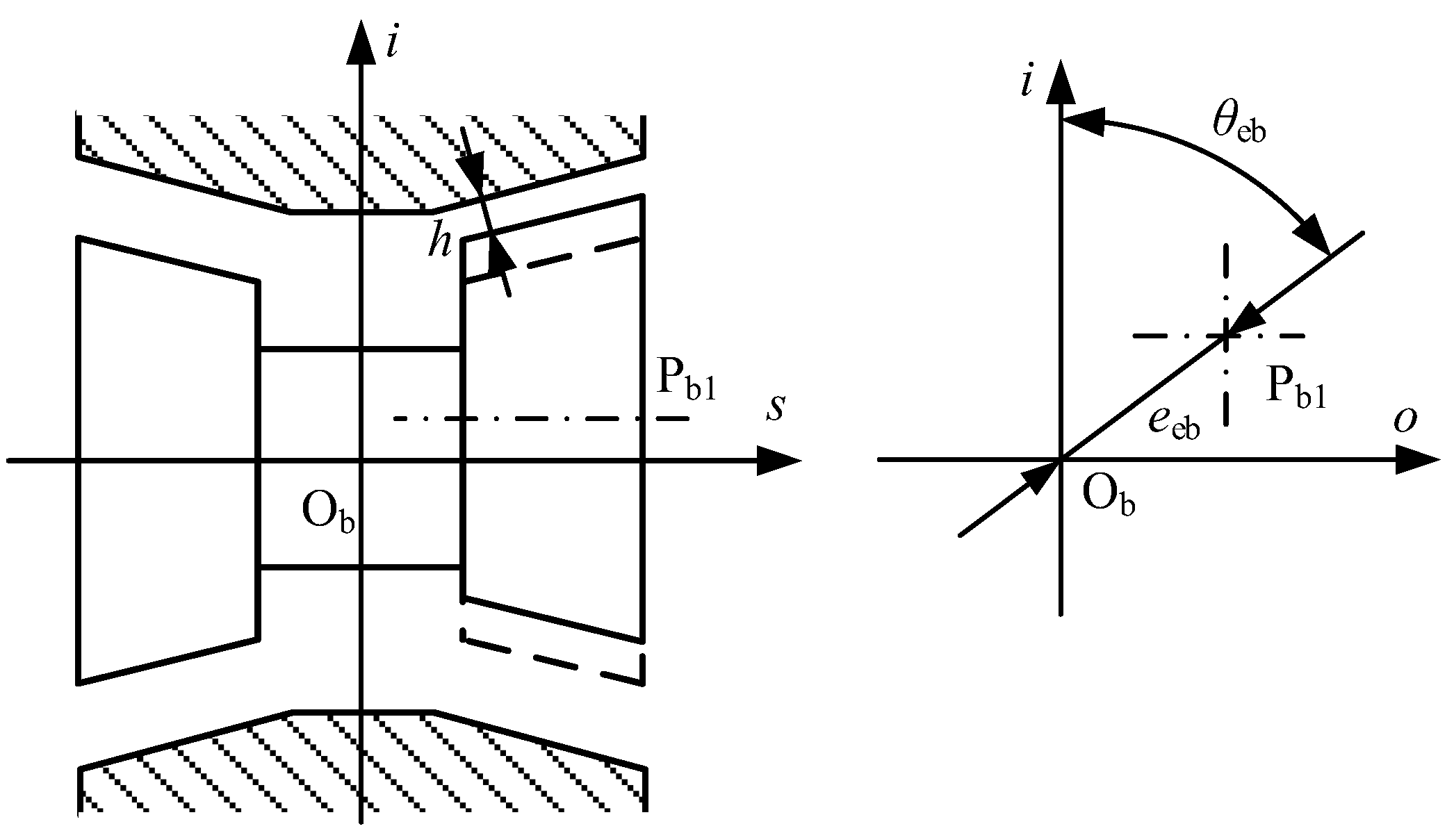
3.3. Eccentricity of the Axis
3.4. Angular Deviation of the Axis
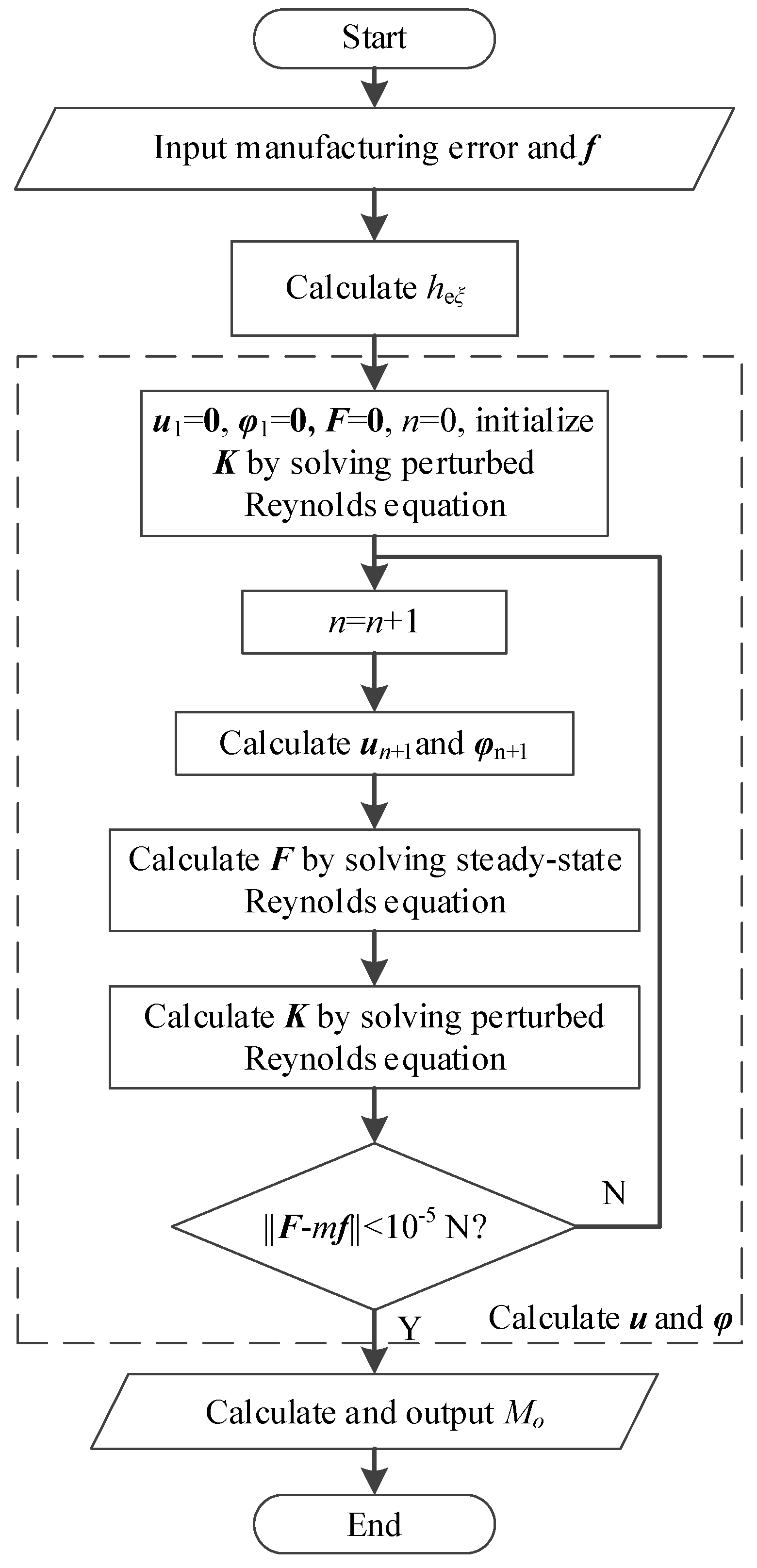
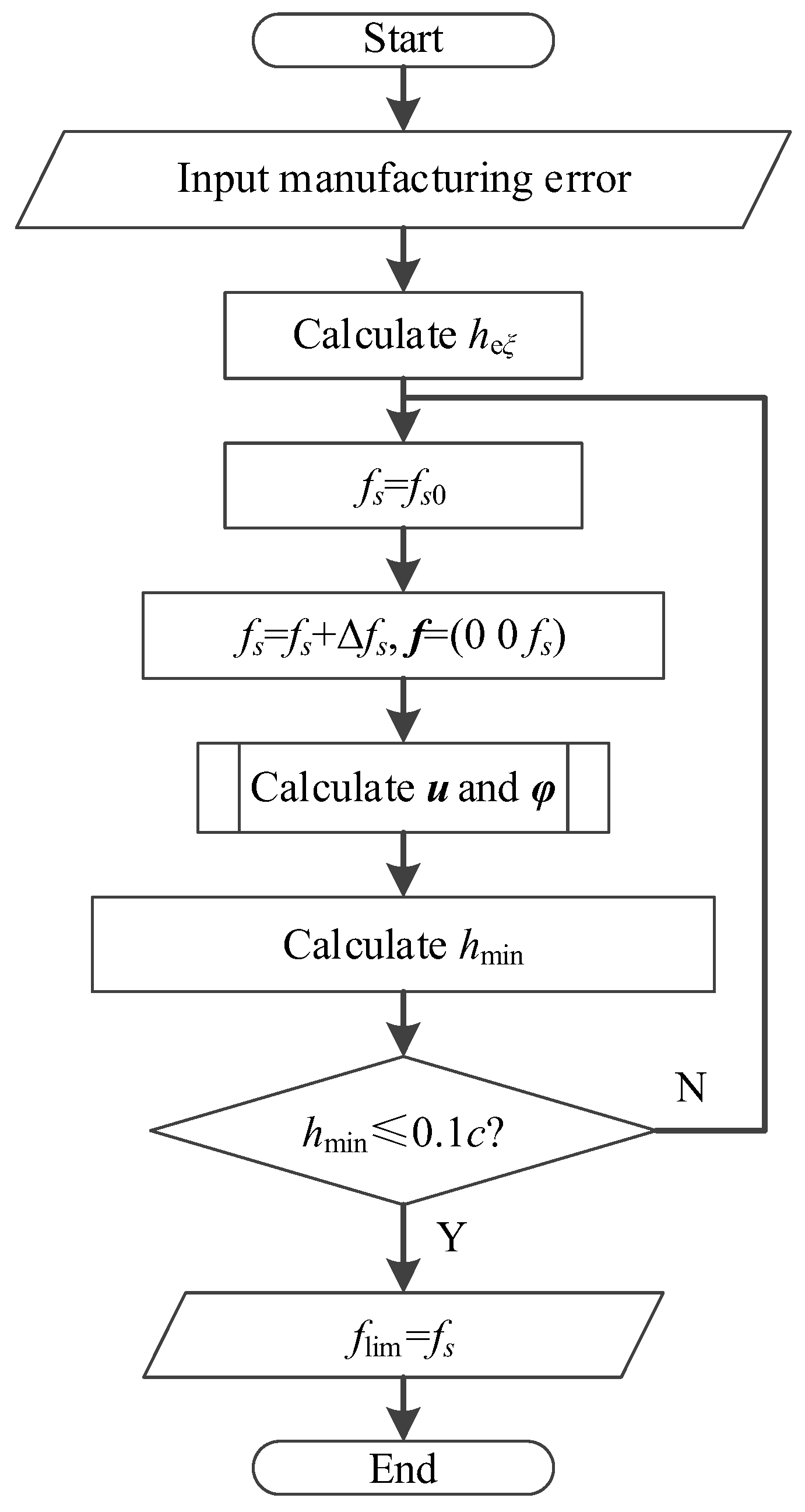
4. Method to Estimate the Effect
4.1. Interference Torque
4.2. Overload limit
5. Results and Discussion
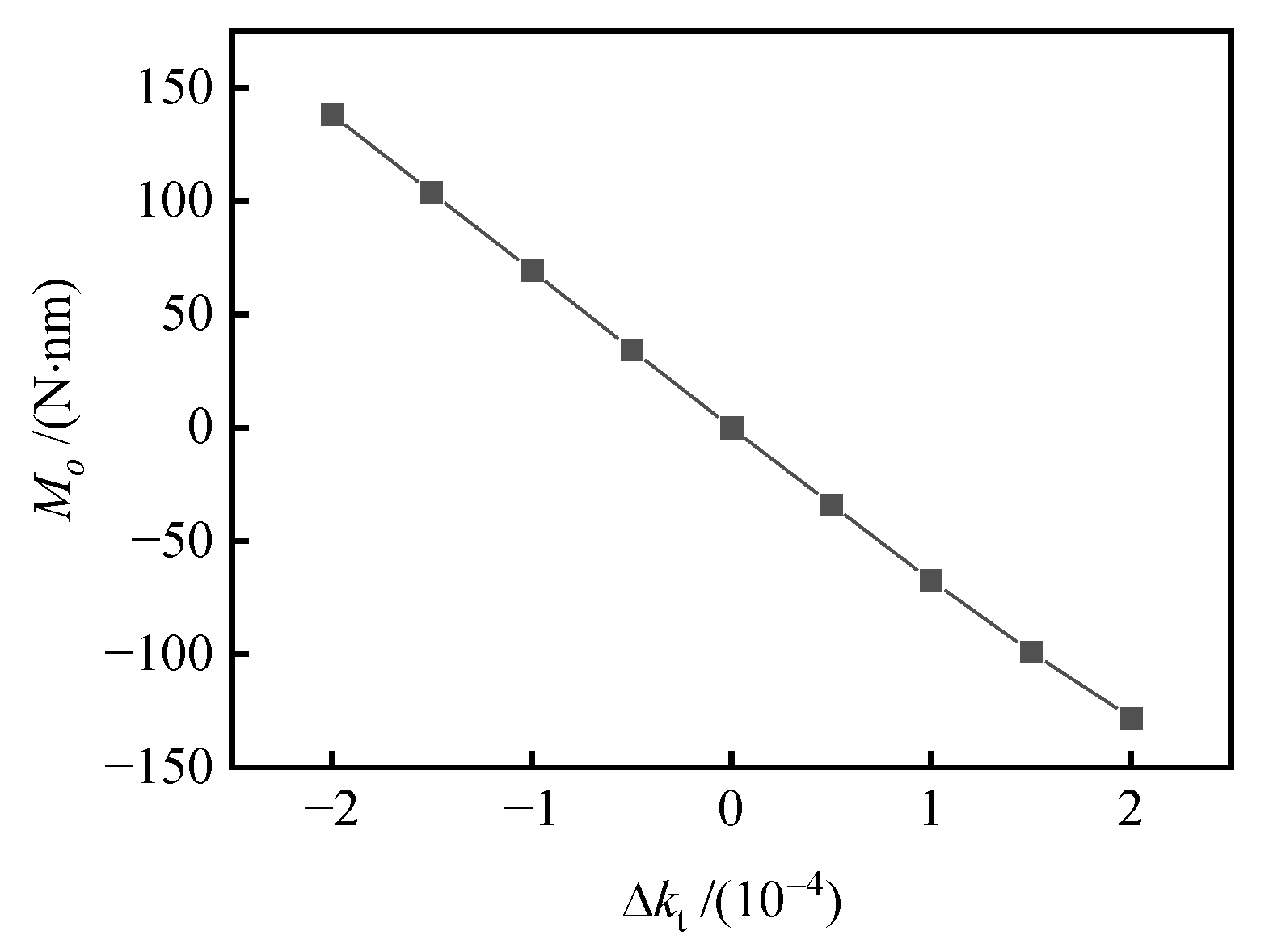
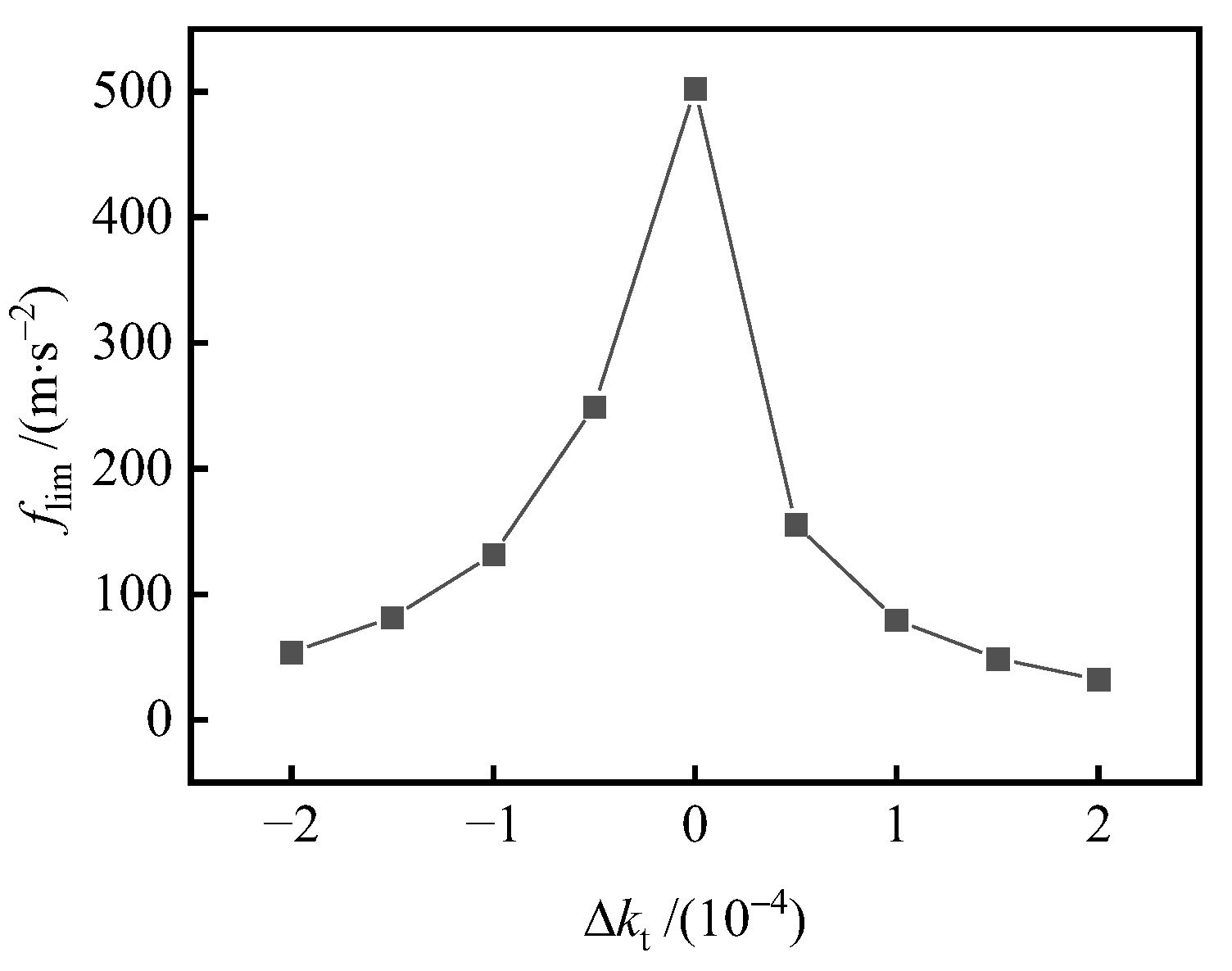
5.1. Effects of Taper Error
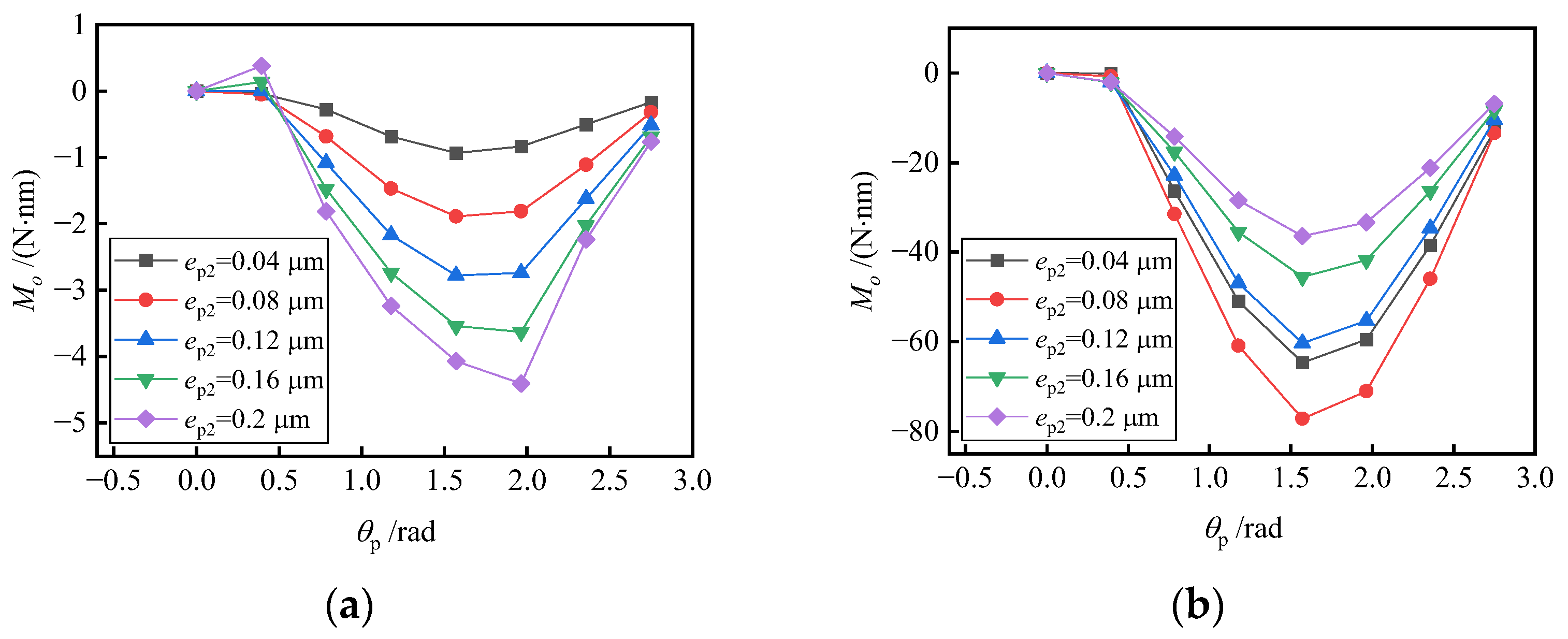
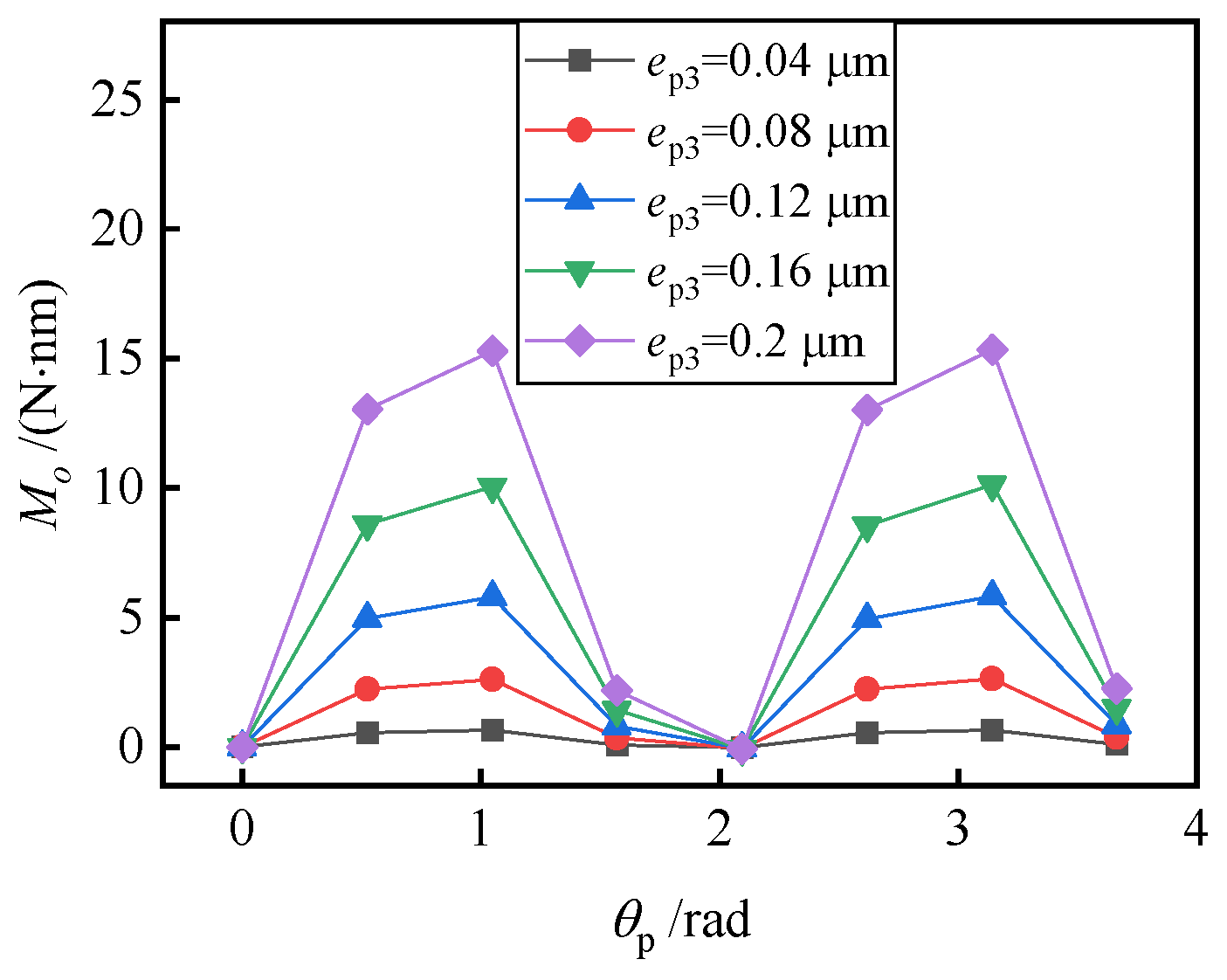
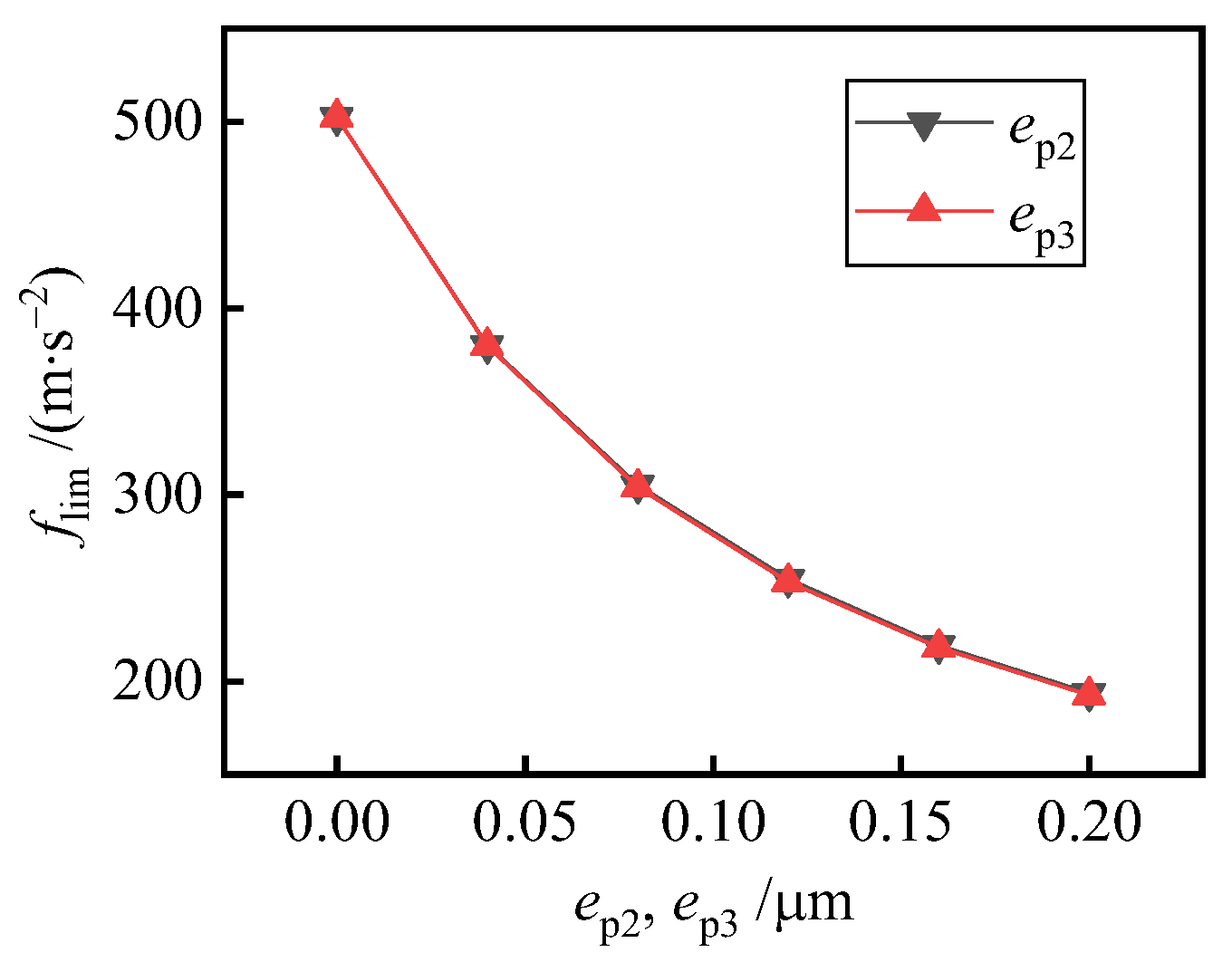
5.2. Effect of Oval Error and Trigone Error
5.3. Effect of Eccentricity of the Axis
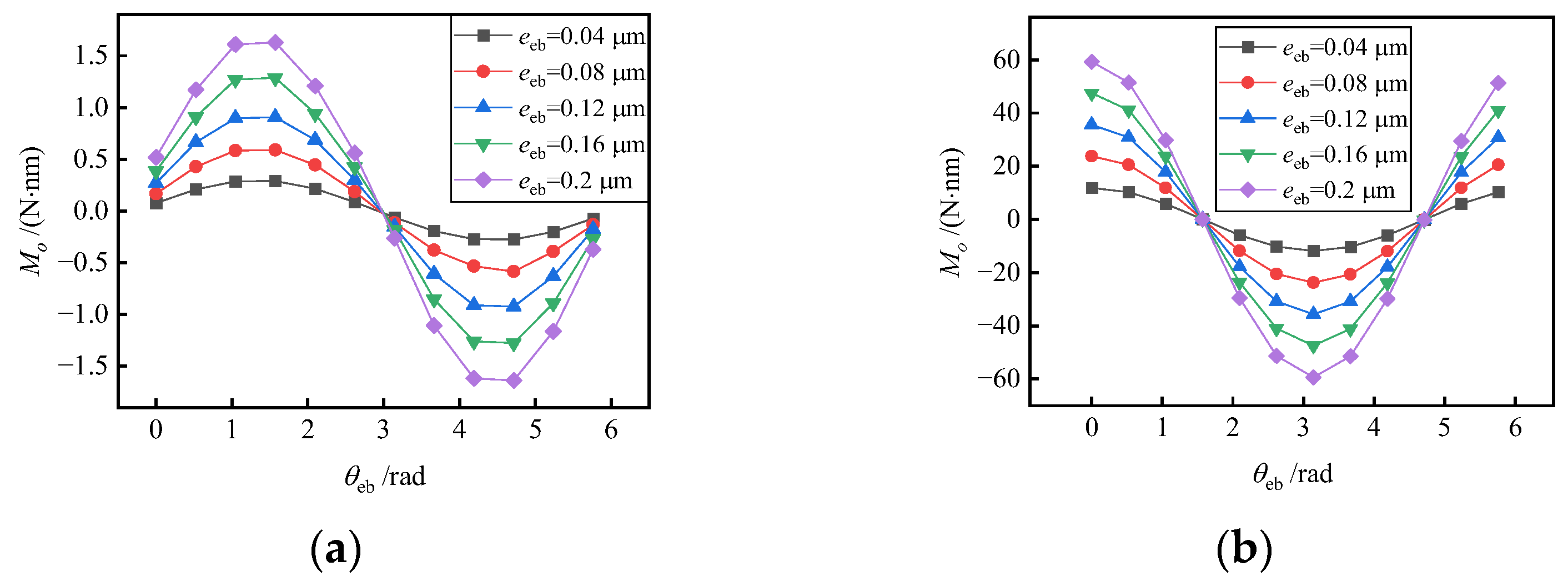
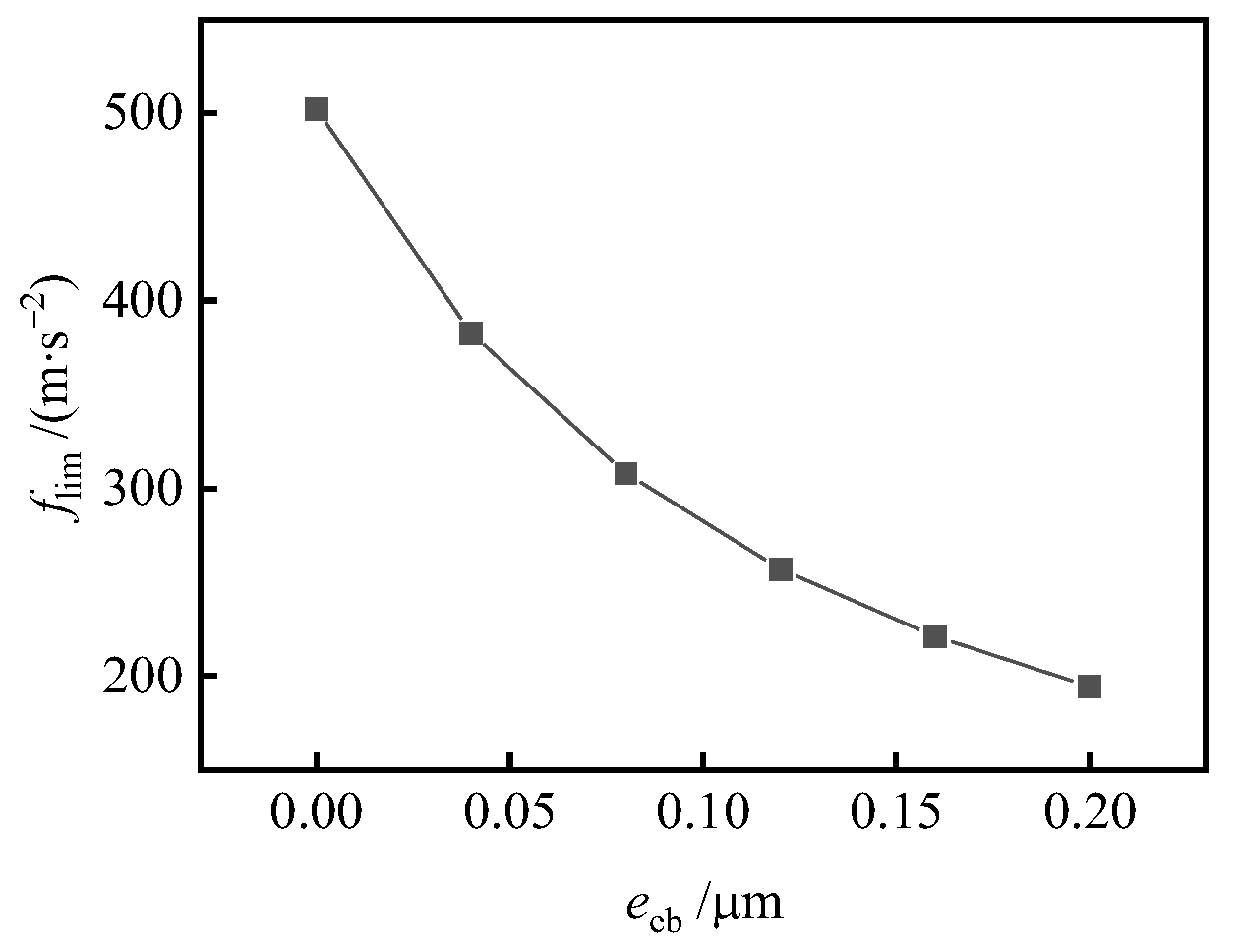
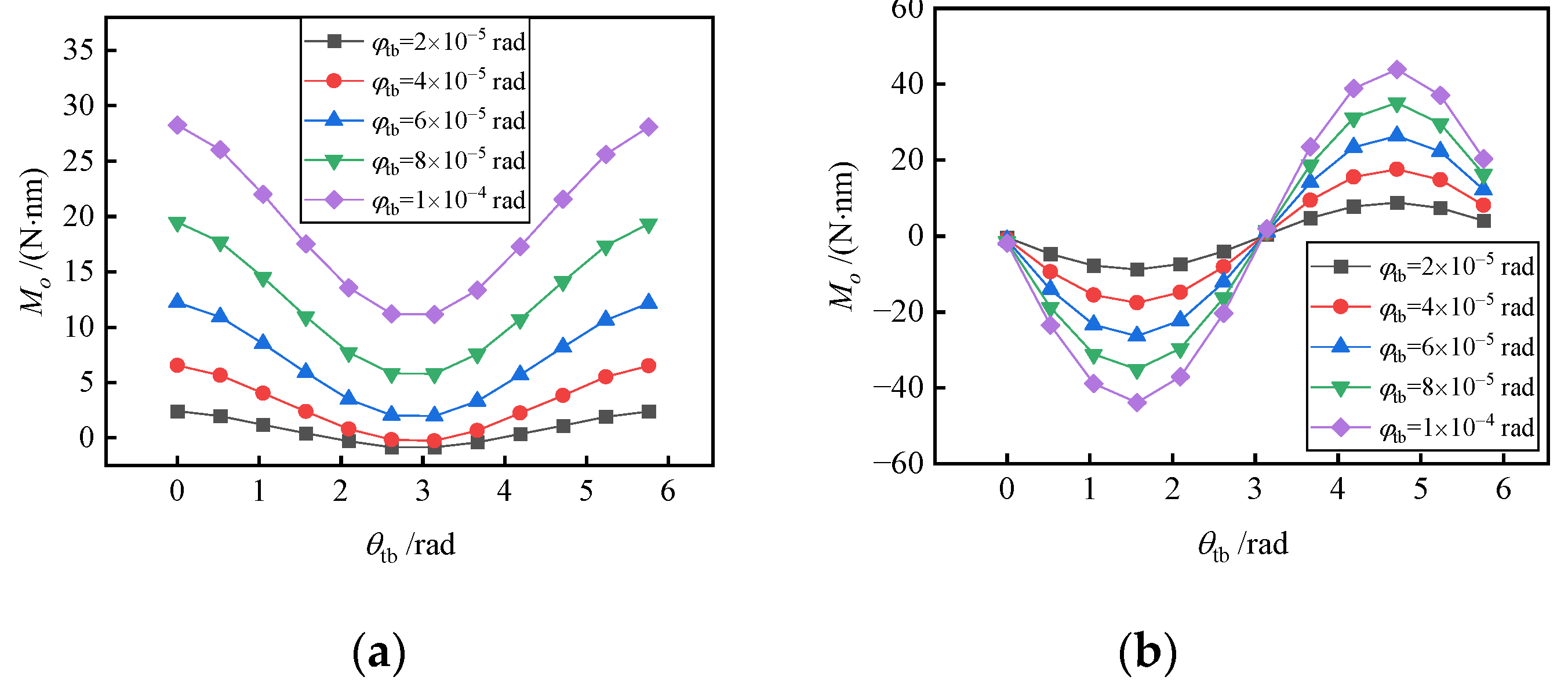
5.4. Effect of the Angular Deviation of the Axis
6. Conclusions
- (1)
- With the effect of manufacturing errors, even only specific force in a single direction could cause the interference torque. Taper error will cause interference torque, whether there is specific force or not. With an oval error or trigone error, radial specific force will cause interference torque. With an eccentricity or angular deviation of the axis, any specific force will cause interference torque. In general, the interference torque is small, which is 10–1000 times smaller than that under the condition of both radial and axial specific forces.
- (2)
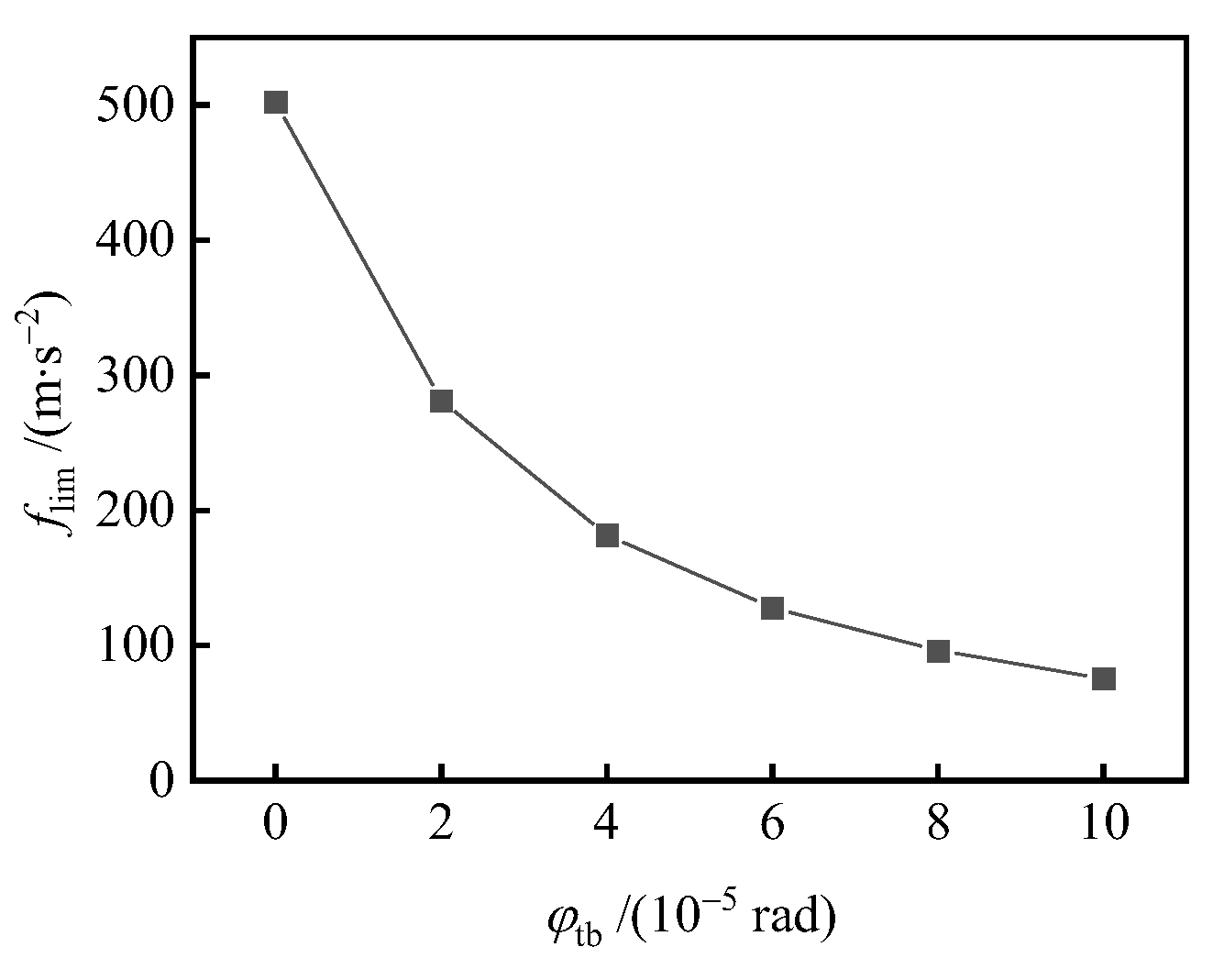
- The increase in taper error, oval error, trigone error, eccentricity of the axis and angular deviation of the axis will increase the interference torque and reduce the ultimate overload, because they cause uneven distribution of gas film. When the attitude angle of bearing axis eccentricity and angular deviation changes, the interference torque will change periodically and may be 0, but the installation angle corresponding to the 0 point is different under different working conditions.
- (3)
- Among the manufacturing errors studied in this paper, the taper error has the greatest influence on the gas-dynamic bearing gyroscope. With the taper error up to 1.5 × 10−4, the interference torque under the condition of f = (10 0 0) m/s2 could reach 100 N·nm, and the overload limit will be reduced to less than 100 m/s2.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | Bearing width | i, o, s | Coordinates in the input axis, output axis, spin axis respectively |
| c | Bearing clearance | k | Tapper |
| d | Distance between the two cones | m | Mass of the rotor |
| ep2 | Oval error, the difference between the major axis and the minor axis | Mo | Interference torque |
| ep3 | Trigone error | nr | Rotating speed |
| eeb | the eccentricity of the axis of the cone | nξ | Normal unit vector of the bearing surface |
| R | Bottom radius | Ng | Number of grooves |
| f | Specific force | p | Gas film pressure |
| fs0 | Initial specific force | Q | Poiseuille flow rate coefficient |
| flim | Ultimate overload | u | Rotor eccentric displacement |
| Ffg | Apparent gravity | μ | Gas viscosity |
| Fsg | Supported force | φ | Rotor tilting angle |
| Ffr | Apparent gravity | ξ | Cone surfaces index |
| h | Gas film thickness | θp | Difference of the phase angle between the two sides for oval error and trigone error |
| hmin | Minimum film thickness | θeb | Attitude angle |
| heξ | Film thickness variation | βg | Attitude angle of grooves |
| hg | Groove depth | ω | Rotating speed |
References
- Feng, K.; Huang, Z.; Guo, Z.-Y. Design of spherical spiral groove bearings for a high-speed air-lubricated gyroscope. Tribol. Trans. 2015, 58, 1084–1095. [Google Scholar] [CrossRef]
- Hu, H.; Feng, M.; Ren, T. Effect of taper error on the performance of gas foil conical bearing. Ind. Lubr. Tribol. 2020, 72, 1189–1197. [Google Scholar] [CrossRef]
- Nielsen, B.B. Combining Gas Bearing and Smart Material Technologies for Improved Machine Performance Theory and Experiment. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2017. [Google Scholar]
- Nielsen, B.B.; Santos, I.F. Transient and steady state behaviour of elasto–aerodynamic air foil bearings, considering bump foil compliance and top foil inertia and flexibility: A numerical investigation. Proc. Inst. Mech. Eng. Part J-J. Eng. Tribol. 2017, 231, 1235–1253. [Google Scholar] [CrossRef]
- Liu, W.; Baettig, P.; Wagner, P.H.; Schiffmann, J. Nonlinear study on a rigid rotor supported by herringbone grooved gas bearings: Theory and validation. Mech. Syst. Signal Process. 2021, 146, 106983. [Google Scholar] [CrossRef]
- Zhang, X.-Q.; Wang, X.-L.; Si, L.-N.; Liu, Y.-D.; Shi, W.-T.; Xiong, G.-J. Effects of temperature on nonlinear dynamic behavior of gas journal bearing-rotor systems for microengine. Tribol. Trans. 2016, 59, 944–956. [Google Scholar] [CrossRef]
- Bailey, N.; Hibberd, S.; Power, H. Dynamics of a small gap gas lubricated bearing with Navier slip boundary conditions. J. Fluid Mech. 2017, 818, 68–99. [Google Scholar] [CrossRef] [Green Version]
- Tkacz, E.; Kozanecki, Z.; Kozanecka, D.; Łagodziński, J. A self-acting gas journal bearing with a flexibly supported foil - numerical model of bearing dynamics. Int. J. Struct. Stab. Dyn. 2017, 17, 1740012. [Google Scholar] [CrossRef]
- Du, J.; Yang, G.; Ge, W.; Liu, T. Nonlinear dynamic analysis of a rigid rotor supported by a spiral-grooved opposed-hemisphere gas bearing. Tribol. Trans. 2016, 59, 781–800. [Google Scholar] [CrossRef]
- Pronobis, T.; Liebich, R. Comparison of stability limits obtained by time integration and perturbation approach for gas foil bearings. J. Sound Vib. 2019, 458, 497–509. [Google Scholar] [CrossRef]
- Feng, K.; Li, W.-J.; Xie, Y.-Q.; Liu, M.-X. Theoretical analysis of the slip flow effect on gas-lubricated micro spherical spiral groove bearings for machinery gyroscope. Microsyst. Technol. 2016, 22, 387–399. [Google Scholar] [CrossRef]
- Feng, K.; Li, W.J.; Wu, S.B.; Liu, W.H. Thermohydrodynamic analysis of micro spherical spiral groove gas bearings under slip flow and surface roughness coupling effect. Microsyst. Technol. 2017, 23, 1779–1792. [Google Scholar] [CrossRef]
- Li, Y.; Duan, F. Interference torque of a three-floated gyroscope with gas-lubricated bearings subject to a sudden change of the specific force. Chin. J. Aeronaut. 2019, 32, 737–747. [Google Scholar] [CrossRef]
- Li, Y.; Duan, F. Static error model of a gyroscope with gas-dynamic hemispherical bearings. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 1705–1711. [Google Scholar]
- Guenat, E.; Schiffmann, J. Multi-objective optimization of grooved gas journal bearings for robustness in manufacturing tolerances. Tribol. Trans. 2019, 62, 1041–1050. [Google Scholar] [CrossRef]
- Liu, J. Research on Influencing Factors of Interference Torque of Gas-Floated Gyroscope. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2011. [Google Scholar]
- Liang, Y.; Liu, J.; Sun, Y.; Lu, L. Surface roughness effects on vortex torque of air supported gyroscope. Chin. J. Aeronaut. 2011, 24, 90–95. [Google Scholar] [CrossRef] [Green Version]
- Yang, G. Research on Dynamic Characteristics of Gas Bearing Rotor System for Gyroscope. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar]
- Li, H.; Yu, H.; Zhang, G.; Zhao, H.; Ma, W. Effect of elliptical error on the characteristics of porous aerostatic journal bearings. Manuf. Technol. Mach. Tool 2015, 6, 84–87. [Google Scholar]
- Ren, T.; Feng, M.; Hu, M.; Liu, Z. Influence of machining errors on stiffness of hydrodynamic gas bearing in gyroscope motor. J. Chin. Inert. Technol. 2019, 27, 378–383. [Google Scholar]
- Li, Y.; Zhang, D.; Duan, F. Interference torque of a gas-dynamic bearing gyroscope subject to a uniform change of the specific force and the carrier angular velocity. Sensors 2020, 20, 6852. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Duan, F.; Fan, L.; Yan, Y. Static error model of a three-floated gyroscope with a rotor supported on gas-lubricated bearings. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2018, 232, 2850–2860. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, D.; Duan, F. Dynamic characteristics of opposed-conical gas-dynamic bearings. Ind. Lubr. Tribol. 2019, 72, 415–425. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| Bottom radius R/mm | 7.5 |
| Tapper k | 0.25 |
| Bearing width b/mm | 6.0 |
| Bearing clearance c/μm | 2.0 |
| Distance between the two cones d/mm | 8.0 |
| Groove depth hg/μm | 0.5 |
| Number of grooves Ng | 6.0 |
| Attitude angle of grooves βg/° | 45 |
| Rotor mass m/g | 60 |
| Viscosity μ/(Pa∙s) | 1.79 × 10−5 |
| Rotating speed nr/(r∙min−1) | 30,000 |
| Ambient pressure Pa/Pa | 1.013 × 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, Y.; Li, Y.; Zhang, D. The Effect of Manufacturing Errors on the Performance of a Gas-Dynamic Bearing Gyroscope. Machines 2022, 10, 1010. https://doi.org/10.3390/machines10111010
Ning Y, Li Y, Zhang D. The Effect of Manufacturing Errors on the Performance of a Gas-Dynamic Bearing Gyroscope. Machines. 2022; 10(11):1010. https://doi.org/10.3390/machines10111010
Chicago/Turabian StyleNing, Yanqiang, Yan Li, and Desheng Zhang. 2022. "The Effect of Manufacturing Errors on the Performance of a Gas-Dynamic Bearing Gyroscope" Machines 10, no. 11: 1010. https://doi.org/10.3390/machines10111010
APA StyleNing, Y., Li, Y., & Zhang, D. (2022). The Effect of Manufacturing Errors on the Performance of a Gas-Dynamic Bearing Gyroscope. Machines, 10(11), 1010. https://doi.org/10.3390/machines10111010






