Air Combat Maneuver Decision Method Based on A3C Deep Reinforcement Learning
Abstract
:1. Introduction
2. Modeling of UCAVs Flight Maneuvers
2.1. UCAV Maneuver Model
2.1.1. Kinematic Model
2.1.2. Kinetic Model
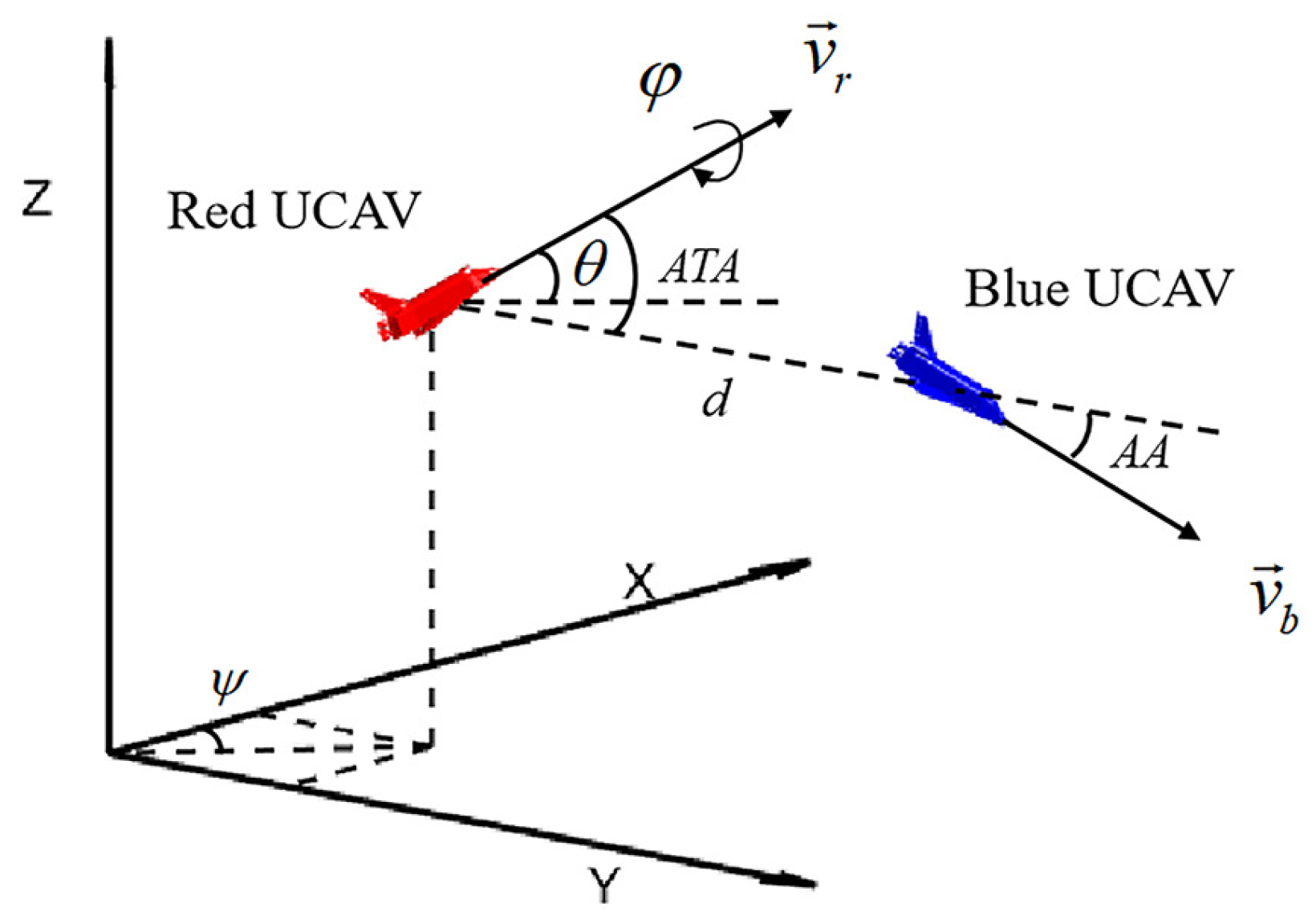
2.2. Air Combat Situation Assessment and Judgment of Victory and Defeat
3. Air Combat Maneuver Decision Scheme
3.1. Introduction to Deep Reinforcement Learning
3.2. A3C Reinforcement Learning Decision Model
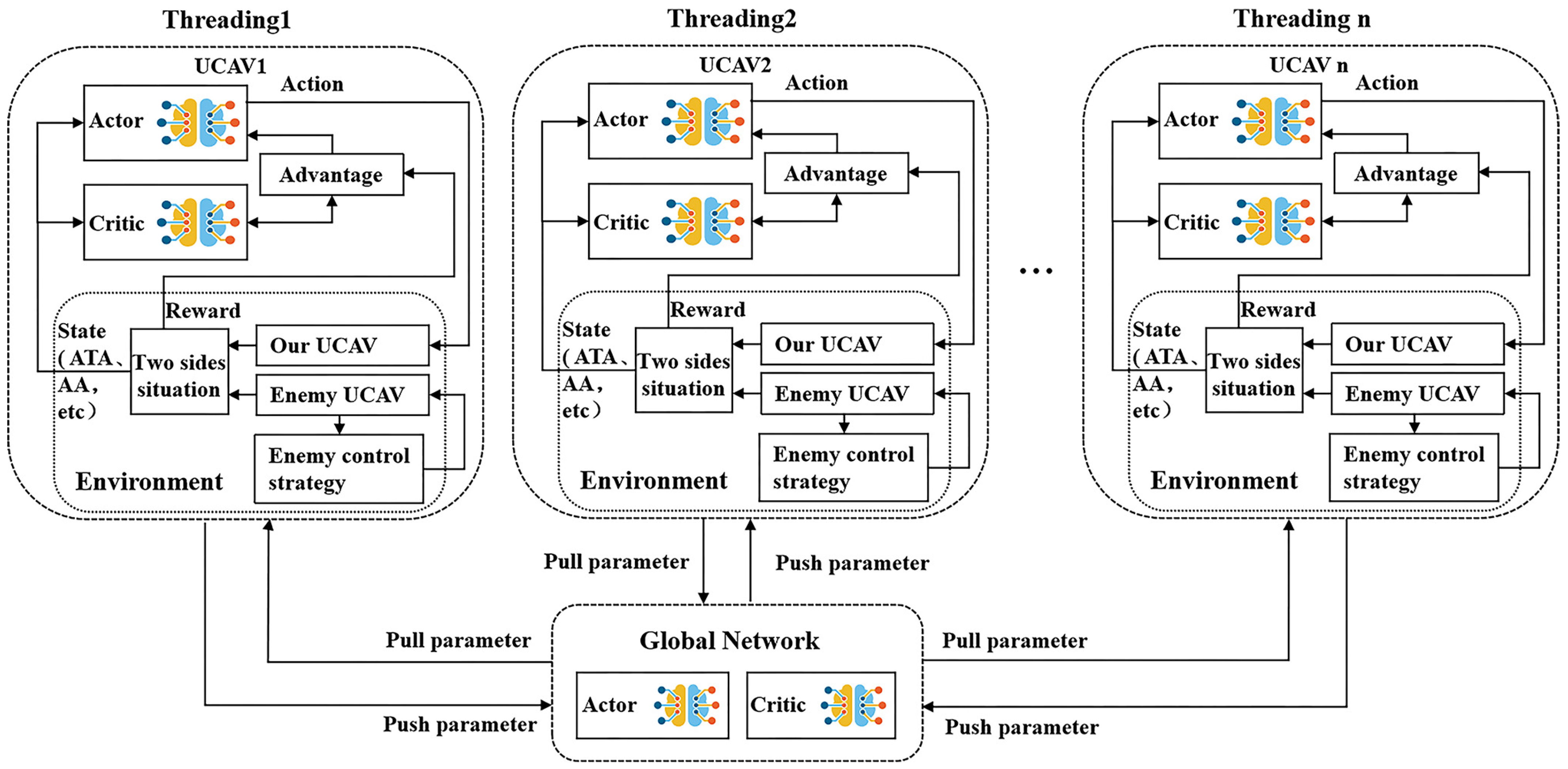
3.2.1. Overall Framework
3.2.2. A3C Related Principles
3.3. State Space and Action Space Descriptions
3.3.1. State Space
3.3.2. Action Space
3.4. Reward Function
4. Experimental Simulation and Discussion
4.1. Experimental Parameter Setting
4.2. Algorithm Flow
| Algorithm 1: Autonomous Maneuver Decision of UCAV based on A3C |
Input: The state feature dimension S, the action dimension A, the global network parameters and , the neural network parameters , of the current thread, the maximum number of iterations, the maximum length of one episode’s time series within a thread. The reward decay factor and the number N of n-step rewards. The entropy coefficient c and the learning rates , . Output: The global network parameters and that have been updated.
|
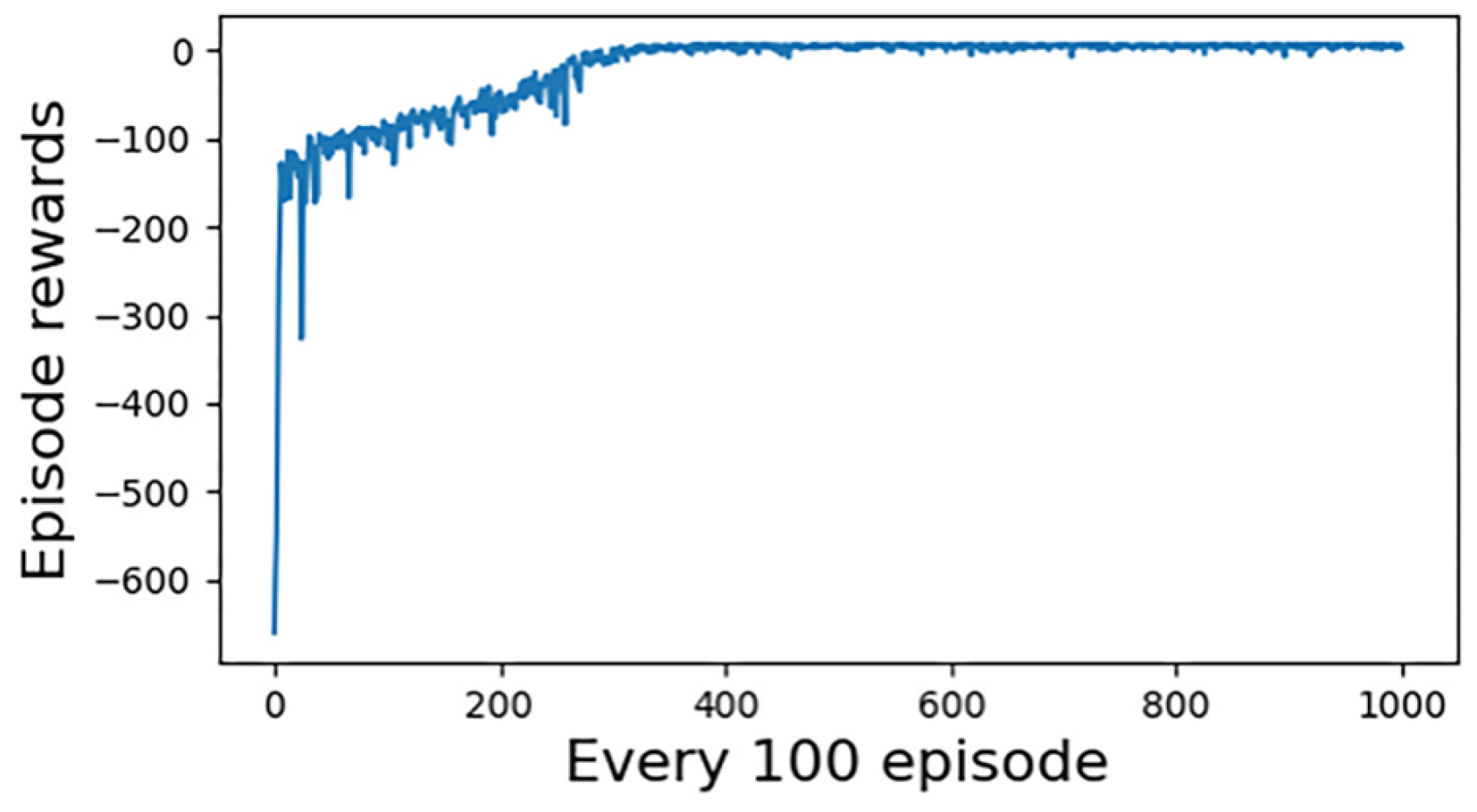
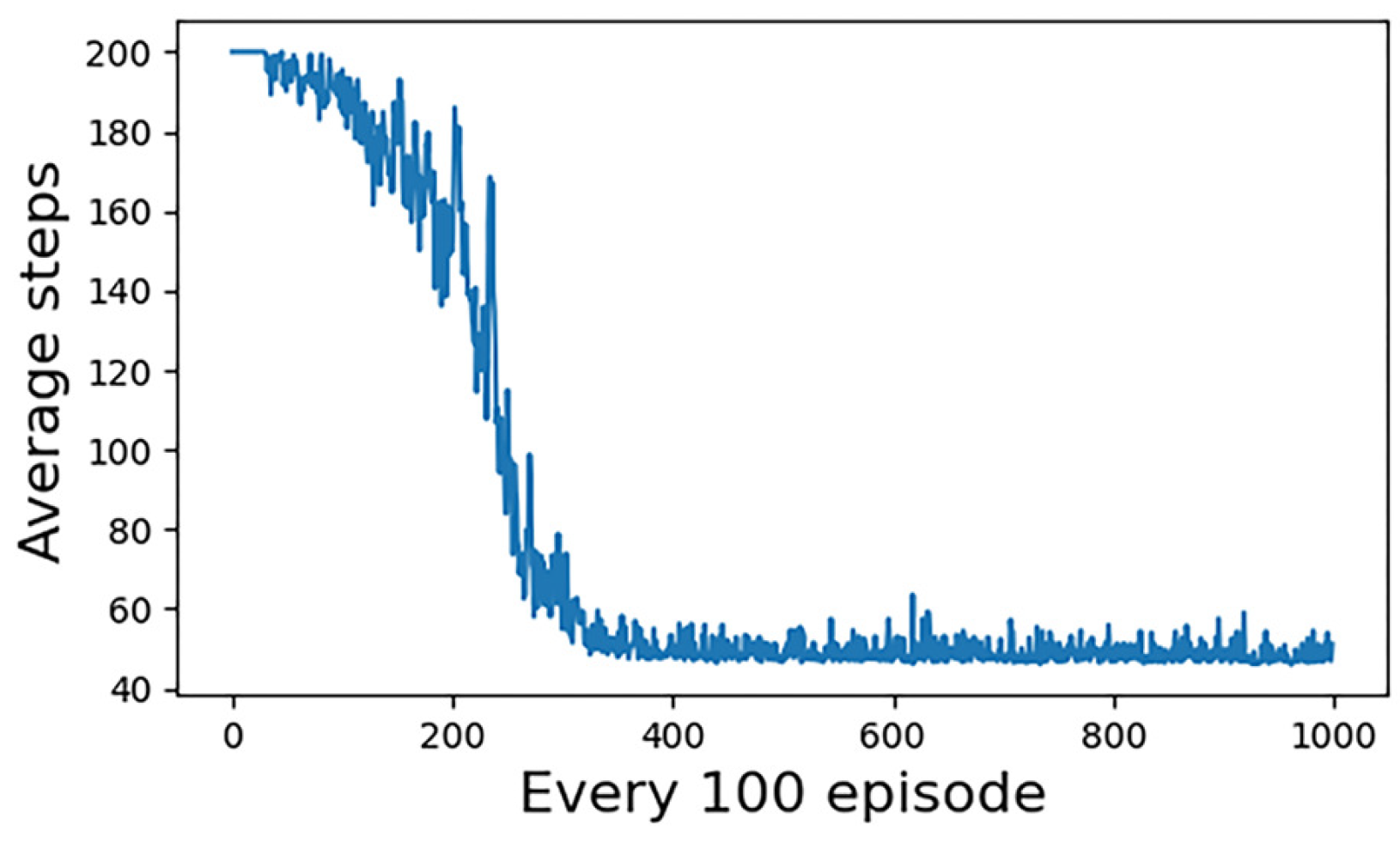
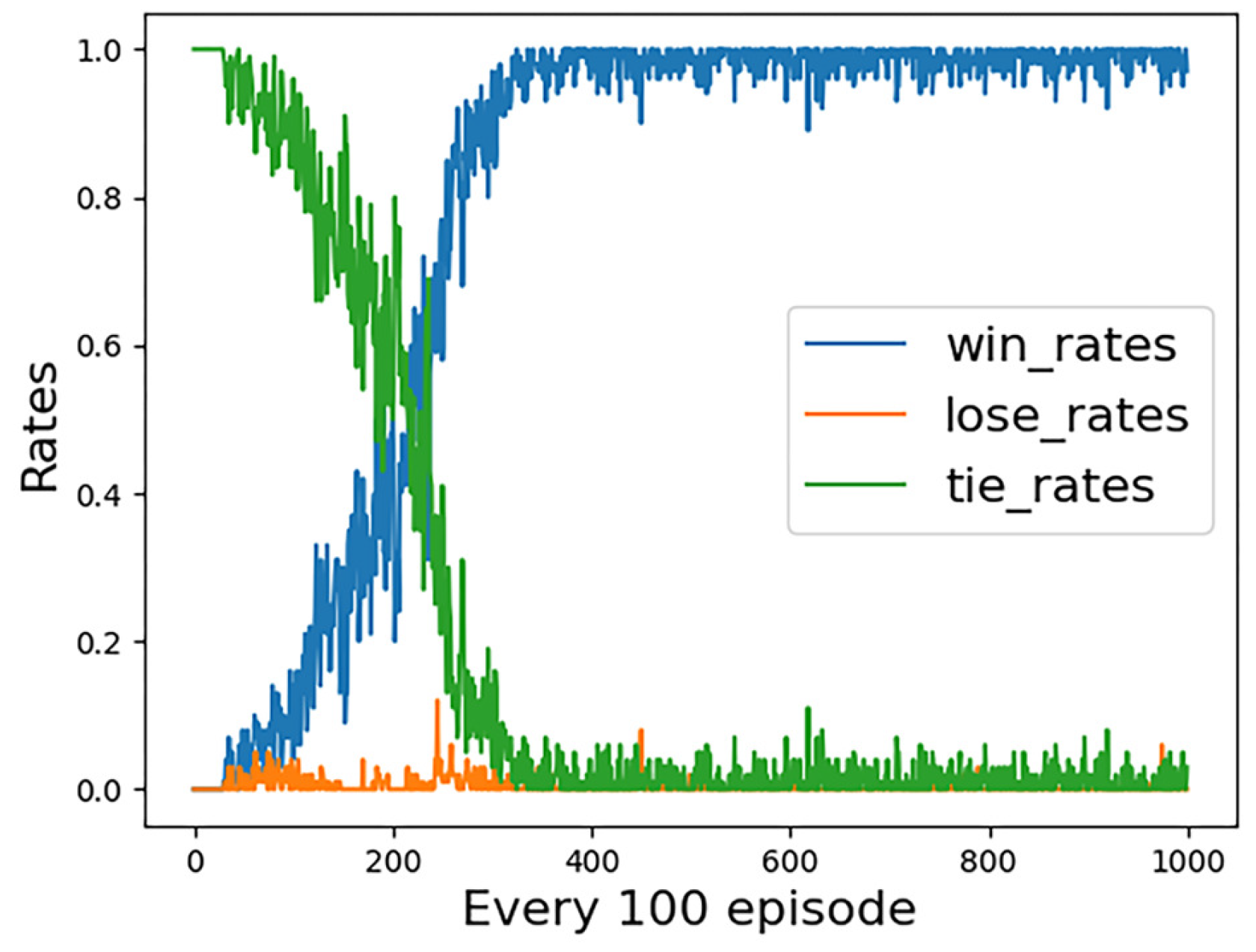
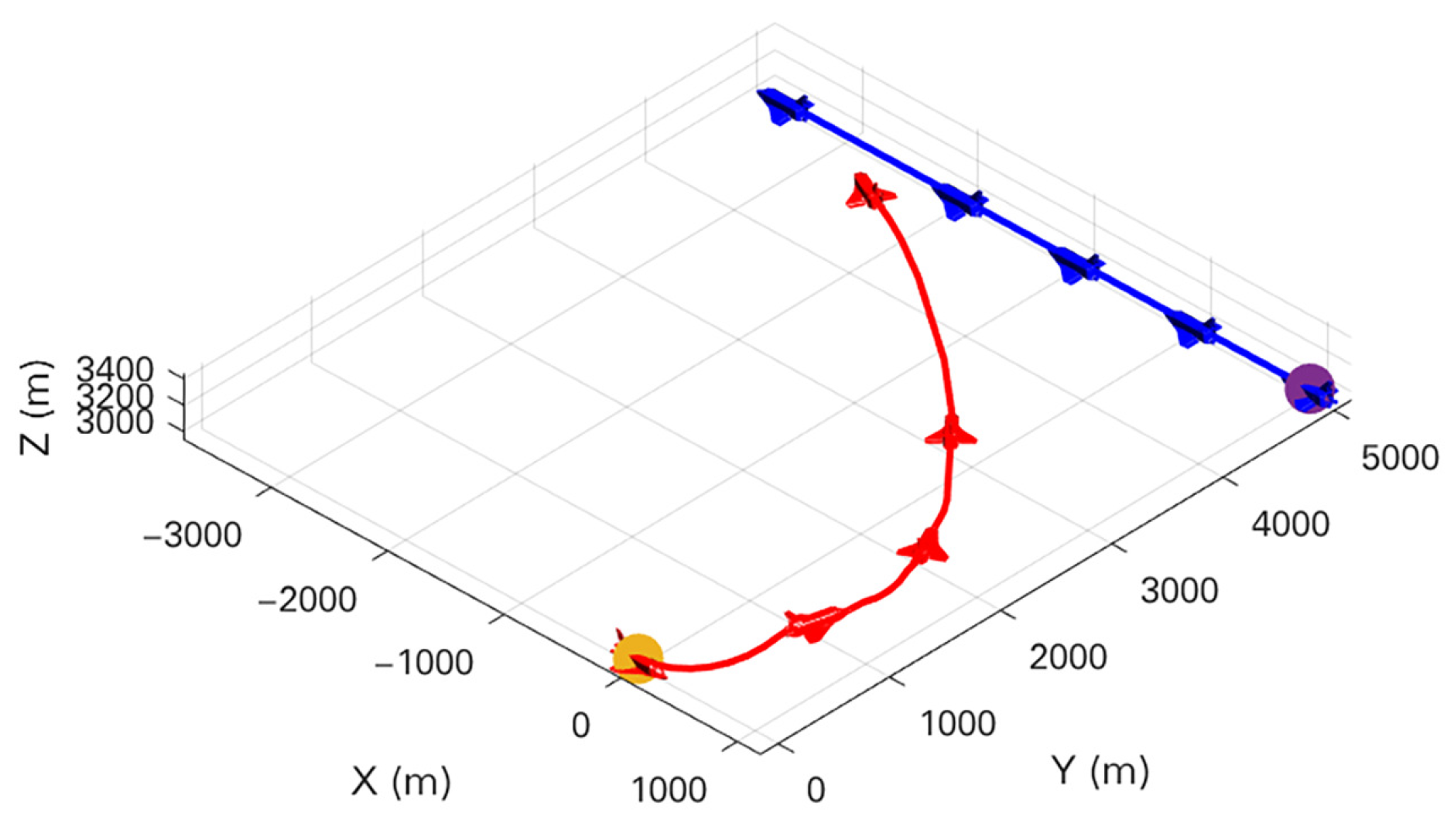
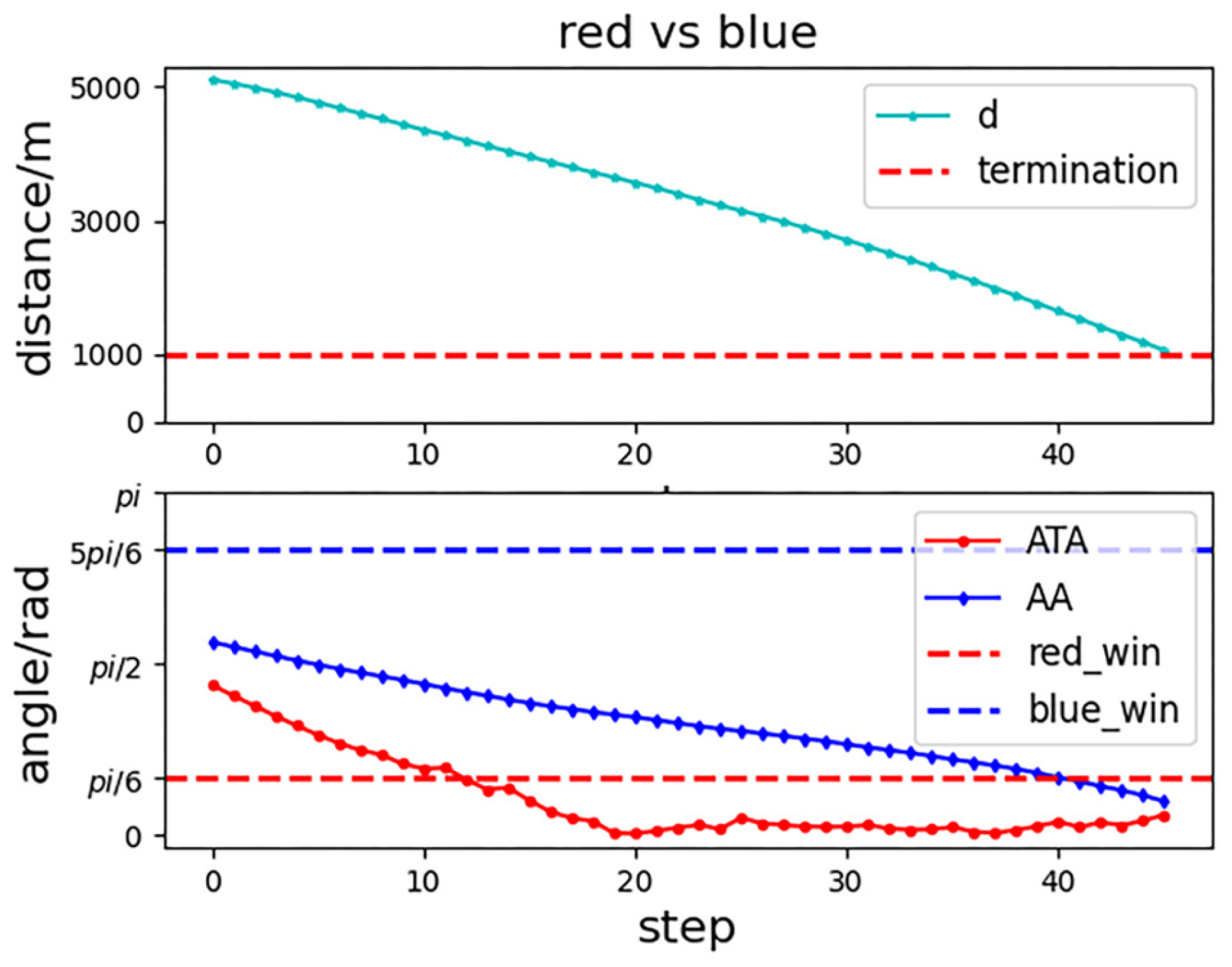
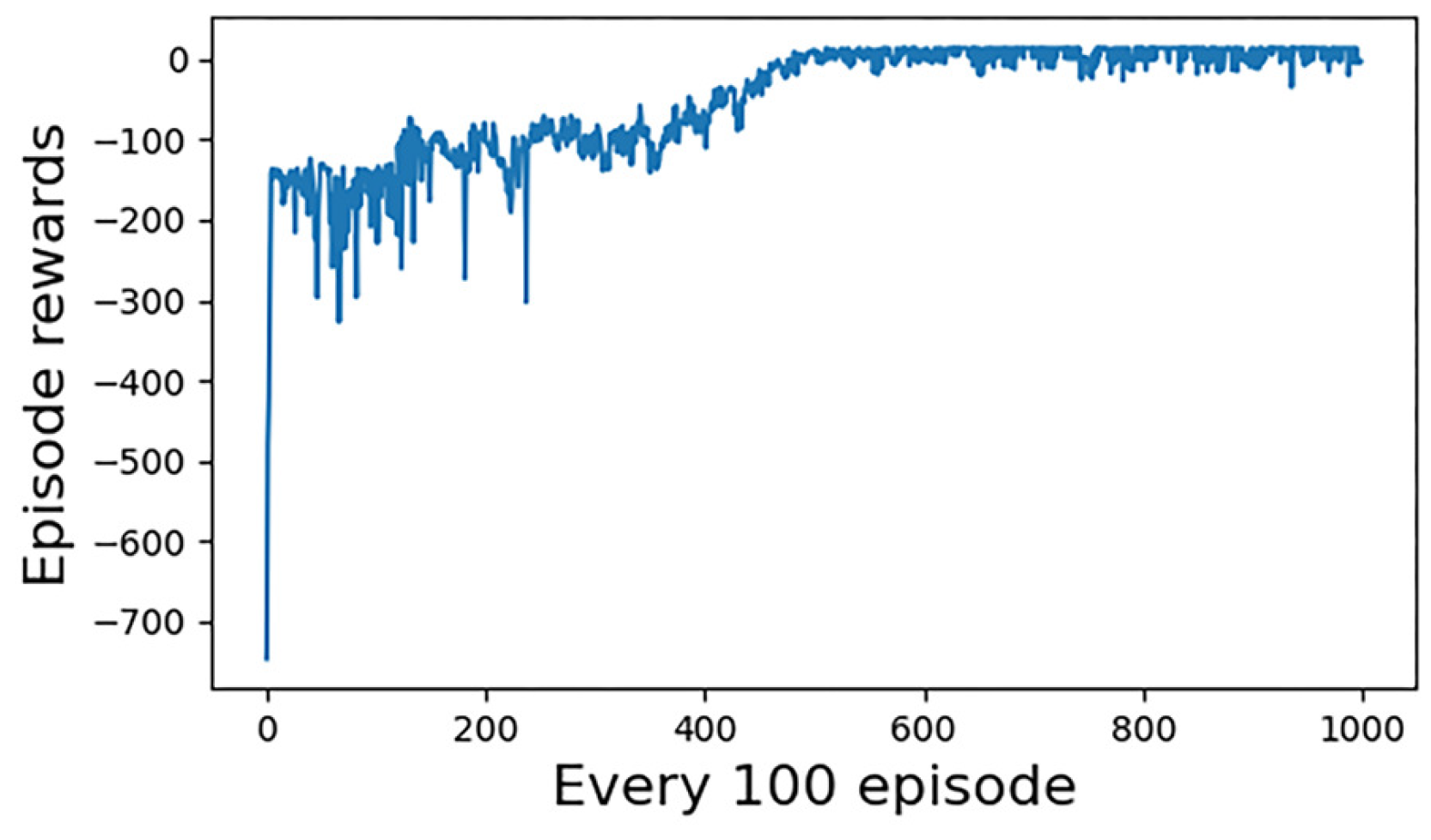
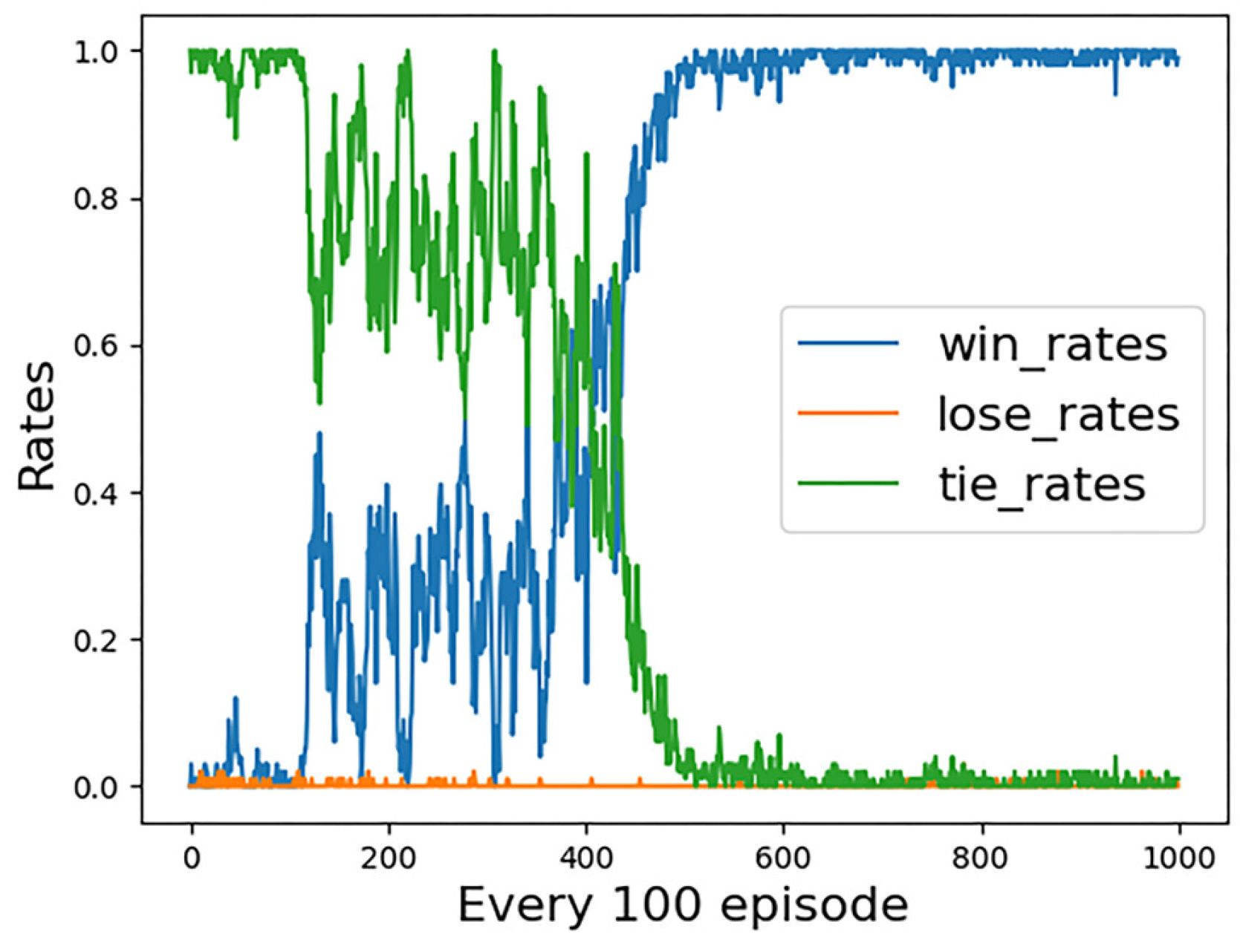
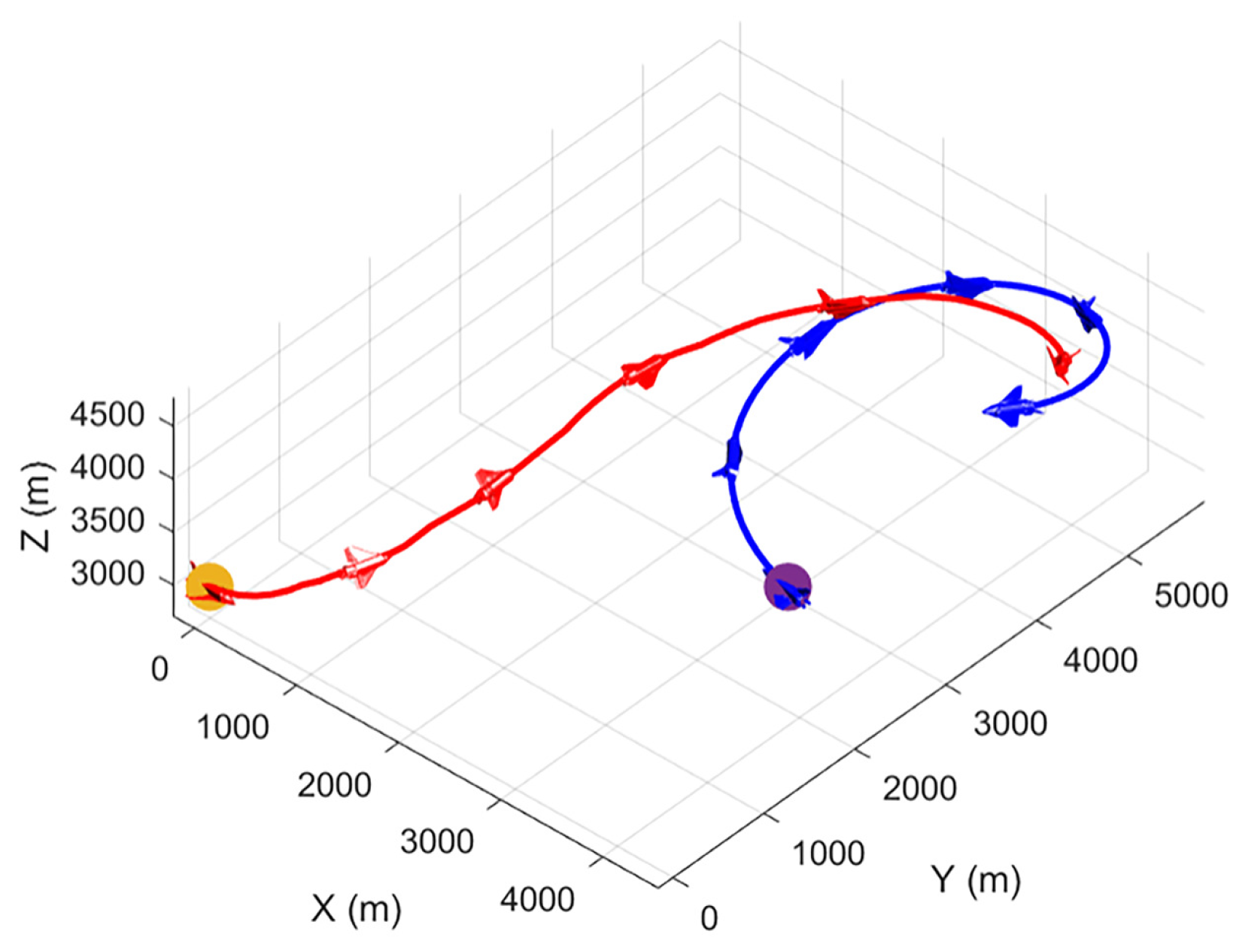
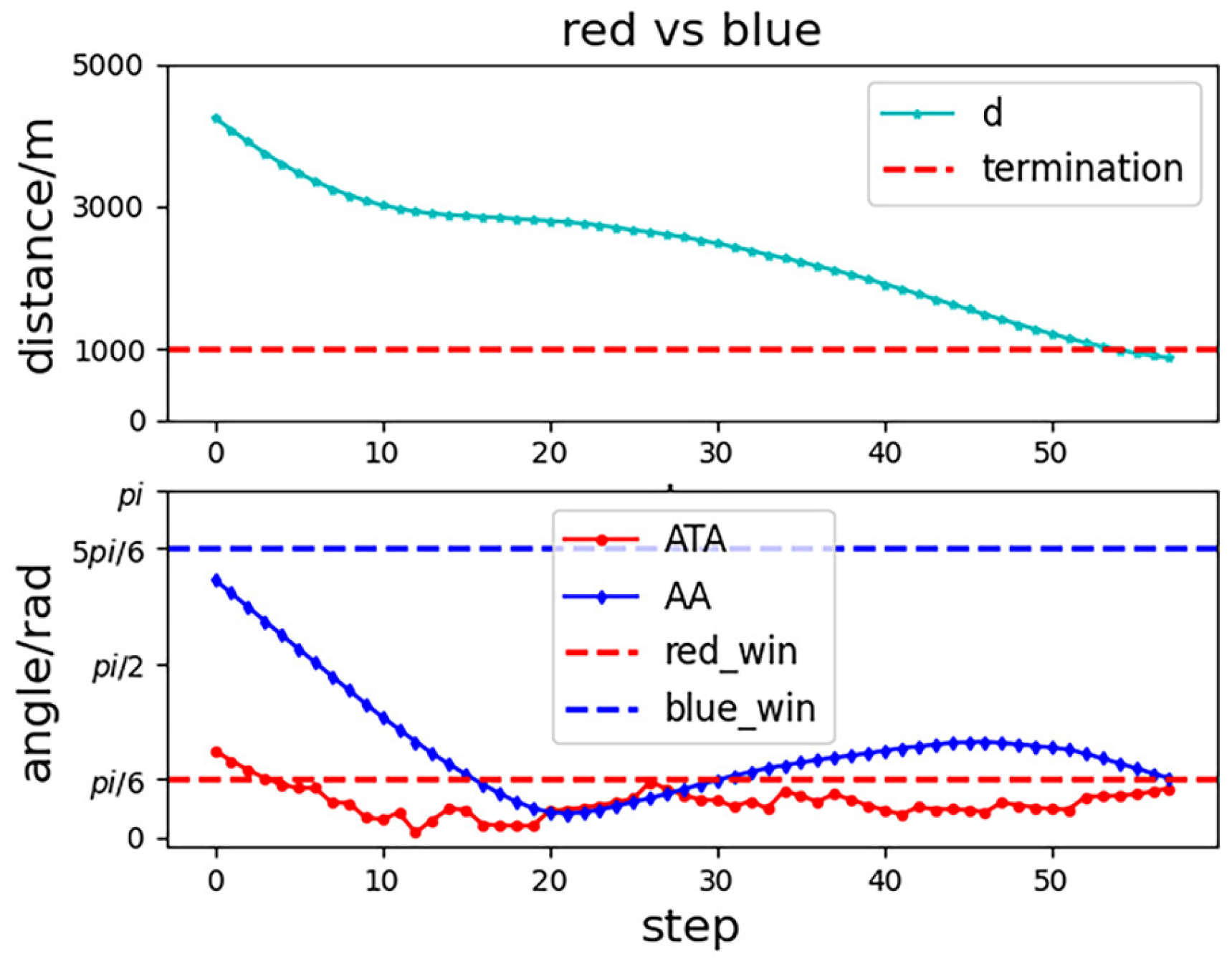
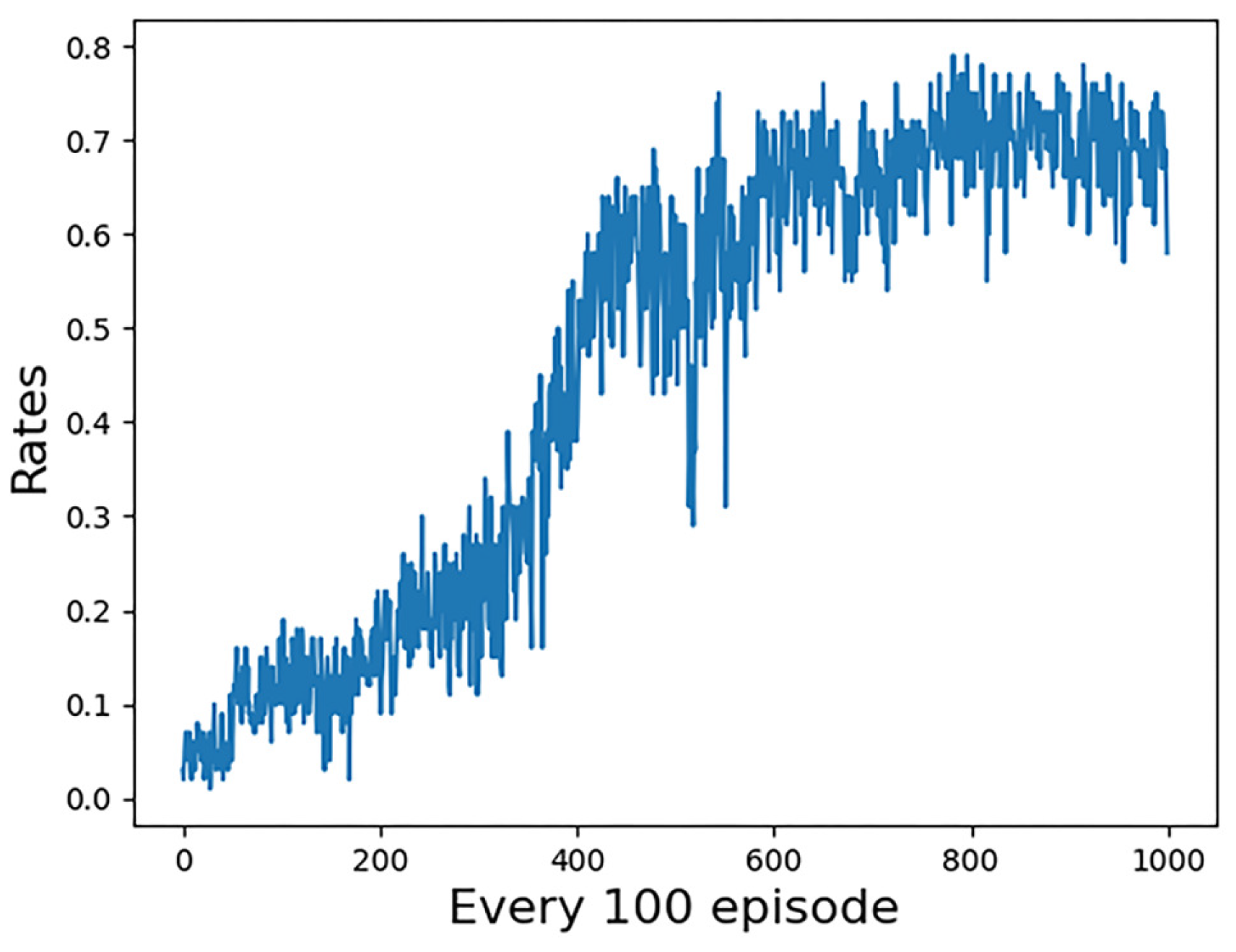
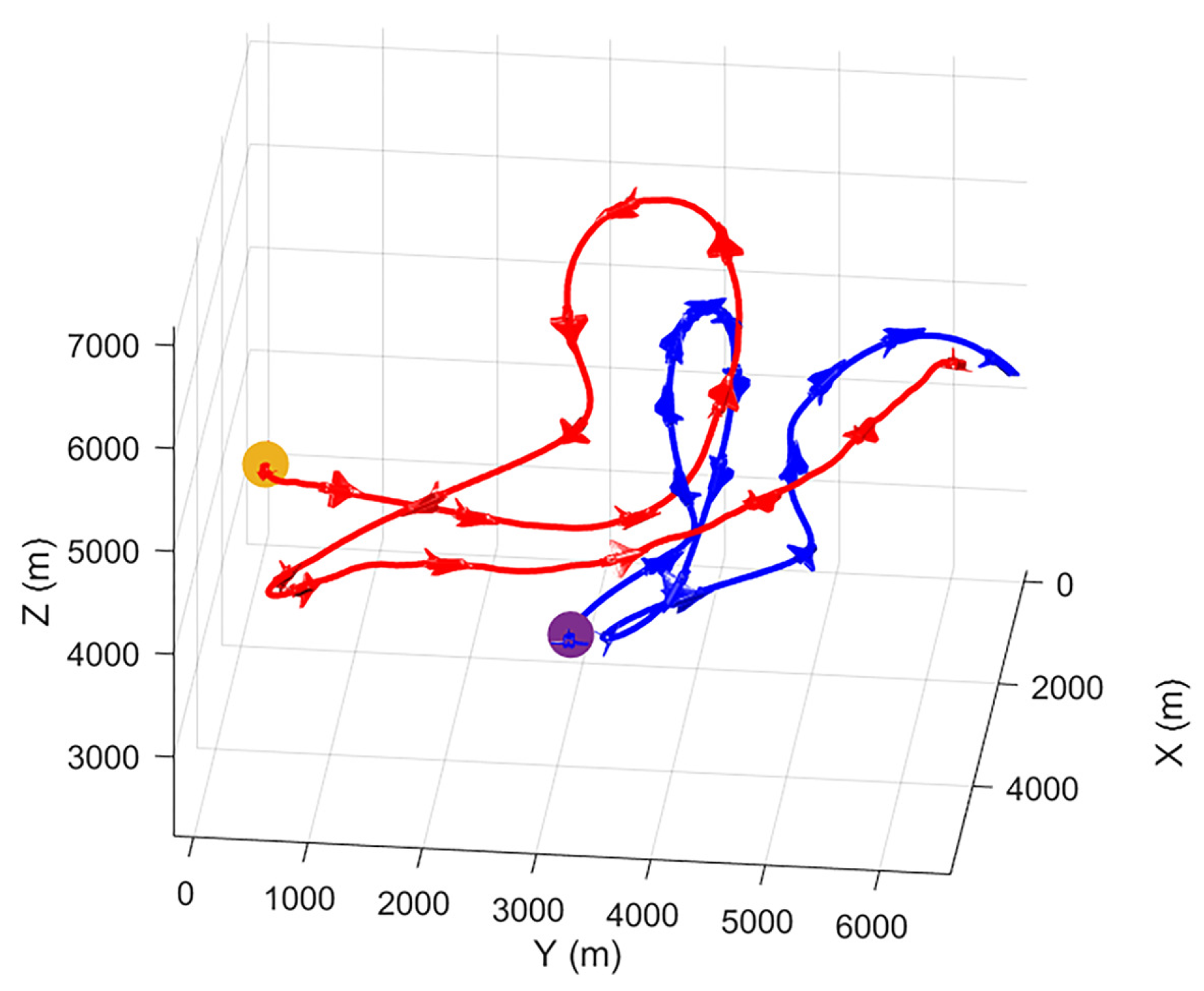
4.3. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Azar, A.T.; Koubaa, A.; Mohamed, N.A. Drone Deep Reinforcement Learning: A Review. Electronics 2021, 10, 999. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, D.L. Editorial of Special Issue on UAV Autonomous, Intelligent and Safe Control. Guid. Navig. Control. 2022, 1, 1–6. [Google Scholar] [CrossRef]
- Burgin, G.H. Improvements to the Adaptive Maneuvering Logic Program; NASA: Washington, DC, USA, 1986. [Google Scholar]
- Wang, X.; Wang, W.; Song, K. UAV Air Combat Decision Based on Evolutionary Expert System Tree. Ordnance Ind. Autom. 2019, 38, 42–47. [Google Scholar]
- Fu, L.; Xie, F.H.; Meng, G.L. An UAV Air-combat Decision Expert System based on Receding Horizon Contro. J. Beijing Univ. Aeronaut. Astronaut. 2015, 41, 1994–1999. [Google Scholar]
- Gracia, E.; Casbeer, D.W.; Pachter, M. Active Target Defence Differential Game: Fast Defender Case. IET Control. Theory Appl. 2017, 11, 2985–2993. [Google Scholar] [CrossRef]
- Hyunju, P. Differential Game Based Air Combat Maneuver Generation Using Scoring Function Matrix. Int. J. Aeronaut. Space Sci. 2016, 17, 204–213. [Google Scholar]
- Ha, J.S.; Chae, H.J.; Choi, H.L. A Stochastic Game-theoretic Approach for Analysis of Multiple Cooperative Air Combat. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 3728–3733. [Google Scholar]
- Deng, K.; Peng, H.Q.; Zhou, D.Y. Study on Air Combat Decision Method of UAV Based on Matrix Game and Genetic Algorithm. Fire Control Command Control 2019, 44, 61–66+71. [Google Scholar]
- Chao, F.; Peng, Y. On Close-range Air Combat based on Hidden Markov Model. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference, Nanjing, China, 2–14 August 2016; pp. 688–695. [Google Scholar]
- Li, B.; Liang, S.Y.; Chen, D.Q.; Li, X.T. A Decision-Making Method for Air Combat Maneuver Based on Hybrid Deep Learning Network. Chin. J. Electron. 2022, 31, 107–115. [Google Scholar]
- Zhang, H.P.; Huang, C.Q.; Xuan, Y.B. Maneuver Decision of Autonomous Air Combat of Unmanned Combat Aerial Vehicle Based on Deep Neural Network. Acta Armamentarii 2020, 41, 1613–1622. [Google Scholar]
- Ernest, N.; Carroll, D.; Schumacher, C. Genetic Fuzzy based Artificial Intelligence for Unmanned Combat AerialVehicle Control in Simulated Air Combat Missions. J. Def. Manag. 2016, 6, 1–7. [Google Scholar]
- Kim, J.; Park, J.H.; Cho, D.; Kim, H.J. Automating Reinforcement Learning With Example-Based Resets. IEEE Robot. Autom. Lett. 2022, 7, 6606–6613. [Google Scholar] [CrossRef]
- Wang, H.T.; Yang, R.P.; Yin, C.S.; Zou, X.F.; Wang, X.F. Research on the Difficulty of Mobile Node Deployment’s Self-Play in Wireless Ad Hoc Networks Based on Deep Reinforcement Learning. Wirel. Commun. Mob. Comput. 2021, 11, 1–13. [Google Scholar]
- Kurzer, K.; Schörner, P.; Albers, A.; Thomsen, H.; Daaboul, K.; Zöllner, J.M. Generalizing Decision Making for Automated Driving with an Invariant Environment Representation using Deep Reinforcement Learning. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 August 2021; Volume 39, pp. 994–1000. [Google Scholar]
- Yang, Q.M.; Zhang, J.D.; Shi, G.Q.; Hu, J.W.; Wu, Y. Maneuver Decision of UAV in Short-range Air Combat Based on Deep Reinforcement Learning. IEEE Access 2020, 8, 363–378. [Google Scholar] [CrossRef]
- Hu, D.Y.; Yang, R.N.; Zuo, J.L.; Zhang, Z.; Wu, J.; Wang, Y. Application of Deep Reinforcement Learning in Maneuver Planning of Beyond-Visual-Range Air Combat. IEEE Access 2021, 9, 32282–32297. [Google Scholar] [CrossRef]
- Yfl, A.; Jpsa, B.; Wei, J.A. Autonomous Maneuver Decision-making for a UCAV in Short-range Aerial Combat Based on an MS-DDQN Algorithm. Def. Technol. 2021, 18, 1697–1714. [Google Scholar]
- Etin, E.; Barrado, C.; Pastor, E. Counter a Drone in a Complex Neighborhood Area by Deep Reinforcement Learning. Sensors 2020, 20, 2320. [Google Scholar]
- Zhang, Y.T.; Zhang, Y.M.; Yu, Z.Q. Path Following Control for UAV Using Deep Reinforcement Learning Approach. Guid. Navig. Control 2021, 1, 2150005. [Google Scholar] [CrossRef]
- Wang, L.; Hu, J.; Xu, Z. Autonomous Maneuver Strategy of Swarm Air Combat based on DDPG. Auton. Intell. Syst. 2021, 1, 1–12. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1928–1937. [Google Scholar]
- Williams, P. Three-dimensional Aircraft Terrain-following Via Real-time Optimal Control. J. Guid. Control Dyn. 1990, 13, 1146–1149. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, W.; Li, Y.; Zhang, F.; Sun, Y.; Liu, D. Research on Cooperation Between Wind Farm and Electric Vehicle Aggregator Based on A3C Algorithm. IEEE Access 2021, 9, 55155–55164. [Google Scholar] [CrossRef]
- Austin, F.; Carbone, G.; Falco, M. Automated Maneuvering Decisions for Air-to-air Combat. AIAA J. 1987, 87, 656–659. [Google Scholar]


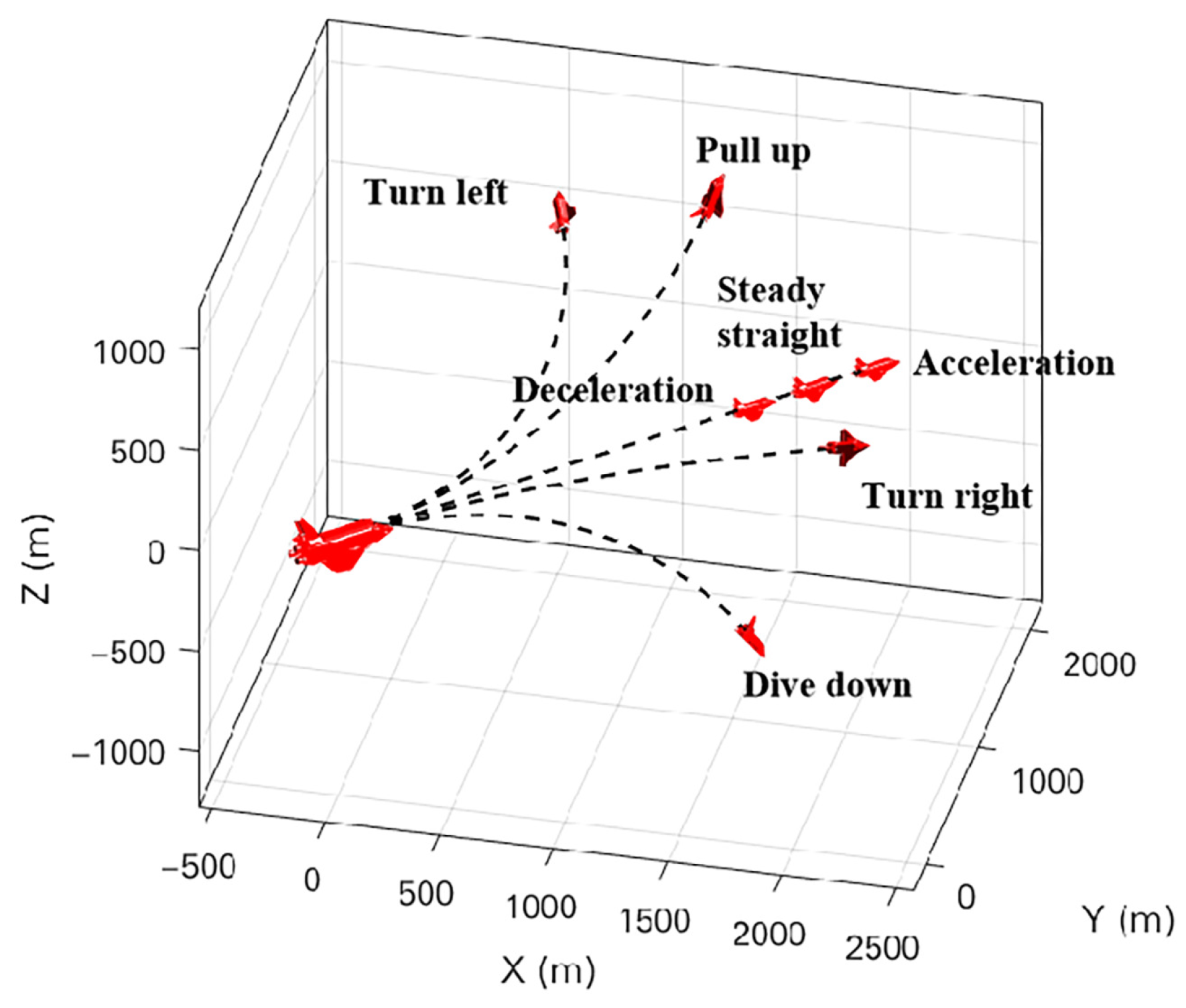



| Basic Actions | Tangential Overload | Method Overload | Roll Angle |
|---|---|---|---|
| steady straight | 0 | 1 | 0 |
| deceleration | 2 | 1 | 0 |
| acceleration | −1 | 1 | 0 |
| turn left | 0 | 8 | |
| turn right | 0 | 8 | |
| pull up | 0 | 8 | 0 |
| dive down | 0 | −8 | 0 |
| Condition | Enemy Strategy | Stating Coordinate (m) | Speed (m/s) | Yaw Angle (Degree) | Pitch Angle (Degree) | |
|---|---|---|---|---|---|---|
| 1 | steady straight | our UCAV | (0, 0, 3000) | 250 | 180 | 0 |
| enemy UCAV | (1000, 5000, 3000) | 200 | 0 | 0 | ||
| 2 | spiral climb | our UCAV | (0, 0, 3000) | 250 | 180 | 0 |
| enemy UCAV | (3000, 3000, 2800) | 250 | 0 | 15 | ||
| 3 | DQN algorithm | our UCAV | (0, 0, 3000) | 250 | 180 | 0 |
| enemy UCAV | (3000, 3000, 3000) | 200 | 0 | 0 |
| Network | Network Layer | Neurons | Activation Function | Learning Rate |
|---|---|---|---|---|
| Actor | input layer | 10 | - | |
| hidden layer1 | 128 | ReLu | ||
| hidden layer2 | 64 | ReLu | ||
| output layer | 7 | Softmax | 0.0001 | |
| Critic | input layer | 10 | - | |
| hidden layer1 | 64 | ReLu | ||
| hidden layer2 | 32 | ReLu | ||
| output layer | 1 | - | 0.0005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Xu, Y.; Kang, Y.; Luo, D. Air Combat Maneuver Decision Method Based on A3C Deep Reinforcement Learning. Machines 2022, 10, 1033. https://doi.org/10.3390/machines10111033
Fan Z, Xu Y, Kang Y, Luo D. Air Combat Maneuver Decision Method Based on A3C Deep Reinforcement Learning. Machines. 2022; 10(11):1033. https://doi.org/10.3390/machines10111033
Chicago/Turabian StyleFan, Zihao, Yang Xu, Yuhang Kang, and Delin Luo. 2022. "Air Combat Maneuver Decision Method Based on A3C Deep Reinforcement Learning" Machines 10, no. 11: 1033. https://doi.org/10.3390/machines10111033
APA StyleFan, Z., Xu, Y., Kang, Y., & Luo, D. (2022). Air Combat Maneuver Decision Method Based on A3C Deep Reinforcement Learning. Machines, 10(11), 1033. https://doi.org/10.3390/machines10111033








