A Nonlinear Vibration Control of a String Using the Method Based on Its Time-Varying Length

Abstract

Strings are common components in various mechanical engineering applications, such as transmission lines, infusion pipes, stay cables in bridges, and wire rope of elevators. The string vibrations can affect the stability and accuracy of systems. In this paper, a time-varying string length method is studied for string vibration suppression. A dynamic model of a string with the time-varying length is formulated. The dimensionless variables are introduced into the nonlinear dynamic model to realize the separation of time and space variables. The finite difference method is used to solve the differential equations of time functions. The vibration characteristics of time-varying length string are analyzed, such as the free vibrations, forced vibrations and damping effect. The influences of the length time-varying frequency and length time-varying range on the suppression performances are discussed. The results show that the time-varying string length method can effectively disperse the resonance peak energy and suppress multimodal resonance at the same time. The suppression performance is better for the time-varying length string with a higher time-varying frequency and a higher time-varying range.

1. Introduction

String structures are often used in various engineering applications, such as cables, transmission lines and marine risers. It is also used to hoist elevators, increase strength on the bridges and other mechanical structures. The vibrations of string structures in the systems can reduce work efficiency, cause fatigue damage and system failures. With the continuous improvement of system stability requirements, the string vibration suppression has also received extensive attention.

The string vibrations often come from the external environment excitations with random and unknown characteristics. The excitation characteristics are challenge works in the string vibration suppression methods. The suppression methods mainly include the passive control and active control. The passive control modes mainly include the damping [1], absorber [2] and structure design [3], etc. He et al. [1] studied the vibration suppressions of axially moving strings by a fixed viscous damper at the right end of a string. They obtained the optimal damping value damping values. Kakou et al. [4] proposed a mobile vibration damping robot to control the wind induced vibrations of the power line. The robot was driven to the antinode position according to the excitation frequencies. It effectively improved the vibration suppressions of the continuous system by the fixed passive tuned vibration absorber. Sorokin et al. [3] controlled the vibrations of the predefined region of string by designing the continuous change of cross-section of string. They proposed a variable amplitude method for this purpose.

Compared with the passive control methods, the flexibility of active control strategy is more conducive to vibration suppression with the random excitations. Thus, the active control methods were widely used to control the string vibrations [5,6,7]. Wijnand et al. [5] used a finite time tracking controller to suppress the mode of vibration of the nonlinear string model. Xing et al. [6] studied the stability of three-dimensional variable length strings based on the adaptive quantization control strategy. Even if the actuator is degraded, the control algorithm can effectively suppress the string vibrations and improve the fault tolerance rate of the control system.

Boundary controls (BC) have become the universal control methods in the active control due to the regulating effect of boundary conditions on the vibrations. Another reason is that it is easier to install the controller in the end of string. Some results have been achieved by the BC in the rapid convergence of amplitude and the stabilization of hyperbolic differential equations [8,9]. The introduction of disturbance observers also solved the problems of vibration suppression with the unknown disturbance [10,11]. Ren et al. [12] improved the control algorithm and proposed an adaptive fault-tolerant BC method, which can effectively suppress the string vibrations in the presence of unknown excitations and actuator failures. By constructing the boundary constraint controller and disturbance observer, Shi et al. [13] ensured the boundary output constraint converges to an arbitrarily small residual set at a greater rate of convergence and realized the asymptotic stability of the system. In addition, the BC methods were also applied to the control of nonlinear vibration models, such as the axially moving strings and variable strings. Liu et al. [14] proposed an adaptive neural network controller to control the vibrations of an axially moving belt. The simulation results show that the method has good vibration suppression performance. Kelleche et al. [15] used adaptive BC to stabilize a nonlinear axial moving string and proved the stability of closed-loop control system. Xing et al. [16] studied the vibration of three-dimensional flexible tubes with variable length. They proposed a boundary control method with the backstepping technology to suppress the vibrations of tubes with the input constraints.

The BC and other active control methods need the reliable control strategies. In the case of unknown disturbance, the control performance depends on the disturbance observer. The BC methods are popular because the boundary conditions can affect the vibration characteristics of strings. Changing the position of damper on the string can affect the vibration suppression performance [4]. Changing the string length can cause the variable of amplitude and natural frequency [17,18]. The variable length strings have always been the controlled object, but the variable length can also be used as a strategy to suppress the resonance of string. The frequency variation of a variable length string can destroy the stable resonance. However, there is few research about the perspective according to authors’ survey. Therefore, a time-varying string length method is proposed to suppression resonance in this paper. The resonant frequency is continuously changed by the time-varying fixed position of end. The mode shape changes before the response stabilizes.

In this work, a nonlinear dynamic model of time-varying length string is formulated to solve the free and forced vibrations. The time-varying length is used to normalize spatial variables when the dimensionless variables are introduced to realize variable separation. The time functions are obtained by the finite difference method. The suppression performances of time-varying length on the free vibrations and forced vibrations are studied. The influences of the time-varying frequency and time-varying range on the vibration suppression of string are discussed.

2. Problem Formulation

Figure 1 shows a schematic diagram of a time-varying length string. The length of string l(t) is the function of time. w(x, t) represents the vibration displacement. T is the static tension. ρ is the distributed mass per unit length. c is the damping coefficient. The partial differential equation of string vibration can be derived according to the Newton’s second law. Without considering the bending stiffness and sag of the string, the motion equation of taut string is [13]

$$\rho \frac{{\partial }^{2}w}{\partial t^2}+c\frac{\partial w}{\partial t}-T\frac{{\partial }^{2}w}{\partial x^2}=0$$

(1)

The boundary conditions of time-varying length string are

$$w(0,t)=0,w(l(t),t)=0$$

(2)

The vibration equation is defined in the space domain related to time. Define the dimensionless variables $s=\frac{x}{l\left(t\right)}$ to obtain stationary space domain [19]. The differential of w(x,t) becomes

$$\left\{\begin{array}{l}\frac{\partial w}{\partial x}=\frac{1}{l\left(t\right)}\frac{\partial w}{\partial s}\\ \frac{\partial w}{\partial t}=\frac{-s\dot{l}\left(t\right)}{l\left(t\right)}\frac{\partial w}{\partial s}+\frac{\partial w}{\partial t}\end{array}\right.$$

(3)

where $\dot{l}(t)$ the derivative of l(t) with respect to time. The second order differentiations are

$$\left\{\begin{array}{l}\frac{{\partial }^{2}w}{\partial x^2}=\frac{1}{l^2\left(t\right)}\frac{\partial w}{\partial s}\\ \frac{{\partial }^{2}w}{\partial t^2}=\left(\frac{-s\ddot{l}\left(t\right)}{l\left(t\right)}+\frac{2s{\dot{l}}^2\left(t\right)}{l^2\left(t\right)}\right)\frac{\partial w}{\partial s}+{\left(\frac{s\dot{l}\left(t\right)}{l\left(t\right)}\right)}^2\frac{{\partial }^{2}w}{\partial s^2}-\frac{s\dot{l}\left(t\right)}{l\left(t\right)}\frac{{\partial }^{2}w}{\partial t\partial s}+\frac{{\partial }^{2}w}{\partial t^2}\end{array}\right.$$

(4)

By substituting Equations (3) and (4) into Equation (1), the partial differential equation becomes

$$\rho \frac{{\partial }^{2}w}{\partial t^2}+\rho \left(\frac{-s\ddot{l}\left(t\right)}{l\left(t\right)}+\frac{2s{\dot{l}}^2\left(t\right)}{l^2\left(t\right)}\right)\frac{\partial w}{\partial s}+\rho {\left(\frac{s\dot{l}\left(t\right)}{l\left(t\right)}\right)}^2\frac{{\partial }^{2}w}{\partial s^2}-\rho \frac{s\dot{l}\left(t\right)}{l\left(t\right)}\frac{{\partial }^{2}w}{\partial t\partial s}-c\frac{s\dot{l}\left(t\right)}{l\left(t\right)}\frac{\partial w}{\partial s}+c\frac{\partial w}{\partial t}-\frac{T}{l^2\left(t\right)}\frac{{\partial }^{2}w}{\partial s^2}=0$$

(5)

Define the variables $a^2=\frac{T}{\rho }$, $\gamma =\frac{c}{\rho }$, $g\left(t\right)=\frac{\dot{l}(t)}{l\left(t\right)}, h\left(t\right)=\frac{\ddot{l}\left(t\right)}{l\left(t\right)}$. Substituting the variables into Equation (5), Equation (5) becomes

$$\frac{{\partial }^{2}w}{\partial t^2}+\gamma \frac{\partial w}{\partial t}-\frac{a^2}{l^2\left(t\right)}\frac{{\partial }^{2}w}{\partial s^2}+\left[-sh\left(t\right)+2s{g}^2\left(t\right)\right]\frac{\partial w}{\partial s}+{\left[sg\left(t\right)\right]}^2\frac{{\partial }^{2}w}{\partial s^2}-sg\left(t\right)\frac{{\partial }^{2}w}{\partial t\partial s}-\gamma sg\left(t\right)\frac{\partial w}{\partial s}=0$$

(6)

The time-varying form of string length designed is l(t) = l₀ + Δlcos(ωt) in this paper. A small time-varying range 2Δl and a small time-varying frequency $\omega$ are designed to ensure the slow changes of string length. When Δl and $\omega$ are both small, $\left|\dot{l}(t)\right|=\left|\Delta l\omega \sin \left(\omega t\right)\right|\ll \left|l\left(t\right)\right|$ and $\left|\ddot{l}\left(t\right)\right|=\left|\Delta l{\omega }^2\cos \left(\omega t\right)\right|\ll \left|l\left(t\right)\right|$. So, g(t)≪1 and h(t)≪1. Since c and ρ have same order, and 0 < s < 1, the coefficients of the last four items in Equation (6) are always obviously less than 1. The last four items in Equation (6) may be neglected [19]. The case under consideration later in the article will give the coefficient range of the last four terms. Equation (6) is simplified as

$$\frac{{\partial }^{2}w}{\partial t^2}+\gamma \frac{\partial w}{\partial t}-\frac{a^2}{l^2\left(t\right)}\frac{{\partial }^{2}w}{\partial s^2}=0$$

(7)

3. Dynamic Analysis of the Time-Varying Length String

3.1. Free Vibrations Equations

The dimensionless parameter s replaces the variable x. Thus, the spatial variable of boundary conditions does not contain time. It is conducive to variable separation. The solution of free vibration is [17]

$$w_A\left(s,t\right)={\displaystyle \sum _{n=1}^N{\phi }_n\left(s\right)q_n\left(t\right)}$$

(8)

in which, n is the number of modes, ${\phi }_n$(s) is the n-th order mode function and $q_n$(t) is the nth order time function. Using the method of separating variables, Equation (7) can be converted into

$$\left\{\begin{array}{l}\frac{{\partial }^2{\phi }_n}{\partial s^2}+{\beta }_n^2{\phi }_n\left(s\right)=0\\ \frac{{\partial }^2{q}_n}{\partial t^2}+r\frac{\partial q_n}{\partial t}+\frac{{\beta }_n{}^2{a}^2}{l^2\left(t\right)}{q}_n=0\end{array}\right.$$

(9)

The boundary conditions of time-varying length string become

$$w(0,t)=0,w(\frac{l(t)}{l(t)},t)=w(1,t)=0$$

(10)

Suppose a mode function satisfying the boundary conditions. The mode function is assumed in the form [17]

$${\phi }_n\left(s\right)=\sin \left(n\pi s\right)$$

(11)

At this time, the natural frequency is

$${\omega }_n^2\left(t\right)=\frac{{\left(n\pi \right)}^2{a}^2}{l^2\left(t\right)}$$

(12)

The differential equation of time function can be written as

$$\frac{{\partial }^2{q}_n}{\partial t^2}+\gamma \frac{\partial q_n}{\partial t}+{\omega }_n\left(t\right)q_n=0$$

(13)

3.2. Forced Vibrations Equations

When the system has external excitations, the right end of Equation (7) is no longer zero. The transverse force is ${f(x, t)=F}_0{\cos \left(\omega t\right)\delta (x-x}_0)$, which is the concentrated load at the x₀ position. Substitute dimensionless variables s into force. The transverse force is

$$f\left(s,t\right)=F_0\cos \left(\omega t\right)\delta \left(s-\frac{x_0}{l(t)}\right)$$

(14)

The forced vibration equation of time-varying length string is

$$\frac{{\partial }^{2}w}{\partial t^2}+\gamma \frac{\partial w}{\partial t}-\frac{a^2}{l^2\left(t\right)}\frac{{\partial }^{2}w}{\partial s^2}=f\left(s,t\right)/\rho$$

(15)

The excitation force of Fourier series is [2]

$$f\left(s,t\right)={\displaystyle \sum _{m=1}^{\infty }{\varphi }_m\left(t\right)\sin \left(m\pi s\right)}$$

(16)

$${\varphi }_m\left(t\right)=2{\displaystyle {\int }_0^{1}f\left(s,t\right)}\sin \left(m\pi s\right)ds$$

(17)

The mode function is obtained according to the boundary conditions. The mode function of forced vibration is same as that of free vibration. The solution of forced vibration can also be the form of Fourier series. It is

$$w_F\left(s,t\right)={\displaystyle \sum _{m=1}^{\infty }\sin \left(m\pi s\right)q_m\left(t\right)}$$

(18)

Substituting Equations (16)–(18) into Equation (15). The differential equation of m-th order time function of forced vibration is

$$\frac{{\partial }^2{q}_m}{\partial t^2}+\gamma \frac{\partial q_m}{\partial t}+{\omega }_m\left(t\right)q_m=\frac{{\varphi }_m\left(t\right)}{\rho }$$

(19)

The differential equation of time function contains time-dependent coefficient. Therefore, the exact solutions of Equations (13) and (19) does not exist. The approximate solutions of differential equation of time function are obtained by numerical method.

3.3. Discretization of the Vibration Equation

The finite difference method is used to solve the differential equation of time functions. For the time functions of free vibration, the time is discrete at region [0, T], and the time step is τ. The difference scheme of Equation (13) is

$$\frac{q_n^{k+1}-2q_n^k+q_n^{k-1}}{{\tau }^2}-{\left({\omega }_n^k\right)}^2{q}_n^k+\gamma \frac{q_n^{k+1}-q_n^{k-1}}{2\tau }+\mathrm{O}({\tau }^2)=0$$

(20)

The truncation error of Equation (20) is $\mathrm{O}\left({\tau }^2\right)$. When τ tend to 0, the truncation error tends to 0. So the difference Equation (20) is compatible with Equation (13). Define $p=\frac{\gamma \tau }{2}$, Equation (20) can be presented as

$$\left(p+1\right)q_n^{k+1}=\left(p-1\right)q_n^{k-1}+\left[2-{\left({\omega }_n^k\right)}^2{\tau }^2\right]q_n^k$$

(21)

The values of first two levels of Equation (21) are obtained from the initial conditions. The initial displacement and initial velocity of string are

$$w\left(x,0\right)=u(x),\frac{\partial w}{\partial t}\left(x,0\right)=v\left(x\right)$$

(22)

The forms of variable separation are

$$w_A\left(x,0\right)={\displaystyle \sum _{n=1}^N\sin \left(\frac{n\pi x}{l\left(0\right)}\right)q_n\left(0\right)}=u\left(x\right)$$

(23)

$$\frac{\partial w_A}{\partial t}\left(x,0\right)={\displaystyle \sum _{n=1}^N\sin \left(\frac{n\pi x}{l\left(0\right)}\right)\frac{\partial q_n}{\partial t}\left(0\right)}=v\left(x\right)$$

(24)

The initial value and velocity of time function can be obtained by integral. They are

$$q_n\left(0\right)=\frac{2}{l\left(0\right)}{\displaystyle {\int }_0^{l\left(0\right)}u\left(x\right)}\sin \left(\frac{n\pi x}{l\left(0\right)}\right)dx$$

(25)

$$\frac{\partial q_n}{\partial t}\left(0\right)=\frac{2}{l\left(0\right)}{\displaystyle {\int }_0^{l\left(0\right)}v\left(x\right)}\sin \left(\frac{n\pi x}{l\left(0\right)}\right)dx$$

(26)

The initial velocity is subjected to central difference at the half layer. The value of first two levels of Equation (21) can be solved

$$\left\{\begin{array}{l}{q}_n^1=q_n\left(0\right),n=1,2,\dots ,N\\ \frac{q_n^2-q_n^1}{\tau }=\frac{\partial q_n}{\partial t}\left(0\right),n=1,2,\dots ,N\end{array}\right.$$

(27)

According to Equations (21) and (27), the difference solution of Equation (13) can be obtained. The solution process of time functions of forced vibration is same as that of free vibration. Considering the excitation item additionally, the difference scheme of Equation (19) is

$$\left(p+1\right)q_m^{k+1}=\left(p-1\right)q_m^{k-1}+\left[2-{\left({\omega }_n^k\right)}^2{\tau }^2\right]q_m^k+{\tau }^2{\varphi }_m^k/\rho$$

(28)

Through the variable separation, the initial displacement and initial velocity of forced vibrations are

$$w_F\left(x,0\right)={\displaystyle \sum _{m=1}^{\infty }\sin \left(\frac{m\pi x}{l\left(0\right)}\right)q_m\left(0\right)}=u\left(x\right)$$

(29)

$$\frac{\partial w_F}{\partial t}\left(x,0\right)={\displaystyle \sum _{m=1}^{\infty }\sin \left(\frac{m\pi x}{l\left(0\right)}\right)\frac{\partial q_m}{\partial t}\left(0\right)}=v\left(x\right)$$

(30)

Since initial conditions and excitation are considered in the difference calculation, the forced vibration solutions include the free vibrations.

4. Results and Discussions

The vibration of time-varying length string is obtained by the finite difference method in a MATLAB code. The vibration suppression performances of time-varying string length method on the free vibrations and forced vibrations are studied. The influences of the time-varying range and time-varying frequency on the vibration suppression performances of string are discussed. The parameters of all models are T = 0.9 N and ρ = 0.001 kg/m.

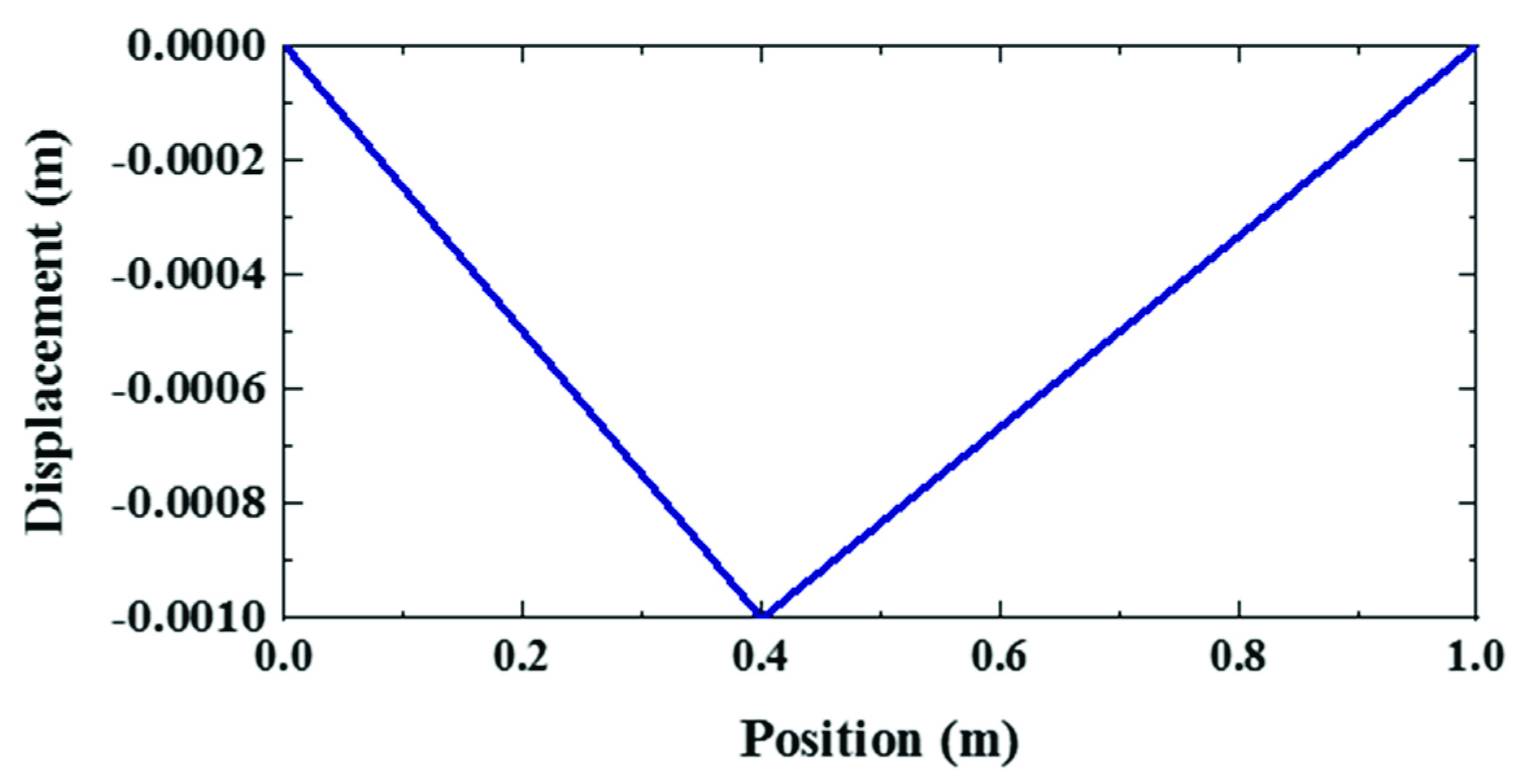
4.1. Free Vibrations of Time-Varying Length String

In the section, the undamped and damped free vibrations of time-varying length string are calculated. The time-varying string length is l(t) = 0.8 + 0.2cos(0.2πt) m, while the contrast string length is 1 m. The coefficient ranges of the last four terms in Equation (6) for the case are −0.13 to 0.08, 0 to 0.026, −0.16 to 0.16 and 0. The coefficient of last four terms can be regarded as small quantities, and the last four terms in Equation (6) may be neglected. The initial velocity is 0; and the initial displacement is

$$\phi \left(x\right)=\left\{\begin{array}{l}-0.0025x,x\le 0.4\\ \frac{0.001x}{6}-\frac{0.005}{3},0.4<x\le 1\end{array}\right.$$

(31)

The initial displacement is shown in Figure 2. The initial displacement of string is reasonable and satisfies the boundary conditions of string. The initial conditions can produce free vibrations of all modes to verify the suppression performance of time-varying length on each mode.

Figure 3 shows the time-domain free vibration comparison of time-varying length string and contrast string without damping. Figure 4 gives the frequency-domain comparison of acceleration level. In Figure 3, the vibration frequency and amplitude of time-varying length string is different from that of contrast string. The vibration frequency varies with the string length. In Figure 4, there are multiple vibration peaks at the natural frequencies of contrast string, while the peaks disappear in the spectrum of time-varying length string. In addition, the response of time-varying length string is larger than that of contrast string in other frequency bands. This is because the change of vibration frequency leads to peak energy dispersion.

When the damping coefficient is c = 0.0005, the time-domain free vibration comparisons are shown in Figure 5, and the frequency-domain comparisons are shown in Figure 6. The coefficient ranges of the last terms in Equation (6) become −0.08 to 0.08. The coefficient of the last terms can still be regarded as small quantities. Figure 5 gives the vibration attenuation of two strings due to damping. The peak attenuations of time-varying length string in Figure 6 are lower than those in Figure 4, because the effect of the damping on the contrast string is greater than that on the time-varying length string. Moreover, the damping reduces the responses of time-varying strings in other frequency bands.

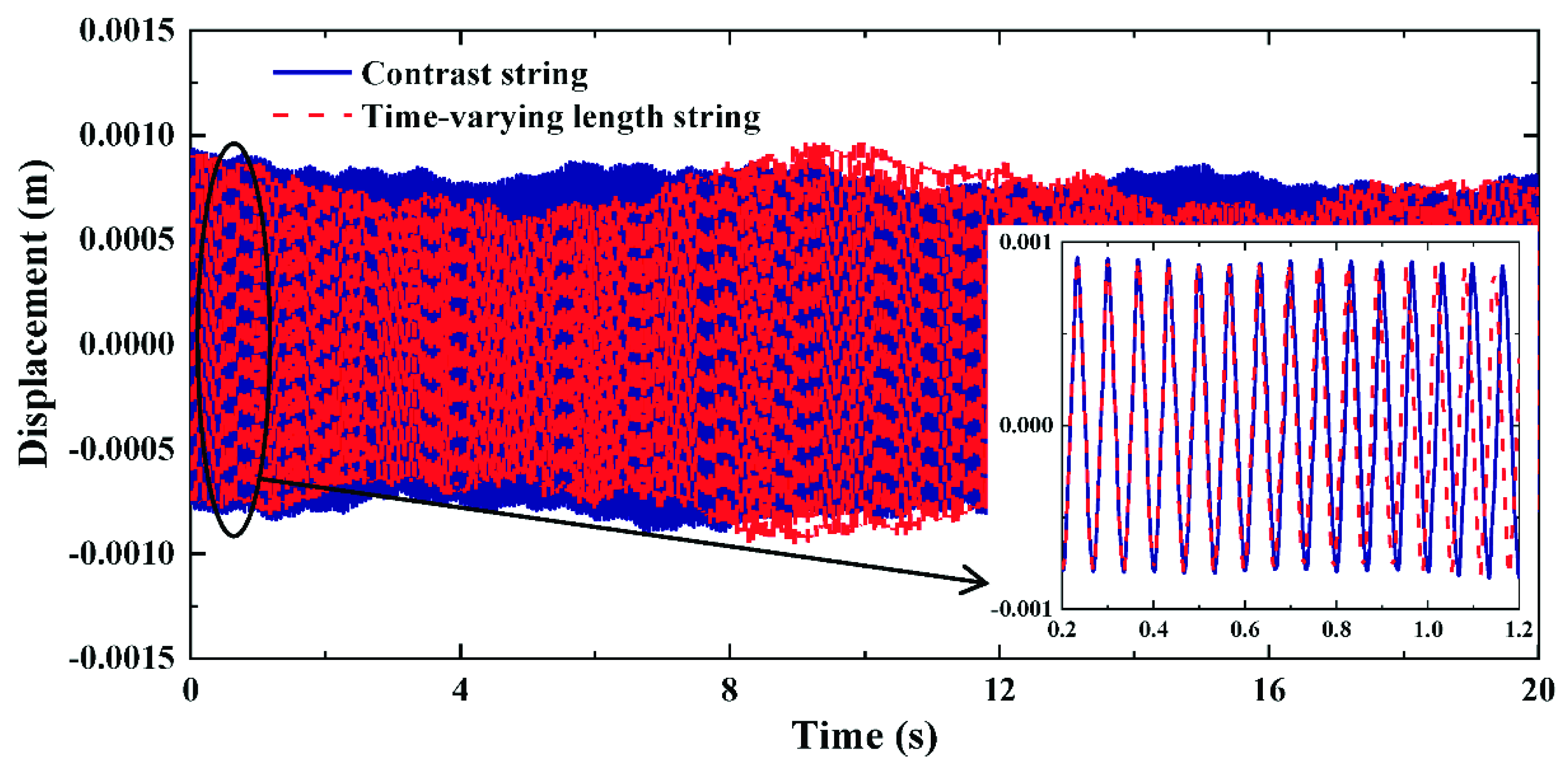
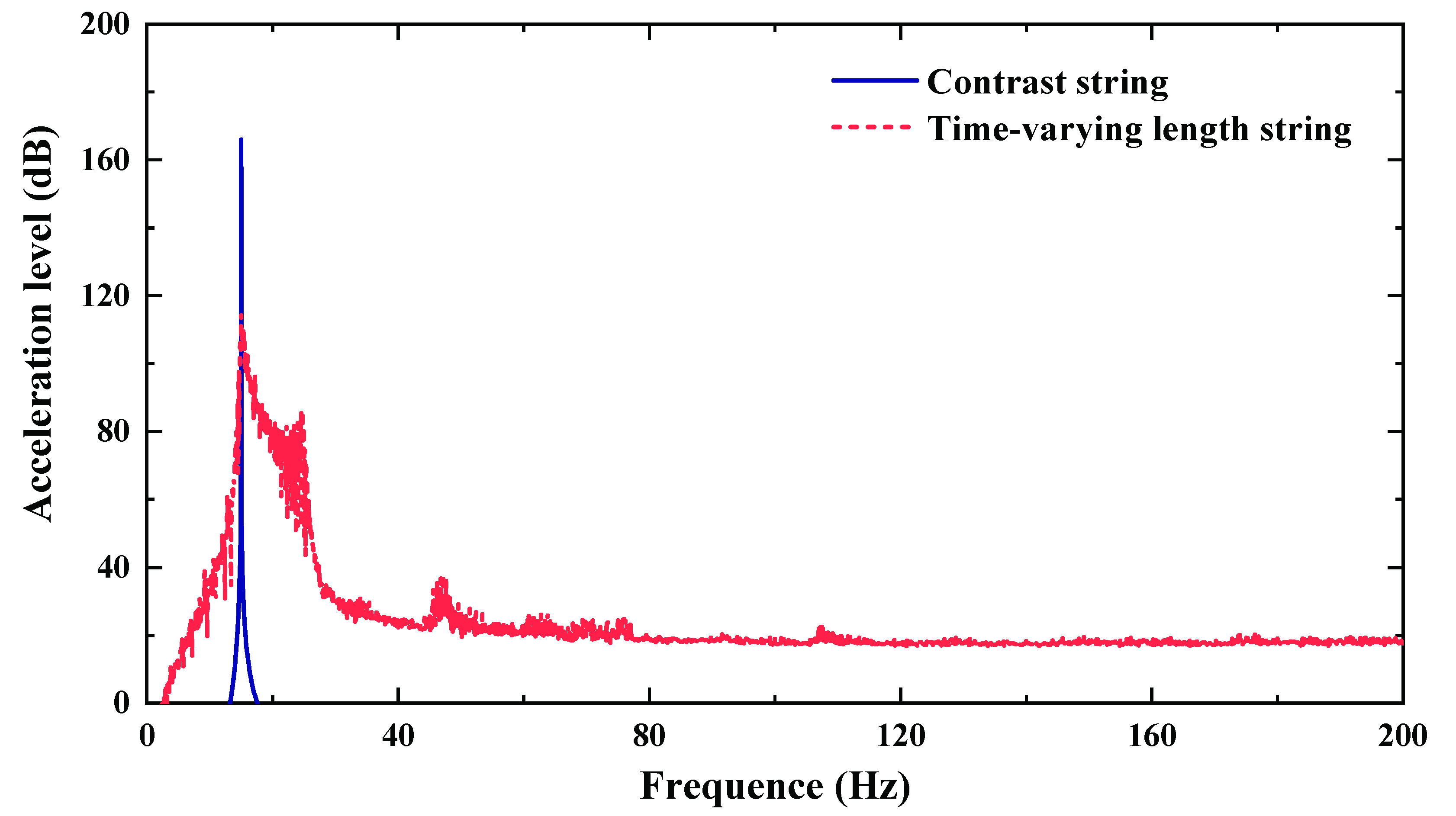
4.2. Forced Vibrations of Time-Varying Length String

To study the resonance suppression performance by the time-varying string length method, the forced vibrations with the single frequency or multifrequency excitation of time-varying length string and contrast string are compared. The single frequency excitation force is f(x,t) = 0.1 sin(30πt)δ(x − 0.5). The excitation frequency is the first natural frequency of contrast string. The other string parameters are same as free vibration cases. The time-domain forced vibrations comparison of time-varying length string and contrast string is shown in Figure 7. In Figure 7, the vibrations are basically stable after 5 s. The time-domain vibrations from 5 s to 20 s are transferred frequency-domain; and the spectrums comparison is shown in Figure 8. In Figure 7, the vibration period of time-varying length string is same as the time-varying period. When the resonant frequencies become far away from the excitation frequency, the response rapidly reduced. The resonance can’t be maintained due to the variety of string length. Therefore, the response of time-varying length string is significantly lower than that of contrast string. In Figure 8, the time-varying length can reduce the peak at the excitation frequency. The responses of frequency band near the excitation frequency are increased. It indicates that the peak energy is dispersed to the nearby frequency band.

To verify whether the time-varying string length method is effective when the multiple order resonance occurs, the structures need the multiple frequencies excitation. The frequencies are the first six resonance frequencies of contrast string. The time-domain and frequency-domain comparisons of the time-varying length string and contrast string are shown in Figure 9 and Figure 10. In Figure 9, the amplitude of time-varying length string is always lower than that of the contrast string in the process of periodic variations. The time-varying string length method can disperse every resonance peak energy at the same time.

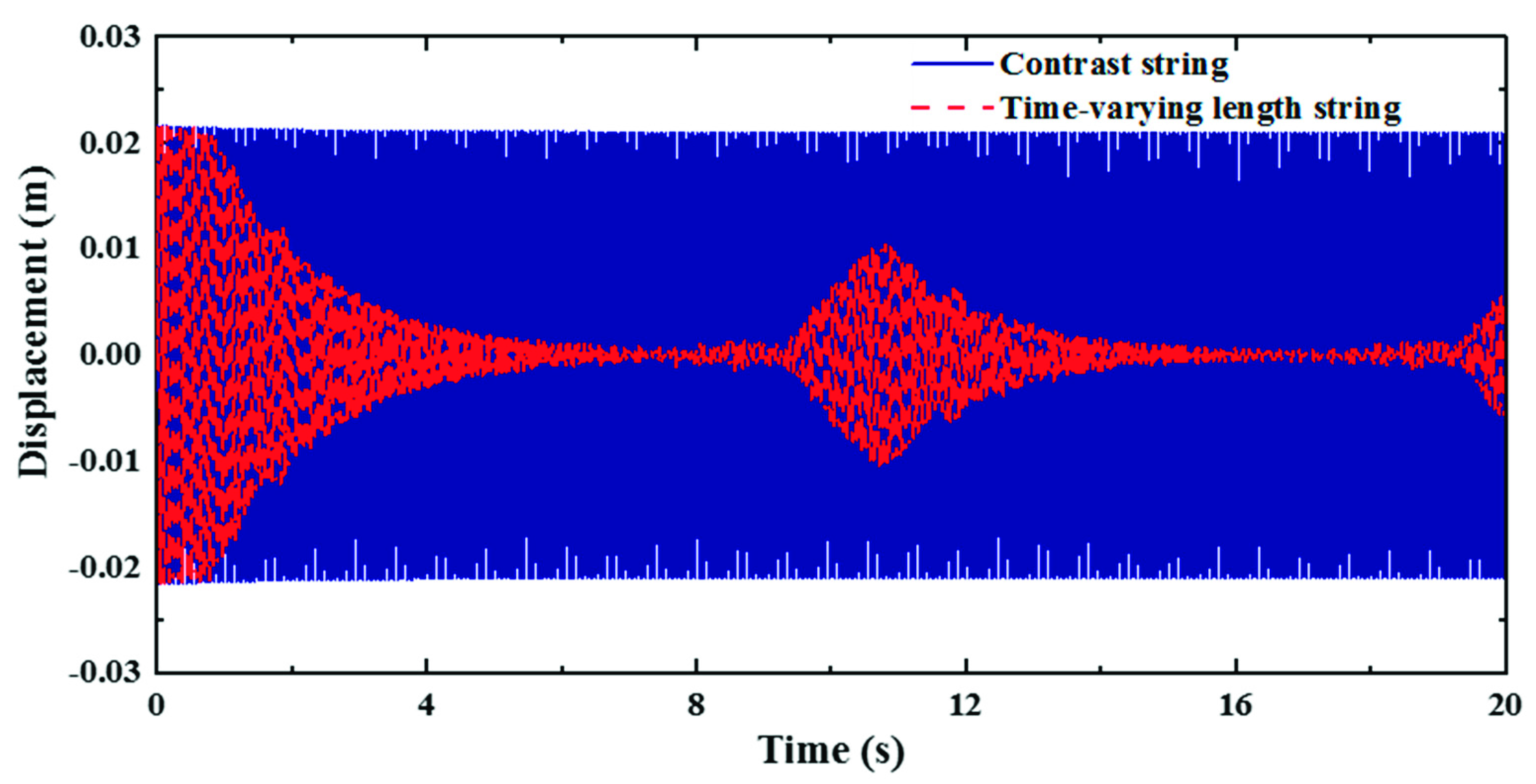
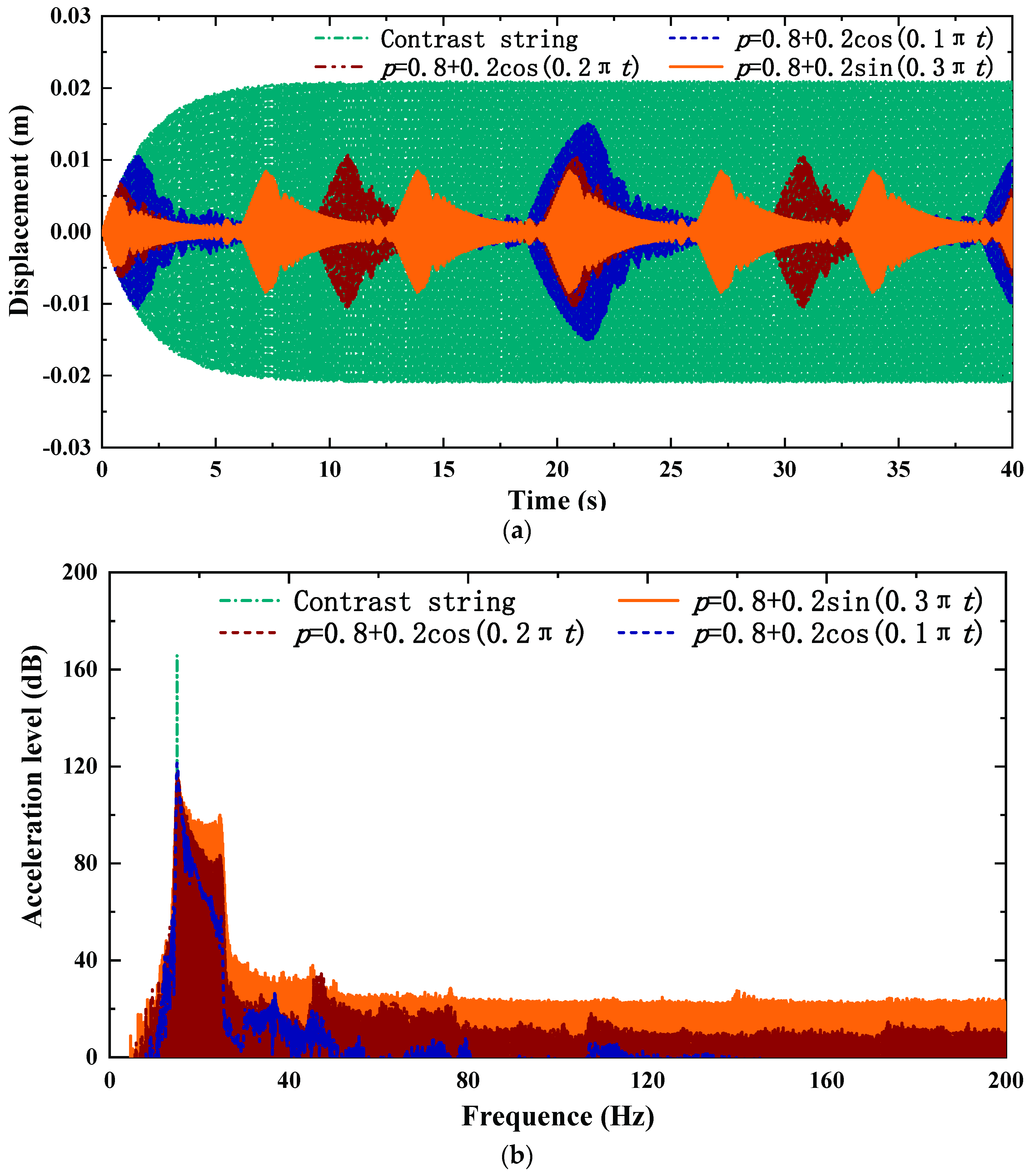
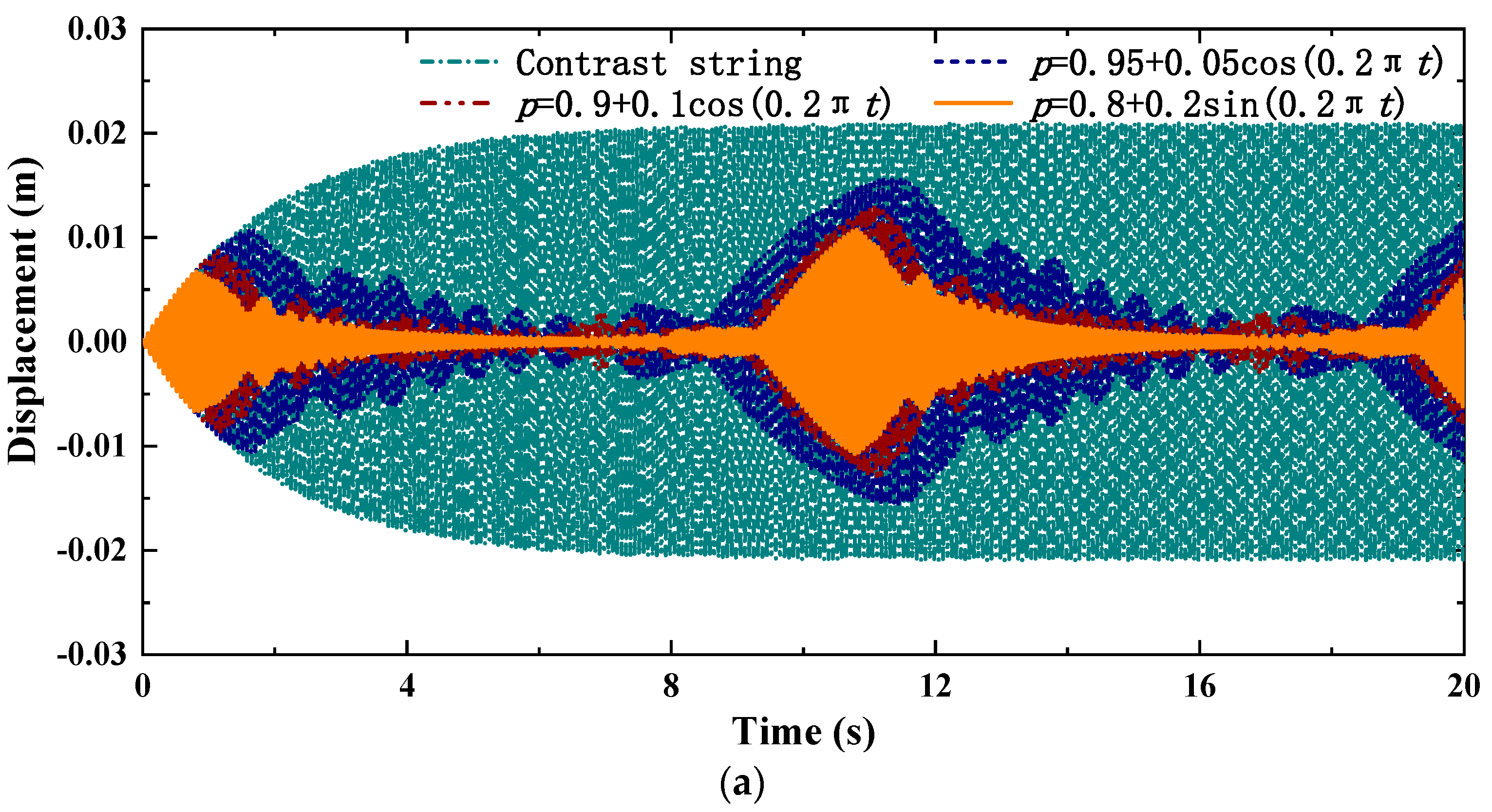
4.3. Influences of the Time-Varying Range and Time-Varying Frequency

In this section, the influences of the time-varying frequency and time-varying range on the vibration suppression performances are studied. The resonant frequency varies with the string length. Therefore, the time-varying range and time-varying frequency of string length can affect the variation characteristics of steady-state amplitude and frequency. The vibration comparison with different time-varying frequencies (0.05 Hz, 0.1 Hz, 0.15 Hz), is shown in Figure 11. The spectrums are converted from 20 s–40 s time-domain results. The maximum coefficient ranges of the last four terms in Equation (6) for these cases are −0.29 to 0.18, 0 to 0.06, −0.24 to 0.24 and −0.24 to 0.24. The coefficients of the last four terms are obviously less than 1. The vibration comparison with different time-varying ranges (0.1 m, 0.2 m, 0.4 m) is shown in Figure 12. Figure 12b gives the spectrums converted from 10 s–20 s time-domain results. In Figure 11, the length time-varying frequency can affect the vibration period and maximum amplitude. The effect of the time-varying frequency on the peak attenuation is slight. The larger time-varying frequency leads to a greater peak energy dispersion performance. Because the greater speed of change leads to the shorter time of resonance frequency stays near the excitation frequency. In Figure 12, the amplitude decreases as the time-varying range increases. The peak energy dispersion performance is greater in the larger time-varying range.

5. Conclusions

In this paper, a time-varying string length method for suppress string vibration is studied. To solve the nonlinear dynamic model of time-varying length string, the dimensionless variables are introduced to separate the variables. The finite difference method is used to obtain the numerical solution of the time function. The vibration suppression performances of the method for free vibration and forced vibration are analyzed. The influences of the time-varying frequency and time-varying range of length are studied. The following conclusions are obtained.

(1)

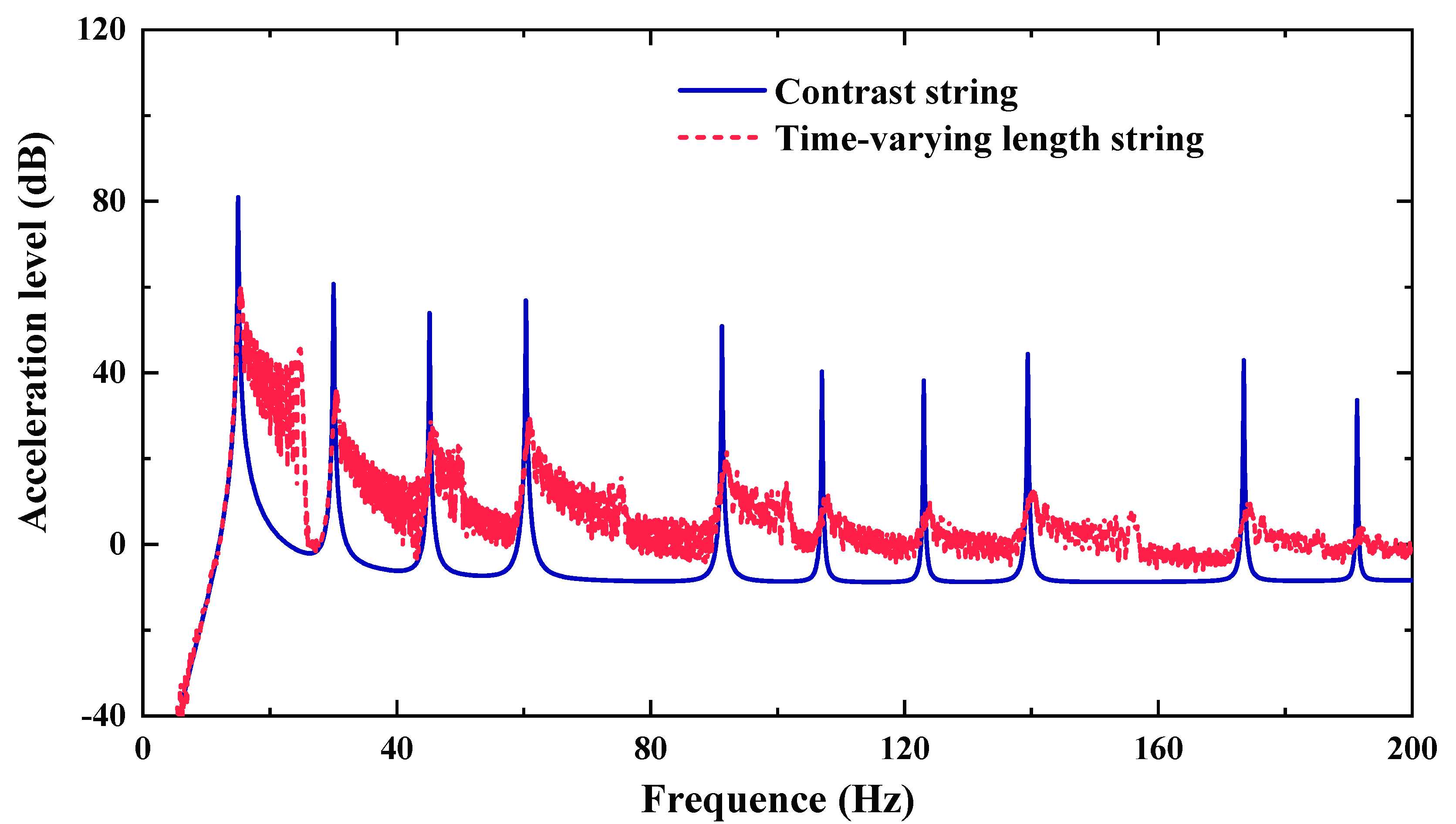
The time-varying string length method can change the free vibration frequencies. Each modal peak decreases significantly at the same time, while the responses in other frequency bands increase. The reason is that the time-varying modal frequency disperses the peak energy to the nearby frequency band. The damping reduces the peak attenuations, but it can consume the energy dispersed to other frequency bands.

(2)

The time-varying string length method causes the change of resonant frequency to suppress the resonance excited by single frequency, which disperses the resonant peak energy to other frequency bands. This method can effectively suppress multi-modal resonances of string at the same time.

(3)

The larger the time-varying frequency and time-varying range, the greater the peak attenuations and the better the resonant peak energy dispersion performance.