Towards a Fault Diagnosis Method for Rolling Bearings with Time-Frequency Region-Based Convolutional Neural Network
Abstract
1. Introduction
2. Preliminaries
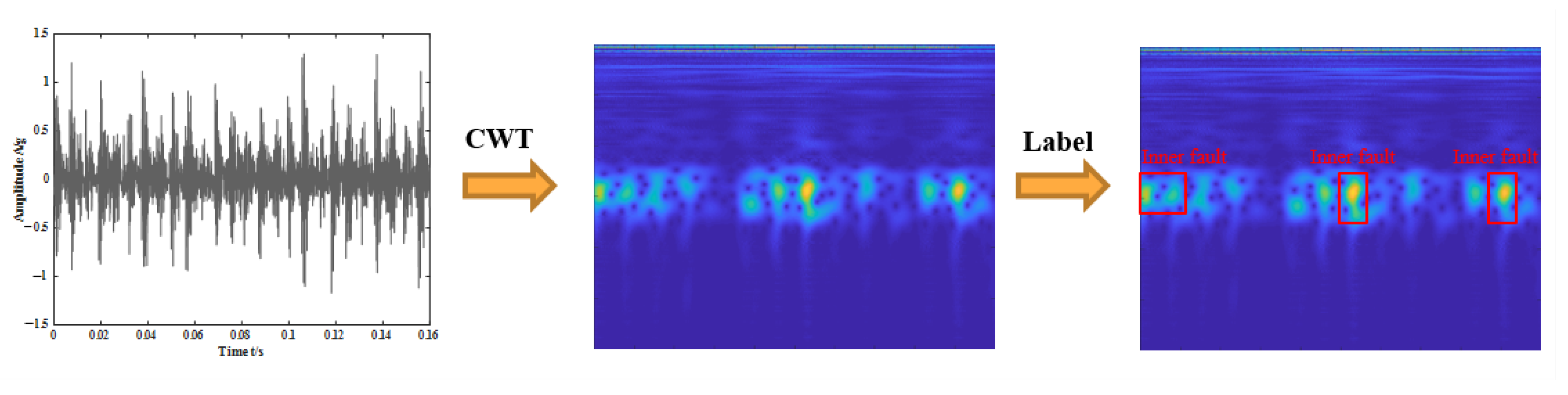
2.1. Time-Frequency Processing with Wavelet Transform
2.2. The Framework of Faster RCNN
2.2.1. Feature Extraction
2.2.2. Region Proposal Network
2.2.3. RoIs Pooling
2.2.4. RCNN Fully Connected Network
3. Time-Frequency RCNN
3.1. Backbone Network with Attention
3.1.1. Attention Module
3.1.2. Architecture of the Attention ResNet
3.2. Classification Strategy
3.3. Overview of Time-Frequency RCNN
4. Fault Diagnosis Framework Based on TF-RCNN
5. Case Analysis
5.1. Case 1: Diagnosis for Artificial Damages
5.1.1. Dataset Description
5.1.2. Model Selection
5.1.3. Result Analysis
5.2. Case 2: Diagnosis for Realistic Damages
5.2.1. Dataset Description
5.2.2. Result Analysis
5.2.3. The Contribution of Attention
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587–106626. [Google Scholar] [CrossRef]
- Sharma, A.; Upadhyay, N.; Kankar, P.K.; Amarnath, M. Nonlinear dynamic investigations on rolling element bearings: A review. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Zhao, H.M.; Liu, H.D.; Jin, Y.; Dang, X.J.; Deng, W. Feature extraction for data-driven remaining useful life prediction of rolling bearings. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Tang, J.; Wu, J.; Hu, B.; Liu, J. Towards a fault diagnosis method for rolling bearing with bi-directional deep belief network. Appl. Acoust. 2022, 192, 108727. [Google Scholar] [CrossRef]
- Liang, H.P.; Zhao, X.Q. Rolling bearing fault diagnosis based on one-dimensional dilated convolution network with residual connection. IEEE Access 2021, 9, 31078–31091. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z.; Xiao, H.; Yu, X. Quaternion singular spectrum analysis using convex optimization and its application to fault diagnosis of rolling bearing. Measurement 2017, 103, 321–332. [Google Scholar] [CrossRef]
- Lai, Z.H.; Wang, S.B.; Zhang, G.Q.; Zhang, C.L.; Zhang, J.W. Rolling bearing fault diagnosis based on adaptive multiparameter-adjusting bistable stochastic resonance. Shock Vib. 2020, 2020, 6096024. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, B.; Xiang, L.; Li, W.; Zhu, C. Information interval spectrum: A novel methodology for rolling-element bearing diagnosis. Measurement 2021, 183, 109899–109916. [Google Scholar] [CrossRef]
- He, Q.; Song, H.; Ding, X. Sparse signal reconstruction based on time-frequency manifold for rolling element bearing fault signature enhancement. IEEE Trans. Instrum. Meas. 2016, 65, 482–491. [Google Scholar] [CrossRef]
- De Moura, E.P.; Souto, C.R.; Silva, A.A.; Irmão, M.A.S. Evaluation of principal component analysis and neural network performance for bearing fault diagnosis from vibration signal processed by rs and df analyses. Mech. Syst. Signal Process. 2011, 25, 1765–1772. [Google Scholar] [CrossRef]
- Ai, Y.-T.; Guan, J.-Y.; Fei, C.-W.; Tian, J.; Zhang, F.-L. Fusion information entropy method of rolling bearing fault diagnosis based on n-dimensional characteristic parameter distance. Mech. Syst. Signal Process. 2017, 88, 123–136. [Google Scholar] [CrossRef]
- Moura, M.D.; Zio, E.; Lins, I.D.; Droguett, E. Failure and reliability prediction by support vector machines regression of time series data. Reliab. Eng. Syst. Saf. 2011, 96, 1527–1534. [Google Scholar] [CrossRef]
- Chen, F.; Cheng, M.; Tang, B.; Chen, B.; Xiao, W. Pattern recognition of a sensitive feature set based on the orthogonal neighborhood preserving embedding and adaboost svm algorithm for rolling bearing early fault diagnosis. Meas. Sci. Technol. 2020, 31, 105007. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H.; Zhang, X.; Wang, H. Optimal multi-kernel local fisher discriminant analysis for feature dimensionality reduction and fault diagnosis. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2021, 235, 1041–1056. [Google Scholar] [CrossRef]
- Wan, L.; Gong, K.; Zhang, G.; Yuan, X.; Li, C.; Deng, X. An efficient rolling bearing fault diagnosis method based on spark and improved random forest algorithm. IEEE Access 2021, 9, 37866–37882. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.G.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L. A new two-level hierarchical diagnosis network based on convolutional neural network. IEEE Trans. Instrum. Meas. 2020, 69, 330–338. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z.; Li, Y.; Tao, J.; Mao, Q.; Zhang, X. An intelligent diagnosis method for machine fault based on federated learning. Appl. Sci. 2021, 11, 12117. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, T.Z.; Jiang, B.; Yang, X. Intelligent bearing fault diagnosis using pca-dbn framework. Neural Comput. Appl. 2020, 32, 10773–10781. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Wang, F.; Wang, Y. Rolling bearing fault diagnosis using adaptive deep belief network with dual-tree complex wavelet packet. ISA Trans. 2017, 69, 187–201. [Google Scholar] [CrossRef]
- Guo, J.; Zheng, P. A method of rolling bearing fault diagnose based on double sparse dictionary and deep belief network. IEEE Access 2020, 8, 116239–116253. [Google Scholar] [CrossRef]
- Song, X.; Zhu, D.; Liang, P.; An, L. A new bearing fault diagnosis method using elastic net transfer learning and lstm. J. Intell. Fuzzy Syst. 2021, 40, 12361–12369. [Google Scholar] [CrossRef]
- Liu, W.; Guo, P.; Ye, L. A low-delay lightweight recurrent neural network (llrnn) for rotating machinery fault diagnosis. Sensors 2019, 19, 3109. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhou, L.; Zhao, W.; Fan, Y.; Ding, X.; Yuan, X. Zero-shot learning for compound fault diagnosis of bearings. Expert Syst. Appl. 2022, 190, 116197. [Google Scholar] [CrossRef]
- Shi, Z.; Chen, J.; Zi, Y.; Zhou, Z. A novel multitask adversarial network via redundant lifting for multicomponent intelligent fault detection under sharp speed variation. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Ma, P.; Zhang, H.; Fan, W.; Wang, C.; Wen, G.; Zhang, X. A novel bearing fault diagnosis method based on 2d image representation and transfer learning-convolutional neural network. Meas. Sci. Technol. 2019, 30, 055402. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Region-based convolutional networks for accurate object detection and segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 142–158. [Google Scholar] [CrossRef] [PubMed]
- Konar, P.; Chattopadhyay, P. Bearing fault detection of induction motor using wavelet and support vector machines (svms). Appl. Soft Comput. 2011, 11, 4203–4211. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using continuous wavelet transform. Appl. Soft Comput. 2011, 11, 2300–2312. [Google Scholar] [CrossRef]
- Su, W.; Wang, F.; Zhu, H.; Zhang, Z.; Guo, Z. Rolling element bearing faults diagnosis based on optimal morlet wavelet filter and autocorrelation enhancement. Mech. Syst. Signal Process. 2010, 24, 1458–1472. [Google Scholar] [CrossRef]
- Tang, B.; Liu, W.; Song, T. Wind turbine fault diagnosis based on morlet wavelet transformation and wigner-ville distribution. Renew. Energy 2010, 35, 2862–2866. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Computer Vision—ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 3–19. [Google Scholar]
- Case Western Reserve University. Available online: http://www.eecs.case.edu/laboratory/bearing/download.htm (accessed on 1 July 2022).
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. In Proceedings of the European Conference of the Prognostics and health Management, Bilbao, Spain, 5–8 July 2016; pp. 5–8. [Google Scholar]















| Bearing Working Condition | Fault Diameter | The Number of Samples |
|---|---|---|
| Normal | — | 200 |
| Inner race fault | 0.1778 | 200 |
| 0.3556 | 200 | |
| 0.5334 | 200 | |
| Outer race fault | 0.1778 | 200 |
| 0.3556 | 200 | |
| 0.5334 | 200 | |
| Ball fault | 0.1778 | 200 |
| 0.3556 | 200 | |
| 0.5334 | 200 |
| Parameter Description | Value |
|---|---|
| Input size | [600, 600] |
| Epochs | 100 |
| Learning rate | |
| Batch size | 4 |
| Optimizer | Adam |
| Attention combining strategy | channel + spatial |
| The base anchor size | 16 |
| Dropout | 0.4 |
| NMS threshold | 0.5 |
| Approach | Backbone | mAP | Diagnosis Accuracy | Standard Deviation |
|---|---|---|---|---|
| Standard Faster RCNN | ResNet50 | 86.34% | 90.13% | 0.61 |
| ResNet101 | 88.62% | 91.06% | 0.54 | |
| SSD | ResNet50 | 87.81% | 92.52% | 0.60 |
| ResNet101 | 88.58% | 94.71% | 0.44 | |
| Yolo | ResNet50 | 85.35% | 91.55% | 0.30 |
| ResNet101 | 85.79% | 93.24% | 0.37 | |
| Proposed method | ResNet50 with attention | 89.09% | 99.74% | 0.36 |
| ResNet101 with attention | 91.13% | 99.61% | 0.34 |
| Model | Structure | Hyperparameter |
|---|---|---|
| CNN | ResNet50 Dense (10) | Dropout = 0.5 Batch size = 32 Optimizer = Adam |
| DBN | three RBMs Structure [1000, 800, 500, 100, 10] Softmax | Learning rate = 0.001 Dropout = 0.5 Batch size = 32 Optimizer = Adam |
| DAE | three hidden layers. structure [1000, 800, 500, 100, 10] Softmax | Learning rate = 0.003 Dropout = 0.4 Batch size = 32 Optimizer = Adam |
| Approach | Diagnosis Accuracy | Standard Deviation | |
|---|---|---|---|
| CNN | 93.78% | 0.63 | |
| DBN | 91.89% | 0.57 | |
| DAE | 94.17% | 0.55 | |
| Proposed method | ResNet50 with attention | 99.74% | 0.36 |
| ResNet101 with attention | 99.64% | 0.34 | |
| Parameter Description | Value |
|---|---|
| Bearing type | 6203 |
| Rotational speed | 1500 rpm |
| Load torque | 0.7 Nm |
| Radial force | 1000 N |
| Sampling time | 4 s |
| Sampling rate | 64 kHz |
| Data Index | Damage Mode | Component | Fault Diameter (mm) | Characteristic of Damage * | Size of Training Testing Samples |
|---|---|---|---|---|---|
| Inner1 | Fatigue: Pitting | Inner race | 6 | A | 180/50 |
| Inner2 | Fatigue: Pitting | Inner race | 1 | B | 180/50 |
| Inner3 | Fatigue: Pitting | Inner race | 2.5 | A | 180/50 |
| Outer1 | Plastic deform: Indentations | Outer race | <1 | A | 180/50 |
| Outer2 | Fatigue. Pitting | Outer race | 2&3 | B | 180/50 |
| Normal | — | — | — | — | 180/50 |
| Approach | Backbone | mAP | Diagnosis Accuracy | Standard Deviation |
|---|---|---|---|---|
| Standard Faster RCNN | ResNet50 | 68.77% | 80.51% | 0.79 |
| ResNet101 | 70.26% | 83.19% | 0.61 | |
| SSD | ResNet50 | 71.65% | 81.99% | 0.68 |
| ResNet101 | 72.18% | 82.70% | 0.50 | |
| Yolo | ResNet50 | 64.05% | 80.36% | 0.49 |
| ResNet101 | 69.44% | 82.94% | 0.43 | |
| Proposed method | ResNet50 with attention | 75.09% | 89.01% | 0.44 |
| ResNet101 with attention | 79.34% | 89.31% | 0.51 |
| Approach | Diagnosis Accuracy | Standard Deviation | |
|---|---|---|---|
| CNN | 85.98% | 0.20 | |
| DBN | 82.38% | 0.33 | |
| DAE | 82.69% | 0.78 | |
| Proposed method | ResNet50 with attention | 89.01% | 0.44 |
| ResNet101 with attention | 89.31% | 0.51 | |
| Approach | Inner1 | Inner2 | Inner3 | Outer1 | Outer2 | Normal |
|---|---|---|---|---|---|---|
| CNN | 84.68% | 82.53% | 88.47% | 88.22% | 76.35% | 90.87% |
| Standard Faster RCNN | 81.41% | 82.66% | 80.71% | 77.47% | 73.41% | 88.63% |
| Proposed method | 90.98% | 90.11% | 90.25% | 89.67% | 79.55% | 93.49% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Wu, J.; Hu, B.; Qing, J. Towards a Fault Diagnosis Method for Rolling Bearings with Time-Frequency Region-Based Convolutional Neural Network. Machines 2022, 10, 1145. https://doi.org/10.3390/machines10121145
Tang J, Wu J, Hu B, Qing J. Towards a Fault Diagnosis Method for Rolling Bearings with Time-Frequency Region-Based Convolutional Neural Network. Machines. 2022; 10(12):1145. https://doi.org/10.3390/machines10121145
Chicago/Turabian StyleTang, Jiahui, Jimei Wu, Bingbing Hu, and Jiajuan Qing. 2022. "Towards a Fault Diagnosis Method for Rolling Bearings with Time-Frequency Region-Based Convolutional Neural Network" Machines 10, no. 12: 1145. https://doi.org/10.3390/machines10121145
APA StyleTang, J., Wu, J., Hu, B., & Qing, J. (2022). Towards a Fault Diagnosis Method for Rolling Bearings with Time-Frequency Region-Based Convolutional Neural Network. Machines, 10(12), 1145. https://doi.org/10.3390/machines10121145







