Weak Fault Feature Extraction of Axle Box Bearing Based on Pre-Identification and Singular Value Decomposition
Abstract
:1. Introduction
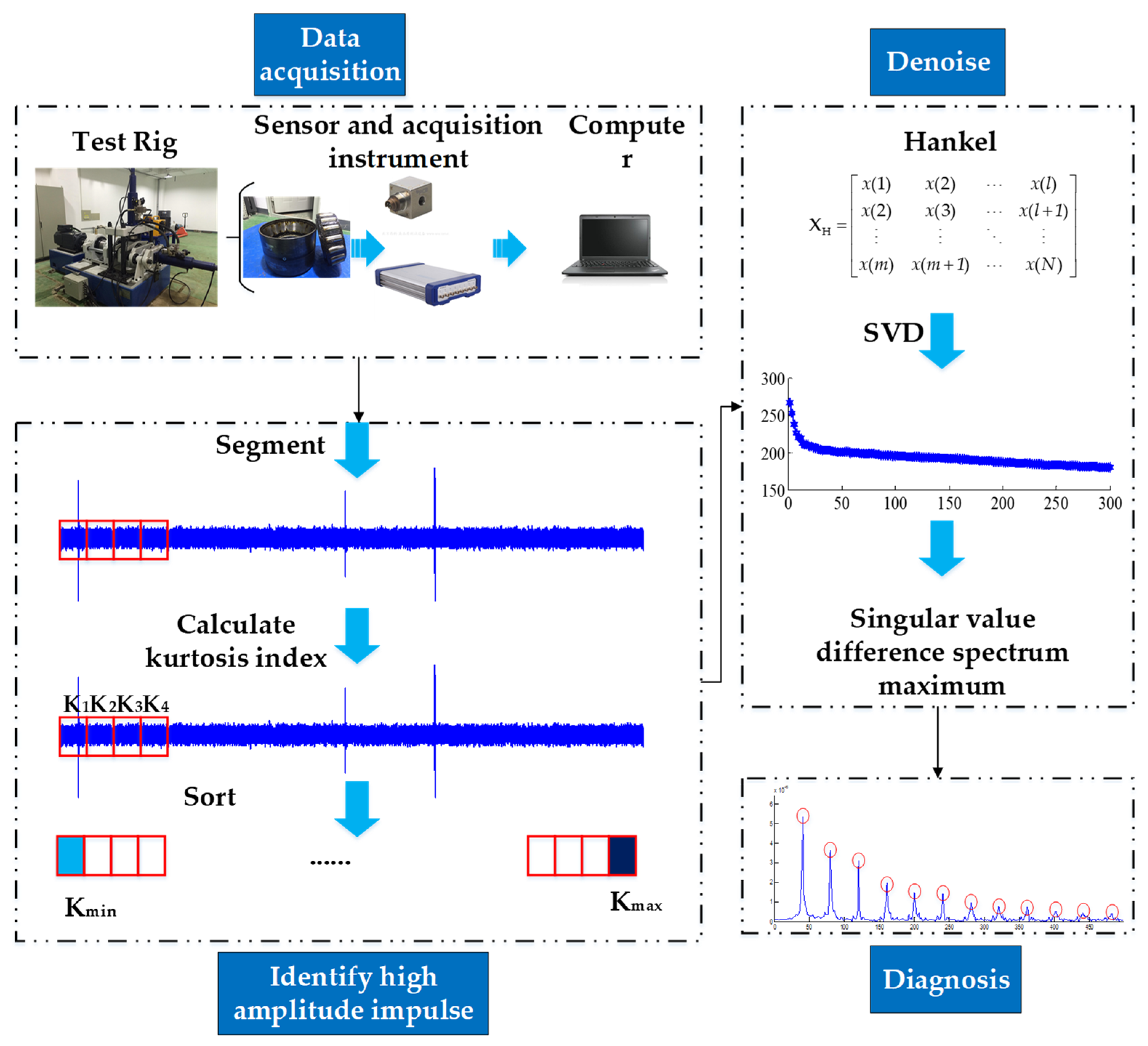
2. Pre-Identifying Singular Value Decomposition Method
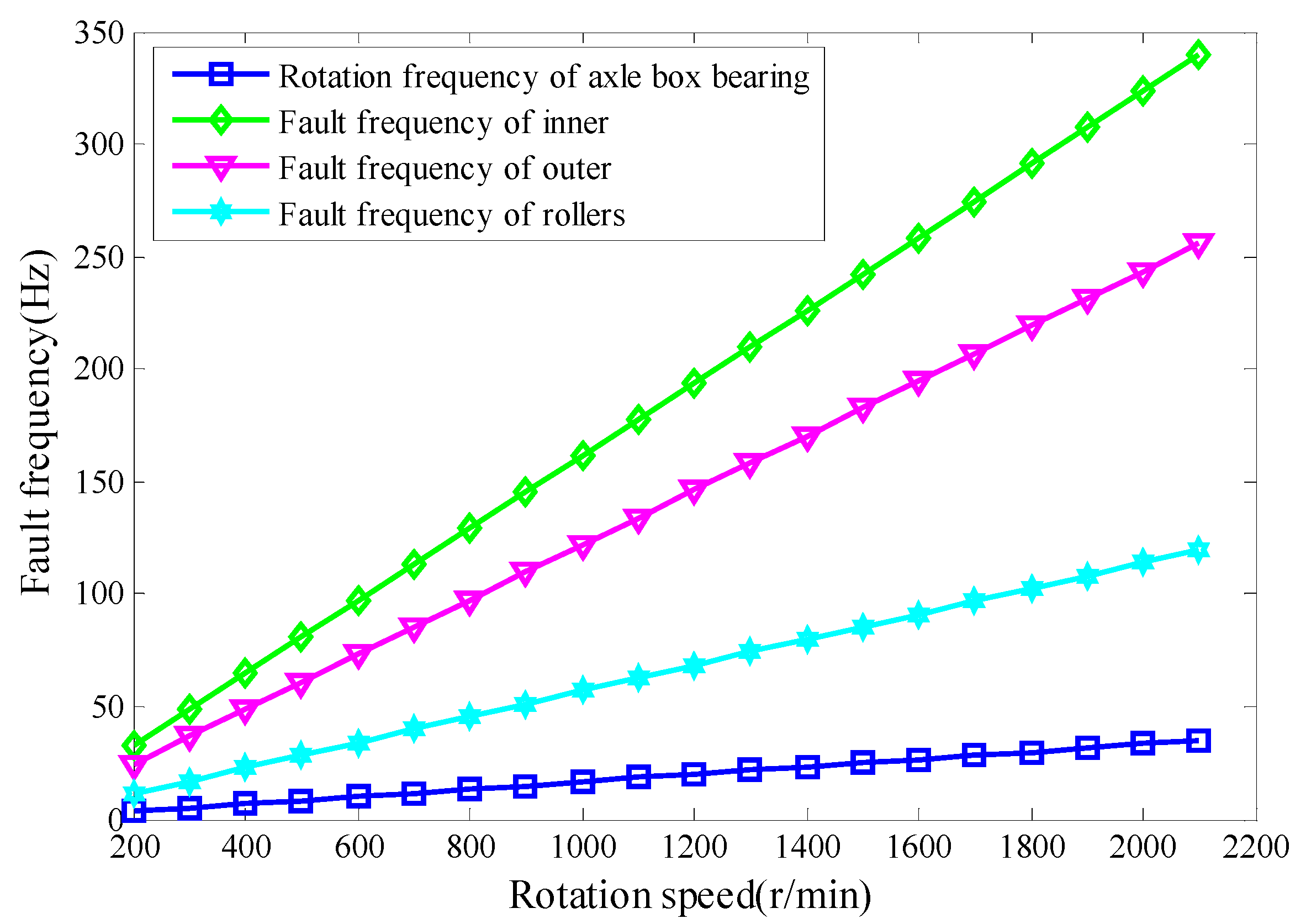
2.1. Failure Characteristic Frequency of Axle Box Bearings
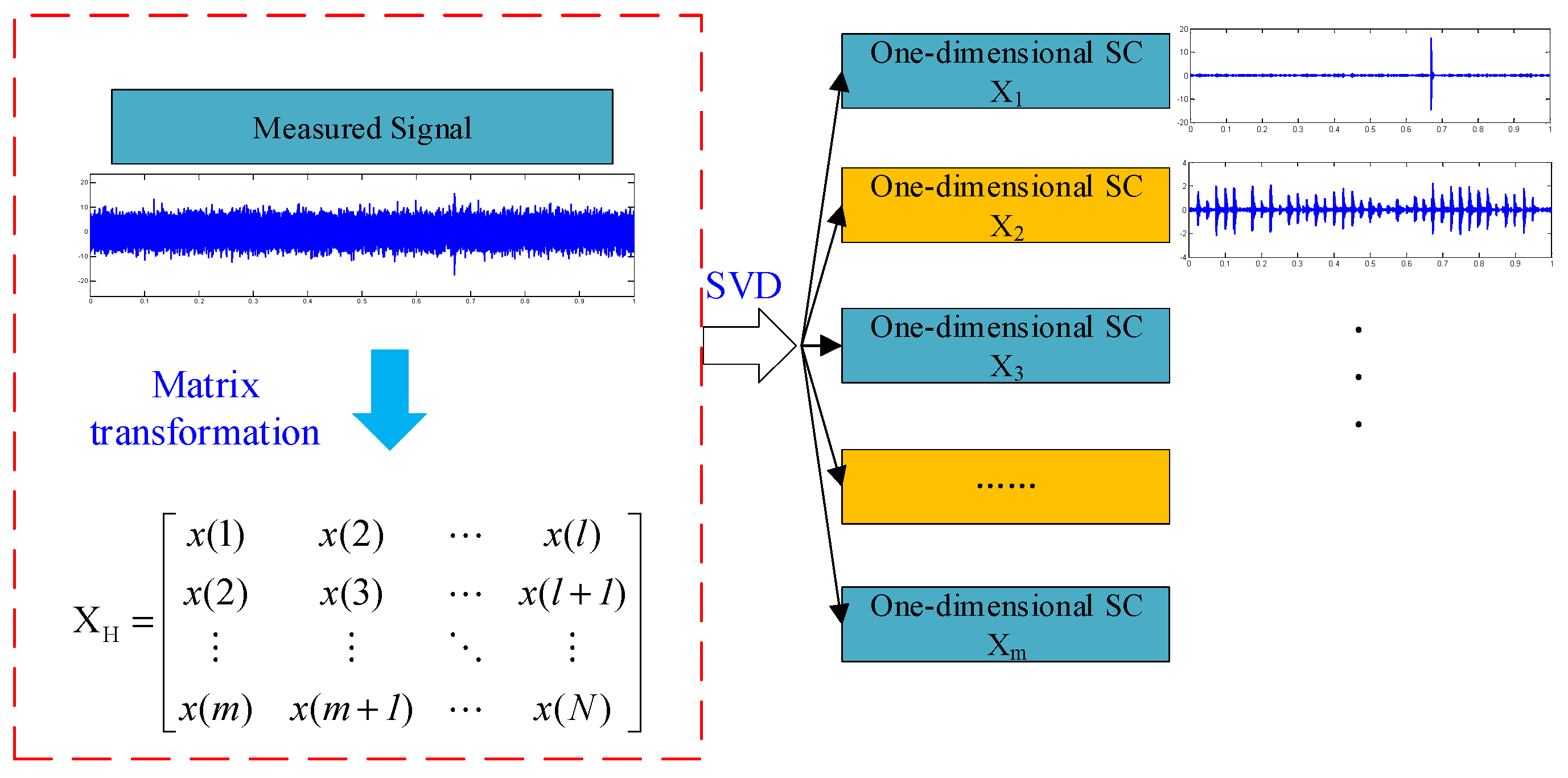
2.2. Singular Value Decomposition Theory
2.3. Pre-Identification of Singular Value Decomposition
| Algorithm 1 Pre-identification |
| Inputs: X-input data 1: Segment X in seconds Xi (i = 1, 2, 3, … t) 2: For i = 1 to t do 3: Ki←kurtosis (Xi) 4: end for 5: Sort Ki from small to large 6: if the bearing speed ≥900 r/min 7: return the signal segment with the smallest kurtosis value 8: else 9: return the signal segment with the kurtosis value in the middle 10: end if Output: Xi |
3. Simulation Analysis and Experimental Validation
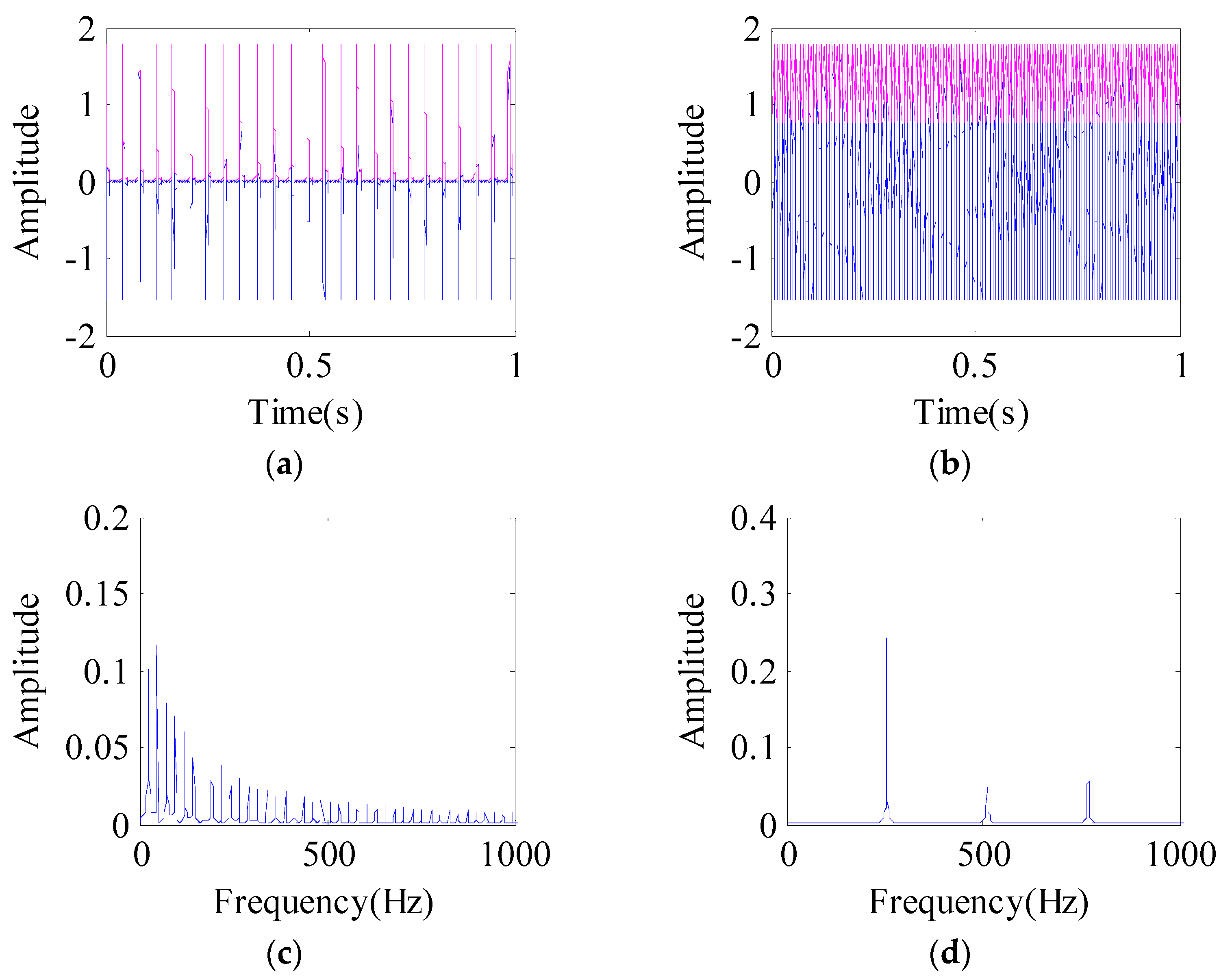
3.1. Simulation Analysis Based on the Formula
3.2. Data Validation Based on the Railway Bearing Comprehensive Test Bench
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Papaelias, M.; Amini, A.; Huang, Z.; Vallely, P.; Dias, D.C.; Kerkyras, S. Online condition monitoring of rolling stock wheels and axle bearings. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 709–723. [Google Scholar] [CrossRef]
- Ding, J. Fault detection of a wheelset bearing in a high-speed train using the shock-response convolutional sparse-coding technique. Measurement 2018, 117, 108–124. [Google Scholar] [CrossRef]
- Deng, F.; Qiang, Y.; Yang, S.; Hao, R.; Liu, Y. Sparse representation of parametric dictionary based on fault impact matching for wheelset bearing fault diagnosis. ISA Trans. 2021, 110, 368–378. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Song, D.; Xu, X.; Lei, L. A Fault Diagnosis Method of Bogie Axle Box Bearing Based on Spectrum Whitening Demodulation. Sensors 2020, 20, 7155. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yang, S.; Liu, Y.; Lin, J.; Gu, X. Adaptive correlated Kurtogram and its applications in wheelset-bearing system fault diagnosis. Mech. Syst. Sig. Process. 2021, 154, 107511. [Google Scholar] [CrossRef]
- Liu, Z.; Peng, D.; Zuo, M.J.; Xia, J.; Qin, Y. Improved Hilbert-Huang transform with soft sifting stopping criterion and its application to fault diagnosis of wheelset bearings. ISA Trans. 2022, 125, 426–444. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Song, H.; Miao, B.; Zhang, W.; Xiong, Q. Improved multiscale weighted-dispersion entropy and its application in fault diagnosis of train bearing. Meas. Sci. Technol. 2021, 32, 075002. [Google Scholar] [CrossRef]
- Gu, X.; Yang, S.; Liu, Y.; Hao, R.; Liu, Z. Multi-sparsity-based blind deconvolution and its application to wheelset bearing fault detection. Measurement 2022, 199, 111449. [Google Scholar] [CrossRef]
- Ding, J.; Zhao, W.; Miao, B.; Lin, J. Adaptive sparse representation based on circular-structure dictionary learning and its application in wheelset-bearing fault detection. Mech. Syst. Sig. Process. 2018, 111, 399–422. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Ding, S.X.; Huang, B. Data-Driven Fault Diagnosis for Traction Systems in High-Speed Trains: A Survey, Challenges, and Perspectives. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1700–1716. [Google Scholar] [CrossRef]
- Entezami, M.; Roberts, C.; Weston, P.; Stewart, E.; Amini, A.; Papaelias, M. Perspectives on railway axle bearing condition monitoring. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 17–31. [Google Scholar] [CrossRef]
- Zhang, Q.; Ding, J.; Zhao, W. An Adaptive Demodulation Band Segmentation Method to Optimize Spectral Boundary and Its Application for Wheelset-Bearing Fault Detection. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Yi, C.; Li, Y.; Huo, X.; Tsui, K.-L. A promising new tool for fault diagnosis of railway wheelset bearings: SSO-based Kurtogram. ISA Trans. 2022, 128, 498–512. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Selesnick, I.; Cai, G.; Feng, Y.; Sui, X.; Chen, X. Nonconvex Sparse Regularization and Convex Optimization for Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 7332–7342. [Google Scholar] [CrossRef]
- Chen, B.; Song, D.; Zhang, W.; Cheng, Y. A novel spectral coherence-based envelope spectrum for railway axle-box bearing damage identification. Struct. Health Monit. 2022. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Chen, Y.; Chen, Z.; Lin, J. Wheelset bearing fault detection using morphological signal and image analysis. Struct. Control Health Monit. 2020, 27, e2619. [Google Scholar] [CrossRef]
- Zhang, Q.; Ding, J.; Zhao, W. An adaptive boundary determination method for empirical wavelet transform and its application in wheelset-bearing fault detection in high-speed trains. Measurement 2021, 171, 108746. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, K.; Ma, C.; Cui, L.; Tian, W. Adaptive Kurtogram and its applications in rolling bearing fault diagnosis. Mech. Syst. Sig. Process. 2019, 130, 87–107. [Google Scholar] [CrossRef]
- Jin, Z.; He, D.; Wei, Z. Intelligent fault diagnosis of train axle box bearing based on parameter optimization VMD and improved DBN. Eng. Appl. Artif. Intell. 2022, 110, 104713. [Google Scholar] [CrossRef]
- He, L.; Yi, C.; Zhou, Q.; Lin, J.-H. Fast Convolutional Sparse Dictionary Learning Based on LocOMP and Its Application to Bearing Fault Detection. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Xing, Z.; Yi, C.; Lin, J.; Zhou, Q. Multi-component fault diagnosis of wheelset-bearing using shift-invariant impulsive dictionary matching pursuit and sparrow search algorithm. Measurement 2021, 178, 109375. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Sig. Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Xin, G.; Li, Z.; Jia, L.; Zhong, Q.; Dong, H.; Hamzaoui, N.; Antoni, J. Fault Diagnosis of Wheelset Bearings in High-Speed Trains Using Logarithmic Short-Time Fourier Transform and Modified Self-Calibrated Residual Network. IEEE Trans. Ind. Inf. 2022, 18, 7285–7295. [Google Scholar] [CrossRef]
- Wang, X.; Lu, Z.; Wei, J.; Zhang, Y. Fault Diagnosis for Rail Vehicle Axle-Box Bearings Based on Energy Feature Reconstruction and Composite Multiscale Permutation Entropy. Entropy 2019, 21, 865. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Yang, J.; Yao, D.; Wang, J. A New Method of Wheelset Bearing Fault Diagnosis. Entropy 2022, 24, 1381. [Google Scholar] [CrossRef]
- Peng, D.; Liu, Z.; Wang, H.; Qin, Y.; Jia, L. A Novel Deeper One-Dimensional CNN With Residual Learning for Fault Diagnosis of Wheelset Bearings in High-Speed Trains. IEEE Access 2019, 7, 10278–10293. [Google Scholar] [CrossRef]
- Lin, R.; Liu, Z.; Jin, Y. Instantaneous frequency estimation for wheelset bearings weak fault signals using second-order synchrosqueezing S-transform with optimally weighted sliding window. ISA Trans. 2021, 115, 218–233. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Lin, J.; Ding, J.; Huang, Y. A Novel Wheelset Bearing Fault Diagnosis Method Integrated CEEMDAN, Periodic Segment Matrix, and SVD. Shock Vib. 2018, 2018, 1382726. [Google Scholar] [CrossRef]
- Huang, D.; Yang, J.; Zhou, D.; Litak, G. Novel Adaptive Search Method for Bearing Fault Frequency Using Stochastic Resonance Quantified by Amplitude-Domain Index. IEEE Trans. Instrum. Meas. 2020, 69, 109–121. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, J.; Dong, G.; Liu, T.; Chen, G. Study on Hankel matrix-based SVD and its application in rolling element bearing fault diagnosis. Mech. Syst. Sig. Process. 2015, 52–53, 338–359. [Google Scholar] [CrossRef]
- Duan, R.; Liao, Y. Impulsive feature extraction with improved singular spectrum decomposition and sparsity-closing morphological analysis. Mech. Syst. Sig. Process. 2022, 180, 109436. [Google Scholar] [CrossRef]
- Cui, L.; Liu, Y.; Zhao, D.; Zhen, D. Egram Based SVD Method for Gear Fault Diagnosis. IEEE Sens. J. 2022, 22, 13188–13200. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Sig. Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Yu, L.; Antoni, J.; Leclere, Q. Spectral matrix completion by Cyclic Projection and application to sound source reconstruction from non-synchronous measurements. J. Sound Vib. 2016, 372, 31–49. [Google Scholar] [CrossRef]
- Buzzoni, M.; Antoni, J.; D’Elia, G. Blind deconvolution based on cyclostationarity maximization and its application to fault identification. J. Sound Vib. 2018, 432, 569–601. [Google Scholar] [CrossRef]


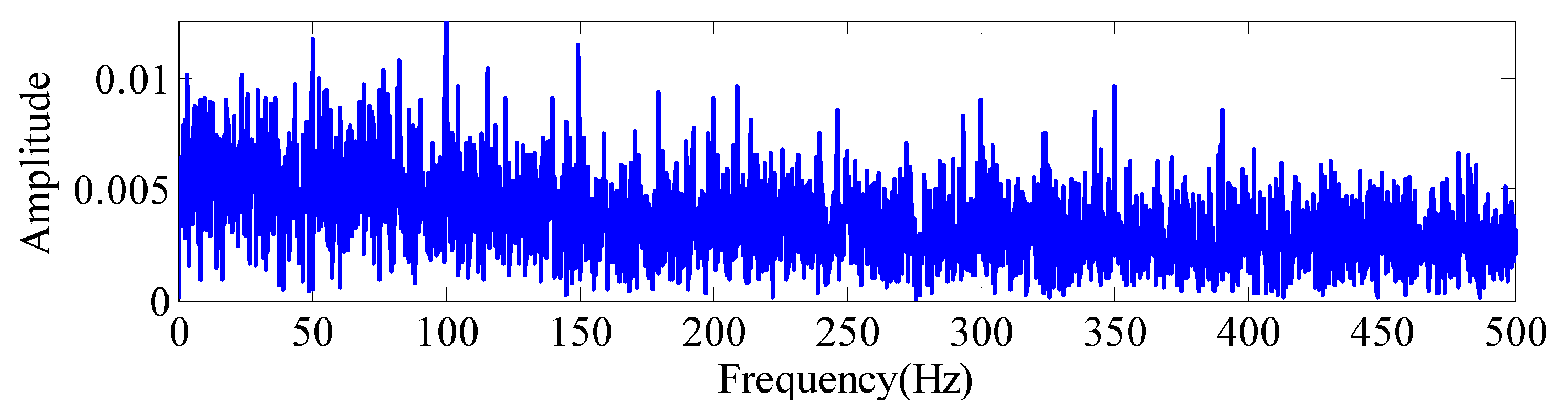
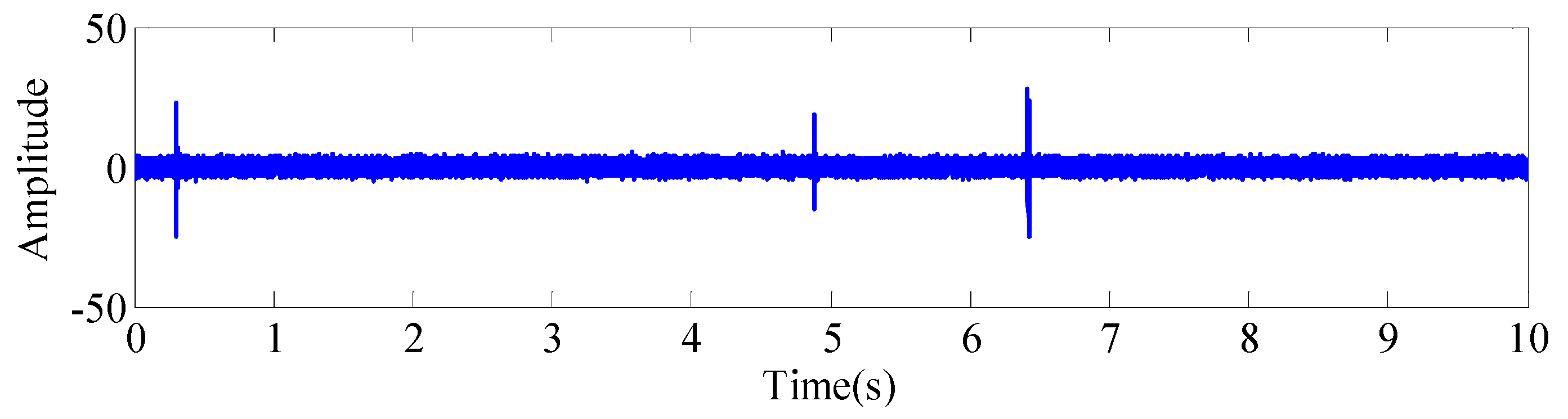
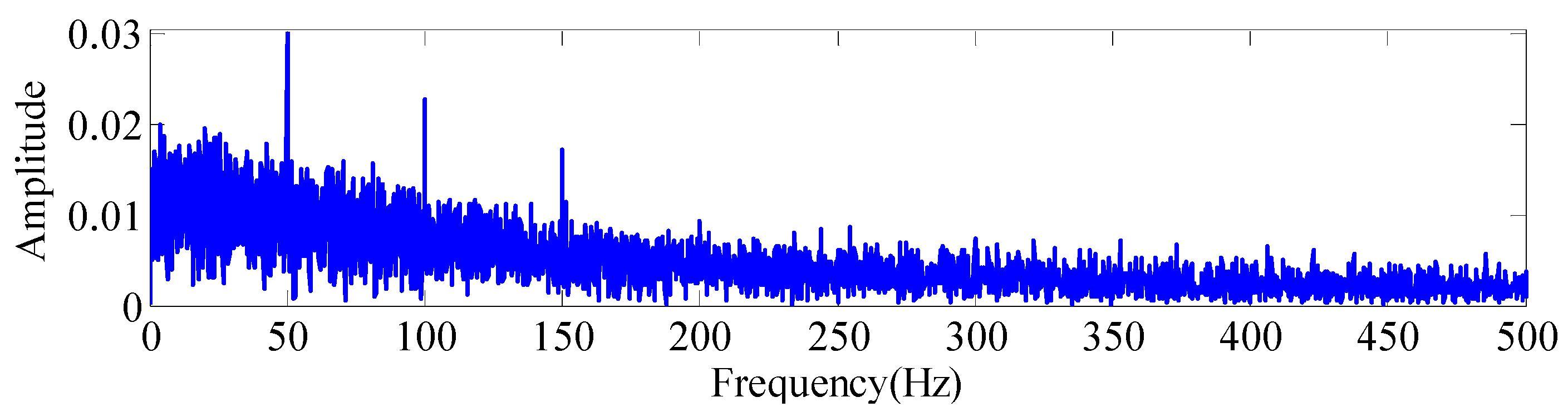


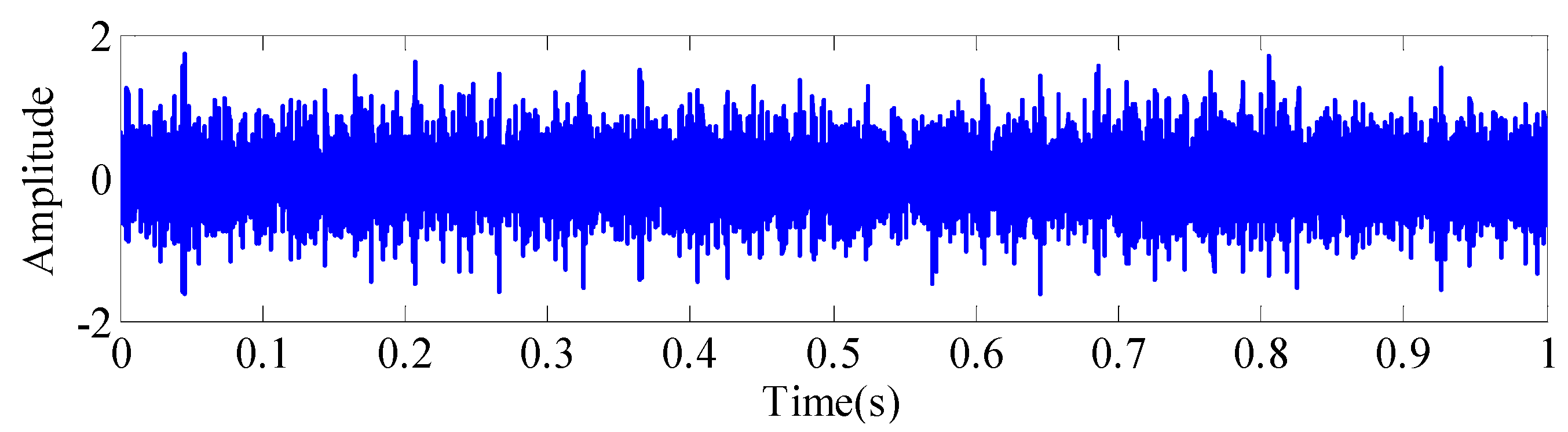


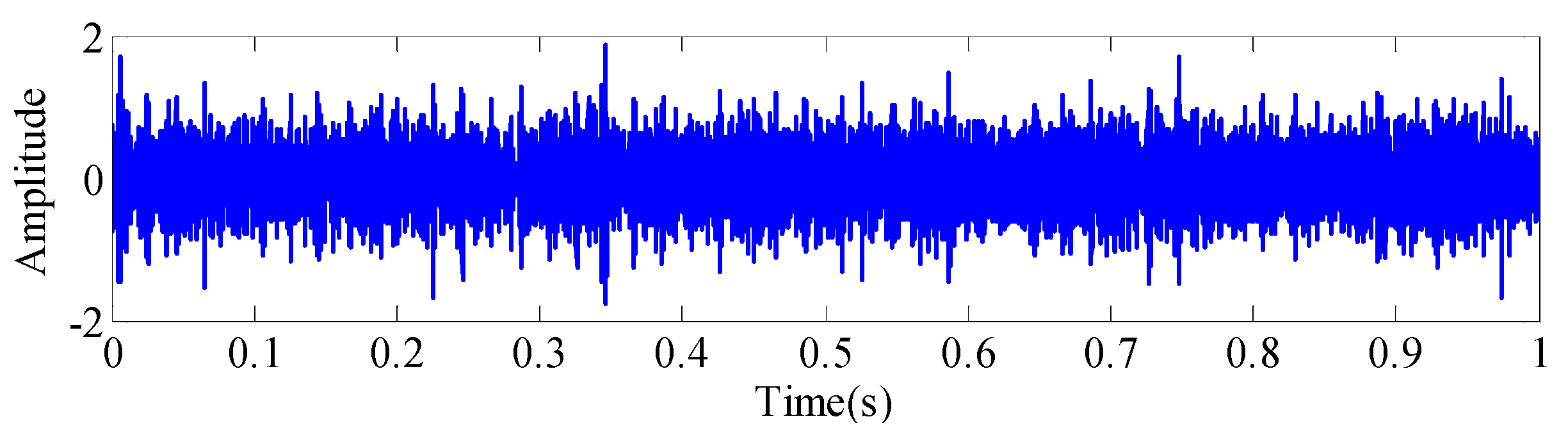
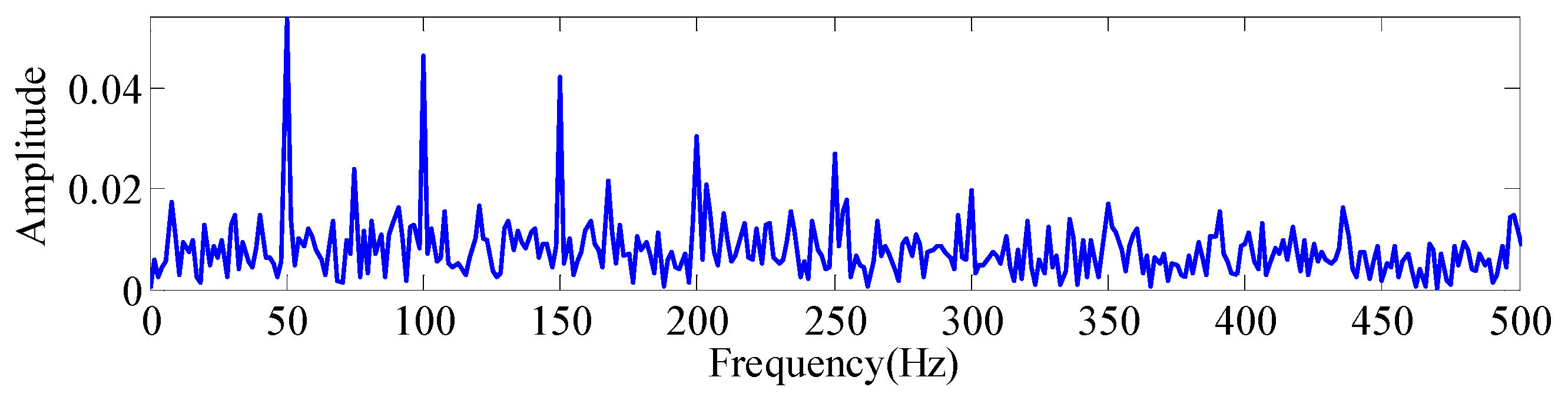
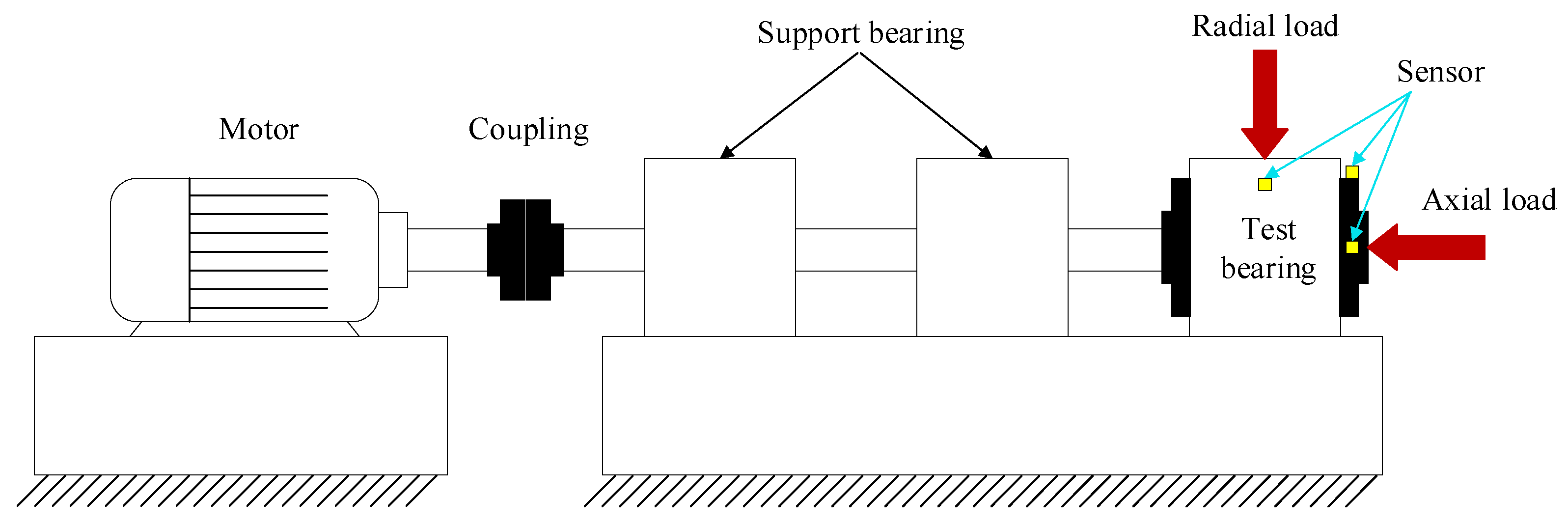


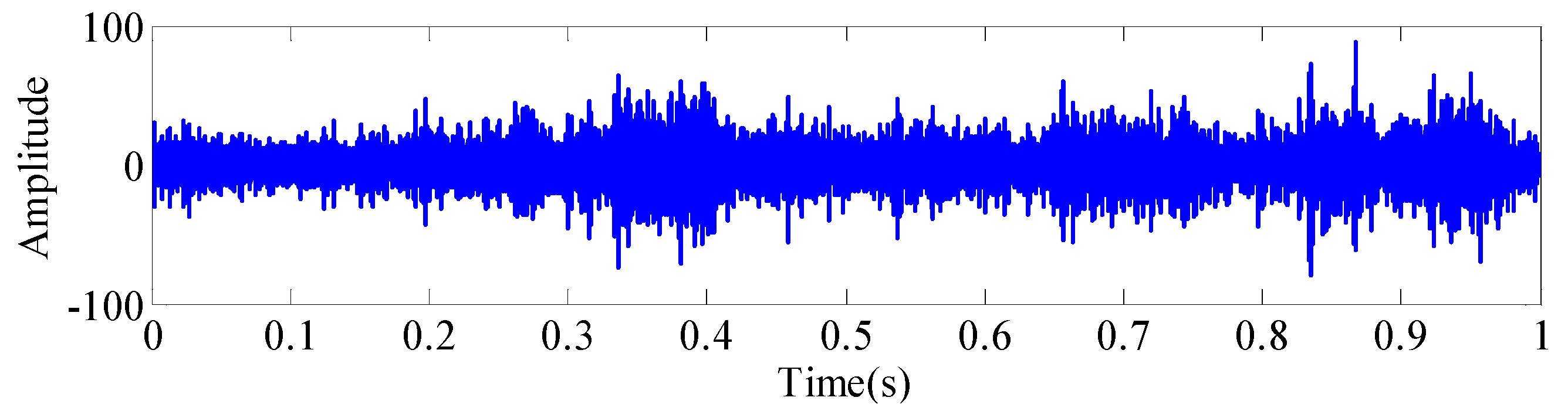
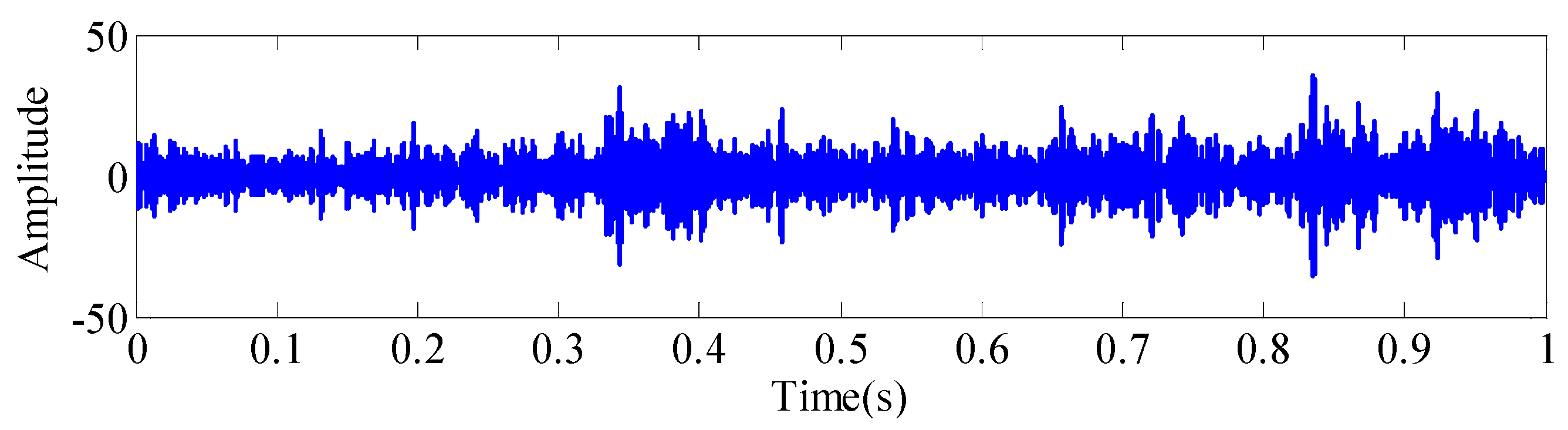

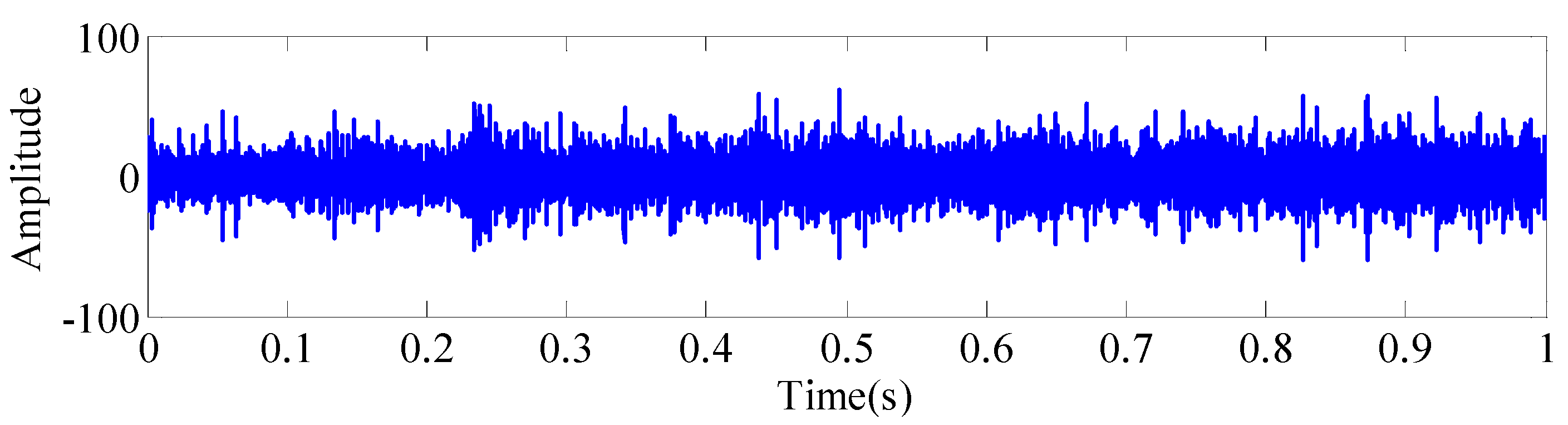
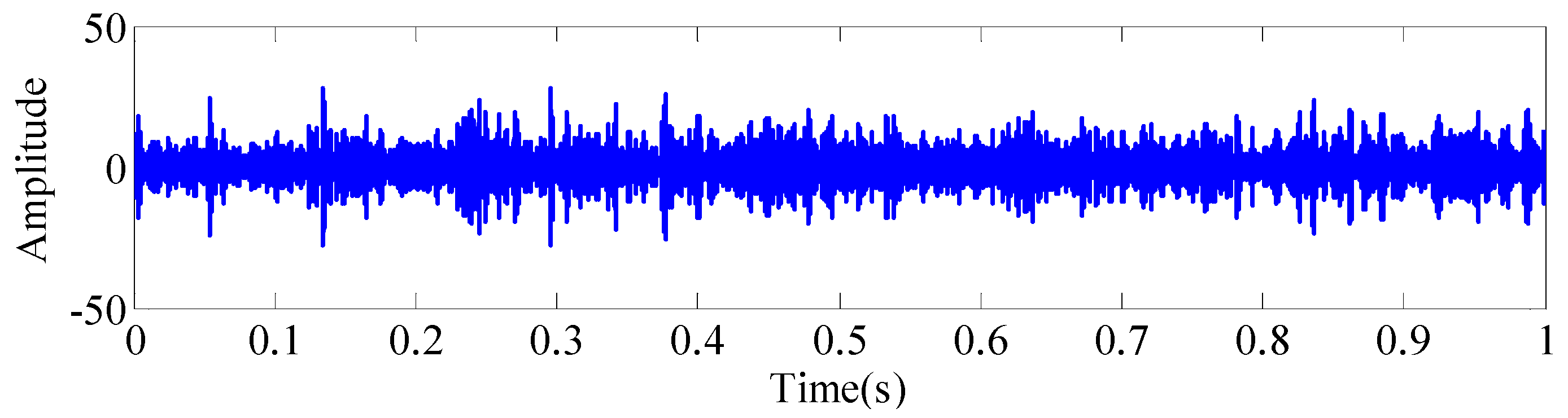



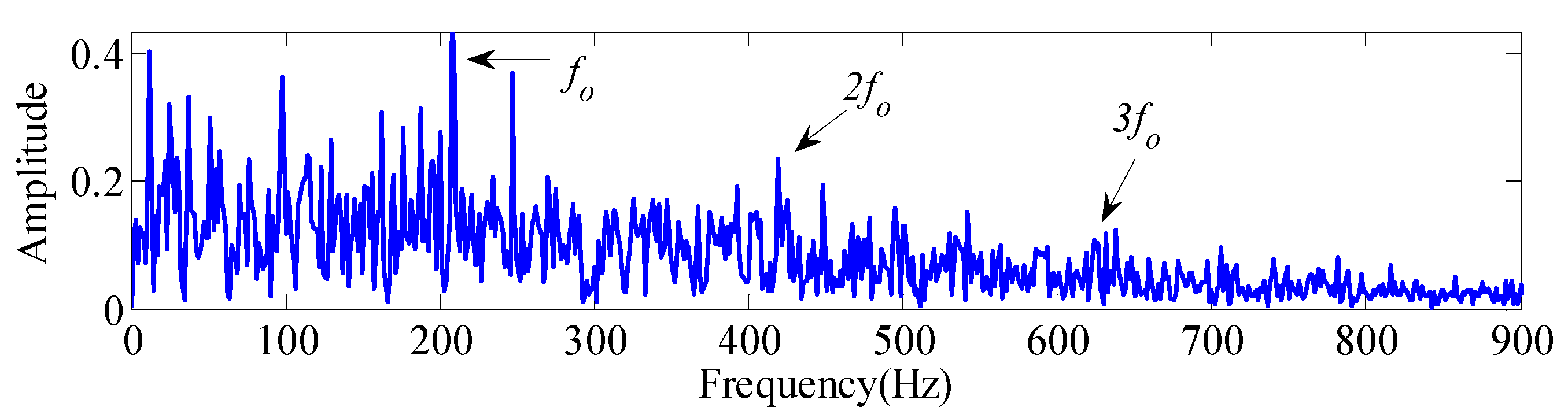
| Speed/(r/min) | 200 | 300 | 600 | 900 | 1200 | 1500 | 1800 | 2100 |
| Kurtosis | 21.824 | 14.545 | 7.276 | 4.887 | 3.722 | 3.052 | 2.642 | 2.322 |
| Position/(s) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Kurtosis | 36.62 | 3.031 | 3.023 | 3.032 | 10.711 | 2.948 | 47.08 | 2.981 | 2.999 | 2.991 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Yang, S.; Liu, Y. Weak Fault Feature Extraction of Axle Box Bearing Based on Pre-Identification and Singular Value Decomposition. Machines 2022, 10, 1213. https://doi.org/10.3390/machines10121213
Zhao L, Yang S, Liu Y. Weak Fault Feature Extraction of Axle Box Bearing Based on Pre-Identification and Singular Value Decomposition. Machines. 2022; 10(12):1213. https://doi.org/10.3390/machines10121213
Chicago/Turabian StyleZhao, Le, Shaopu Yang, and Yongqiang Liu. 2022. "Weak Fault Feature Extraction of Axle Box Bearing Based on Pre-Identification and Singular Value Decomposition" Machines 10, no. 12: 1213. https://doi.org/10.3390/machines10121213
APA StyleZhao, L., Yang, S., & Liu, Y. (2022). Weak Fault Feature Extraction of Axle Box Bearing Based on Pre-Identification and Singular Value Decomposition. Machines, 10(12), 1213. https://doi.org/10.3390/machines10121213






