Advances and Prospects of Vision-Based 3D Shape Measurement Methods
Abstract
:1. Introduction
2. Basics of Vision-Based 3D Measurement
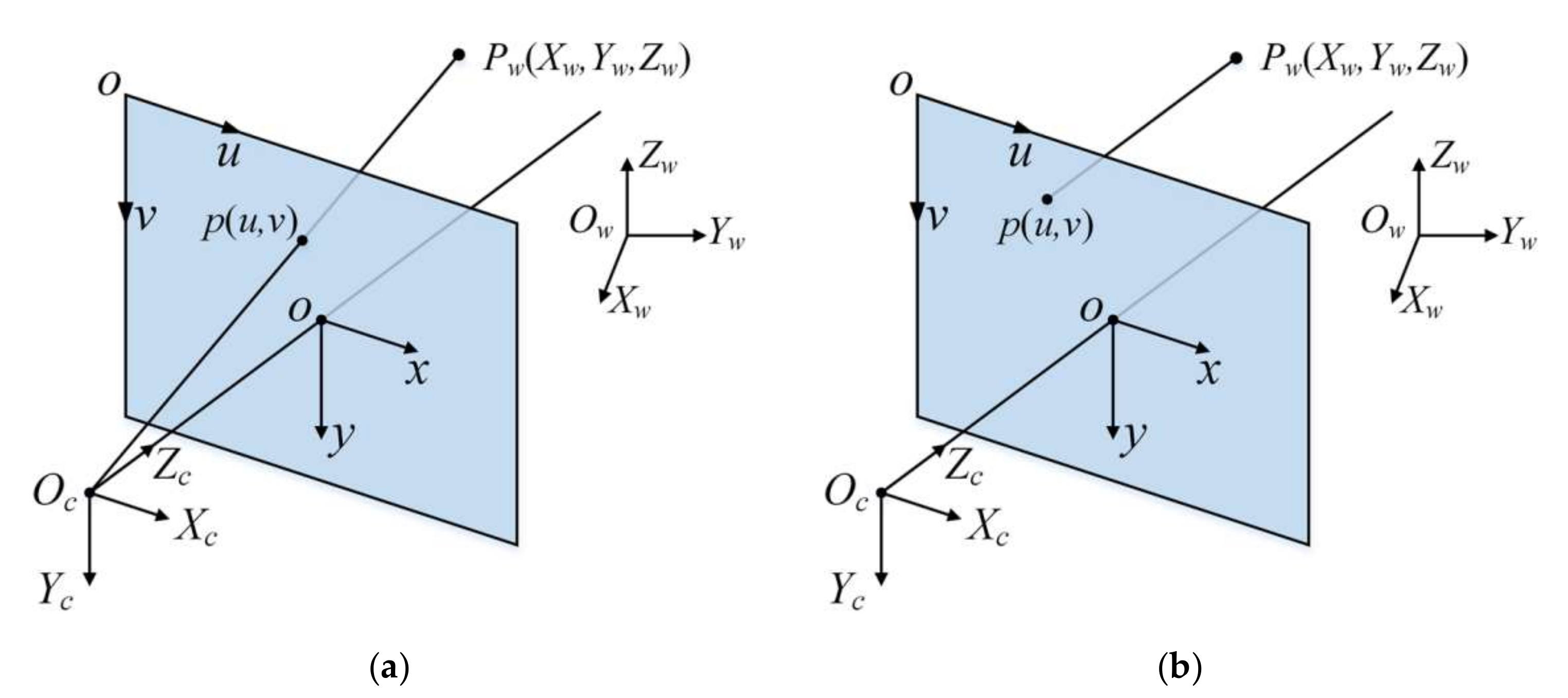
2.1. Camera Model
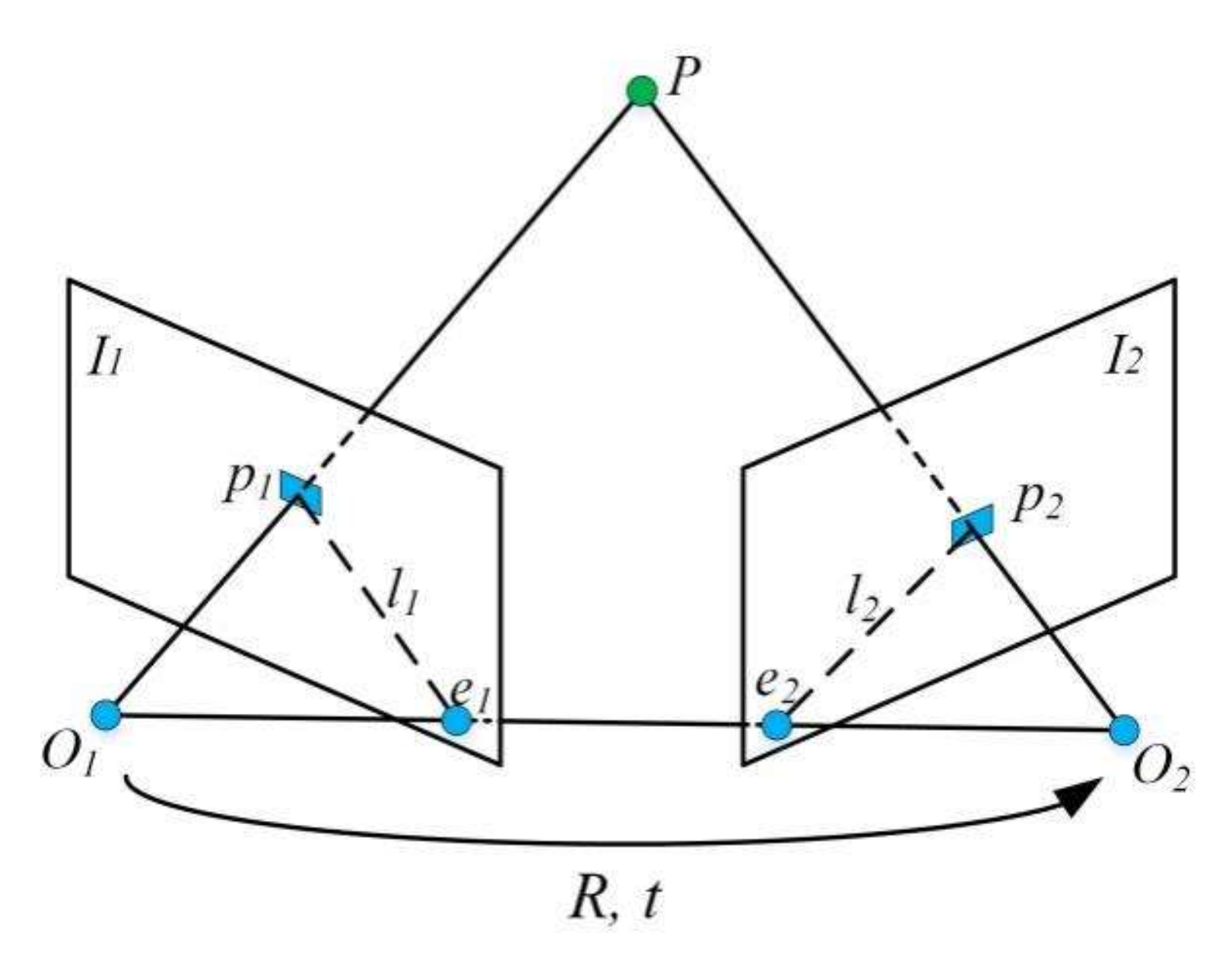
2.2. Epipolar Geometry
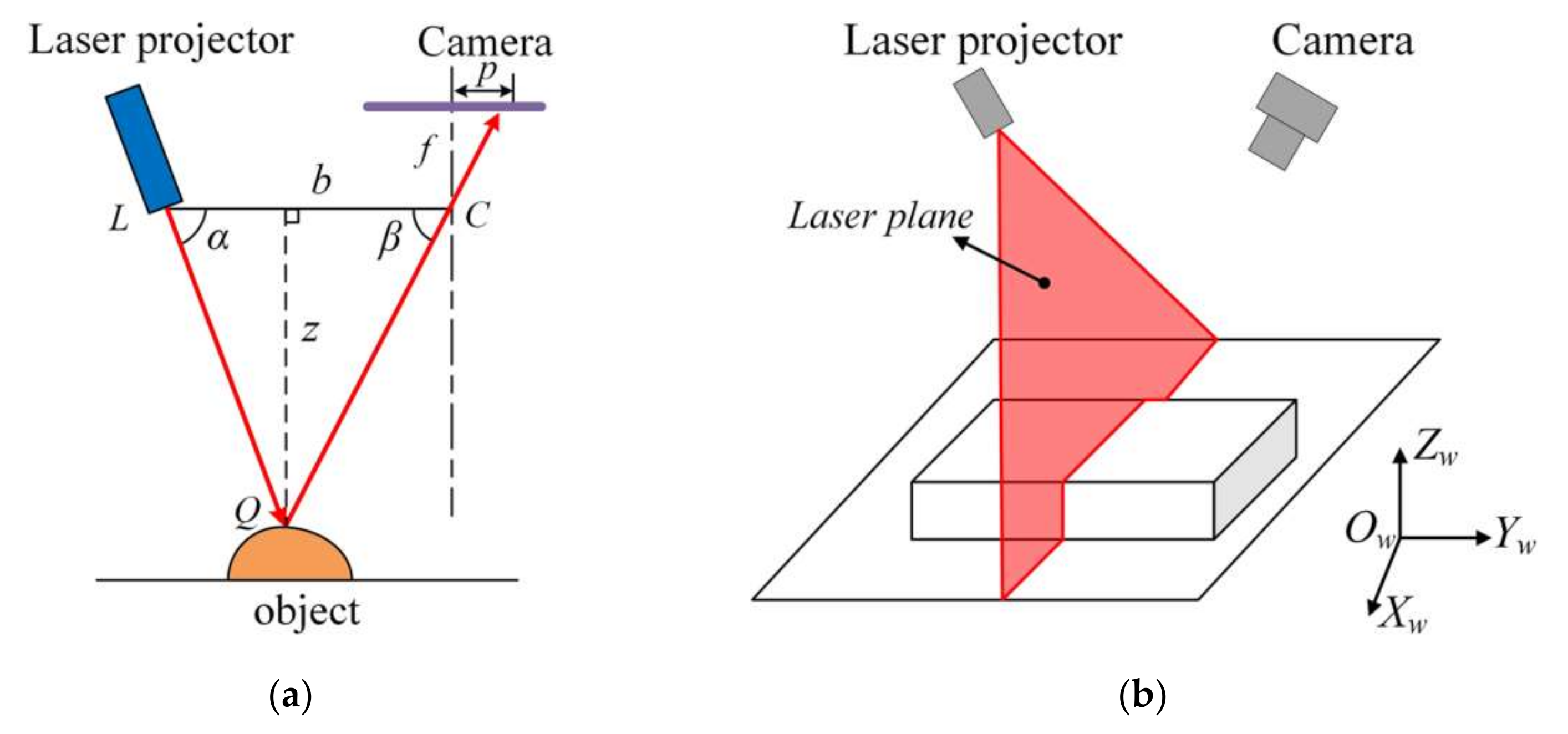
2.3. Laser Triangulation
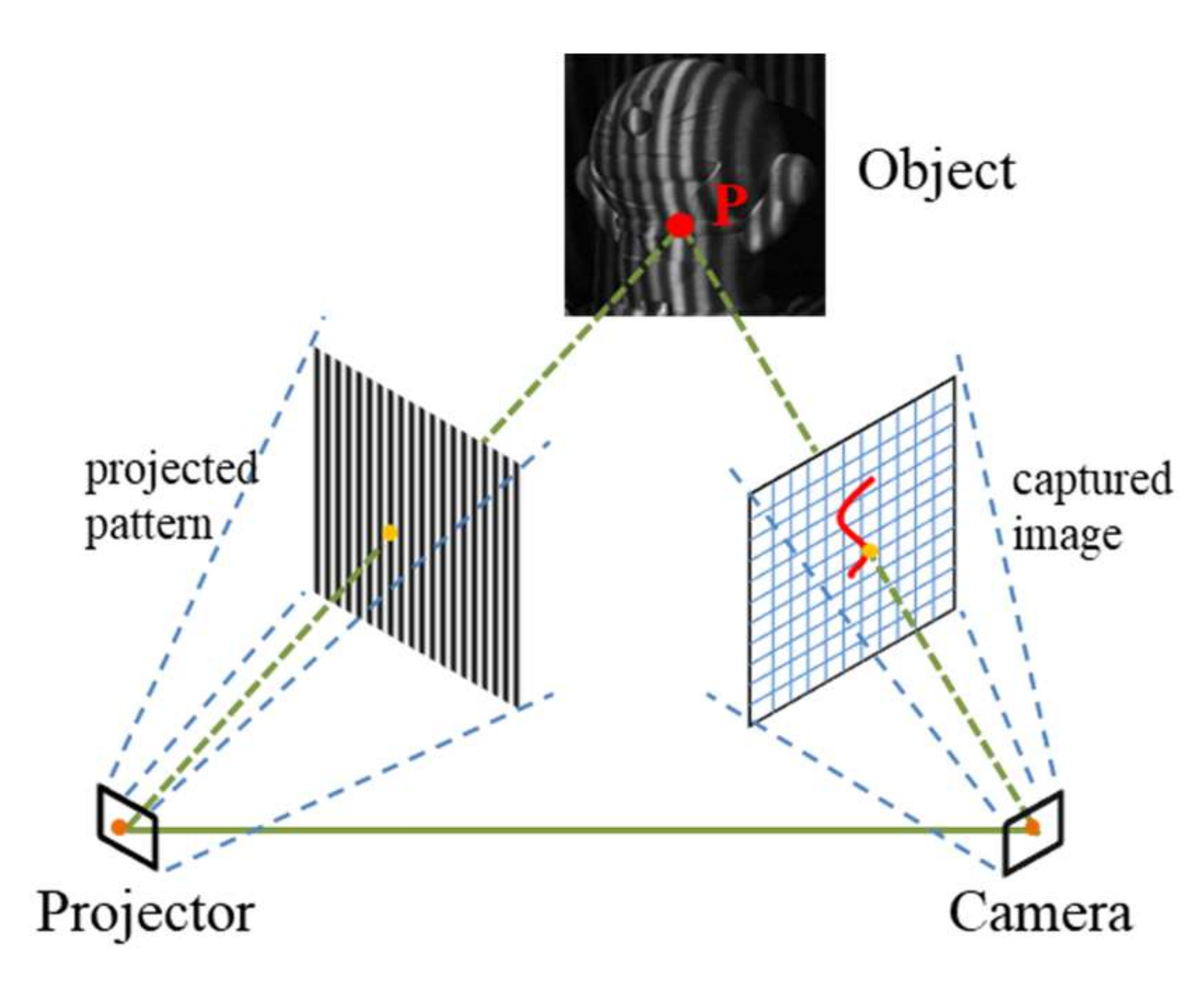
2.4. Structured Light System Model
3. Vision-Based 3D Shape Measurement Techniques
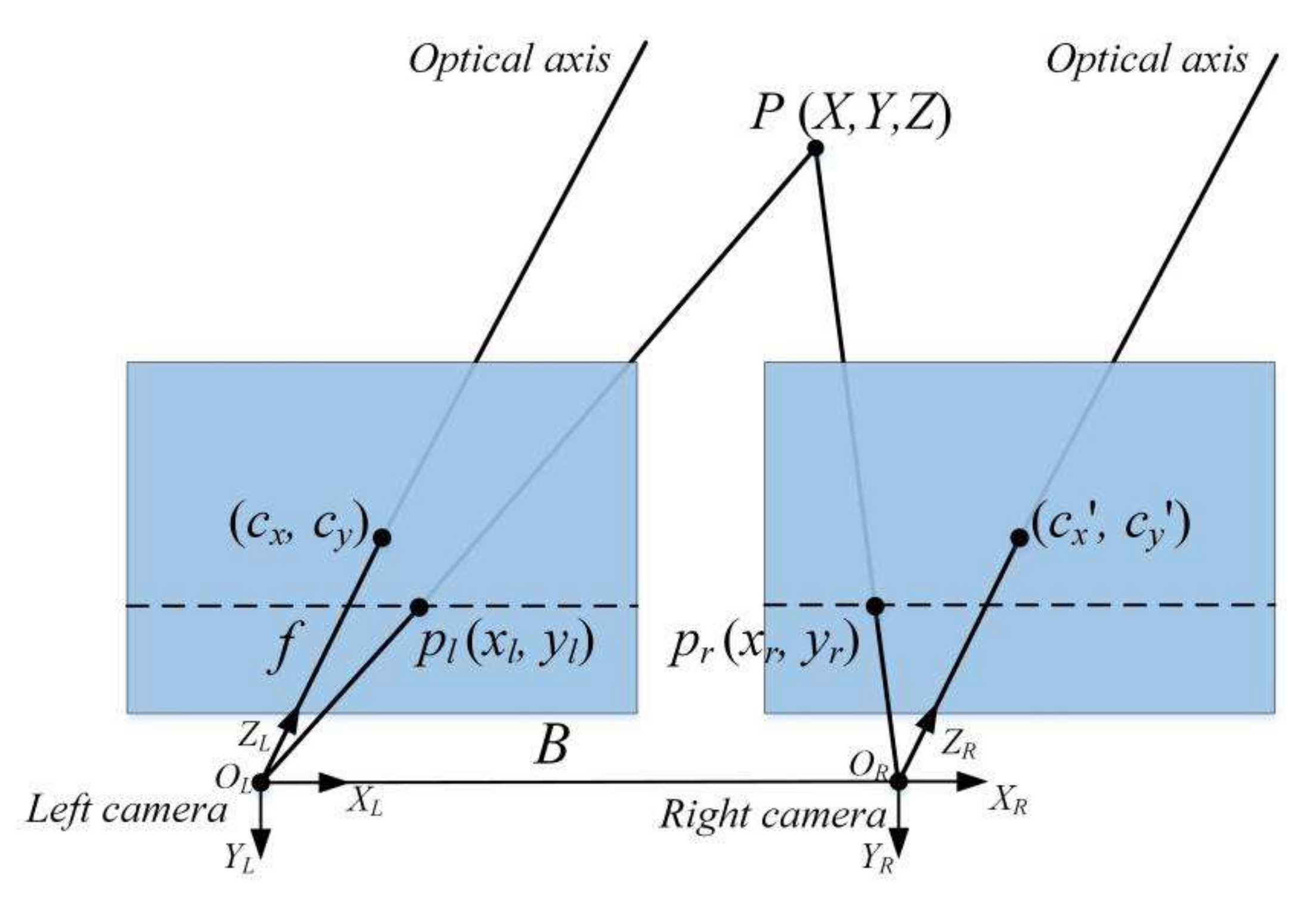
3.1. Stereo Vision Technique
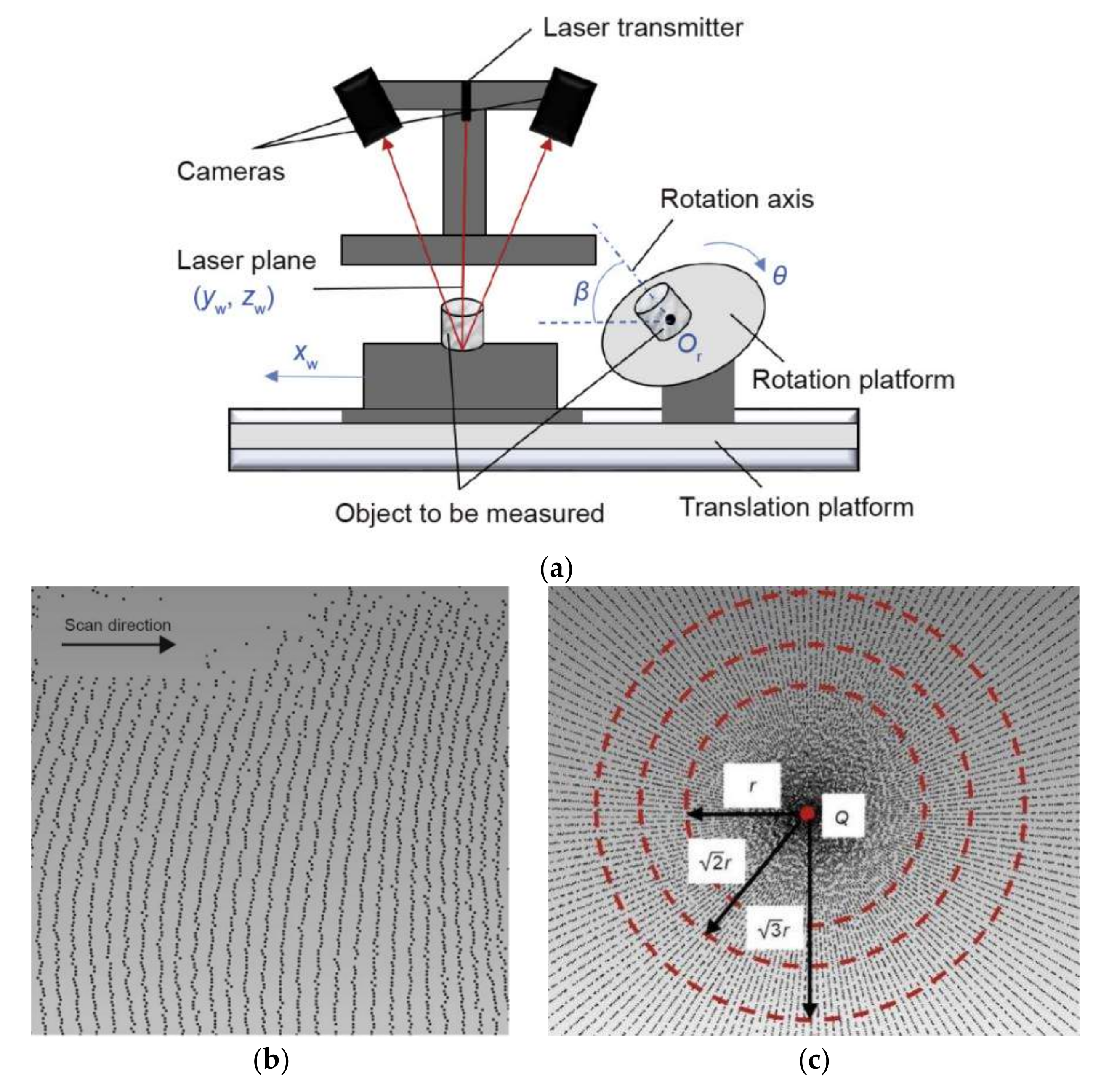
3.2. Three-Dimensional Laser Scanning Technique
3.3. Structured Light Technique
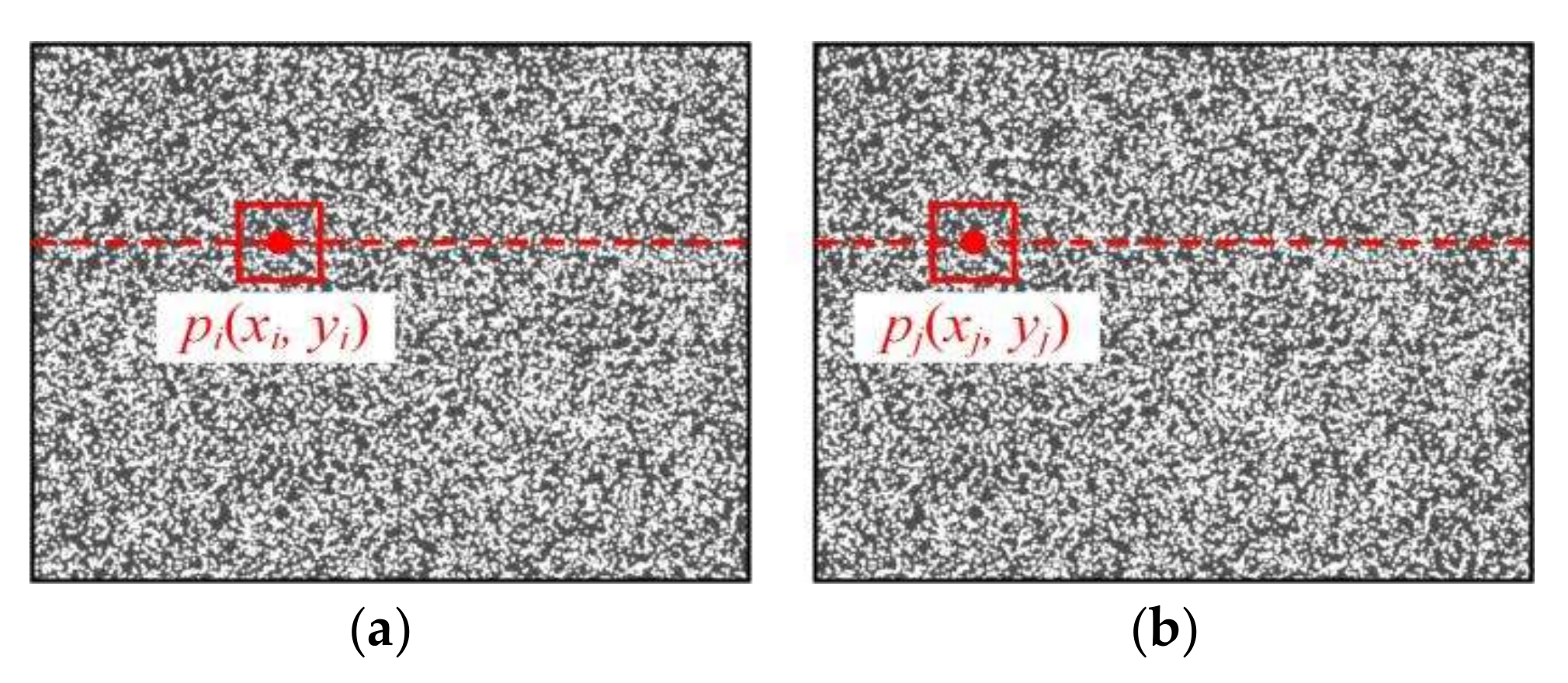
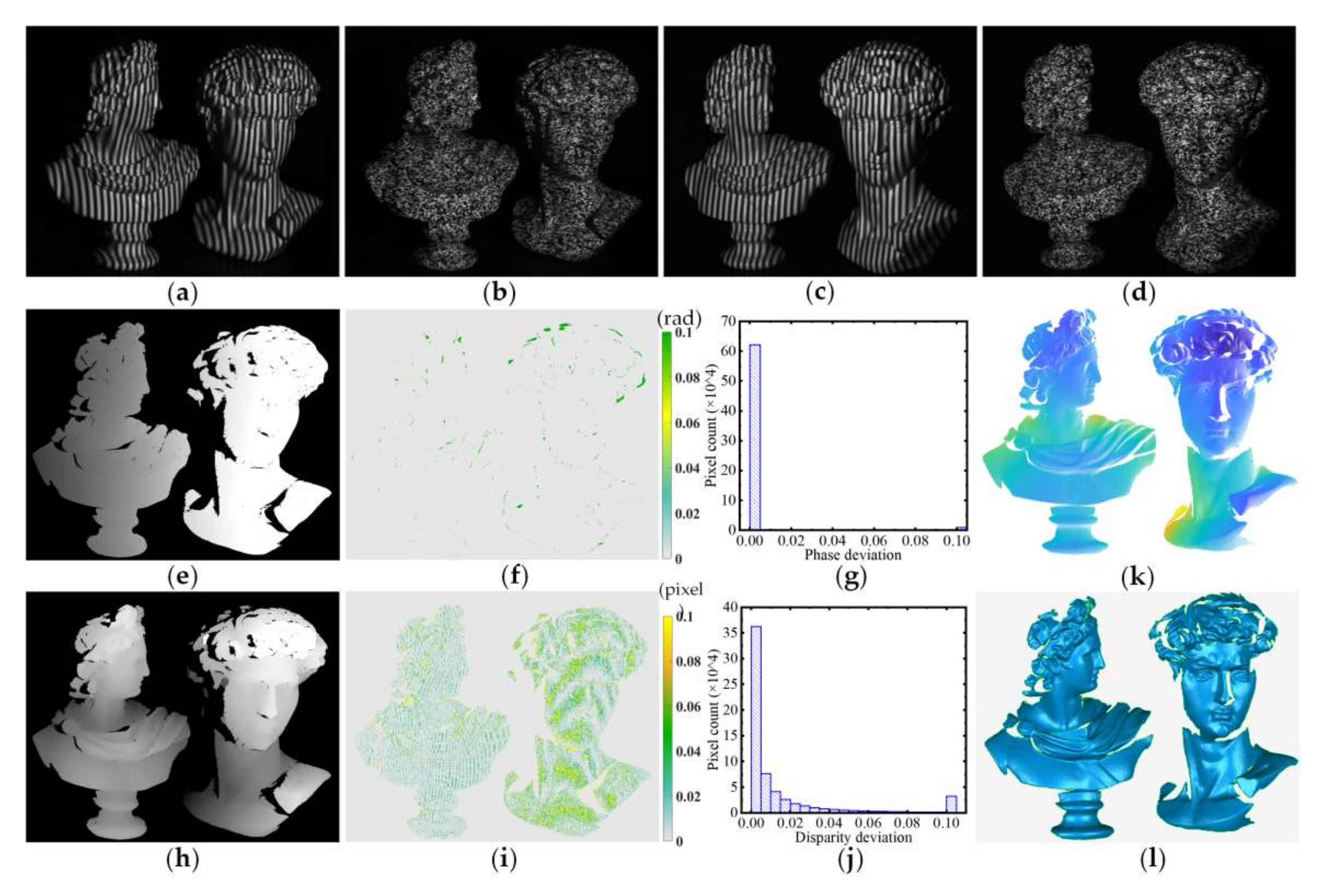
3.3.1. Random Speckle Projection
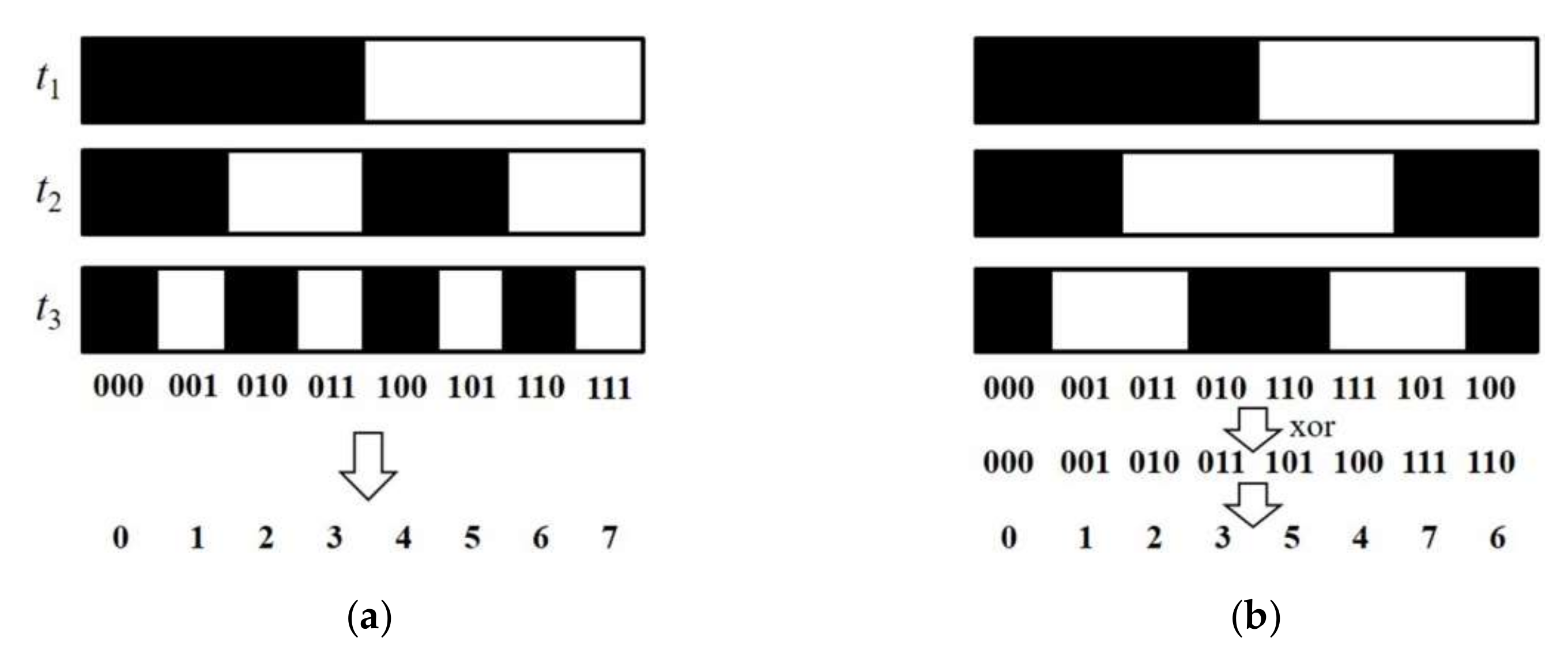
3.3.2. Binary Coding Projection
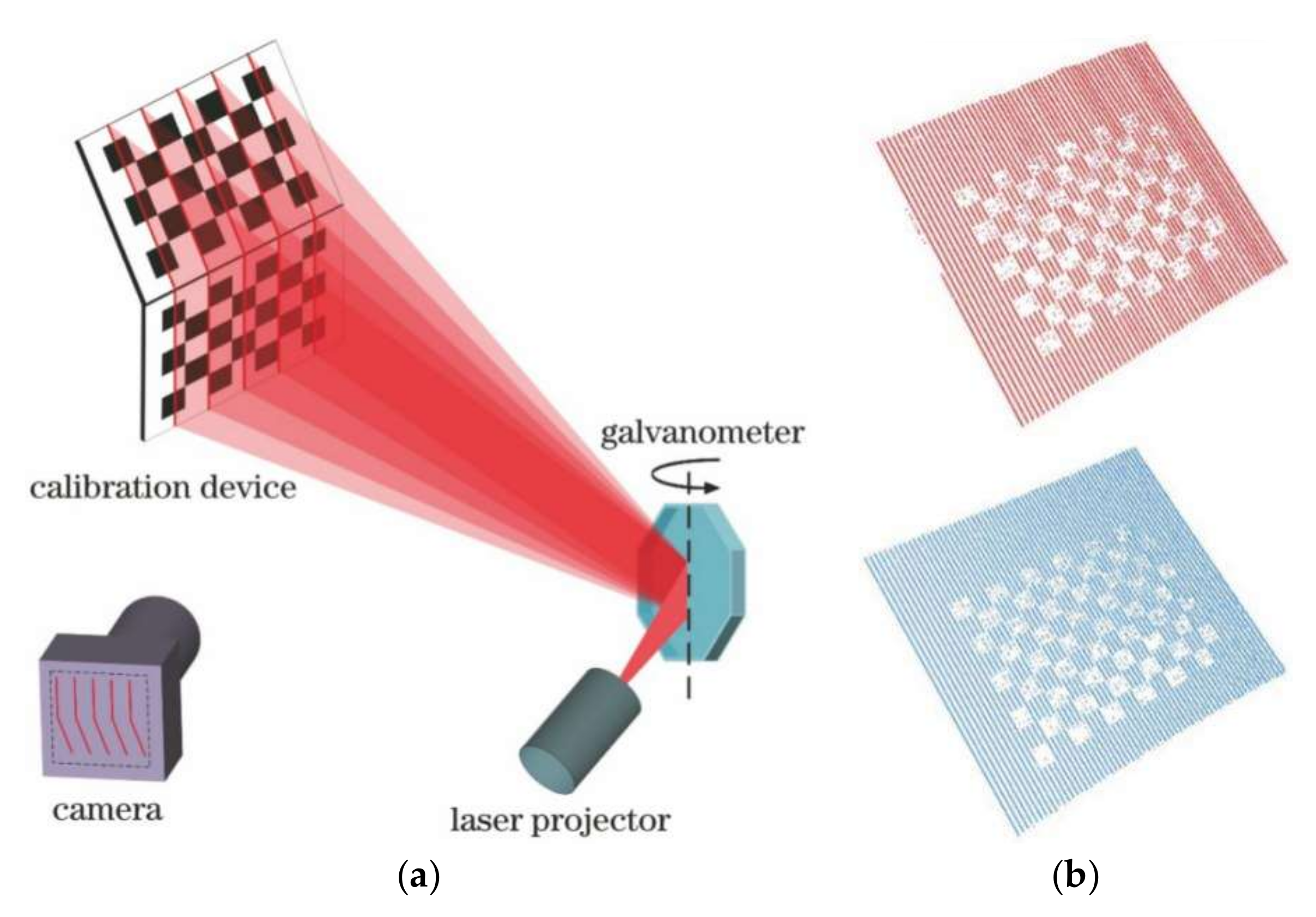
3.3.3. Fringe Projection
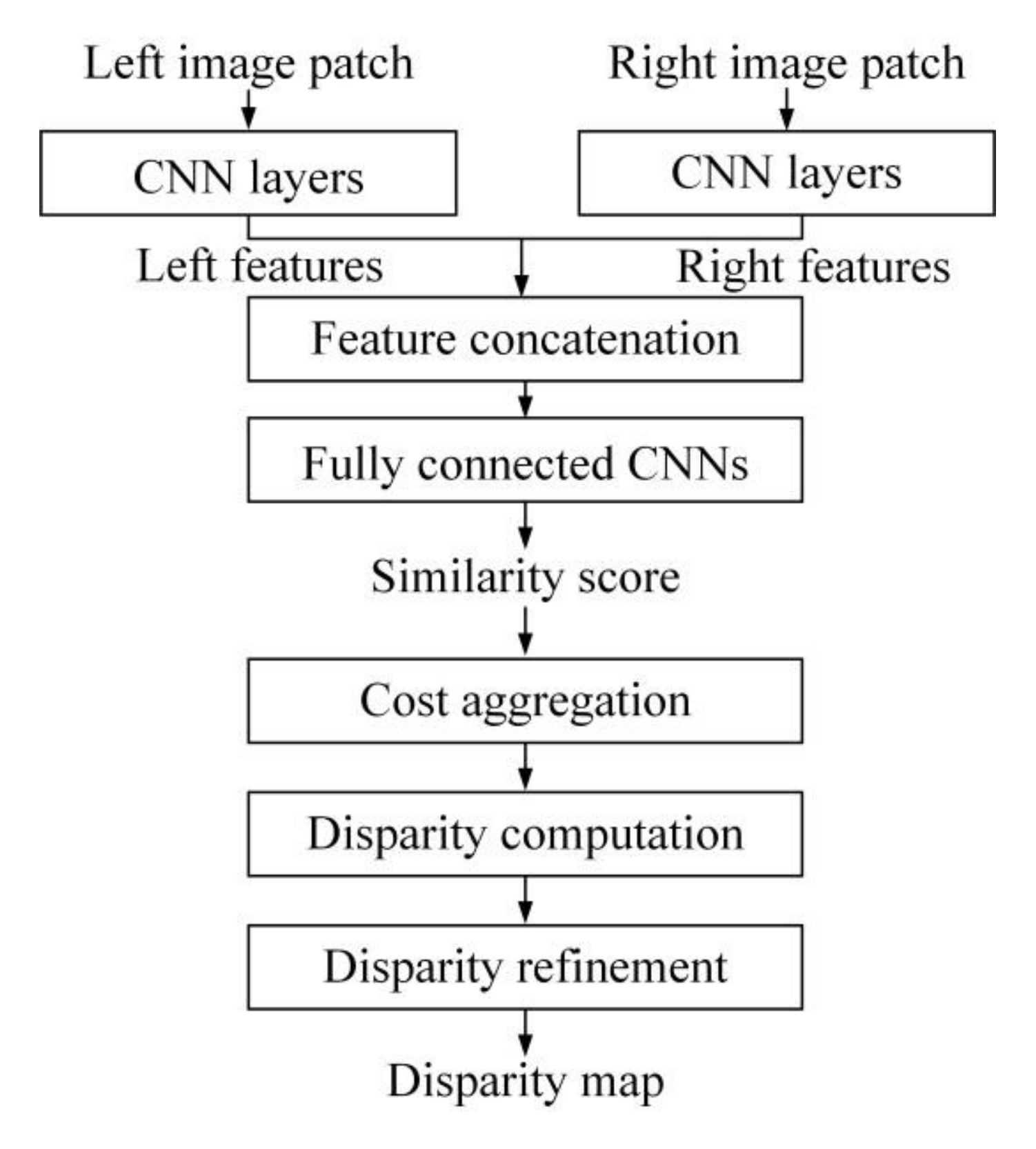
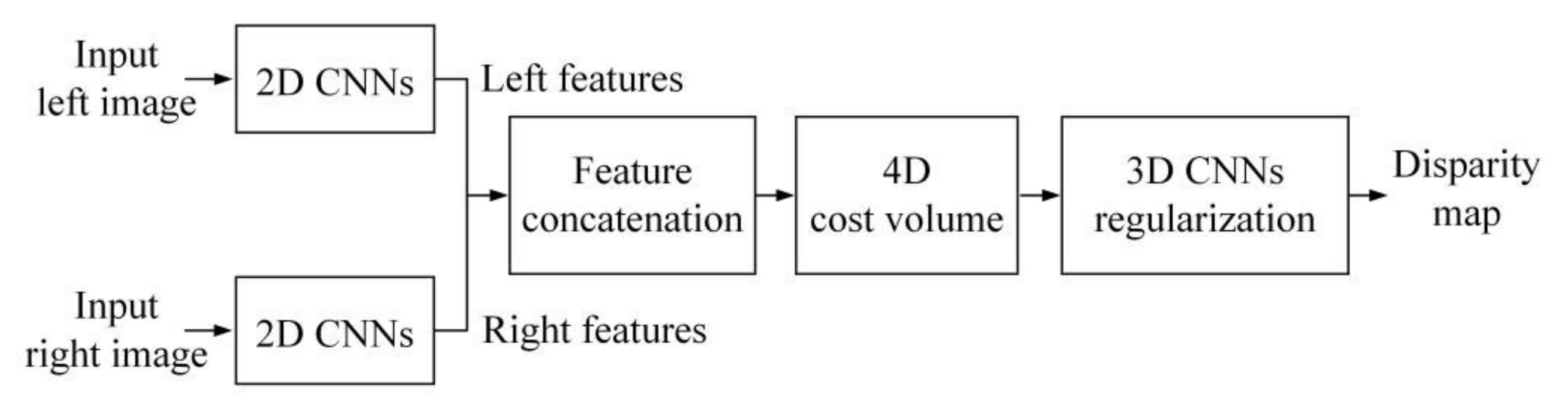
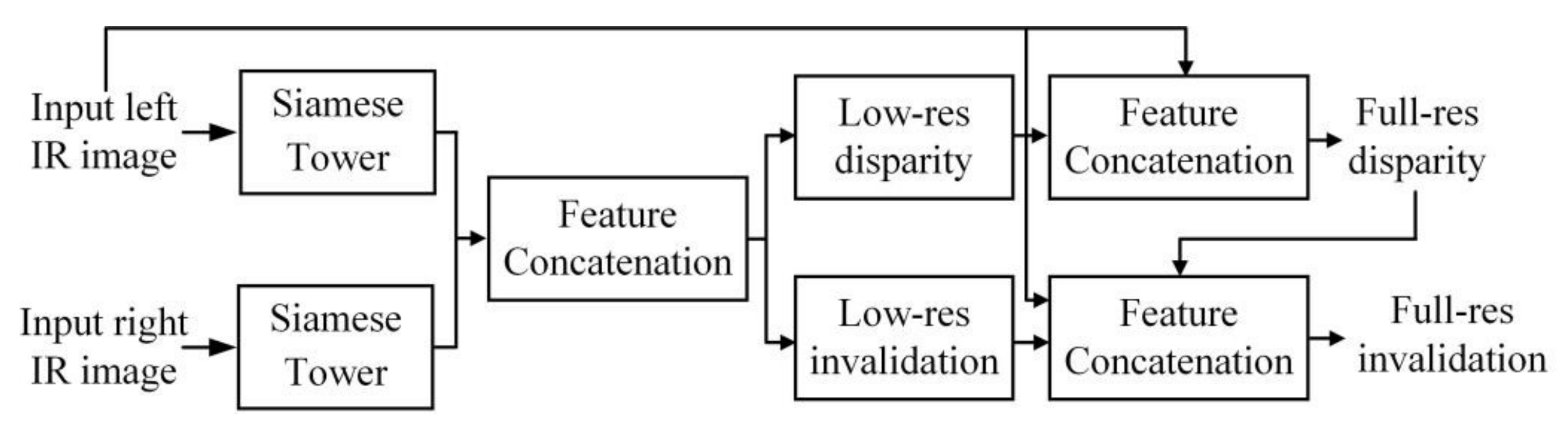
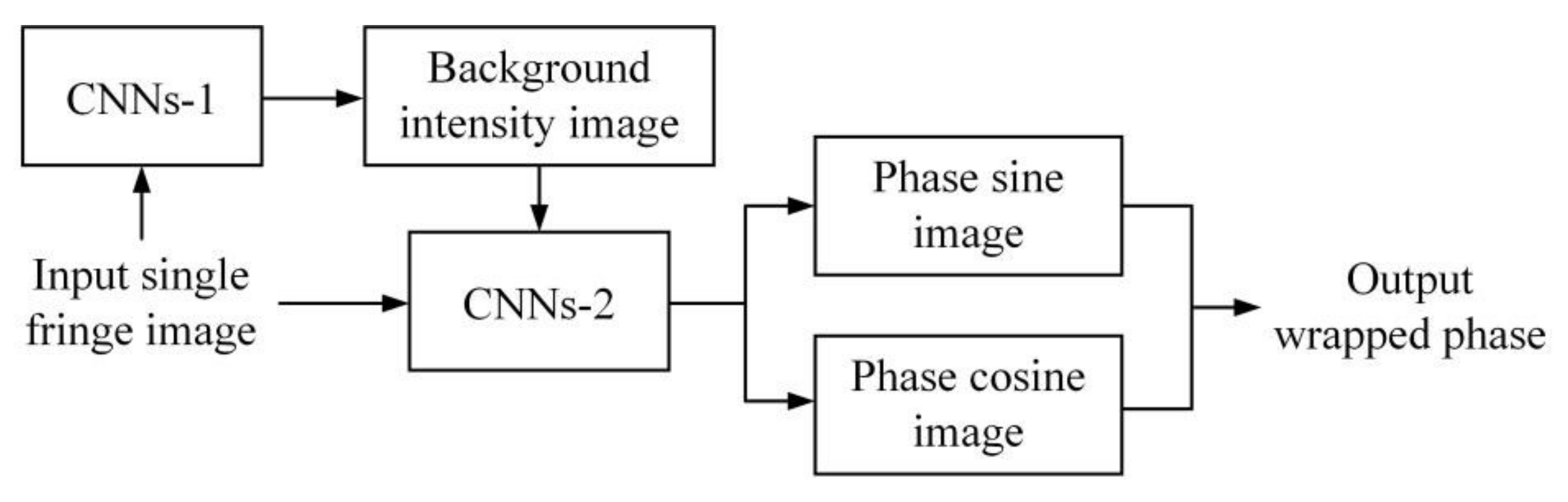
3.4. Deep Learning-Based Techniques
4. Discussion
4.1. Comparison and Analysis
4.2. Uncertainty of Vision-Based Measurement
- (1)
- Image acquisition: a camera system is composed of lens, hardware and software components, all of which affect the final image taken with the camera if it is not predefined. The camera pose also affects the position and shape of the measured object in the image. Thus, the camera system should be accurately calibrated, and the systematic effects should be considered and compensated. The random effects should also be taken into account, related to fluctuations of the camera position because of imperfections of the bearing structure, environmental vibrations, etc.
- (2)
- Lighting conditions: the lighting of the scene directly determines the pixel values of the image, which may have an adverse impact on image processing and measurement results if the lighting condition varies. Lighting conditions can be considered either as systematic effects (the background that does not change during the measurement process) and random effects (fluctuations of the lighting conditions), and both have to be taken into consideration when evaluating uncertainty.
- (3)
- Image processing and 3D mapping algorithms: uncertainties introduced in the image processing and measurement extraction algorithms must also be taken into consideration. For instance, noise reduction algorithms are not 100% efficient and there is still some noise in the output image. This contribution to uncertainty should be evaluated and combined with all the other contributions to define the uncertainty associated with the final measurement results.
4.3. Challenges and Prospects
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marr, D.; Nishihara, H.K. Representation and recognition of the spatial organization of three-dimensional shapes. Proc. R. Soc. London Ser. B. Biol. Sci. 1978, 200, 269–294. [Google Scholar]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Brown, G.M.; Chen, F.; Song, M. Overview of three-dimensional shape measurement using optical methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar] [CrossRef]
- Khan, F.; Salahuddin, S.; Javidnia, H. Deep Learning-Based Monocular Depth Estimation Methods—A State-of-the-Art Review. Sensors 2020, 20, 2272. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. MVSNet: Depth Inference for Unstructured Multi-View Stereo; Springer: Munich, Germany, 2018; pp. 785–801. [Google Scholar] [CrossRef] [Green Version]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Liu, Y.; Peng, J. Advances techniques of the structured light sensing in intelligent welding robots: A review. Int. J. Adv. Manuf. Technol. 2020, 110, 1027–1046. [Google Scholar] [CrossRef]
- Hirschmuller, H. Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 1, pp. 519–528. [Google Scholar]
- Nayar, S.K.; Nakagawa, Y. Shape from focus. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 824–883. [Google Scholar] [CrossRef] [Green Version]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Yang, S.; Hu, P.; Qu, X. A Robust Optical Flow Tracking Method Based On Prediction Model for Visual-Inertial Odometry. IEEE Robot. Autom. Lett. 2021, 6, 5581–5588. [Google Scholar] [CrossRef]
- Han, X.F.; Laga, H.; Bennamoun, M. Image-based 3D object reconstruction: State-of-the-art and trends in the deep learning era. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 1578–1604. [Google Scholar] [CrossRef] [Green Version]
- Foix, S.; Alenya, G.; Torras, C. Lock-in Time-of-Flight (ToF) Cameras: A Survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Shi, X.; Zhang, G.; Lv, C. A Dual-Platform Laser Scanner for 3D Reconstruction of Dental Pieces. Engineering 2018, 4, 796–805. [Google Scholar] [CrossRef]
- Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Huang, L.; Idir, M.; Zuo, C.; Asundi, A. Review of phase measuring deflectometry. Opt. Lasers Eng. 2018, 107, 247–257. [Google Scholar] [CrossRef]
- Arnison, M.R.; Larkin, K.G.; Sheppard, C.J.; Smith, N.I.; Cogswell, C.J. Linear phase imaging using differential interference contrast microscopy. J. Microsc. 2004, 214, 7–12. [Google Scholar] [CrossRef]
- Li, D.; Tian, J. An accurate calibration method for a camera with telecentric lenses. Opt. Lasers Eng. 2013, 51, 538–541. [Google Scholar] [CrossRef]
- Sun, C.; Liu, H.; Jia, M.; Chen, S. Review of Calibration Methods for Scheimpflug Camera. J. Sens. 2018, 2018, 3901431. [Google Scholar] [CrossRef] [Green Version]
- Blais, F. Review of 20 years of range sensor development. J. Electron. Imaging 2004, 13, 231–243. [Google Scholar] [CrossRef]
- Wang, M.; Yin, Y.; Deng, D.; Meng, X.; Liu, X.; Peng, X. Improved performance of multi-view fringe projection 3D microscopy. Opt. Express 2017, 25, 19408–19421. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z. Flexible Camera Calibration by Viewing a Plane from Unknown Orientations. In Proceedings of the 7th IEEE International Conference on Computer Vision (ICCV’99), Kerkyra, Greece, 20–27 September 1999; pp. 666–673. [Google Scholar]
- Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef] [Green Version]
- Hartley, R.I. Self-calibration from multiple views with a rotating camera. In Proceedings of the 1994 European Conference on Computer Vision, Stockholm, Sweden, 2–6 May 1994; Springer: Stockholm, Sweden, 2018; pp. 471–478. [Google Scholar]
- Maybank, S.J.; Faugeras, O.D. A theory of self-calibration of a moving camera. Int. J. Comput. Vis. 1992, 8, 123–151. [Google Scholar] [CrossRef]
- Caprile, B.; Torre, V. Using vanishing points for camera calibration. Int. J. Comput. Vis. 1990, 4, 127–139. [Google Scholar] [CrossRef]
- Habed, A.; Boufama, B. Camera self-calibration from bivariate polynomials derived from Kruppa’s equations. Pattern Recognit. 2008, 41, 2484–2492. [Google Scholar] [CrossRef]
- Louhichi, H.; Fournel, T.; Lavest, J.M.; Ben Aissia, H. Self-calibration of Scheimpflug cameras: An easy protocol. Meas. Sci. Technol. 2007, 18, 2616–2622. [Google Scholar] [CrossRef]
- Steger, C. A Comprehensive and Versatile Camera Model for Cameras with Tilt Lenses. Int. J. Comput. Vis. 2016, 123, 121–159. [Google Scholar] [CrossRef] [Green Version]
- Hartley, R.I. In defense of the eight-point algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 580–593. [Google Scholar] [CrossRef] [Green Version]
- Fusiello, A.; Trucco, E.; Verri, A. A compact algorithm for rectification of stereo pairs. Mach. Vis. Appl. 2000, 12, 16–22. [Google Scholar] [CrossRef]
- Steger, C. An unbiased detector of curvilinear structures. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 113–125. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, J. Summary on Calibration Method of Line-Structured Light. Laser Optoelectron. Prog. 2018, 55, 020001. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Li, F.; Zhang, G. Calibration method for line-structured light vision sensor based on a single ball target. Opt. Lasers Eng. 2015, 69, 20–28. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, G. Complete calibration of a structured light stripe vision sensor through planar target of unknown orientations. Image Vis. Comput. 2005, 23, 59–67. [Google Scholar] [CrossRef]
- Wei, Z.; Cao, L.; Zhang, G. A novel 1D target-based calibration method with unknown orientation for structured light vision sensor. Opt. Laser Technol. 2010, 42, 570–574. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, P.S. Novel method for structured light system calibration. Opt. Eng. 2006, 45, 083601. [Google Scholar]
- Li, B.; Karpinsky, N.; Zhang, S. Novel calibration method for structured-light system with an out-of-focus projector. Appl. Opt. 2014, 53, 3415–3426. [Google Scholar] [CrossRef] [PubMed]
- Bell, T.; Xu, J.; Zhang, S. Method for out-of-focus camera calibration. Appl. Opt. 2016, 55, 2346. [Google Scholar] [CrossRef]
- Barnard, S.T.; Fischler, M.A. Computational Stereo. ACM Comput. Surv. 1982, 14, 553–572. [Google Scholar] [CrossRef]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Gupta, R.K.; Cho, S.-Y. Window-based approach for faststereo correspondence. IET Comput. Vis. 2013, 7, 123–134. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.G.; Pollefeys, M. Multi-resolution real-time stereo on commodity graphics hardware. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; pp. 211–217. [Google Scholar]
- Hirschmuller, H.; Scharstein, D. Evaluation of cost functions for stereo matching. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Zabih, R.; Woodfill, J. Non-parametric local transforms for computing visual correspondence. In Proceedings of the 1994 European Conference on Computer Vision, Stockholm, Sweden, 2–6 May 1994; pp. 151–158. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary robust independent elementary features. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Fuhr, G.; Fickel, G.P.; Dal’Aqua, L.P.; Jung, C.R.; Malzbender, T.; Samadani, R. An evaluation of stereo matching methods for view interpolation. In Proceedings of the 2013 IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 403–407. [Google Scholar] [CrossRef]
- Hong, L.; Chen, G. Segment-based stereo matching using graph cuts. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. 74–81. [Google Scholar]
- Yang, Q.X.; Wang, L.; Yang, R.G.; Stewenius, H.; Nister, D. Stereo Matching with Color-Weighted Correlation, Hierarchical Belief Propagation, and Occlusion Handling. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 492–504. [Google Scholar] [CrossRef]
- Hamzah, R.A.; Ibrahim, H. Literature survey on stereo vision disparity map algorithms. J. Sens. 2016, 2016, 8742920. [Google Scholar] [CrossRef] [Green Version]
- Quan, Y.; Li, S.; Mai, Q. On-machine 3D measurement of workpiece dimensions based on binocular vision. Opt. Precis. Eng. 2013, 21, 1054–1061. [Google Scholar] [CrossRef]
- Wei, Z.; Gu, Y.; Huang, Z.; Wu, J. Research on Calibration of Three Dimensional Coordinate Reconstruction of Feature Points in Binocular Stereo Vision. Acta Metrol. Sin. 2014, 35, 102–107. [Google Scholar]
- Song, L.; Sun, S.; Yang, Y.; Zhu, X.; Guo, Q.; Yang, H. A Multi-View Stereo Measurement System Based on a Laser Scanner for Fine Workpieces. Sensors 2019, 19, 381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, B.; Xue, T.; Zhang, T.; Ye, S. A novel method for round steel measurement with a multi-line structured light vision sensor. Meas. Sci. Technol. 2010, 21, 025204. [Google Scholar] [CrossRef]
- Li, J.; Chen, M.; Jin, X.; Chen, Y.; Dai, Z.; Ou, Z.; Tang, Q. Calibration of a multiple axes 3-D laser scanning system consisting of robot, portable laser scanner and turntable. Optik 2011, 122, 324–329. [Google Scholar] [CrossRef]
- Winkelbach, S.; Molkenstruck, S.; Wahl, F.M. Low-Cost Laser Range Scanner and Fast Surface Registration Approach. In Proceedings of the 2006 Annual Symposium of the German-Association-for-Pattern-Recognition, Berlin, Germany, 12–14 September 2006; pp. 718–728. [Google Scholar]
- Theiler, P.W.; Wegner, J.D.; Schindler, K. Keypoint-based 4-Points Congruent Sets—Automated marker-less registration of laser scans. J. Photogramm. Remote Sens. 2014, 96, 149–163. [Google Scholar] [CrossRef]
- Yang, S.; Yang, L.; Zhang, G.; Wang, T.; Yang, X. Modeling and Calibration of the Galvanometric Laser Scanning Three-Dimensional Measurement System. Nanomanufacturing Metrol. 2018, 1, 180–192. [Google Scholar] [CrossRef]
- Wang, T.; Yang, S.; Li, S.; Yuan, Y.; Hu, P.; Liu, T.; Jia, S. Error Analysis and Compensation of Galvanometer Laser Scanning Measurement System. Acta Opt. Sin. 2020, 40, 2315001. [Google Scholar]
- Yang, L.; Yang, S. Calibration of Galvanometric Line-structured Light Based on Neural Network. Tool Eng. 2019, 53, 97–102. [Google Scholar]
- Kong, L.B.; Peng, X.; Chen, Y.; Wang, P.; Xu, M. Multi-sensor measurement and data fusion technology for manufacturing process monitoring: A literature review. Int. J. Extrem. Manuf. 2020, 2, 022001. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Yan, J.W.; Kuriyagawa, T. Manufacturing technologies toward extreme precision. Int. J. Extrem. Manuf. 2019, 1, 022001. [Google Scholar] [CrossRef] [Green Version]
- Khan, D.; Shirazi, M.A.; Kim, M.Y. Single shot laser speckle based 3D acquisition system for medical applications. Opt. Lasers Eng. 2018, 105, 43–53. [Google Scholar] [CrossRef]
- Eschner, E.; Staudt, T.; Schmidt, M. 3D particle tracking velocimetry for the determination of temporally resolved particle trajectories within laser powder bed fusion of metals. Int. J. Extrem. Manuf. 2019, 1, 035002. [Google Scholar] [CrossRef] [Green Version]
- Schaffer, M.; Grosse, M.; Harendt, B.; Kowarschik, R. High-speed three-dimensional shape measurements of objects with laser speckles and acousto-optical deflection. Opt. Lett. 2011, 36, 3097–3099. [Google Scholar] [CrossRef] [PubMed]
- Harendt, B.; Große, M.; Schaffer, M.; Kowarschik, R. 3D shape measurement of static and moving objects with adaptive spatiotemporal correlation. Appl. Opt. 2014, 53, 7507. [Google Scholar] [CrossRef] [PubMed]
- Stark, A.W.; Wong, E.; Weigel, D.; Babovsky, H.; Schott, T.; Kowarschik, R. Subjective speckle suppression in laser-based stereo photogrammetry. Opt. Eng. 2016, 55, 121713. [Google Scholar] [CrossRef]
- Khan, D.; Kim, M.Y. High-density single shot 3D sensing using adaptable speckle projection system with varying preprocessing. Opt. Lasers Eng. 2020, 136, 106312. [Google Scholar] [CrossRef]
- Inokuchi, S.; Sato, K.; Matsuda, F. Range-imaging system for 3-D object recognition. In Proceedings of the 1984 International Conference on Pattern Recognition, Montreal, QC, Canada, 30 July–2 August 1984; pp. 806–808. [Google Scholar]
- Trobina, M. Error Model of a Coded-Light Range Sensor; Communication Technology Laboratory, ETH Zentrum: Zurich, Germany, 1995. [Google Scholar]
- Song, Z.; Chung, R.; Zhang, X.T. An accurate and robust strip-edge-based structured light means for shiny surface micromeasurement in 3-D. IEEE Trans. Ind. Electron. 2013, 60, 1023–1032. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, X.; Xiang, L.; Sun, X. 3-D shape measurement based on complementary Gray-code light. Opt. Lasers Eng. 2012, 50, 574–579. [Google Scholar] [CrossRef]
- Zheng, D.; Da, F.; Huang, H. Phase unwrapping for fringe projection three-dimensional measurement with projector defocusing. Opt. Eng. 2016, 55, 034107. [Google Scholar] [CrossRef]
- Zheng, D.; Da, F.; Kemao, Q.; Seah, H.S. Phase-shifting profilometry combined with Gray-code patterns projection: Unwrapping error removal by an adaptive median filter. Opt. Eng. 2016, 55, 034107. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, W.; Zhang, Q. High-speed three-dimensional shape measurement based on shifting Gray-code light. Opt. Express 2019, 27, 22631–22644. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Lasers Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Lasers Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Zuo, C.; Tao, T.; Feng, S.; Huang, L.; Asundi, A.; Chen, Q. Micro Fourier Transform Profilometry (μFTP): 3D shape measurement at 10,000 frames per second. Opt. Lasers Eng. 2018, 102, 70–91. [Google Scholar] [CrossRef] [Green Version]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 1983, 22, 3977–3982. [Google Scholar] [CrossRef]
- Cao, S.; Cao, Y.; Zhang, Q. Fourier transform profilometry of a single-field fringe for dynamic objects using an interlaced scanning camera. Opt. Commun. 2016, 367, 130–136. [Google Scholar] [CrossRef]
- Guo, L.; Li, J.; Su, X. Improved Fourier transform profilometry for the automatic measurement of 3D object shapes. Opt. Eng. 1990, 29, 1439–1444. [Google Scholar] [CrossRef]
- Kemao, Q. Windowed Fourier transform for fringe pattern analysis. Appl. Opt. 2004, 43, 2695–2702. [Google Scholar] [CrossRef]
- Zhong, J.; Weng, J. Spatial carrier-fringe pattern analysis by means of wavelet transform: Wavelet transform profilometry. Appl. Opt. 2004, 43, 4993–4998. [Google Scholar] [CrossRef] [PubMed]
- Gdeisat, M.; Burton, D.; Lilley, F.; Arevalillo-Herráez, M. Fast fringe pattern phase demodulation using FIR Hilbert transformers. Opt. Commun. 2016, 359, 200–206. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Gao, N.; Xiao, Y.; Gao, F.; Jiang, X. Single-shot 3D shape measurement of discontinuous objects based on a coaxial fringe projection system. Appl. Opt. 2019, 58, A169–A178. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S. Absolute phase retrieval methods for digital fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 107, 28–37. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Zhao, M.; Huang, L.; Zhang, Q.; Su, X.; Asundi, A.; Kemao, Q. Quality-guided phase unwrapping technique: Comparison of quality maps and guiding strategies. Appl. Opt. 2011, 50, 6214–6224. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Towers, C.E.; Towers, D.P.; Jones, J.D. Absolute fringe order calculation using optimised multi-frequency selection in full-field profilometry. Opt. Lasers Eng. 2005, 43, 788–800. [Google Scholar] [CrossRef]
- Sansoni, G.; Carocci, M.; Rodella, R. Three-dimensional vision based on a combination of gray-code and phase-shift light projection: Analysis and compensation of the systematic errors. Appl. Opt. 1999, 38, 6565–6573. [Google Scholar] [CrossRef] [Green Version]
- Van der Jeught, S.; Dirckx, J.J. Real-time structured light profilometry: A review. Opt. Lasers Eng. 2016, 87, 18–31. [Google Scholar] [CrossRef]
- Nguyen, H.; Nguyen, D.; Wang, Z.; Kieu, H.; Le, M. Real-time, high-accuracy 3D imaging and shape measurement. Appl. Opt. 2014, 54, A9–A17. [Google Scholar] [CrossRef]
- Cong, P.; Xiong, Z.; Zhang, Y.; Zhao, S.; Wu, F. Accurate Dynamic 3D Sensing With Fourier-Assisted Phase Shifting. IEEE J. Sel. Top. Signal Process. 2014, 9, 396–408. [Google Scholar] [CrossRef]
- An, Y.; Hyun, J.-S.; Zhang, S. Pixel-wise absolute phase unwrapping using geometric constraints of structured light system. Opt. Express 2016, 24, 18445–18459. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Li, B.; Zhang, S. Pixel-by-pixel absolute phase retrieval using three phase-shifted fringe patterns without markers. Opt. Lasers Eng. 2017, 91, 232–241. [Google Scholar] [CrossRef]
- Gai, S.; Da, F.; Dai, X. Novel 3D measurement system based on speckle and fringe pattern projection. Opt. Express 2016, 24, 17686–17697. [Google Scholar] [CrossRef] [PubMed]
- Hu, P.; Yang, S.; Zheng, F.; Yuan, Y.; Wang, T.; Li, S.; Liu, H.; Dear, J.P. Accurate and dynamic 3D shape measurement with digital image correlation-assisted phase shifting. Meas. Sci. Technol. 2021, 32, 075204. [Google Scholar] [CrossRef]
- Hu, P.; Yang, S.; Zhang, G.; Deng, H. High-speed and accurate 3D shape measurement using DIC-assisted phase matching and triple-scanning. Opt. Lasers Eng. 2021, 147, 106725. [Google Scholar] [CrossRef]
- Wu, G.; Wu, Y.; Li, L.; Liu, F. High-resolution few-pattern method for 3D optical measurement. Opt. Lett. 2019, 44, 3602–3605. [Google Scholar] [CrossRef] [PubMed]
- Lei, S.; Zhang, S. Flexible 3-D shape measurement using projector defocusing. Opt. Lett. 2009, 34, 3080–3082. [Google Scholar] [CrossRef]
- Zhang, S.; Van Der Weide, D.; Oliver, J. Superfast phase-shifting method for 3-D shape measurement. Opt. Express 2010, 18, 9684–9689. [Google Scholar] [CrossRef] [Green Version]
- Weise, T.; Leibe, B.; Van Gool, L. Fast 3d scanning with automatic motion compensation. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 18–23 June 2007; pp. 2695–2702. [Google Scholar]
- Feng, S.; Zuo, C.; Tao, T.; Hu, Y.; Zhang, M.; Chen, Q.; Gu, G. Robust dynamic 3-D measurements withmotion-compensated phase-shifting profilometry. Opt. Lasers Eng. 2018, 103, 127–138. [Google Scholar] [CrossRef]
- Liu, Z.; Zibley, P.C.; Zhang, S. Motion-induced error compensation for phase shifting profilometry. Opt. Express 2018, 26, 12632–12637. [Google Scholar] [CrossRef]
- Lu, L.; Yin, Y.; Su, Z.; Ren, X.; Luan, Y.; Xi, J. General model for phase shifting profilometry with an object in motion. Appl. Opt. 2018, 57, 10364–10369. [Google Scholar] [CrossRef]
- Liu, X.; Tao, T.; Wan, Y.; Kofman, J. Real-time motion-induced-error compensation in 3D surface-shape measurement. Opt. Express 2019, 27, 25265–25279. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Wu, Z.; Li, Y.; Liu, Y.; Zhang, Q. Real-time 3D shape measurement with dual-frequency composite grating and motion-induced error reduction. Opt. Express 2020, 28, 26882–26897. [Google Scholar] [CrossRef]
- Zhou, K.; Meng, X.; Cheng, B. Review of Stereo Matching Algorithms Based on Deep Learning. Comput. Intell. Neurosci. 2020, 2020, 8562323. [Google Scholar] [CrossRef] [PubMed]
- Zbontar, J.; LeCun, Y. Computing the stereo matching cost with a convolutional neural network. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1592–1599. [Google Scholar]
- Seki, A.; Pollefeys, M. SGM-Nets: Semi-global matching with neural networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 June 2017; pp. 6640–6649. [Google Scholar]
- Mayer, N.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. Large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4040–4048. [Google Scholar]
- Liang, Z.; Feng, Y.; Guo, Y.; Liu, H.; Chen, W.; Qiao, L.; Zhou, L.; Zhang, J. Learning for disparity estimation through feature constancy. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2811–2820. [Google Scholar]
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. End-to-End Learning of Geometry and Context for Deep Stereo Regression. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 66–75. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.; Chen, Y. Pyramid stereo matching network. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5410–5418. [Google Scholar]
- Zhang, F.; Prisacariu, V.; Yang, R.; Torr, P.H.S. GA-Net: Guided aggregation net for end-To-End stereo matching. In Proceedings of the 2019 IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 185–194. [Google Scholar]
- Fanello, S.R.; Rhemann, C.; Tankovich, V.; Kowdle, A.; Escolano, S.O.; Kim, D.; Izadi, S. Hyperdepth: Learning depth from structured light without matching. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2016; pp. 5441–5450. [Google Scholar]
- Fanello, S.R.; Valentin, J.; Rhemann, C.; Kowdle, A.; Tankovich, V.; Davidson, P.; Izadi, S. Ultrastereo: Efficient learning-based matching for active stereo systems. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 June 2017; pp. 6535–6544. [Google Scholar]
- Zhang, Y.; Khamis, S.; Rhemann, C.; Valentin, J.; Kowdle, A.; Tankovich, V.; Schoenberg, M.; Izadi, S.; Funkhouser, T.; Fanello, S. ActiveStereoNet: End-to-End Self-supervised Learning for Active Stereo Systems. In Proceedings of the 2018 European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 802–819. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Liu, R.; Guan, B.; Pan, Y.; Sun, S. Stereo-Matching Network for Structured Light. IEEE Signal Process. Lett. 2018, 26, 164–168. [Google Scholar] [CrossRef]
- Feng, S.; Chen, Q.; Gu, G.; Tao, T.; Zhang, L.; Hu, Y.; Yin, W.; Zuo, C. Fringe pattern analysis using deep learning. Adv. Photon. 2019, 1, 025001. [Google Scholar] [CrossRef] [Green Version]
- Spoorthi, G.; Gorthi, S.; Gorthi, R.K.S.S. PhaseNet: A deep convolutional neural network for two-dimensional phase unwrapping. IEEE Signal Process. Lett. 2019, 26, 54–58. [Google Scholar] [CrossRef]
- Yin, W.; Chen, Q.; Feng, S.; Tao, T.; Huang, L.; Trusiak, M.; Asundi, A.; Zuo, C. Temporal phase unwrapping using deep learning. Sci. Rep. 2019, 9, 20175. [Google Scholar] [CrossRef]
- Yan, K.; Yu, Y.; Huang, C.; Sui, L.; Qian, K.; Asundi, A. Fringe pattern denoising based on deep learning. Opt. Commun. 2018, 437, 148–152. [Google Scholar] [CrossRef]
- Van der Jeught, S.; Dirckx, J.J.J. Deep neural networks for single shot structured light profilometry. Opt. Express 2019, 27, 17091–17101. [Google Scholar] [CrossRef]
- Machineni, R.C.; Spoorthi, G.E.; Vengala, K.S.; Gorthi, S.; Gorthi, R.K.S.S. End-to-end deep learning-based fringe projection framework for 3D profiling of objects. Comput. Vis. Image Underst. 2020, 199, 103023. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Zhang, Z.; Zuo, C.; Zhang, Y.; Zheng, D.; Han, J. Dynamic 3-D measurement based on fringe-to-fringe transformation using deep learning. Opt. Express 2020, 28, 9405–9418. [Google Scholar] [CrossRef]
- Gupta, M.; Agrawal, A.; Veeraraghavan, A.; Narasimhan, S.G. A practical approach to 3D scanning in the presence of interreflections; subsurface scattering defocus. Int. J. Comput. Vis. 2013, 102, 33–55. [Google Scholar] [CrossRef]
- Rao, L.; Da, F. Local blur analysis phase error correction method for fringe projection profilometry systems. Appl. Opt. 2018, 57, 4267–4276. [Google Scholar] [CrossRef] [PubMed]
- Waddington, C.; Kofman, J. Analysis of measurement sensitivity to illuminance fringe-pattern gray levels for fringe-pattern projection adaptive to ambient lighting. Opt. Lasers Eng. 2010, 48, 251–256. [Google Scholar] [CrossRef]
- Ribo, M.; Brandner, M. State of the art on vision-based structured light systems for 3D measurements. In Proceedings of the 2005 IEEE International Workshop on Robotic Sensors: Robotic & Sensor Environments, Ottawa, ON, Canada, 30 September–1 October 2005; pp. 2–6. [Google Scholar]
- Liu, P.; Li, A.; Ma, Z. Error analysis and parameter optimization of structured-light vision system. Comput. Eng. Des. 2013, 34, 757–760. [Google Scholar]
- Jia, X.; Jiang, Z.; Cao, F.; Zeng, D. System model and error analysis for coded structure light. Opt. Precis. Eng. 2011, 19, 717–727. [Google Scholar]
- Fan, L.; Zhang, X.; Tu, D. Structured light system calibration based on digital phase-shifting projection technology. Machinery 2014, 52, 73–76. [Google Scholar]
- ISO 15530; Geometrical Product Specifications (GPS)—Coordinate Measuring Machines (CMM): Technique for Determining the Uncertainty of Measurement. ISO: Geneva, Switzerland, 2013.
- ISO 25178; Geometrical product specifications (GPS)—Surface texture: Areal. ISO: Geneva, Switzerland, 2019.
- Giusca, C.L.; Leach, R.K.; Helery, F.; Gutauskas, T.; Nimishakavi, L. Calibration of the scales of areal surface topography-measuring instruments: Part 1. Measurement noise residual flatness. Meas. Sci. Technol. 2013, 23, 035008. [Google Scholar] [CrossRef]
- Giusca, C.L.; Leach, R.K.; Helery, F. Calibration of the scales of areal surface topography measuring instruments: Part 2. Amplification; linearity squareness. Meas. Sci. Technol. 2013, 23, 065005. [Google Scholar] [CrossRef]
- Giusca, C.L.; Leach, R.K. Calibration of the scales of areal surface topography measuring instruments: Part 3. Resolut. Meas. Sci. Technol. 2013, 24, 105010. [Google Scholar] [CrossRef]
- Ren, M.J.; Cheung, C.F.; Kong, L.B. A task specific uncertainty analysis method for least-squares-based form characterization of ultra-precision freeform surfaces. Meas. Sci. Technol. 2012, 23, 054005. [Google Scholar] [CrossRef]
- Ren, M.J.; Cheung, C.F.; Kong, L.B.; Wang, S.J. Quantitative Analysis of the Measurement Uncertainty in Form Characterization of Freeform Surfaces based on Monte Carlo Simulation. Procedia CIRP 2015, 27, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Cheung, C.F.; Ren, M.J.; Kong, L.B.; Whitehouse, D. Modelling analysis of uncertainty in the form characterization of ultra-precision freeform surfaces on coordinate measuring machines. CIRP Ann.-Manuf. Technol. 2014, 63, 481–484. [Google Scholar] [CrossRef]
- Vukašinović, N.; Bračun, D.; Možina, J.; Duhovnik, J. The influence of incident angle, object colour and distance on CNC laser scanning. Int. J. Adv. Manuf. Technol. 2010, 50, 265–274. [Google Scholar] [CrossRef]
- Ge, Q.; Li, Z.; Wang, Z.; Kowsari, K.; Zhang, W.; He, X.; Zhou, J.; Fang, N.X. Projection micro stereolithography based 3D printing and its applications. Int. J. Extrem. Manuf. 2020, 2, 022004. [Google Scholar] [CrossRef]
- Schaffer, M.; Grosse, M.; Harendt, B.; Kowarschik, R. Coherent two-beam interference fringe projection for highspeed three-dimensional shape measurements. Appl. Opt. 2013, 52, 2306–2311. [Google Scholar] [CrossRef]
- Duan, X.; Duan, F.; Lv, C. Phase stabilizing method based on PTAC for fiber-optic interference fringe projection profilometry. Opt. Laser Eng. 2013, 47, 137–143. [Google Scholar]
- Duan, X.; Wang, C.; Wang, J.; Zhao, H. A new calibration method and optimization of structure parameters under the non-ideal condition for 3D measurement system based on fiber-optic interference fringe projection. Optik 2018, 172, 424–430. [Google Scholar] [CrossRef]
- Gayton, G.; Su, R.; Leach, R.K. Modelling fringe projection based on linear systems theory and geometric transformation. In Proceedings of the 2019 International Symposium on Measurement Technology and Intelligent Instruments, Niigata, Japan, 1–4 September 2019. [Google Scholar]
- Petzing, J.; Coupland, J.; Leach, R.K. The Measurement of Rough Surface Topography Using Coherence Scanning Interferometry; National Physical Laboratory: London, UK, 2010. [Google Scholar]
- Salahieh, B.; Chen, Z.; Rodriguez, J.J.; Liang, R. Multi-polarization fringe projection imaging for high dynamic range objects. Opt. Express 2014, 22, 10064–10071. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Bell, T.; Zhang, S. High dynamic range real-time 3D shape measurement. Opt. Express 2016, 24, 7337–7346. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Jiang, H.; Lin, H.; Tang, S. A high dynamic range structured light means for the 3D measurement of specular surface. Opt. Lasers Eng. 2017, 95, 8–16. [Google Scholar] [CrossRef]
- Lin, H.; Gao, J.; Mei, Q.; Zhang, G.; He, Y.; Chen, X. Three-dimensional shape measurement technique for shiny surfaces by adaptive pixel-wise projection intensity adjustment. Opt. Lasers Eng. 2017, 91, 206–215. [Google Scholar] [CrossRef]
- Zhong, C.; Gao, Z.; Wang, X.; Shao, S.; Gao, C. Structured Light Three-Dimensional Measurement Based on Machine Learning. Sensors 2019, 19, 3229. [Google Scholar] [CrossRef] [Green Version]




| Methods | Hardware Configuration | Performance | Applicable Occasion | |||
|---|---|---|---|---|---|---|
| Number of Cameras | Lighting Device | Resolution | Representative Accuracy | Anti-Interference Capability | ||
| Stereo vision | 2 | None | Low | 0.18/13.95 mm (1.3%) [52]; 0.029/24.976 mm (0.12%) [53] | Medium | Target positioning and tracking |
| 3D laser scanning | 1 or 2 | Laser | Medium or high | 0.016/2 mm (0.8%) [15]; 0.05/60 mm (0.8%) [60,61]; 0.025 mm with the scanning area of 310 × 350 mm2 (CREAFORM HandySCAN) | High (against ambient light) | Static measurement for surfaces with high diffuse reflectance |
| RSP | 1 or 2 | Projector or laser | Medium | 0.392/20 mm (2%) [64]; 0.845/20 mm (Kinect v1) | Low (high sensitivity to noise) | Easy to miniaturize for use in consumer products |
| Binary coding projection | 1 or 2 | Projector | Medium | 0.098/12.6994 mm (0.8%) [76] | Medium | Static measurement with fast speed but relatively low accuracy |
| FTP | 1 or 2 | Projector | High | 0.2/35 mm (0.6%) [82] | Medium | Dynamic measurement for surfaces without strong texture |
| PSP | 1 or 2 | Projector | High | 0.02 mm within a 200 × 180 mm2 field of view [101]; up to 0.0025 mm (GOM ATOS Core) | Medium or high | Static measurement for complex surfaces with high accuracy and dense point cloud |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Yang, S.; Hu, P.; Deng, H. Advances and Prospects of Vision-Based 3D Shape Measurement Methods. Machines 2022, 10, 124. https://doi.org/10.3390/machines10020124
Zhang G, Yang S, Hu P, Deng H. Advances and Prospects of Vision-Based 3D Shape Measurement Methods. Machines. 2022; 10(2):124. https://doi.org/10.3390/machines10020124
Chicago/Turabian StyleZhang, Guofeng, Shuming Yang, Pengyu Hu, and Huiwen Deng. 2022. "Advances and Prospects of Vision-Based 3D Shape Measurement Methods" Machines 10, no. 2: 124. https://doi.org/10.3390/machines10020124
APA StyleZhang, G., Yang, S., Hu, P., & Deng, H. (2022). Advances and Prospects of Vision-Based 3D Shape Measurement Methods. Machines, 10(2), 124. https://doi.org/10.3390/machines10020124





