Theoretical Roughness Modeling of Hard Turned Surfaces Considering Tool Wear

Abstract

Surface roughness is an important factor in metal cutting, and usually different surface roughness characteristics are used to control the quality of the machined surfaces. However, as the cutting tool wears out during the cutting process, the roughness values change. In most cases, theoretical roughness values are calculated without taking the wear characteristics of the tool into account. For this reason, the calculated and measured roughness values may differ from each other, and the tendency of their change may also be different. This paper presents a method for the determination of the theoretical roughness of hard turned surfaces considering the wear of the cutting tool. The purpose of the analyses performed was to show the effect of wear trace on the tool and the roughness of the machined surface and to give a possible method to take the wear into account when calculating the theoretical roughness values. During the investigations, the shape of the actual (worn) edge section of the cutting tool was recorded by an optical microscope, and the theoretical surface roughness values were calculated with that profile by a CAD modeling method developed earlier. Cutting experiments were conducted on a lathe machine with two similar cutting tools, one of them has significant tool wear, while the other was a completely new one. The calculated theoretical roughness values were compared with real measured roughness values, and the error of the estimates was between 8.7 and 68.3%, larger errors were found at lower feeds.

1. Introduction

Hard turning is a widely used process to cut the surfaces of hard materials that have hardness values over 45 HRC. This process is especially important in the manufacturing of automotive parts [1] alongside other industry segments, e.g., marine [2], aerospace [3], punch and die or mold making [4], among others. It can be used to semi-finish the surface before grinding [5], or it can totally eliminate the need for grinding if the process parameters are carefully controlled [6]. One of the indisputable advantages of the hard turning process over grinding is the possibility of creating more favorable residual stress conditions [7]. Hard turning can be considered a more environmentally friendly technology [8] than grinding as well: in a typical grinding process, an excessive amount of coolant is used which will be mixed up with the removed workpiece and tool particles, thus generating an abrasive slurry [9]. Hard turning is usually performed in dry conditions [10] or with a minimal amount of coolant and lubricant fluids [11,12]. Bartarya and Choudhury [13] have concluded that when using the right combination of insert nose radii, feed rate and other cutting parameters, hard turning can produce a better surface finish than grinding. The surface roughness in hard turning is relatively easy to estimate, as the process is performed with a single point cutting tool having definite edge geometry (i.e., the exact form of the cutting edge is known, and its lengths and angles are exactly defined in contrast with abrasive processes, where the edge geometry is not defined) [14]. As a consequence of this, several researchers have already dealt with estimating the surface roughness achievable in hard turning with different modeling techniques applied [15]. In the following, some of the works considered more important by the authors are presented.

State of the Art of Surface Roughness and Wear Modeling in Hard Turning

Researchers use different methods to model surface roughness. These modeling procedures were classified into four groups by Benardos and Vosniakos [16]: a machining theory-based approach, experimental investigation approach, designed experiments approach and artificial intelligence approach. Every approach has its own characteristics, advantages and disadvantages. However, Lu [17] has divided the modeling procedures into three main groups: pure modeling, a signal-based approach and artificial intelligence-based approach. This is essentially a similar approach for the classification as the previous one, only from a slightly different perspective: the above-mentioned article by Benardos and Vosniakos was written earlier, and the perception of modeling procedures changes over time: what seemed to be a novelty 5 or 10 years ago (e.g., the use of experimental design methods) later became routine for conducting experiments. The classification developed by Lu was also born more than ten years ago, and since then we have seen tremendous advances in both modeling and the application of artificial intelligence methods, as well as sensor technology. Nowadays, with the development of sensor technologies and the rise of Industry 4.0 and the Internet of Things (IoT) [18,19], the goal is to approach real roughness values as accurately as possible when estimating theoretical roughness, e.g., by constructing the digital twin of the whole machining system [20].

There are significant differences in the calculation of the theoretical roughness for cutting modes with different kinematic conditions. Khorasani et al. [21] have shown that surface roughness is fundamentally influenced by six factors: tool and workpiece properties, cutting parameters, machine tool properties and thermal and dynamic parameters. For processes with relatively simple movements, such as turning [22], the calculation of theoretical roughness is relatively simple if the goal is to determine the theoretical roughness in the classical sense, i.e., based solely on tool and workpiece geometry and the feed value [23]. For other methods with more complex kinematics, surface roughness modeling also becomes more difficult [24].

As it was seen from the above groupings, one way to examine the surface roughness is to perform cutting experiments, measure the surfaces using sensor technology and then set up models based on them to estimate the expected roughness. Taha et al. [25] have used this experimental roughness estimation method for turning AISI D2 steel. Zhao et al. have also utilized this method [26,27] to establish a correlation between the cutting tool edge radius and surface roughness and sub-surface deformation using FE simulation and cutting experiments. Zak [28] has also considered the tool corner radius when measuring the cutting forces and surface roughness and has made some correlation between them. Mane and Kumar [29] have investigated the effects of the different cutting parameters (cutting speed, feed, depth of cut) on Ra surface roughness in hard turning with Minimal Cutting Fluid Application (MCFA). They have used Response Surface Methodology (RSM) and Analysis of Variance (ANOVA) methods. Based on the results of CNC turning experiments on hardened C45 steel, Selvam and Senthil [30] set up a mathematical model to estimate the Ra arithmetical average roughness. Ferreira et al. [31] have evaluated surface roughness using conventional and multi-radii ceramic tools for the hard turning of AISI H13 steel. The measured values were compared with theoretical data which was calculated by empirical formulas. D’Addona and Raykar [32] have used wiper inserts in the hard turning of oil hardening non-shrinking steel, and they analyzed the effect of the insert geometry on the surface roughness by using ANOVA and Analysis of Means (AOM) plots. Singh and Rao [33] have investigated the effects of the nose radius and the effective rake angle of the cutting insert on the surface roughness alongside two technological parameters, the cutting speed v and the feed f. Struzikiewicz et al. [34] have made cutting experiments to compare the surface roughness at longitudinal turning of sintered and cast AlSi10MG alloy samples, and a correlation was established between the measurement data and the theoretical roughness values. Pinheiro et al. [35] have investigated the effect of cutting parameters on surface roughness, consumed power, vibration and tool wear indicators using the Taguchi method for a difficult-to-machine material, Inconel 718 superalloy. Masoudi et al. [36] experimentally investigated the effect of applying minimum quantity lubrication on the roughness of the machined surface, cutting forces and tool wear when turning AISI 1045 steel. Similar studies have been performed by Limin [37], but for the turning of Ti6Al4V alloy. Yousefi and Zohoor [38] proposed a knowledge-based expert system to predict surface roughness based on their experiments, while Li et al. [39] used Adaptive Genetic Algorithms to estimate roughness using experimental data. Dhilip et al. [40] reported their experiments to maximize material removal rate and to minimize machining time and surface roughness. Gray relational analysis was performed to optimize these output parameters. Hessainia et al. [41] optimized the technological parameters (cutting speed, feed rate, depth of cut) in hard turning using the RSM method to reduce vibrations and improve surface roughness. Grzesik [42] presented a combined method for estimating Rz and Sz surface roughness parameters in precision hard turning with a CBN tool, where the empirical model generated from the experimental data was improved by advanced numerical modeling. Tuan et al. [43] investigated the effect of MoS₂ nanoparticle concentration and technological parameter cutting speed, feed-on surface roughness and surface microstructure during the hard turning of 90CrSi steel with minimal lubrication. The Box–Behnken experimental design was used to analyze the effect and interactions of the input parameters and to determine the optimal parameter set. An article by Abbas et al. [44] presents an experimental hard turning study for the comparative analysis of Wiper and TiCN + AL₂O₃ + TiN-coated carbide inserts having conventional radius. The cutting was performed with the optimal technological parameters determined by the preliminary experiments for both insert types. The quality of the machined surface, tool wear and specific cutting energy were determined for the different cutting lengths. Aslantas et al. [45] investigated surface roughness and tool wear characteristics during the micro-turning of Ti-6Al-4V alloy. Micro-turning is a special machining process because further reduction of surface roughness could only be done in a very complicated way, so technological parameters must be chosen for turning that provide adequate results.

Different modeling techniques (analytical, numerical, FEM-based, etc.) are also commonly used to predict the surface roughness values. Some of the researchers consider only the effect of tool geometry and technological data during the modeling. As an example, Adamczak and Cus [23] have introduced a generalized model of roughness formation which can be applied for most of the typical machining operations, e.g., turning, milling, etc. Sung et al. [46] developed an analytical model in which surface roughness parameters (Ra, Rt) were calculated based on feed, nose radius and two cutting edge angles: the inclination angle and the rake angle. Some others also consider the workpiece characteristics. Chavoshi and Tajdari [47] have used an Artificial Neural Network (ANN) to study the effects of the workpiece hardness and spindle speed on surface roughness.

There are also studies where more complex models have been used to model the theoretical roughness. He et al. have developed a combined model that takes into account the kinematic and dynamic characteristics of the process and also defects in the workpiece material [48,49]. Tool edge waviness, material spring back and plastic side flow are all integrated in the kinematic part of the model. The simulation of the dynamical effects was performed by a multifrequency vibration model. Kiyak [50] developed a theoretical model where the distortion of the marks of the cutting insert in the theoretical roughness profile was calculated based on the torsional momentum acting on the tool holder. The obtained results were validated using FEM analysis. Tian et al. [51] studied the surface roughness in hard turning both theoretically and experimentally, taking into account the basic machining parameters as well as the relative vibrations in both the cutting and feed directions. Tomov et al. [52] presented a theoretical model for estimating surface roughness in longitudinal turning in which a distorting profile was superimposed on a kinematically geometrically calculated one to form the final roughness profile. Spindle imbalance is also an important factor which may be considered during the roughness calculations, as it was shown in [53]. Rashid et al. [54] performed experiments to determine the available surface roughness in hard turning by drilling holes in the surface before machining. This generated intermittent relaxation to the tool during cutting and they concluded that this can improve the surface roughness and decrease the temperature and forces. This method is termed “surface defect machining” [55].

In the case of significant tool wear (which is essentially unavoidable during cutting), roughness values will change, and the well-known kinematics-based formula for theoretical roughness calculations [56] will become inaccurate. In the case of hard turning, the cutting tool must withstand a high load [57]. Due to the high temperature generated during the process, burn-ins and so-called Built-up-Edges (BUEs) may be formed both on the rake face and on the flank of the cutting insert, which sooner or later significantly affect the edge geometry of the tool and the microgeometry of the created surface [58]. These are also the main cause of the so-called white-layer formation in hard turning [59], which is a very hard layer at the machined surface and can lead to crack permeation and product failure [60]. Therefore, tool wear in hard turning and its effect on surface roughness was analyzed by many researchers. Mondal et al. [61] has investigated how the different cooling options (dry, wet) and the main cutting parameters (cutting speed and feed) affect the tool wear when hard turning of 16MnCrS5 steel by TiC-coated carbide inserts. Colantonio et al. [62] analyzed cutting tool wear during turning using artificial intelligence techniques. Wu et al. [63] investigated the possibilities of increasing the wear resistance and cutting efficiency of a micro-grooved tool with “Deform” finite element software in AISI 201 material-grade steel turning. Modern metalworking centers cannot yet reliably estimate the wear status of a tool used in metal cutting. The aim of Lapshin’s article [64] was to estimate the wear rate of a tool indirectly, based on a consistent model between systems designed for the force, heat and vibration conditions of the cutting process. In an article by Airao et al. [65], they investigated how ultrasonic vibration affects tool wear when a coated carbide insert is used for machining Nimonic-90 nickel-based superalloy in dry and wet conditions.

Several researchers have addressed the relationship between tool wear and surface roughness in hard machining. Zawada-Tomkiewicz [66] showed how the wear of the cutting edge and its surroundings (such as the flank wear) can have a significant effect on surface roughness in hard turning. Tamizharasan et al. [67] have analyzed the effect of the cutting speed, feed, depth of cut, tool grade, workpiece hardness and flank wear on tool life, material removal, economics of operation and surface roughness. They have shown that flank wear can significantly change the nominal cutting geometry, and it is a typical factor of qualifying the cutting tool condition. Dureja et al. [68] also investigated the effect of technological parameters on tool wear and surface roughness using S/N ratio, ANOVA analysis and Taguchi methods when hard turning AISI D3 steel. Yallese et al. [69] have investigated the effect of cutting parameters on ceramic and CBN tool wear in the hard turning of X200Cr12 steel, and they have determined the correlation between surface roughness and tool wear. The aim of the studies by del Risco-Alfonso et al. [70] was to determine the relationship between the main cutting force, the initial speed of tool wear and the surface roughness. In their paper, they proposed a multi-purpose optimization model to minimize energy consumption and initial wear rate, as well as to maximize productivity. García-Martínez et al. [71] analyzed surface integrity and tool wear when turning copper-nickel 70/30 ASTM B122 alloy with low initial lubrication.

Palanisamy and Shanmugasundaram [72] have used regression and Artificial Neural Network (ANN) models for predicting tool wear and surface roughness by using cutting speed, feed and depth of cut as input parameters. A similar method was used by Senthilkumar and Tamizharasan [73], who also dealt with the estimation of tool wear and roughness, also using ANN. Özel and Karpat [74] utilized Neural Network modeling combined with regression models to predict the surface roughness and flank wear for a variety of cutting conditions when hard turning of hardened AISI 52100 and AISI H-13 steels. Kundrak et al. [75] analyzed the tool life functions in hard turning, and they concluded that the tool wear that determines the tool life originates from very complex mechanical, chemical thermal, electrical and other processes, so it seems to be difficult to describe the wearing process analytically. However, Penalva and others [76] have found that tool wear is a partly deterministic process and examining the roughness of the machined surface provides an opportunity to map the wear condition of the tool. Pimenov et al. [77] proposed an artificial intelligence-based method for the automatic estimation of surface roughness in face milling by monitoring cutting insert wear. The AI-based roughness prediction has the main drive power and tool wear among others as input parameters, and several AI methods were tested: random forest (RF), standard multilayer perceptron, regression trees and radial-based function, of which the RF method proved to be the most accurate.

As it can be seen from the mentioned works, tool wear is an important factor to consider during surface roughness modeling in hard turning. The aim of the research was to investigate how tool wear can be taken into account in the calculation of theoretical roughness in hard turning. Based on our investigations, a new method is proposed for the calculation of theoretical roughness, which is targeted at the more accurate description of the machined surface topography. The hypothesis of the research is that the wear mark on the working edge of the cutting tool significantly influences the roughness of the created surface, so if the contour of the worn tool edge can be modeled, then the theoretical roughness can be more accurately estimated. This represents a new application of a theoretical surface roughness determination method based on the CAD modeling presented earlier [78]. Based on the investigations and their results presented in the paper, the relationship between surface roughness and tool wear can be better understood.

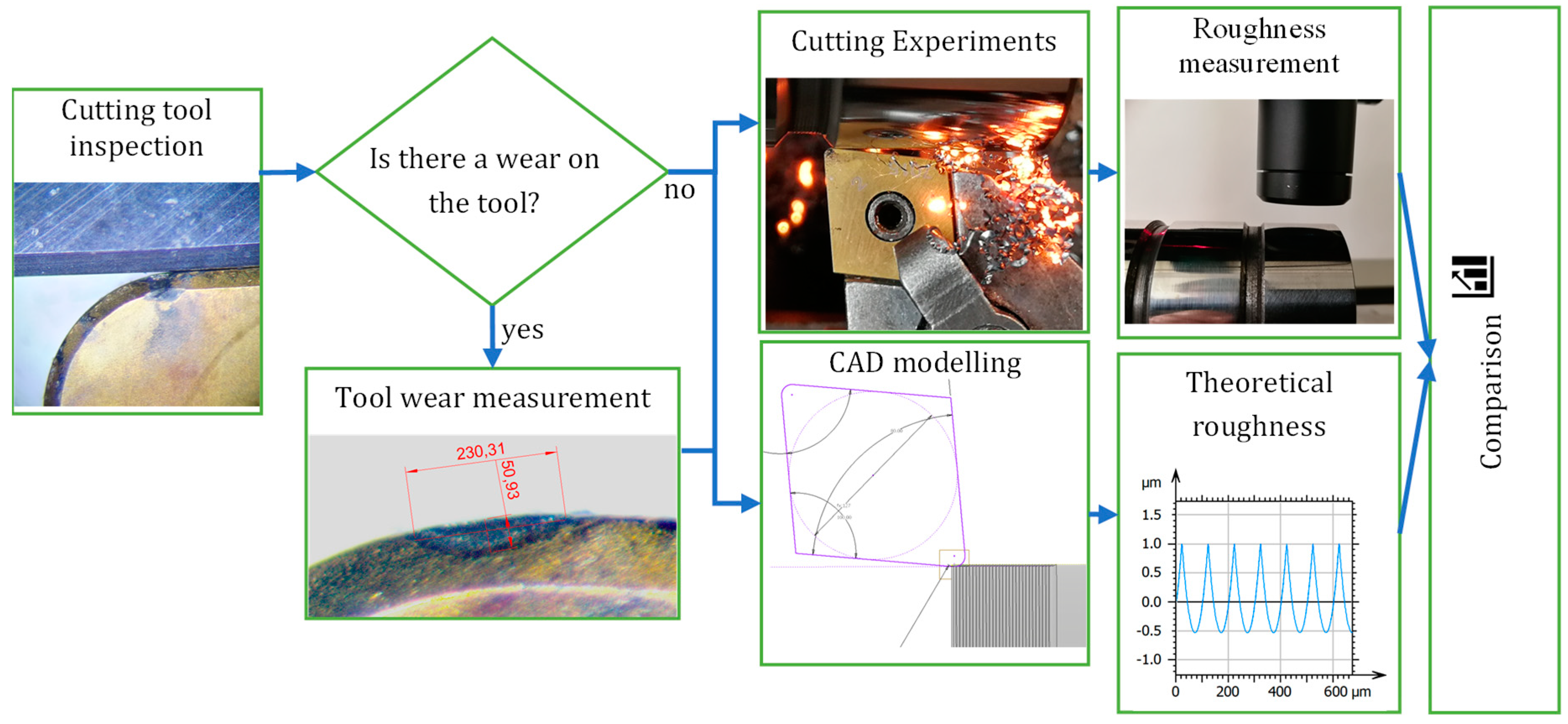
2. Materials and Methods

The overview of the applied investigation method is showed in Figure 1.

Initially, the cutting tool was analyzed by a Zeiss Stereo Discovery V8 stereo microscope with 80X magnification. If there are any wear marks on the tool, then the wear characteristics should be measured, and the outer contour of the worn insert should be recorded. At that stage, it is important to place the cutting tool according to its working position during the cutting, i.e., it is favorable to use the tool holder for these investigations and fix the insert into its pocket. The next step is the actual creation of the machined surface: on the one hand to perform the cutting experiments, while on the other hand to generate the theoretical surface by means of CAD modeling considering the wear characteristics of the insert. After that, the surface roughness can be obtained either by measurements in the case of real cutting or by getting the model points of the simulated surface by an expediently developed interface software which is able to communicate with the CAD system. After that, the roughness data could be evaluated with the help of a commercial surface roughness evaluation software, the Altimap (Mountains) software was utilized for that in the actual research work. Then, the two datasets can be compared, and maybe the relation can be described between them. This method has the ability to estimate the expected roughness values for a given insert before starting the actual cutting process.

2.1. Investigation Conditions

Both the physical cutting tests and the theoretical simulations were conducted with identical cutting conditions. Two cutting inserts were applied during the investigations. Both were the same type CNGA 80° rhombic-shaped CBN inserts with nose radius of 0.8 mm from the same manufacturer, the only difference between them was that Insert2 had a clear wear on it, as it is shown in Figure 2 from two different view angles. The measured flank wear was about 40 µm, while the crater on the rake face was measured as approximately 230 µm long and 51 µm wide. Examination of the development of tool wear was not the subject of the present research, so the worn insert was obtained after previous cutting experiments. The cutting insert type was chosen for practical reasons: it is a very common tool for hard turning, and the 0.8 mm nose radius can be considered as a mean value, as inserts with a radius of 0.4 to 1.2 mm are usually used for turning.

An MCLNR-16-4D tool holder was used during the cutting tests. With this configuration, the following working tool geometry was achieved: κ_r = 95°; γ_p = −6°; γ_f = −6°.

The test samples were Ø48 mm rods made from CMO3 (34CRMO4 equivalent, WNr. 1.7220) steel in a hardened state. Its hardness was measured at around 53–55 HRC. As the varied parameter was the feed per revolution value, the work part has to be prepared for the feed change, thus 5 mm wide grooves were cut after every measurement area, which was 20 mm long as it is shown in Figure 3, where the cutting inserts are also depicted.

The cutting experiments were conducted on an EU 400-01 universal lathe machine. This is a traditional lathe machine, which has enough rigidity to perform this operation. Moreover, it has a brand new NSK rotating center placed in the tailstock, as the work holding is extremely important in hard turning operations.

The wear of the cutting tool was measured by a Zeiss Stereo Discovery V8 microscope. The surface roughness measurements were performed by an Altisurf 520 3D surface roughness measurement equipment. The applied probe was a CL2 type Confocal Chromatic Sensor (CCS), with an MG140 magnifier. The measurement range of this setup is 300 µm, while the theoretical resolution is up to 0.5 nm. A standard Gaussian filter was used for the evaluation, and the recommendations of ISO 4288 were followed for the cut-off and evaluation length.

In terms of cutting parameters, the values of spindle speed and depth of cut were constant during the experiments: n = 1060 1/min; a_p = 0.15 mm. The parameter change for each experimental step was the value of the feed per revolution, and the following values were used: f = 0.05; 0.1; 0.15; 0.2 and 0.25 mm. As the value of the feed is known to have the greatest effect on the surface roughness, this was chosen as a variable.

2.2. Surface Roughness Modeling

A method was developed earlier for the three-dimensional modeling of theoretical surface roughness in the case of cutting with tools having defined edge geometry [78]. This method is based on CAD modeling of the machined surface, and by obtaining the coordinate points of the modeled surface along a so-called theoretical measurement line and evaluating them in a suitable software for surface roughness calculation. The schematic overview of the developed modeling method is illustrated in Figure 4.

The modeling of the machined surface was done in the following basic steps:

• First, the uncut workpiece geometry (in the actual case, it is a cylinder) was modeled in the CAD system (the AutoDesk Inventor software was used in the current work).
• After that, the two-dimensional cutting edge geometry was created in the tool reference plane. This is an ideal representation of the cutting tool edge, without its own irregularities and/or wear characteristics.
• Next, the trajectory of the cutting tool was created on the surface. In the case of turning, it is a helical path, where the value of the pitch of the helix corresponds to the feed per revolution (f) value of the turning process. The axis of the helix is the rotational axis of the workpiece.
• The next step is the actual simulation of the cutting process: the cutting edge geometry is guided along the tool path and the resulting volume is cut from the workpiece material. Thus, the machined surface was obtained. However, it should be noted here that most CAD systems do not allow to intersect the cut volume by itself (self-intersection). This problem can be easily solved by reducing the rotational angle below 360°, and then creating a linear pattern along the rotational axis from the cut volume with the spacing distance of feed (f).
• The next step is to create a so-called measurement line: a measurement plane was defined, which intersects the generated surface in the given radial position, thus cutting out the 2D “measured” profile of the simulated surface. This is basically the theoretical profile, but the points of this profile are not available by default in the CAD system.
• The following step is to query the points of this profile from the CAD system, for which a specially designed interface program (Add-In) had to be developed. There is a programming interface for almost every CAD system, which can be used to interact with it, and to perform various modeling and other tasks.
• This is followed by storing the obtained profile coordinates in an appropriate file format, which can be evaluated later with a dedicated surface analysis software. In the current investigations, the AltiMap (Mountains) software was used, which is developed by Digital Surf Inc. It has its own format for 2D profiles (.pro) and surfaces (.sur) as well, and there is an application programming interface for saving the data points in one of those formats.
• The final step is to load the generated data files into the AltiMap software and evaluate them according to the parameters needed. Thus, the theoretical and the measured data can be evaluated with the same software, with the same method.

This method was successfully applied for face milling [79] and conventional turning operations [80]. However, if the cutting tool has a significant wear, the generated surface topography may look quite different. An example of this is shown in Figure 5, where the measured roughness profiles for identical tools having a nose radius of r_ε = 0.8 mm for f = 0.25 mm can be seen. The tool on Figure 5b has a significant flank wear (VB ≈ 40 µm), and a crater on the rake face as well (see Figure 2), which results in a distorted roughness profile diagram.

Therefore, the previously introduced modeling method was modified in order to facilitate the consideration of the wear of the cutting insert. To do this, the first step was to obtain the microscope image of the insert. A Zeiss Discovery V8 stereo microscope was used for this purpose. The insert was clamped in the tool holder, and then the working part of the insert was recorded with the mentioned equipment. Several measurements were performed both on the rake and on the flank surface of the tool as well to find the appropriate wear characteristic for the roughness modeling. After the wear of the insert was measured by the stereo microscope, it was realized that neither the flank wear nor the crater on the rake face is what really matters during the cut surface formation, but the outer contour of the insert. As it can be seen from Figure 6, there are two “cusps” on the cutting edge, and this form was observed on the roughness profile diagrams as well.

Thus, it was concluded that the outer contour of the insert should be used as insert geometry in the CAD system during the theoretical surface generation. Thus, the original modeling method, which was introduced earlier, needs to be slightly modified to enable the consideration of tool wear during the theoretical modeling. The previously taken insert image file was imported into the CAD System, and a spline curve was created on the outer contour of the insert, as is shown in Figure 5. This spline replaces the cutting tool shape on the tool reference plane.

Figure 7 shows the theoretical profiles from the original and the modified modeling method (i.e., without and with considering the tool wear). The roughness shape in Figure 7b may be compared with its measured counterpart in Figure 5b, and then their similarity becomes apparent. The courses of these two roughness curves are very close to each other, and their cusp heights are also similar.

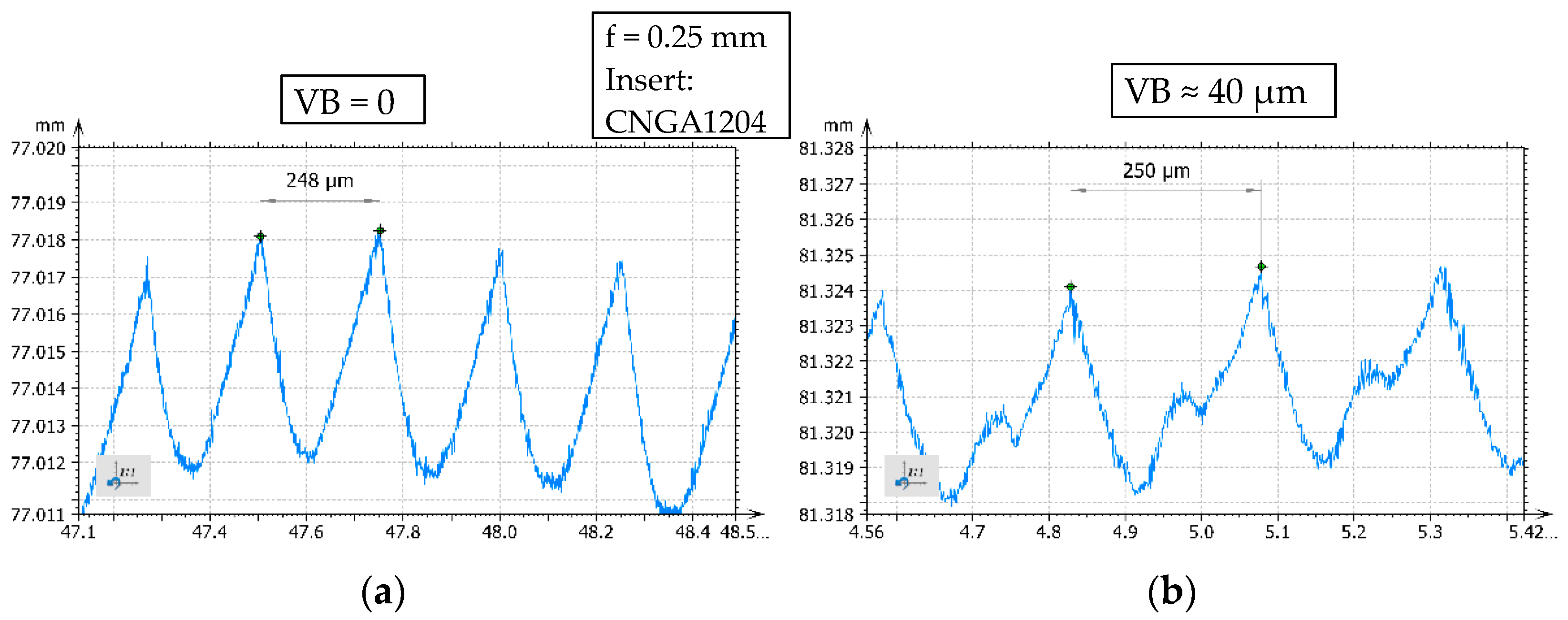
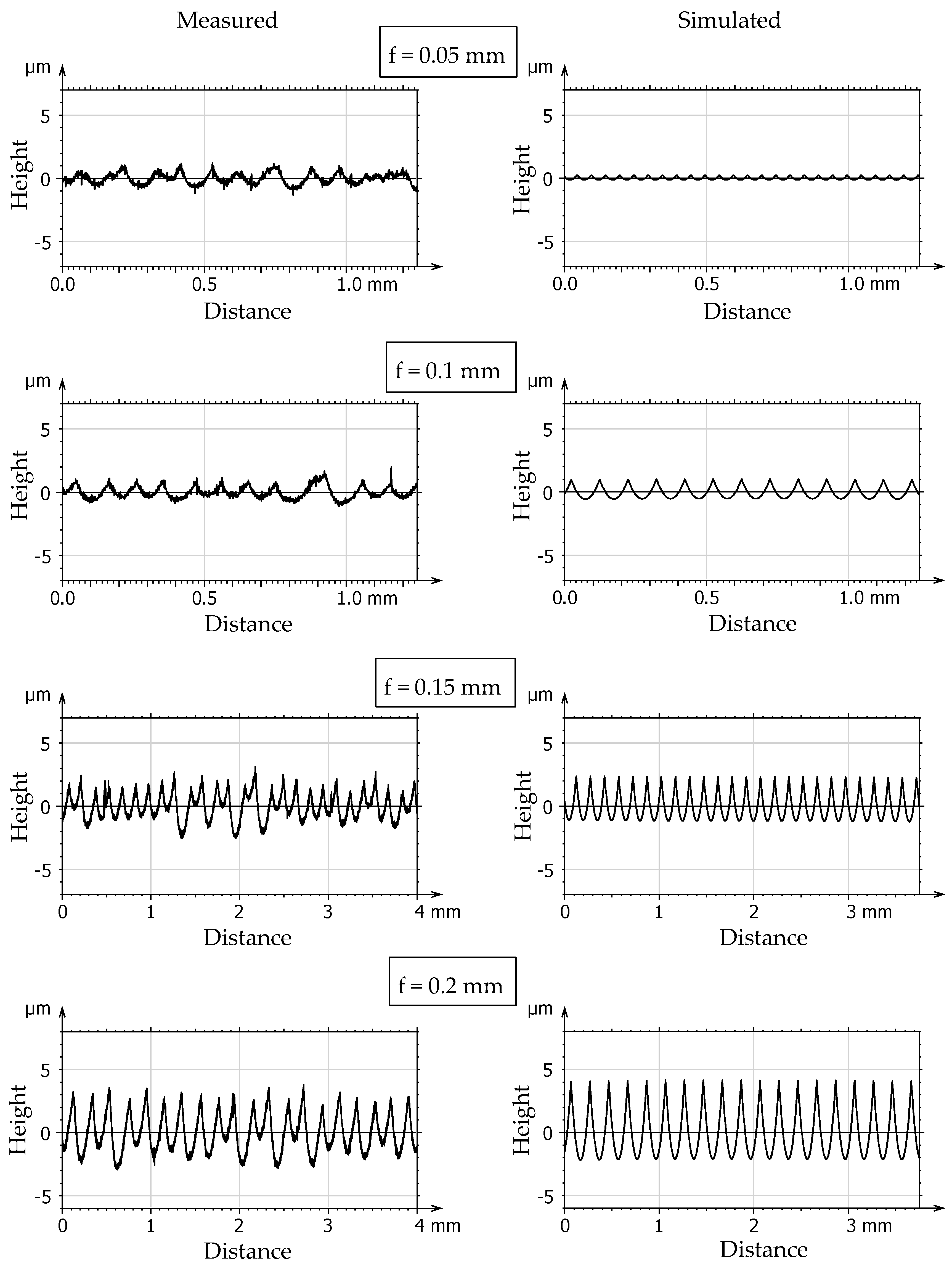
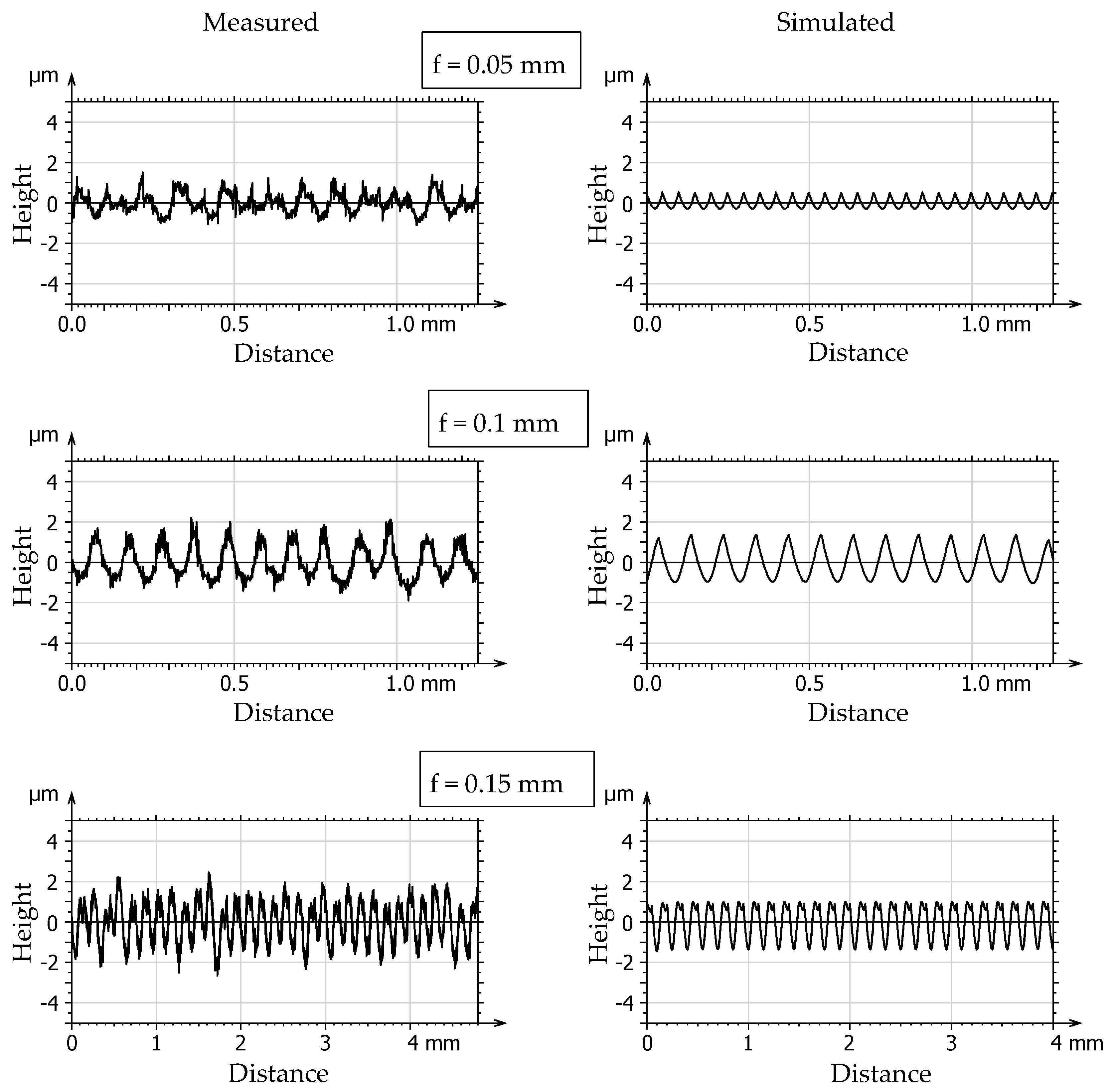
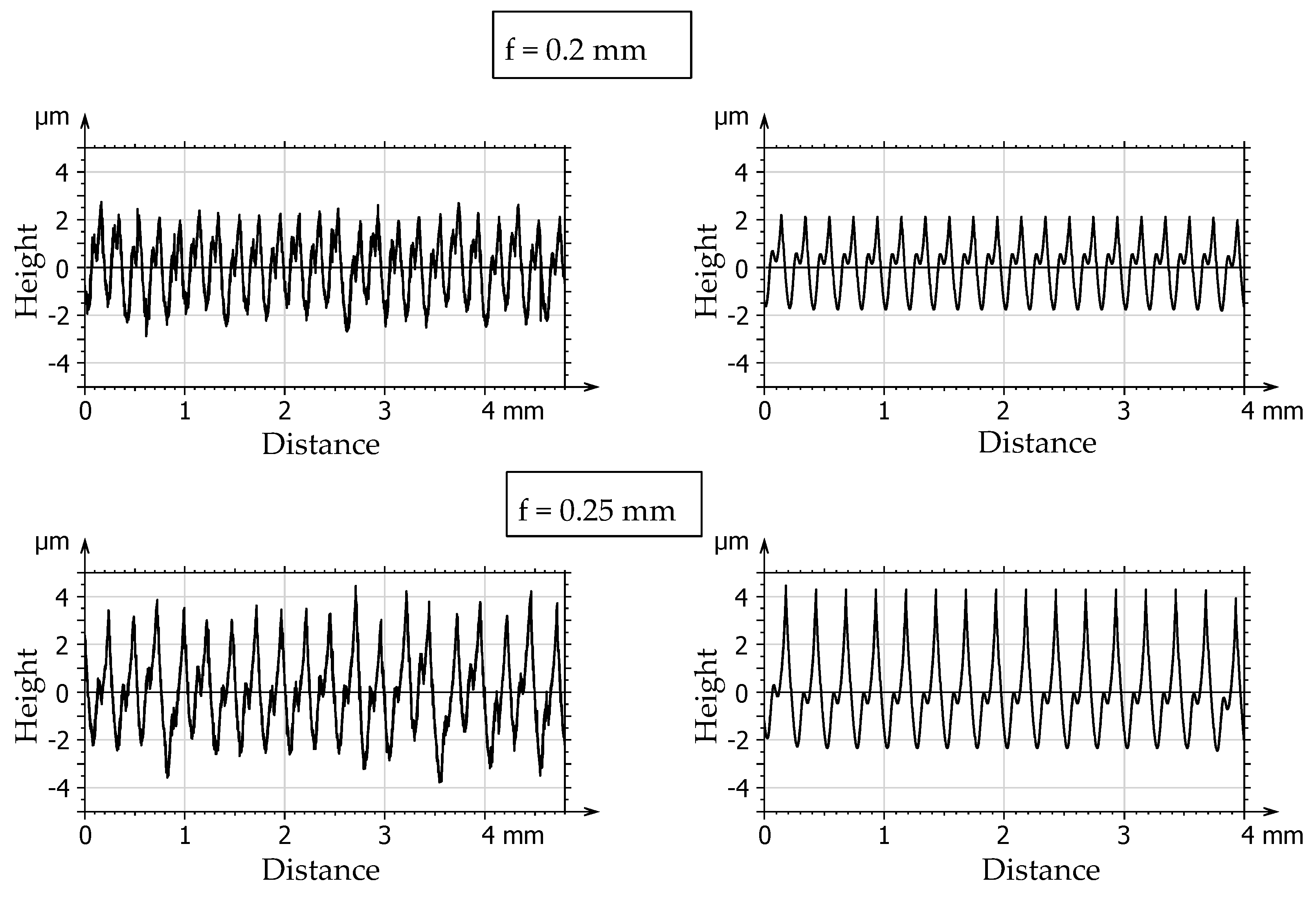
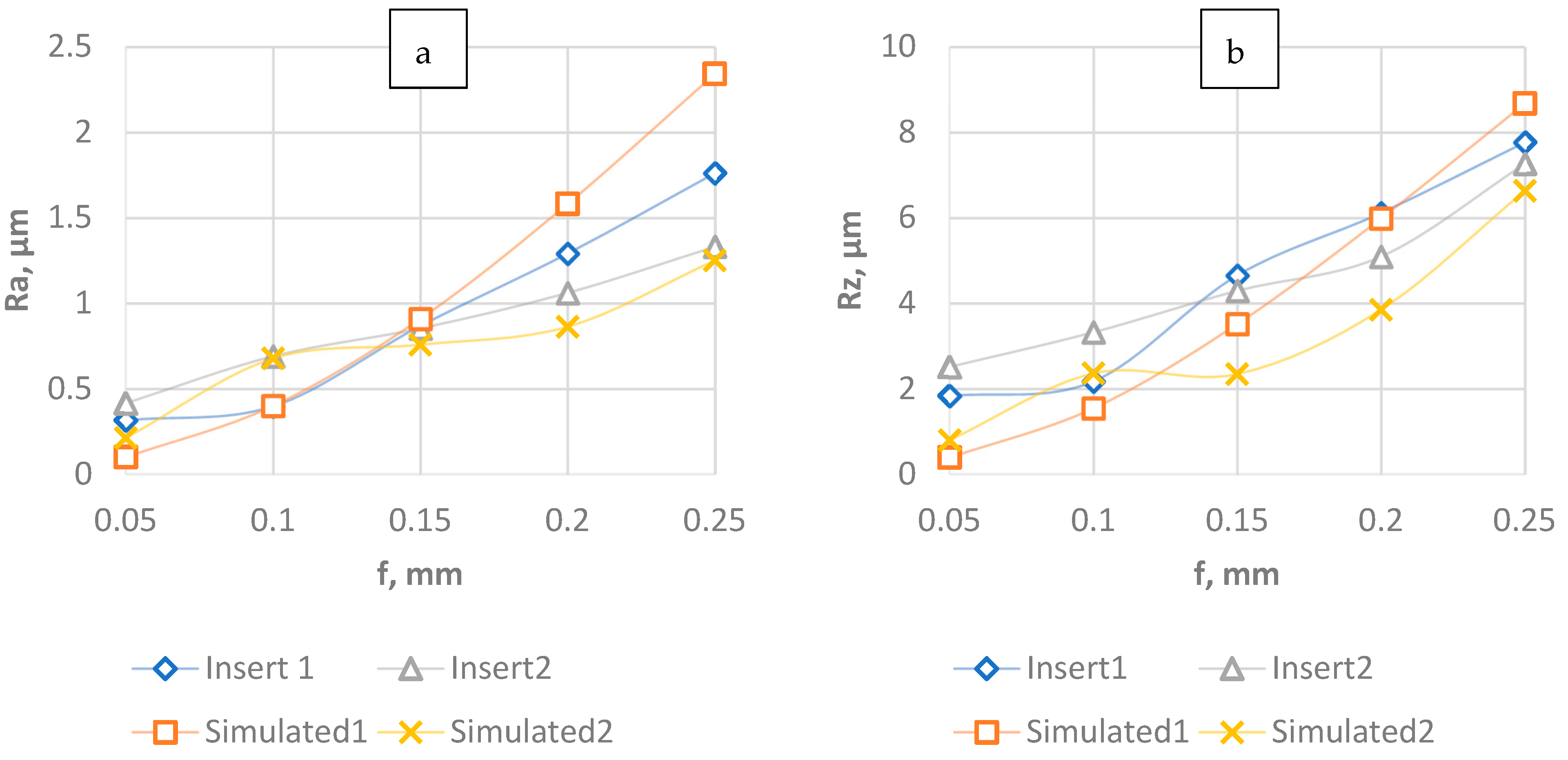
3. Results and Discussion

First, the theoretical profiles obtained for Insert1 are shown in Figure 8. Here, the applied cutting insert was a completely new one, so no tool wear was observed on its cutting edge (on the working section of it). Indeed, the roughness profiles shown in the figure do not show traces of any wear.

Figure 8 shows that obviously there are differences between the theoretical and measured values, but this difference becomes smaller with increasing feed. At low feed rates, the dynamic characteristics of the cutting process have a much greater influence on the resulting roughness profile [81].

In the case of the real roughness profile, the vibrations of the cutting system, which also depend on the components of the cutting force, are visibly reflected in the roughness profile. In hard turning, the cutting forces are usually much larger than in normal turning [82]. This inevitably causes an increase in vibrations, which is why it is important to use the right machines and equipment when machining hard surfaces. It can be also observed here that as the feed value increases, the theoretical and the measured cusp heights get closer to each other, as the effect of the vibrations and other dynamic effects are much less in proportion to the effect of the feed at higher feed values.

In the case of the measured profile visible at the smallest feed rate of f = 0.05 mm, another factor is worth considering: the effect of the so-called minimum chip thickness on the formation of the roughness profile [83]. Below a certain minimum undeformed chip thickness, the cutting edge of the tool is unable to remove material from the workpiece, so a so-called “ploughing effect” (partial material removal) occurs. The value of the minimum chip thickness (h_min) depends on several factors but is basically calculated from the edge radius (r_β) of the tool [84]. The tool radius is not reported by the manufacturers and is not easy to measure, so estimates are usually given. The edge radius of analogous tools used in the present research was measured to be around 50 µm [83]. In the same research, the approximate formula for the minimum chip thickness was determined to be 0.4 × r_β. Based on this, the value of the minimum chip thickness in the present case is around h_min ≈ 20 µm (0.02 mm). As the tool has a relatively large nose radius (0.8 mm), the actual undeformed chip thickness is changing along the curved tool edge from h_max = 0.029 to 0 mm. This was calculated from h = f × sinκ_r, where κ_r is the main cutting edge angle, which is changing continuously from 0 to 35.66° with the given nose radius of 0.8 mm and depth of cut a_p = 0.15 mm (see [85]). Even the maximum value of the calculated h (h_max = 0.029 mm) is very close to the h_min = 0.02 mm, so the effect of this phenomena can be seen in the roughness profiles. The measured roughness profiles seen at low feed rates is thus likely to be shaped by the combined effect of several factors, the detailed examination of which goes beyond the objectives of this paper.

Figure 9 shows the measured and theoretical profiles for Insert2, which has a significant wear on the working part of its cutting edge as it was already discussed before. If the profile graphs for f = 0.05 mm are compared to their counterparts in Figure 8, it can be observed that the cusps heights are significantly greater especially for the simulated profile. This is due to the fact that the cutting edge was modeled as a spline with two cusps, and thus the relatively large nose radius (r_ε = 0.8 mm) has been changed to something like a radius of a few micrometers (as it can be seen in Figure 6). It is known that as the radius gets smaller, higher cusp heights will appear in the roughness profile [86]. However, as the f value increases, the cusp heights get smaller, especially above f = 0.15 mm, where the “notch” starts to appear at the peak of the roughness profile cusps. This can be attributed to the two peaks on the tool shape caused by the tool wear as it was discussed earlier.

Two surface roughness parameters were considered in the actual investigation: the Ra arithmetical average roughness and the Rz maximum height of the profile (according to ISO 4287). These two parameters are frequently used in industrial practice to characterize machined surfaces. Three measurements were made on each surface, the average of which was taken as the measured value. The measured and simulated Ra and Rz values are summarized in Table 1 and Table 2, respectively. The accuracy of the approximation was calculated using the following well-known formula in Equation (1):

$$Error=\frac{\left|SV-MV\right|}{MV}·100[\%]$$

(1)

where:

• SV: Simulated value
• MV: Measured value

Table 1. Measured and simulated Ra values and prediction errors.

f, mm		Ra, µm
		0.05	0.1	0.15	0.2	0.25
Insert1	Measured	0.316	0.397	0.867	1.29	1.76
	Simulated	0.099	0.399	0.908	1.58	2.34
	Error, %	68.7	0.5	4.7	22.5	32.9
Insert2	Measured	0.415	0.69	0.853	1.06	1.33
	Simulated	0.212	0.677	0.7575	0.8623	1.25
	Error, %	48.9	1.9	11.2	18.6	6

Table 1. Measured and simulated Ra values and prediction errors.

f, mm		Ra, µm
		0.05	0.1	0.15	0.2	0.25
Insert1	Measured	0.316	0.397	0.867	1.29	1.76
	Simulated	0.099	0.399	0.908	1.58	2.34
	Error, %	68.7	0.5	4.7	22.5	32.9
Insert2	Measured	0.415	0.69	0.853	1.06	1.33
	Simulated	0.212	0.677	0.7575	0.8623	1.25
	Error, %	48.9	1.9	11.2	18.6	6

Table 2. Measured and simulated Rz values and prediction errors.

f, mm		Rz, µm
		0.05	0.1	0.15	0.2	0.25
Insert1	Measured	1.83	2.17	4.65	6.11	7.76
	Simulated	0.388	1.54	3.51	5.98	8.67
	Error, %	78.8	29	24.5	2.2	11.7
Insert2	Measured	2.51	3.32	4.29	5.09	7.26
	Simulated	0.796	2.36	2.342	3.849	6.63
	Error, %	68.3	28.9	45.4	24.4	8.7

Table 2. Measured and simulated Rz values and prediction errors.

f, mm		Rz, µm
		0.05	0.1	0.15	0.2	0.25
Insert1	Measured	1.83	2.17	4.65	6.11	7.76
	Simulated	0.388	1.54	3.51	5.98	8.67
	Error, %	78.8	29	24.5	2.2	11.7
Insert2	Measured	2.51	3.32	4.29	5.09	7.26
	Simulated	0.796	2.36	2.342	3.849	6.63
	Error, %	68.3	28.9	45.4	24.4	8.7

Figure 10 shows both the measured and simulated surface roughness parameters in the conducted hard turning investigations. The “Simulated1” data series should be compared with “Insert1”, while the “Simulated2” with the “Insert2” results, due to the previously introduced tool wear effect. As is shown in Figure 10a, which illustrates the Ra parameter, the drawn points of those corresponding data pairs are fairly close to each other. The roughness values get higher with the increase of the feed per revolution f, but there is a clear breakage on the curves at around f = 0.15 mm for both the measured and the simulated data for the worn insert. This is mainly due to the fact that the tool wear mark just starts to appear in the generated profile from that feed value, as it can be seen on the profile diagrams in Figure 9. The other two curves for unworn insert show regular increasing form. However, in the case of Rz, things get more complicated. Simulated roughness curves exhibit nearly the same characteristics as in the case of Ra, but the measured ones, especially for the worn insert showing greater deviations from it, and for f = 0.15 mm, so one can say that the worn insert roughness value is closer to the “Simulated1” data, which is for unworn insert. However, this can be considered as an exception, as for the other feed values, the “Simulated2” data is closer to the measured one. Additionally, it should be also noted here that the Rz parameter is not the best one for characterizing hard turned surfaces; it is usually better suited for other machining processes (e.g., grinding), and the Ra value is more appropriate to be used in the case of hard turning [87]. Another important characteristic which can be derived from Figure 10 is that simulated roughness values for the unworn insert are higher than the measured ones for high feed values (especially for f > 0.2 mm). This seems to be somewhat controversial, as usually the real values are higher because of the dynamic components superimposing onto the theoretical roughness values. However, the insert which has a relatively high edge blending cannot cut the material perfectly, and thus the tenuous roughness cusps which can be seen on theoretical roughness profile diagrams (Figure 8) cannot be formed during the real cutting process, so the final measured roughness value may be smaller.

4. Conclusions

A new method was introduced in the paper for the determination of theoretical roughness values in turning processes. The actual investigations were concentrated on the hard turning process, which can be used to finish the surface of hardened parts. The conducted simulations and real cutting tests showed that the method is suitable for estimating the roughness of the surfaces cut by inserts which were already used before, and a significant wear can be observed in their cutting edge. During the proposed simulation method, the profile of the cutting tool was examined by an optical microscope, and the contour of the cutting edge was recorded. This image was imported into a parametric CAD system, and then the contour was described by a spline. This method can be used for the more accurate modeling of the cutting tool during the theoretical roughness calculations, as in the case of tool wear (which is unavoidable during cutting) the roughness profile will be significantly changed. It has been shown in the paper that even in the case of a relatively small amount of tool wear, significant distortions can be observed in the roughness profile, therefore the accuracy of the theoretical roughness values calculated with the methods used for sharp inserts decreases. Based on the comparison of the simulated and the measured data, it can be stated that with the help of the proposed new method the topography of the surface formed during the real cutting process can be well approximated. It was concluded that the accuracy of the approximation improves with an increasing feed rate. The presented method provides a new approach to the investigation and determination of surface roughness during turning. The practical applicability of the method may be the accurate prediction of the relatively permissible tool wear value, which will limit the relatively permissible change of the parameter Ra of the machined surface.

However, it should be mentioned that the introduced method may be further improved. In practice, cutting tools are usually used continuously until the end of their life is reached (the amount of wear exceeds a specified critical value), and this is followed automatically by a tool change (or switching of the cutting edge). Therefore, in the next step of the research, it would be expedient to examine how the wear of the cutting tool could be measured during machining and how the roughness values could be continuously estimated, on the basis of which the process could be intervened directly. This would be of great importance for process monitoring. Because the workpiece rotates during turning, optical roughness measurement during machining is not possible, so the in-process tool wear measurement may be a potential solution for that. Several researchers have already dealt with this topic (e.g., [88,89,90,91]), but it would be worthwhile to examine the applicability of this idea from the perspective of the introduced method.