A Study for Improved Prediction of the Cutting Force and Chip Shrinkage Coefficient during the SKD11 Alloy Steel Milling
Abstract
:1. Introduction
2. Material
2.1. Chemical Compositions and Material Properties
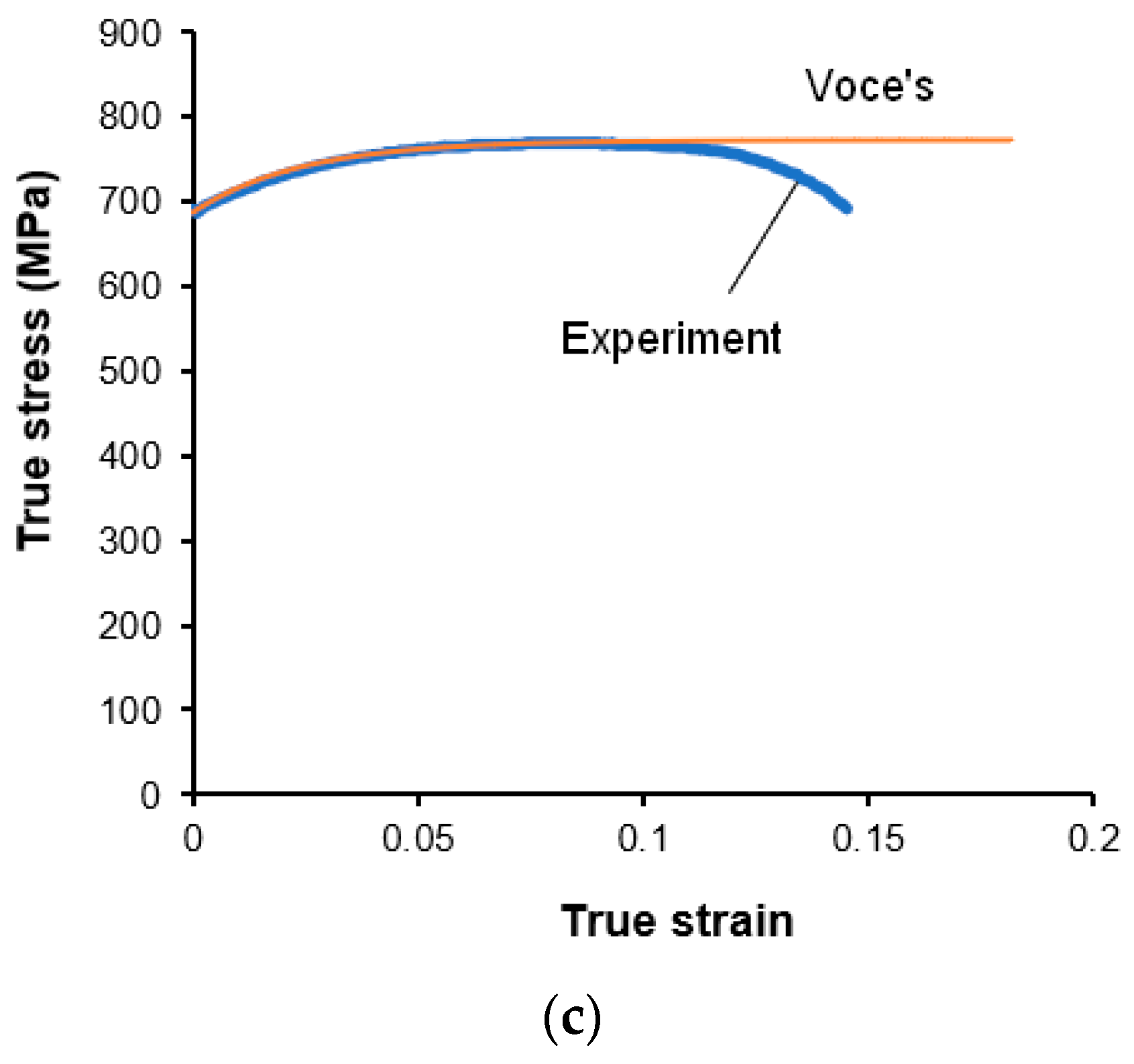
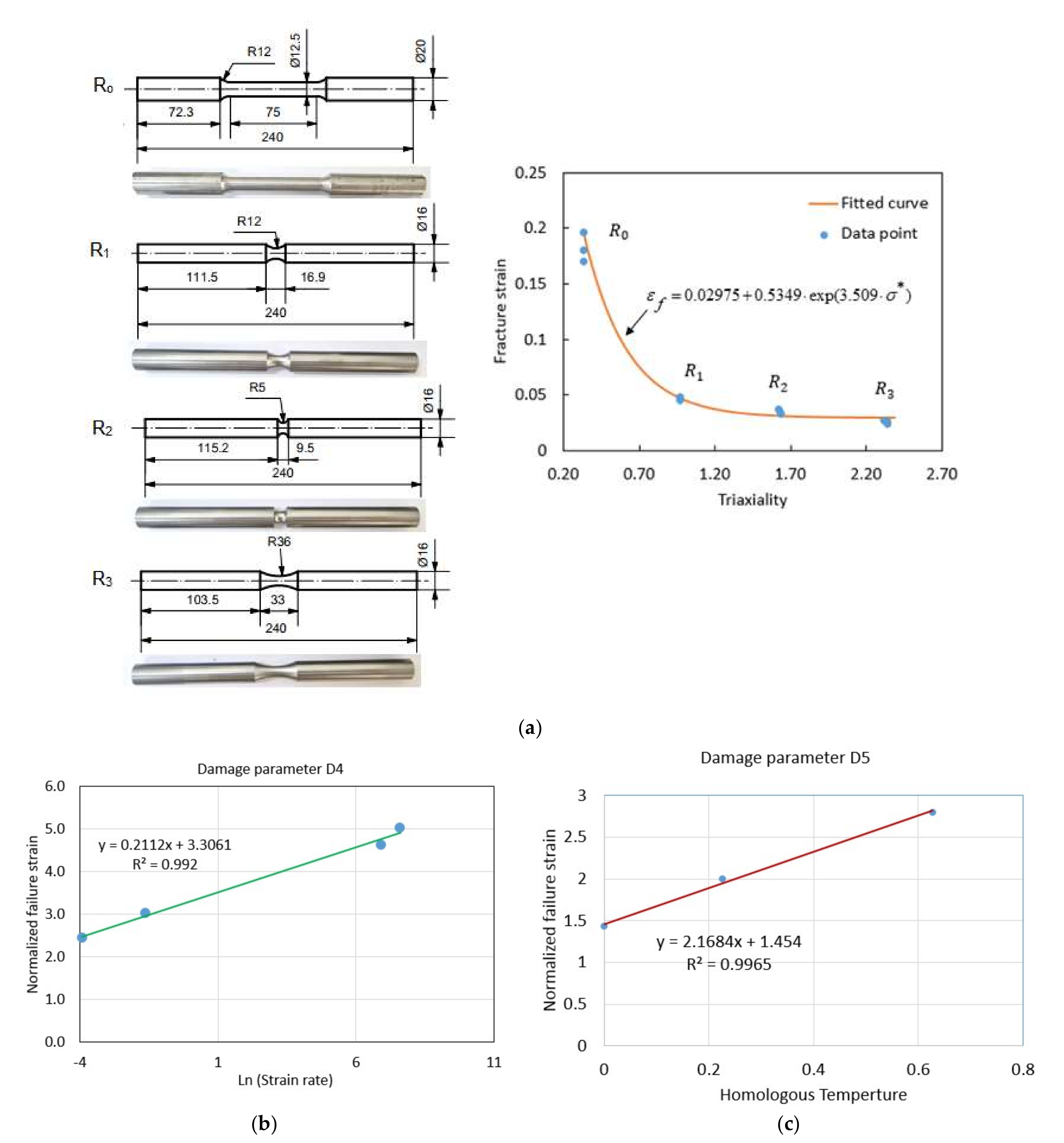
2.2. J-C Fracture Model
3. Experiments
3.1. Experiment Setup
3.2. Cutting-Force Measurement
3.3. Chip Shrinkage Coefficient (K) Determination
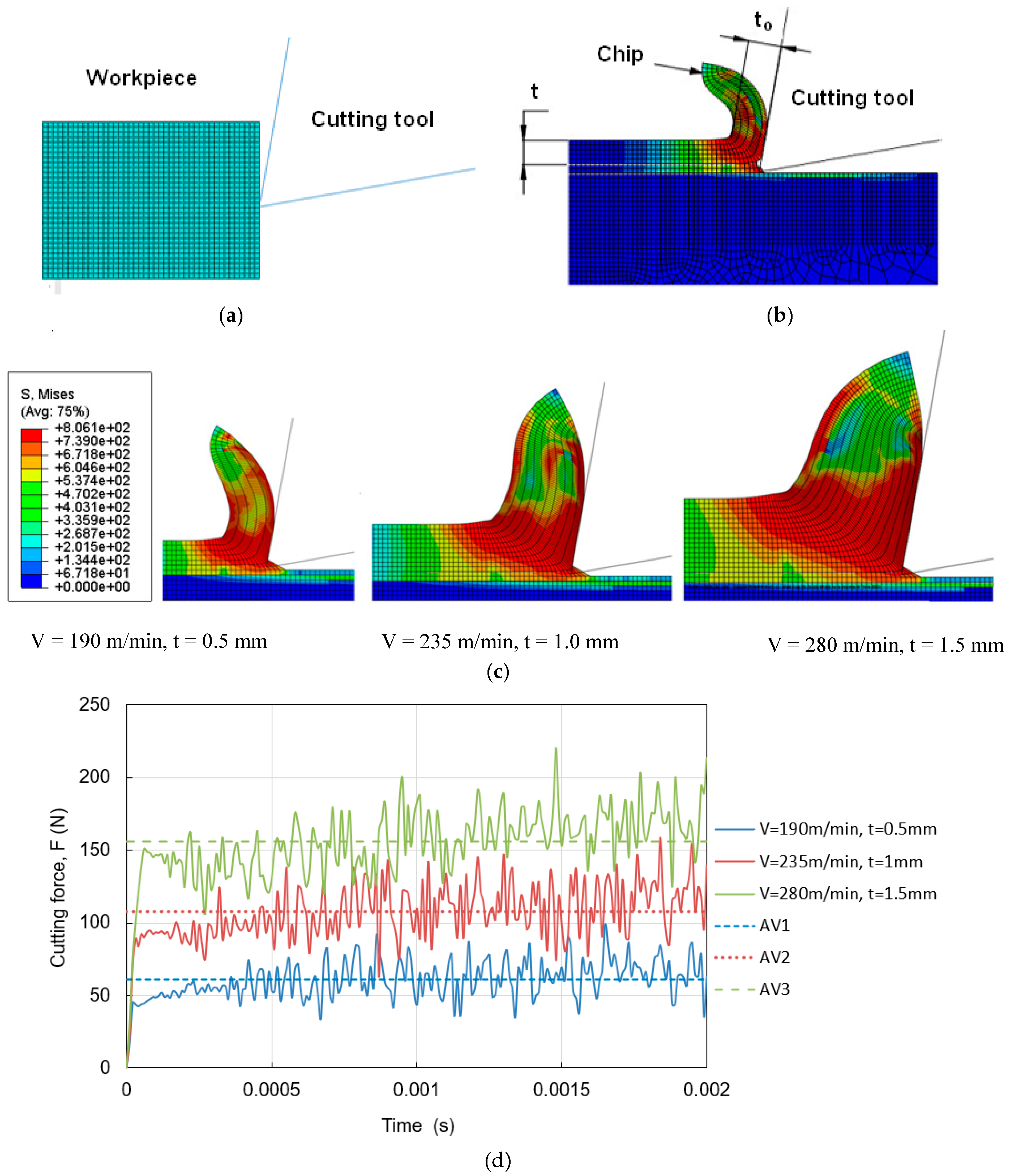
4. Finite Element Simulations
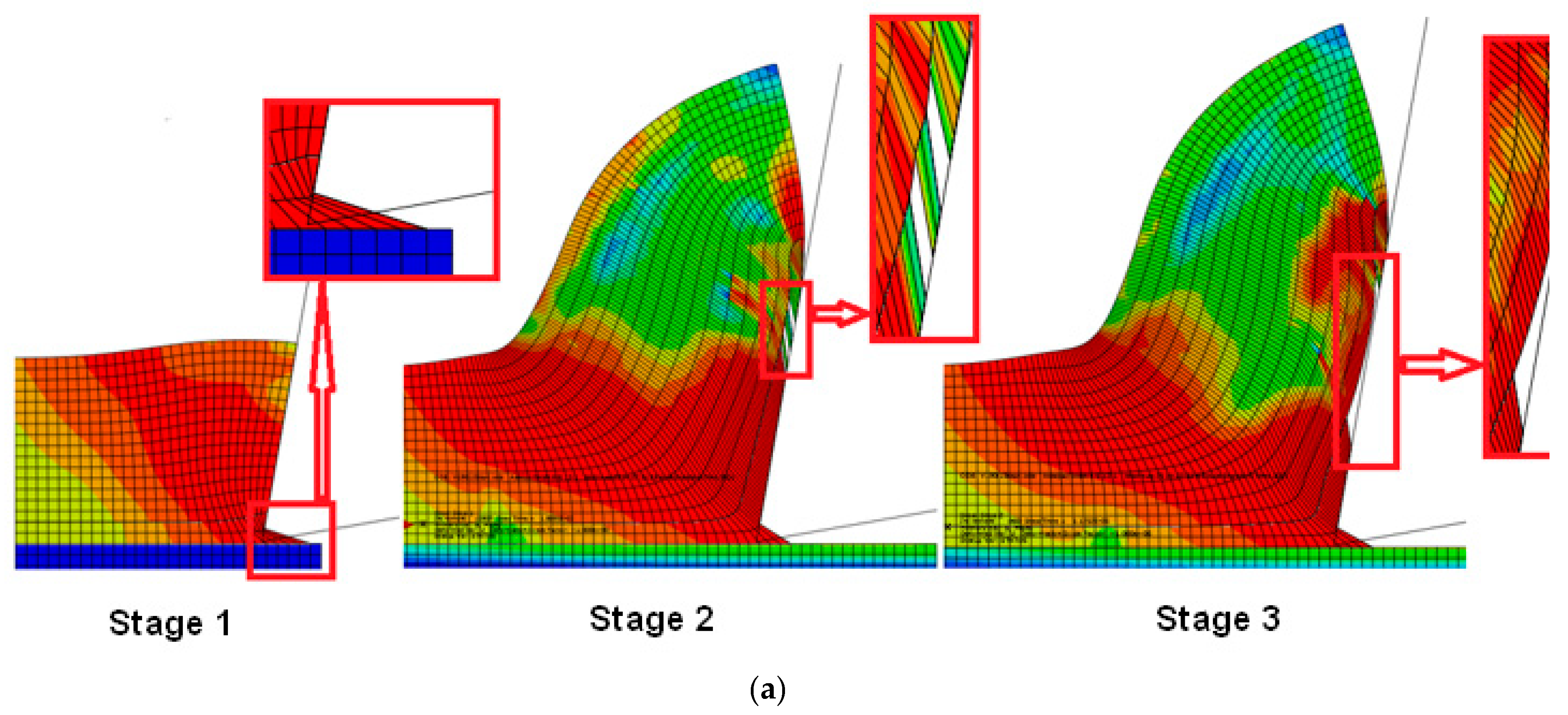
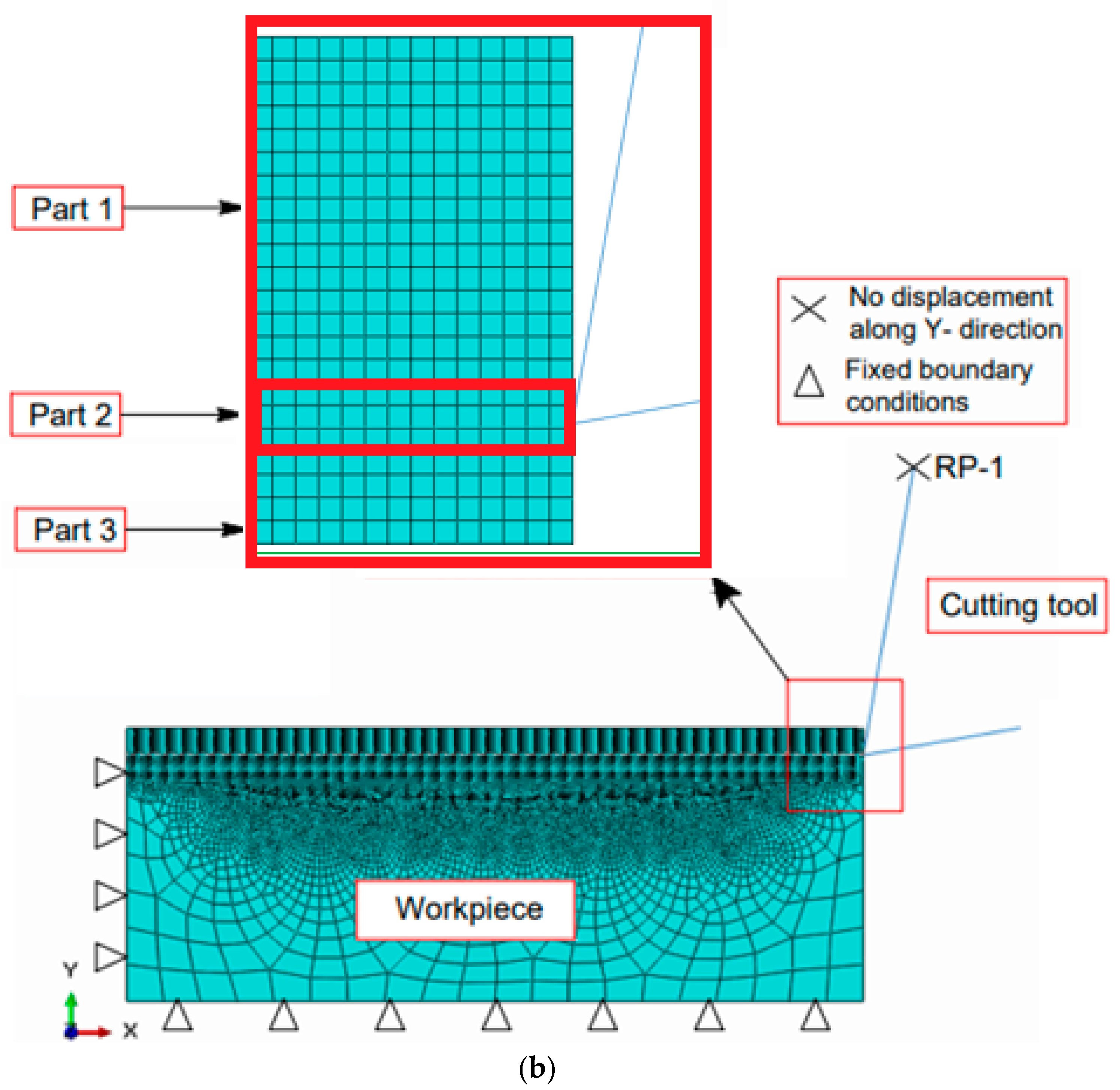
4.1. FEM-Based Model
4.2. Cutting Force (F) and Chip Shrinkage Coefficient (K) Determination
5. Modification of the FEM-Based Model
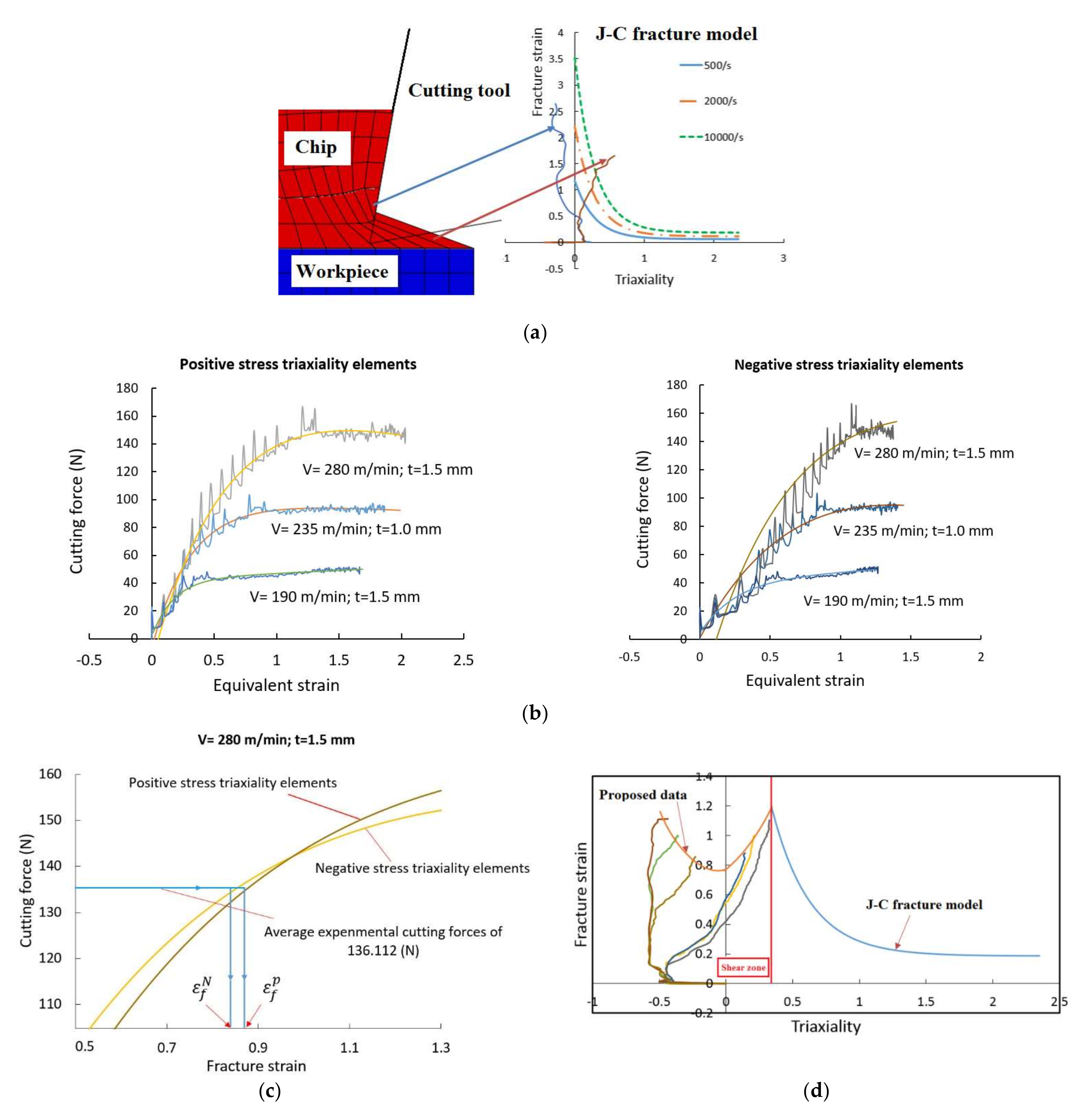
5.1. Proposed Method for the Modified Fracture Model
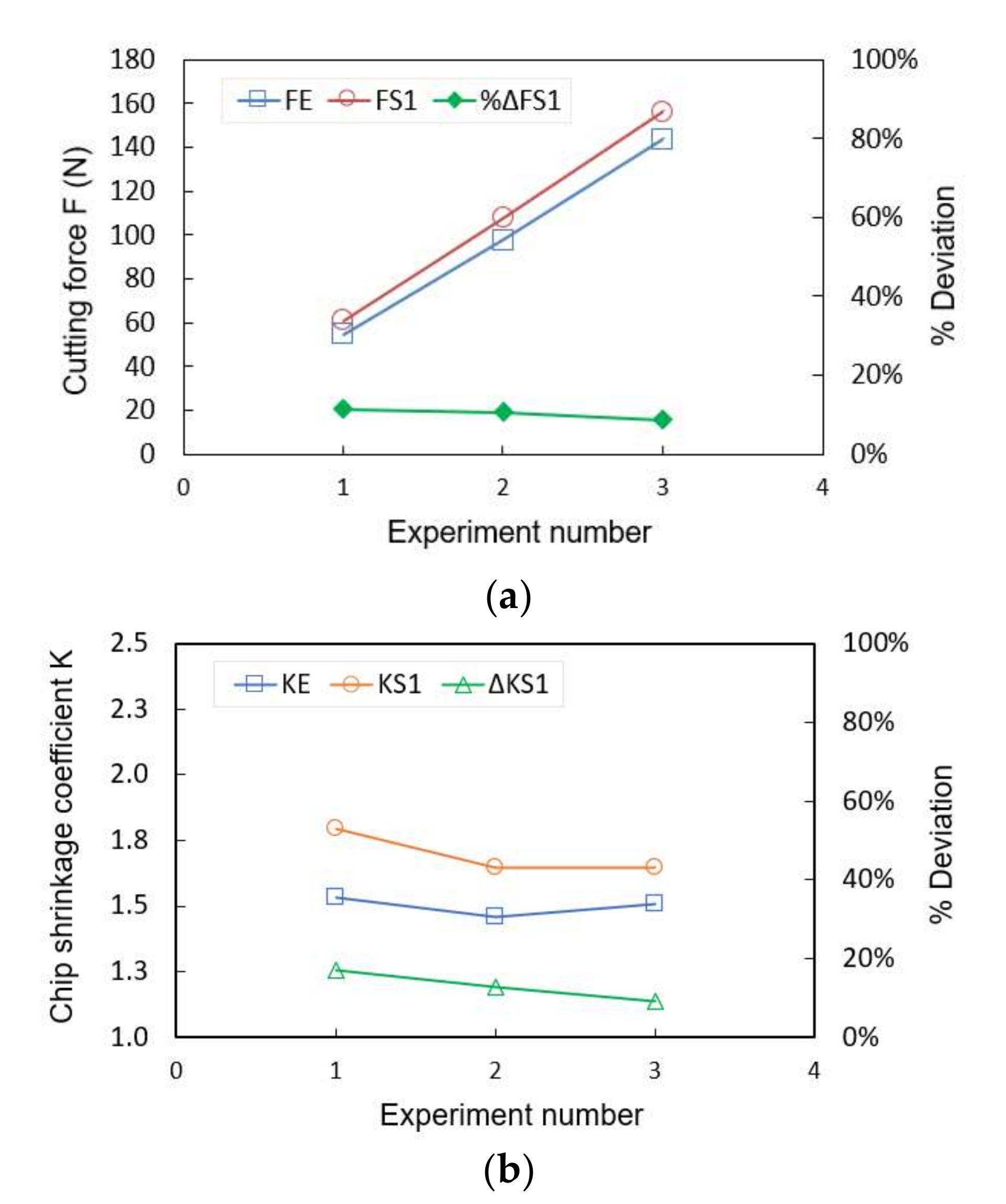
5.2. Validation of Proposed Fracture Model
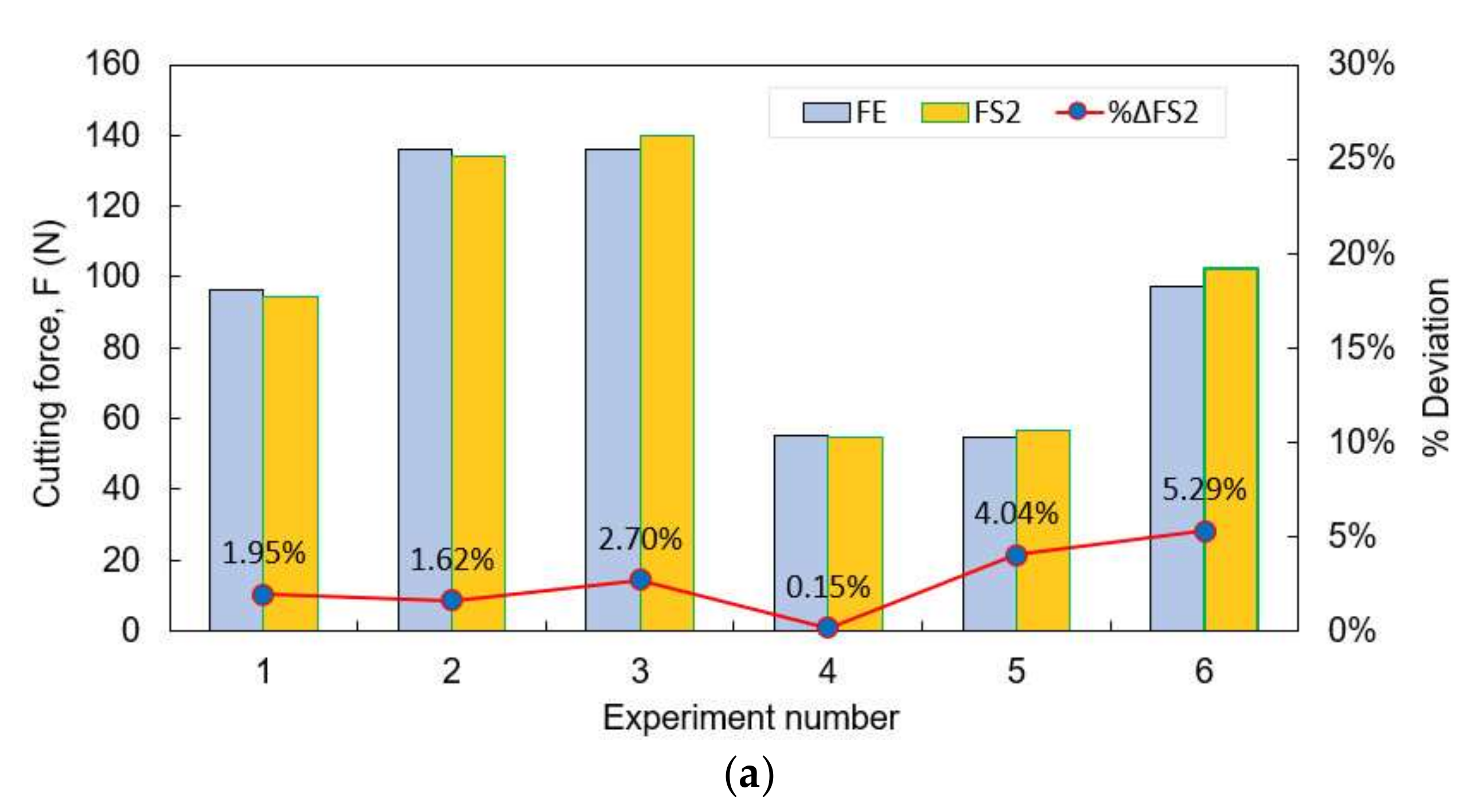
5.3. Verification of Proposed Fracture Model
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| σ, = equivalent stress, equivalent strain, stress triaxiality |
| A, B = plastic coefficients |
| Di (i = 1, 2, 3, 4, 5) = The material constants |
| F = the synthetic cutting force |
| Fx, Fy, Fz = three the cutting forces components |
| t, to = the uncut and actual chip thickness |
| V, fr, t = cutting speed, feed rate, cutting depth |
| K= chip shrinkage coefficient |
| Q = mass of the chip |
| ρ = destiny of the workpiece material |
| G, H, L, M = force equational parameters |
References
- Banh, T.L.; Tran, T.L.; Tran, S.T. Metal Cutting Principles, 2nd ed.; Science and Technics Publishing House: Hanoi, Vietnam, 2013. (In Vietnamese) [Google Scholar]
- Pham, T.H.; Mac, T.B.; Tong, V.C.; Banh, T.L.; Nguyen, D.T. Simulation and experimental studies to verify the effect of cutting parameters on chip shrinkage coefficient and cutting forces in machining of A6061 aluminum alloy. Adv. Mech. Eng. 2016, 8, 1687814016673297. [Google Scholar] [CrossRef] [Green Version]
- Umbrello, D.; M’Saoubi, R.; Outeiro, J.C. The influence of Johnson-Cook material constants on finite element simulation of machining of AISI 316L steel. Int. J. Mach. Tools Manuf. 2007, 47, 462–470. [Google Scholar] [CrossRef]
- Thepsonthi, T.; Özel, T. 3-D finite element process simulation of micro-end milling Ti-6Al-4V titanium alloy: Experimental validations on chip flow and tool wear. J. Mater. Process. Technol. 2015, 221, 128–145. [Google Scholar] [CrossRef]
- Liu, P.; Quan, Y.; Wan, J. Finite element simulations of rail milling based on the modified Johnson-Cook constitutive model. J. Phys. Conf. Ser. 2021, 1759, 012025. [Google Scholar] [CrossRef]
- Silva, R.G.; Teicher, U.; Brosius, A.; Ihlenfeldt, S. 2D finite element modeling of the cutting force in peripheral milling of cellular metals. Materials 2020, 13, 555. [Google Scholar] [CrossRef] [Green Version]
- Arisoy, Y.M.; Özel, T. Prediction of machining induced microstructure in Ti-6Al-4V alloy using 3-D FE-based simulations: Effects of tool micro-geometry, coating and cutting conditions. J. Mater. Process. Technol. 2015, 220, 1–26. [Google Scholar] [CrossRef]
- Yk, K.O. The residual stress produced by metal cutting. Ann. CIRP 1971, 20, 13–14. [Google Scholar]
- Tzotzis, A.; García-Hernández, C.; Huertas-Talón, J.L.; Kyratsis, P. Influence of the nose radius on the machining forces induced during AISI-4140 hard turning: A CAD-based and 3D FEM approach. Micromachines 2020, 11, 798. [Google Scholar] [CrossRef]
- Rao, S.S. The Finite Element Method in Engineering, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Tzotzis, A.; García-Hernández, C.; Huertas-Talón, J.L.; Kyratsis, P. FEM based mathematical modelling of thrust force during drilling of Al7075-T6. Mech. Ind. 2020, 21, 415. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr-Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1. [Google Scholar] [CrossRef]
- Zhang, W.; Zhuang, K.; Pu, D. A novel finite element investigation of cutting force in orthogonal cutting considering plough mechanism with rounded edge tool. Int. J. Adv. Manuf. Technol. 2020, 108, 3323–3334. [Google Scholar] [CrossRef]
- Korkmaz, M.E.; Günay, M. Finite Element Modelling of Cutting Forces and Power Consumption in Turning of AISI 420 Martensitic Stainless Steel. Arab. J. Sci. Eng. 2018, 43, 4863–4870. [Google Scholar] [CrossRef]
- Leksycki, K.; Feldshtein, E.; Lisowicz, J.; Chudy, R.; Mrugalski, R. Cutting forces and chip shaping when finish turning of 17-4 ph stainless steel under dry, wet, and mql machining conditions. Metals 2020, 10, 1187. [Google Scholar] [CrossRef]
- Thi-Hoa, P.; Thi-Bich, M.; Van-Canh, T.; Tien-Long, B.; Duc-Toan, N. A study on the cutting force and chip shrinkage coefficient in high-speed milling of A6061 aluminum alloy. Int. J. Adv. Manuf. Technol. 2018, 98, 177–188. [Google Scholar] [CrossRef]
- Gupta, M.K.; Korkmaz, M.E.; Sarıkaya, M.; Krolczyk, G.M.; Günay, M.; Wojciechowski, S. Cutting forces and temperature measurements in cryogenic assisted turning of AA2024-T351 alloy: An experimentally validated simulation approach. J. Meas. 2022, 188, 110594. [Google Scholar] [CrossRef]
- Gupta, M.K.; Korkmaz, M.E.; Sarıkaya, M.; Krolczyk, G.M.; Günay, M. In-process detection of cutting forces and cutting temperature signals in cryogenic assisted turning of titanium alloys: An analytical approach and experimental study. J. Mech. Syst. Signal Processing 2022, 169, 108772. [Google Scholar] [CrossRef]
- Xavierarockiaraj, S.; Kuppan, P. Investigation of cutting forces, surface roughness and tool wear during Laser assisted machining of SKD11Tool steel. Procedia Eng. 2014, 97, 1657–1666. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Xie, Y.; Zheng, L.; Qin, Z.; Tang, D.; Song, Y. Research on the Chip Formation Mechanism during the high-speed milling of hardened steel. Int. J. Mach. Tools Manuf. 2014, 79, 31–48. [Google Scholar] [CrossRef]
- Wang, C.; Ding, F.; Tang, D.; Zheng, L.; Li, S.; Xie, Y. Modeling and simulation of the high-speed milling of hardened steel SKD11 (62 HRC) based on SHPB technology. Int. J. Mach. Tools Manuf. 2016, 108, 13–26. [Google Scholar] [CrossRef]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Patwari MA, U.; Amin, A.N.; Faris, W.F. Influence of chip serration frequency on chatter formation during end milling of Ti6Al4V. J. Manuf. Sci. Eng. Trans. ASME 2011, 133, 011013. [Google Scholar] [CrossRef] [Green Version]



| C | Cr | Mo | Si | Mn | Ni | V |
|---|---|---|---|---|---|---|
| 1.4–1.6 | 11–13 | 0.7–1.2 | ≤0.6 | ≤0.6 | - | 0.15–0.3 |
| Materials | SKD11 |
|---|---|
| Yield stress (MPa) | 688 |
| Tensile strength (MPa) | 786 |
| A (MPa) | 84.332 |
| B | 41.265 |
| Density (ρ kg/mm3) | 8400 |
| Elastic modulus (E, kN/mm2) | 210 |
| Poisson ratio () | 0.3 |
| Thermal expansion coefficient (10−6/K) | 11 |
| Melt temperature Tm (K) | 1733 |
| Specific heat (J/kg.°C) | 461 |
| Thermal conductivity coefficient (w/m.K) | 20.5 |
| D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|
| 0.02975 | 0.5349 | −3.5090 | 0.2112 | 2.1684 |
| Exp. No. | V (m/min) | t (mm) | FE (N) | KE |
|---|---|---|---|---|
| 1 | 190 | 0.5 | 54.833 | 1.5312 |
| 2 | 235 | 1 | 100.435 | 1.4594 |
| 3 | 280 | 1.5 | 136.112 | 1.5089 |
| No. | V (m/min) | t (mm) | to (mm) | FE (N) | FS1 (N) | ΔF1 (%) | KE | KS1 | ΔK1 (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 190 | 0.5 | 0.896 | 54.833 | 61.107 | 11.44 | 1.5312 | 1.7920 | 17.03 |
| 2 | 235 | 1 | 1.647 | 100.435 | 107.746 | 10.57 | 1.4594 | 1.6470 | 12.85 |
| 3 | 280 | 1.5 | 2.471 | 136.112 | 156.214 | 8.71 | 1.5089 | 1.6473 | 9.17 |
| Stress Triaxiality Elements | ||||||
|---|---|---|---|---|---|---|
| Cutting Conditions | V = 190 m/min t = 0.5 mm | V = 235 m/min t = 1.0 mm | V = 280 m/min t = 1.5 mm | |||
| Parameter | Positive | Negative | Positive | Negative | Positive | Negative |
| G | 43.08 | 42.55 | 101.7 | 2196 | −252.2 | 2188 |
| H | 0.088 | 0.125 | −0.047 | −0.689 | −1.519 | −0.6897 |
| L | −41.21 | −38.03 | −108.6 | −2195 | 239.1 | −2192 |
| M | −5.63 | −3.89 | −3.164 | −3.164 | −0.206 | −08312 |
| No. | V (m/min) | t (mm) | FE (N) | FS2 (N) | ΔF2 (%) | KE | KS2 | ΔK2 (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 190 | 0.5 | 54.833 | 52.312 | 4.60 | 1.5312 | 1.4720 | 3.87 |
| 2 | 235 | 1 | 100.435 | 97.561 | 0.12 | 1.4594 | 1.4350 | 1.67 |
| 3 | 280 | 1.5 | 136.112 | 147.789 | 2.85 | 1.5089 | 1.4693 | 2.62 |
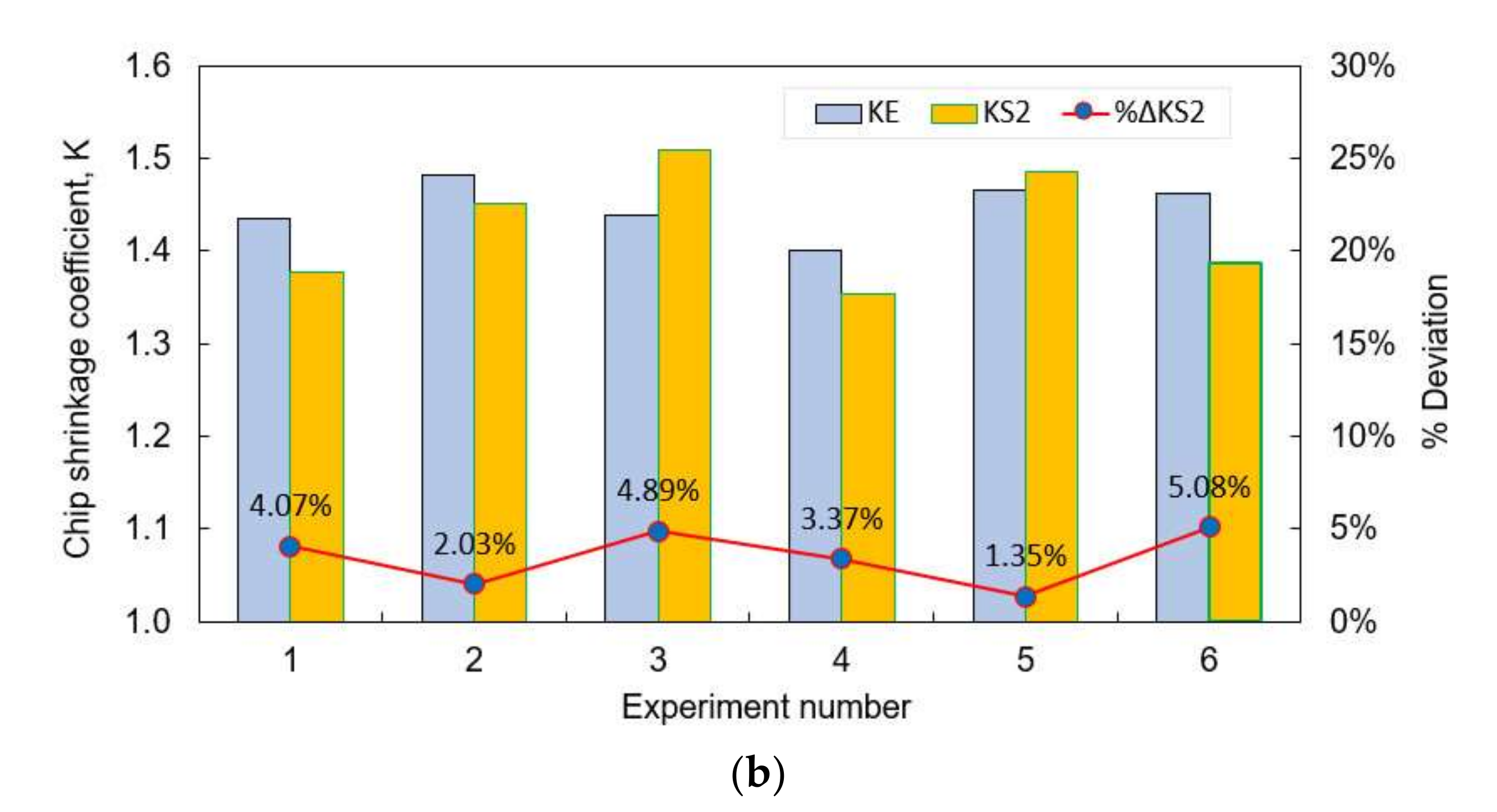
| Exp. No. | V (m/min) | t (mm) | FE (N) | KE | FS2 (N) | KS2 | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 190 | 1 | 96.201 | 1.4354 | 94.322 | 1.3770 | 1.95% | 4.07% |
| 2 | 190 | 1.5 | 136.121 | 1.4821 | 133.915 | 1.4520 | 1.62% | 2.03% |
| 3 | 235 | 1.5 | 136.1122 | 1.4396 | 139.783 | 1.5100 | 2.70% | 4.89% |
| 4 | 235 | 0.5 | 55.03434 | 1.4012 | 54.954 | 1.3540 | 0.15% | 3.37% |
| 5 | 280 | 0.5 | 54.639 | 1.4662 | 56.845 | 1.4860 | 4.04% | 1.35% |
| 6 | 280 | 1 | 97.123 | 1.4623 | 102.257 | 1.3880 | 5.29% | 5.08% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mac, T.-B.; Luyen, T.-T.; Nguyen, D.-T. A Study for Improved Prediction of the Cutting Force and Chip Shrinkage Coefficient during the SKD11 Alloy Steel Milling. Machines 2022, 10, 229. https://doi.org/10.3390/machines10040229
Mac T-B, Luyen T-T, Nguyen D-T. A Study for Improved Prediction of the Cutting Force and Chip Shrinkage Coefficient during the SKD11 Alloy Steel Milling. Machines. 2022; 10(4):229. https://doi.org/10.3390/machines10040229
Chicago/Turabian StyleMac, Thi-Bich, The-Thanh Luyen, and Duc-Toan Nguyen. 2022. "A Study for Improved Prediction of the Cutting Force and Chip Shrinkage Coefficient during the SKD11 Alloy Steel Milling" Machines 10, no. 4: 229. https://doi.org/10.3390/machines10040229
APA StyleMac, T.-B., Luyen, T.-T., & Nguyen, D.-T. (2022). A Study for Improved Prediction of the Cutting Force and Chip Shrinkage Coefficient during the SKD11 Alloy Steel Milling. Machines, 10(4), 229. https://doi.org/10.3390/machines10040229








