Meshing Stiffness Calculation of Disposable Harmonic Drive under Full Load
Abstract
:1. Introduction
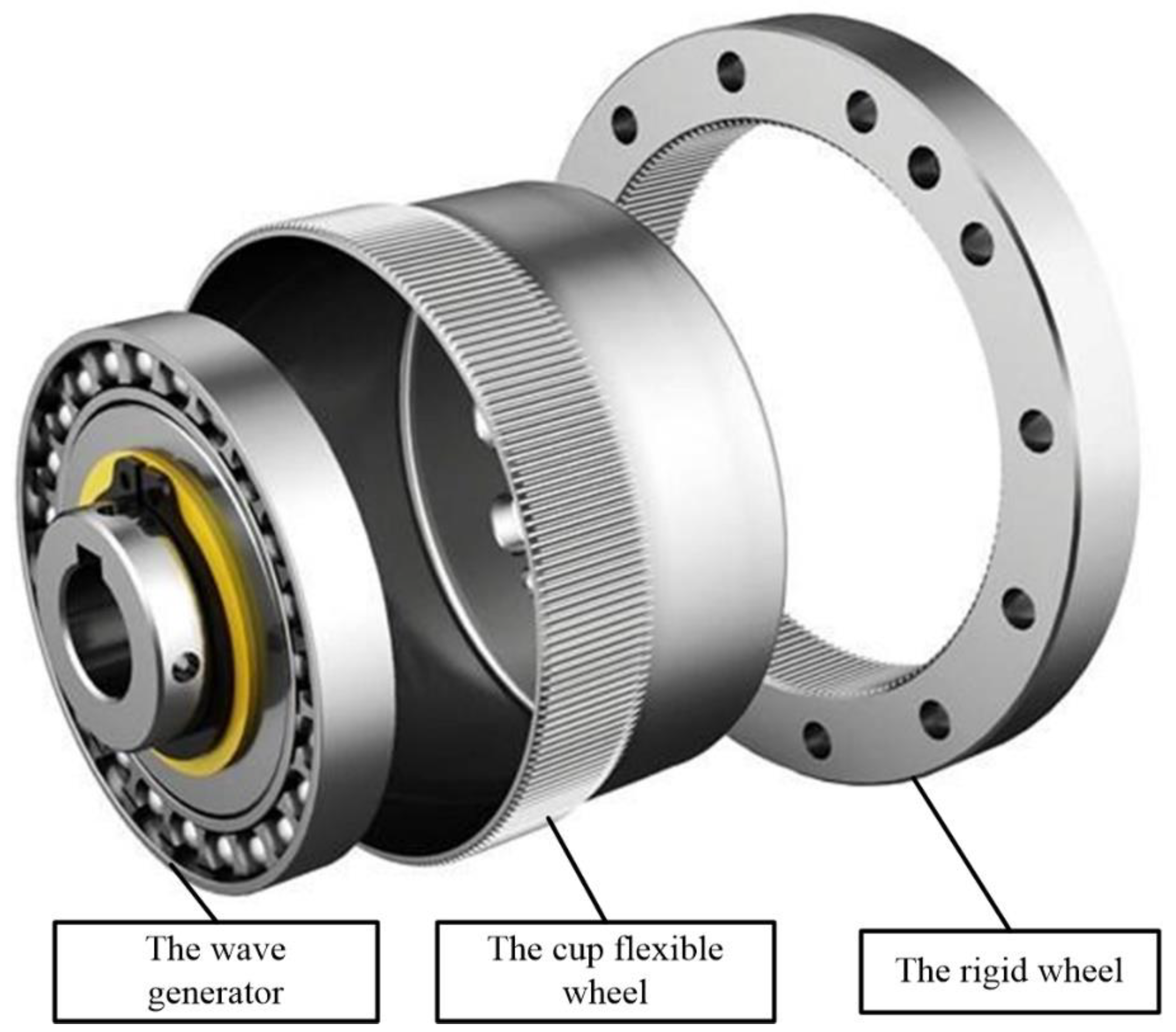
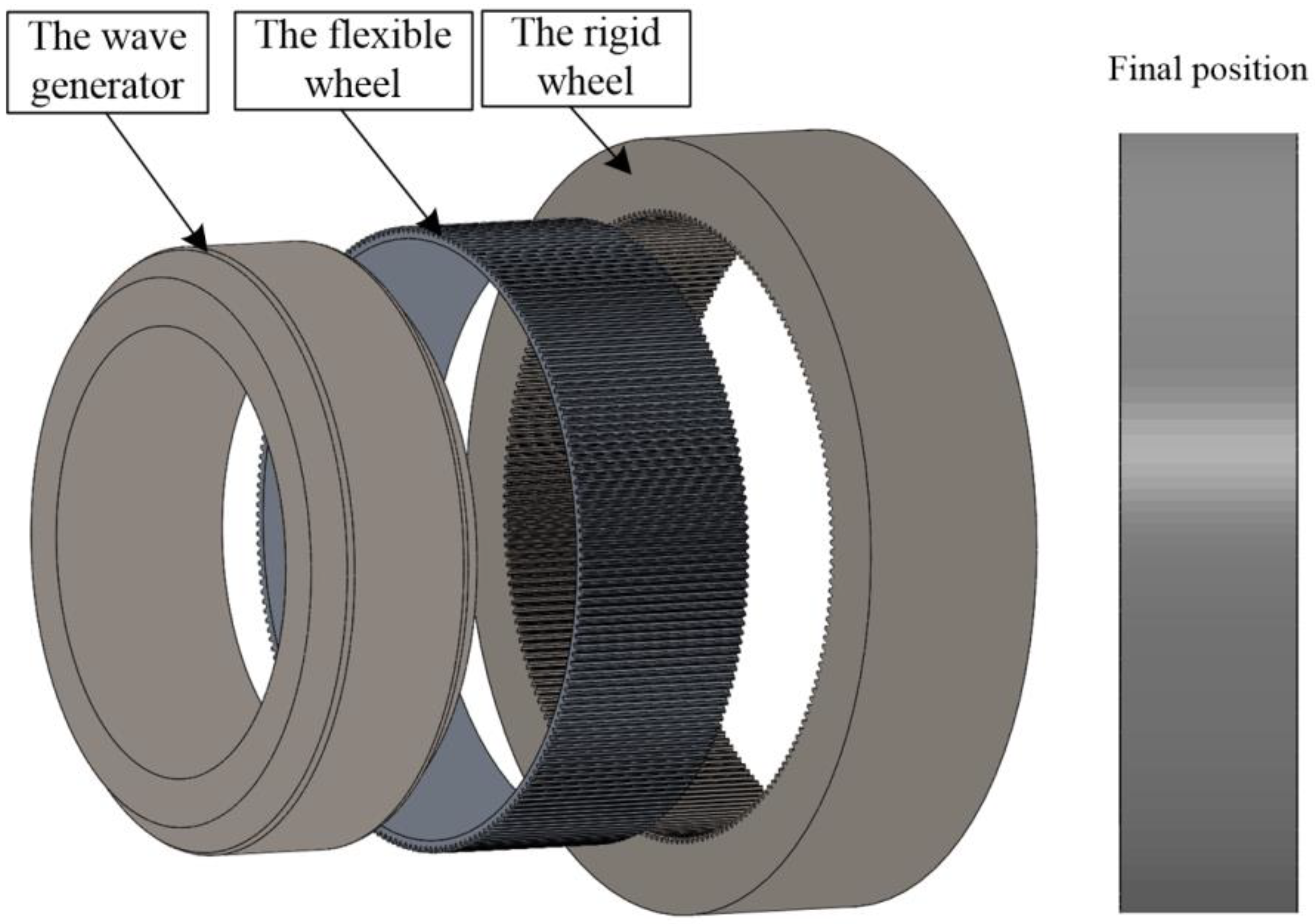
2. Design Scheme of the Disposable Harmonic Drive
2.1. Design of the Disposable Harmonic Flexible Wheel
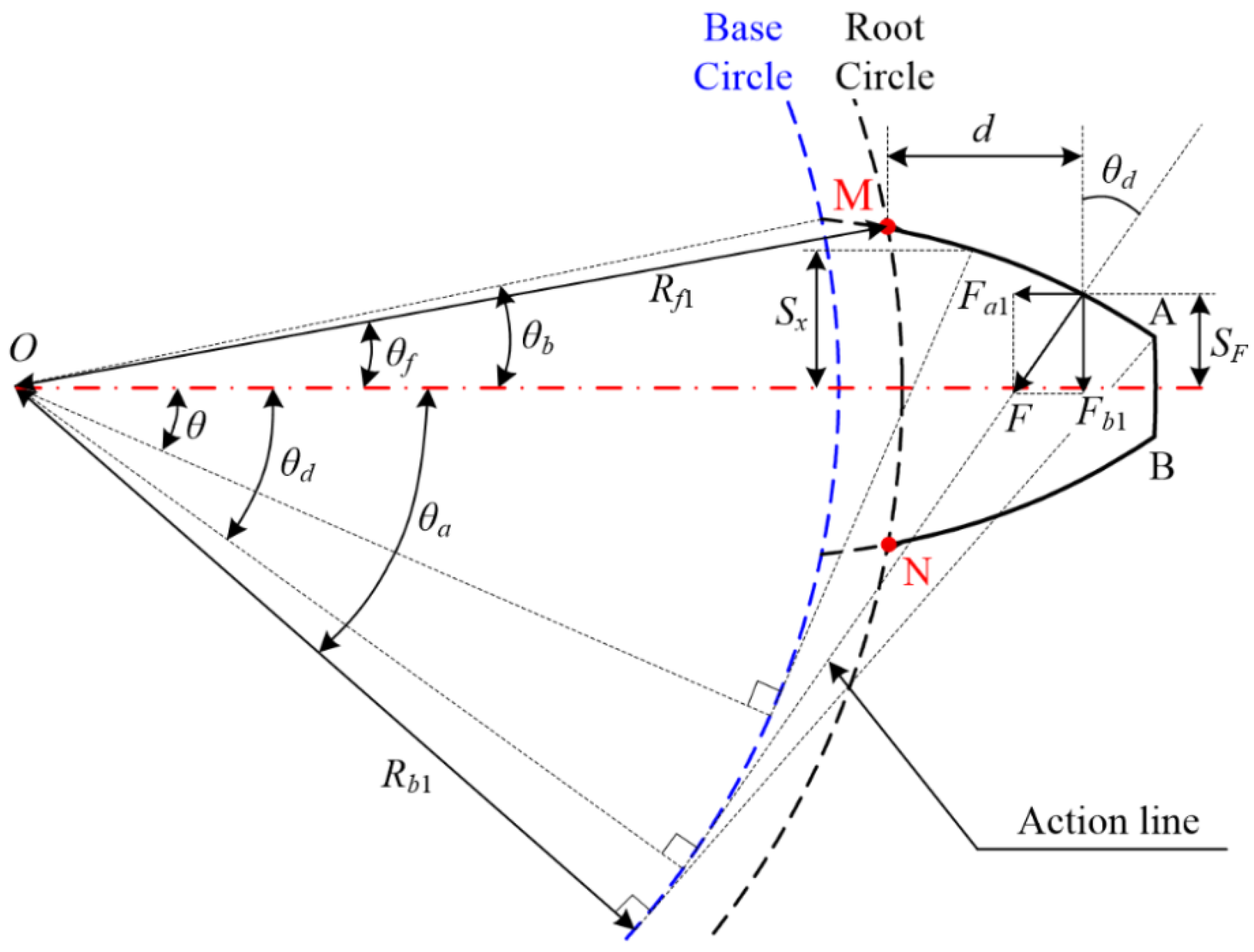
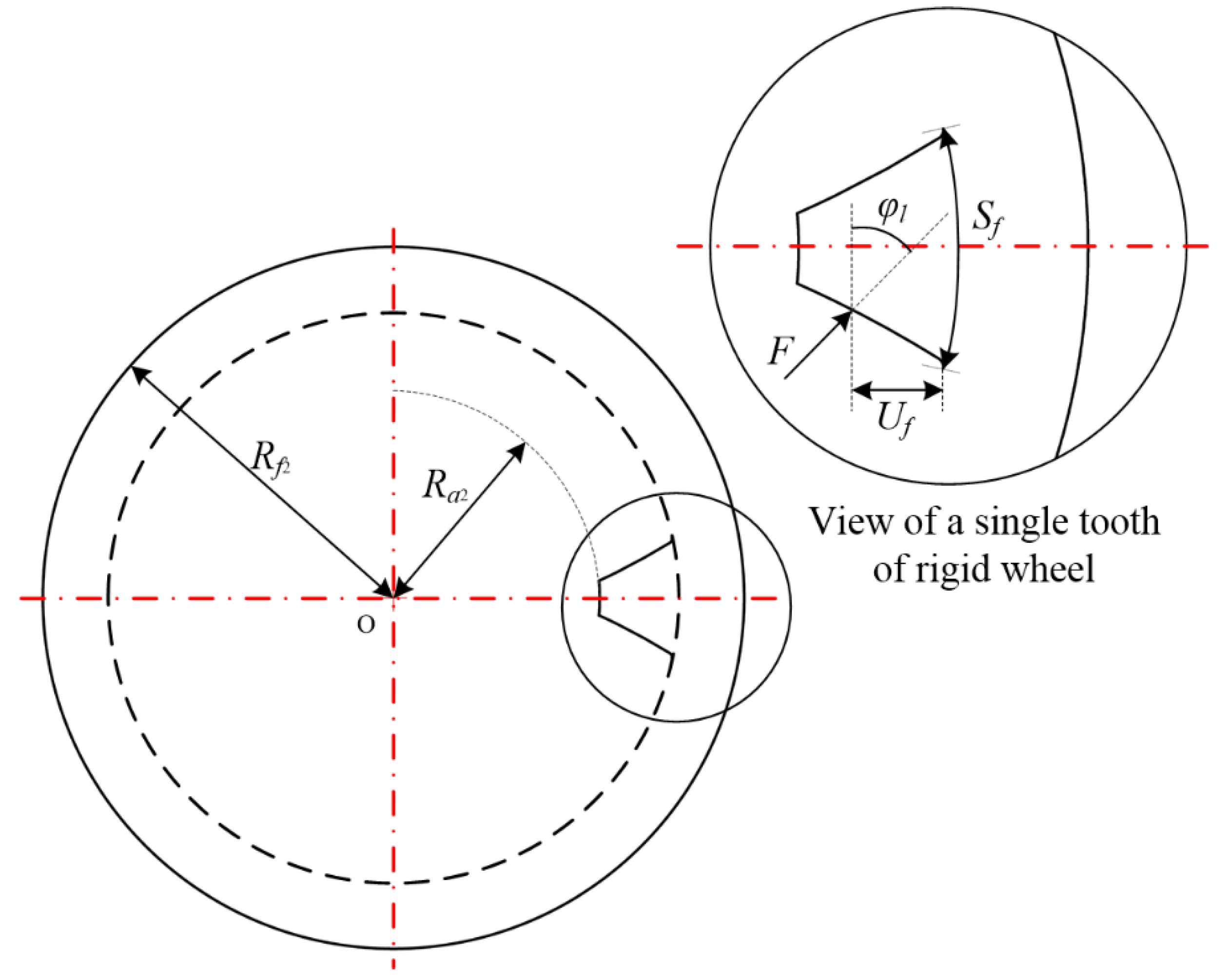
2.2. Tooth Profile Design of the Disposable Harmonic Rigid Wheel
- (1)
- The distortion of the flexible wheel is not considered during transmission, and the length of the neutral layer of the flexible wheel remains unchanged;
- (2)
- The tooth profile of the flexible wheel does not change during assembly and transmission;
- (3)
- The symmetrical section of the flexible teeth is still perpendicular to the neutral layer of the flexible wheel after deformation;
- (4)
- The neutral layer of the flexible wheel remains stable during meshing.
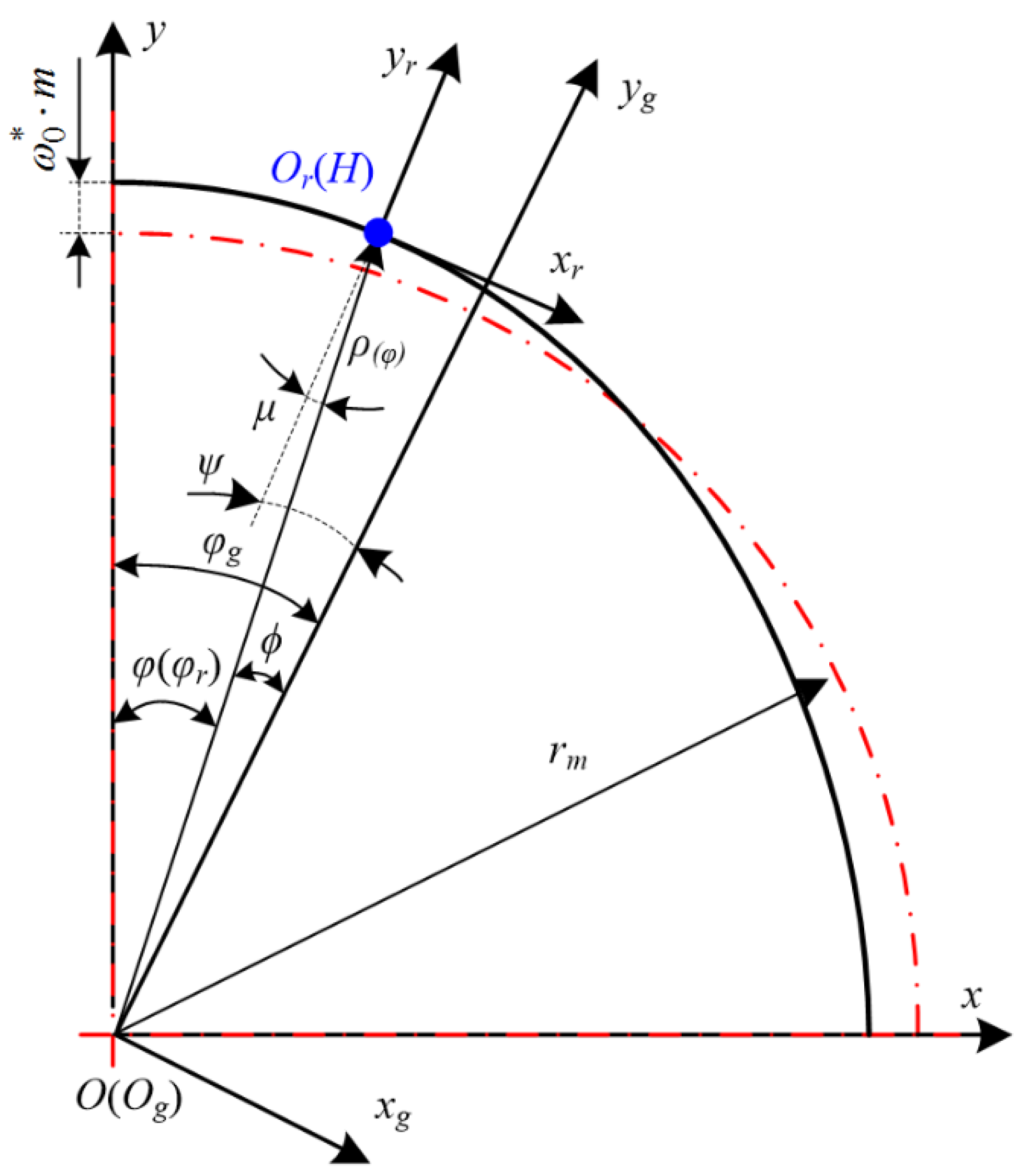
3. Analytical Model to Compute the Meshing Stiffness of the Disposable Harmonic Drive under Full Load
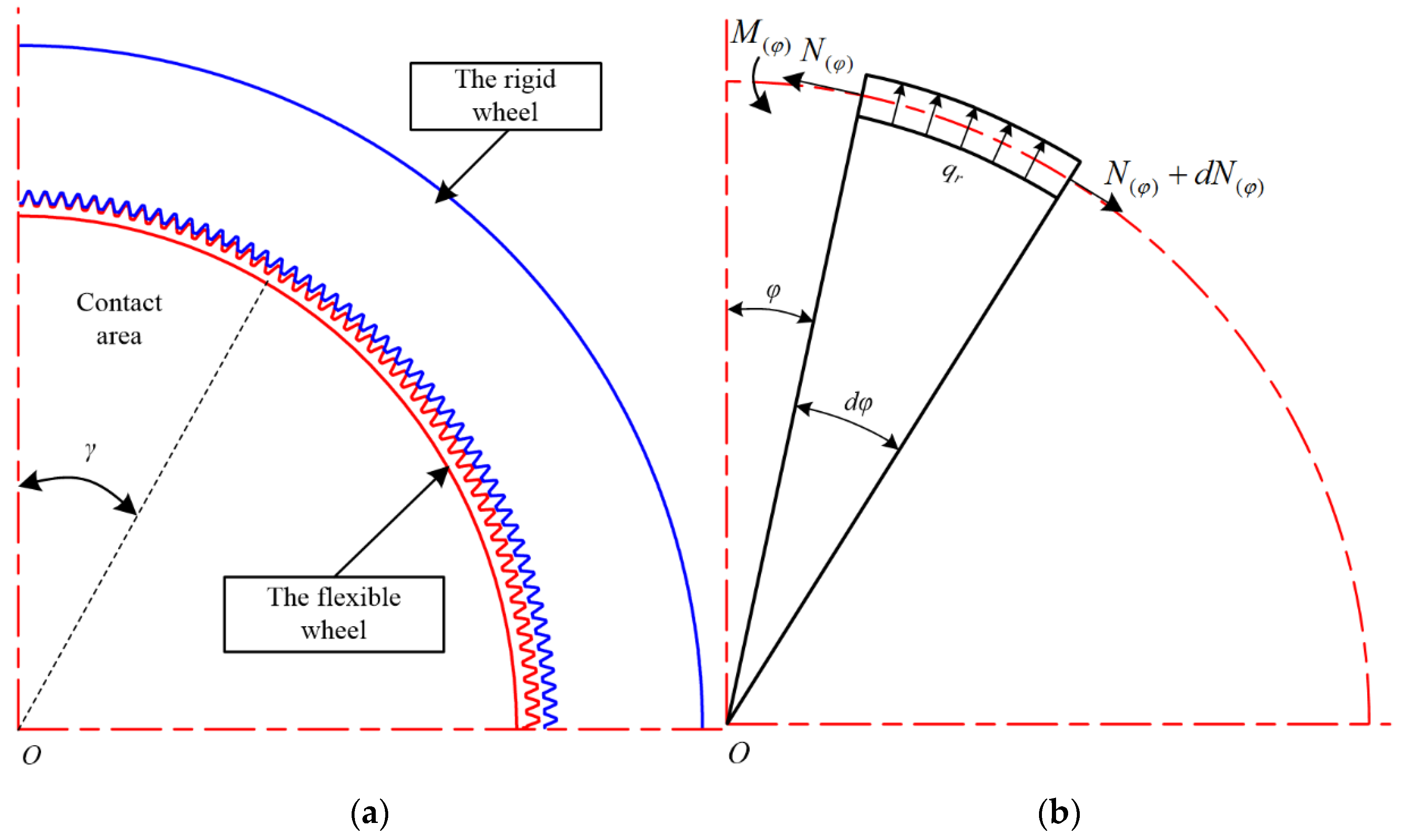
3.1. Stiffness of the Flexible Wheel Tooth
3.2. Stiffness of the Rigid Wheel Tooth
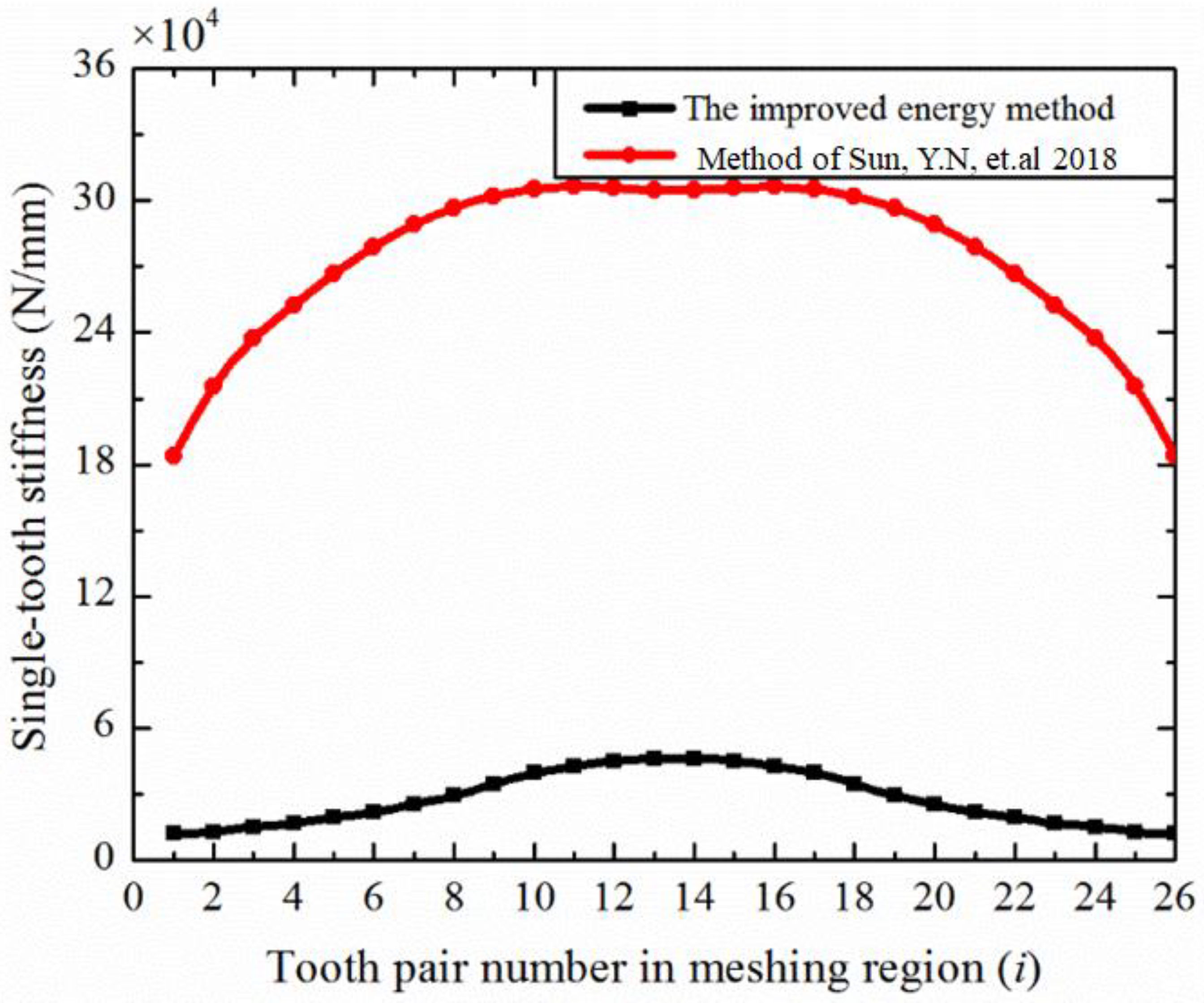
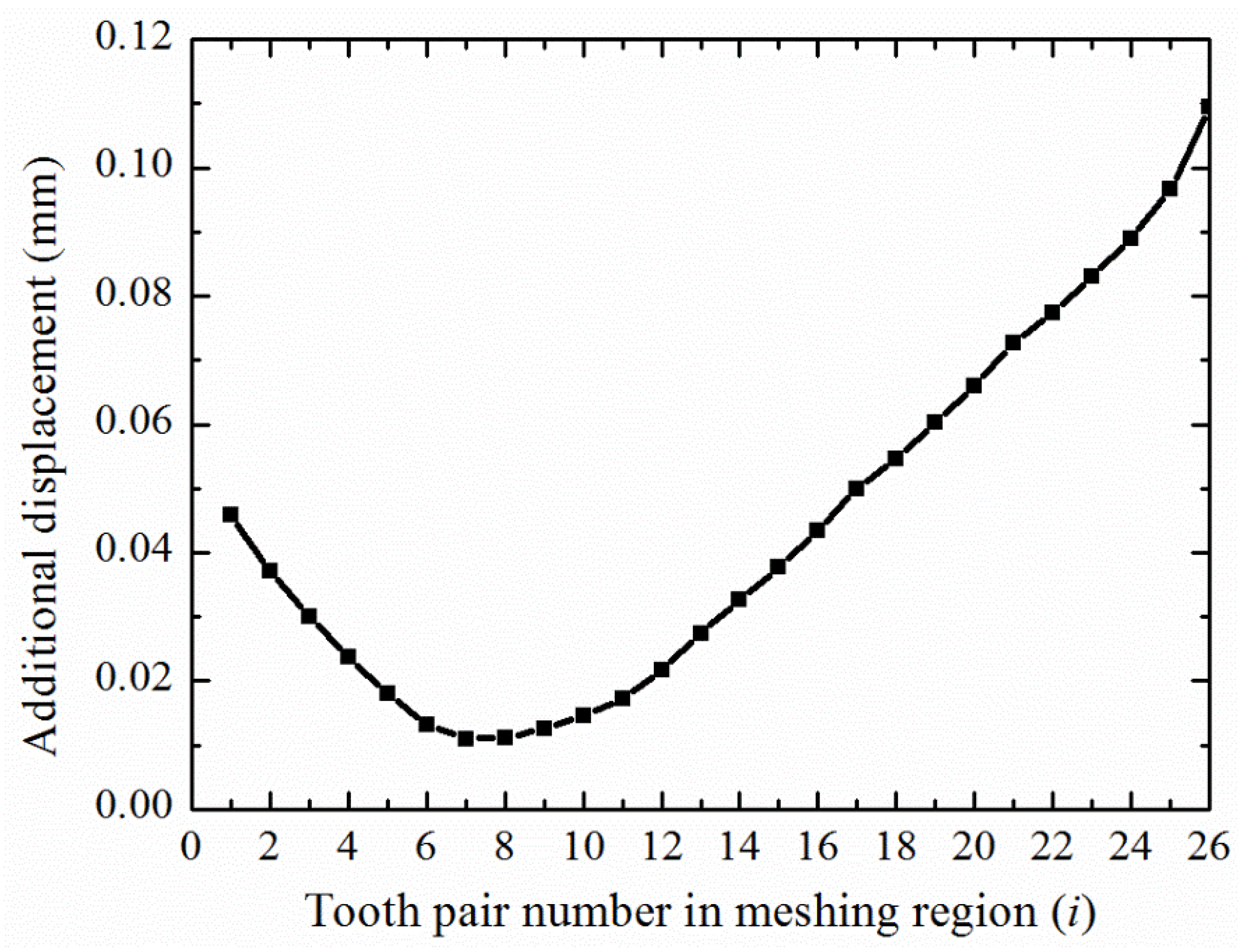
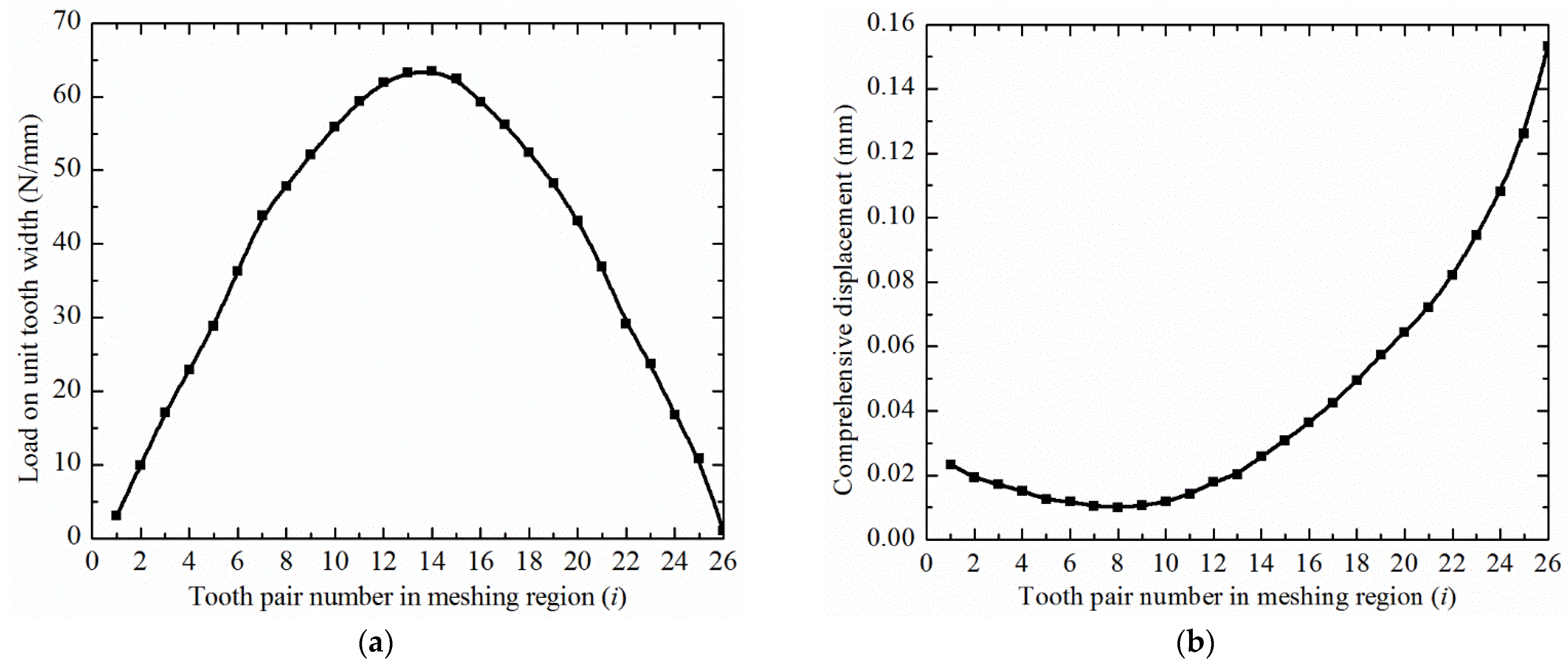
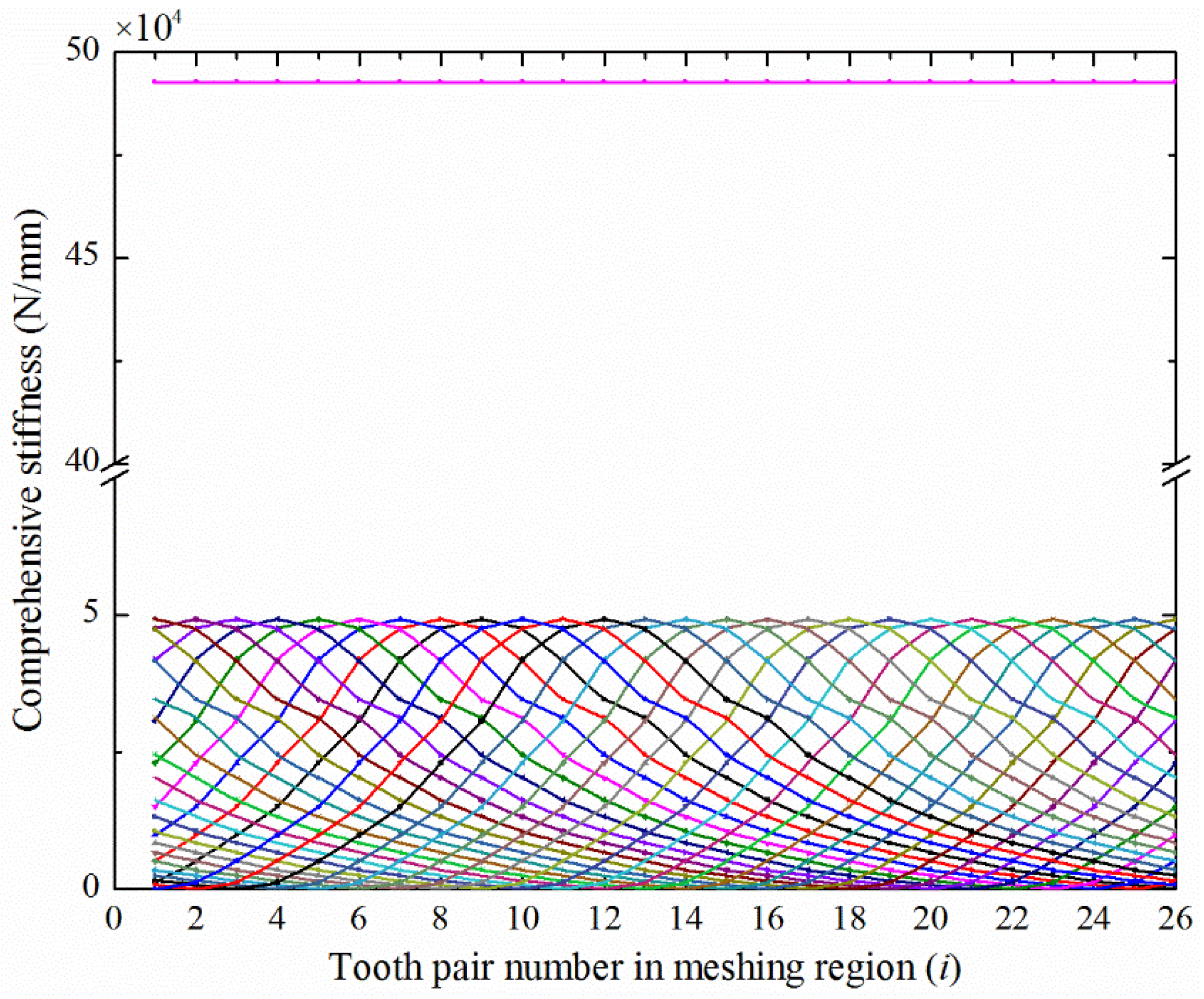
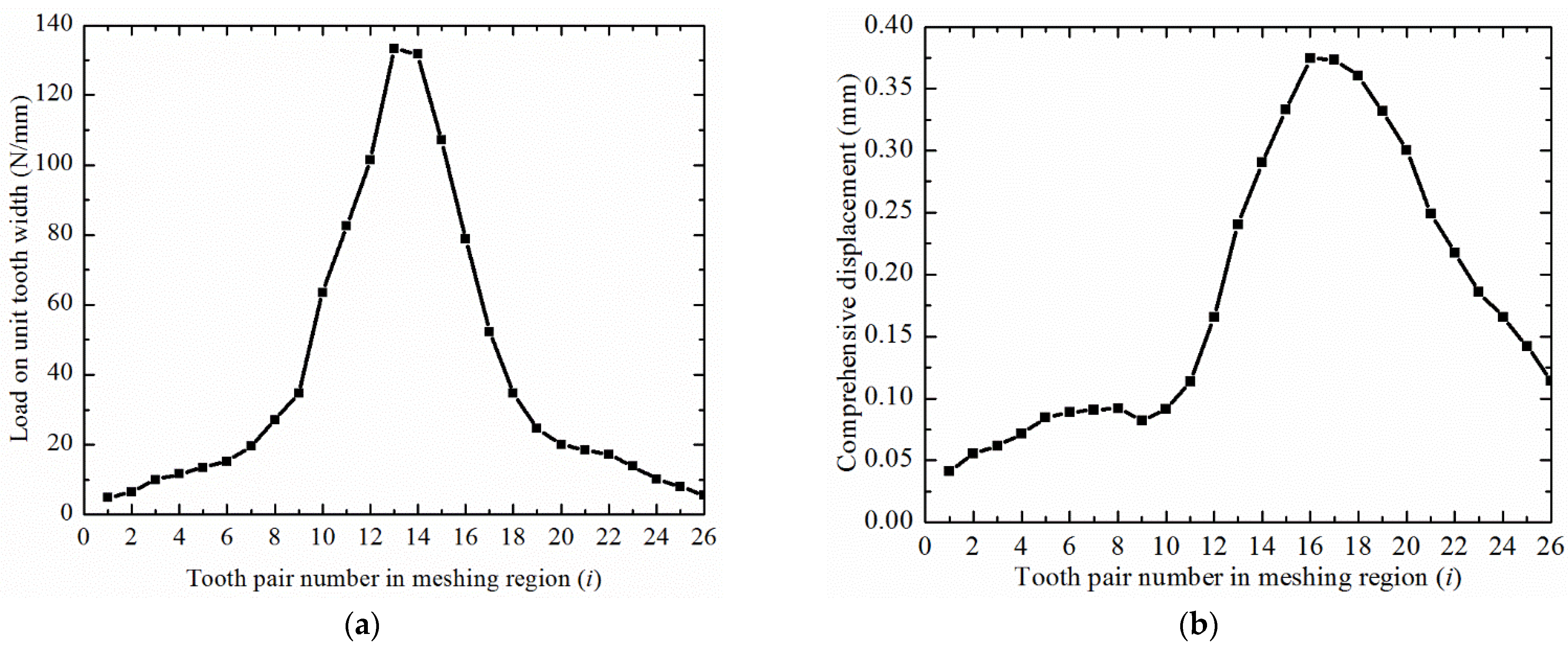
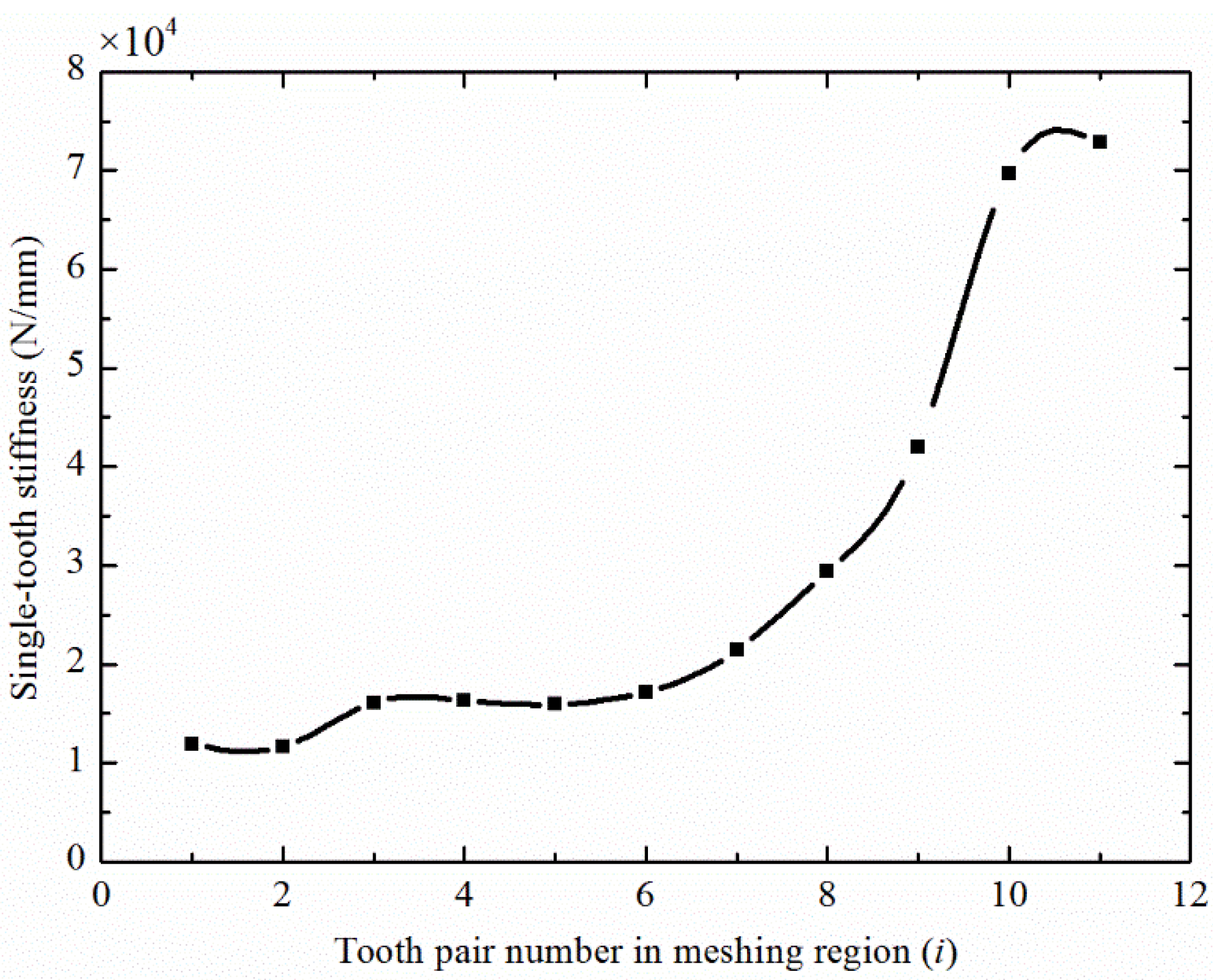
3.3. Stiffness of Multi-Tooth Meshing
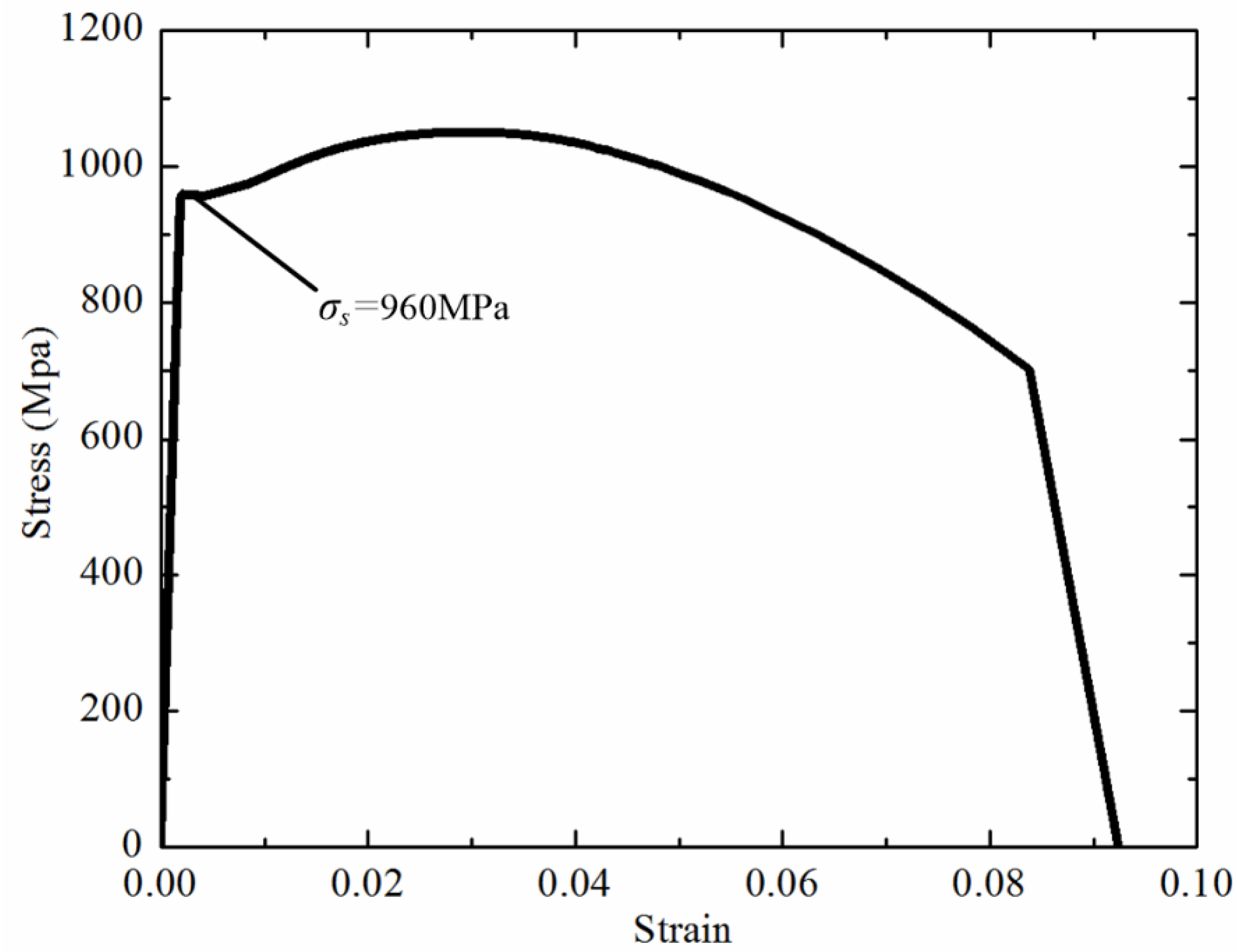
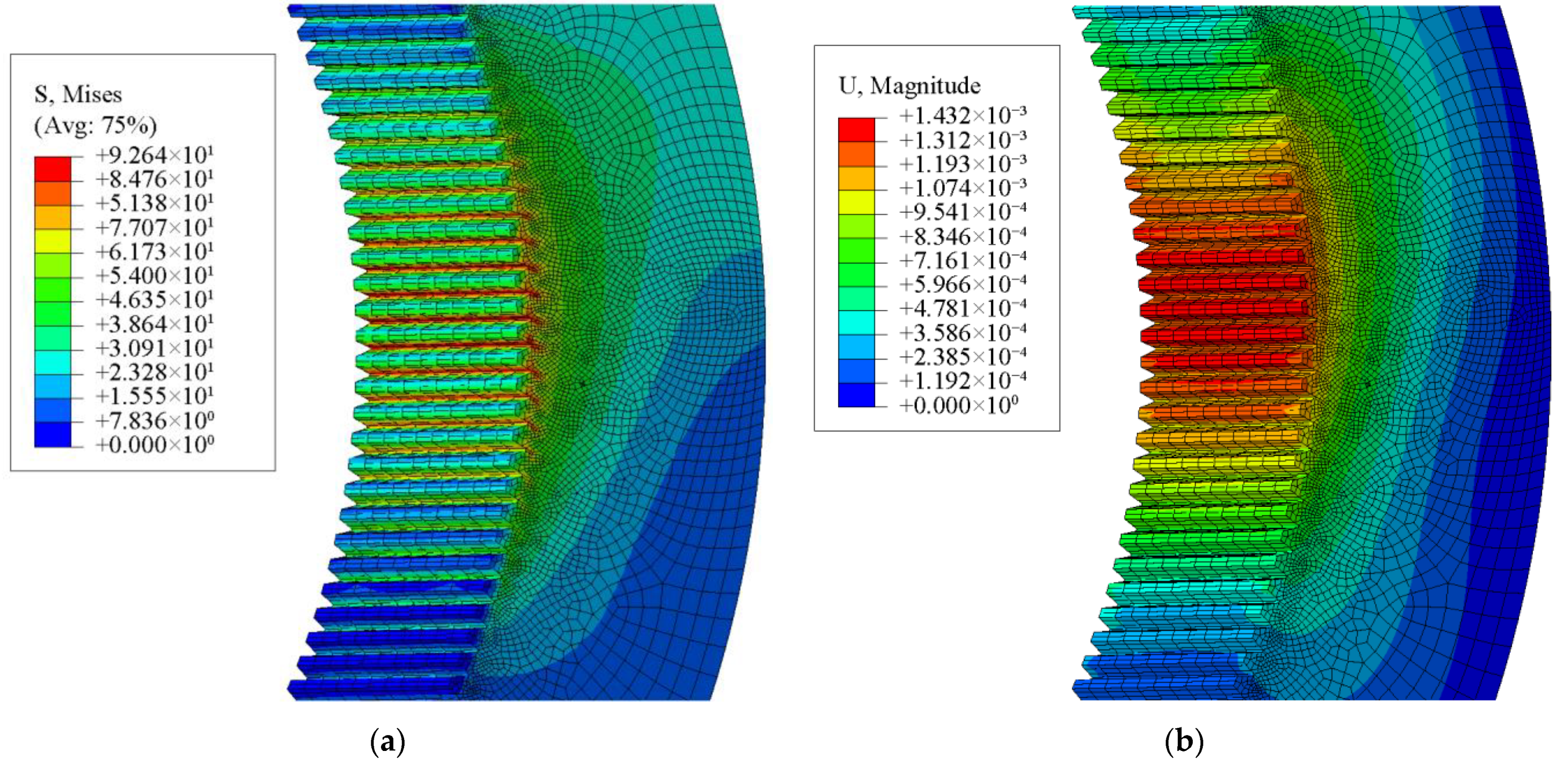
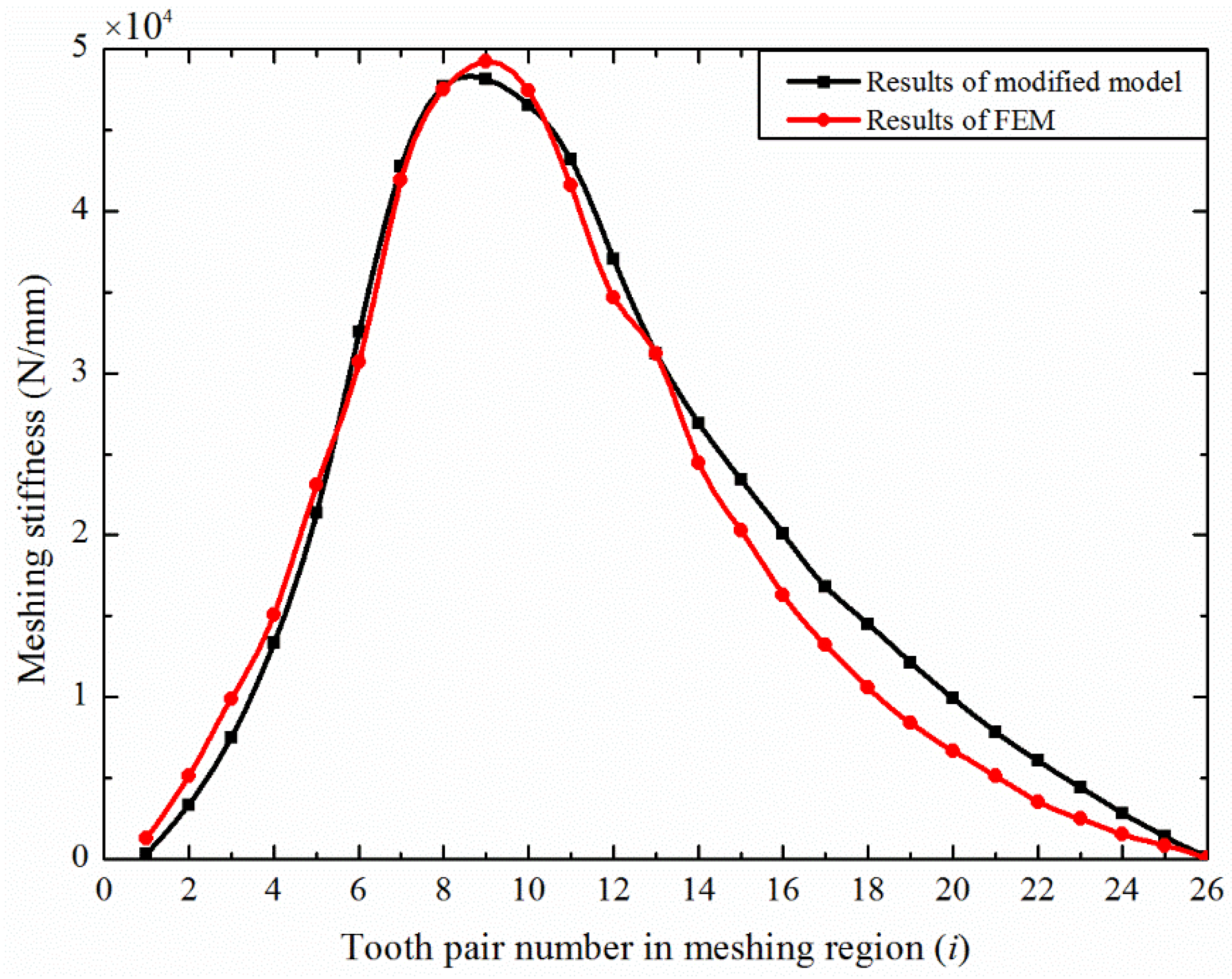
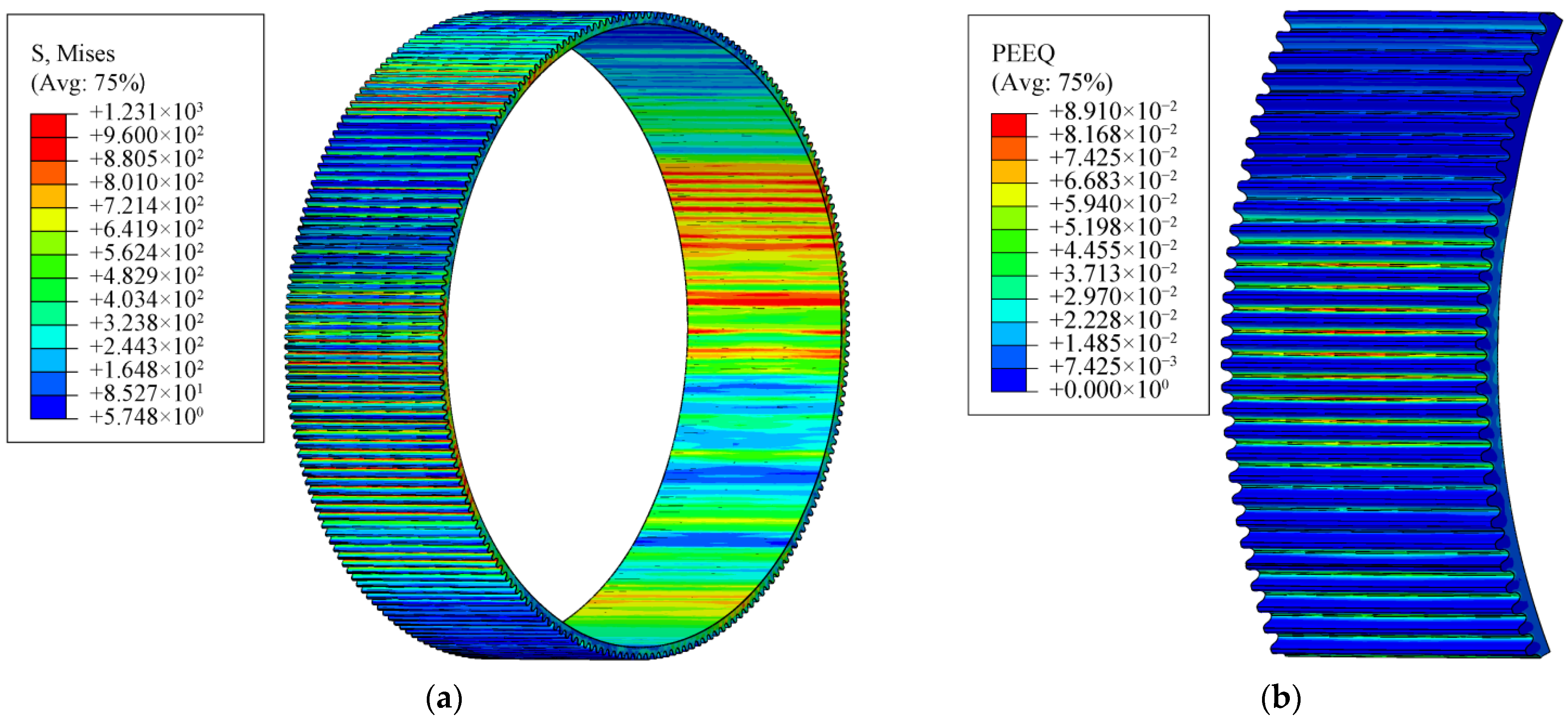
4. Meshing Stiffness Using Finite Element Model
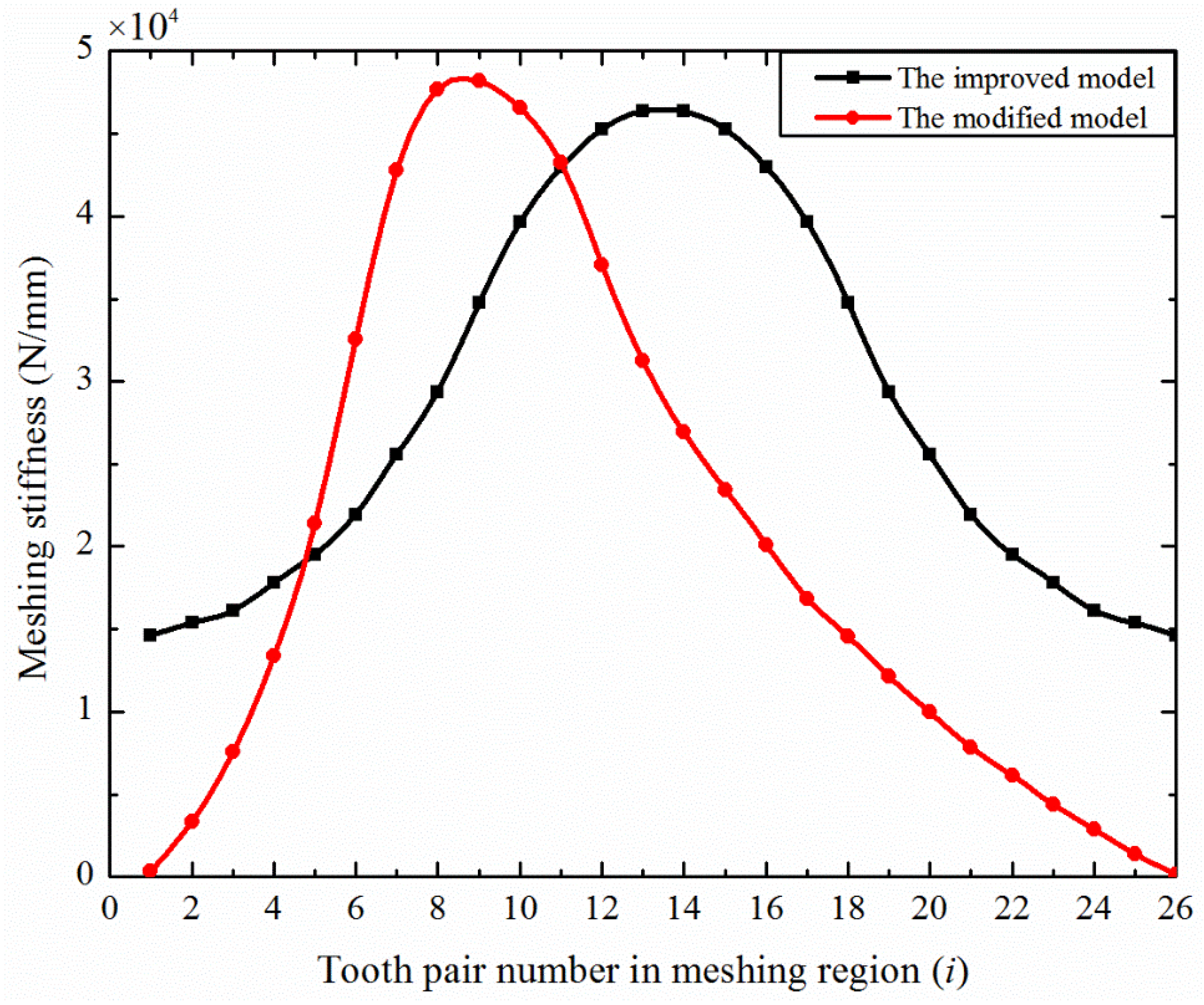
5. Conclusions
- (1)
- Different from other gear transmissions, the calculation of disposable harmonic gears needs to be conducted separately by distinguishing the structural characteristics of the two gears. The model of the teeth that considers the thin rim of the flexible wheel can accurately describe the amplitude of the meshing stiffness of the disposable harmonic gear under full load;
- (2)
- The modified improved energy method considers the influence of multi-tooth meshing on the stiffness of the flexible gear and can accurately reflect the comprehensive stiffness of the disposable harmonic gear in the meshing region under full load;
- (3)
- The comprehensive stiffness of the disposable harmonic drive is higher than that of conventional gear drive. The disposable harmonic gear can operate under full load for a short time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Taghirad, H.D.; Belanger, P.R. Modeling and Parameter Identification of Harmonic Drive Systems. J. Dyn. Syst. Measur. Control 1998, 120, 439–444. [Google Scholar] [CrossRef]
- Ma, D.; Rao, P.; Yan, S. Kinematics Analysis of Meshed Teeth Pairs of Harmonic Drive Gears Considering the Load Effect Using Computer Vision. In Proceedings of the Automation and Robotics of the 5th International Conference on Control, Beijing, China, 19–22 April 2019; pp. 212–217. [Google Scholar]
- Yang, D.C.H.; Lin, J.Y. Hertzian damping, tooth friction and bending elasticity in gear impact dynamics. J. Mech. Des. 1987, 109, 189–196. [Google Scholar] [CrossRef]
- Tian, X.H. Dynamic Simulation for System Response of Gearbox Including Localized Gear Faults. Master Thesis, University of Alberta, Edmonton, AB, Canada, 2004. [Google Scholar]
- Weber, C.; Banaschek, K. The Deformation of Loaded Gears and the Effect on Their Load Carrying Capacity; Department of Scientific and Industrial Research: London, UK, 1951; p. 3. [Google Scholar]
- Attia, A.Y. Deflection of spur gear teeth cut in thin rims. J. Eng. Ind. 1964, 86, 333–341. [Google Scholar] [CrossRef]
- Cornell, R.W. Compliance and stress sensitivity of spur gear teeth. J. Mech. Des. 1981, 103, 447–459. [Google Scholar] [CrossRef] [Green Version]
- Sainsot, P.; Velex, P.; Duverger, O. Contribution of Gear Body to Tooth Deflections—A New Bidimensional Analytical Formula. J. Mech. Des. 2004, 126, 748–752. [Google Scholar] [CrossRef]
- Chaari, F.; Baccar, W.; Abbes, M.S. Effect of spalling or tooth breakage on gear mesh stiffness and dynamic response of a one-stage spur gear transmission. Eur. J. Mech. A Solid. 2008, 27, 691–705. [Google Scholar] [CrossRef]
- Sun, Y.N.; Ma, H.; Huangfu, Y.F. A revised time-varying mesh stiffness model of spur gear pairs with tooth modifications. Mech. Mach. Theory 2018, 129, 261–278. [Google Scholar] [CrossRef]
- Wang, Q.B.; Chen, K.K.; Zhao, B. An analytical-finite-element method for calculating mesh stiffness of spur gear pairs with complicated foundation and crack. Eng. Fail. Anal. 2018, 94, 339–353. [Google Scholar] [CrossRef]
- Chen, W.; Lei, Y.; Fu, Y. A study of effects of tooth surface wear on time-varying mesh stiffness of external spur gear considering wear evolution process. Mech. Mach. Theory 2021, 155, 104055. [Google Scholar] [CrossRef]
- Sánchez, M.B.; Pleguezuelos, M. Influence of profile modifications on meshing stiffness, load sharing, and trasnsmission error of involute spur gears. Mech. Mach. Theory. 2019, 139, 506–525. [Google Scholar] [CrossRef]
- Ma, H.; Pang, X.; Feng, R. Fault features analysis of cracked gear considering the effects of the extended tooth contact. Eng. Fail. Anal. 2015, 48, 105–120. [Google Scholar] [CrossRef]
- Zhan, J.X.; Fard, M.; Jazar, R. A CAD-FEM-QSA integration technique for determining the time-varying meshing stiffness of gear pairs. Measurement 2017, 100, 139–149. [Google Scholar] [CrossRef]
- Chen, K.; Huangfu, Y.F.; Ma, H. Calculation of mesh stiffness of spur gears considering complex foundation types and crack propagation paths. Mech. Syst. Signal Process. 2019, 130, 273–292. [Google Scholar] [CrossRef]
- Kayabasi, O.; Erzincanli, F. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modelling. Mater. Des. 2007, 28, 441–447. [Google Scholar] [CrossRef]
- Ma, D.H.; Wu, J.N.; Liu, T. Deformation analysis of the flexspline of harmonic drive gears considering the driving speed effect using laser sensors. Sci. China Technol. Sci. 2017, 60, 1175–1187. [Google Scholar] [CrossRef]
- Dong, H.M.; Wang, D. Elastic deformation characteristic of the flexspline in harmonic drive. In ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots (ReMAR); IEEE: London, UK, 2009; pp. 363–369. [Google Scholar]
- Dong, H.M.; Zhu, Z.D.; Zhou, W.D. Dynamic Simulation of Harmonic Gear Drives Considering Tooth Profiles Parameters Optimization. J. Comput. 2012, 7, 1429–1436. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.X.; Lin, S.Z.; Xing, J.Z. Deformation of flexspline under transmission force in harmonic drive. Adv. Mat. Res. 2010, 97–101, 3536–3539. [Google Scholar] [CrossRef]
- Chen, X.X.; Liu, Y.S.; Xing, J.Z. A novel method based on mechanical analysis for the stretch of the neutral line of the flexible wheel cup of a harmonic drive. Mech. Mach. Theory 2014, 76, 1–19. [Google Scholar] [CrossRef]
- Chen, X.X.; Liu, Y.S.; Xing, J.Z. Neutral line of flexible wheel in harmonic driver. J. Mech. Eng. 2014, 50, 1–19. [Google Scholar] [CrossRef]
- Hrcek, S.; Brumercik, F.; Slavomir, L.; Lukac, M.; Patin, B.; Glowacz, A. Global Sensitivity Analysis of Chosen Harmonic Drive Parameters Affecting Its Lost Motion. Materials 2021, 14, 5057. [Google Scholar] [CrossRef]
- Hu, S.Y.; Fang, Z.D. The Analysis and Modeling of the Synthetical Meshing Stiffness of Inner Gearing considering the Flexible Inner Ring Gear. Shock Vib. 2019, 2019, 2324546. [Google Scholar] [CrossRef]
- Dong, H.M.; Wang, D.L.; Ting, K. Kinematic Effect of the Compliant Cup in Harmonic Drives. J. Mech. Des. 2011, 133, 051004. [Google Scholar] [CrossRef]
- Gravagno, F.; Mucino, V.H.; Pennestrì, E. Influence of wave generator profile on the pure kinematic error and centrodes of harmonic drive. Mech. Mach. Theory. 2016, 104, 100–117. [Google Scholar] [CrossRef]
- Tjahjowidodo, T.; Al-Bender, F.; Brussel, H.V. Theoretical modelling and experimental identification of nonlinear torsional behaviour in harmonic drives. Mechatronics 2013, 23, 497–504. [Google Scholar] [CrossRef]
- Zhang, H.; Ahmad, S.; Liu, G. Modeling of Torsional Compliance and Hysteresis Behaviors in Harmonic Drives. IEEE ASME Trans. Mechatron. 2014, 20, 178–185. [Google Scholar] [CrossRef]
- Rheaume, F.E.; Champliaud, H.; Liu, Z. On the computing of the torsional rigidity of a harmonic drive using FEA. In Proceedings of the ANSYS Conference and Exhibition, Pittsburgh, PA, USA, 2–4 May 2006. [Google Scholar]
- Rhéaume, F.E.; Champliaud, H.; Liu, Z. Understanding and modelling the torsional stiffness of harmonic drives through finite-element method. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2009, 223, 515–524. [Google Scholar] [CrossRef]
- Timofeev, G.A.; Kostikov, Y.V. Torsional rigidity of harmonic gear drives. Rus. Eng. Res. 2016, 36, 995–998. [Google Scholar] [CrossRef]
- Ma, J.F.; Li, C.; Luo, Y.C. Simulation of meshing characteristics of harmonic reducer and experimental verification. Adv. Mech. Eng. 2018, 10, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.H.; Wang, R.; Rao, P.F. Automated Analysis of Meshing Performance of Harmonic Drive Gears under Various Operating Conditions. IEEE Access 2018, 6, 68137–68154. [Google Scholar] [CrossRef]
- Wei, L.Y.; Wang, C.L.; Zhang, L.Y. Finite Element Analysis of Meshing Stiffness of Harmonic Gear. J. Mech. Transm. 2018, 42, 147–150. [Google Scholar]
- Zhang, Y.X.; Wang, G.L.; Pan, X.D. Calculating the Load Distribution and Contact Stress of the Disposable Harmonic Drive under Full Load. Machines 2022, 10, 96. [Google Scholar] [CrossRef]
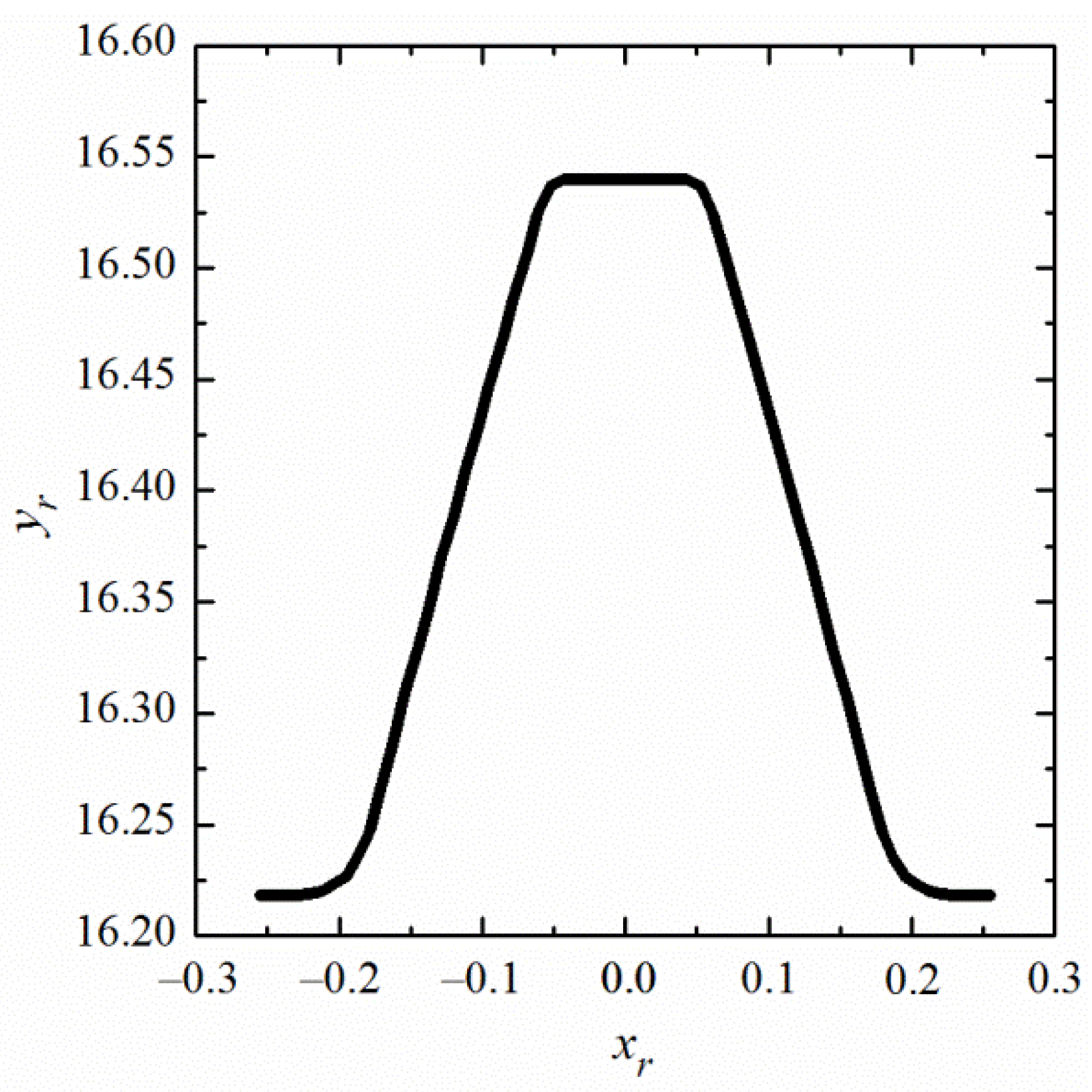
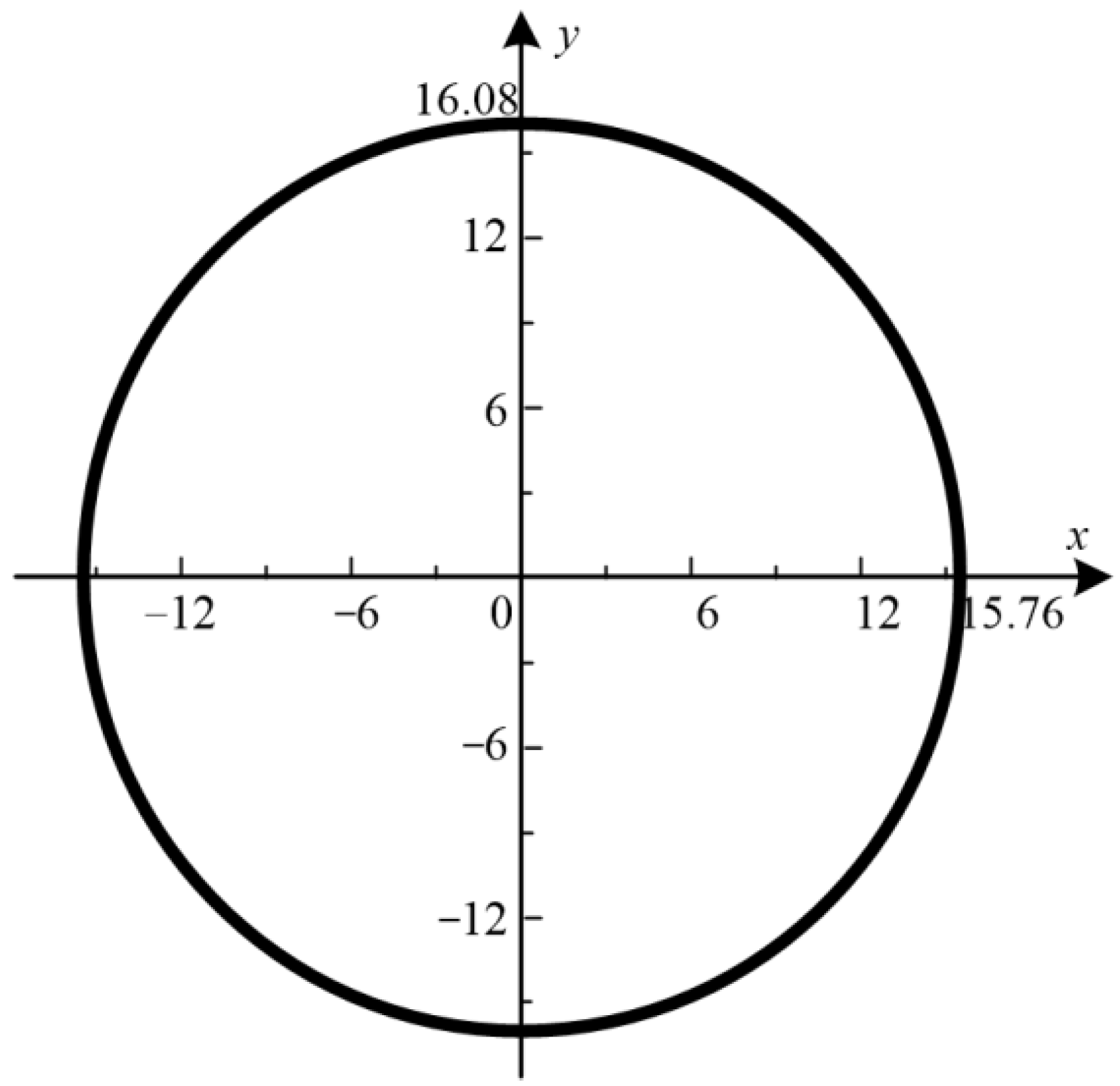
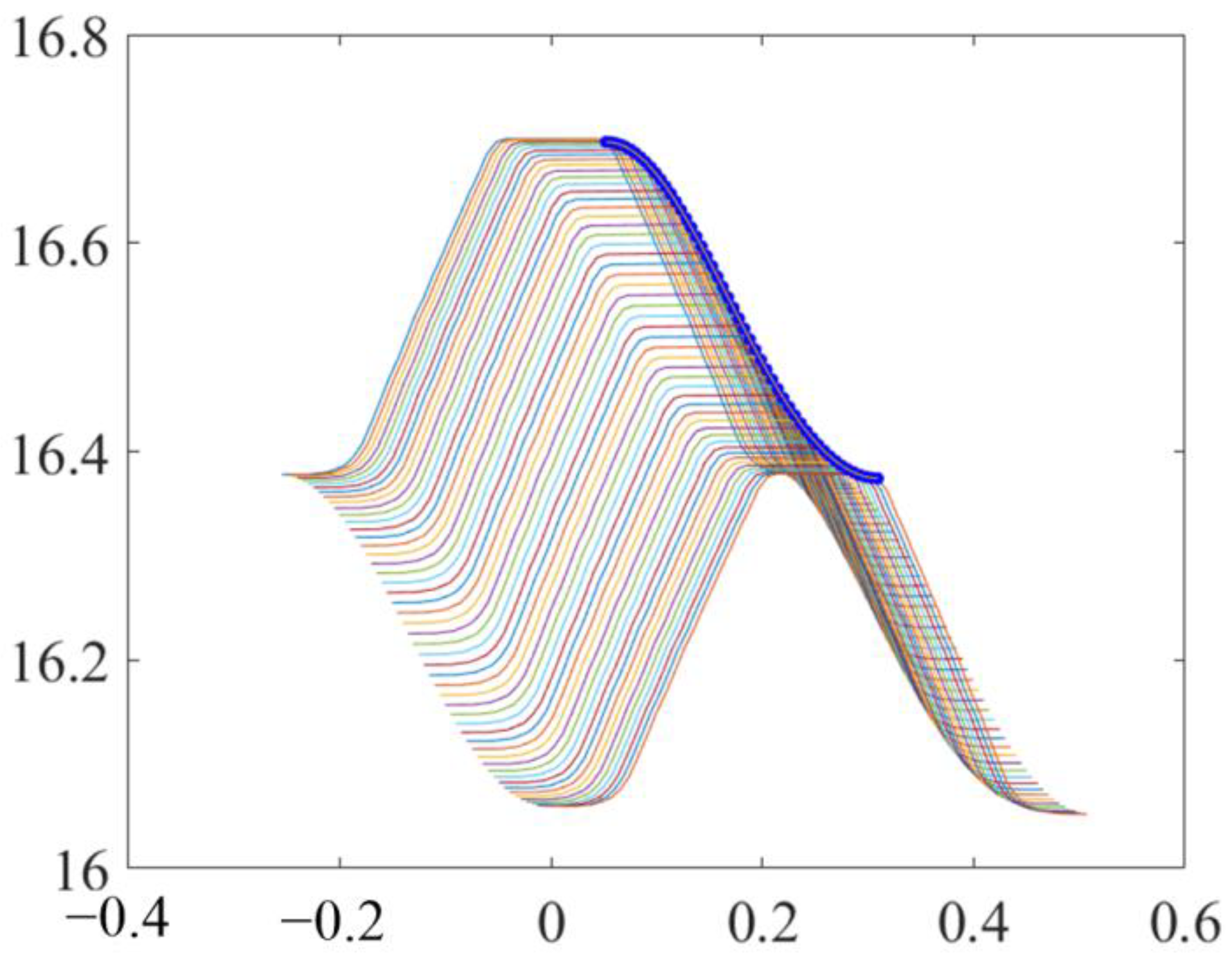






| L* | M* | P* | Q* | |
|---|---|---|---|---|
| Weber [5]–Attia [6] | 5.2 | 1 | 1.4 | 0.294–0.32 |
| Cornell [7] | 5.306 | 1.4 (plane stress) 1.14 (plane strain) | 1.534 | 0.32 |
| Parameter | Flexible Wheel | Rigid Wheel |
|---|---|---|
| Number of teeth Z | 200 | 202 |
| Module m (mm) | 0.16 | 0.16 |
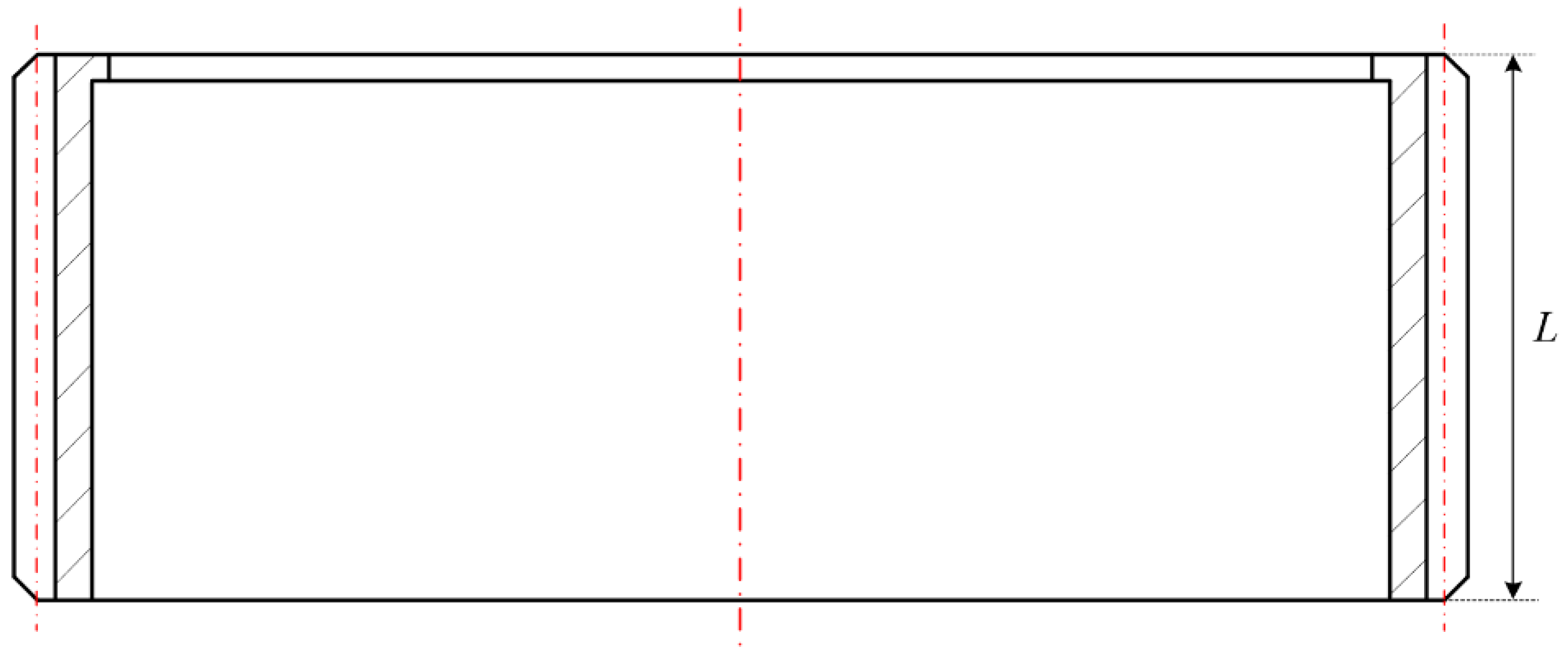
| Teeth width L (mm) | 10 | 10 |
| Pressure angle α0 (°) | 20 | |
| Transmission ratio | 100 | |
| Flexible Wheel | Rigid Wheel and Wave Generator | |
|---|---|---|
| Material | 40CrNiMoA | 45 Steel |
| Density ρ (kg/m3) | 7850 | 7870 |
| Young’s modulus E (MPa) | 211,000 | 209,000 |
| Poisson’s ratio ν | 0.3 | 0.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Pan, X.; Li, Y.; Wang, G.; Wu, G. Meshing Stiffness Calculation of Disposable Harmonic Drive under Full Load. Machines 2022, 10, 271. https://doi.org/10.3390/machines10040271
Zhang Y, Pan X, Li Y, Wang G, Wu G. Meshing Stiffness Calculation of Disposable Harmonic Drive under Full Load. Machines. 2022; 10(4):271. https://doi.org/10.3390/machines10040271
Chicago/Turabian StyleZhang, Yuxin, Xudong Pan, Yuefeng Li, Guanglin Wang, and Guicheng Wu. 2022. "Meshing Stiffness Calculation of Disposable Harmonic Drive under Full Load" Machines 10, no. 4: 271. https://doi.org/10.3390/machines10040271





