Feedforward–Feedback Controller Based on a Trained Quaternion Neural Network Using a Generalised
Abstract
:1. Introduction
2. Feedforward–Feedback Controller Based on a Quaternion Neural Network
2.1. Generalised Calculus
2.2. Quaternion Neural Network
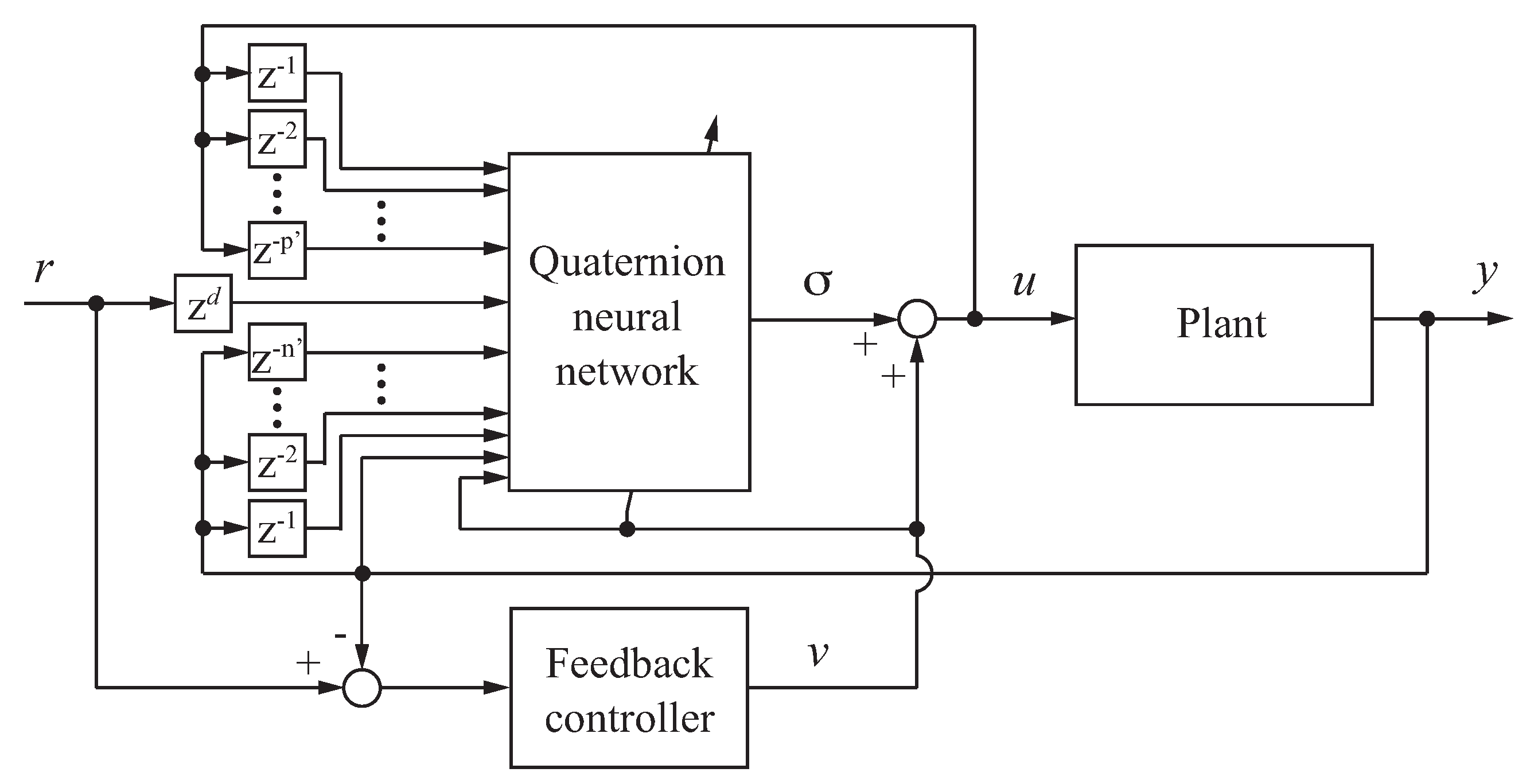
2.3. Feedforward–Feedback Controller
2.4. Remarks on the Stability Condition of the Controller
- (i)
- The plant is represented by Equation (13), where the orders of the plant, the dead time and the sign of the high–frequency gain are known.
- (ii)
- The QNN’s activation function is a split-type function using a component-wise linear function even though it is not analytic in the field of quaternion number.
- (iii)
- The feedback controller is a P–controller, and the QNN’s connection weights allow the feedback controller output to be sufficiently small.
3. Computational Experiments
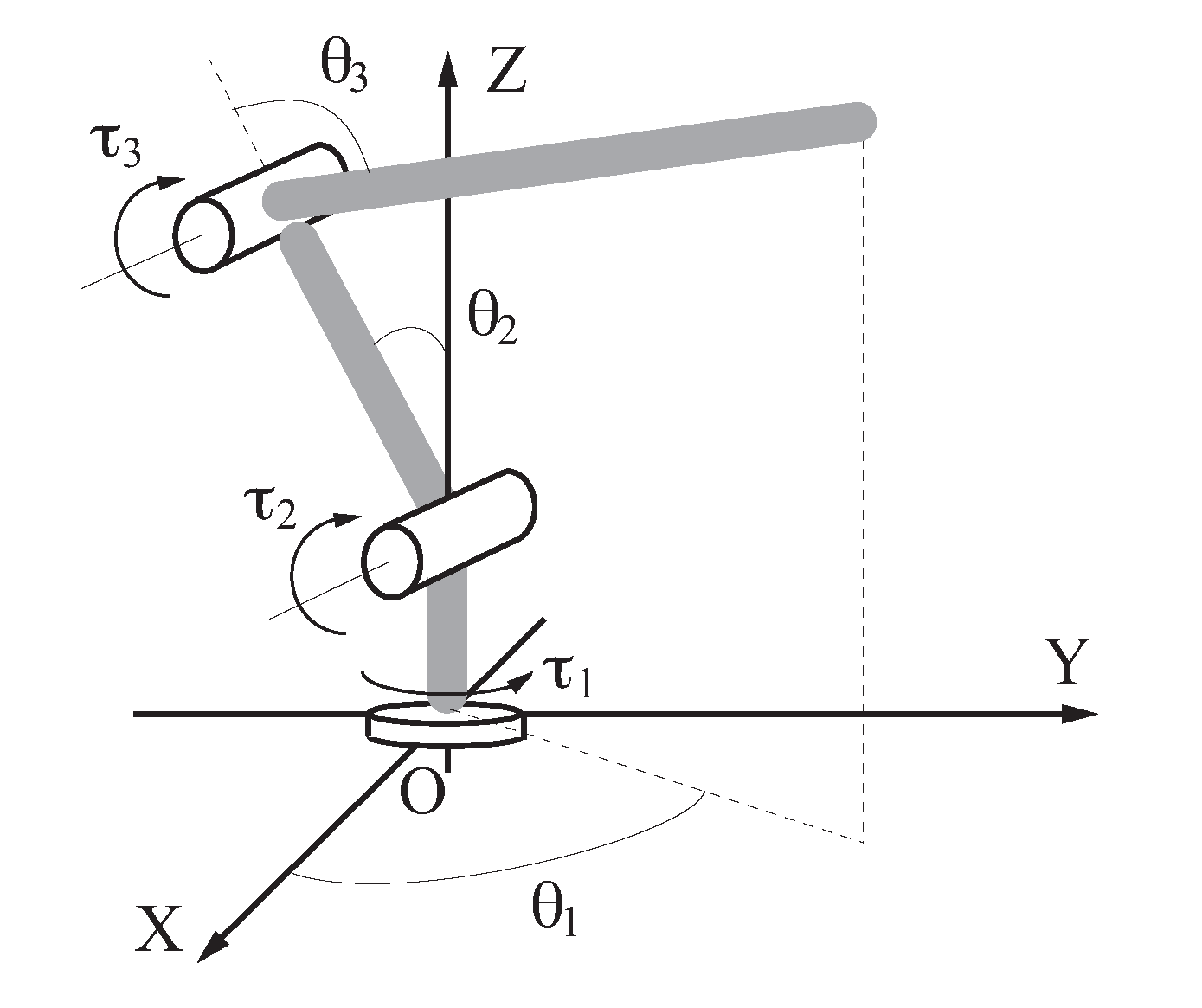
3.1. Robot Manipulator
3.2. Controller Condition
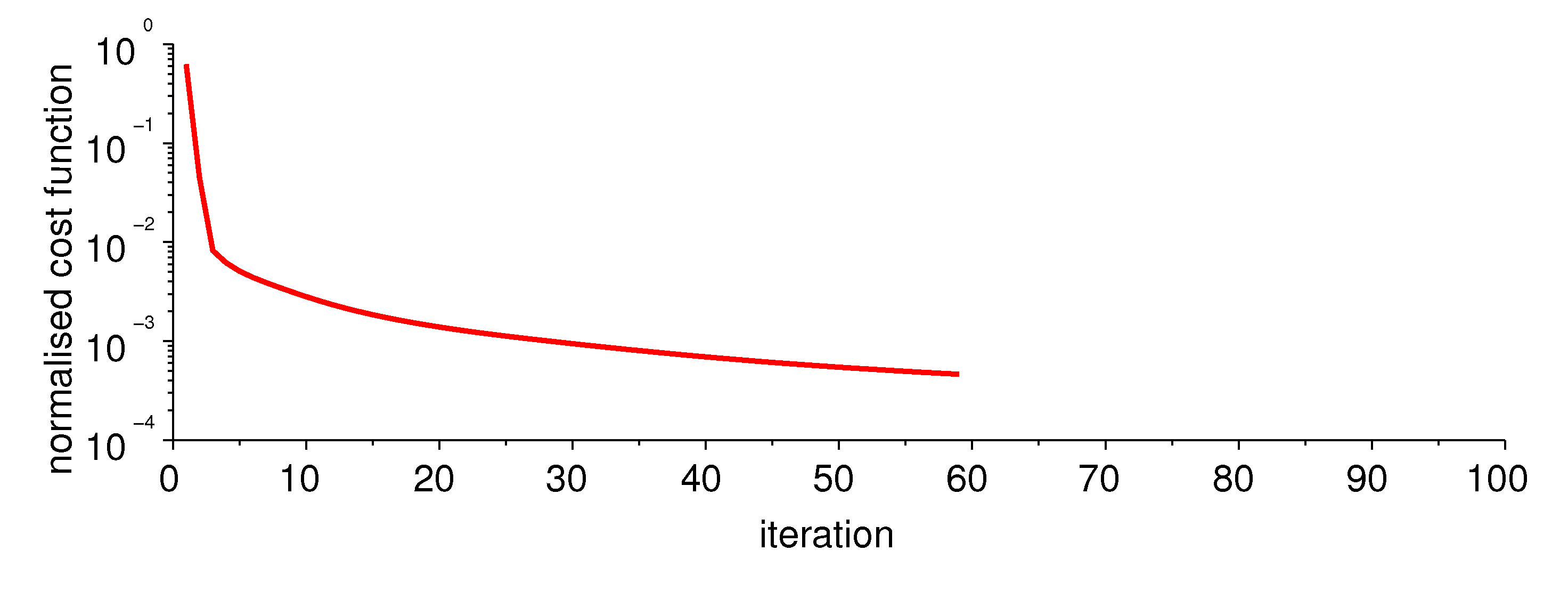
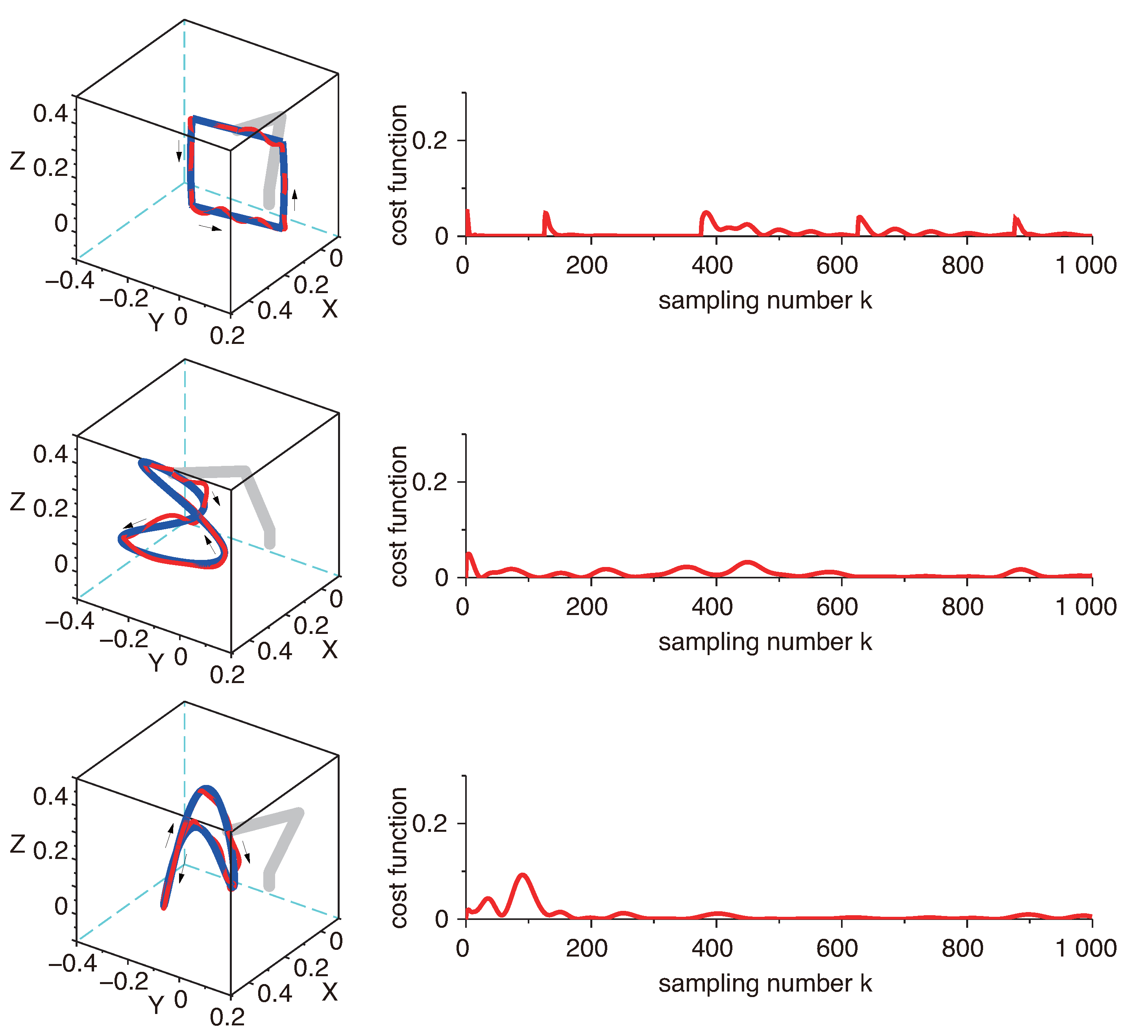
3.3. Numerical Simulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, Y. Artificial Intelligence: A survey on evolution, models, applications and future trends. J. Manag. Anal. 2019, 6, 1–29. [Google Scholar] [CrossRef]
- Ingrand, F.; Ghallab, M. Robotics and artificial intelligence: A perspective on deliberation functions. AI Commun. 2014, 27, 63–80. [Google Scholar] [CrossRef] [Green Version]
- Prieto, A.; Prieto, B.; Ortigosa, E.M.; Ros, E.; Pelayo, F.; Ortega, J.; Rojas, I. Neural networks: An overview of early research, current frameworks and new challenges. Neurocomputing 2016, 214, 242–268. [Google Scholar] [CrossRef]
- Dargan, S.; Kumar, M.; Ayyagari, M.R.; Kumar, G. A survey of deep learning and its applications: A new paradigm to machine learning. Arch. Comput. Methods Eng. 2020, 27, 1071–1092. [Google Scholar] [CrossRef]
- Wang, H.; Liu, N.; Zhang, Y.; Feng, D.; Huang, F.; Li, D.; Zhang, Y. Deep reinforcement learning: A survey. Front. Inf. Technol. Electron. Eng. 2020, 21, 1726–1744. [Google Scholar] [CrossRef]
- Alfsmann, D.; Göckler, H.G.; Sangwine, S.J.; Ell, T.A. Hypercomplex algebras in digital signal processing: Benefits and drawbacks. In Proceedings of the 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007; pp. 1322–1326. [Google Scholar]
- Nitta, T. (Ed.) Complex–Valued Neural Networks—Utilizing High–Dimensional Parameters; Information Science Reference: Hershey, PA, USA, 2009. [Google Scholar]
- Hirose, A. (Ed.) Complex–Valued Neural Networks—Advances and Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2013. [Google Scholar]
- Tripathi, B.K. (Ed.) High Dimensional Neurocomputing—Growth, Appraisal and Applications; Springer: New Delhi, India, 2015. [Google Scholar]
- Parcollet, T.; Morchid, M.; Linares, G. A survey of quaternion neural networks. Artif. Intell. Rev. 2020, 53, 2957–2982. [Google Scholar] [CrossRef]
- García–Retuerta, D.; Casado–Vara, R.; Rey, A.M.; Prieta, F.D.; Prieto, J.; Corchado, J.M. Quaternion neural networks: State–of–the–art and research challenges. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Guimaraes, Portugal, 4–5 November 2020; pp. 456–467. [Google Scholar]
- Bayro-Corrochano, E. A survey on quaternion algebra and geometric algebra applications in engineering and computer science 1995–2020. IEEE Access 2021, 9, 104326–104355. [Google Scholar] [CrossRef]
- Takahashi, K.; Isaka, A.; Fudaba, T.; Hashimoto, M. Remarks on quaternion neural network–based controller trained by feedback error learning. In Proceedings of the 2017 IEEE/SICE International Symposium on System Integration, Taipei, Taiwan, 11–14 December 2017; pp. 875–880. [Google Scholar]
- Takahashi, K. Comparison of neural network–based adaptive controllers using hypercomplex numbers for controlling robot manipulator. In Proceedings of the 13th IFAC Workshop on Adaptive and Learning Control Systems, Winchester, UK, 4–6 December 2019; pp. 67–72. [Google Scholar]
- Takahashi, K.; Watanabe, L.; Yamasaki, H.; Hiraoka, S.; Hashimoto, M. Remarks on control of a robot manipulator using a quaternion recurrent neural–network–based compensator. In Proceedings of the 2020 Australian & New Zealand Control Conference, Gold Coast, Australia, 25–26 November 2020; pp. 244–247. [Google Scholar]
- Takahashi, K. Comparison of high–dimensional neural networks using hypercomplex numbers in a robot manipulator control. Artif. Life Robot. 2021, 26, 367–377. [Google Scholar] [CrossRef]
- Parcollet, T.; Ravanelli, M.; Morchid, M.; Linarés, G.; Trabelsi, C.; Mori, R.D.; Bengio, Y. Quaternion recurrent neural networks. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019; pp. 1–9. [Google Scholar]
- Mandic, D.P.; Jahanchahi, C.; Took, C.C. A quaternion gradient operator and its applications. IEEE Signal Process. Lett. 2011, 18, 47–50. [Google Scholar] [CrossRef]
- Xu, D.; Jahanchahi, C.; Took, C.C.; Mandic, D.P. Enabling quaternion derivatives: The generalized HR calculus. R. Soc. Open Sci. 2015, 2, 150255. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, D.; Mandic, D.P. The theory of quaternion matrix derivatives. IEEE Trans. Signal Process. 2015, 63, 1543–1556. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Gao, H.; Mandic, D.P. A new proof of the generalized Hamiltonian–Real calculus. R. Soc. Open Sci. 2016, 3, 160211. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Xia, Y.; Mandic, D.P. Optimization in quaternion dynamic systems: Gradient, hessian, and learning algorithms. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 249–261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popa, C.A. Learning algorithms for quaternion–valued neural networks. Neural Process. Lett. 2018, 47, 949–973. [Google Scholar] [CrossRef]
- Takahashi, K.; Tano, E.; Hashimoto, M. Remarks on feedforward-feedback controller using a trained quaternion neural network based on generalised HR calculus and its application to controlling a robot manipulator. In Proceedings of the 2021 (11th) International Conference on Advanced Mechatronic Systems, Tokyo, Japan, 9–12 December 2021; pp. 81–86. [Google Scholar]
- Kawato, M.; Furukawa, K.; Suzuki, R. A hierarchical neural-network model for control and learning of voluntary movement. Biol. Cybern. 1987, 57, 169–185. [Google Scholar] [CrossRef] [PubMed]
- Yamada, T. Remarks on feedback loop gain characteristics of adaptive type neural network feedforward feedback controller. In Proceedings of the SICE Annual Conference 2008, Tokyo, Japan, 20–22 August 2008; pp. 2244–2249. [Google Scholar]

| Steel–Dwass Test | Iteration | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | Median (IQR) | ||
| Number of units | 1 | – | 42.5 (32.5–59.5) | |||
| 2 | * | – | 60.5 (38.5–81) | |||
| 3 | ns | – | 63 (44.75–82.25) | |||
| 4 | ns | ns | – | 75 (60.75–87) | ||
| Steel–Dwass Test | Reset | |||||
| 1 | 2 | 3 | 4 | Median (IQR) | ||
| Number of units | 1 | – | 48.5 (20.75–83.75) | |||
| 2 | ns | – | 75 (33.75–143.25) | |||
| 3 | – | 256.5 (92.25–634.5) | ||||
| 4 | – | 1006.5 (317.75–2378.75) | ||||
| Steel–Dwass Test | Iteration | ||||||
|---|---|---|---|---|---|---|---|
| 0.006 | 0.012 | 0.018 | 0.024 | 0.030 | Median (IQR) | ||
| Learning factor | 0.006 | – | 72 (55.25–87.25) | ||||
| 0.012 | ns | – | 60.5 (38.5–81) | ||||
| 0.018 | ns | – | 48.5 (37–67.5) | ||||
| 0.024 | * | ns | – | 45 (29–66.25) | |||
| 0.030 | † | ns | ns | – | 43.5 (29.25–66) | ||
| Steel–Dwass Test | Reset | ||||||
| 0.006 | 0.012 | 0.018 | 0.024 | 0.030 | Median (IQR) | ||
| Learning factor | 0.006 | – | 219.5 (91–681.5) | ||||
| 0.012 | – | 75 (33.75–143.25) | |||||
| 0.018 | ns | – | 75.5 (31.75–141.25) | ||||
| 0.024 | † | ns | † | – | 129 (47.75–270.5) | ||
| 0.030 | ns | * | ns | – | 193.5 (64.5–392.25) | ||
| Steel–Dwass Test | Iteration | |||||
|---|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 10 | Median (IQR) | ||
| Scale factor | 0.5 | – | 62.5 (45.25–78.5) | |||
| 1 | ns | – | 60.5 (38.5–81) | |||
| 2 | ns | ns | – | 71 (53–87.75) | ||
| 10 | ns | ns | ns | – | 71 (54.75–92) | |
| Steel–Dwass Test | Reset | |||||
| 0.5 | 1 | 2 | 10 | Median (IQR) | ||
| Scale factor | 0.5 | – | 287.5 (124.5–432) | |||
| 1 | – | 75 (33.75–143.25) | ||||
| 2 | ns | – | 72 (27.75–119.25) | |||
| 10 | * | – | 483.5 (236.25–758.5) | |||
| Iteration | Reset | Success Rate [%] | |
|---|---|---|---|
| Median (IQR) | Median (IQR) | ||
| G calculus | 69.5 (51.25–85.75) | 874.5 (460.5–2038.5) | 100 |
| Pseudo–derivative | 45.5 (29.75–75.25) | 2106 (935–4656.5) | 94 |
| Mann–Whitney U test |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, K.; Tano, E.; Hashimoto, M.
Feedforward–Feedback Controller Based on a Trained Quaternion Neural Network Using a Generalised
Takahashi K, Tano E, Hashimoto M.
Feedforward–Feedback Controller Based on a Trained Quaternion Neural Network Using a Generalised
Takahashi, Kazuhiko, Eri Tano, and Masafumi Hashimoto.
2022. "Feedforward–Feedback Controller Based on a Trained Quaternion Neural Network Using a Generalised
Takahashi, K., Tano, E., & Hashimoto, M.
(2022). Feedforward–Feedback Controller Based on a Trained Quaternion Neural Network Using a Generalised





