Numerical Simulations and Experiments on Single-Tooth Rock-Breaking
Abstract
:1. Introduction
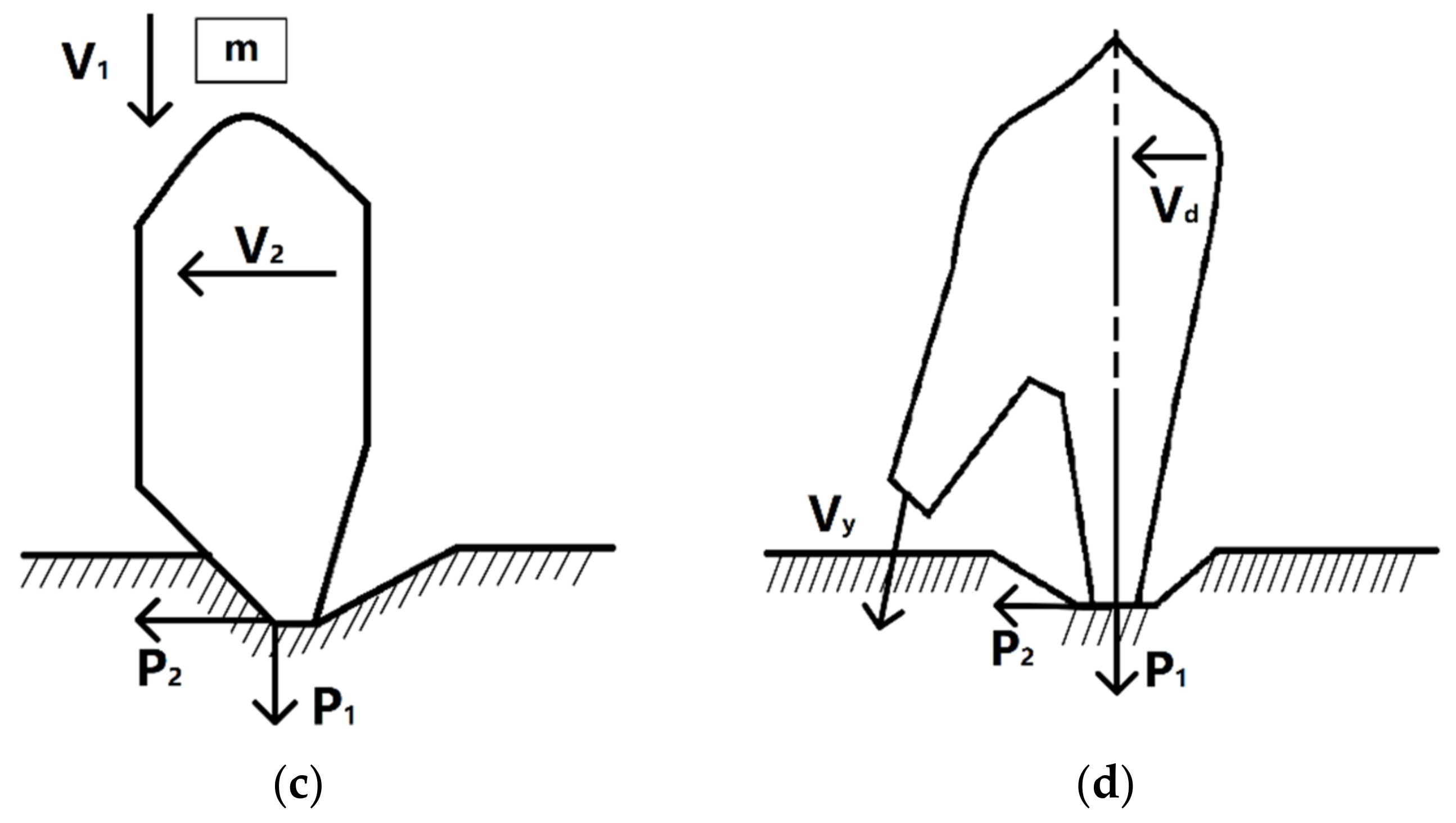
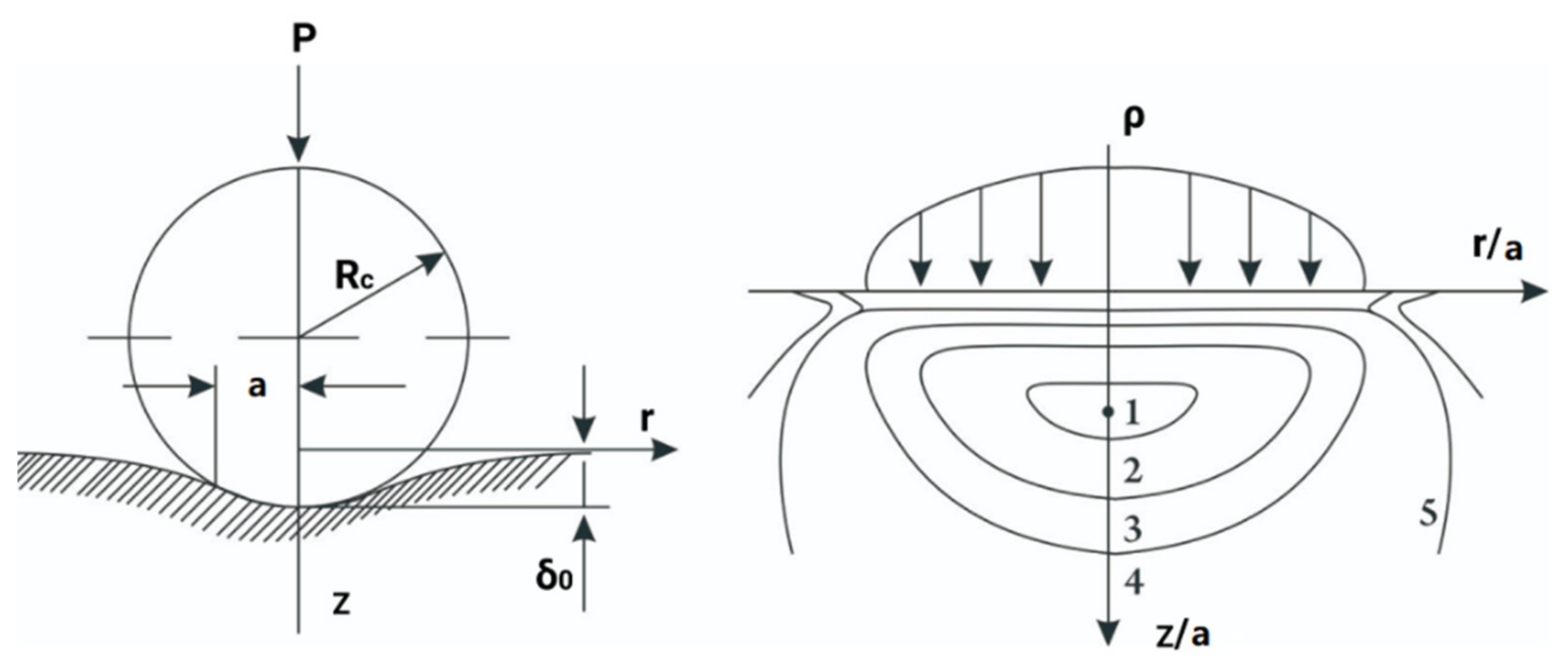
2. Force Analysis of Single-Tooth Vertical Rock-Breaking
3. Finite Element Model and Convergence Verification of Single-Tooth Dynamic Rock-Breaking
3.1. Subsection-Defined Contact Types and Boundary Conditions
3.2. Simulation Test Scheme
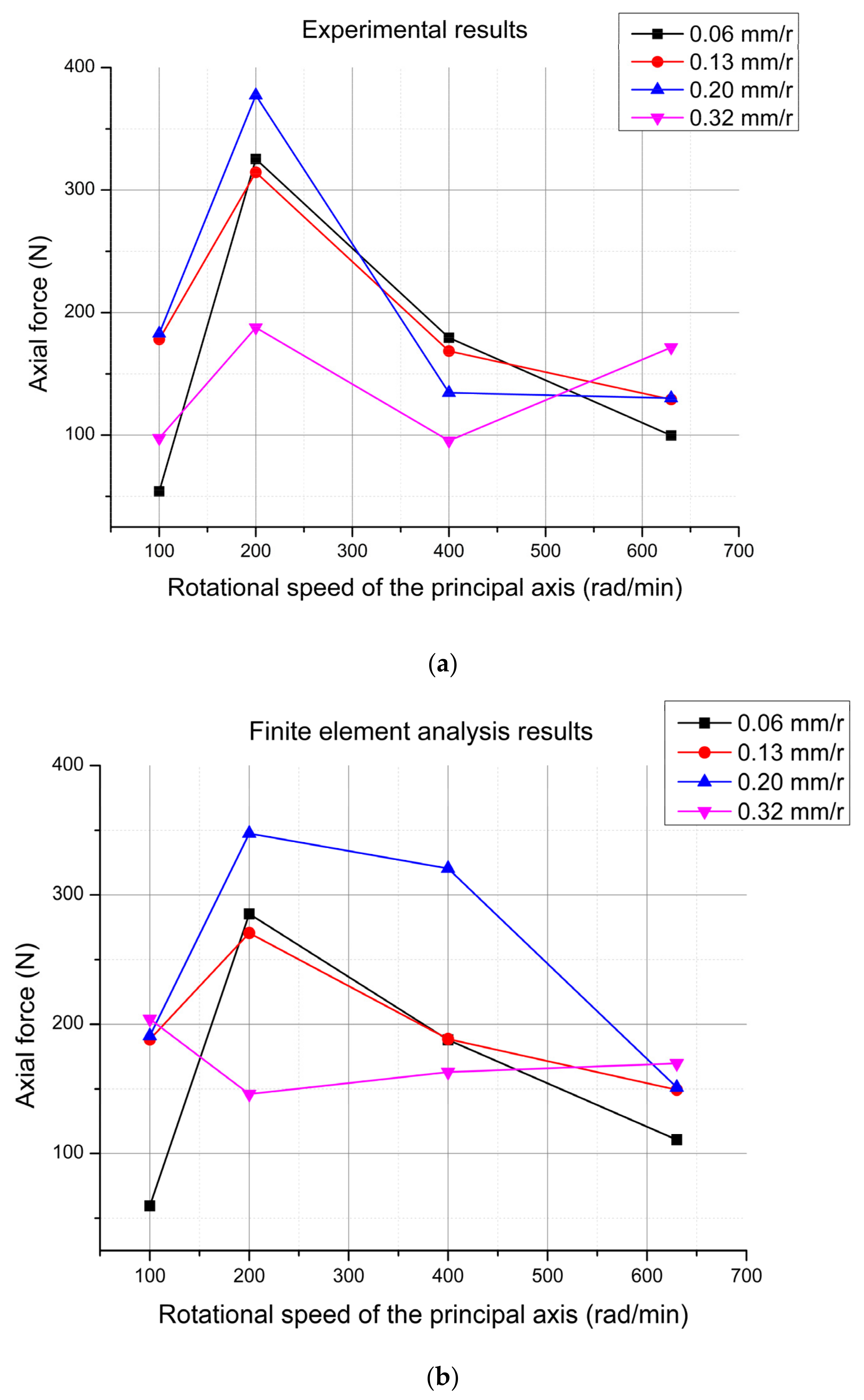
3.3. Results and Discussion
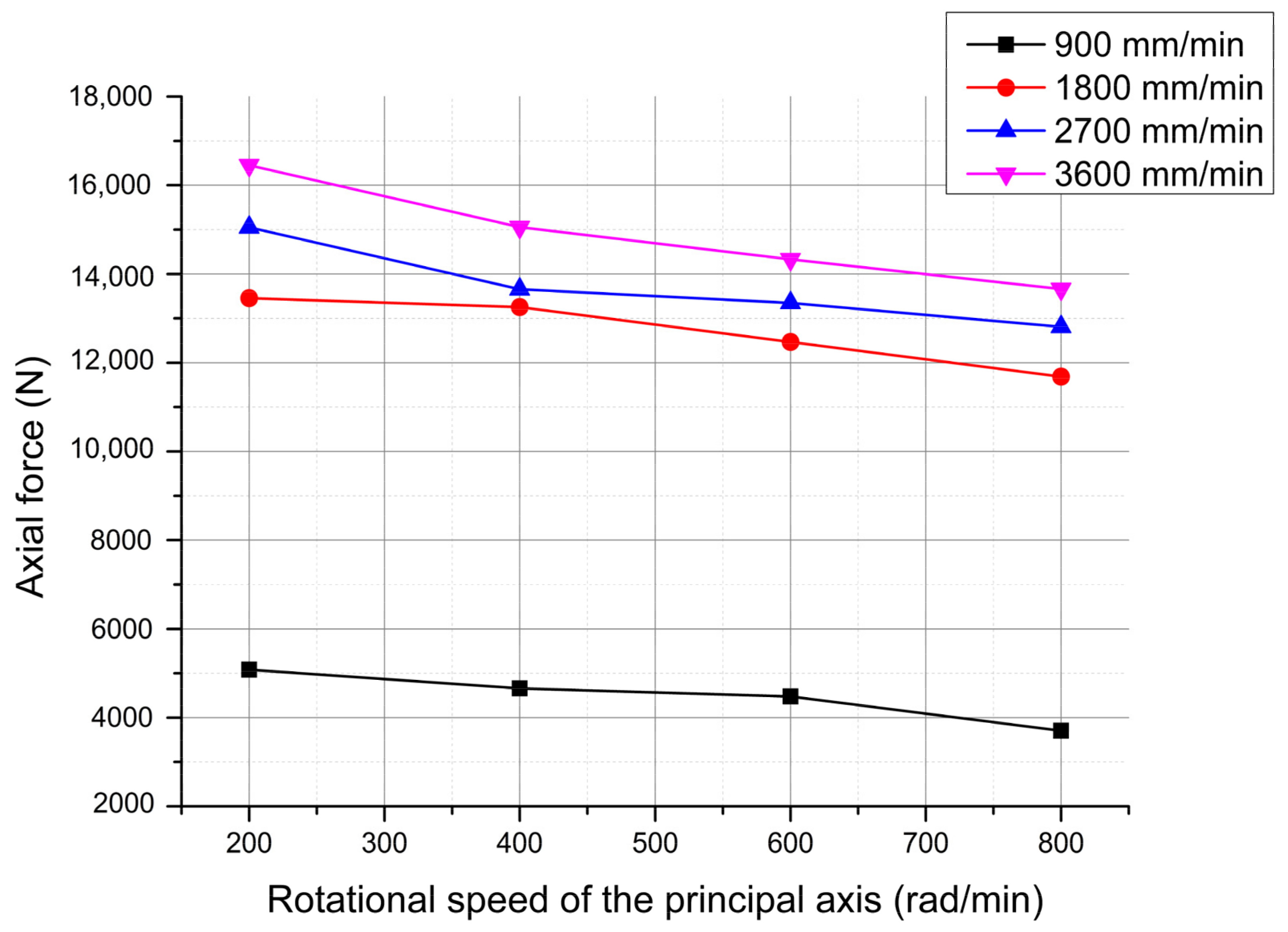
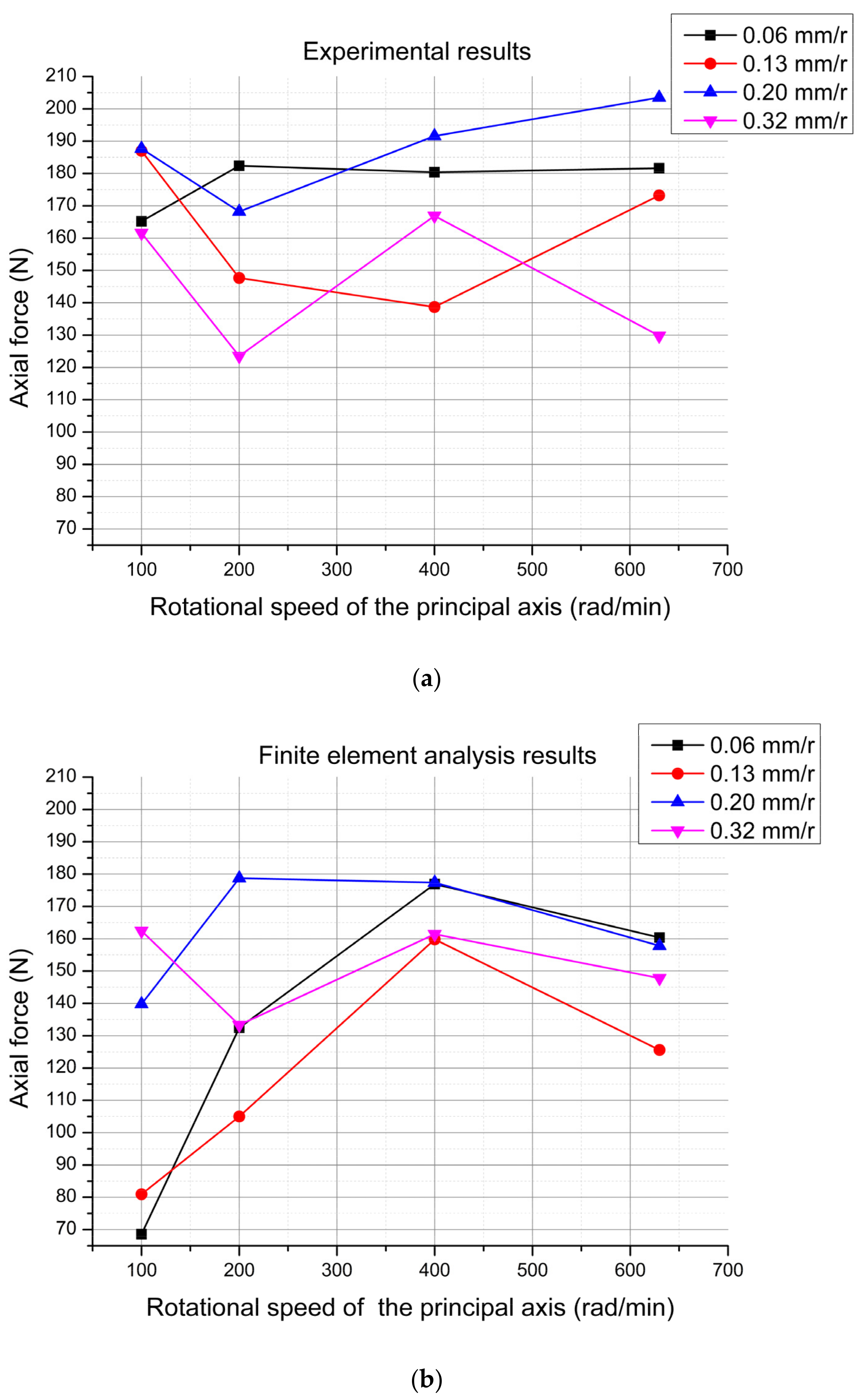
3.3.1. Influence of the Rotational Speed on the Axial Drilling Force
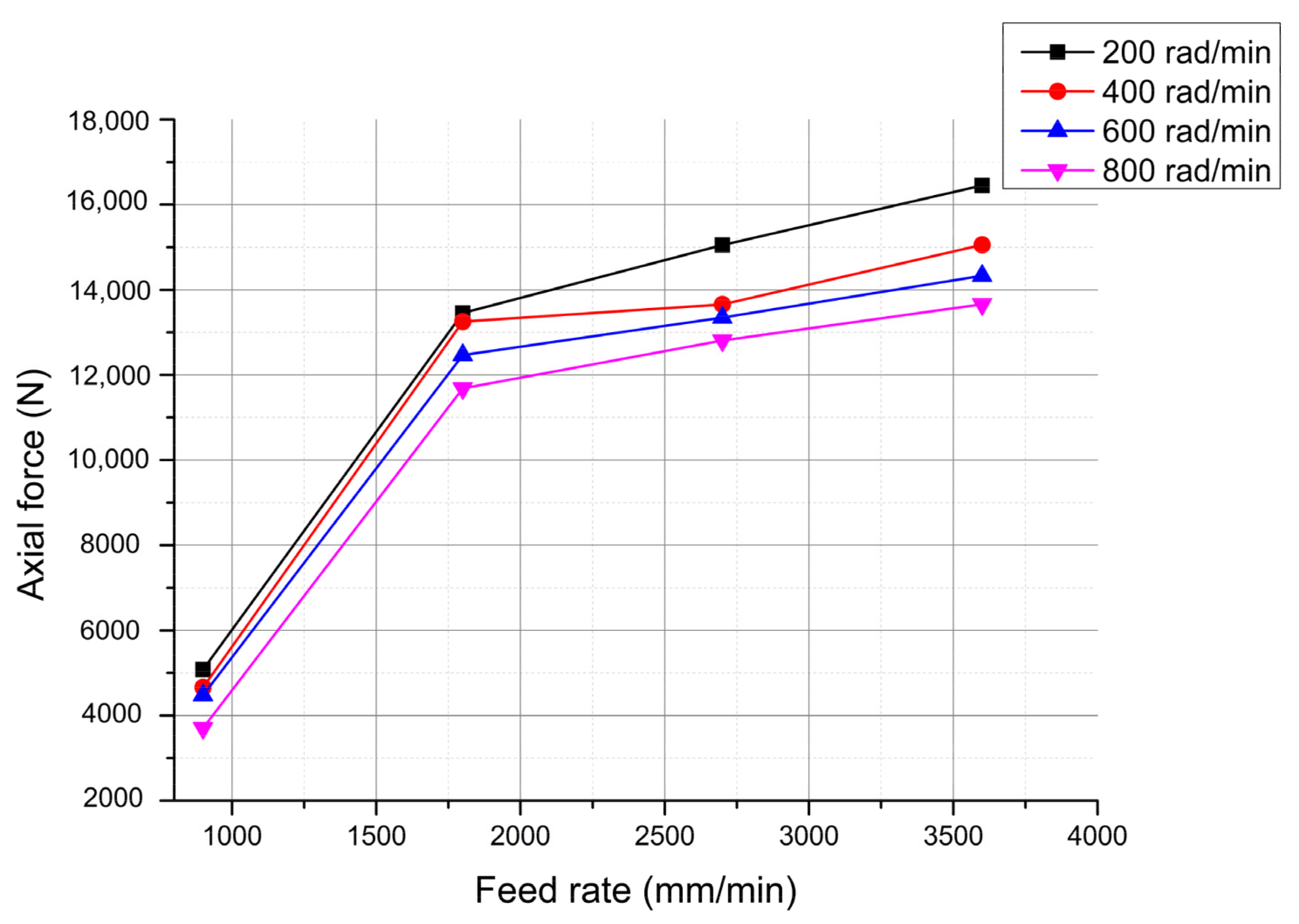
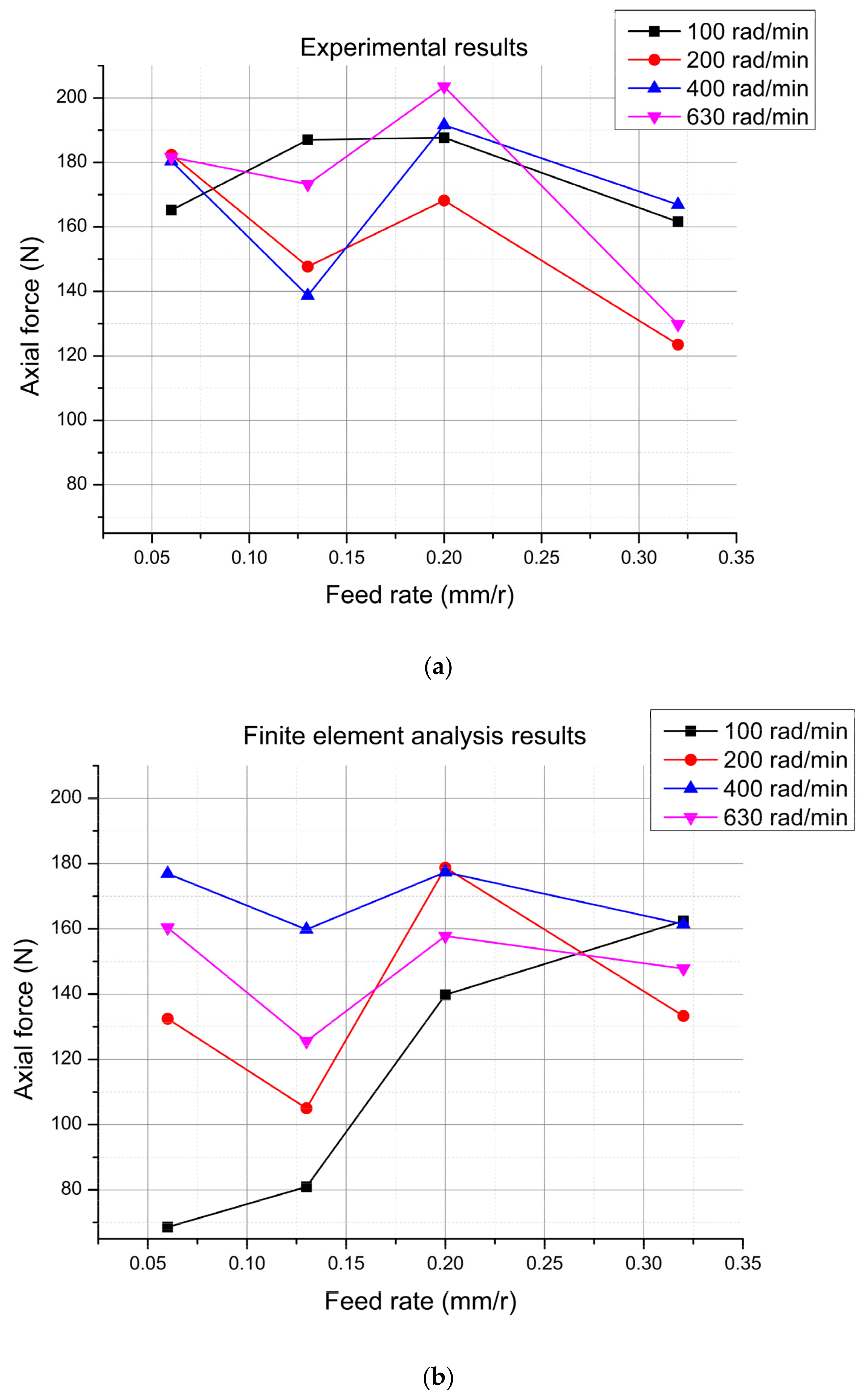
3.3.2. Effect of the Feed Rate on the Axial Drilling Force
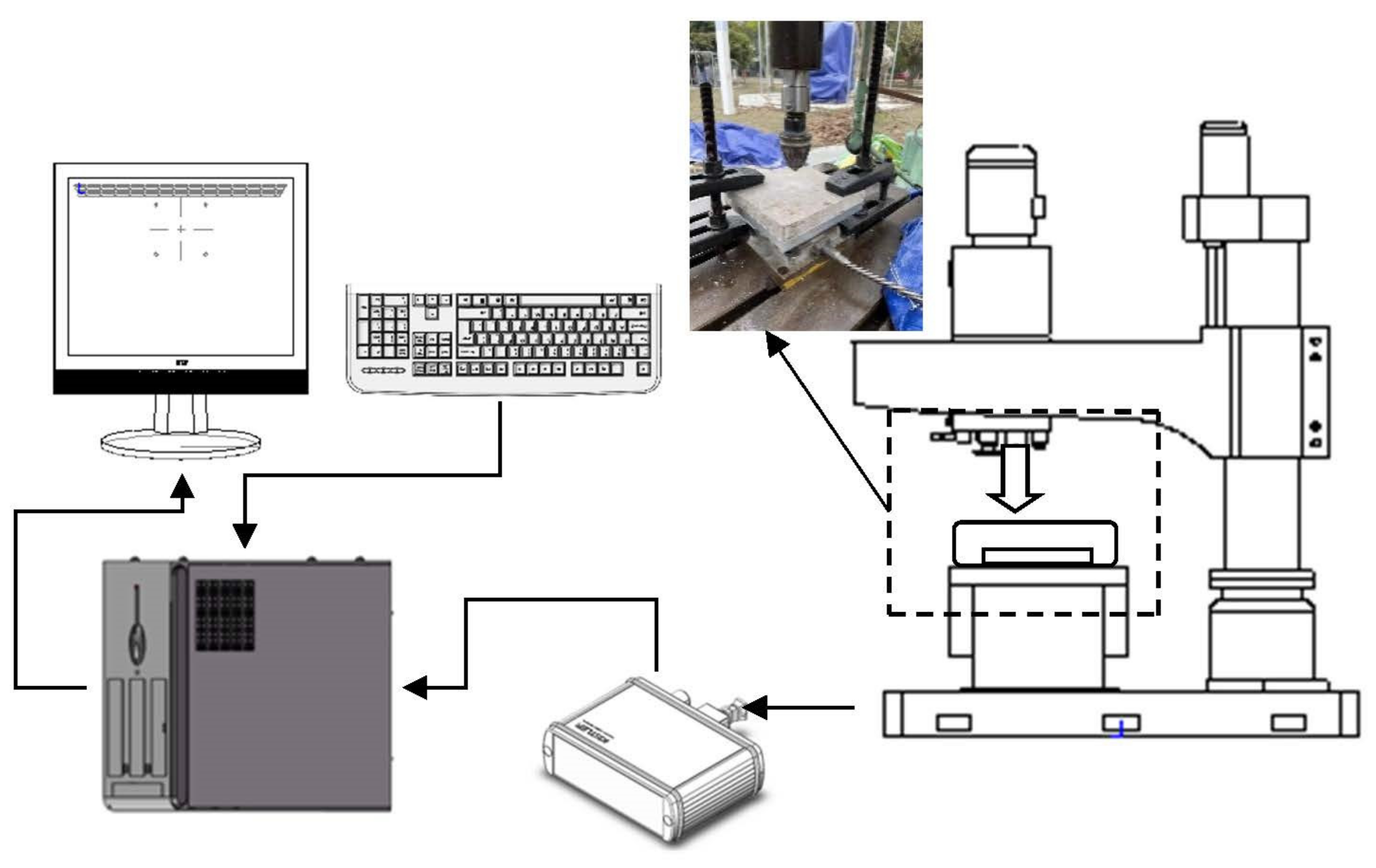
4. Single-Tooth Rock-Breaking Experiment
4.1. Analysis from the Numerical Size of Data
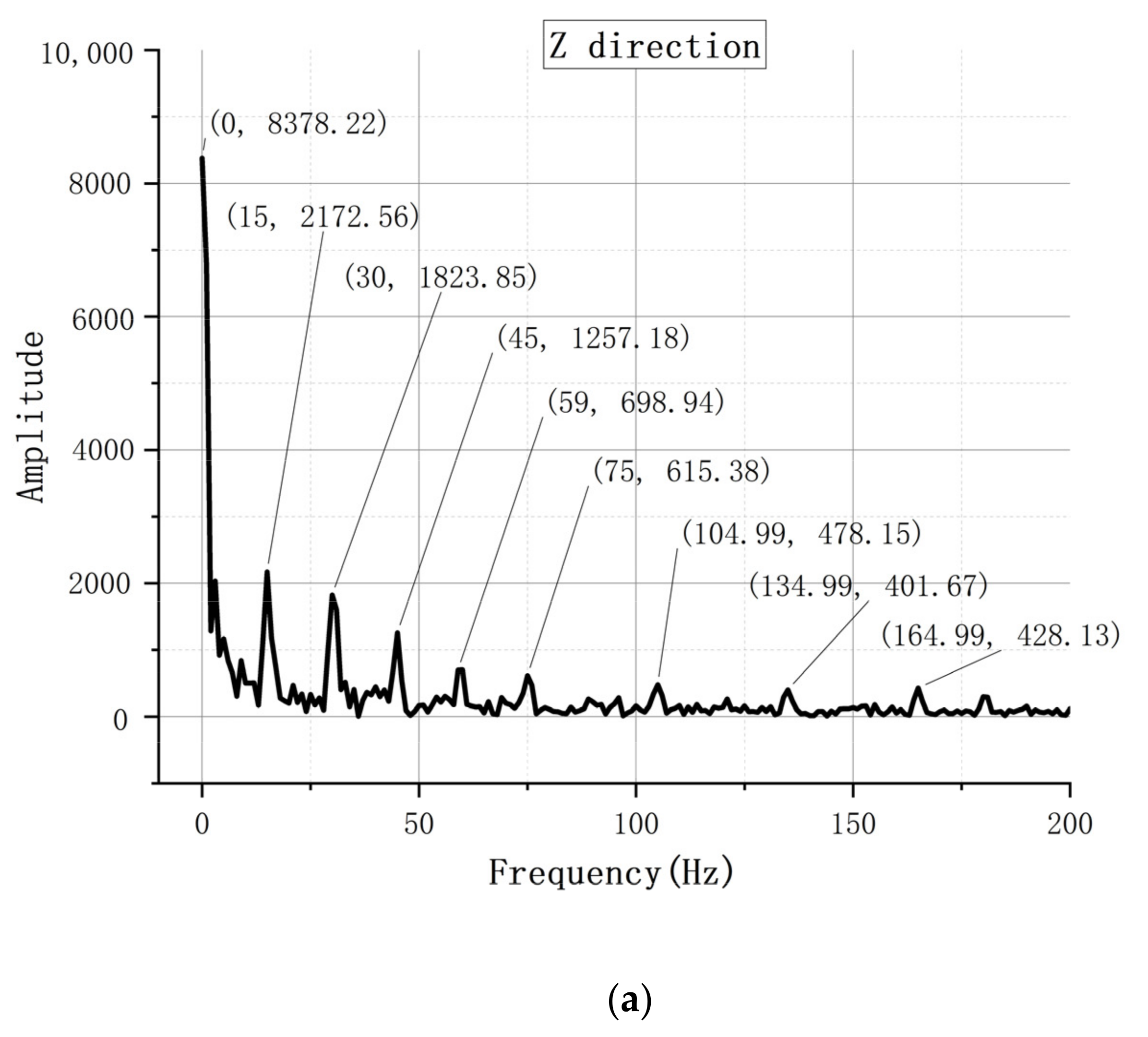
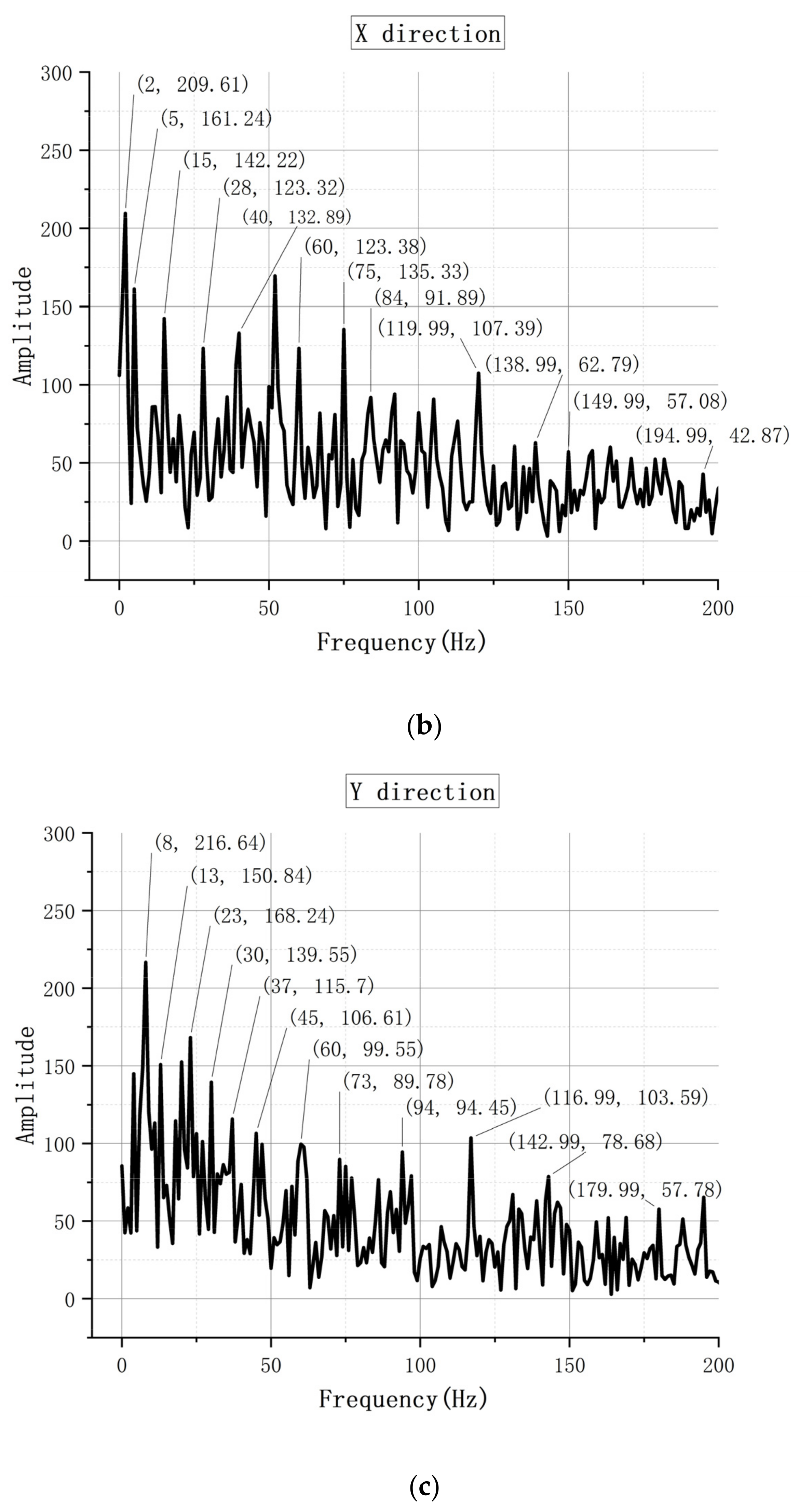
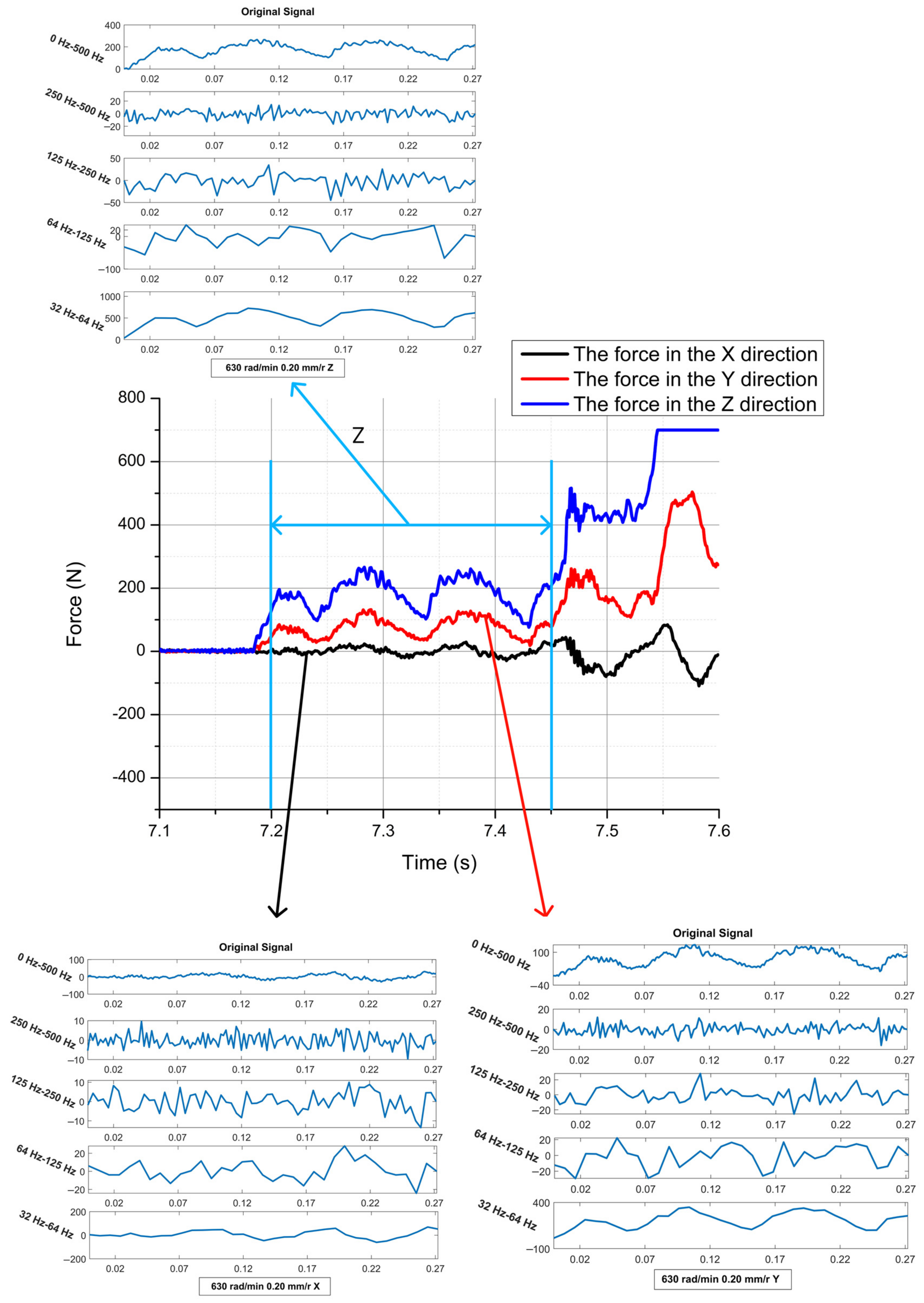
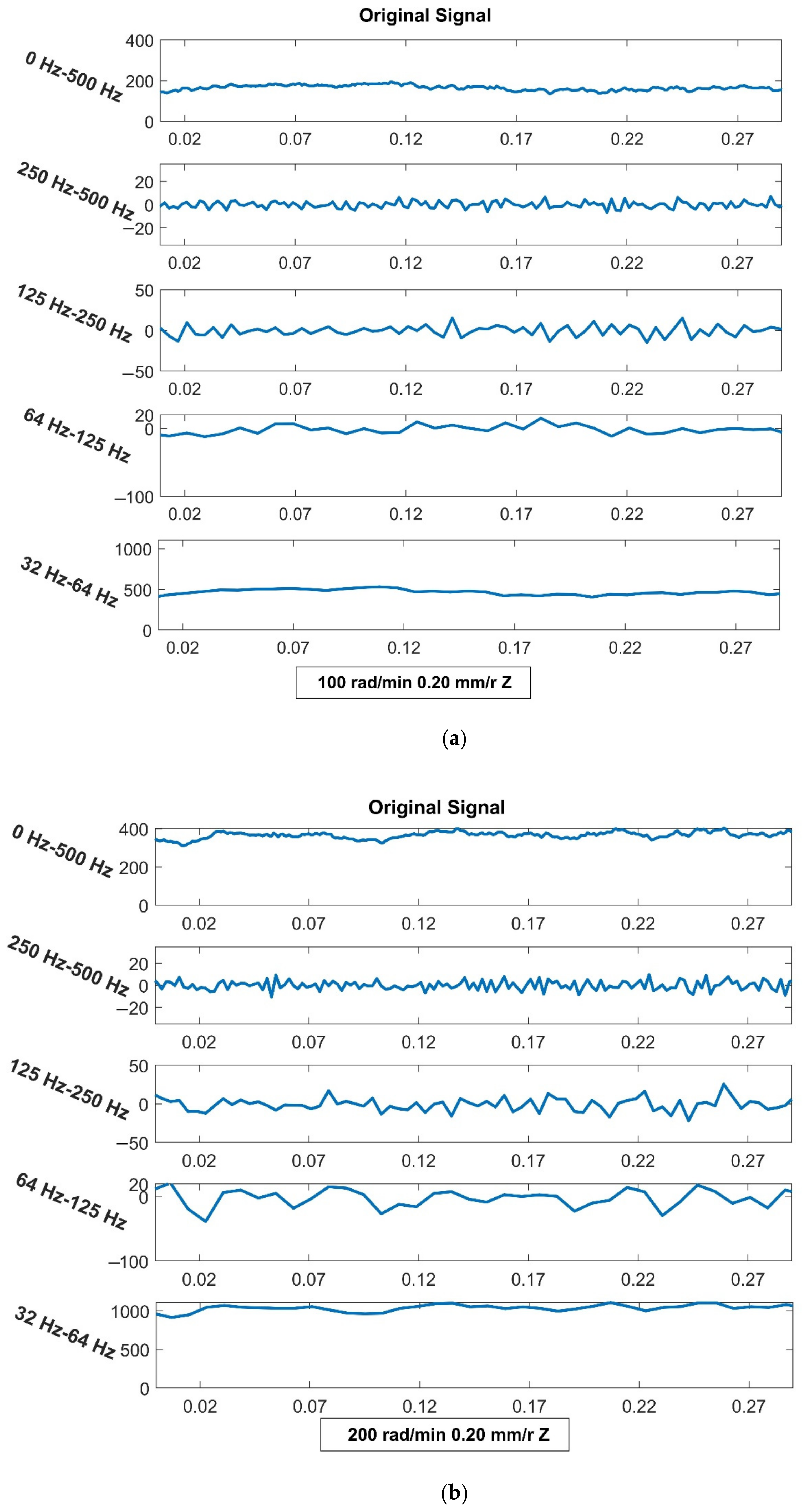
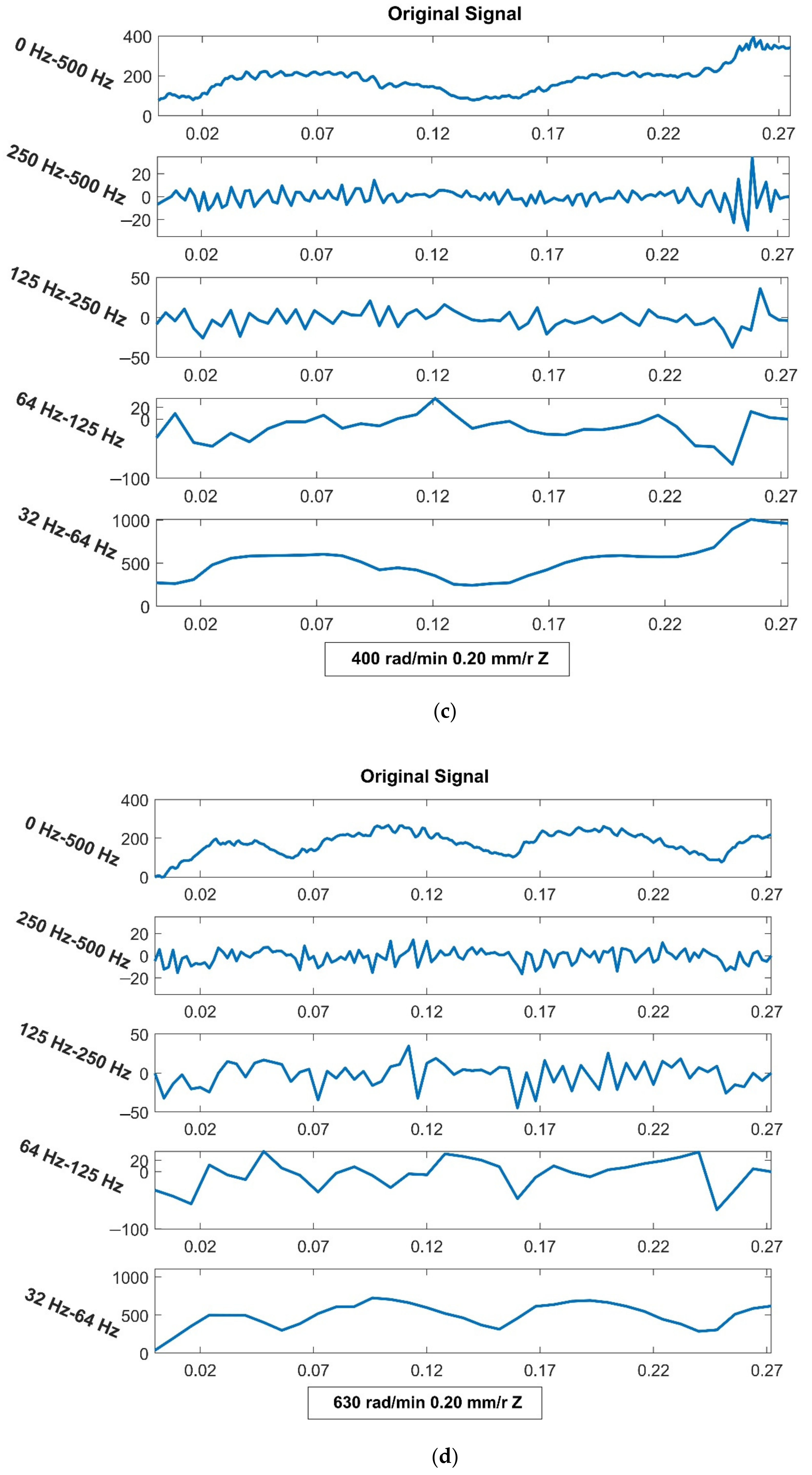
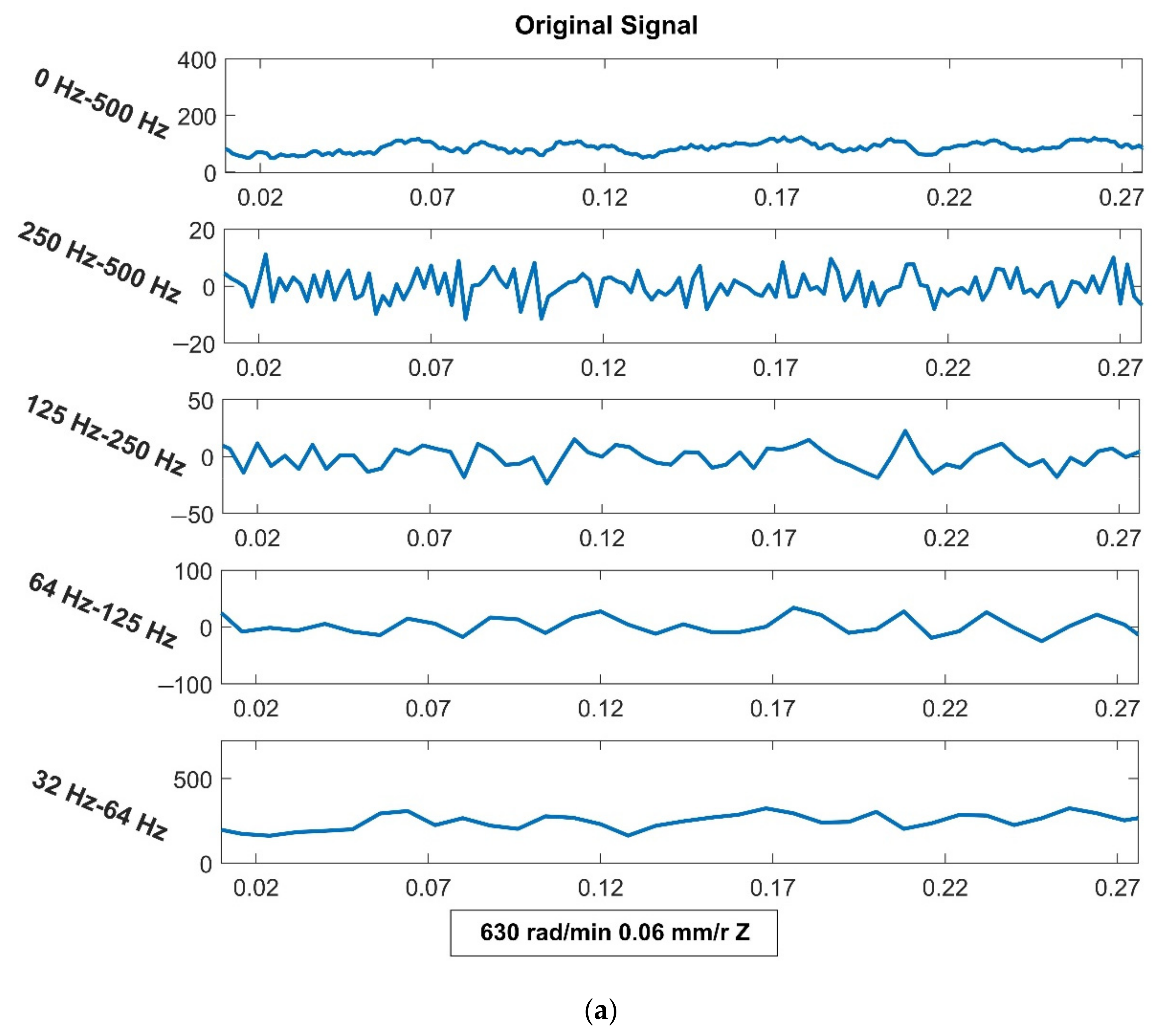
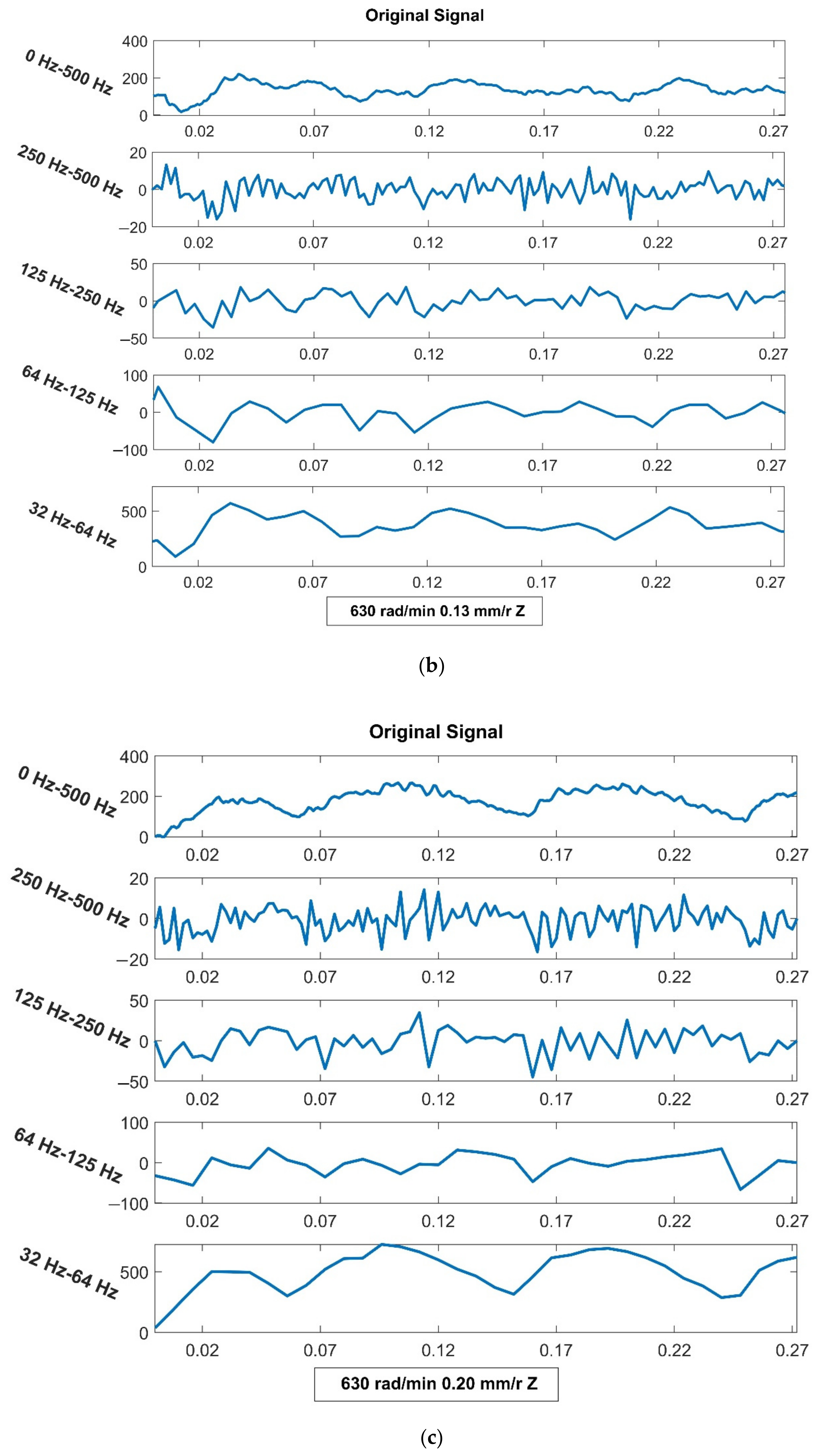
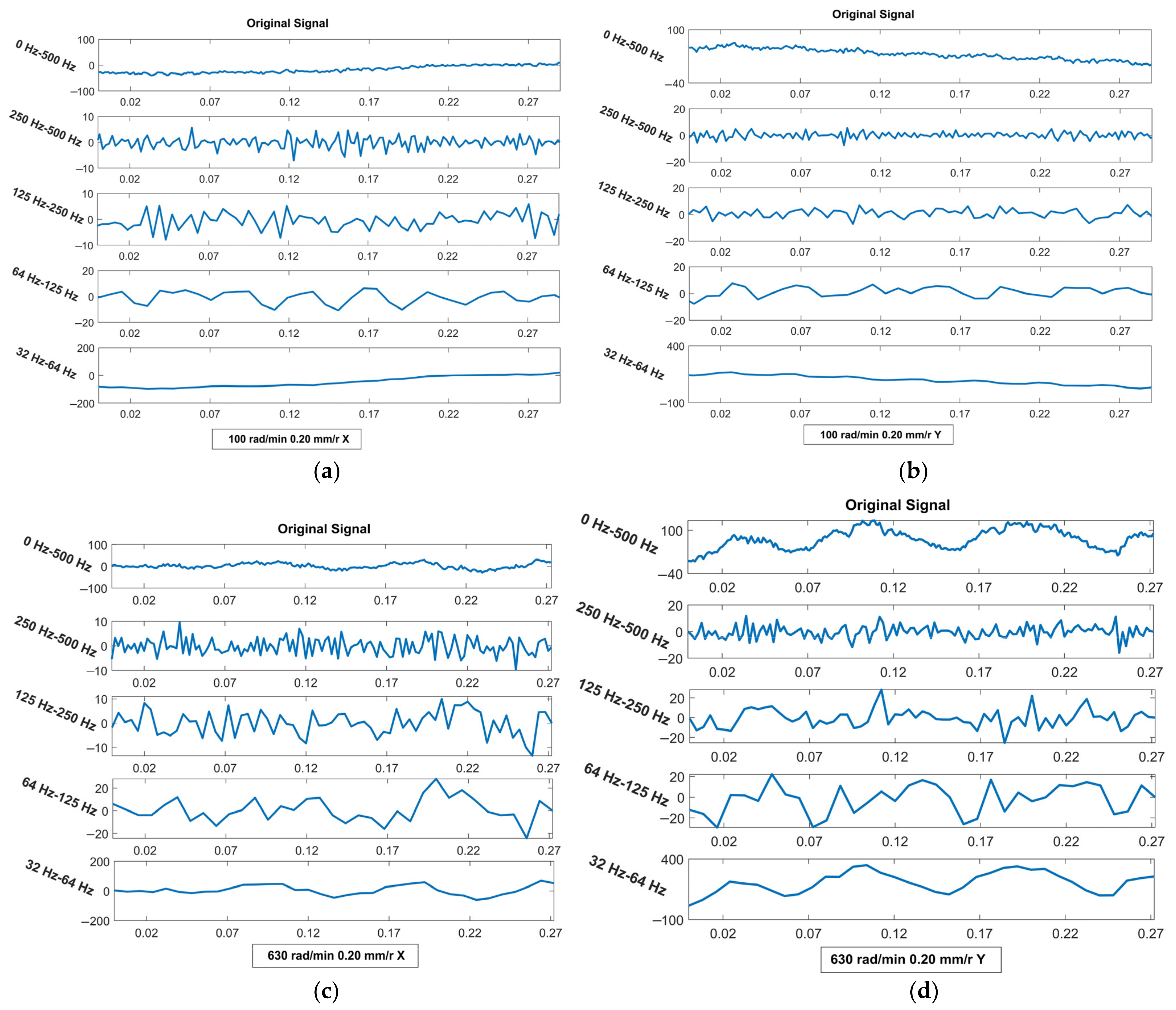
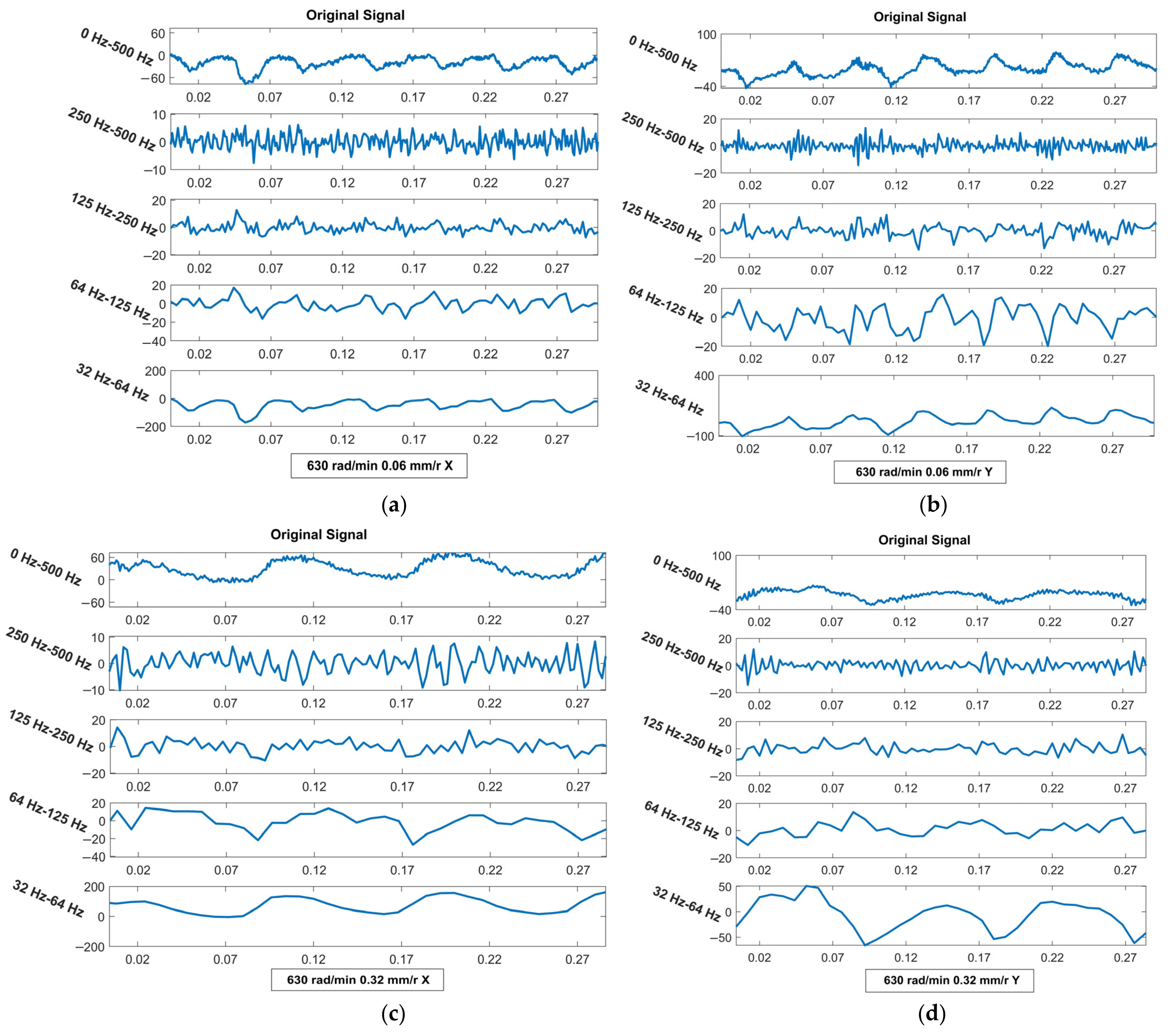
4.2. Analysis from the Vibration Aspect
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Cai, M.; Masoumi, H. A constitutive model for modified cable bolts exhibiting cone shaped failure mode. Int. J. Rock Mech. Min. Sci. 2021, 145, 104855. [Google Scholar] [CrossRef]
- Detournay, E.; Richard, T.; Shepherd, M. Drilling response of drag bits: Theory and experiment. Int. J. Rock Mech. Min. Sci. 2008, 45, 1347–1360. [Google Scholar] [CrossRef]
- Panayirci, H.M. An experimental study on steering response of PDC drill bits. J. Pet. Sci. Eng. 2022, 208, 109440. [Google Scholar] [CrossRef]
- Huang, K.; Yang, Y.; Li, G.; Wang, Y.; Ren, H.; Niu, S. Torsion and vibration reduction mechanism of roller PDC hybrid bit. J. Pet. Sci. Eng. 2022, 208, 109491. [Google Scholar] [CrossRef]
- He, Z.; Shi, L.; Li, L.; Kong, L.; Zhang, X.; Liu, X. Study on the Mechanism of Stick-Slip Vibration Based on Single-Cutter Rock Breaking Finite Element Simulation. China Pet. Mach. 2021, 49, 17–26. [Google Scholar]
- Liu, B.; Ni, P.; Tan, X.; Zhang, C. Research on rock breaking efficiency of rotary punching drilling rig. J. Mech. Electr. Eng. 2020, 37, 801–805. [Google Scholar]
- Liu, B.; Wu, J.; Zhang, J.; Shi, X.; Li, S. Numerical Simulation on the Rock Breaking of Cutter Teeth of PDC Cutter Based on Discrete Element Method. Min. R & D 2021, 41, 165–169. [Google Scholar] [CrossRef]
- Liu, S.; Ni, H.; Wang, Y.; Zhang, H. Mechanism of multi-dimensional impact loads applied in increasing the rock cutting efficiency of a PDC bit. J. Vib. Shock. 2021, 40, 258–264. [Google Scholar]
- Lu, Z.; Zheng, J.; Jiang, Z.; Zhao, F. An Experimental Study on Rock Breaking Efficiency with Ultrasonic High-Frequency Rotary-Percussive Drilling Technology. Pet. Drill. Tech. 2021, 49, 20–25. [Google Scholar] [CrossRef]
- Zhu, X.; He, L.; Liu, W.; Luo, Y.; Yang, F. Research on particle jet and its auxiliary drill tooth breaking law. J. Southwest Pet. Univ. 2020, 1–11. [Google Scholar]
- Błaż, S.; Zima, G.; Jasiński, B.; Kremieniewski, M. Invert Drilling Fluids with High Internal Phase Content. Energies 2021, 14, 4532. [Google Scholar] [CrossRef]
- Wu, B.; Liu, T.; Zhang, X.; Wu, B.; Jeffrey, R.; Bunger, A. A Transient Analytical Model for Predicting Wellbore/Reservoir Temperature and Stresses during Drilling with Fluid Circulation. Energies 2017, 11, 42. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Ni, H.; Wang, R.; Song, W. The effect of thermal stresses on the relation between rock failure and temperature and pressure of supercritical carbon dioxide jet. Greenh. Gases Sci. Technol. 2018, 8, 218–237. [Google Scholar] [CrossRef]
- Liu, Z.; Ni, F.; Wei, C.; Li, H. Experimental and numerical investigation of roadheader for breaking rock containing predrill holes. Energy Sci. Eng. 2020, 8, 2511–2526. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Zhou, Z.; Ge, Z.; Zhang, X.; Li, Q. Research on and Design of a Self-Propelled Nozzle for the Tree-Type Drilling Technique in Underground Coal Mines. Energies 2015, 8, 14260–14271. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Xiao, S.; Ge, Z.; Zhou, Z.; Deng, K. Rock-Breaking Properties of Multi-Nozzle Bits for Tree-Type Drilling in Underground Coal Mines. Energies 2016, 9, 249. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Zhao, B.; Ni, H.; Li, Z.; Liu, Y.; Chen, X. Research on the modulation mechanism and rock breaking efficiency of a cuttings waterjet. Energy Sci. Eng. 2019, 7, 1687–1704. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Sun, P.; Wang, G.; Fu, B.; Yao, J. Rock-breaking mechanism and efficiency of straight-swirling mixed nozzle for the nondiagenetic natural gas hydrate in deep-sea shallow. Energy Sci. Eng. 2020, 8, 3740–3752. [Google Scholar] [CrossRef]
- Tang, Q.; Zhao, D.; Zhou, Y.; Zhang, Z. Discrete element simulation for investigating fragmentation mechanism of hard rock under ultrasonic vibration loading. Energy Sci. Eng. 2020, 8, 3805–3822. [Google Scholar] [CrossRef]
- Wang, W.; Liu, G.; Li, J.; Zha, C.; Lian, W. Numerical simulation study on rock-breaking process and mechanism of compound impact drilling. Energy Rep. 2021, 7, 3137–3148. [Google Scholar] [CrossRef]
- Shao, F.; Liu, W.; Gao, D.; Ye, Y. Study on rock-breaking mechanism of axe-shaped PDC cutter. J. Pet. Sci. Eng. 2021, 205, 108922. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, D.; Zhao, Y.; Gao, K.; Zhang, C.; Lü, X. 3D numerical simulation study of rock breaking of the wavy PDC cutter and field verification. J. Pet. Sci. Eng. 2021, 203, 108578. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.; Zhang, Z.; Gao, K.; Li, J.; Xie, X. The rock breaking mechanism analysis of axial ultra-high frequency vibration assisted drilling by single PDC cutter. J. Pet. Sci. Eng. 2021, 205, 108859. [Google Scholar] [CrossRef]
- Knez, D.; Khalilidermani, M. A Review of Different Aspects of Off-Earth Drilling. Energies 2021, 14, 7351. [Google Scholar] [CrossRef]
- Yu, G.; Hu, Q.; Feng, X.; Meng, G.; Nie, Y. Research on Drilling Rate Optimization of a UCS Identification System While Drilling for Coal Mine Roadway Roofs. Machines 2021, 9, 242. [Google Scholar] [CrossRef]
- Liu, Q.; Zha, Y.; Liu, T.; Lu, C. Research on Adaptive Control of Air-Borne Bolting Rigs Based on Genetic Algorithm Optimization. Machines 2021, 9, 240. [Google Scholar] [CrossRef]
- Bołoz, Ł. Interpretation of the results of mechanical rock properties testing with respect to mining methods. Acta Montan. Slovaca 2020, 25, 81–93. [Google Scholar] [CrossRef]
- Fan, X.; Lin, H.; Lai, H.; Cao, R.; Liu, J. Numerical analysis of the compressive and shear failure behavior of rock containing multi-intermittent joints. Comptes Rendus Mécanique 2019, 347, 33–48. [Google Scholar] [CrossRef]
- Korayem, M.H.; Taheri, M.; Badkoobehhezaveh, H.; Khaksar, H. Simulating the AFM-based biomanipulation of cylindrical micro/nanoparticles in different biological environments. J. Braz. Soc. Mech. Sci. Eng. 2016, 39, 1883–1894. [Google Scholar] [CrossRef]
- Adams, G.G.; Nosonovsky, M. Contact modeling—Forces. Tribol. Int. 2000, 33, 10. [Google Scholar] [CrossRef]
- Gonzalez-Perez, I.; Iserte, J.L.; Fuentes, A. Implementation of Hertz theory and validation of a finite element model for stress analysis of gear drives with localized bearing contact. Mech. Mach. Theory 2011, 46, 765–783. [Google Scholar] [CrossRef]
- Nasseri, M.H.B.; Rao, K.S.; Ramamurthy, T. Anisotropic strength and deformational behavior of Himalayan schists. Int. J. Rock Mech. Min. Sci. 2003, 40, 3–23. [Google Scholar] [CrossRef]
- Özbek, A.; Gül, M.; Karacan, E.; Alca, Ö. Anisotropy effect on strengths of metamorphic rocks. J. Rock Mech. Geotech. Eng. 2018, 10, 164–175. [Google Scholar] [CrossRef]
- Ozcelik, Y.; Yilmazkaya, E. The effect of the rock anisotropy on the efficiency of diamond wire cutting machines. Int. J. Rock Mech. Min. Sci. 2011, 48, 626–636. [Google Scholar] [CrossRef]
- Qin, M.; Wang, K.; Pan, K.; Sun, T.; Liu, Z. Analysis of signal characteristics from rock drilling based on vibration and acoustic sensor approaches. Appl. Acoust. 2018, 140, 275–282. [Google Scholar] [CrossRef]
- Peng, X.; Li, L.; Yang, Y.; Zhao, G.; Zeng, T. Experimental study on rotary ultrasonic vibration assisted drilling rock. Adv. Space Res. 2021, 67, 546–556. [Google Scholar] [CrossRef]
- Chen, X.; Chen, G.; Song, G.; Chen, X. Analysis of drilling vibration response based on rock properties. Explor. Eng. 2019, 46, 20–26. [Google Scholar]
- Zhao, D.; Wu, J.; Li, Z. Simulation and experimental research on ultrasonic vibration high temperature rock. J. Pet. Sci. Eng. 2022, 212, 110255. [Google Scholar] [CrossRef]





| Density | Modulus of Elasticity | Poisson’s Ratio |
|---|---|---|
| 7850 kg/m3 | 21,000 MPa | 0.3 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Density(kg/m3) | 2.5 × 103 | Amount of plastic strain before fracture | 0.008 |
| Shear modulus (Pa) | 8.38 × 109 | Material tensile strength (Pa) | 7.54 × 106 |
| Static uniaxial compressive strength (MPa) | 147.88 | Crush pressure (Pa) | 49.3 × 106 |
| Characteristic cohesive strength | 0.79 | Volume strain of crushing | 0.0044 |
| Characteristic pressure hardening coefficient | 1.6 | Compaction pressure (Pa) | 1.0 × 109 |
| Strain rate coefficient | 0.007 | Compacting volume strain | 0.12 |
| Pressure hardening exponent | 0.61 | Pressure constant (Pa) | 85 × 109 |
| Normalized maximum strength | 7.0 | Pressure constant (Pa) | −171 × 109 |
| Material damage parameter1 | 0.04 | Pressure constant (Pa) | 208 × 109 |
| Material damage parameter2 | 1.0 | Parameter value of the failure type | 0.004 |
| Experiment Number | Rotational Speed of Spindle (rad/min) | Feed Speed (mm/min) |
|---|---|---|
| 1 | 200 | 900, 1800, 2700, 3600 |
| 2 | 400 | 900, 1800, 2700, 3600 |
| 3 | 600 | 900, 1800, 2700, 3600 |
| 4 | 800 | 900, 1800, 2700, 3600 |
| Feed Rate (mm/min) | Slope |
|---|---|
| 900 | −2.16 |
| 1800 | −3.05 |
| 2700 | −3.52 |
| 3600 | −4.55 |
| Rotational Speed of Axis (rad/min) | Slope |
|---|---|
| 200 | 3.97 |
| 400 | 3.51 |
| 600 | 3.38 |
| 800 | 3.44 |
| Technical Parameters | Unit | Specific Numerical |
|---|---|---|
| Bed dimension | mm | 800 × 630 × 500 |
| Travel of spindle | mm | 400 |
| Large bore diameter | mm | 63 |
| Distance from spindle center line to column bus | mm | 450–2000 |
| Distance between spindle end face and base working face | mm | 400–1600 |
| Spindle taper | Morse No. | 5# |
| Spindle speed range | rpm | 20–1600 |
| Spindle speed series | Step | 16 |
| Spindle feed range | mm/r * | 0.04–3.2 |
| Spindle feed series | Step | 16 |
| Horizontal movement distance of headstock | mm | 1600 |
| Spindle motor power | kW | 5.5 |
| Total weight | kg | 7000 |
| Overall dimension | mm | 3080 × 1250 × 3400 |
| Parameters | Granite | Sandstone |
|---|---|---|
| Density (g/cm3) | 2.63~2.73 2.80~3.10 3.10~3.30 | 1.2~1.5 2.2~3.0 |
| Uniaxial compressive strength of rock (MPa) | 75~110 120~180 180~200 | 4.5~10 47~180 |
| Hardness | Hard rock | Relatively hard rock |
| Drillability level | Ⅹ | Ⅸ |
| Coefficient of strength | 16~18 | 14~16 |
| Specific work of rock-breaking (J/cm3) | 383~480 | 187~284 |
| Abrasiveness | Neutral | Neutral |
| Abrasiveness index (mg) | 45~65 | 18~30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, J.; Mei, Q.; Huang, K.; Luo, Q.; Dong, J. Numerical Simulations and Experiments on Single-Tooth Rock-Breaking. Machines 2022, 10, 455. https://doi.org/10.3390/machines10060455
Li H, Wang J, Mei Q, Huang K, Luo Q, Dong J. Numerical Simulations and Experiments on Single-Tooth Rock-Breaking. Machines. 2022; 10(6):455. https://doi.org/10.3390/machines10060455
Chicago/Turabian StyleLi, Heyuqiu, Jie Wang, Qi Mei, Kunlan Huang, Qingyi Luo, and Jie Dong. 2022. "Numerical Simulations and Experiments on Single-Tooth Rock-Breaking" Machines 10, no. 6: 455. https://doi.org/10.3390/machines10060455
APA StyleLi, H., Wang, J., Mei, Q., Huang, K., Luo, Q., & Dong, J. (2022). Numerical Simulations and Experiments on Single-Tooth Rock-Breaking. Machines, 10(6), 455. https://doi.org/10.3390/machines10060455





