A Rolling Bearing Fault Diagnosis Method Based on Enhanced Integrated Filter Network
Abstract
:1. Introduction
- This method is an end-to-end bearing fault diagnosis system that integrates noise reduction, feature extraction, and fault recognition. It does not need signal processing and does not rely on expert experience and knowledge.
- The method integrates multiple convolutional layers (weak filters) with different scales to form an enhanced integrated filter, which is connected in a parallel and cascaded way to achieve the effect of the enhanced filter. It can capture useful signals in the middle and low frequencies and filter high-frequency noise.
- Finally, the method integrates the feature information of different receptive fields into vector space. It uses the peculiarity of vector to mine correlations between fault features at the time dimension, so as to improve the fault diagnosis precision of the model in a strong noise environment.
2. Basic Theory
2.1. One Dimensional Convolution and Signal Filtering
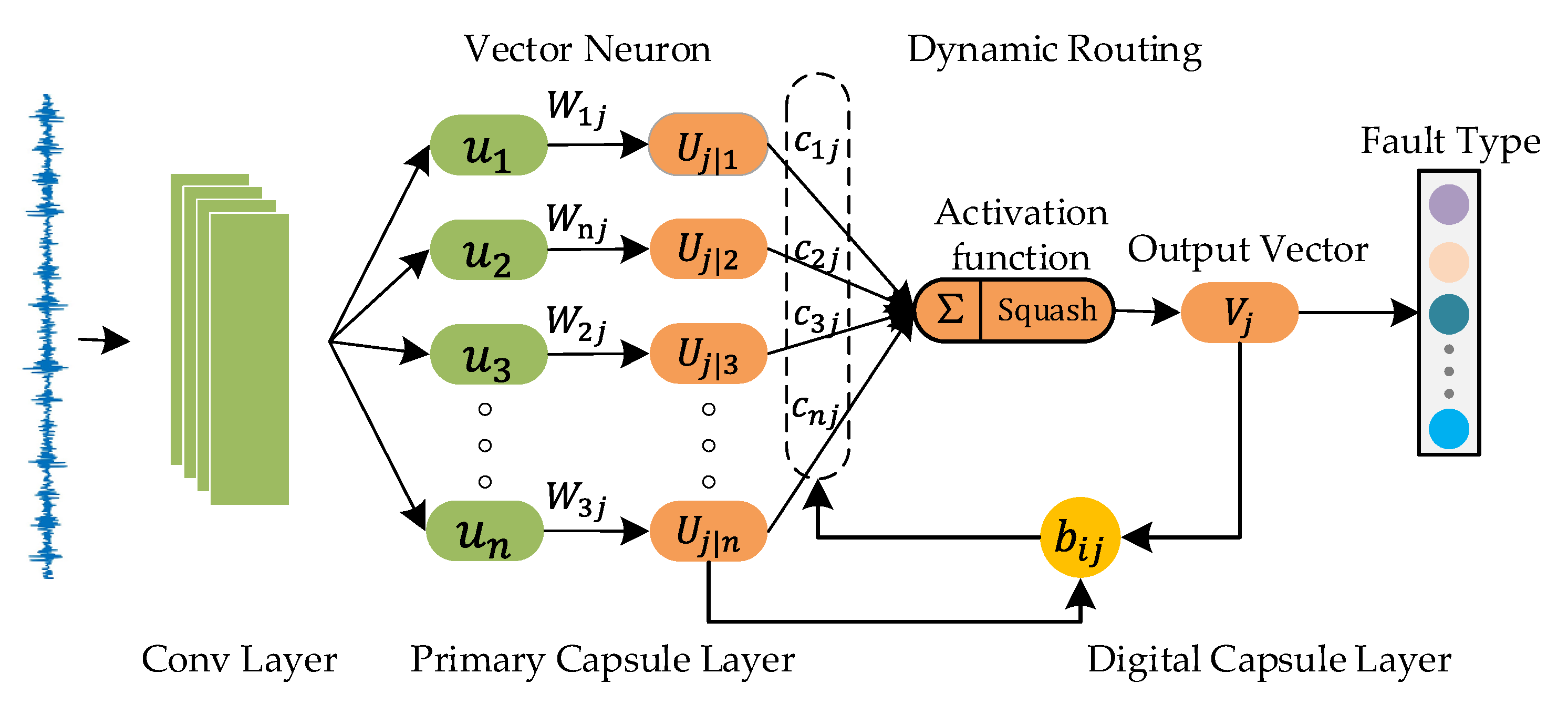
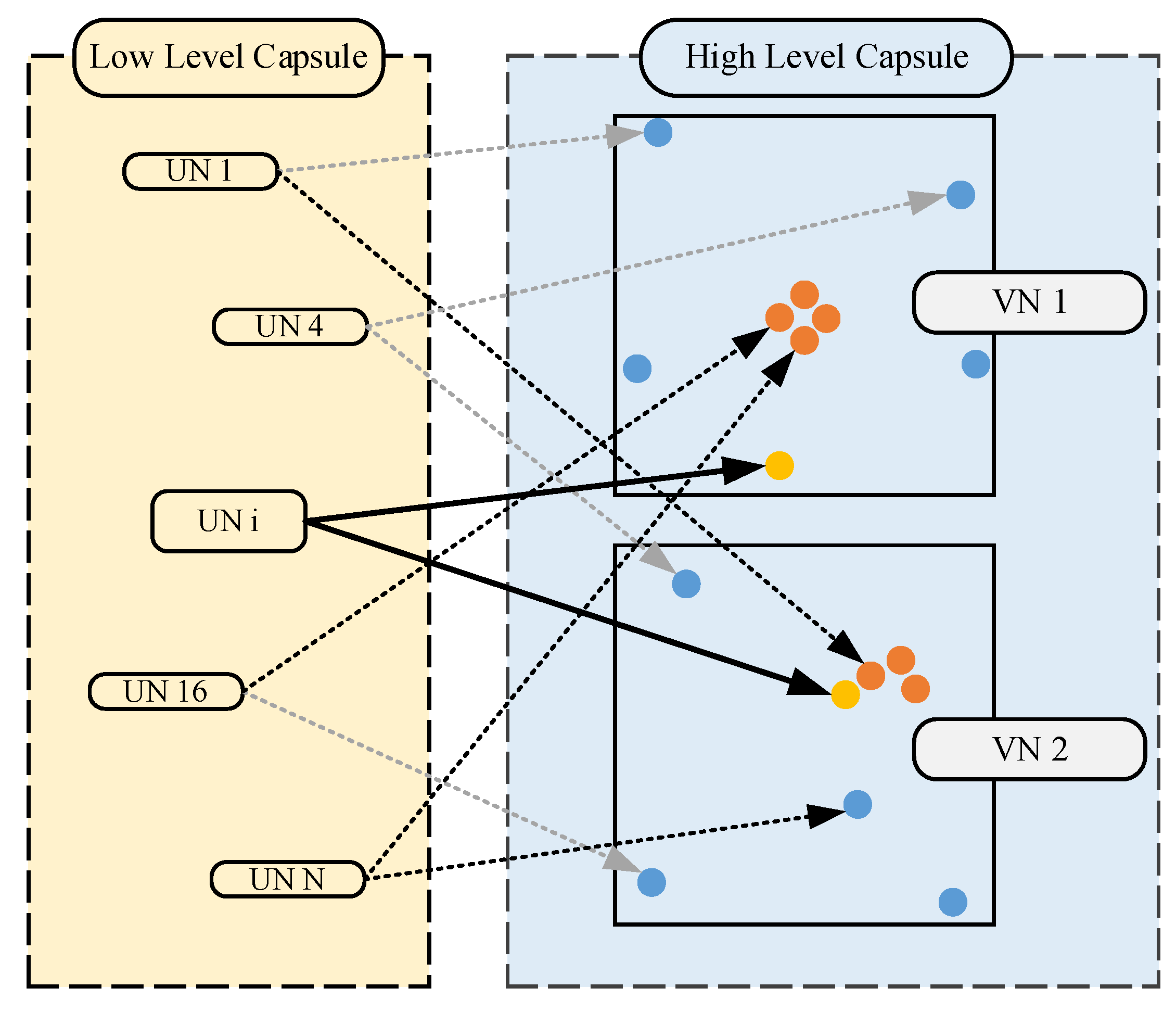
2.2. Vector Neuron and Dynamic Routing
3. Proposed Methodology
3.1. Enhanced Integrated Filter
3.2. The Architecture of EIFN
4. Experiments and Results
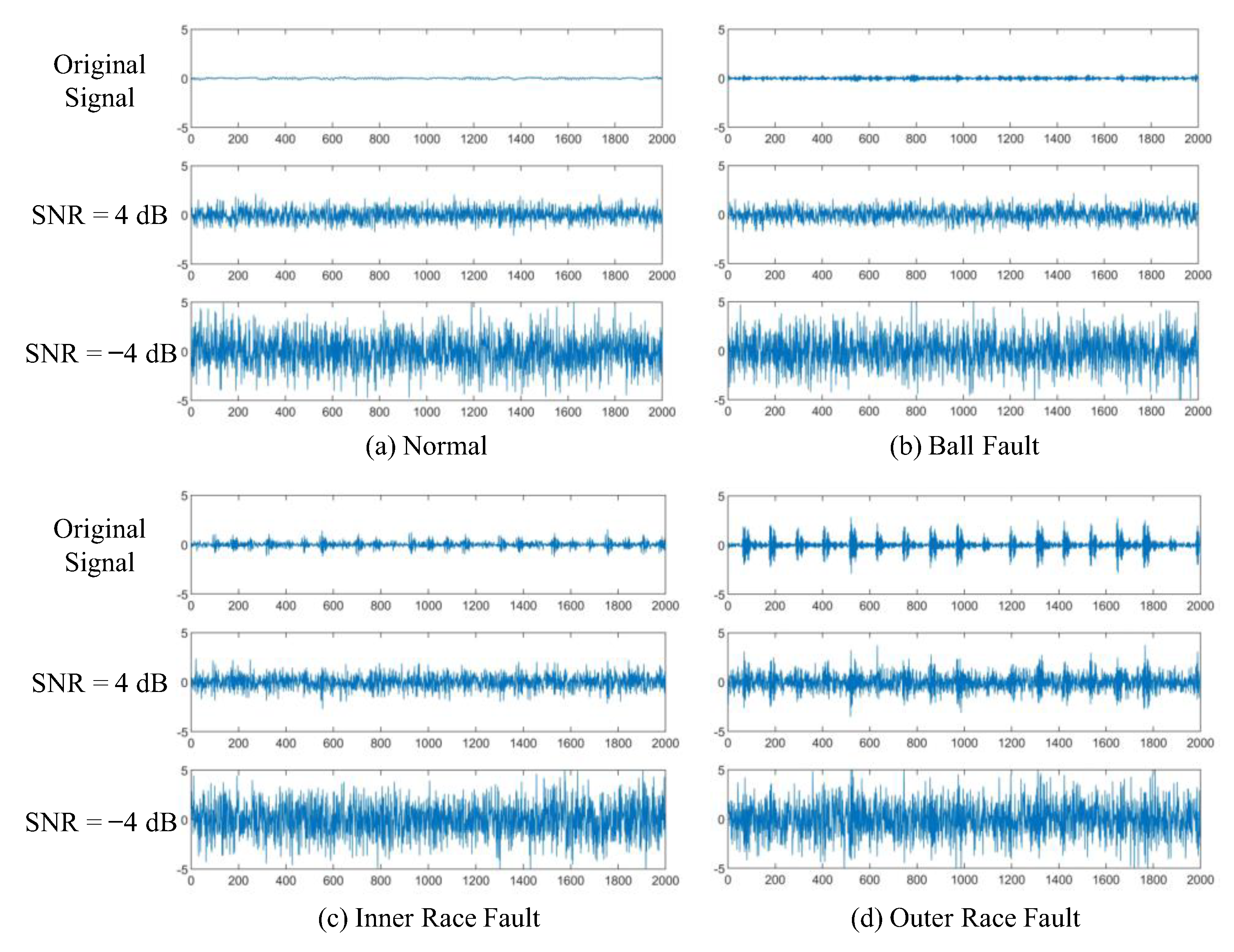
4.1. The Experimental Data
4.1.1. Case 1: CWRU Bearing Dataset
4.1.2. Case 2: IMS Bearing Dataset
4.2. Model Parameters of EIFN
4.3. Experimental Verification of EIFN’s Effectiveness
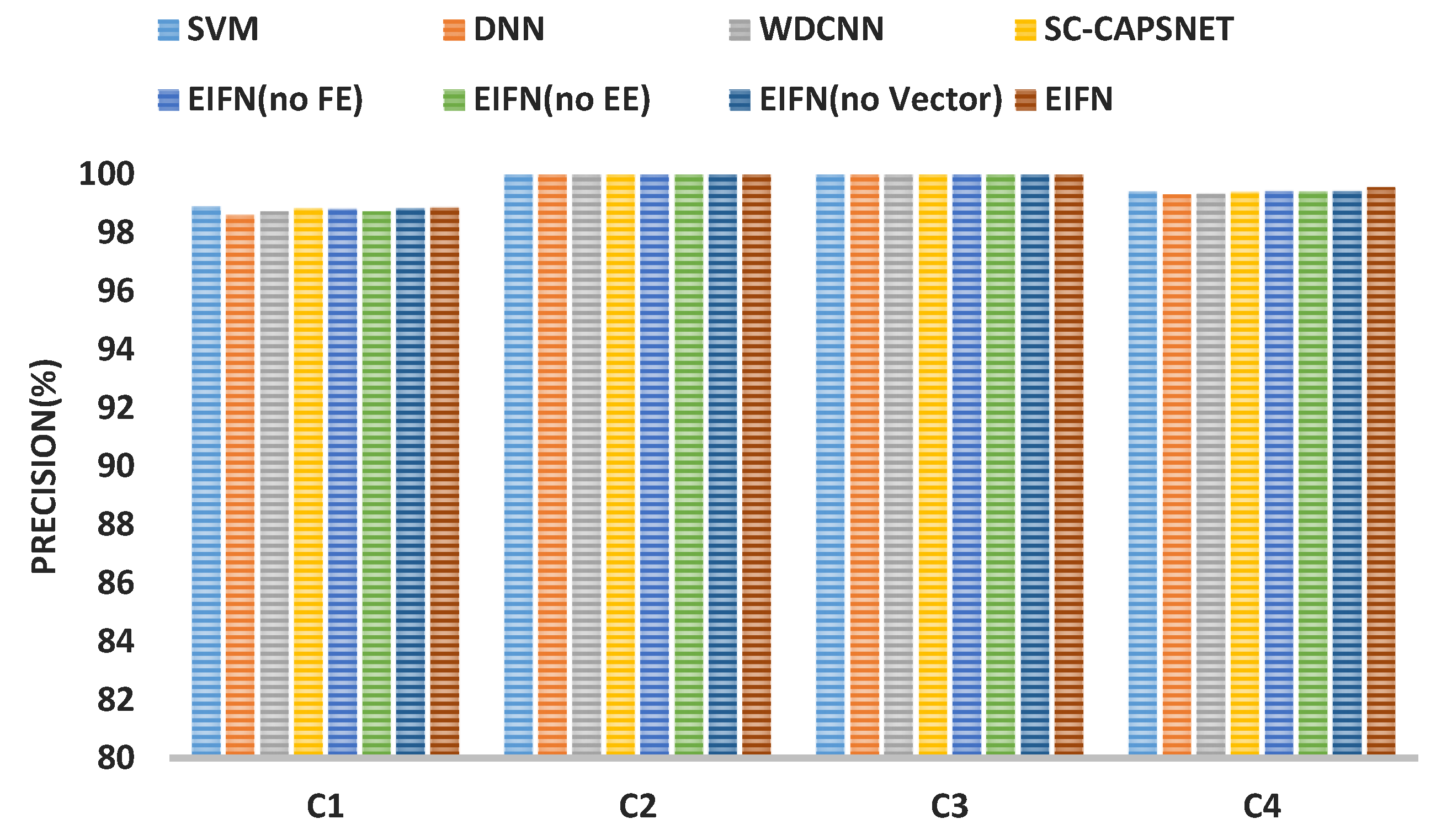
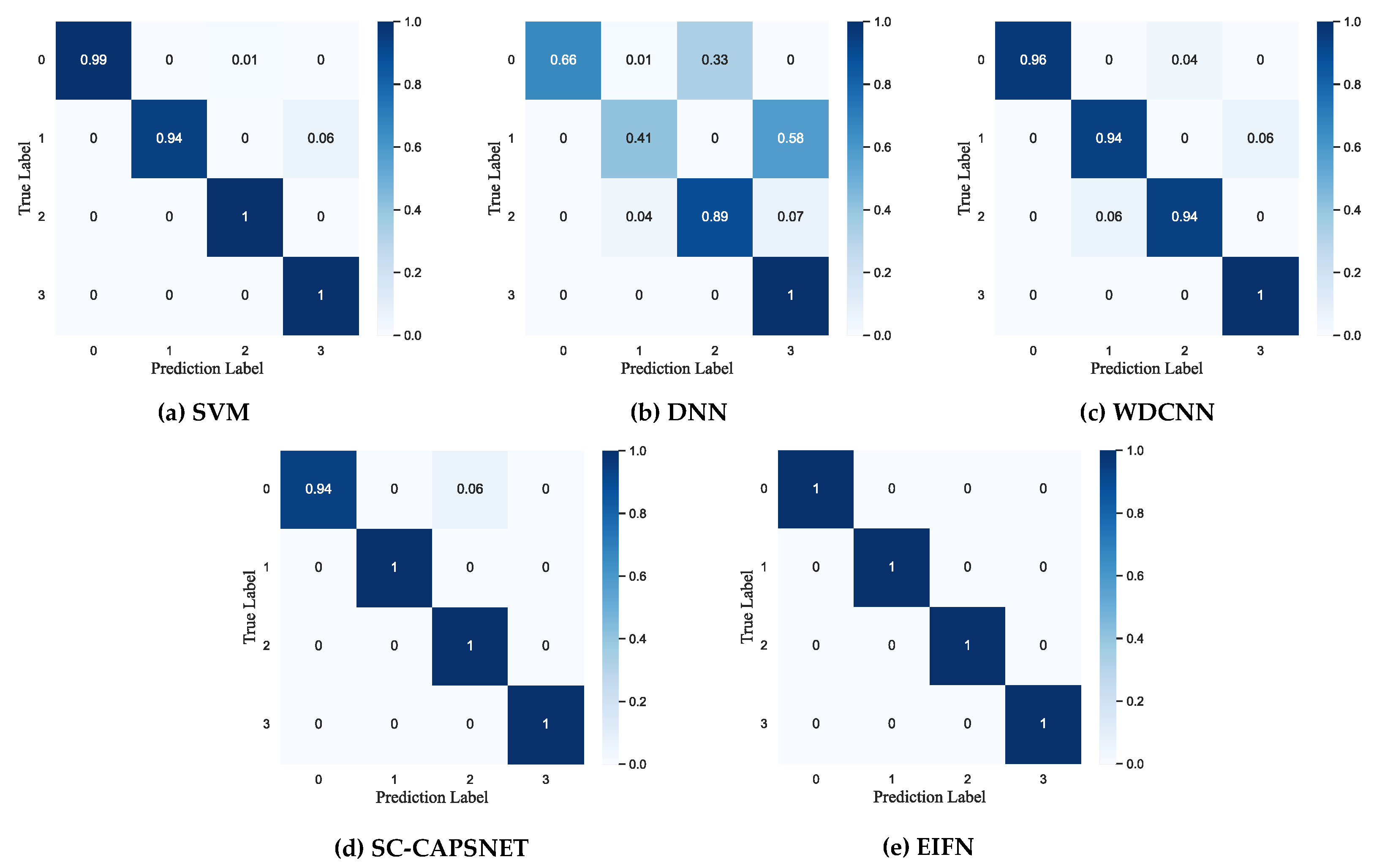
4.3.1. The Fault Diagnosis Result on CWRU Bearing Dataset
4.3.2. The Fault Diagnosis Result on IMS Bearing Dataset
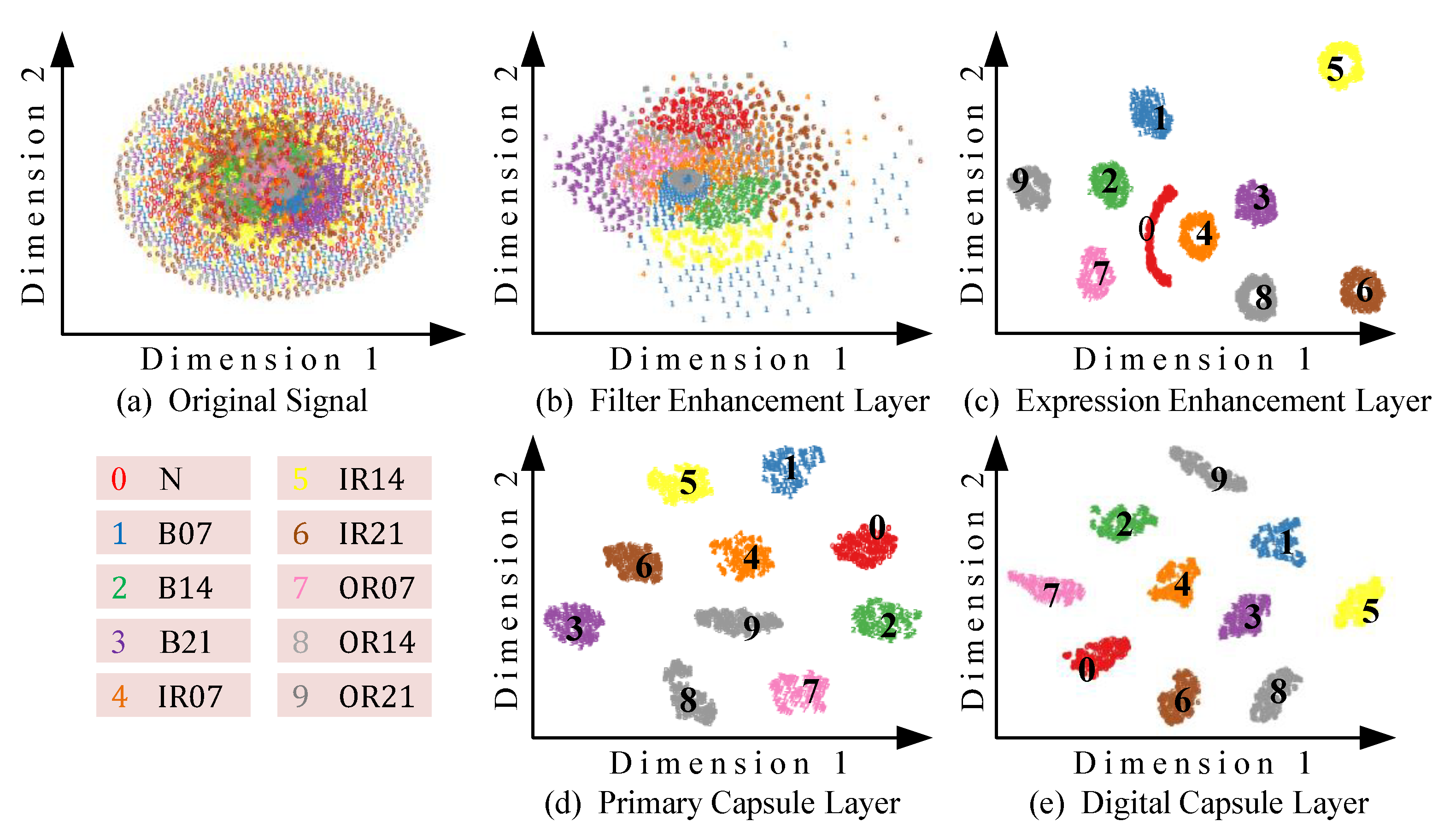
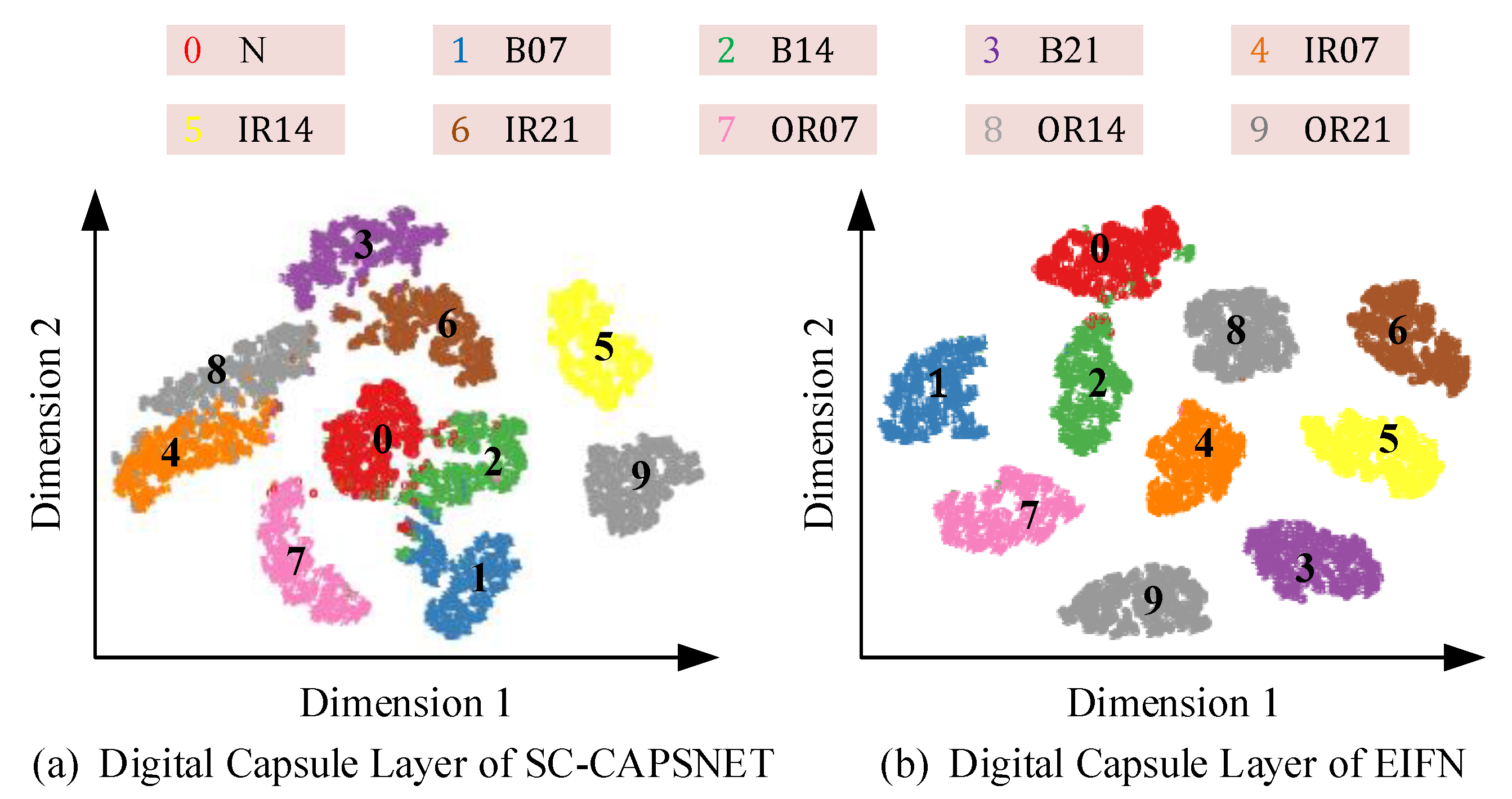
4.3.3. Visual Analysis of Feature Extraction Process
4.4. Comparative Analysis in Strong Noise Environment
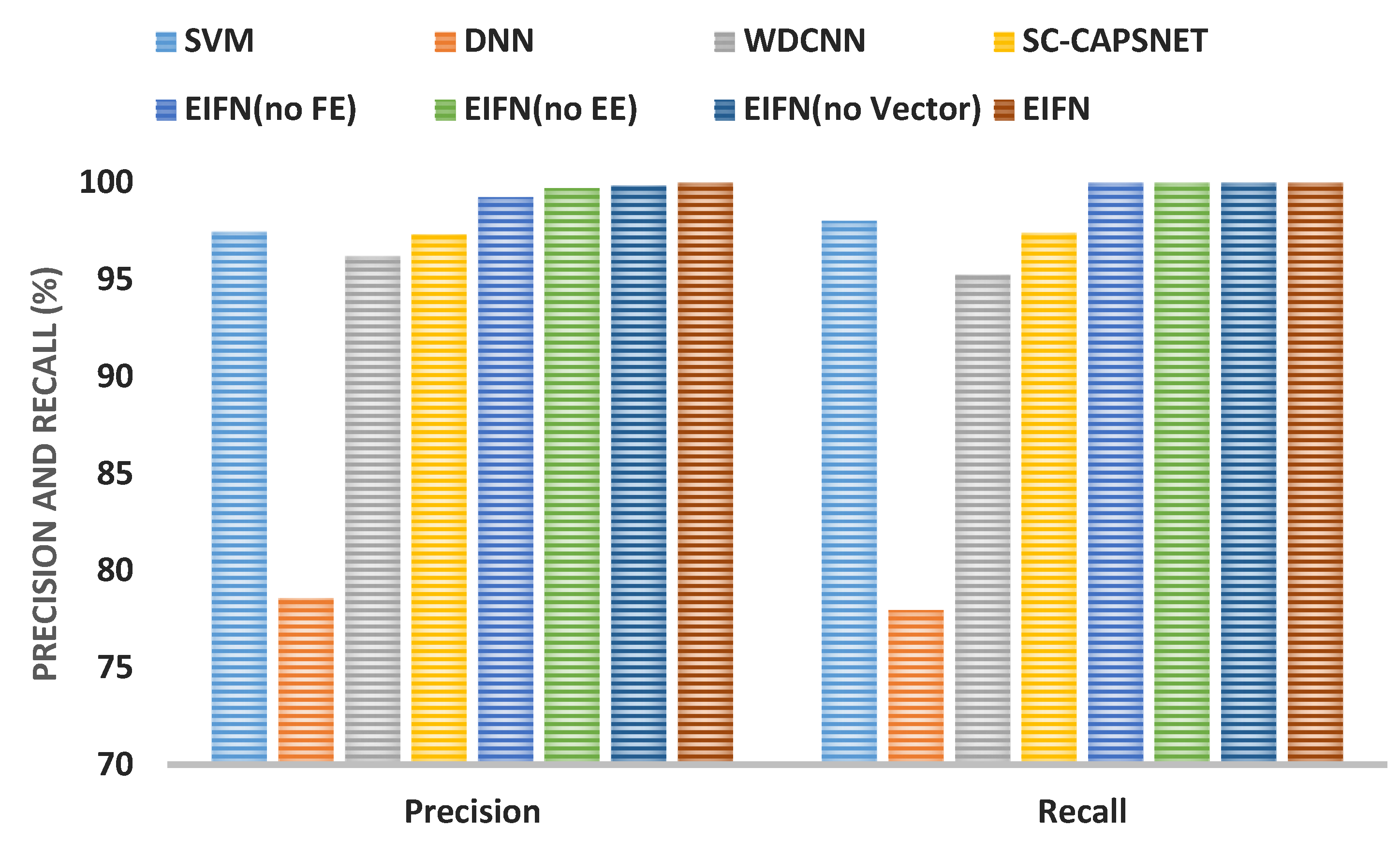
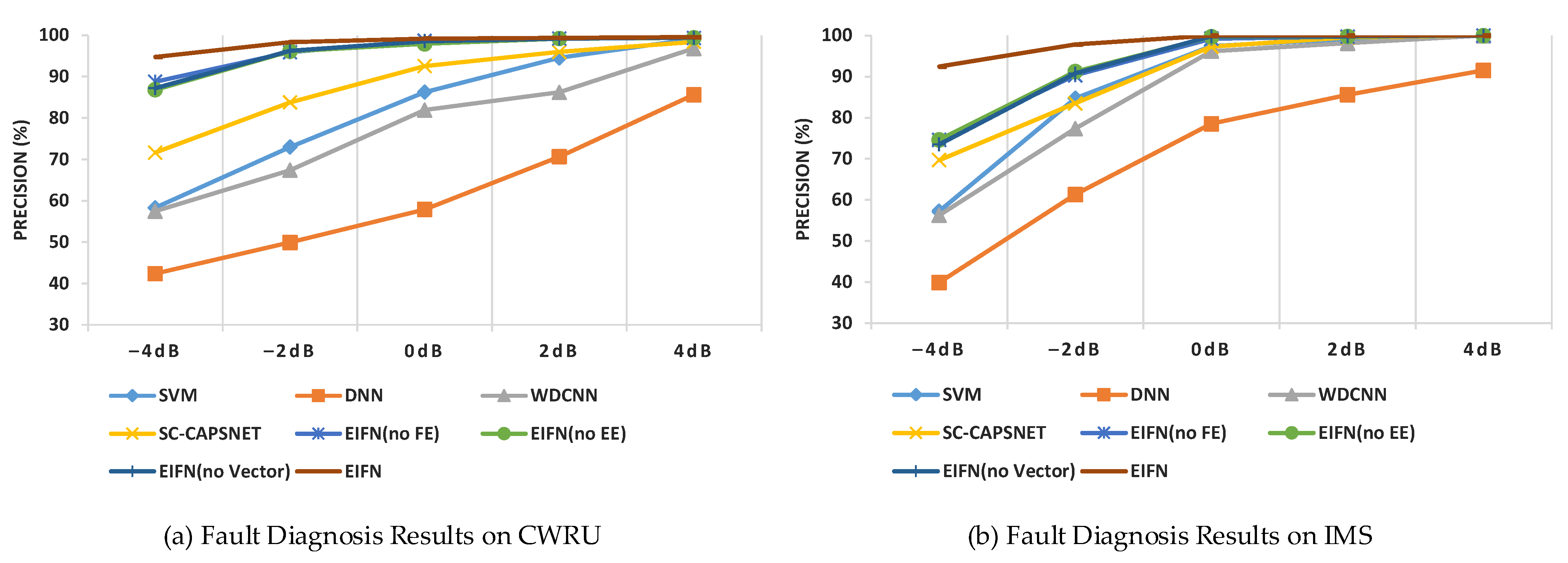
4.4.1. Fault Diagnosis Results and Comparative Analysis
4.4.2. Discussion on Experimental Results
4.4.3. Feature Visualization Analysis
5. Conclusions
- (1)
- EIFN integrates multiple primary filters in parallel and cascaded mode to form the enhanced integrated filter. It can not only filter high-frequency noise and extract useful feature information of low and middle frequency but also maintain frequency and time resolution to a certain extent.
- (2)
- EIFN uses vector neurons to incorporate scalar feature information into vector spaces. The relationship between low-level features and high-level features is established by dynamic routing. The key information of multi-scale fault features of signal in the time dimension is highlighted to improve the precision of bearing fault diagnosis in a strong noise environment.
- (3)
- The experimental results show that EIFN can effectively identify various types of rolling bearing states, and the bearing fault diagnosis precisions are more than 92% when strong noise of SNR = −4 dB. The visualization results verify that EIFN can effectively extract low and medium-frequency feature information and filter high-frequency noise through the enhanced integrated filter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hoang, D.T.; Kang, H.J. A survey on Deep Learning based bearing fault diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; De Silva, C.W. Fault diagnosis for rotating machinery using multiple sensors and convolutional neural networks. IEEE/ASME Trans. Mechatron. 2017, 23, 101–110. [Google Scholar] [CrossRef]
- El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60, 252–272. [Google Scholar] [CrossRef]
- Yan, X.; She, D.; Xu, Y.; Jia, M. Deep regularized variational autoencoder for intelligent fault diagnosis of rotor–bearing system within entire life-cycle process. Knowl. Based Syst. 2021, 226, 107142. [Google Scholar] [CrossRef]
- Li, G.; Tang, G.; Luo, G.; Wang, H. Underdetermined blind separation of bearing faults in hyperplane space with variational mode decomposition. Mech. Syst. Signal Process. 2019, 120, 83–97. [Google Scholar] [CrossRef]
- Qin, C.; Wang, D.; Xu, Z.; Tang, G. Improved empirical wavelet transform for compound weak bearing fault diagnosis with acoustic signals. Appl. Sci. 2020, 10, 682. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Wang, Z.; Chen, B.; Zhang, W.; Huang, G. An improved complementary ensemble empirical mode decomposition with adaptive noise and its application to rolling element bearing fault diagnosis. ISA Trans. 2019, 91, 218–234. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Pan, H.; Cheng, J.; Cheng, J. A novel deep stacking least squares support vector machine for rolling bearing fault diagnosis. Comput. Ind. 2019, 110, 36–47. [Google Scholar] [CrossRef]
- Gunerkar, R.S.; Jalan, A.K.; Belgamwar, S.U. Fault diagnosis of rolling element bearing based on artificial neural network. J. Mech. Sci. Technol. 2019, 33, 505–511. [Google Scholar] [CrossRef]
- Zhang, N.; Wu, L.; Yang, J.; Guan, Y. Naive bayes bearing fault diagnosis based on enhanced independence of data. Sensors 2018, 18, 463. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep learning algorithms for bearing fault diagnostics—A comprehensive review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Case Stud. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Eren, L.; Ince, T.; Kiranyaz, S. A generic intelligent bearing fault diagnosis system using compact adaptive 1D CNN classifier. J. Signal Process Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Han, T.; Zhang, L.; Yin, Z.; Tan, A.C. Rolling bearing fault diagnosis with combined convolutional neural networks and support vector machine. Measurement 2021, 177, 109022. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Zhao, K.; Wang, R. A deep transfer nonnegativity-constraint sparse autoencoder for rolling bearing fault diagnosis with few labeled data. IEEE Access 2019, 7, 91216–91224. [Google Scholar] [CrossRef]
- Zhao, K.; Jiang, H.; Li, X.; Wang, R. An optimal deep sparse autoencoder with gated recurrent unit for rolling bearing fault diagnosis. Meas. Sci. Technol. 2019, 31, 015005. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, H.; Zhao, K.; Li, X. An adaptive deep transfer learning method for bearing fault diagnosis. Measurement 2020, 151, 107227. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, Y.; Deng, J.; Jiang, Y.; Zhang, W. A novel transfer learning method for bearing fault diagnosis under different working conditions. Measurement 2021, 171, 108767. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, L. A combination of residual and long–short-term memory networks for bearing fault diagnosis based on time-series model analysis. Meas. Sci. Technol. 2020, 32, 015904. [Google Scholar] [CrossRef]
- Hao, S.; Ge, F.X.; Li, Y.; Jiang, J. Multisensor bearing fault diagnosis based on one-dimensional convolutional long short-term memory networks. Measurement 2020, 159, 107802. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Chen, L.; Han, P. Rolling bearing fault diagnosis using improved deep residual shrinkage networks. Shock. Vib. 2021, 2021, 9942249. [Google Scholar] [CrossRef]
- Tong, Y.; Wu, P.; He, J.; Zhang, X.; Zhao, X. Bearing fault diagnosis by combining a deep residual shrinkage network and bidirectional LSTM. Meas. Sci. Technol. 2021, 33, 034001. [Google Scholar] [CrossRef]
- Chen, Z.; Mauricio, A.; Li, W.; Gryllias, K. A deep learning method for bearing fault diagnosis based on cyclic spectral coherence and convolutional neural networks. Mech. Syst. Signal Process. 2020, 140, 106683. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault diagnosis of rolling bearing of wind turbines based on the variational mode decomposition and deep convolutional neural networks. Appl. Soft Comput. 2020, 95, 106515. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 3859–3869. [Google Scholar]
- Chen, T.; Wang, Z.; Yang, X.; Jiang, K. A deep capsule neural network with stochastic delta rule for bearing fault diagnosis on raw vibration signals. Measurement 2019, 148, 106857. [Google Scholar] [CrossRef]
- Yang, P.; Su, Y.C.; Zhang, Z. A study on rolling bearing fault diagnosis based on convolution capsule network. J. Vib. Shock 2020, 39, 55–62+68. [Google Scholar]
- Huang, R.; Li, J.; Wang, S.; Li, G.; Li, W. A robust weight-shared capsule network for intelligent machinery fault diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 6466–6475. [Google Scholar] [CrossRef]
- Han, T.; Ma, R.; Zheng, J. Combination bidirectional long short-term memory and capsule network for rotating machinery fault diagnosis. Measurement 2021, 176, 109208. [Google Scholar] [CrossRef]
- Li, L.; Zhang, M.; Wang, K. A fault diagnostic scheme based on capsule network for rolling bearing under different rotational speeds. Sensors 2020, 20, 1841. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Peng, G.; Chen, Y.; Gao, H. A convolutional neural network based on a capsule network with strong generalization for bearing fault diagnosis. Neurocomputing 2019, 323, 62–75. [Google Scholar] [CrossRef]
- Sun, Z.; Yuan, X.; Fu, X.; Zhou, F.; Zhang, C. Multi-Scale Capsule Attention Network and Joint Distributed Optimal Transport for Bearing Fault Diagnosis under Different Working Loads. Sensors 2021, 21, 6696. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, L.; Du, W.; Cai, W.; Zhou, J.; Wang, J.; He, G. A novel method for intelligent fault diagnosis of bearing based on capsule neural network. Complexity 2019, 2019, 6943234. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ning, D.; Feng, S. A novel capsule network based on wide convolution and multi-scale convolution for fault diagnosis. Appl. Sci. 2020, 10, 3659. [Google Scholar] [CrossRef]
- Li, Y.; Wang, N.; Shi, J.; Liu, J.; Hou, X. Revisiting Batch Normalization for Practical Domain Adaptation. arXiv 2016, arXiv:1603.04779. [Google Scholar]







| Fault Label | Fault Category | Fault Diameter | Sample Size |
|---|---|---|---|
| 0 | Normal | 0 | 1000 |
| 1 | Ball fault | 0.007 | 1000 |
| 2 | Ball fault | 0.014 | 1000 |
| 3 | Ball fault | 0.021 | 1000 |
| 4 | Inner race fault | 0.007 | 1000 |
| 5 | Inner race fault | 0.014 | 1000 |
| 6 | Inner race fault | 0.021 | 1000 |
| 7 | Outer race fault | 0.007 | 1000 |
| 8 | Outer race fault | 0.014 | 1000 |
| 9 | Outer race fault | 0.021 | 1000 |
| Fault Label | Fault Category | Training Set | Testing Set |
|---|---|---|---|
| 0 | Normal | 700 | 300 |
| 1 | Inner race fault | 700 | 300 |
| 2 | Ball fault | 700 | 300 |
| 3 | Outer race fault | 700 | 300 |
| Layer Type | Operation | Kernel Size | Stride | Kernel Number | Output Size | Parallel Output Size | Padding |
|---|---|---|---|---|---|---|---|
| Filter enhancement layer | Convolution 1 | 96 × 1 | 32 | 32 | 64 × 32 | 64 × 128 | Yes |
| Convolution 2 | 120 × 1 | 32 | 32 | 64 × 32 | Yes | ||
| Convolution 3 | 144 × 1 | 32 | 32 | 64 × 32 | Yes | ||
| Convolution 4 | 168 × 1 | 32 | 32 | 64 × 32 | Yes | ||
| Pooling layer | Sampling | 2 × 1 | 2 | 32 | 32 × 128 | No | |
| Expression enhancement layer | Convolution 1 | 7 × 1 | 2 | 32 | 16 × 32 | 16 × 128 | Yes |
| Convolution 2 | 10 × 1 | 2 | 32 | 16 × 32 | Yes | ||
| Convolution 3 | 13 × 1 | 2 | 32 | 16 × 32 | Yes | ||
| Convolution 4 | 16 × 1 | 2 | 32 | 16 × 32 | Yes | ||
| Pooling layer | Sampling | 2 × 1 | 2 | 32 | 8 × 128 | No | |
| Primary capsule layer | Construct of vector neurons | 4 × 1 | 2 | 32 | 24 × 4 | No | |
| Digital capsule layer | Dynamic routing | 10/4 | 1 | 10 × 8/4 × 8 | No |
| Model | C1 | C2 | C3 | C4 | ||||
|---|---|---|---|---|---|---|---|---|
| Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | |
| SVM | 91.43 | 92.07 | 97.08 | 97.21 | 98.74 | 99.12 | 86.23 | 87.16 |
| DNN | 65.11 | 64.52 | 77.63 | 77.81 | 78.28 | 79.34 | 57.89 | 58.74 |
| WDCNN | 86.24 | 86.01 | 96.71 | 96.76 | 96.13 | 95.01 | 81.92 | 82.34 |
| SC-CAPSNET | 95.87 | 96.21 | 97.13 | 97.64 | 99.48 | 99.56 | 92.54 | 93.23 |
| EIFN (no FE) | 97.21 | 97.38 | 98.73 | 99.91 | 99.72 | 99.78 | 98.71 | 98.83 |
| EIFN (no EE) | 96.74 | 96.91 | 98.97 | 99.83 | 99.87 | 99.91 | 97.91 | 98.23 |
| EIFN (no Vector) | 96.56 | 96.73 | 99.76 | 99.92 | 100 | 100 | 98.54 | 98.62 |
| EIFN | 98.73 | 99.21 | 100 | 100 | 100 | 100 | 99.18 | 99.23 |
| Model | −4 dB | −2 dB | 0 dB | 2 dB | 4 dB | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | |
| SVM | 58.31 | 57.56 | 72.97 | 73.43 | 86.23 | 87.16 | 94.52 | 95.87 | 99.11 | 98.79 |
| DNN | 42.37 | 41.28 | 49.92 | 50.62 | 57.89 | 58.74 | 70.62 | 70.88 | 85.63 | 86.35 |
| WDCNN | 57.45 | 56.78 | 67.38 | 66.94 | 81.92 | 82.34 | 86.21 | 85.75 | 96.81 | 97.03 |
| SC-CAPSNET | 71.63 | 72.01 | 83.78 | 84.25 | 92.54 | 93.23 | 95.97 | 96.71 | 98.41 | 98.56 |
| EIFN (no FE) | 88.76 | 88,63 | 95.91 | 95.77 | 98.71 | 98.83 | 99.23 | 99.14 | 99.33 | 99.36 |
| EIFN (no EE) | 86.84 | 87.72 | 96.11 | 96.71 | 97.91 | 98.23 | 99.19 | 99.15 | 99.38 | 99.32 |
| EIFN (no Vector) | 87.21 | 88.19 | 96.22 | 96.81 | 98.54 | 98.62 | 99.18 | 99.21 | 99.42 | 99.44 |
| EIFN | 94.73 | 95.64 | 98.33 | 98.78 | 99.18 | 99.23 | 99.34 | 99.41 | 99.54 | 99.56 |
| Model | −4 dB | −2 dB | 0 dB | 2 dB | 4 dB | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | |
| SVM | 57.24 | 56.87 | 84.71 | 83.24 | 97.46 | 98.01 | 99.17 | 100 | 100 | 100 |
| DNN | 39.87 | 40.26 | 61.27 | 60.62 | 78.54 | 77.97 | 85.59 | 85.72 | 91.52 | 90.87 |
| WDCNN | 56.23 | 55.32 | 77.32 | 76.54 | 96.21 | 95.25 | 98.16 | 97.64 | 100.00 | 100.00 |
| SC-CAPSNET | 69.67 | 68.43 | 83.51 | 82.97 | 97.33 | 97.38 | 99.56 | 100.00 | 100.00 | 100.00 |
| EIFN (no FE) | 74.58 | 75.45 | 90.33 | 91.43 | 99.25 | 100 | 99.75 | 100.00 | 100.00 | 100.00 |
| EIFN (no EE) | 74.63 | 75.88 | 91.21 | 90.75 | 99.72 | 100 | 99.78 | 100.00 | 100.00 | 100.00 |
| EIFN (no Vector) | 73.52 | 74.78 | 90.78 | 90.11 | 99.83 | 100.00 | 99.81 | 100.00 | 100.00 | 100.00 |
| EIFN | 92.45 | 93.81 | 97.82 | 98.54 | 100 | 100 | 100.00 | 100.00 | 100.00 | 100.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Tao, J.; Yang, D.; Xie, H.; Li, Z. A Rolling Bearing Fault Diagnosis Method Based on Enhanced Integrated Filter Network. Machines 2022, 10, 481. https://doi.org/10.3390/machines10060481
Wu K, Tao J, Yang D, Xie H, Li Z. A Rolling Bearing Fault Diagnosis Method Based on Enhanced Integrated Filter Network. Machines. 2022; 10(6):481. https://doi.org/10.3390/machines10060481
Chicago/Turabian StyleWu, Kang, Jie Tao, Dalian Yang, Hu Xie, and Zhiying Li. 2022. "A Rolling Bearing Fault Diagnosis Method Based on Enhanced Integrated Filter Network" Machines 10, no. 6: 481. https://doi.org/10.3390/machines10060481
APA StyleWu, K., Tao, J., Yang, D., Xie, H., & Li, Z. (2022). A Rolling Bearing Fault Diagnosis Method Based on Enhanced Integrated Filter Network. Machines, 10(6), 481. https://doi.org/10.3390/machines10060481






