Utilizing Human Feedback in Autonomous Driving: Discrete vs. Continuous
Abstract
:1. Introduction
2. Related Works
3. Background
Soft Actor–Critic
- (1)
- A state-value network V is parameterized by and approximates the soft value function. This network is trained by minimizing the squared residual error:
- (2)
- The soft Q-network parameterized by and was trained by minimizing the soft Bellman residual error:whereand is the parameter of the target value function that exponentially moves the mean of value network weights and can make the training more stable [39]. The aim of Equation (4) is to minimize the squared error for all of the state–action pairs from the replay buffer by getting the difference between the predicted Q-function and the current reward added to the discounted expected value of the next step. Again, the optimization of the parameters was computed by stochastic gradients:
- (3)
- The last function is policy function parameterized by that is trained by minimizing the expected KL divergence [25]:
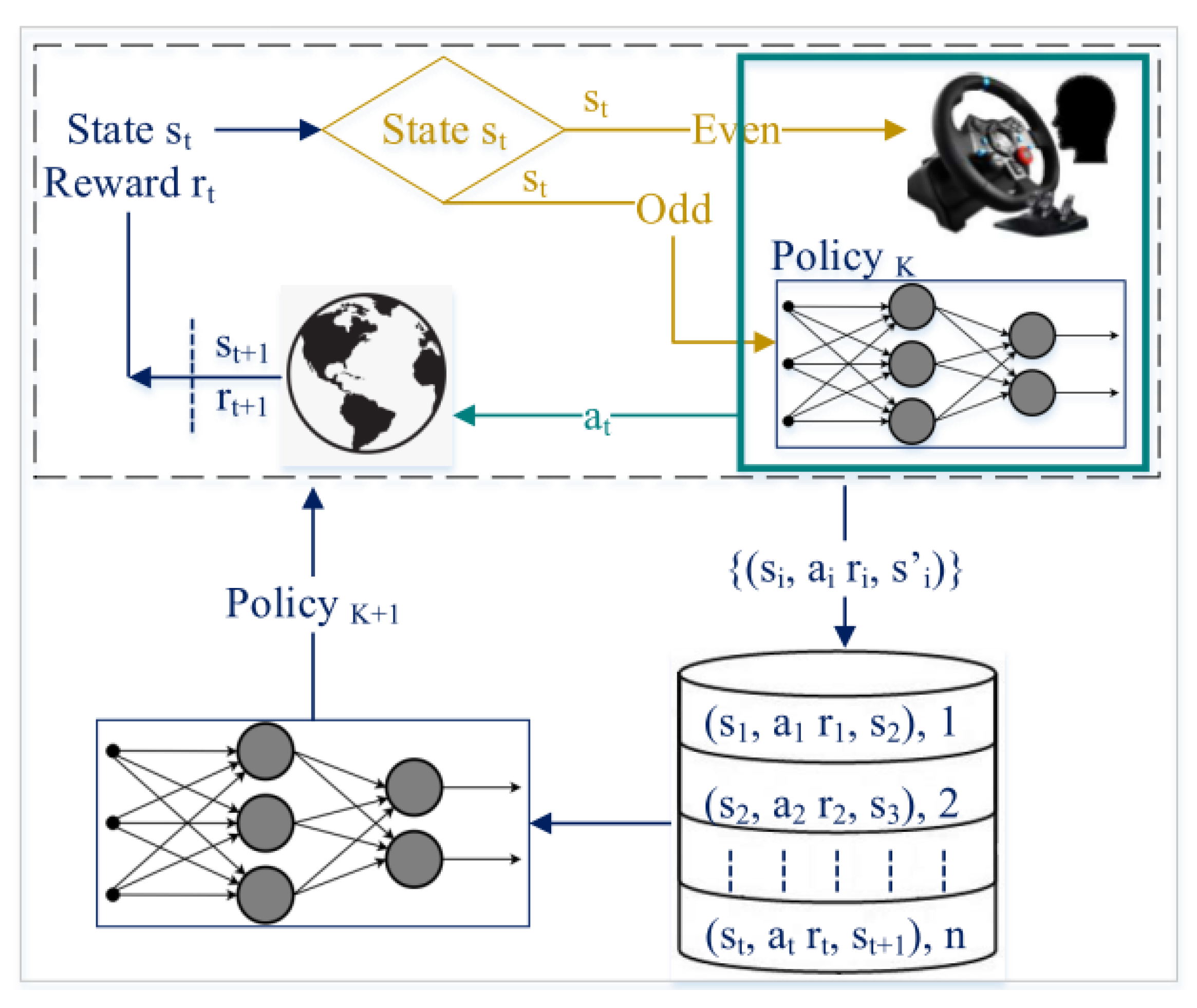
4. Method
5. Task 1: Autonomous Driving in CARLA
5.1. Experiment
5.2. Results
5.2.1. Results: Continuous Steer Feedback from Human and SAC Algorithm
5.2.2. Results: Discrete Steer Feedback from Human and SAC Algorithm
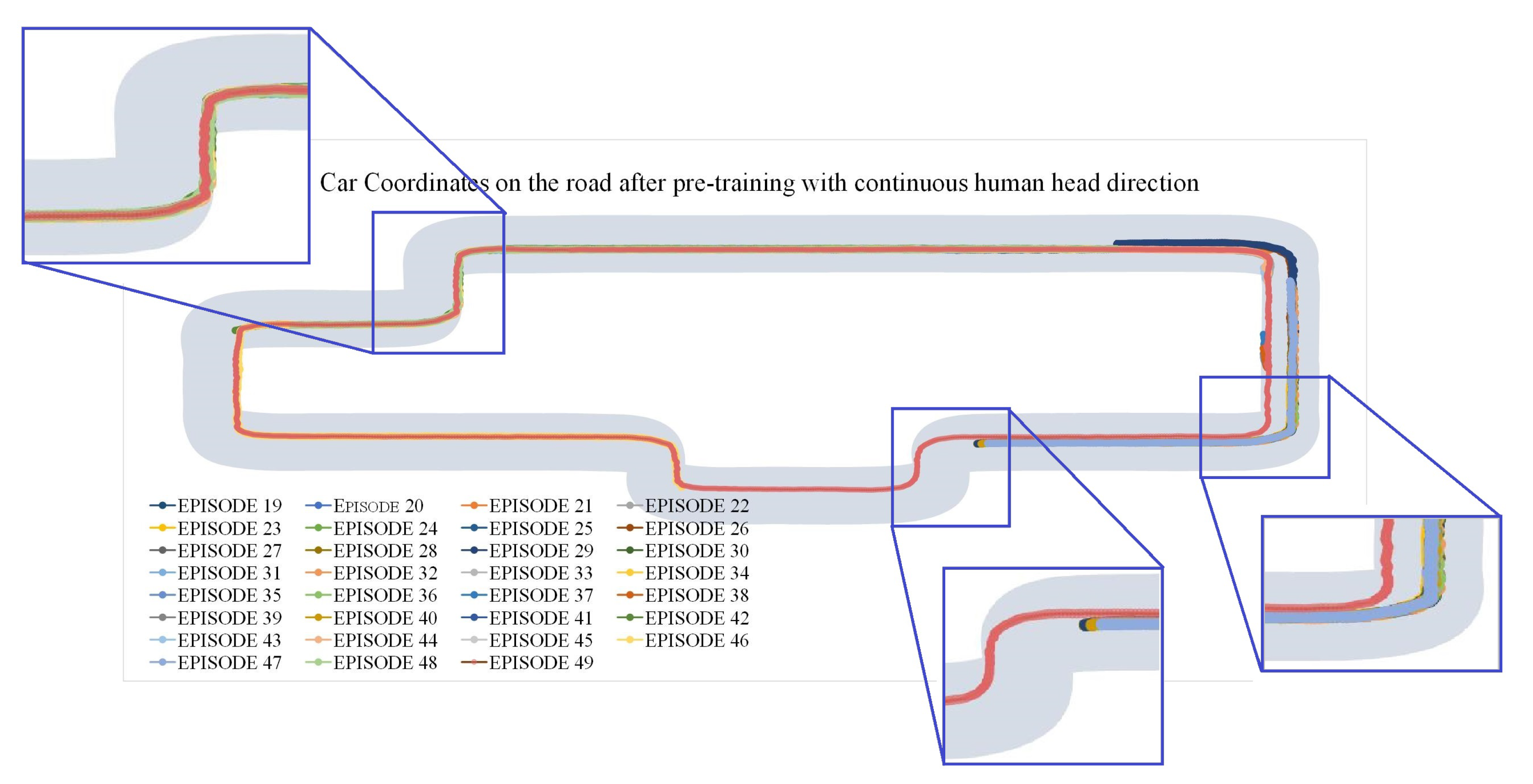
5.2.3. Results: Continuous Human Head Direction Feedback and SAC Algorithm
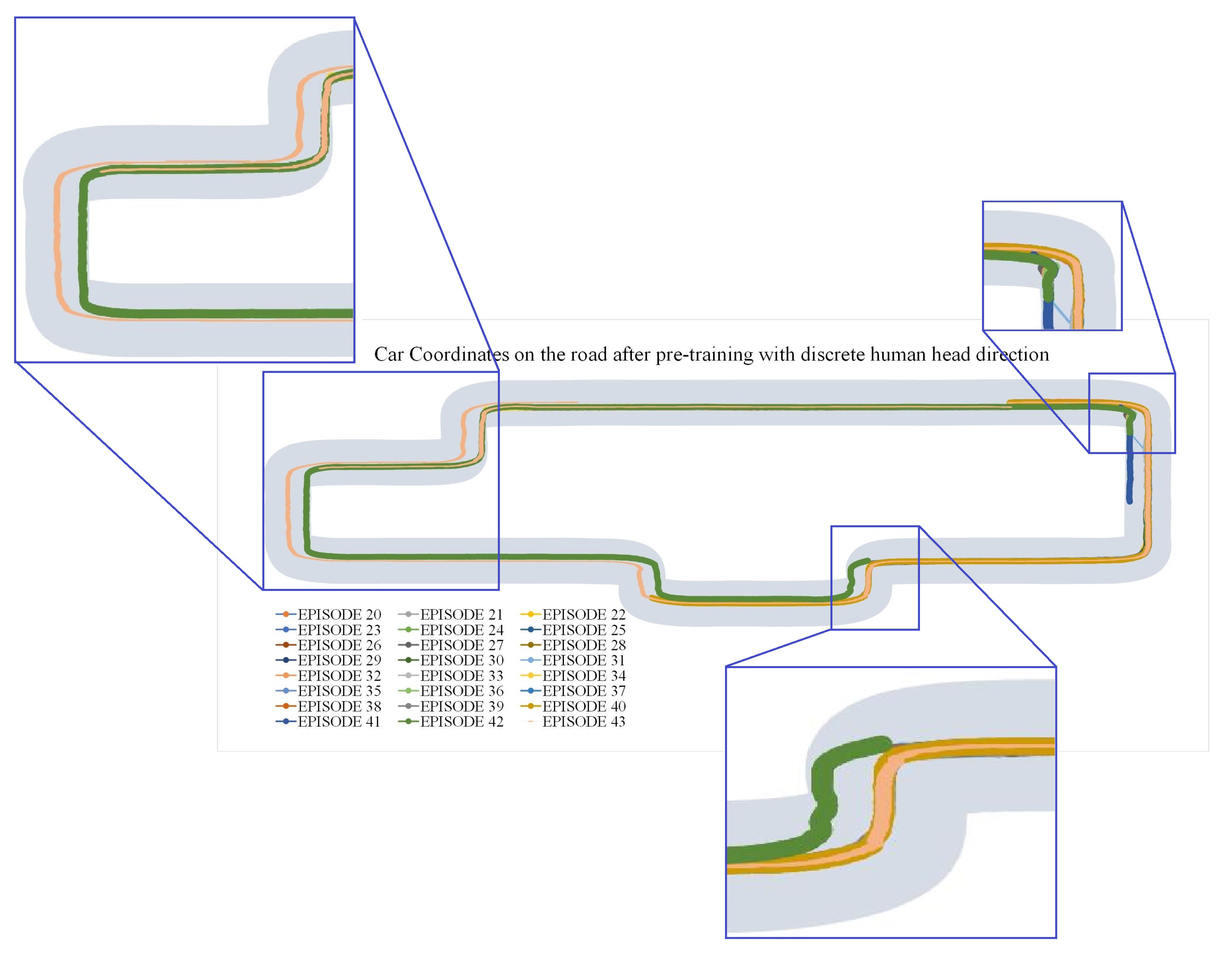
5.2.4. Results: Discrete Human Head Direction Feedback and SAC Algorithm
5.3. Results: Behavior
6. Task 2: Inverted Pendulum
6.1. Experiment
6.2. Result
7. Summary of Results
8. Discussion
Contribution
- Continuous human steer feedback;
- Discrete human steer feedback;
- Continuous human head direction feedback;
- Discrete human head direction feedback;
- Continuous algorithmic expert feedback;
- Discrete algorithmic expert feedback.
- When a driver faces a curve, they receive the rotational and acceleration stimulation and control the head to the curve direction [29,30]. Therefore, the human head direction is closely related to the direction of the road curve [30,31]. We used human head direction to train the policy without any effort from the human during training.
- This method significantly improved the data efficiency. Therefore, the human expert is not gathering any data samples before the SAC training time, and human effort for training SAC was significantly reduced (5000 steps of human training) compared to other human demonstration methods such as LfD.
- Discrete action–space has a faster training time but is unsuitable for covering all the aspects of a complex environment. In this work, we took advantage of discrete actions to tune the policy faster without changing the action–space of the SAC algorithm to discrete.
- In a LfI method, when the agent performs any mistake in the environment, the human expert intervenes to correct the fault action. Therefore, there exists a non-neglected delay from humans to take control over the policy. This delay was removed in our method since the human and policy alternately generated actions to take control over the policy.
- The training time was significantly reduced, especially when the feedback was discrete.
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smart, W.D.; Kaelbling, L.P. Practical Reinforcement Learning in Continuous Spaces. 2000. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.97.9314&rep=rep1&type=pdf (accessed on 17 July 2022).
- Lange, S.; Riedmiller, M.; Voigtländer, A. Autonomous reinforcement learning on raw visual input data in a real world application. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Liu, H.; Huang, Z.; Lv, C. Improved deep reinforcement learning with expert demonstrations for urban autonomous driving. arXiv 2021, arXiv:2102.09243. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 1889–1897. [Google Scholar]
- Bi, J.; Dhiman, V.; Xiao, T.; Xu, C. Learning from interventions using hierarchical policies for safe learning. Proc. AAAI Conf. Artif. Intell. 2020, 34, 10352–10360. [Google Scholar] [CrossRef]
- Liu, K.; Wan, Q.; Li, Y. A deep reinforcement learning algorithm with expert demonstrations and supervised loss and its application in autonomous driving. In Proceedings of the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 2944–2949. [Google Scholar]
- Kendall, A.; Hawke, J.; Janz, D.; Mazur, P.; Reda, D.; Allen, J.-M.; Lam, V.-D.; Bewley, A.; Shah, A. Learning to drive in a day. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8248–8254. [Google Scholar]
- Hancock, P.A.; Nourbakhsh, I.; Stewart, J. On the future of transportation in an era of automated and autonomous vehicles. Proc. Natl. Acad. Sci. USA 2019, 116, 7684–7691. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Zhang, Q.; Zhao, D.; Chen, Y. Lane change decision-making through deep reinforcement learning with rule-based constraints. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–6. [Google Scholar]
- Ward, P.N.; Smofsky, A.; Bose, A.J. Improving exploration in soft-actor-critic with normalizing flows policies. arXiv 2019, arXiv:1906.02771. [Google Scholar]
- Dossa, R.F.J.; Lian, X.; Nomoto, H.; Matsubara, T.; Uehara, K. A human-like agent based on a hybrid of reinforcement and imitation learning. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Shin, M.; Kim, J. Adversarial imitation learning via random search. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. Deep reinforcement learning framework for autonomous driving. Electron. Imaging 2017, 19, 70–76. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ma, H. Pretraining deep actor-critic reinforcement learning algorithms with expert demonstrations. arXiv 2018, arXiv:1801.10459. [Google Scholar]
- Wu, J.; Huang, Z.; Huang, C.; Hu, Z.; Hang, P.; Xing, Y.; Lv, C. Human-in-the-loop deep reinforcement learning with application to autonomous driving. arXiv 2021, arXiv:2104.07246. [Google Scholar]
- Gao, Y.; Xu, H.; Lin, J.; Yu, F.; Levine, S.; Darrell, T. Reinforcement learning from imperfect demonstrations. arXiv 2018, arXiv:1802.05313. [Google Scholar]
- Hussein, A.; Gaber, M.M.; Elyan, E.; Jayne, C. Imitation learning: A survey of learning methods. ACM Comput. Surv. (CSUR) 2017, 50, 1–35. [Google Scholar] [CrossRef]
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. In Advances in Neural Information Processing Systems; NeurIPS: Lake Tahoe, NV, USA, 2000; pp. 1008–1014. Available online: https://papers.nips.cc/paper/1999/hash/6449f44a102fde848669bdd9eb6b76fa-Abstract.html (accessed on 17 July 2022).
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Codevilla, F.; Santana, E.; López, A.M.; Gaidon, A. Exploring the limitations of behavior cloning for autonomous driving. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 9329–9338. [Google Scholar]
- Savari, M.; Choe, Y. Online virtual training in soft actor-critic for autonomous driving. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021. [Google Scholar]
- Saunders, W.; Sastry, G.; Stuhlmueller, A.; Evans, O. Trial without error: Towards safe reinforcement learning via human intervention. arXiv 2017, arXiv:1707.05173. [Google Scholar]
- Goecks, V.G.; Gremillion, G.M.; Lawhern, V.J.; Valasek, J.; Waytowich, N.R. Efficiently combining human demonstrations and interventions for safe training of autonomous systems in real-time. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolului, HI, USA, 27 January–1 February 2019; Volume 33, pp. 2462–2470. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Chen, S.; Wang, M.; Song, W.; Yang, Y.; Li, Y.; Fu, M. Stabilization approaches for reinforcement learning-based end-to-end autonomous driving. IEEE Trans. Veh. Technol. 2020, 69, 4740–4750. [Google Scholar] [CrossRef]
- Millán, C.; Fernandes, B.J.; Cruz, F. Human feedback in continuous actor-critic reinforcement learning. In Proceedings of the 27th European Symposium on Artificial Neural Networks, Bruges, Belgium, 24–26 April 2019. [Google Scholar]
- Hasselt, H.V.; Wiering, M.A. Reinforcement learning in continuous action spaces. In Proceedings of the IEEE International Symposium on Approximate Dynamic Programming and Reinforcement Learning, Honolulu, HI, USA, 1–5 April 2007. [Google Scholar]
- Fujisawa, S.; Wada, T.; Kamiji, N.; Doi, S. Analysis of head tilt strategy of car drivers. In Proceedings of the ICROS-SICE International Joint Conference, Fukuoka, Japan, 18–21 August 2009; pp. 4161–4165. [Google Scholar]
- Land, M.F.; Tatler, B.W. Steering with the head: The visual strategy of a racing driver. Curr. Biol. 2001, 11, 1215–1220. [Google Scholar] [CrossRef] [Green Version]
- Braunagel, C.; Kasneci, E.; Stolzmann, W.; Rosenstiel, W. Driver-activity recognition in the context of conditionally autonomous driving. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 1652–1657. [Google Scholar]
- Huang, Z.; Wu, J.; Lv, C. Efficient deep reinforcement learning with imitative expert priors for autonomous driving. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Cheng, C.-A.; Saigol, K.; Lee, K.; Yan, X.; Theodorou, E.; Boots, B. Agile autonomous driving using end-to-end deep imitation learning. arXiv 2017, arXiv:1709.07174. [Google Scholar]
- Zuo, S.; Wang, Z.; Zhu, X.; Ou, Y. Continuous reinforcement learning from human demonstrations with integrated experience replay for autonomous driving. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 2450–2455. [Google Scholar]
- Pal, A.; Mondal, S.; Christensen, H.I. Looking at the right stuff-guided semantic-gaze for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11883–11892. [Google Scholar]
- Huang, G.; Liang, N.; Wu, C.; Pitts, B.J. The impact of mind wandering on signal detection, semi-autonomous driving performance, and physiological responses. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Seattle, WA, USA, 28 October–2 November 2019; SAGE Publications Sage: Los Angeles, CA, USA, 2019; Volume 63, pp. 2051–2055. [Google Scholar]
- Du, Z.; Miao, Q.; Zong, C. Trajectory planning for automated parking systems using deep reinforcement learning. Int. J. Automot. Technol. 2020, 21, 881–887. [Google Scholar] [CrossRef]
- Sutton, R.S. On the significance of markov decision processes. In Proceedings of the International Conference on Artificial Neural Networks, Lausanne, Switzerland, 8–10 October 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 273–282. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An open urban driving simulator. In Proceedings of the 1st Annual Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; pp. 1–16. [Google Scholar]
- Palanisamy, P. Multi-agent connected autonomous driving using deep reinforcement learning. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Raffin, A.; Sokolkov, R. Learning to Drive Smoothly in Minutes. 27 January 2019. Available online: https://github.com/araffin/learning-to-drive-in-5-minutes/ (accessed on 17 July 2022).
- Todorov, E.; Erez, T.; Tassa, Y. Mujoco: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar]
- Wang, D.; Devin, C.; Cai, Q.-Z.; Yu, F.; Darrell, T. Deep object-centric policies for autonomous driving. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 22–24 May 2019; pp. 8853–8859. [Google Scholar]









| Approaches | Method | Human Feedback | ||||
|---|---|---|---|---|---|---|
| Algorithm | Discrete | Continuous | Discrete | Continuous | Type | |
| [32] | SAC | - | ✔ | - | ✔ | Steer |
| [16] | TD3 | - | ✔ | - | ✔ | Steer |
| [33] | DNN | - | ✔ | - | ✔ | Steer |
| [34] | DDPG | - | ✔ | - | ✔ | Steer |
| [3] | DQfD | - | ✔ | - | ✔ | Steer |
| [26] | DDPG | - | ✔ | - | ✔ | Steer |
| [35] | NN | - | - | - | ✔ | Gaze |
| [36] | NN | - | - | - | - | Eye tracking, heart rate, physiological data |
| [37] | DQN&DRQN | ✔ | - | ✔ | - | Steer |
| Ours (matching) | SAC | - | ✔ | - | ✔ | Steer |
| Ours (matching) | SAC | - | ✔ | - | ✔ | Head |
| Ours (mismatching) | SAC | - | ✔ | ✔ | - | Steer |
| Ours (mismatching) | SAC | - | ✔ | ✔ | - | Head |
| Type | CARLA: Steer | CARLA: Head | Pendulum |
|---|---|---|---|
| Continuous | 37.9% | 10.3% | 43.6% |
| Discrete | 91.1% | 62.9% | 74.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savari, M.; Choe, Y. Utilizing Human Feedback in Autonomous Driving: Discrete vs. Continuous. Machines 2022, 10, 609. https://doi.org/10.3390/machines10080609
Savari M, Choe Y. Utilizing Human Feedback in Autonomous Driving: Discrete vs. Continuous. Machines. 2022; 10(8):609. https://doi.org/10.3390/machines10080609
Chicago/Turabian StyleSavari, Maryam, and Yoonsuck Choe. 2022. "Utilizing Human Feedback in Autonomous Driving: Discrete vs. Continuous" Machines 10, no. 8: 609. https://doi.org/10.3390/machines10080609
APA StyleSavari, M., & Choe, Y. (2022). Utilizing Human Feedback in Autonomous Driving: Discrete vs. Continuous. Machines, 10(8), 609. https://doi.org/10.3390/machines10080609






