Dynamic Response and Synchronizing Characteristic for the Dual-Motor Driving System in Non-Inertial System
Abstract
:1. Introduction
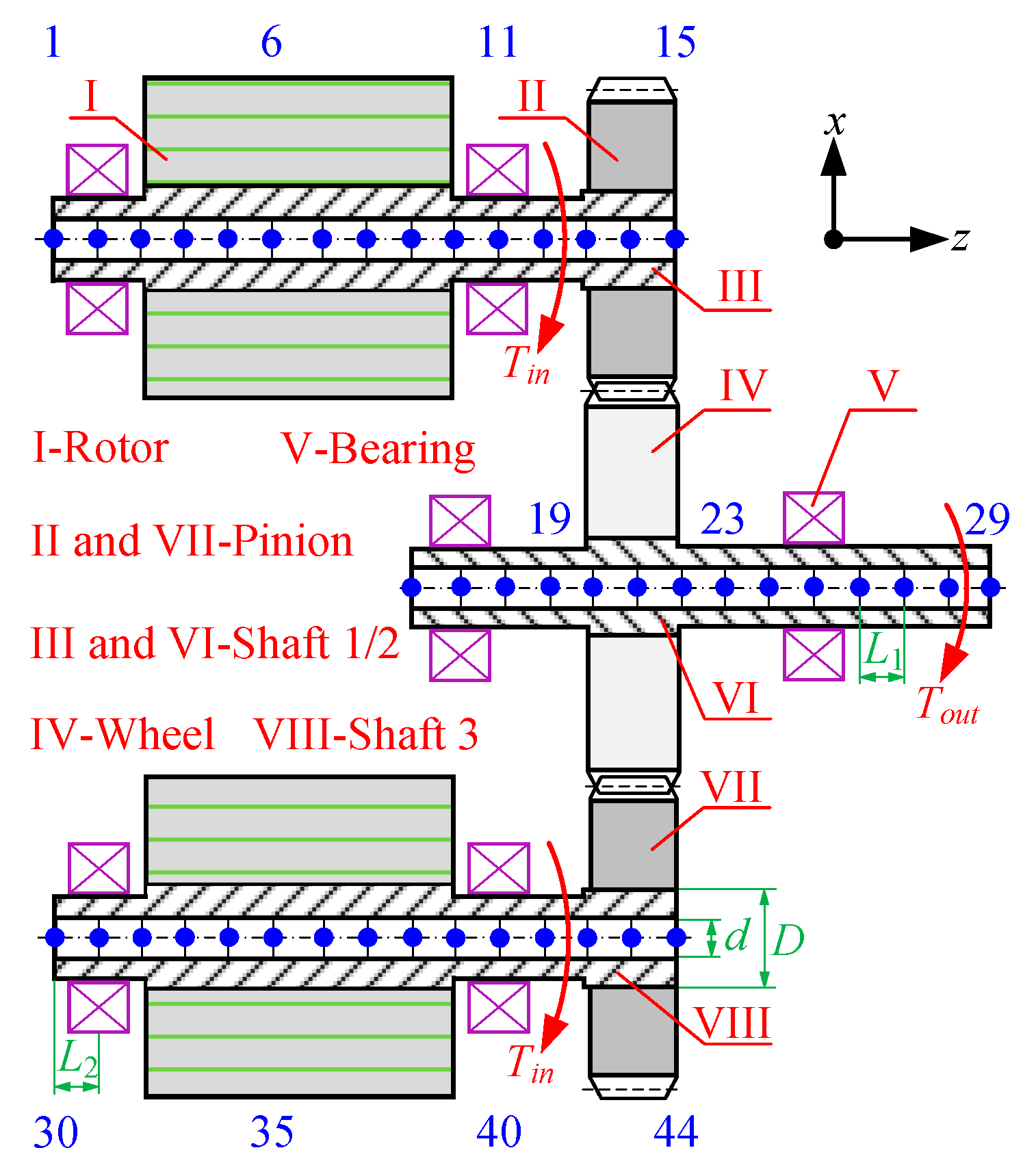
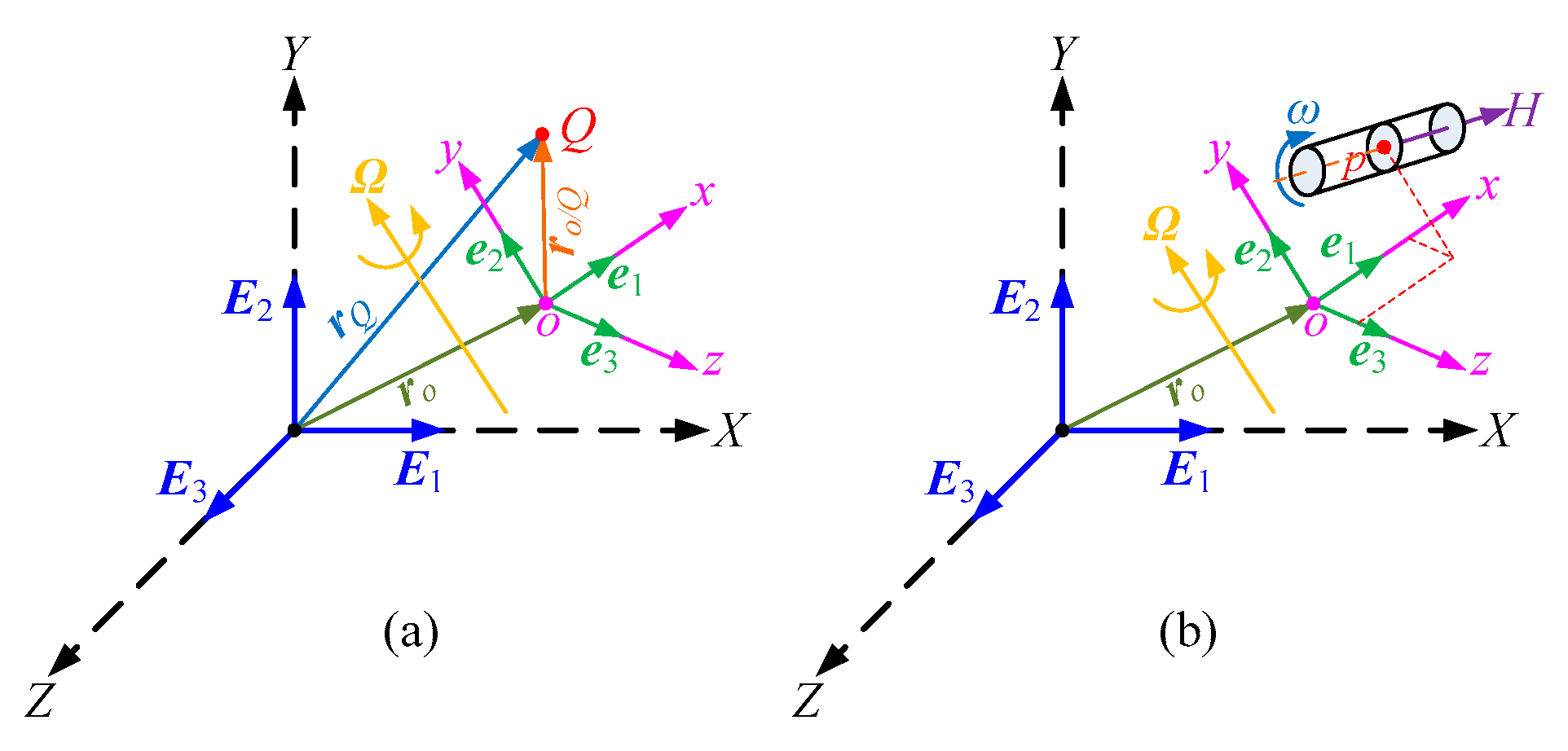
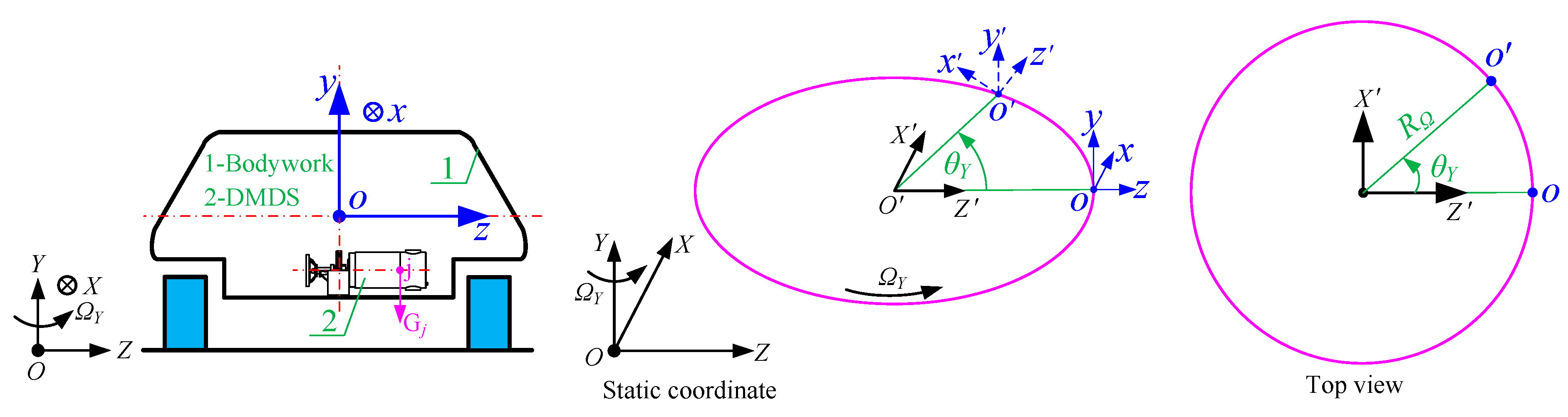
2. Dynamic Model of Dual-Motor Driving System in Non-Inertial System
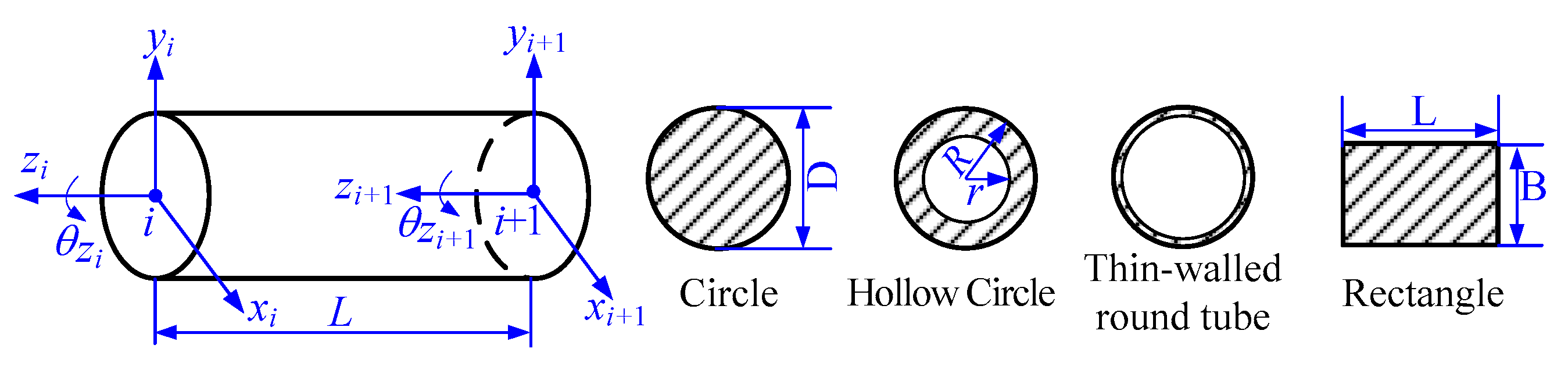
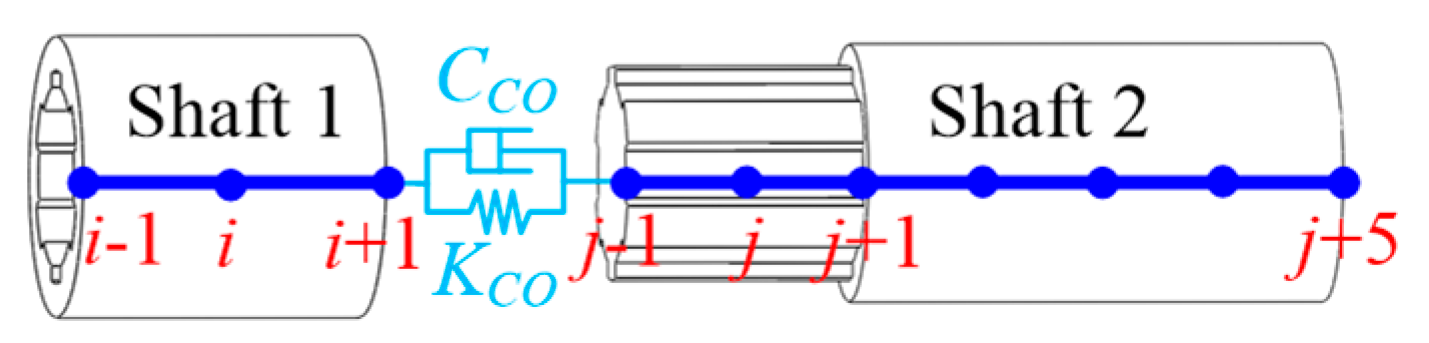
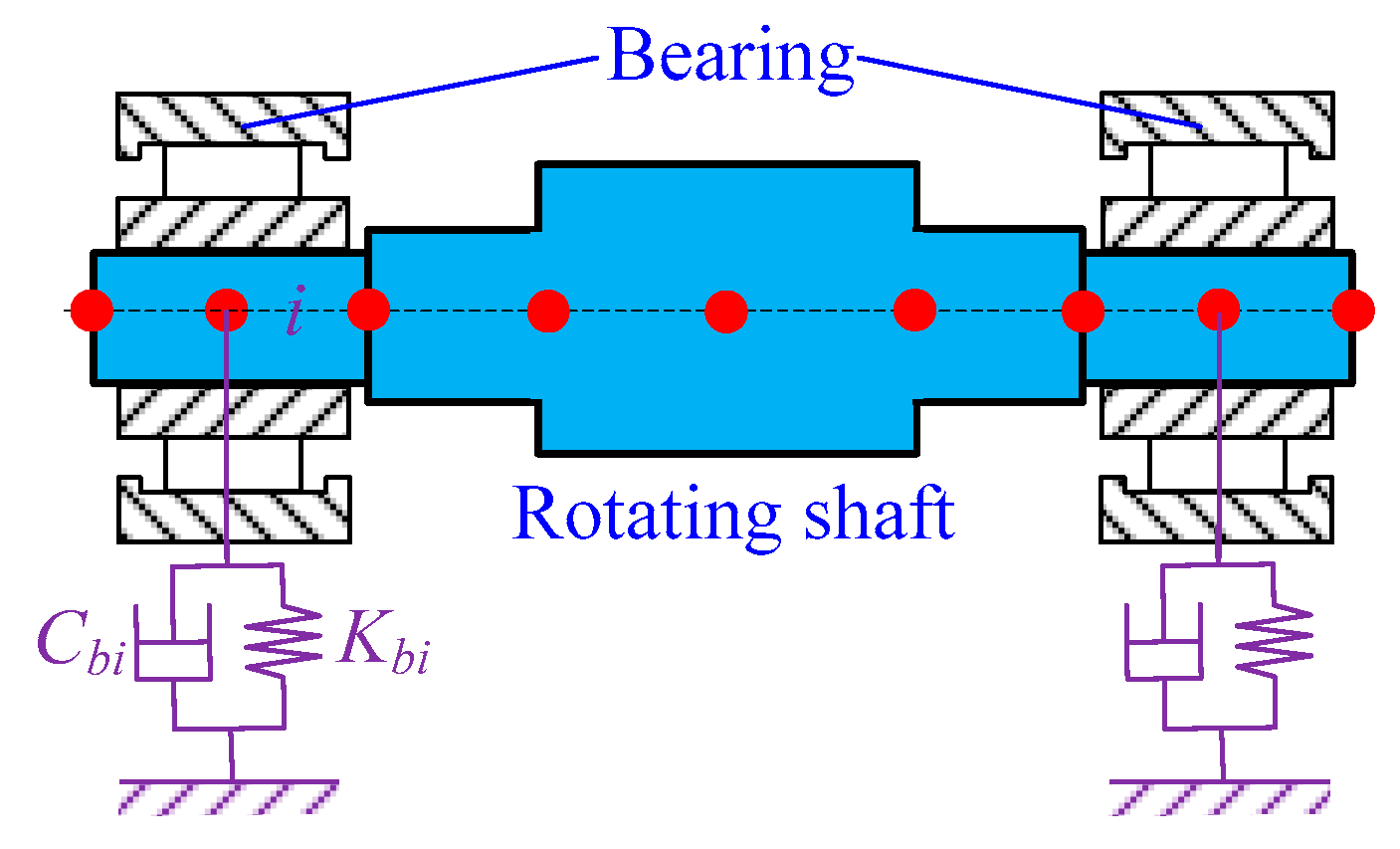
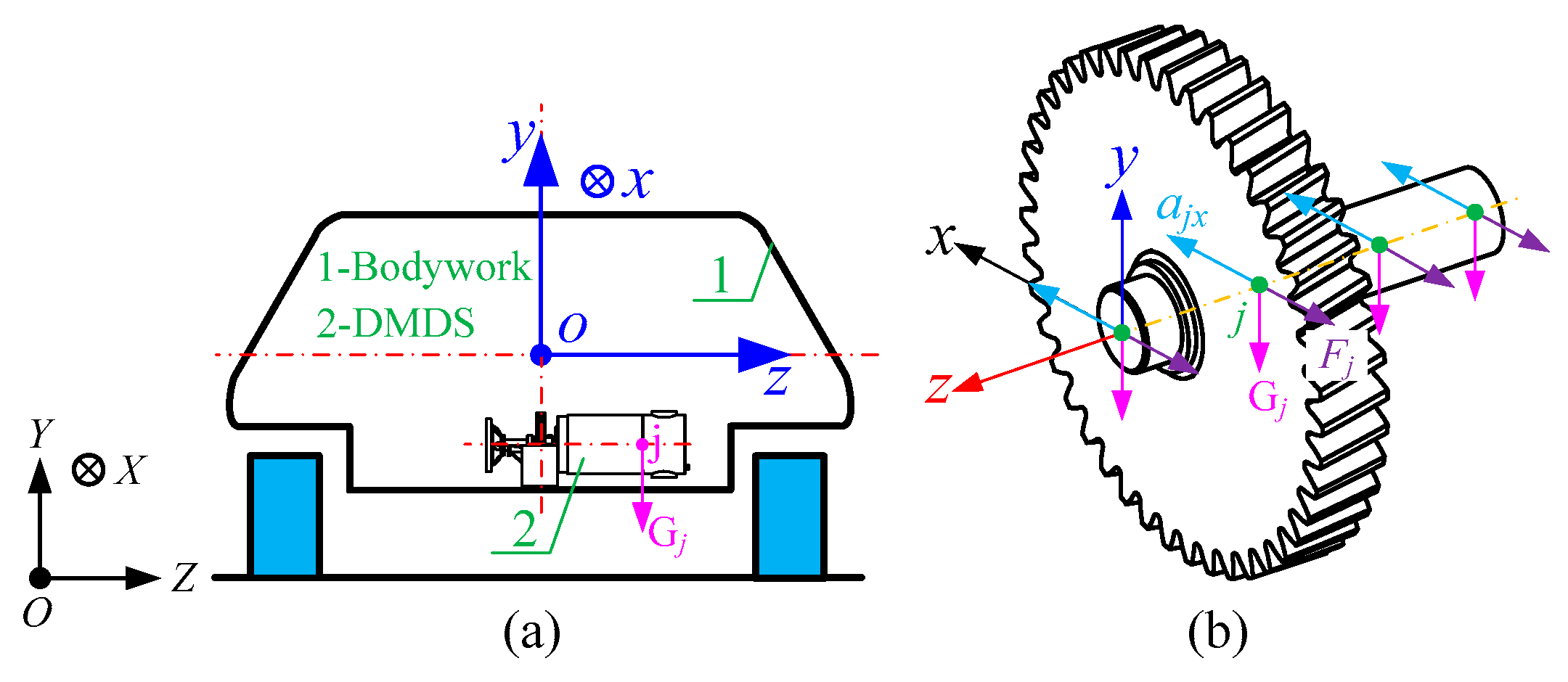
2.1. Dynamic Model of Basic Coupling Elements
2.2. Dynamic Model of Dual-Motor Driving System in Non-Inertial System
3. Dynamic Response and Synchronizing Characteristic Analysis in Non-Inertial System
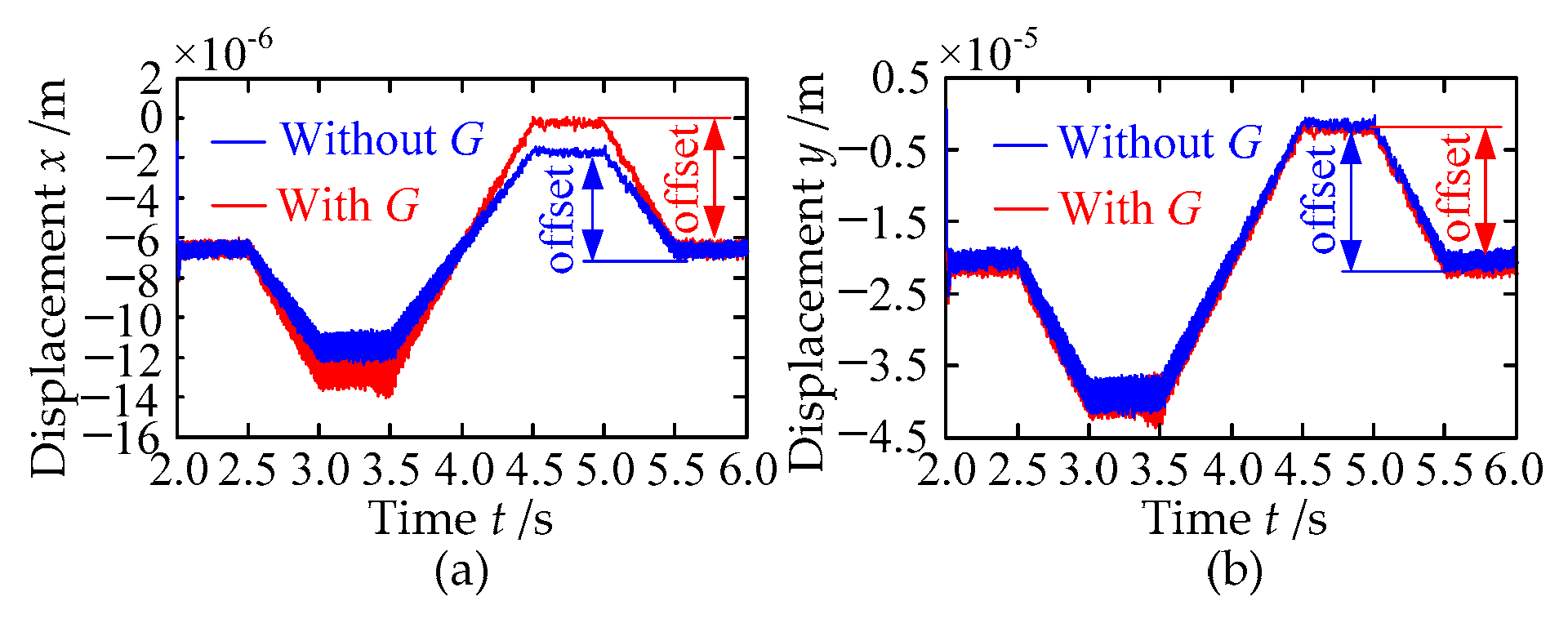
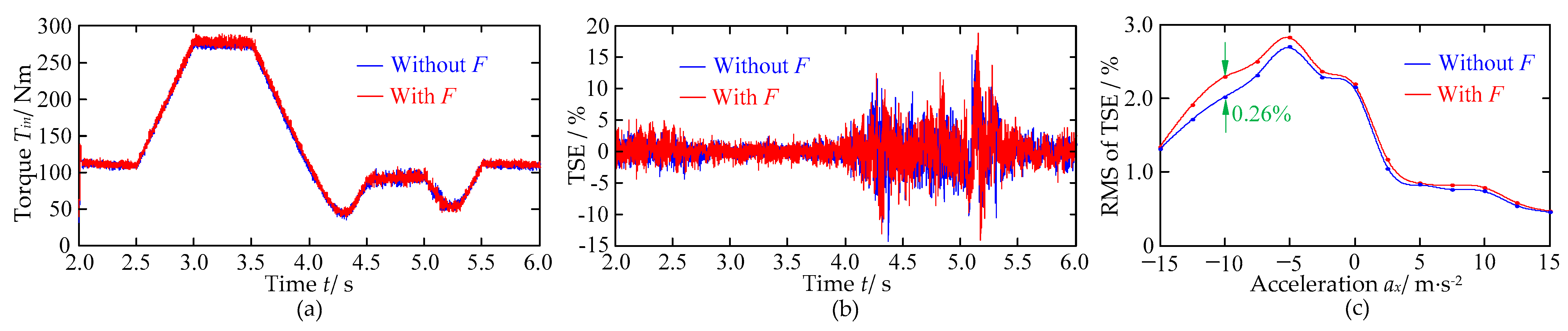
3.1. Case I: The NEVs Perform a Variable Speed Translational Motion
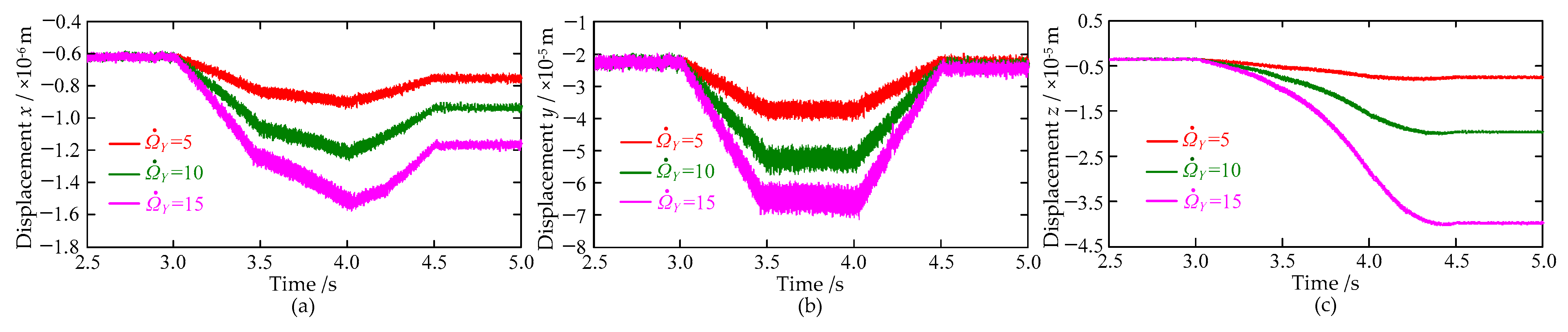
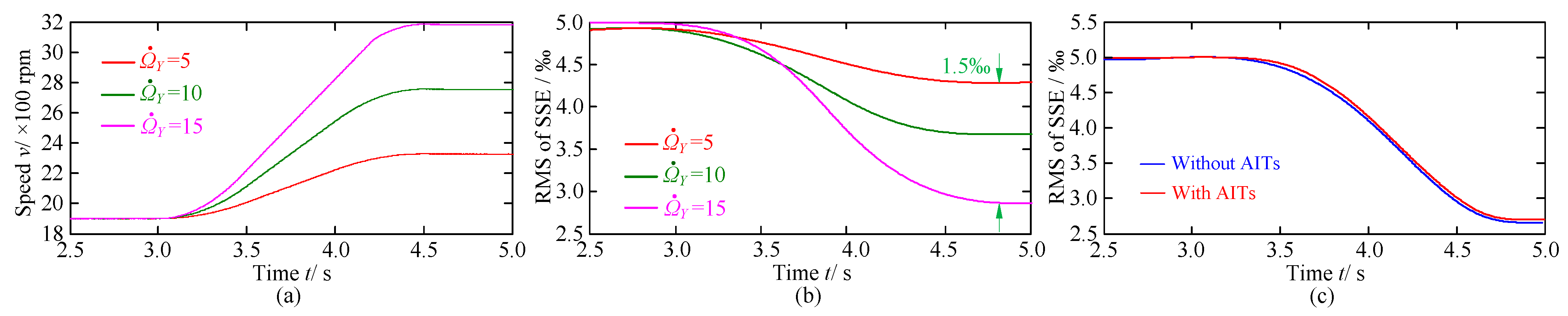
3.2. Case II: The NEVs Perform a Variable Speed Circular Motion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, H.; Zhang, J.; Wen, X. High Power Dual Motor Drive System Used in Fuel Cell Vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008. [Google Scholar]
- Tang, Y. Dual Motor Drive and Control System for an Electric Vehicle. U.S. Patent 8453770B2, 4 June 2013. [Google Scholar]
- Inalpolat, M.; Handschuh, M.; Kahraman, A. Influence of indexing errors on dynamic response of spur gear pairs. Mech. Syst. Signal Process. 2015, 60, 391–405. [Google Scholar] [CrossRef]
- Giagopulos, D.; Salpistis, C.; Natsiavas, S. Effect of non-linearities in the identification and fault detection of gear-pair systems. Int. J. Non-Linear Mech. 2006, 41, 213–230. [Google Scholar] [CrossRef]
- Setiawan, Y.D.; Roozegar, M.; Zou, T.; Angeles, J. A Mathematical Model of Multi-Speed Transmissions in Electric Vehicles in the Presence of Gear-Shifting. IEEE Trans. Veh. Technol. 2018, 67, 397–408. [Google Scholar] [CrossRef]
- Sun, W.; Ding, X.; Wei, J.; Wang, X.; Zhang, A. Hierarchical modeling method and dynamic characteristics of cutter head driving system in tunneling boring machine. Tunn. Undergr. Space Technol. 2016, 52, 99–110. [Google Scholar] [CrossRef]
- Liu, C.; Fang, Z.D.; Liu, X.; Hu, S.Y. Multibody dynamic analysis of a gear transmission system in electric vehicle using hybrid user-defined elements. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2018, 233, 30–42. [Google Scholar] [CrossRef]
- Tang, X.; Hu, X.; Yang, W.; Yu, H. Novel Torsional Vibration Modeling and Assessment of a Power-Split Hybrid Electric Vehicle Equipped with a Dual Mass Flywheel. IEEE Trans. Veh. Technol. 2018, 67, 1990–2000. [Google Scholar] [CrossRef]
- Zhang, Y.; Spanos, P.D. Efficient response determination of a M-D-O-F gear model subject to combined periodic and stochastic excitations. Int. J. Non-Linear Mech. 2019, 120, 103378. [Google Scholar] [CrossRef]
- Yan, H.S.; Wu, Y.C. A Novel Design of a Brushless DC Motor Integrated with an Embedded Planetary Gear Train. IEEE/ASME Trans. Mechatron. 2005, 11, 551–557. [Google Scholar] [CrossRef]
- Mashimo, T.; Urakubo, T.; Shimizu, Y. Micro Geared Ultrasonic Motor. IEEE/ASME Trans. Mechatron. 2018, 23, 781–787. [Google Scholar] [CrossRef]
- Kim, B.S.; Song, J.B.; Park, J.J. A Serial-Type Dual Actuator Unit With Planetary Gear Train: Basic Design and Applications. IEEE/ASME Trans. Mechatron. 2009, 15, 108–116. [Google Scholar]
- Lee, H.; Choi, Y. A New Actuator System Using Dual-Motors and a Planetary Gear. IEEE/ASME Trans. Mechatron. 2012, 17, 192–197. [Google Scholar] [CrossRef]
- Wei, J.; Shu, R.; Qin, D.; Lim, T.C.; Zhang, A.; Meng, F. Study of synchronization characteristics of a multi-source driving transmission system under an impact load. Int. J. Precis. Eng. Manuf. 2016, 17, 1157–1174. [Google Scholar] [CrossRef]
- Zhao, D.Z.; Li, C.W.; Ren, J. Speed synchronisation of multiple induction motors with adjacent cross-coupling control. Iet Control Theory Appl. 2009, 4, 119–128. [Google Scholar] [CrossRef]
- Xiong, H.; Zhang, M.; Zhang, R.; Zhu, X.; Yang, L.; Guo, X.; Cai, B. A new synchronous control method for dual motor electric vehicle based on cognitive-inspired and intelligent interaction. Future Gener. Comput. Syst. 2019, 94, 536–548. [Google Scholar] [CrossRef]
- Shi, T.; Liu, H.; Geng, Q.; Xia, C. Improved Relative Coupling Control Structure for Multi-motor Speed Synchronous Driving System. IET Electr. Power Appl. 2016, 10, 451–457. [Google Scholar]
- Yang, Y.; Li, M.; Hu, M.; Qin, D. Influence of controllable parameters on load sharing behavior of torque coupling gear set. Mech. Mach. Theory 2018, 121, 286–298. [Google Scholar] [CrossRef]
- Kahrobaiyan, M.H.; Asghari, M.; Ahmadian, M.T. A Timoshenko beam element based on the modified couple stress theory. Int. J. Mech. Sci. 2014, 79, 75–83. [Google Scholar] [CrossRef]
- Zhang, A.; Wei, J.; Qin, D.; Hou, S.; Lim, T.C. Coupled Dynamic Characteristics of Wind Turbine Gearbox Driven by Ring Gear Considering Gravity. J. Dyn. Syst. Meas. Control 2018, 140, 1–15. [Google Scholar] [CrossRef]
- Hu, Z.; Tang, J.; Zhong, J.; Chen, S. Frequency spectrum and vibration analysis of high speed gear-rotor system with tooth root crack considering transmission error excitation. Eng. Fail. Anal. 2016, 60, 405–441. [Google Scholar] [CrossRef]
- Lu, Z.; Sheng, H.; Hess, H.L.; Buck, K.M. The modeling and simulation of a permanent magnet synchronous motor with Direct Torque Control based on Matlab/Simulink. In Proceedings of the Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 1150–1156. [Google Scholar]
- Zhang, A.; Wei, J.; Shi, L.; Qin, D.; Lim, T.C. Modeling and dynamic response of parallel shaft gear transmission in non-inertial system. Nonlinear Dyn. 2019, 98, 997–1017. [Google Scholar] [CrossRef]












| Stator | Rotor | Unit | |
|---|---|---|---|
| Resistance | 8.296 × 10−3 | 7.11 × 10−2 | Ω |
| Rated speed | — | 2400 | rpm |
| Rated voltage | 540 | — | VDC |
| Leakage inductance | 5.05 × 10−5 | 5.05 × 10−5 | H |
| Rotational inertia | — | 8.86 × 10−1 | kg·m2 |
| Magnetizing inductance | 8.49 × 10−5 | 8.49 × 10−5 | H |
| Dimensions | φ380 × L399 | mm | |
| Mass | 130 | kg | |
| Rated power | 100 | kW | |
| Rated torque | 400 | Nm | |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Tooth number (pinion/wheel) | 23/69 | Length of shaft 1 (or 3) L1 (mm) | 32 |
| Module (mm) | 4 | Diameter of shaft 2 D/d (mm) | 65/45 |
| Width (mm) | 35 | Length of shaft 2 L2 (mm) | 20 |
| Pressure angle α (°) | 20 | Bearing translational stiffness (Nm−1) | kx = ky = 1.2 × 108; kz = 9.5 × 107 |
| Helix angle β (°) | 15 | Bearing torsional stiffness (Nm−1) | kθx = kθy = 1.0 × 107 |
| Diameter of shaft 1 (or 3) D/d (mm) | 60/45 | Transmission error amplitude (µm) | 20 |
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| Length (mm) | 4675 | High (mm) | 1500 | Front/rear track (mm) | 1525/1520 |
| Width (mm) | 1770 | Wheelbase (mm) | 2670 | Weight (kg) | 1531 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Shu, R.; Huang, J.; Fu, B.; Zou, Z.; Tan, R. Dynamic Response and Synchronizing Characteristic for the Dual-Motor Driving System in Non-Inertial System. Machines 2022, 10, 620. https://doi.org/10.3390/machines10080620
Xie Z, Shu R, Huang J, Fu B, Zou Z, Tan R. Dynamic Response and Synchronizing Characteristic for the Dual-Motor Driving System in Non-Inertial System. Machines. 2022; 10(8):620. https://doi.org/10.3390/machines10080620
Chicago/Turabian StyleXie, Zhengqiu, Ruizhi Shu, Jin Huang, Benyuan Fu, Zheng Zou, and Rulong Tan. 2022. "Dynamic Response and Synchronizing Characteristic for the Dual-Motor Driving System in Non-Inertial System" Machines 10, no. 8: 620. https://doi.org/10.3390/machines10080620






