A Method for Measurement of Workpiece form Deviations Based on Machine Vision
Abstract
:1. Introduction
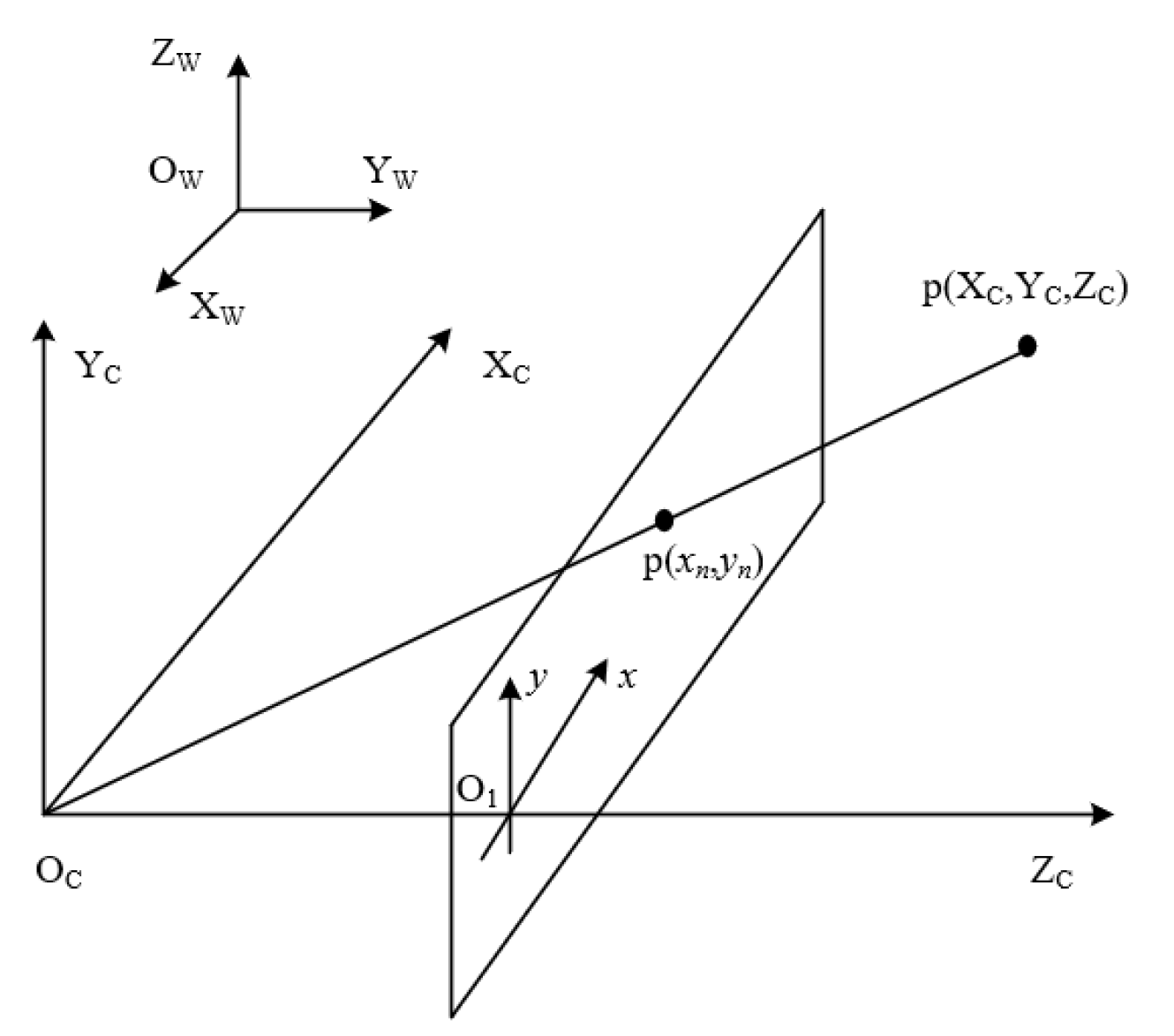
2. Image Acquisition System and Camera Calibration
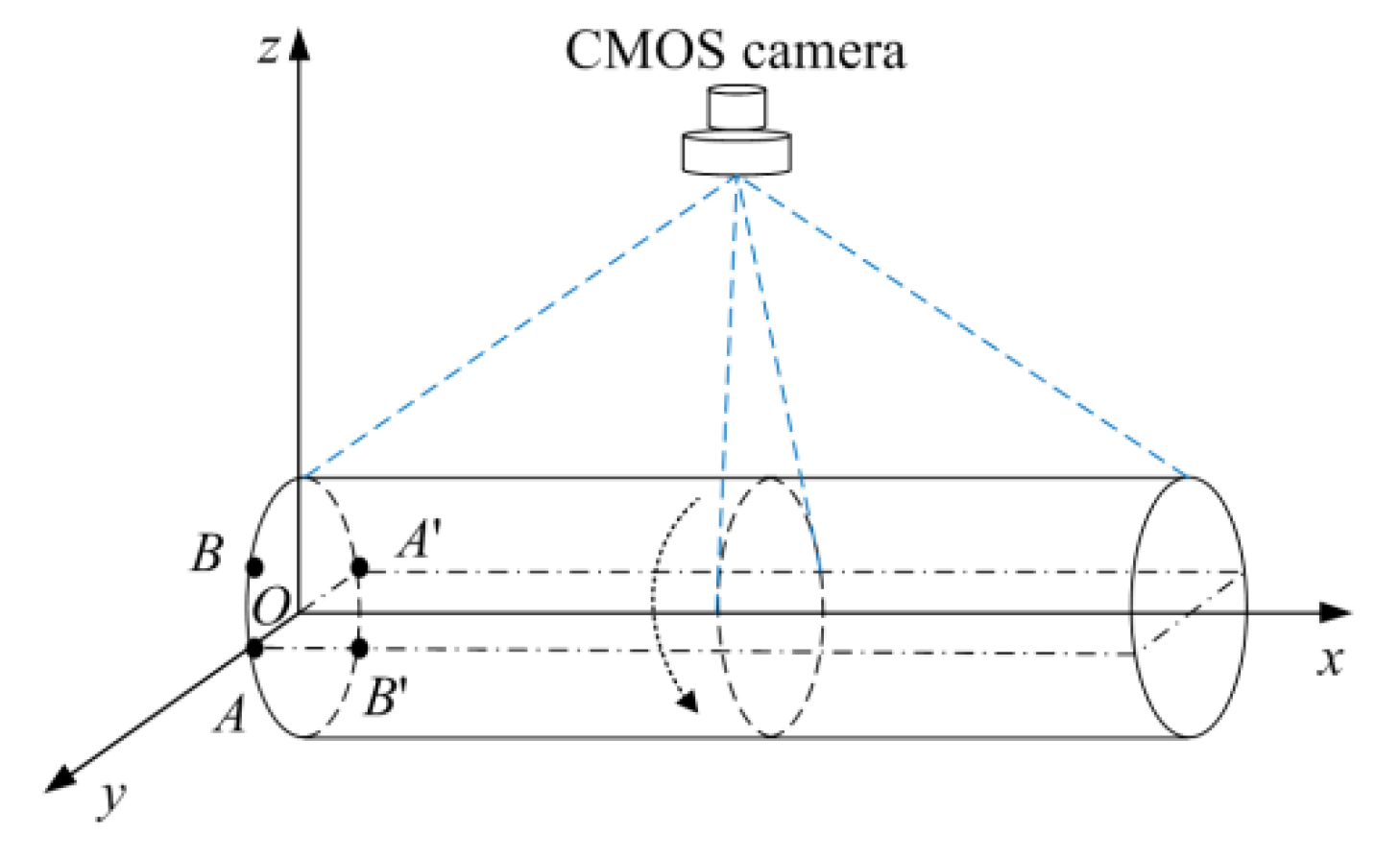
2.1. Composition of the Image Acquisition System
2.2. Camera Calibration
3. Main Algorithms
3.1. Image Correction
3.2. Sub-Pixel Edge Detection Algorithm
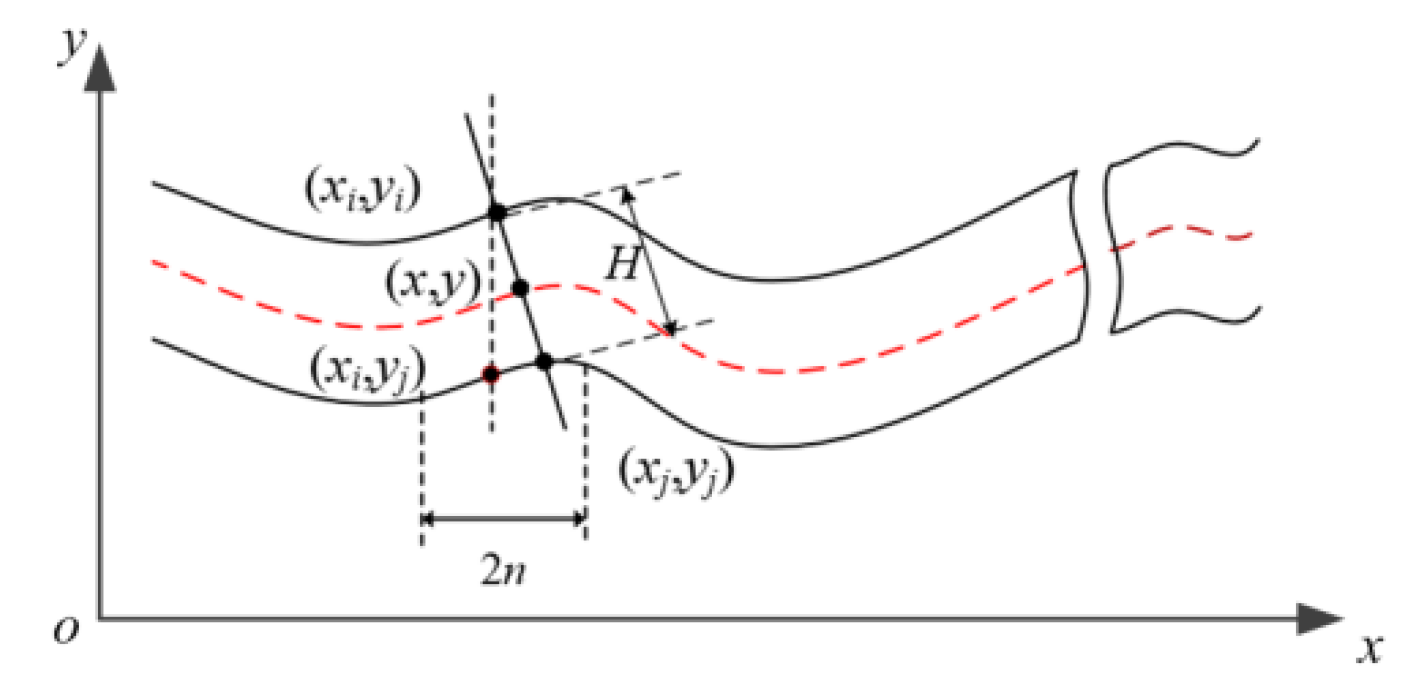
3.3. Calculation of Straightness Deviation
3.3.1. Axis of workpiece fitting
3.3.2. Straightness deviation algorithm
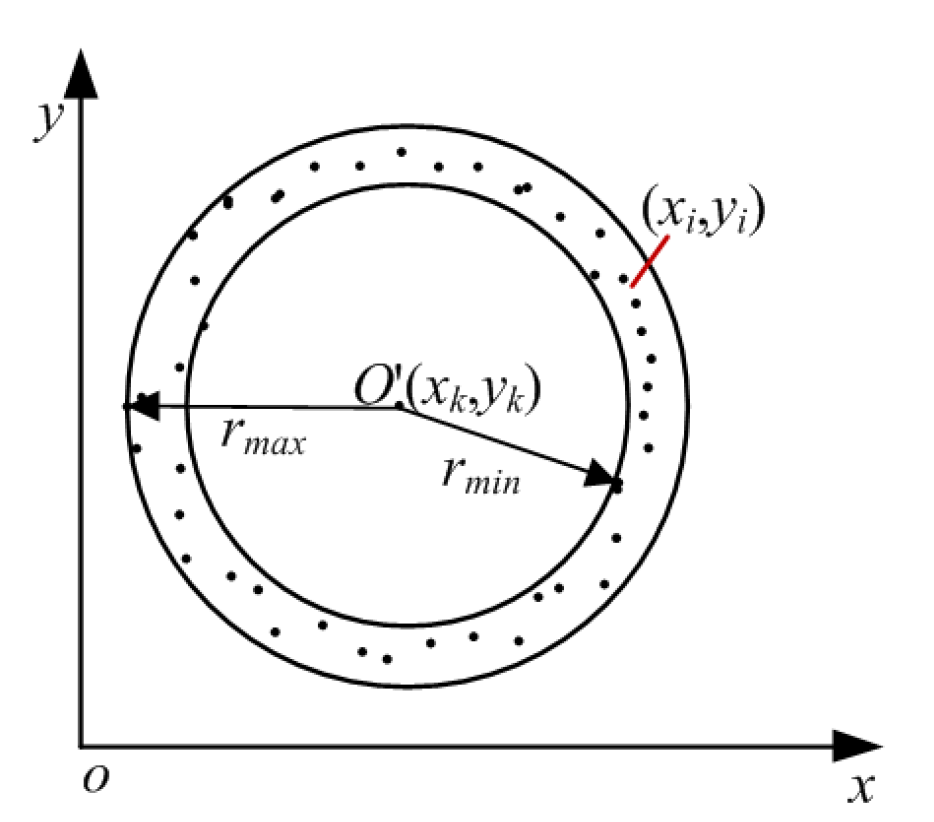
3.4. Calculation of Roundness Deviation
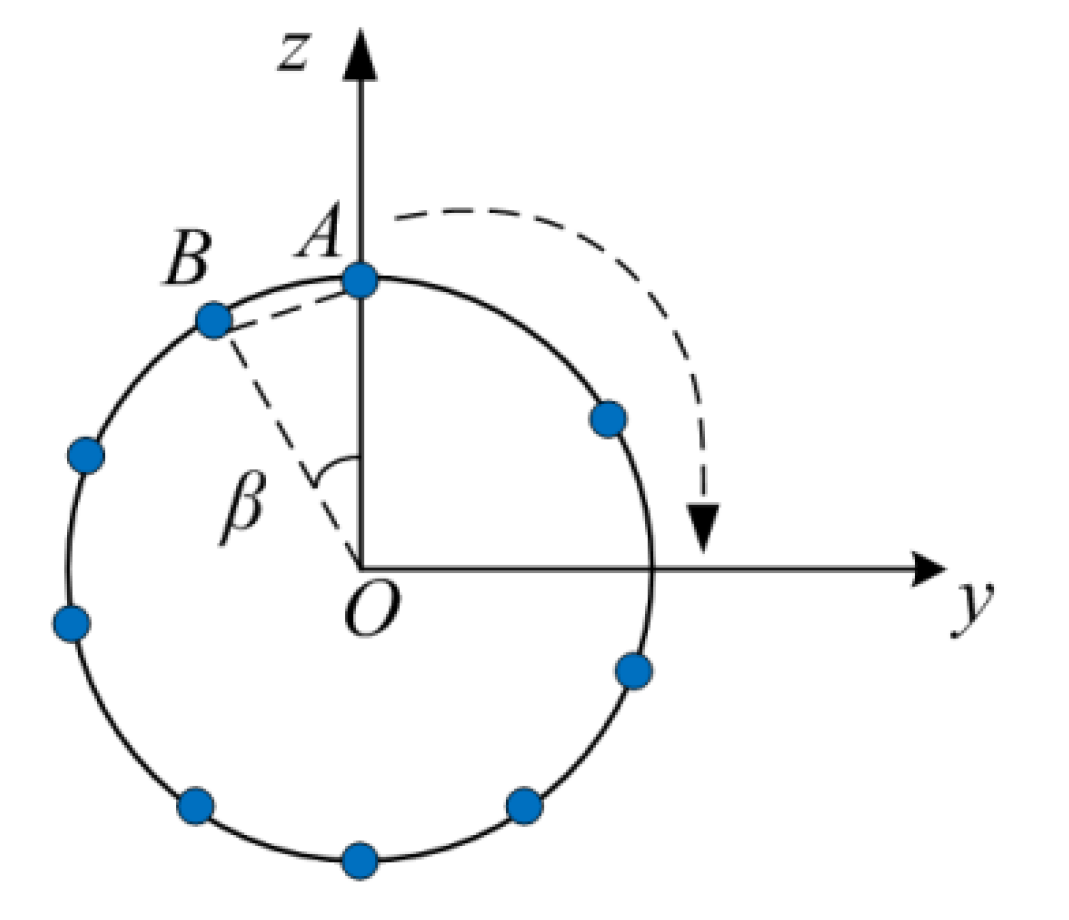
3.4.1. Three-Dimensional Reconstruction by Monocular Camera
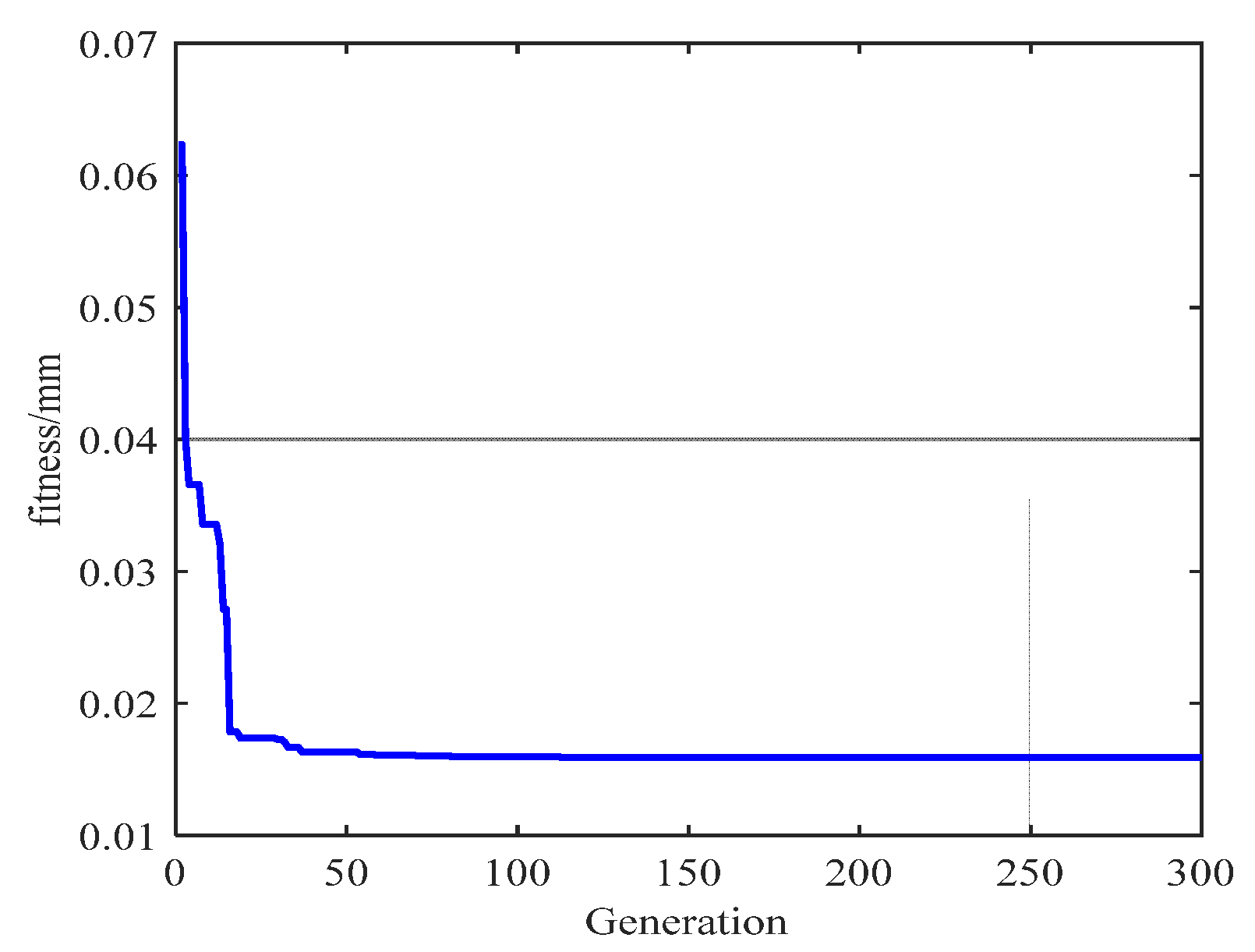
3.4.2. Roundness Deviation Algorithm
3.4.3. Cylindricity Deviation Algorithm
4. Experiment and Results Analysis
4.1. Calibration Results
4.2. Image Pre-Processing
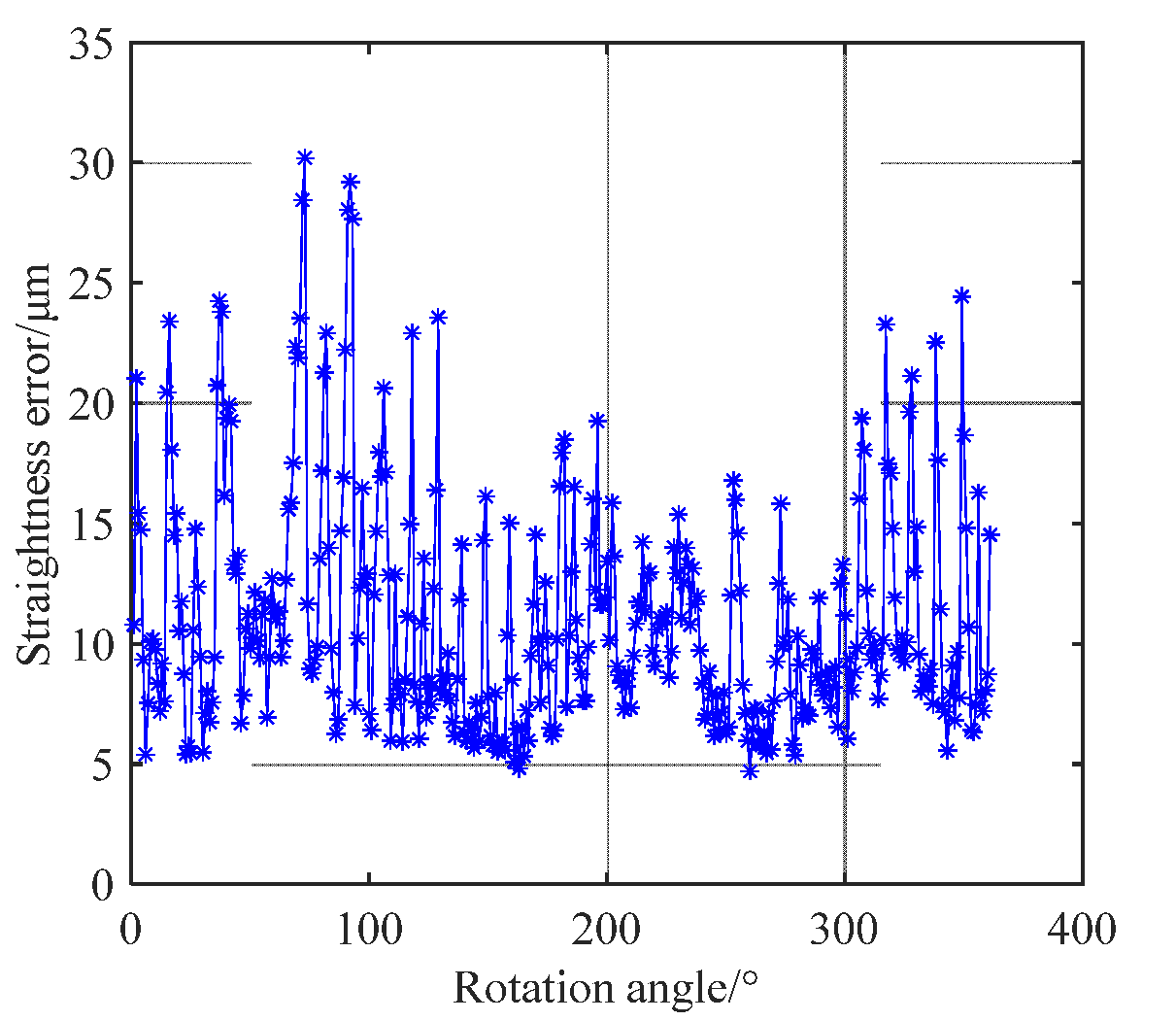
4.3. Straightness Deviation Results
4.4. Roundness Deviation Results
4.5. Cylindricity Deviation Results
4.6. Verification of Measurement Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, G.; Li, Y.; Xia, Q.; Cheng, X.; Chen, W. Research on the on-line dimensional accuracy measurement method of conical spun workpieces based on machine vision technology. Measurement 2019, 148, 106881. [Google Scholar] [CrossRef]
- Derganc, J.; Likar, B.; Pernuš, F. A machine vision system for measuring the eccentricity of bearings. Comput. Ind. 2003, 50, 103–111. [Google Scholar] [CrossRef]
- Kakaley, D.E.; Altieri, R.E.; Buckner, G.D. Non-contacting measurement of torque and axial translation in high-speed rotating shafts. Mech. Syst. Signal Process. 2020, 138, 106520. [Google Scholar] [CrossRef]
- Dong, C.Z.; Ye, X.W.; Jin, T. Identification of structural dynamic characteristics based on machine vision technology. Measurement 2018, 126, 405–416. [Google Scholar] [CrossRef]
- Lu, R.S.; Li, Y.F.; Yu, Q. On-line measurement of the straightness of seamless steel pipes using machine vision technique. Sens. Actuators A Phys. 2001, 94, 95–101. [Google Scholar] [CrossRef]
- Cho, S.; Kim, J.-Y.; Asfour, S.S. Machine learning-based algorithm for circularity analysis. Int. J. Inf. Decis. Sci. 2014, 6, 70–86. [Google Scholar] [CrossRef]
- Liu, W.; Li, X.; Jia, Z.; Li, H.; Ma, X.; Yan, H.; Ma, J. Binocular-vision-based error detection system and identification method for PIGEs of rotary axis in five-axis machine tool. Precis. Eng. 2018, 51, 208–222. [Google Scholar] [CrossRef]
- Tan, Q.; Kou, Y.; Miao, J.; Liu, S.; Chai, B. A Model of Diameter Measurement Based on the Machine Vision. Symmetry 2021, 13, 187. [Google Scholar] [CrossRef]
- Li, B. Research on geometric dimension measurement system of shaft parts based on machine vision. EURASIP J. Image Video Process. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Luo, J.; Liu, Z.; Zhang, P.; Liu, X.; Liu, Z. A method for axis straightness error evaluation based on improved differential evolution algorithm. Int. J. Adv. Manuf. Technol. 2020, 110, 413–425. [Google Scholar] [CrossRef]
- Hao, F.; Shi, J.; Meng, C.; Gao, H.; Zhu, S. Measuring straightness errors of slender shafts based on coded references and geometric constraints. J. Eng. 2020, 2020, 221–227. [Google Scholar] [CrossRef]
- Min, J. Measurement method of screw thread geometric error based on machine vision. Meas. Control. 2018, 51, 304–310. [Google Scholar] [CrossRef]
- Chai, Z.; Lu, Y.; Li, X.; Cai, G.; Tan, J.; Ye, Z. Non-contact measurement method of coaxiality for the compound gear shaft composed of bevel gear and spline. Measurement 2021, 168, 108453. [Google Scholar] [CrossRef]
- Zhengyou, Z. Camera calibration with one-dimensional objects. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 892–899. [Google Scholar] [CrossRef]
- Lv, Y.; Feng, J.; Li, Z.; Liu, W.; Cao, J. A new robust 2D camera calibration method using RANSAC. Optik 2015, 126, 4910–4915. [Google Scholar] [CrossRef]
- Bu, L.; Huo, H.; Liu, X.; Bu, F. Concentric circle grids for camera calibration with considering lens distortion. Opt. Lasers Eng. 2021, 140, 106527. [Google Scholar] [CrossRef]
- Bao, P.; Lei, Z.; Xiaolin, W. Canny edge detection enhancement by scale multiplication. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1485–1490. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, J.; Fu, G.; Poudel, U.P. High-accuracy edge detection with Blurred Edge Model. Image Vis. Comput. 2005, 23, 453–467. [Google Scholar] [CrossRef]
- Xie, X.; Ge, S.; Xie, M.; Hu, F.; Jiang, N. An improved industrial sub-pixel edge detection algorithm based on coarse and precise location. J. Ambient. Intell. Humaniz. Comput. 2019, 11, 2061–2070. [Google Scholar] [CrossRef]
- Sun, Q.; Hou, Y.; Tan, Q. A subpixel edge detection method based on an arctangent edge model. Optik 2016, 127, 5702–5710. [Google Scholar] [CrossRef]
- Li, C.-M.; Xu, G.-S. Sub-pixel Edge Detection Based on Polynomial Fitting for Line-Matrix CCD Image. In Proceedings of the 2009 Second International Conference on Information and Computing Science, Manchester, UK, 21–29 May 2009; pp. 262–264. [Google Scholar]
- Xu, X.; Xu, S.; Jin, L.; Song, E. Characteristic analysis of Otsu threshold and its applications. Pattern Recognit. Lett. 2011, 32, 956–961. [Google Scholar] [CrossRef]
- ISO 1101; Geometrical Product Specification (GPS)—Geometrical Tolerancing—Tolerances of Form, Orientation, Location and Run-Out. ISO: Geneva, Switzerland, 2017.
- Henzold, G. Geometrical Dimensioning and Tolerancing for Design, Manufacturing and Inspection, 2nd ed.; Butterworth-Heinemann: Oxford, UK; Elsevier: Burlington, VT, USA, 2006. [Google Scholar]
- Pratheesh Kumar, M.R.; Prasanna Kumaar, P.; Kameshwaranath, R.; Thasarathan, R. Roundness error measurement using teaching learning based optimization algorithm and comparison with particle swarm optimization algorithm. Int. J. Data Netw. Sci. 2018, 2, 63–70. [Google Scholar] [CrossRef]
- Srinivasu, D.S.; Venkaiah, N. Minimum zone evaluation of roundness using hybrid global search approach. Int. J. Adv. Manuf. Technol. 2017, 92, 2743–2754. [Google Scholar] [CrossRef]
- Rossi, A.; Antonetti, M.; Barloscio, M.; Lanzetta, M. Fast genetic algorithm for roundness evaluation by the minimum zone tolerance (MZT) method. Measurement 2011, 44, 1243–1252. [Google Scholar] [CrossRef] [Green Version]
- Pathak, V.K.; Singh, A.K. Effective Form Error Assessment Using Improved Particle Swarm Optimization. Mapan 2017, 32, 279–292. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 1–38. [Google Scholar] [CrossRef] [Green Version]














| Computer | CMOS Camera | Lens | Light Source |
|---|---|---|---|
| ADLINK IPC-610 | DAHENG MER-2000-19U3C | Computer V1228-MPY | KOMA JS-LT-180-32 |
| Motorized Stage | Parameters | |||
|---|---|---|---|---|
| Travel Range (mm) | Resolution (µm) | Repeatability Positioning (µm) | ||
| X | KXL06200-C2-F | 200 | 0.2 | ±1 |
| Y, Z | KXG06030-C | 30 | 0.1 | ±1 |
| Rotating | KS401-40 | 360° | 0.003° | ±0.05° |
| Section Position | Roundness Deviation of Group A/μm | Roundness Deviation of Group B/μm |
|---|---|---|
| 1 | 15.89 | 14.53 |
| 2 | 14.90 | 14.91 |
| 3 | 13.83 | 13.77 |
| 4 | 13.24 | 13.68 |
| 5 | 12.82 | 13.25 |
| 6 | 13.05 | 12.86 |
| 7 | 12.36 | 13.71 |
| Average value | 13.73 | 13.82 |
| Average Value by RD602/μm | Average Value by the Designed Instrument/μm | Error/μm | |
|---|---|---|---|
| Straightness | 15.80 | 11.11 | −4.69 |
| Roundness | 9.95 | 13.82 | 3.87 |
| Cylindricity | 21.30 | 29.81 | 8.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Han, Z.; Li, Y.; Zheng, H.; Cheng, X. A Method for Measurement of Workpiece form Deviations Based on Machine Vision. Machines 2022, 10, 718. https://doi.org/10.3390/machines10080718
Zhang W, Han Z, Li Y, Zheng H, Cheng X. A Method for Measurement of Workpiece form Deviations Based on Machine Vision. Machines. 2022; 10(8):718. https://doi.org/10.3390/machines10080718
Chicago/Turabian StyleZhang, Wei, Zongwang Han, Yang Li, Hongyu Zheng, and Xiang Cheng. 2022. "A Method for Measurement of Workpiece form Deviations Based on Machine Vision" Machines 10, no. 8: 718. https://doi.org/10.3390/machines10080718
APA StyleZhang, W., Han, Z., Li, Y., Zheng, H., & Cheng, X. (2022). A Method for Measurement of Workpiece form Deviations Based on Machine Vision. Machines, 10(8), 718. https://doi.org/10.3390/machines10080718







