Integrated Impacts of Non-Ideal Factors on the Vibration Characteristics of Permanent Magnet Synchronous Motors for Electric Vehicles
Abstract
:1. Introduction
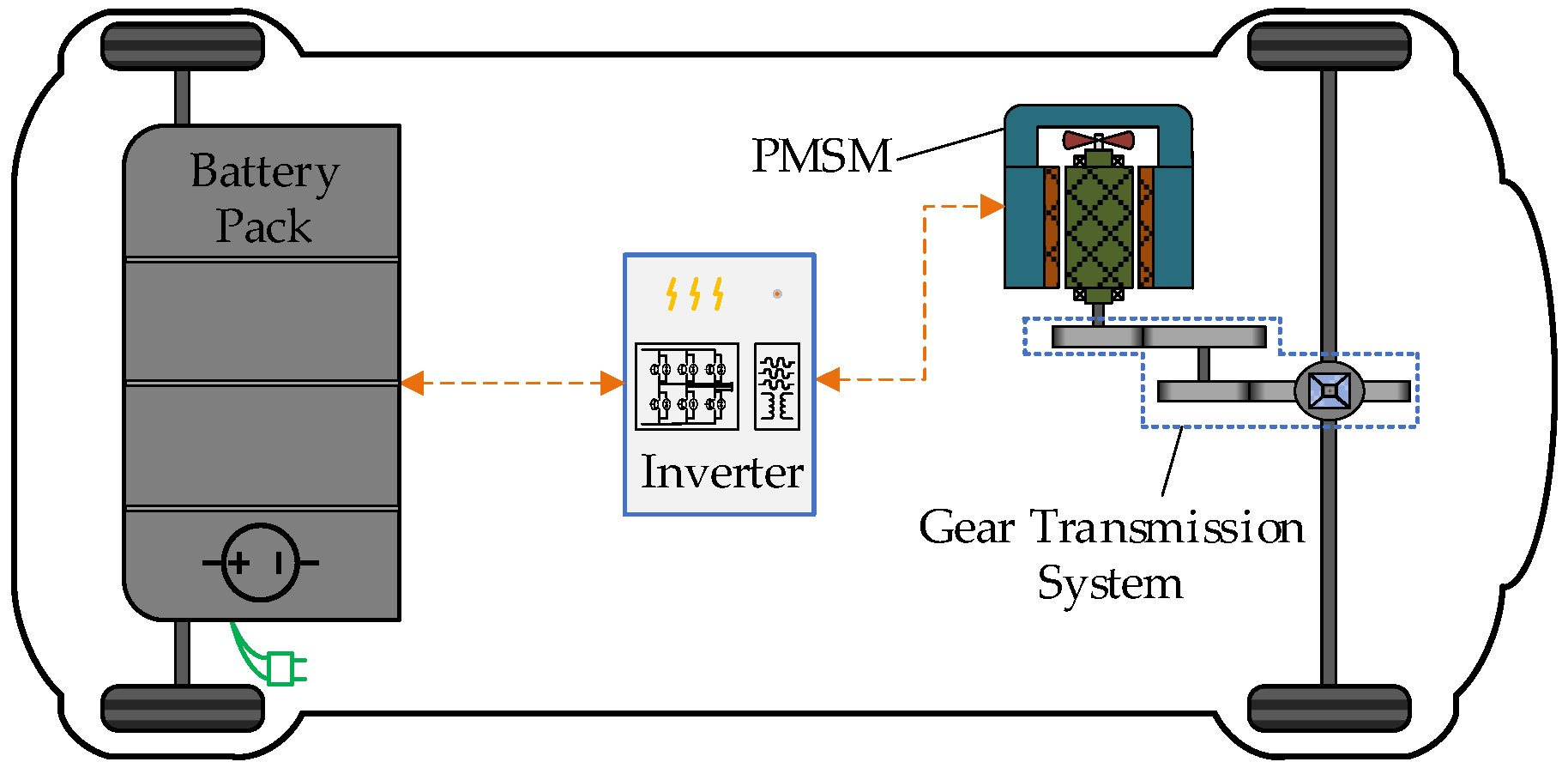
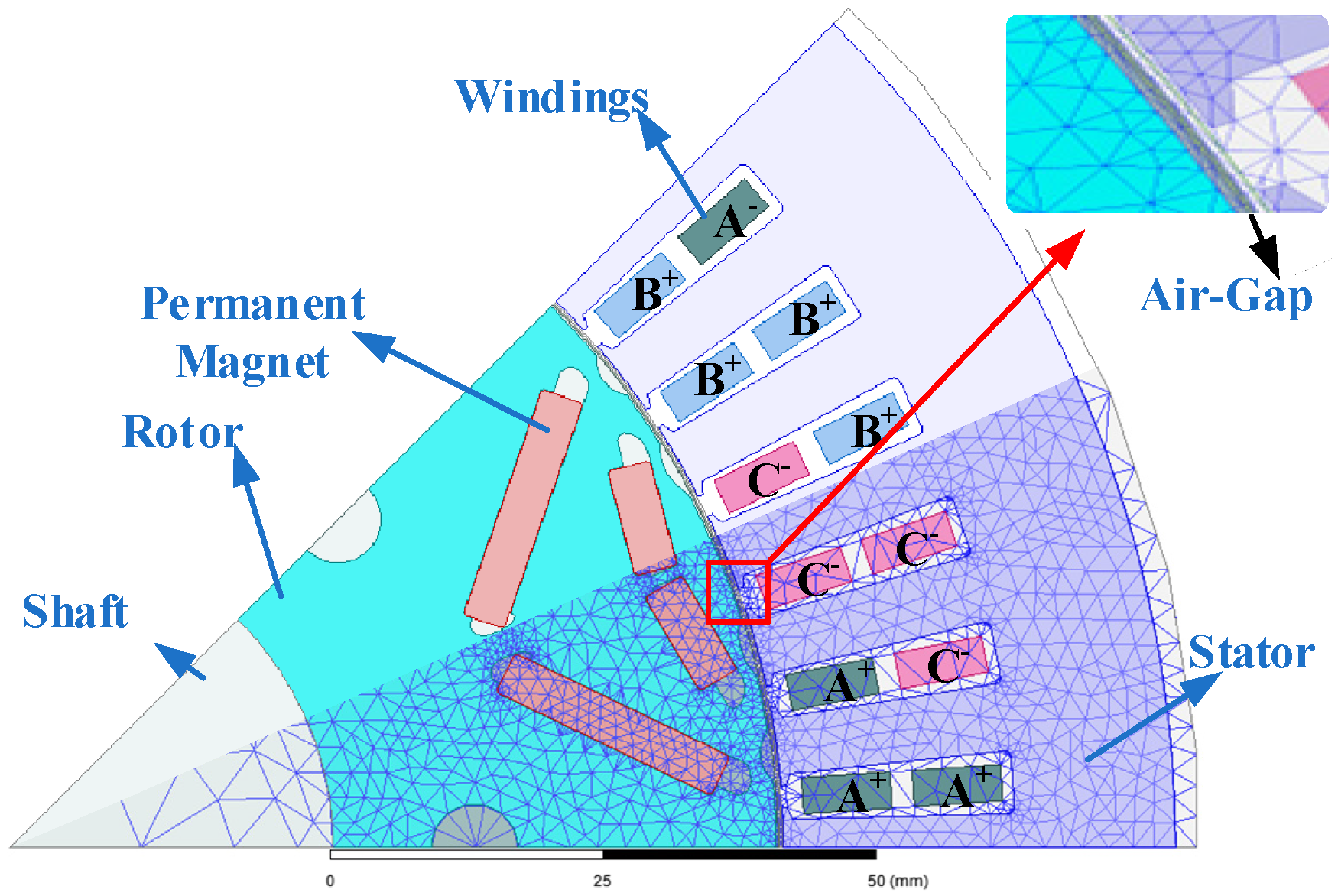
2. Two-Dimensional Electromagnetic Finite Element Model
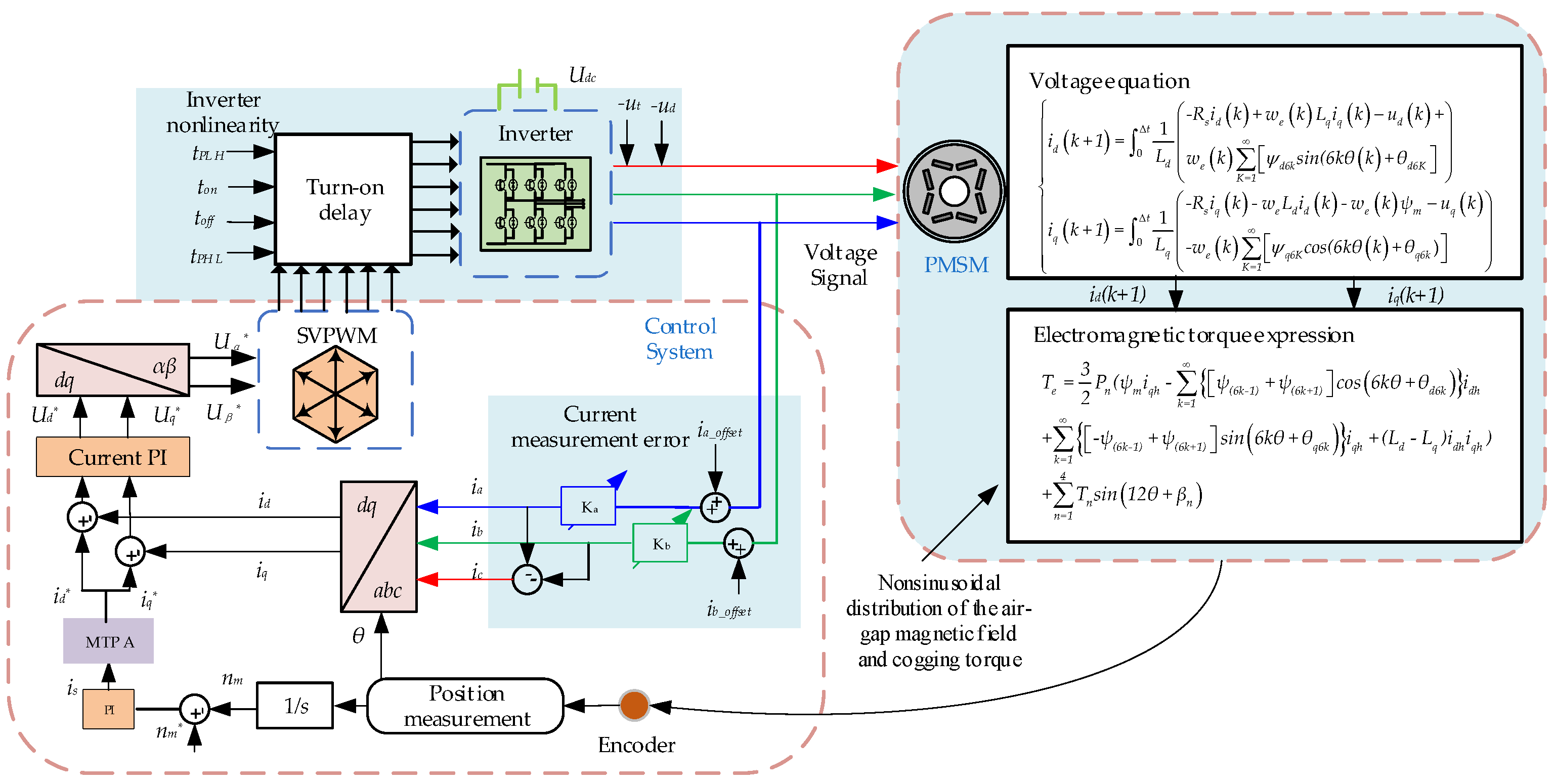
3. Mathematical Modeling of the PMSM and Control System of Electric Vehicles Considering Non-Ideal Factors
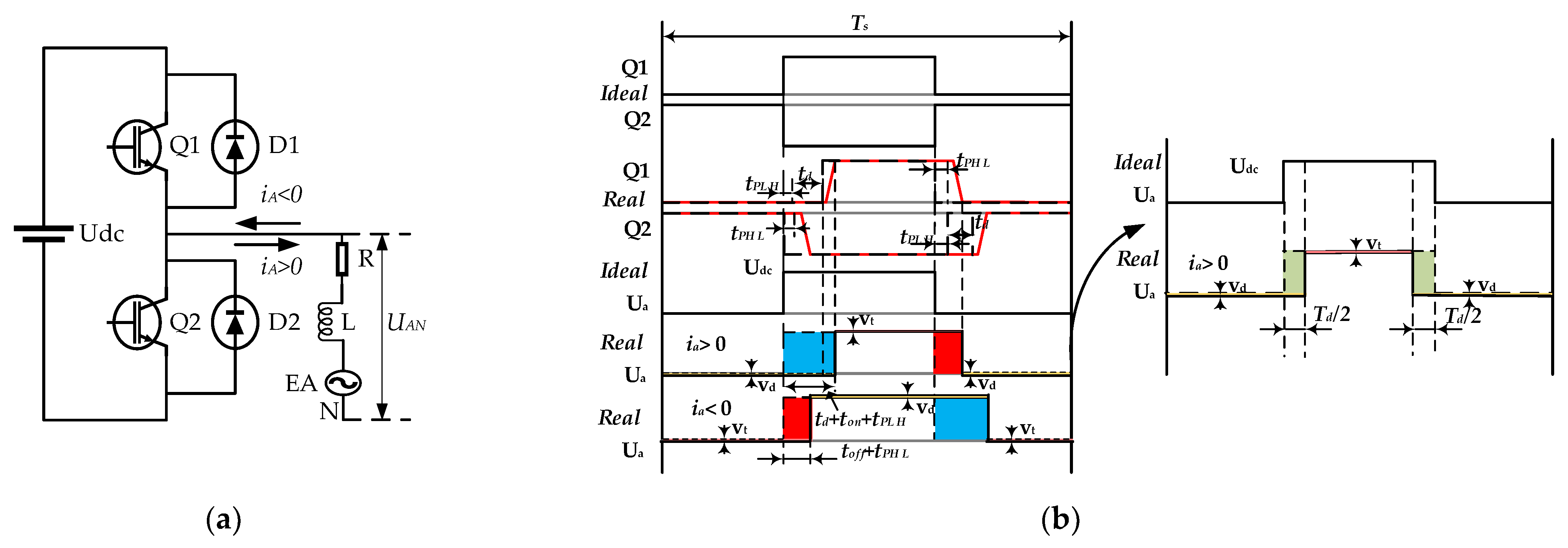
3.1. Mathematical Equations for the Nonlinear Characteristics of the Inverter
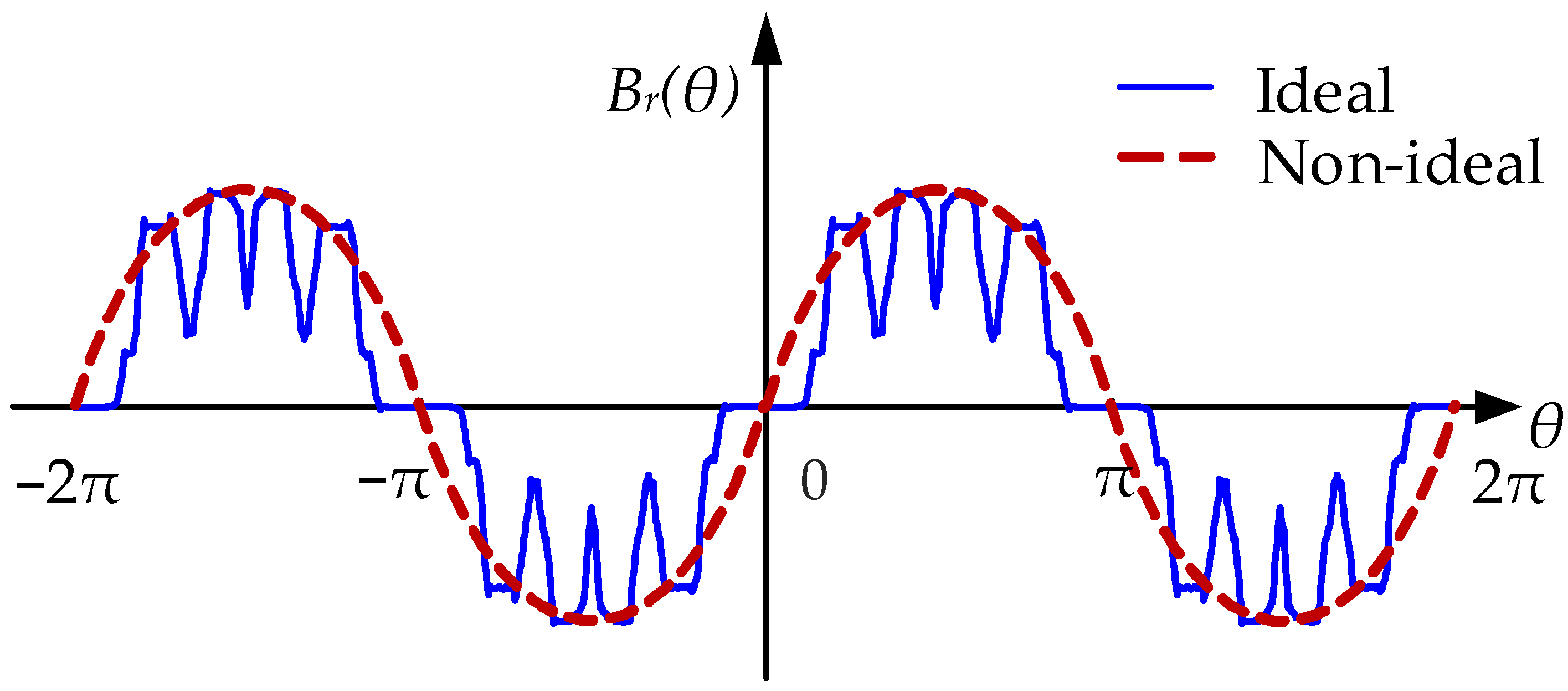
3.2. Mathematical Equations of the Nonsinusoidal Distribution of the Air-Gap Magnetic Field
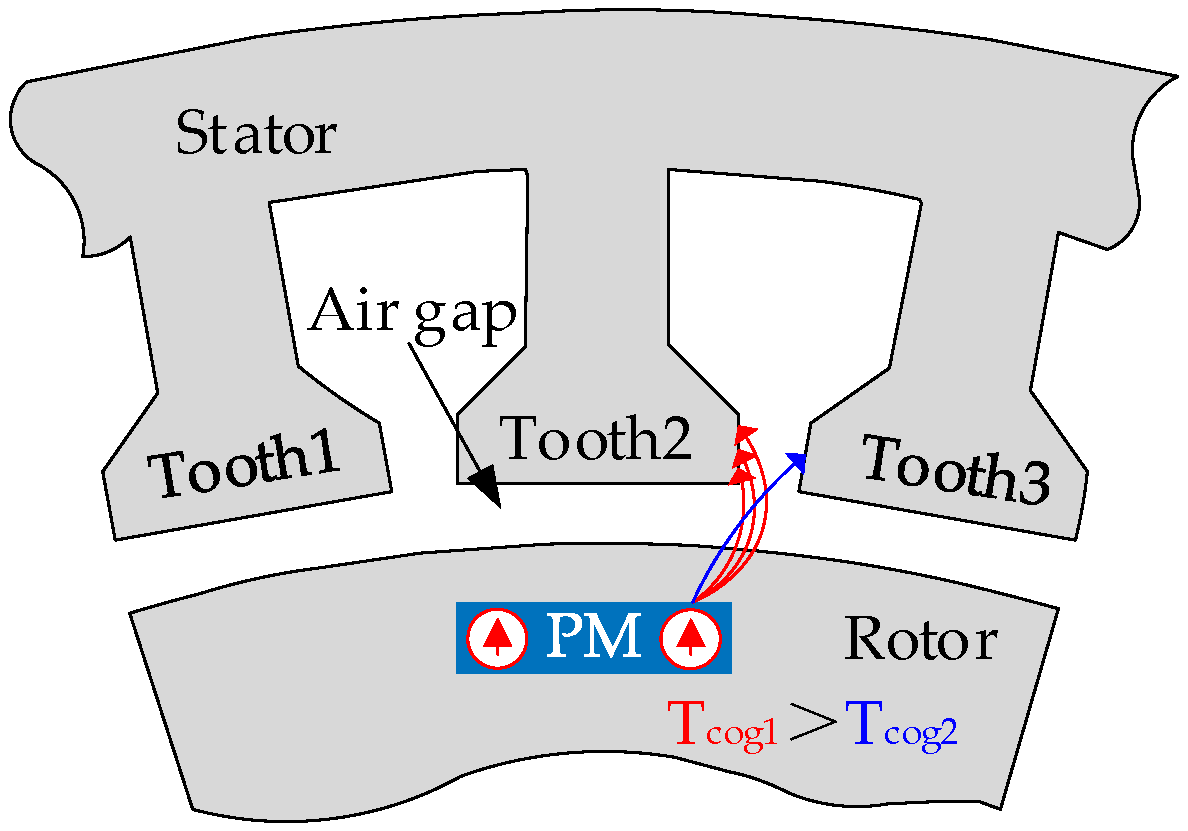
3.3. Mathematical Equation of the Cogging Torque
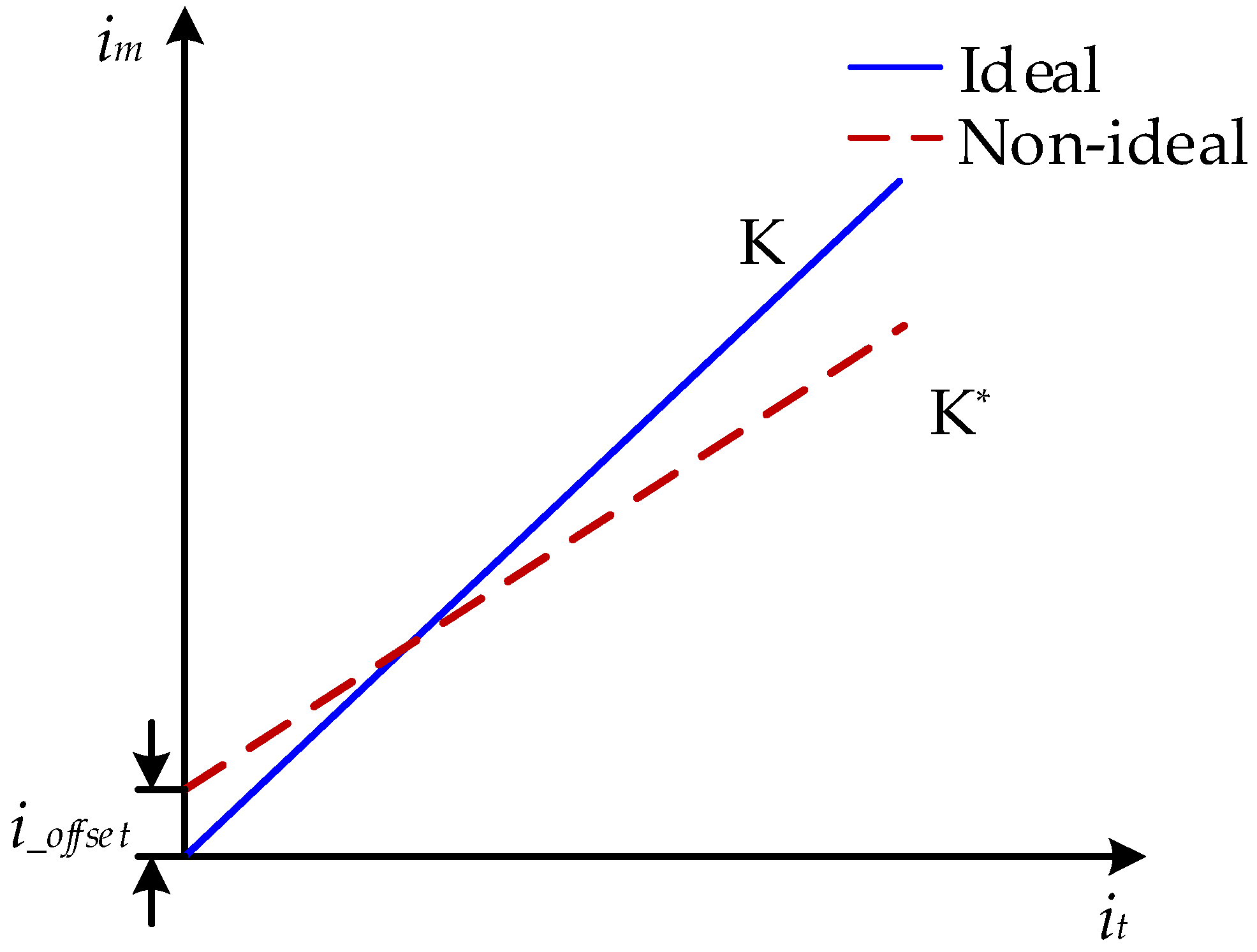
3.4. Mathematical Equations of the Current Measurement Error
3.5. Mathematical Model of the PMSM Considering Non-Ideal Factors
4. Simulation Analysis of the Dynamic Characteristics of the PMSM for Electric Vehicles under Different Speed–Load Conditions
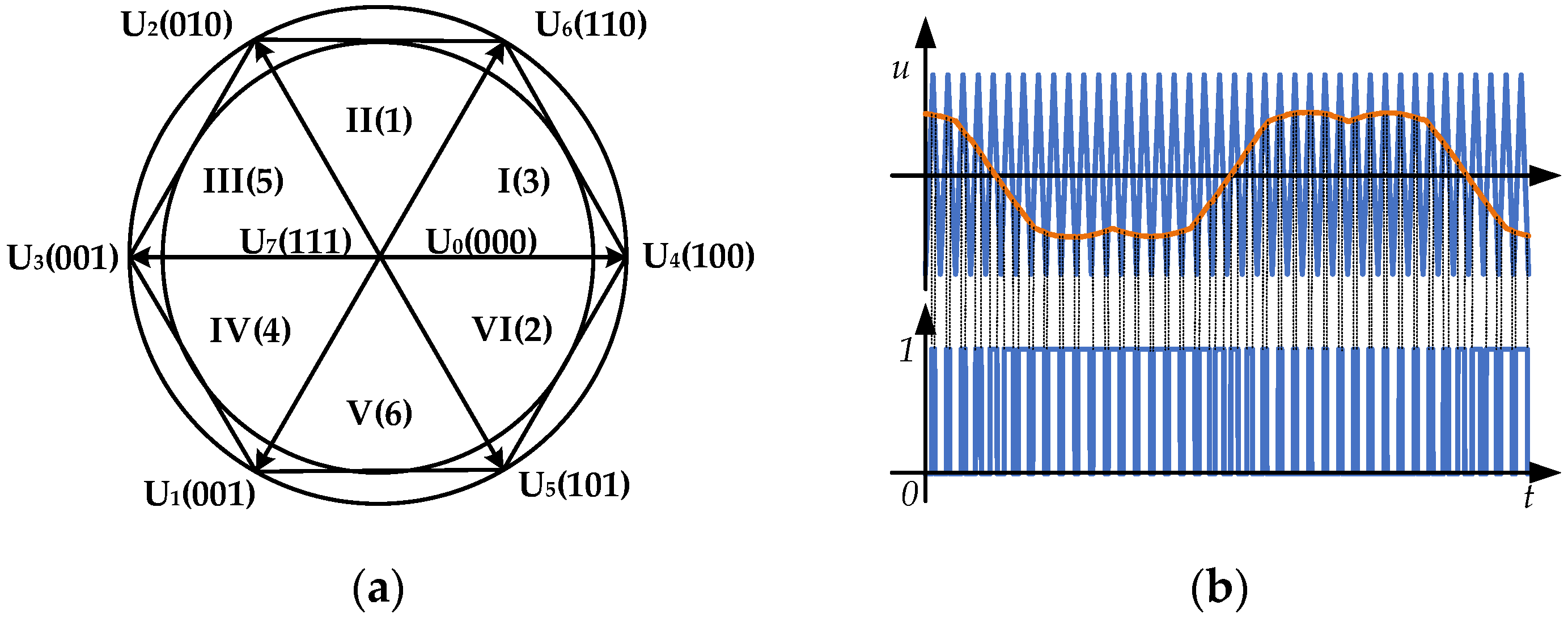
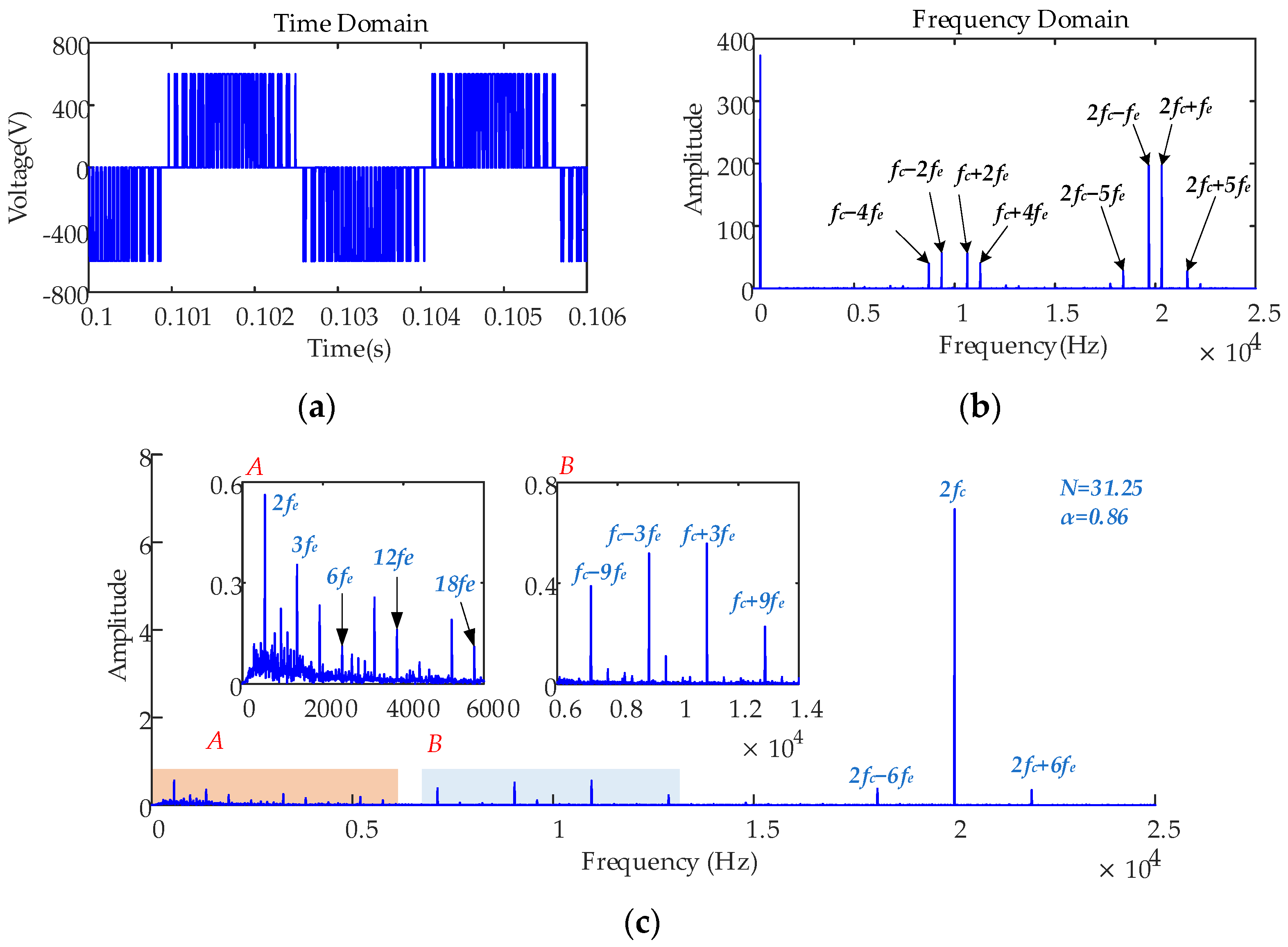
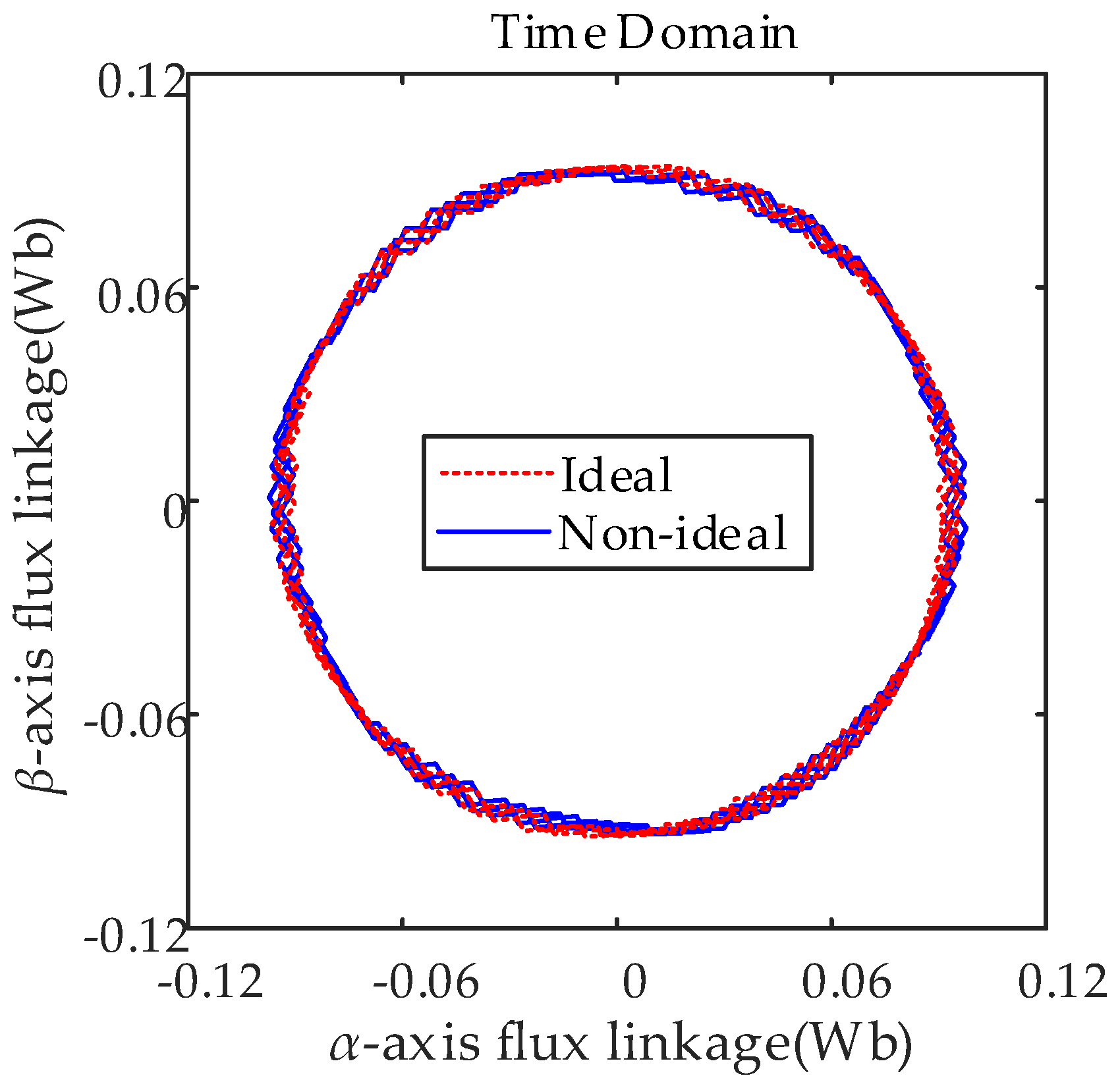
4.1. Influence of SVPWM on the PMSM
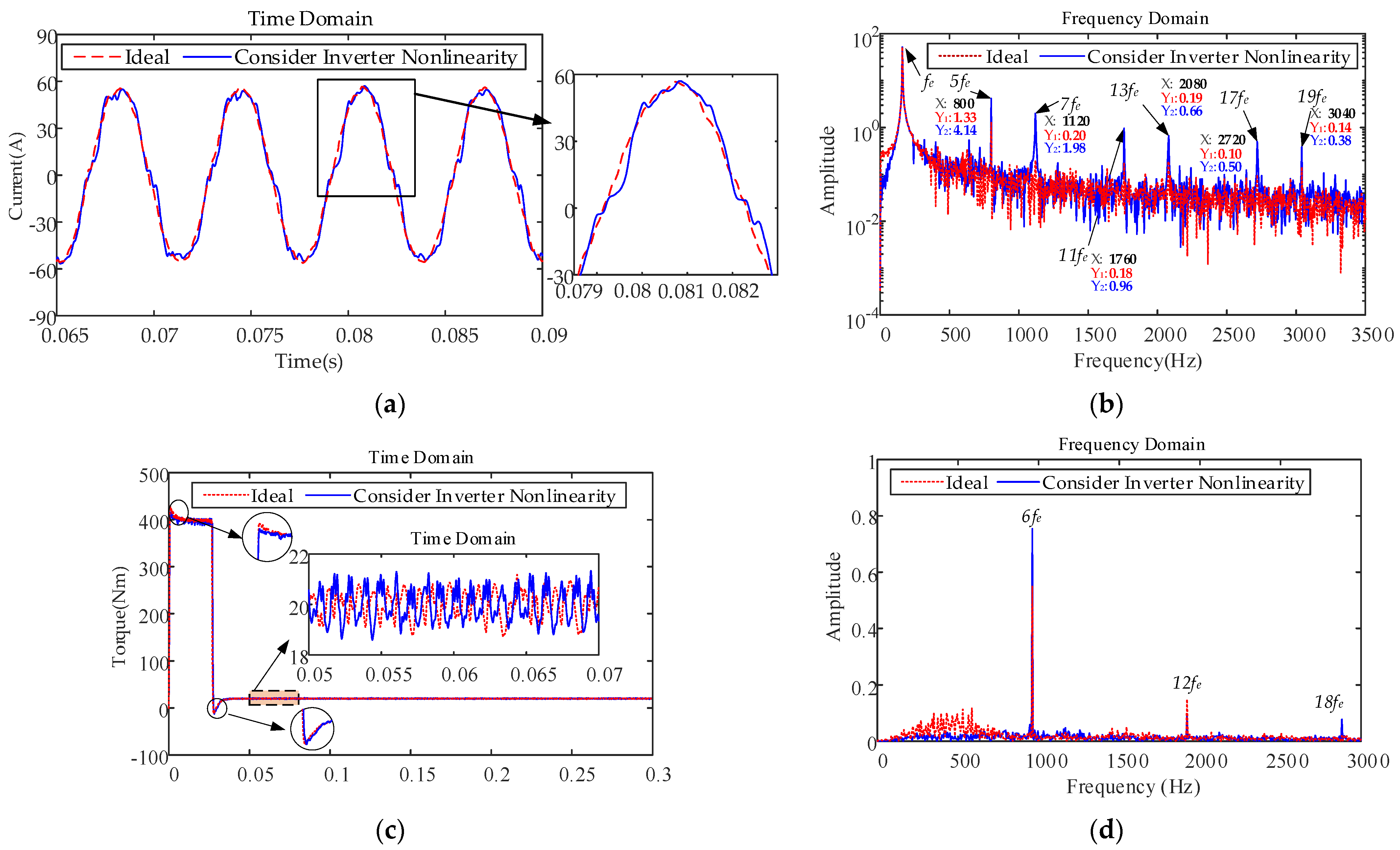
4.2. Consideration of the Nonlinear Characteristics of the Inverter
4.2.1. Constant Speed, Constant Load Condition
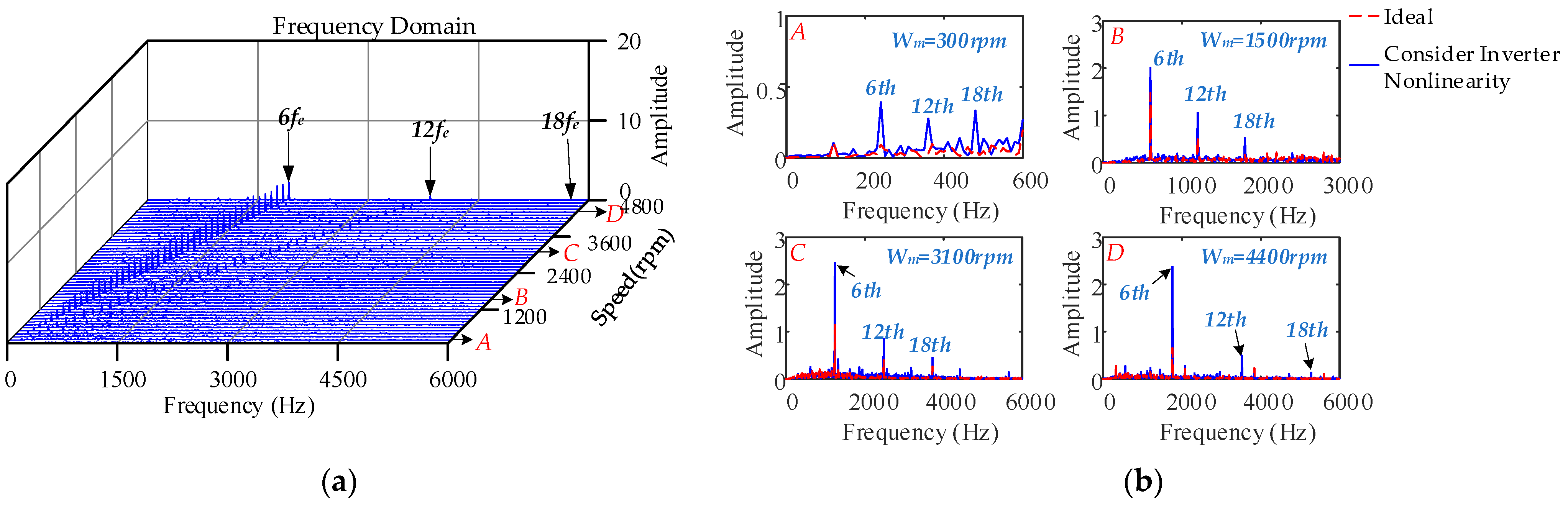
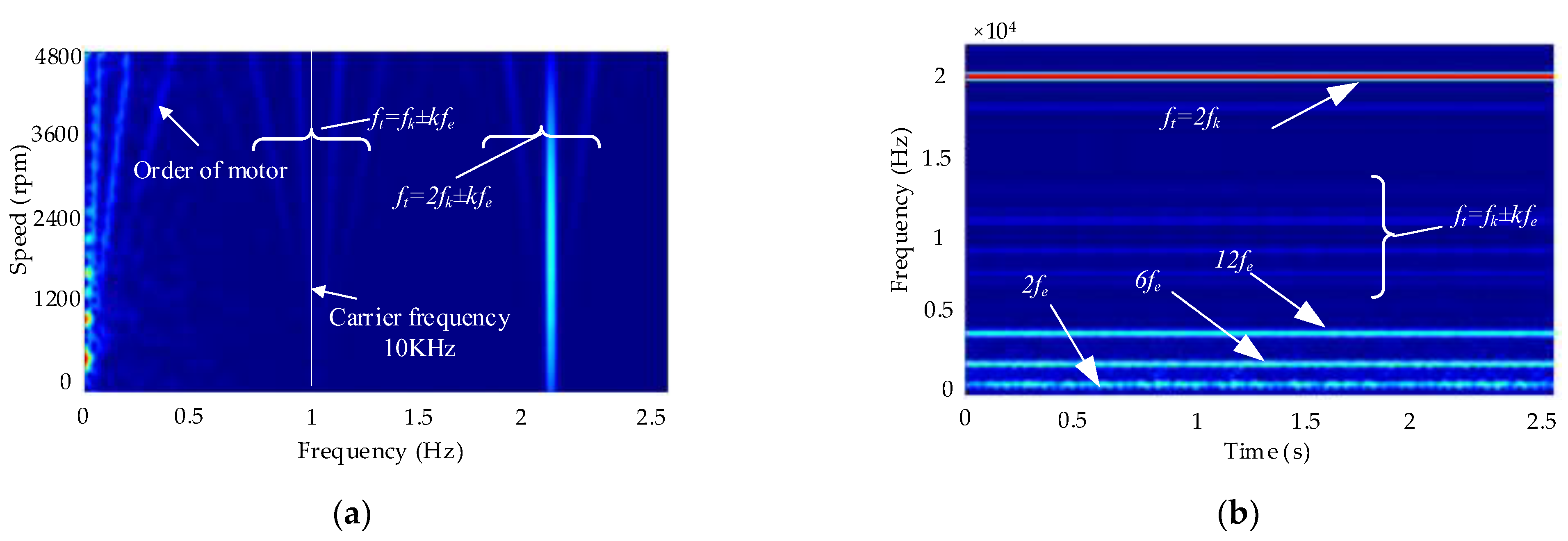
4.2.2. Different Speeds, Constant Load Condition
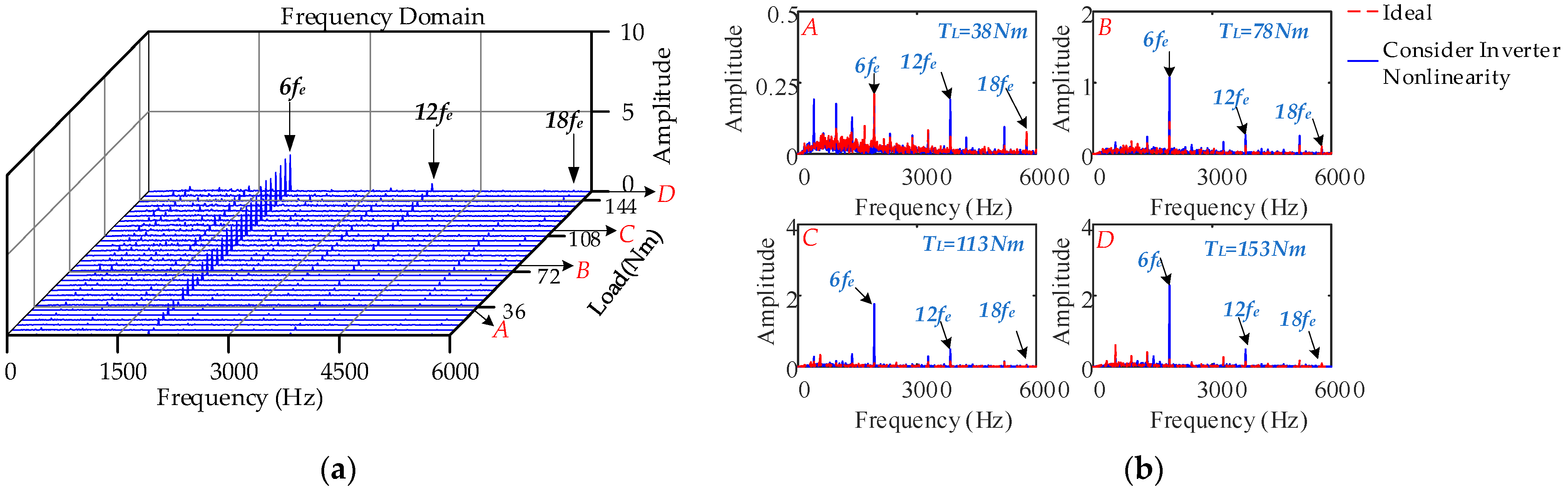
4.2.3. Different Loads, Constant Speed Condition
4.3. Consideration of the Nonsinusoidal Distribution of the Air-Gap Magnetic Field
4.3.1. Constant Speed, Constant Load Condition
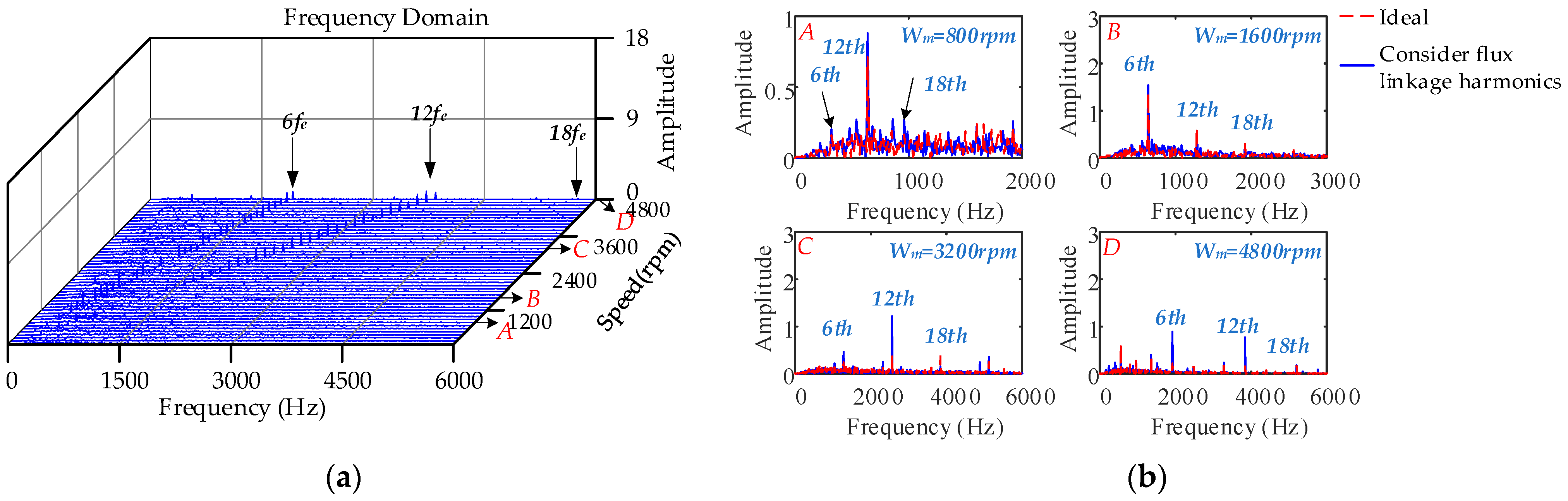
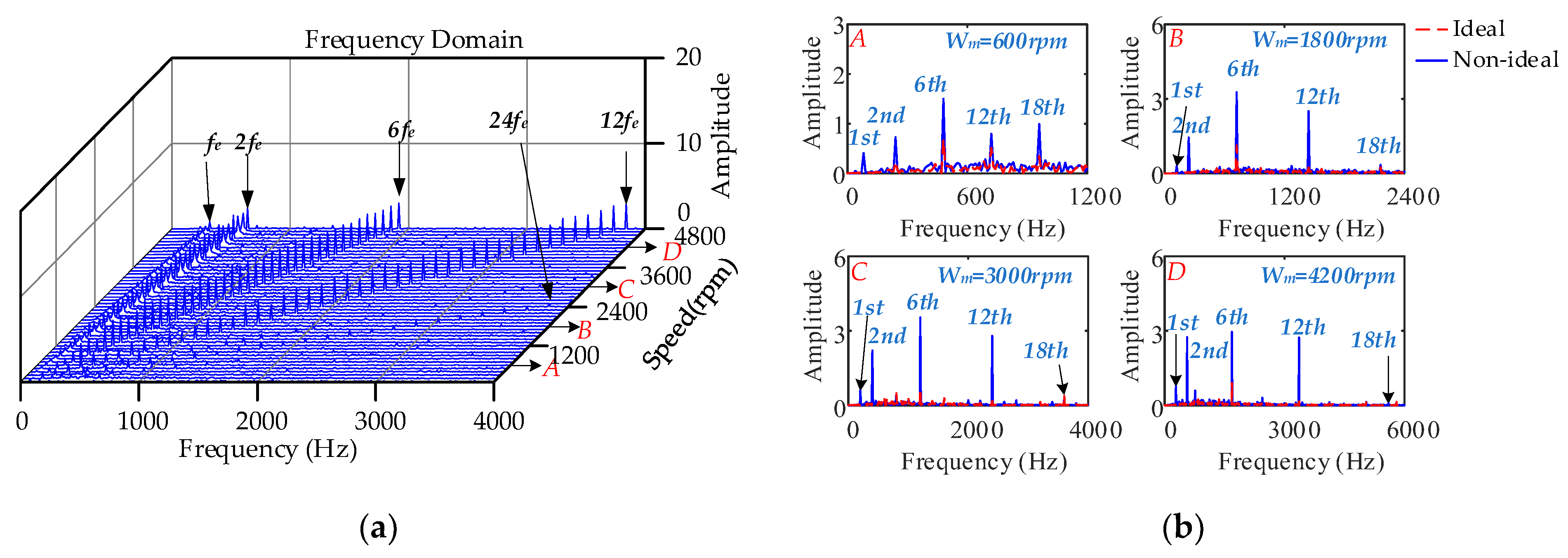
4.3.2. Different Speeds, Constant Load Condition
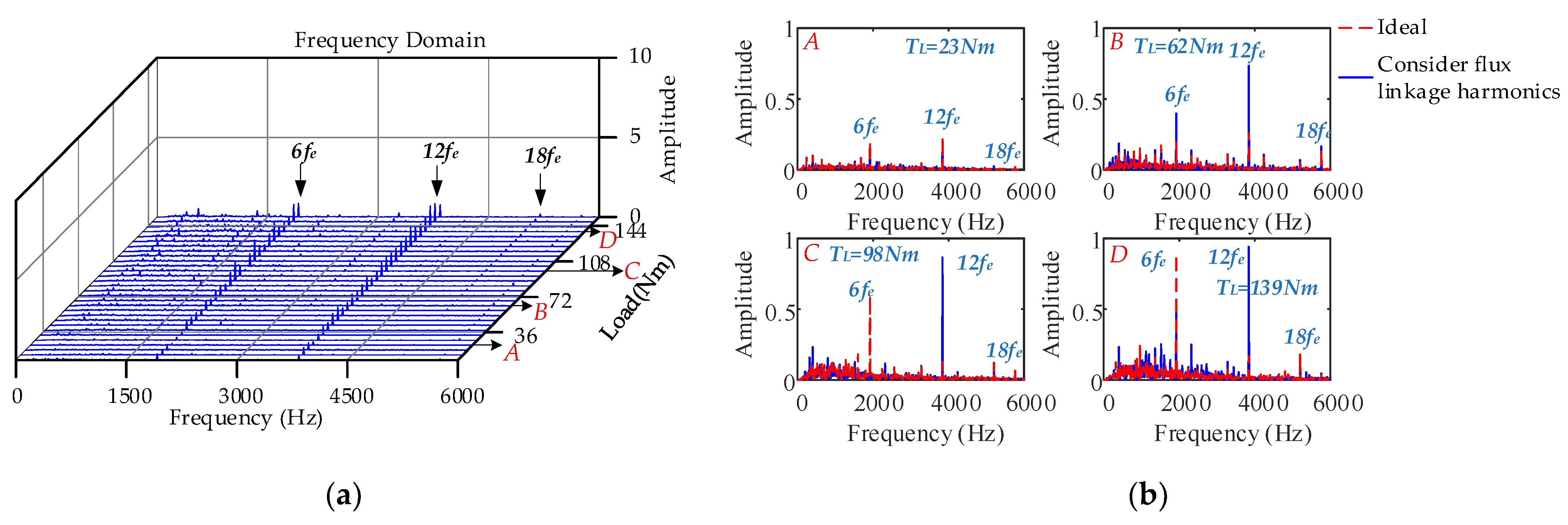
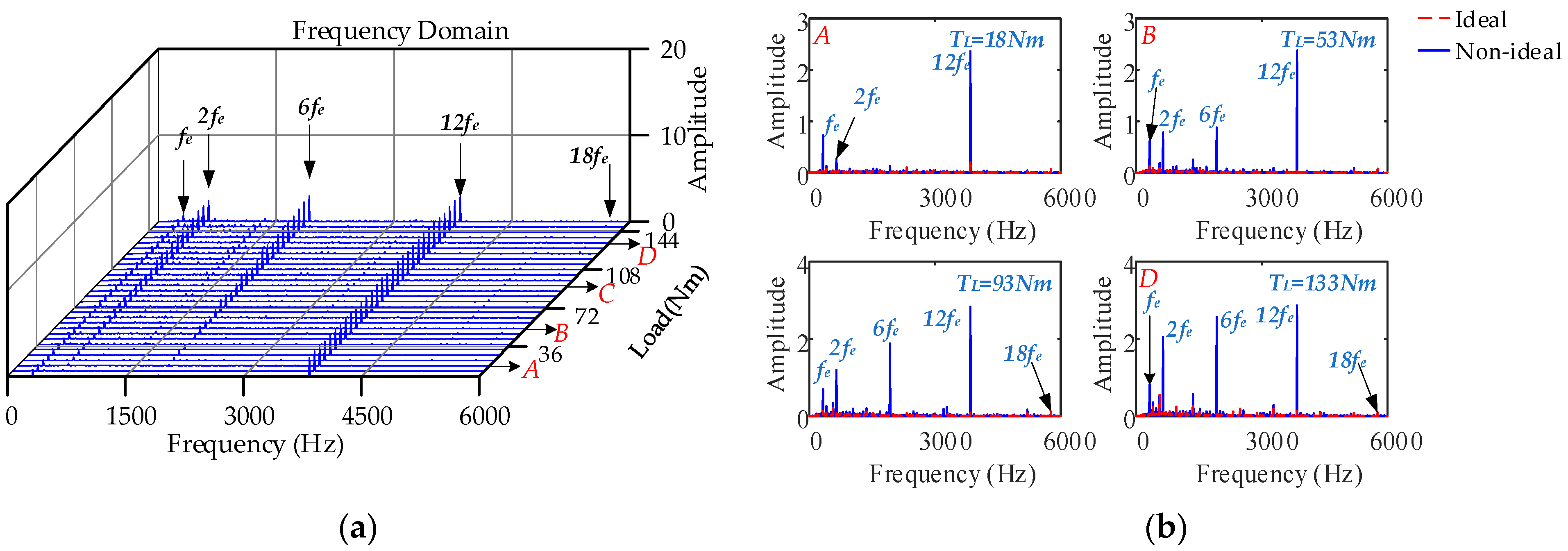
4.3.3. Different Loads, Constant Speed Condition
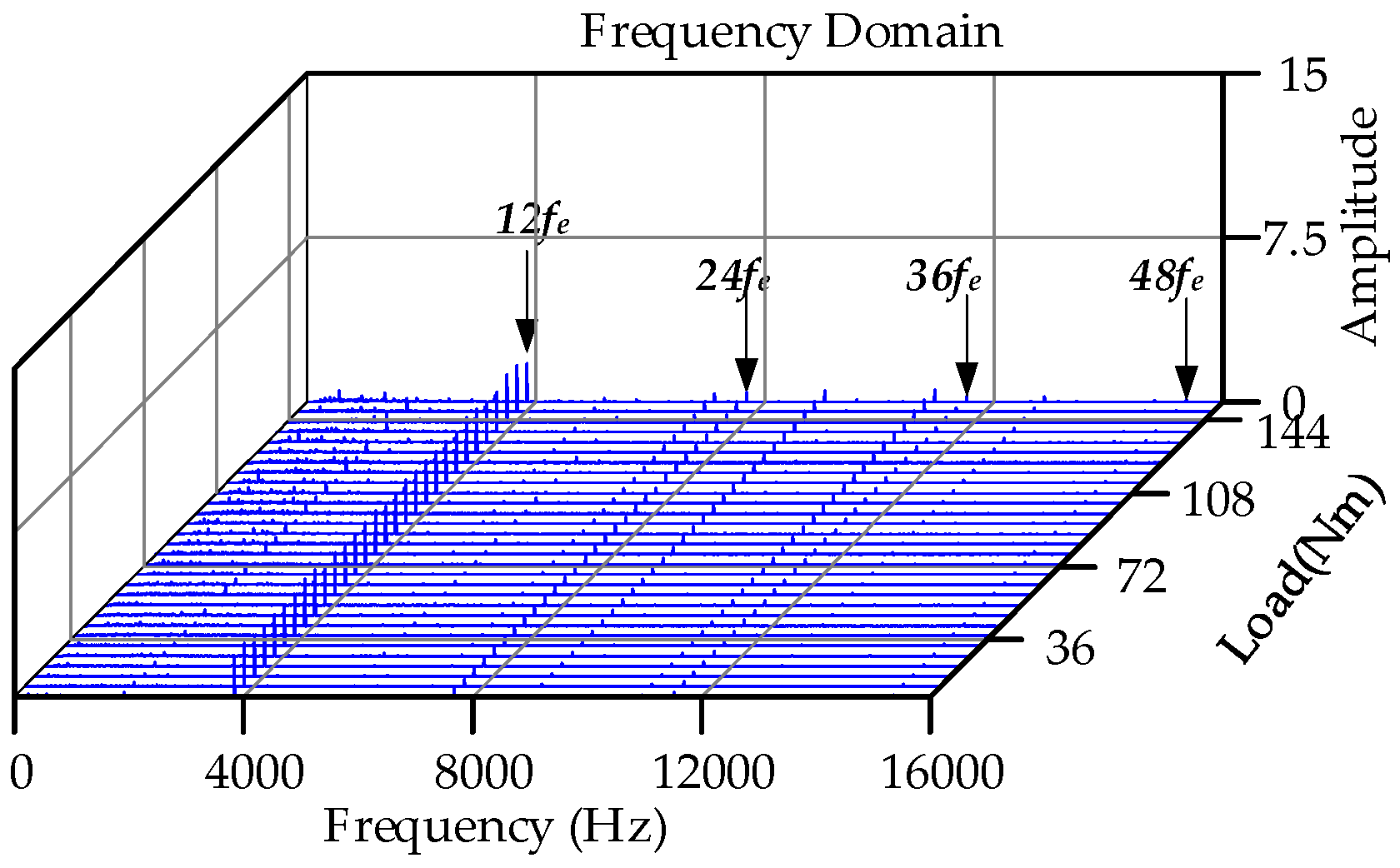
4.4. Consideration of the Cogging Torque
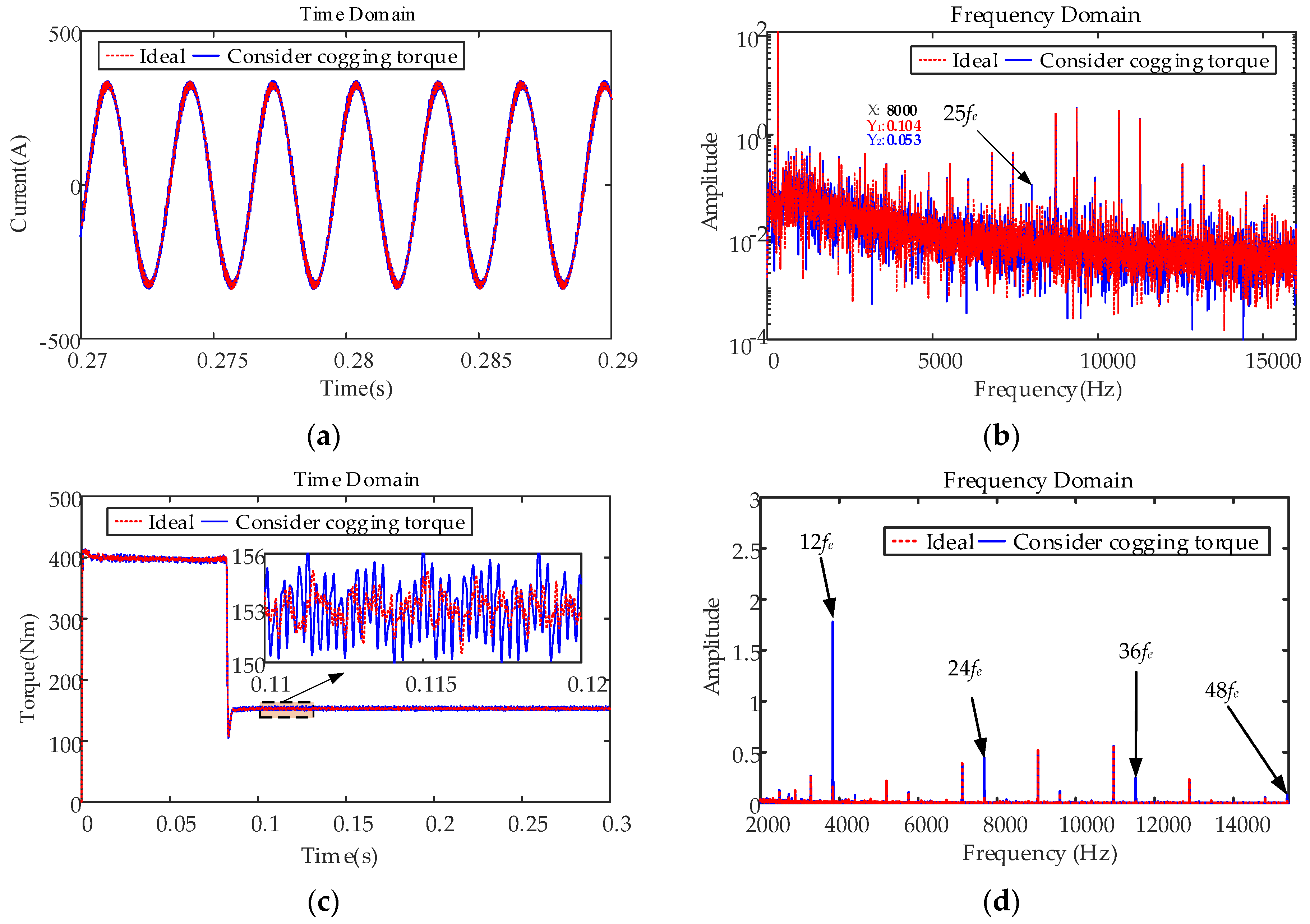
4.4.1. Constant Speed, Constant Load Condition
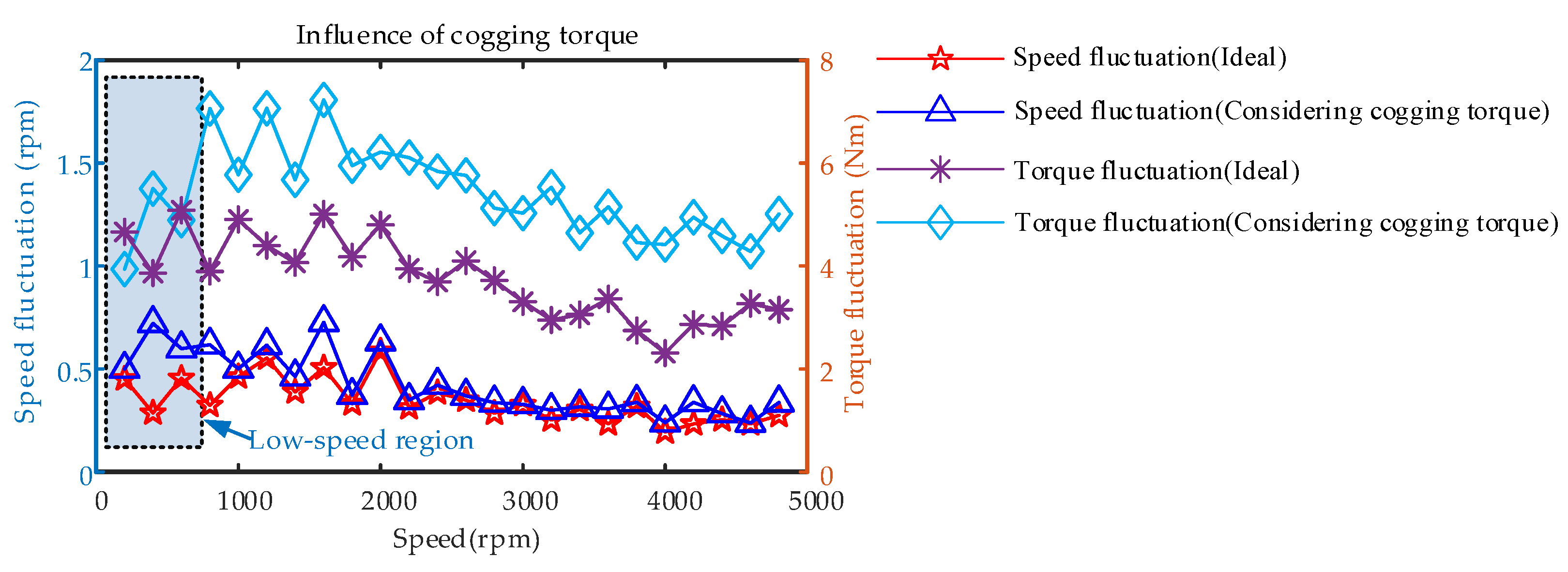
4.4.2. Different Speeds, Constant Load Condition
4.4.3. Different Loads, Constant Speed Condition
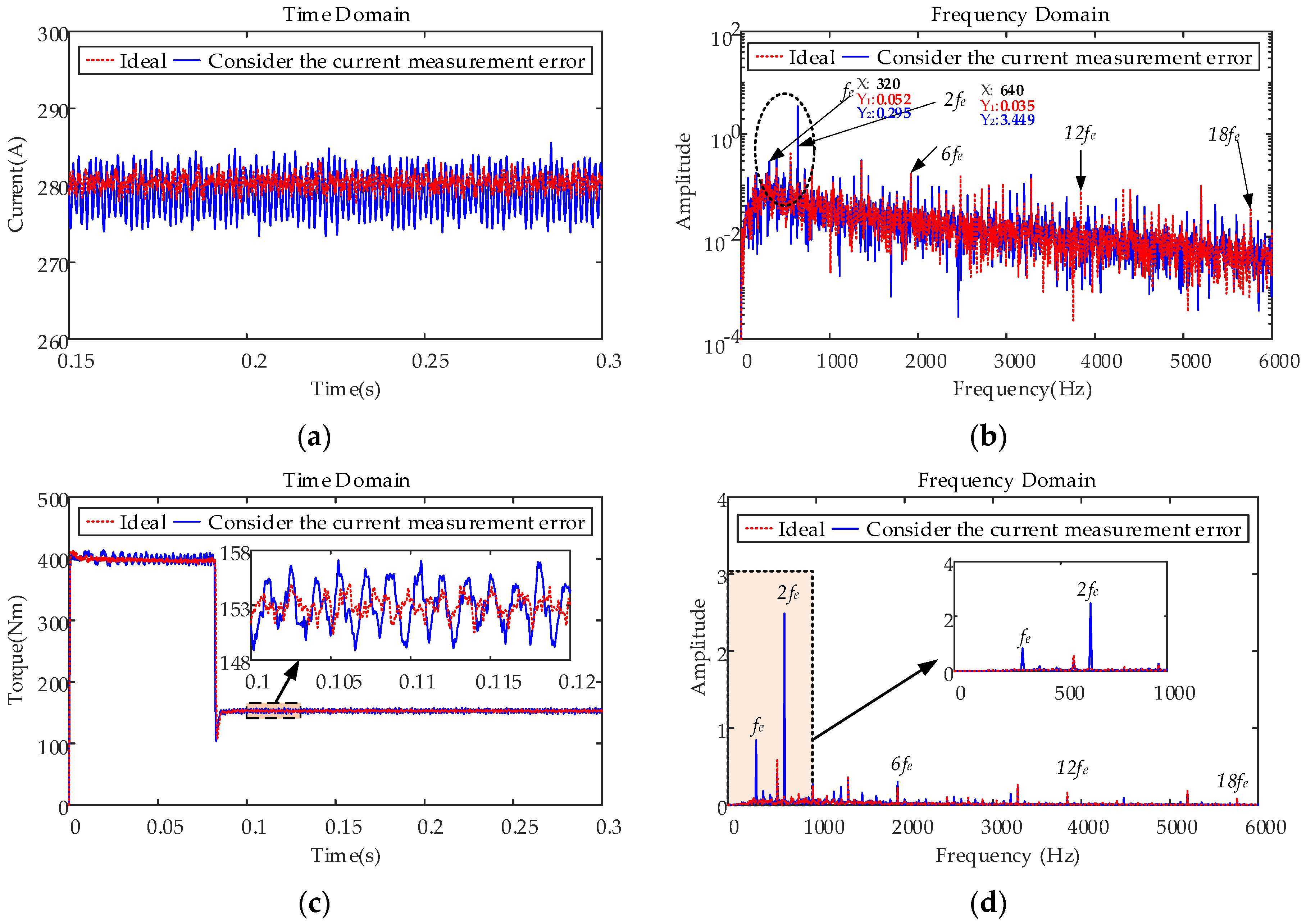
4.5. Consideration of the Current Measurement Error
4.5.1. Constant Speed, Constant Load Condition
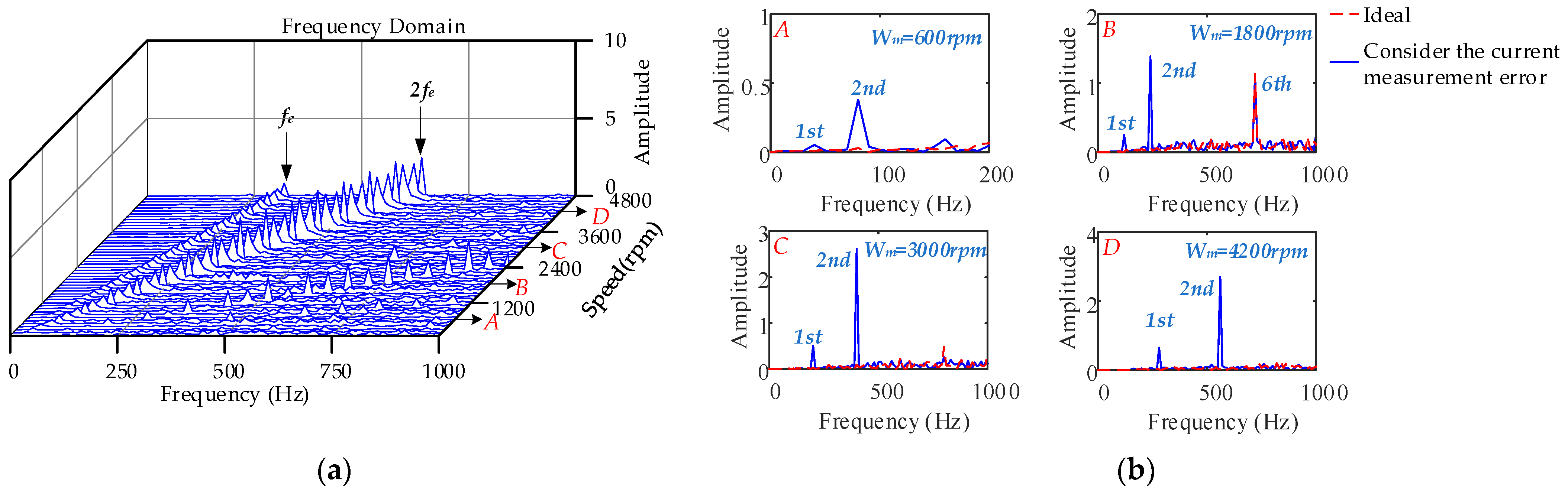
4.5.2. Different Speeds, Constant Load Condition
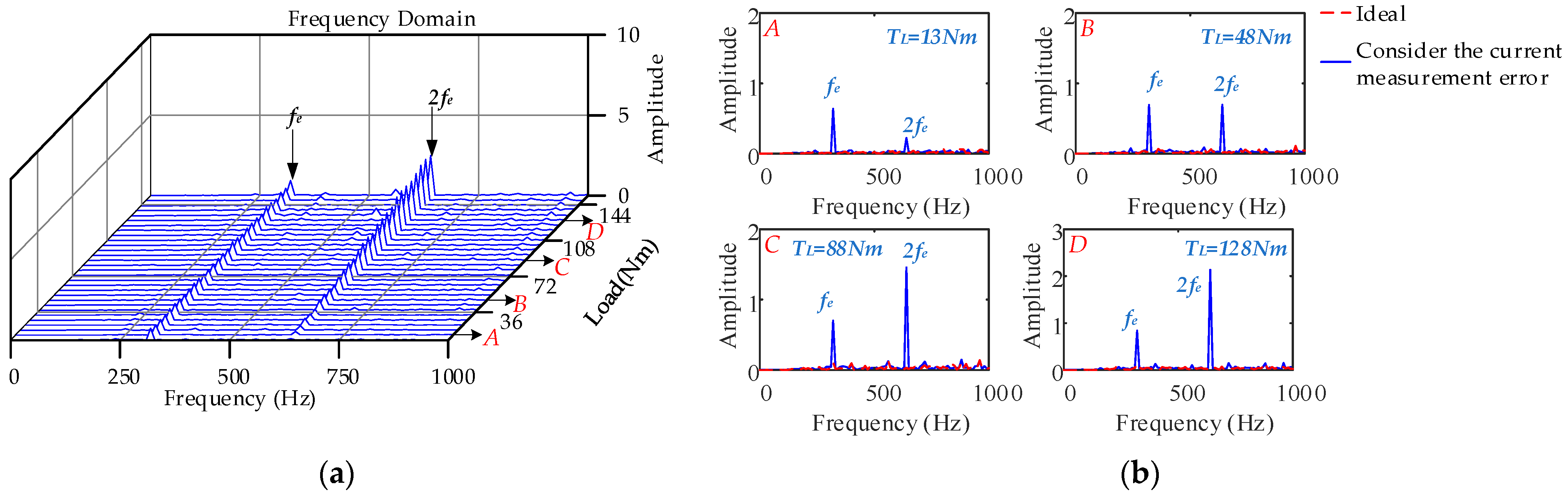
4.5.3. Different Loads, Constant Speed Condition
4.6. Consideration of the Nonlinear Characteristics of the Inverter, Nonsinusoidal Distribution of the Air-Gap Magnetic Field, and Current Measurement Error
4.6.1. Constant Speed, Constant Load Condition
4.6.2. Different Speeds, Constant Load Condition
4.6.3. Different Loads, Constant Speed Condition
4.6.4. Comparison of the Degree of Influence of Each Factor
5. Discussion
6. Conclusions and Future Work
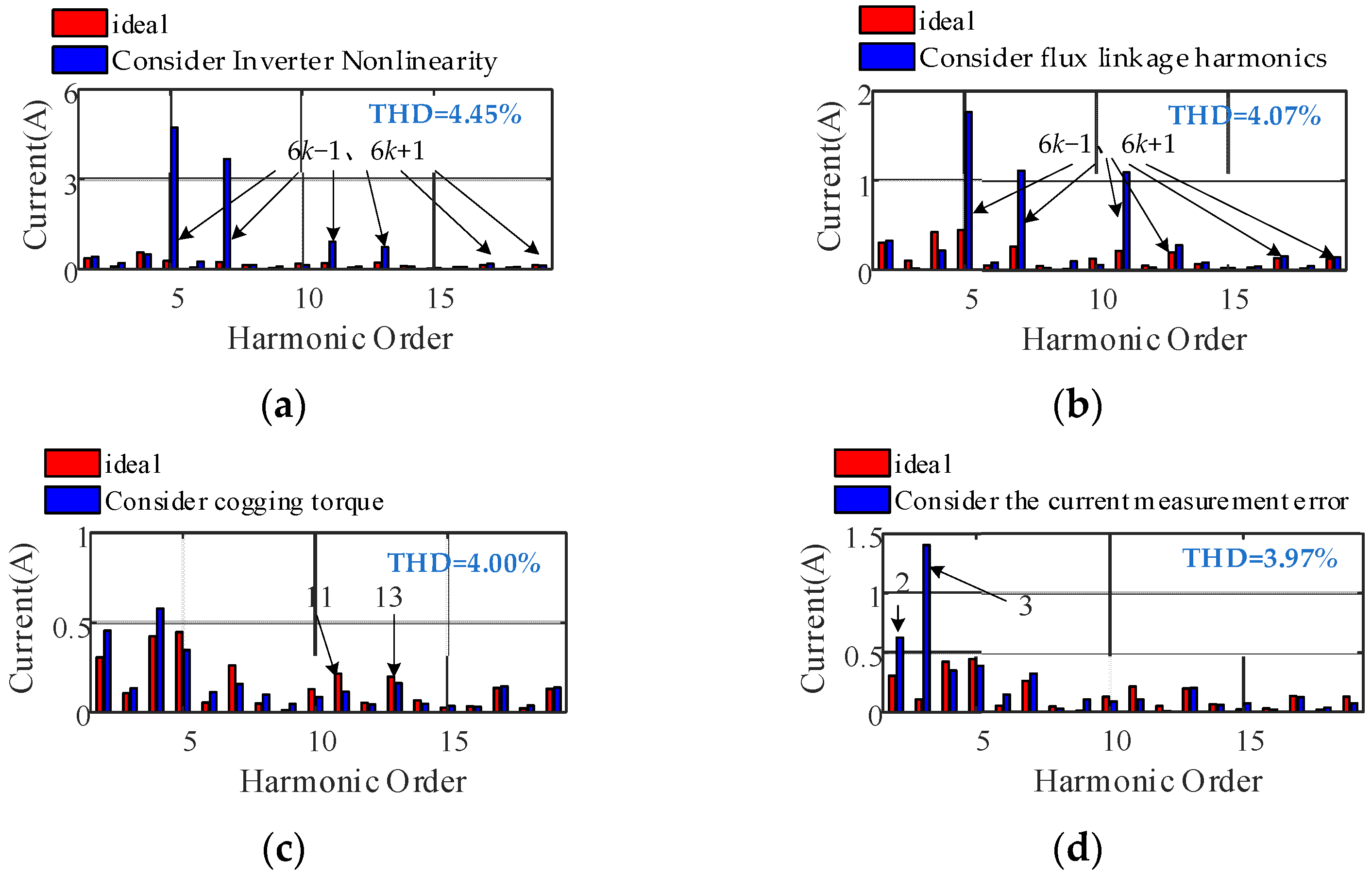
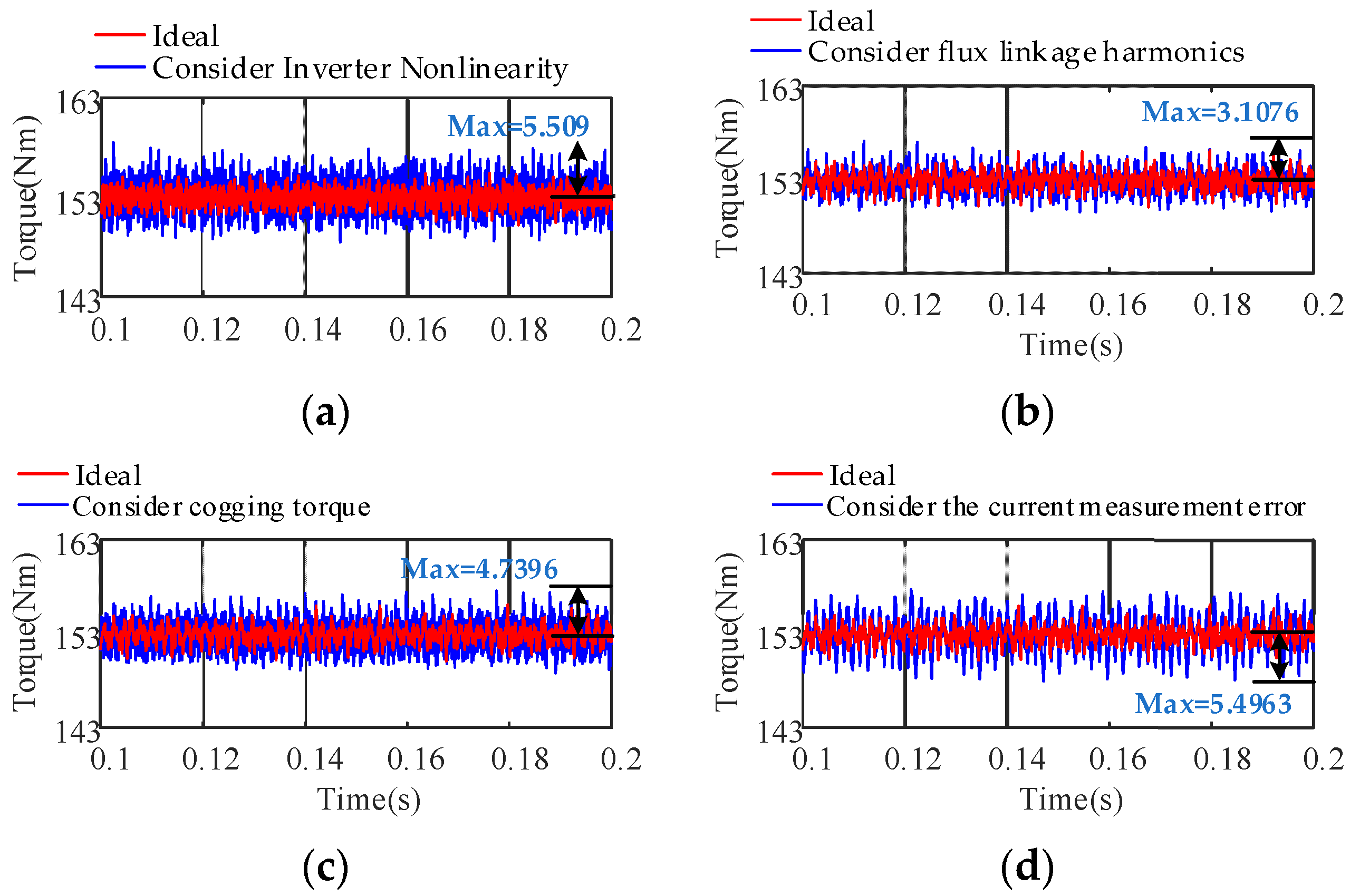
- A large number of 6k − 1th and 6k + 1th harmonic components exist in the motor phase current owing to the nonlinear characteristics of the inverter, which cause distortion of the stator flux linkage and 6nth order torque fluctuation of the electromagnetic torque. The nonsinusoidal distribution of the air-gap magnetic field produces the 6k − 1th and 6k + 1th harmonic components in the back electromotive force and rotor flux linkage, which result in 6nth order torque fluctuations. The current measurement error leads to the existence of 1st and 2nd harmonics in the d- and q-axes current harmonic components, which cause 1st and 2nd order torque fluctuations. The cogging torque leads to a 12nth order torque ripple of the electromagnetic torque.
- Under high-speed operating conditions, the interaction between the low-frequency harmonic current generated by SVPWM and the 6k − 1th and 6k + 1th harmonic currents generated by the nonsinusoidal distribution of the air-gap magnetic field causes the peak frequency of the fluctuation to shift to a high frequency, which leads to a larger amplitude of the 12th order. The electromagnetic torque fluctuations produced by the nonlinearity of the inverter are more violent, and the 1st and 2nd current harmonic frequencies caused by the current measurement error are larger and generate low-frequency electromagnetic torque vibrations. The influence of cogging torque on control performance is reduced. With an increase in load, the current harmonics caused by SVPWM and the nonsinusoidal distribution of the air-gap magnetic field jointly affect the 6nth order torque fluctuation distribution: the larger the load, the greater the electromagnetic torque 6nth order fluctuation caused by the inverter nonlinearity. The amplitude of the 2nd order electromagnetic torque fluctuation produced by the current measurement error is significantly increased.
- The non-ideal factors produce a large number of time harmonics and space harmonics in the PMSM and cause multiple-order torque ripples. Under the coupling actions of the nonlinear characteristics of the inverter and the nonsinusoidal distribution of the air-gap magnetic field, the 6nth order torque ripple is aggravated. With an increase in load, the 1st order torque fluctuation amplitude remains unchanged, and the torque fluctuation components of other orders increase, especially under high-speed and heavy-load conditions. The nonlinear characteristics of the inverter, the nonsinusoidal distribution of the air-gap magnetic field, the cogging torque, and the current measurement error lead to a sharp deterioration of its vibration state. Therefore, the non-ideal factors should be comprehensively considered in the analysis of the nonlinear vibration characteristics of complex motors. This study provides a theoretical reference for the mathematical modeling and electromagnetic vibration research on the PMSMs of electric vehicles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
- The current offset error.
- b.
- The current scaling error.
References
- Hu, J.J.; Peng, T.; Jia, M.; Yang, Y.; Guan, Y. Study on Electromechanical Coupling Characteristics of an Integrated Electric Drive System for Electric Vehicle. IEEE Access 2019, 7, 166493–166508. [Google Scholar] [CrossRef]
- Hu, J.J.; Yang, Y.; Jia, M.; Guan, Y.; Peng, T. A Novel Energy Optimization Control Strategy for Electric Drive System Based on Current Angle. Appl. Sci. 2020, 10, 3778. [Google Scholar] [CrossRef]
- Yang, F.; Jiang, F.; Xu, Z.J.; Qiu, L.; Xu, B.; Zhang, Y.; Yang, K. Complex Coefficient Active Disturbance Rejection Controller for Current Harmonics Sup-pression of IPMSM Drives. IEEE Trans. Power Electron. 2022, 37, 10443–10454. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, G.Q.; Wang, Q.W.; Ding, D.; Li, B.; Wang, G.; Xu, D. High-Gain Nonlinear Active Disturbance Rejection Control Strategy for Traction Permanent Magnet Motor Drives. IEEE Trans. Power Electron. 2022, 37, 13135–13146. [Google Scholar] [CrossRef]
- Hwang, S.-H.; Kim, J.-M. Dead Time Compensation Method for Voltage-Fed PWM Inverter. IEEE Trans. Energy Convers. 2010, 25, 1–10. [Google Scholar] [CrossRef]
- Hou, X.H.; Chen, Z.H.; Wu, S.; Yang, X.J.; Wang, Y.F.; Wang, J. Synchronous Frame Filter Based Harmonic Current Compensation Caused by Dead Time in PMSM Vector Control System. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Korea, 31 October–3 November 2021; pp. 1993–1998. [Google Scholar]
- Hu, J.J.; Yang, Y.; Jia, M.; Guan, Y.; Fu, C.; Liao, S. Research on Harmonic Torque Reduction Strategy for Integrated Electric Drive System in Pure Electric Vehicle. Electronics 2020, 9, 1241. [Google Scholar] [CrossRef]
- Zhu, C.; Zeng, Z.; Zhao, R. Torque ripple elimination based on inverter voltage drop compensation for a three-phase four-switch inverter-fed PMSM drive under low speeds. IET Power Electron. 2017, 10, 1430–1437. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, Y. The Online Parameter Identification Method of Permanent Magnet Synchronous Machine under Low-Speed Region Considering the Inverter Nonlinearity. Energies 2022, 15, 4314. [Google Scholar] [CrossRef]
- Joryo, S.; Tatsumi, K.; Morizane, T.; Taniguchi, K.; Kimura, N.; Omori, H. Study of Torque ripple reduction and Torque boost by Modified Trapezoidal Modulation. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018–ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 1202–1205. [Google Scholar] [CrossRef]
- Zhang, K.; Fan, M.D.; Yang, Y.; Zhu, Z.K.; Garcia, C.; Rodriguez, J. An Improved Adaptive Selected Harmonic Elimination Al-gorithm for Current Measurement Error Correction of PMSMs. IEEE Trans. Power Electron. 2021, 36, 13128–13138. [Google Scholar] [CrossRef]
- Song, Z.F.; Ma, X.H.; Yu, Y. Design of Zero-Sequence Current Controller for Open-End Winding PMSMs Considering Current Measurement Errors. IEEE Trans. Power Electron. 2020, 35, 6127–6139. [Google Scholar] [CrossRef]
- Heo, H.-J.; Hwang, S.-L.; Kim, J.-M.; Choi, J.-W. Compensating of common scaling current-measurement error for perma-nent magnet synchronous motor drives. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016; pp. 374–378. [Google Scholar]
- Lee, S.; Kim, K.H.; Lee, K. Current Measurement Offset Error Compensation in Vector-Controlled SPMSM Drive Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2619–2628. [Google Scholar] [CrossRef]
- Barman, D.; Sengupta, S.; Bhattacharya, T.K. Cogging torque reduction in surface mounted permanent magnet synchronous machine. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Trivandrum, India, 14–17 December 2016; pp. 1–5. [Google Scholar]
- Arias, A.; Caum, J.; Ibarra, E.; Grino, R. Reducing the Cogging Torque Effects in Hybrid Stepper Machines by Means of Resonant Controllers. IEEE Trans. Ind. Electron. 2019, 66, 2603–2612. [Google Scholar] [CrossRef]
- Scheer, R.; Bergheim, Y.; Heintges, D.; Rahner, N.; Gries, R.; Andert, J. An FPGA-Based Real-Time Spatial Harmonics Model of a PMSM Considering Iron Losses and the Thermal Impact. IEEE Trans. Transp. Electrif. 2022, 8, 1289–1301. [Google Scholar] [CrossRef]
- Wu, Z.P.; Zuo, S.G.; Chen, S.Y. Analytical Modeling and Calculation of Electromagnetic Torque of Interior Permanent Magnet Synchronous Motor Considering Ripple Characteristics. SAE Int. J. Adv. Curr. Prac. 2021, 3, 2088–2099. [Google Scholar]
- Gao, J.; Xiang, Z.M.; Dai, L.T.; Huang, S.D.; Ni, D.C.; Yao, C. Cogging Torque Dynamic Reduction Based on Harmonic Torque Counteract. IEEE Trans. Magn. 2022, 58, 1–5. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, H.K.; Bang, T.K.; Lee, J.I.; Kim, S.M.; Choi, J.Y. Performance Characteristics Analysis According to Design Pa-rameters of a 13 kW Interior Permanent Magnet Synchronous Motor for Reducing Cogging Torque. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Korea, 31 October–3 November 2021; pp. 1284–1288. [Google Scholar]
- Wu, D.; Zhu, Z. Design trade-off between cogging torque and torque ripple in fractional slot surface-mounted permanent magnet machines. In Proceedings of the 2015 IEEE International Magnetics Conference (INTERMAG), Beijing, China, 11–15 May 2015; p. 1. [Google Scholar] [CrossRef]
- Nakao, K.; Akatsu, K. Torque ripple suppression of permanent magnet synchronous motors considering total loss reduction. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 3880–3887. [Google Scholar]
- Petrovic, V.; Ortega, R.; Stankovic, A.M.; Tadmor, G. Design and implementation of an adaptive controller for torque ripple minimization in PM synchronous motors. IEEE Trans. Power Electron. 2000, 15, 871–880. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Sen, B.; Lazari, P.; Sun, T. A High-Fidelity and Computationally Efficient Model for Interior Perma-nent-Magnet Machines Considering the Magnetic Saturation, Spatial Harmonics, and Iron Loss Effect. IEEE Trans. Ind. Electron. 2015, 62, 4044–4055. [Google Scholar] [CrossRef]
- Hu, D.; Alsmadi, Y.M.; Xu, L. High-Fidelity Nonlinear IPM Modeling Based on Measured Stator Winding Flux Linkage. IEEE Trans. Ind. Appl. 2015, 51, 3012–3019. [Google Scholar] [CrossRef]
- Fasil, M.; Antaloae, C.; Mijatovic, N.; Jensen, B.B.; Holboll, J. Improved dq-Axes Model of PMSM Considering Airgap Flux Harmonics and Saturation. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Hu, J.B.; Chen, K.; Peng, Z.X. Modeling of electromagnetic torque considering saturation and magnetic field harmonics in permanent magnet synchronous motor for HEV. Simul. Model. Pract. Theory 2016, 66, 212–225. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.-H.; Li, S.; Guo, L.; Yan, Y. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives—A Survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef]
- Song, D.F.; Wu, J.J.; Yang, D.P.; Chen, H.X.; Zeng, X.H. An adaptive torque ripple suppression algorithm for permanent magnet synchronous motor considering the influence of a transmission system. J. Vib. Eng. Technol. 2022, 1–15. [Google Scholar] [CrossRef]




| Parameters | Value | Unit |
|---|---|---|
| Number of poles | 8 | |
| Number of slots | 48 | |
| Stator outer diameter | 108 | mm |
| Rotor outer diameter | 71 | mm |
| Stator inner diameter | 71.7 | mm |
| Rotor inner diameter | 30 | mm |
| Air-gap length | 0.7 | mm |
| Axial length | 125 | mm |
| Length of PM | 22 | mm |
| Thickness of PM | 4 | mm |
| Coercivity of PM | 92,300 | A/m |
| Recovery permeability of PM | 1.06 |
| Parameters | Value | Unit |
|---|---|---|
| Rated power | 80 | kW |
| Rated torque | 153 | Nm |
| Rated speed | 4800 | rpm |
| Rotary inertia | 0.04 | Jm/Kg·m2 |
| Polar logarithm | 4 | - |
| Stator resistance | 0.01 | Ω |
| Flux of PM | 0.0589 | Wb |
| Inductance of axis D | 1.0146 × 10−4 | H |
| Inductance of axis Q | 2.968 × 10−4 | H |
| Parameters | Value | Unit |
|---|---|---|
| Battery DC voltage | 600 | V |
| Modulation carrier period TPWM | 100 | us |
| Modulation carrier frequency fPWM | 10 | kHz |
| IGBT turn-on time ton | 1 | us |
| IGBT turn-off time toff | 2 | us |
| Dead time td | 4 | us |
| Voltage drop of IGBT switch ut | 3 | V |
| Conduction voltage drop of freewheeling diode ud | 2 | V |
| Delay time of gate pulse rise propagation tPLH | 0.5 | us |
| Delay time of gate pulse drop propagation tPHL | 0.53 | us |
| Order | Magnitude [Wb] | Percent |
|---|---|---|
| 5 | 5.4 × 10−5 | 0.092% |
| 7 | 7.48 × 10−5 | 0.127% |
| 11 | 1.113 × 10−4 | 0.189% |
| 13 | 8.304 × 10−6 | 0.014% |
| 17 | 4.6 × 10−7 | 0.0008% |
| 19 | 1.96 × 10−6 | 0.003% |
| Parameter | Value (N·m) | Parameter | Value (rad) |
|---|---|---|---|
| T1 | 1.89897 | β1 | 0.0000672 |
| T2 | 0.379 | β2 | 3.13 |
| T3 | 0.2254 | β3 | 3.12 |
| T4 | 0.0918 | β4 | 3.236 |
| Parameters | Before Considering the Non-Ideal Factors | After Considering the Non-Ideal Factors |
|---|---|---|
| 2nd harmonic current amplitude(A) | 0.36 | 1.06 |
| 3rd harmonic current amplitude(A) | 0.08 | 1.22 |
| 5th harmonic current amplitude(A) | 0.27 | 5.55 |
| 7th harmonic current amplitude(A) | 0.23 | 4.28 |
| 11th harmonic current amplitude(A) | 0.19 | 1.77 |
| 13th harmonic current amplitude(A) | 0.20 | 0.98 |
| 17th harmonic current amplitude(A) | 0.11 | 0.2 |
| 19th harmonic current amplitude(A) | 0.12 | 0.08 |
| Current distortion rate | 3.99% | 4.59% |
| Overall fluctuation amplitude of motor torque(N·m) | 2.78 | 10.37 |
| Fluctuation amplitude of motor shaft speed (rpm) | 0.12 | 0.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, S.; Qiu, L.; Zhang, Z.; Guo, D.; Ren, H. Integrated Impacts of Non-Ideal Factors on the Vibration Characteristics of Permanent Magnet Synchronous Motors for Electric Vehicles. Machines 2022, 10, 739. https://doi.org/10.3390/machines10090739
Ge S, Qiu L, Zhang Z, Guo D, Ren H. Integrated Impacts of Non-Ideal Factors on the Vibration Characteristics of Permanent Magnet Synchronous Motors for Electric Vehicles. Machines. 2022; 10(9):739. https://doi.org/10.3390/machines10090739
Chicago/Turabian StyleGe, Shuaishuai, Longhui Qiu, Zhigang Zhang, Dong Guo, and Honghai Ren. 2022. "Integrated Impacts of Non-Ideal Factors on the Vibration Characteristics of Permanent Magnet Synchronous Motors for Electric Vehicles" Machines 10, no. 9: 739. https://doi.org/10.3390/machines10090739
APA StyleGe, S., Qiu, L., Zhang, Z., Guo, D., & Ren, H. (2022). Integrated Impacts of Non-Ideal Factors on the Vibration Characteristics of Permanent Magnet Synchronous Motors for Electric Vehicles. Machines, 10(9), 739. https://doi.org/10.3390/machines10090739







