Technical Risk Assessment for the Safe Design of a Man-Rider Chair Lift System

Abstract

Underground mining is a difficult area for miners to work. Miners must go to the working faces by walking, which is not only time consuming but also physically demanding. In mines, a man-rider chair lift system (MRCL) has been developed to alleviate the strain stresses caused by walking lengthy and uneven distances up to the working faces. All parameters, including horizontal and vertical distances, variation and inclination of underground mines, slope forces considering the weight of persons and chair, forces acting towards return and drive unit, curves angles, power to operate, and rope safety factor, are calculated mathematically while modelling a man-rider chair lift system for both the installation and extension phases. We analyzed the analytical approach in conjunction with practical installation of the man-rider chair lift system to establish if the installation and extension of MRCL is genuinely feasible in the current scenario. We also created a simulation model of steel wire rope in Creo 8.0 for analyzing the various stresses on it with the Ansys R 16.2 software. In both phase I and phase II, the factor of safety is above that recommended, and the system is a hundred percent reliable, risk-free, and safe for operation.

1. Introduction

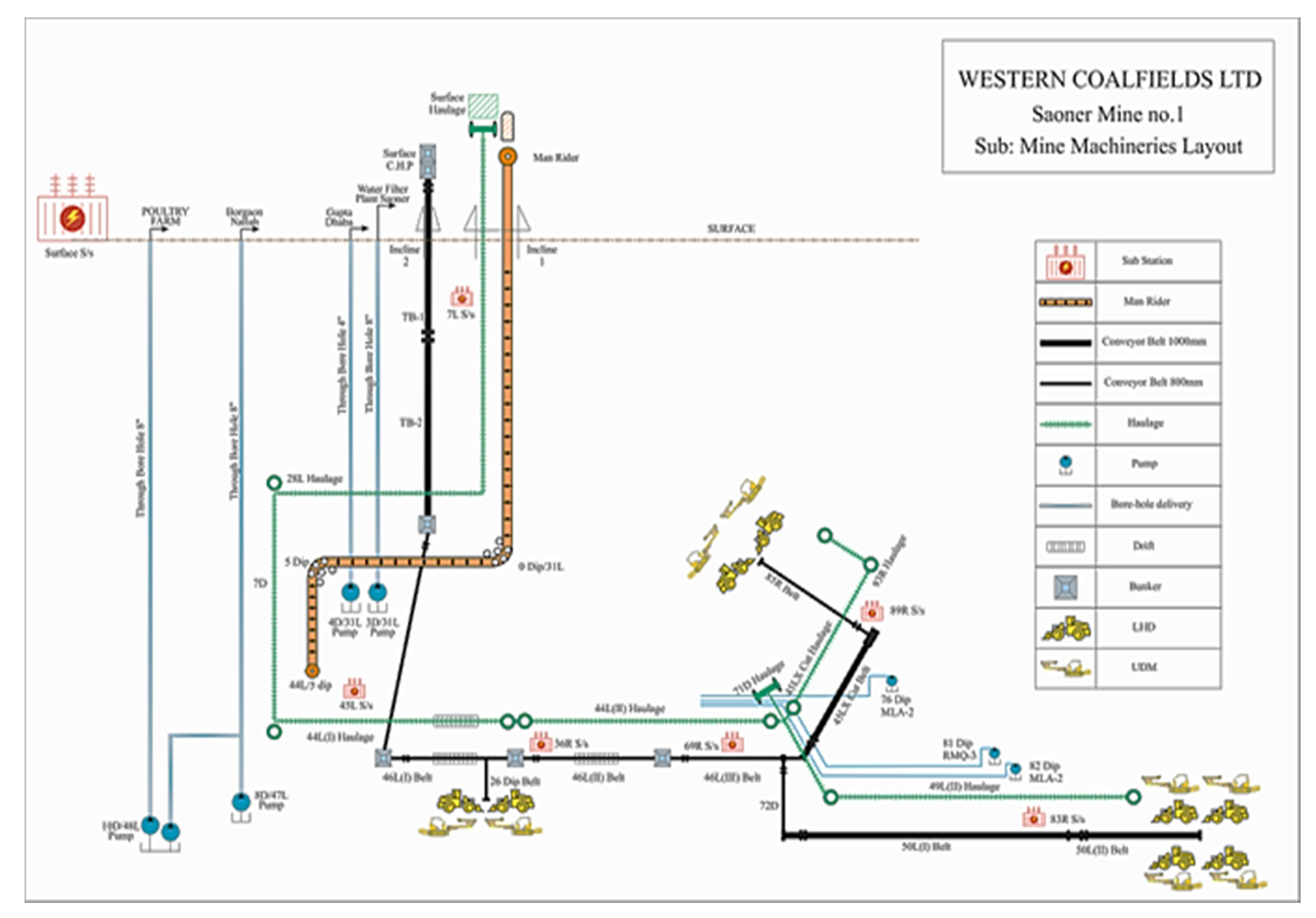
Saoner Mine No. 1 is a multi-working seam, underground coal mine located in India’s Nagpur District of Maharashtra that uses the board and pillar technique of development. The depth of its coal seams ranged from 50 to 200 m below ground [1]. A combination of LHD, UDM, and belt conveyors is used to bring coal from subterranean mines to the surface [2,3]. Figure 1 depicts a detailed plan layout demonstrating the deployment of several types of mining machinery. There are two approaches to the subterranean properties of coal. The first is by a vertical shaft-winding engine and cage lift setup, while the second is via drifted inclines accessed by walking in underground mines. Underground coal-mining technologies are used to excavate deep-down coal seam strata in the earth. Mines are open 24 h a day, seven days a week, and progress is made using the board and pillar development approach during every coal-mining operation. The advancement of working faces lengthens the distance that miners must travel to reach their work places. This constant increase in travel distance causes fatigue among miners and reduces productive working time. A man-rider chair lift system is the solution to overcome these situations of the underground mines [4,5,6].

A man-riding system is employed in deeper mines to aid miners in overcoming major transportation obstacles. It helps to reduce travel time without tiring out miners working in subterranean mines while also increasing output. It is a safe, quick, and pleasant method of transporting miners across long distances with uneven horizontal and vertical bends and grades. As production losses are caused by ever-longer underground travel distances, these systems have become increasingly important in modern mining.

The man-rider chair lift system is an electro-hydraulic mechanism with an endless rope. The driving pulley sheave is operated by a hydraulic motor that receives flow from a hydraulic pump and is powered by an electric prime mover. The drive pulley sheave rotates on its axis and revolves the rope due to tension-induced friction between the drive pulley sheave lining and the steel wire rope [7]. Its rope runs between the hang carrying and depression pulleys on the roof, which are maintained in place by grouted tubes at underground gallery roof, as shown in Figure 2. The man-riding chairs are securely held on an endless wire rope by positive friction. Roller stations set at regular intervals guide the wire rope itself. The wire rope is driven at the appropriate speed by a drive station located at the system’s head. Specification of MRCL is given in

Table 1. Specification of MRCL.

Type and Make	Drive Power	Rope Speed	Maximum Horizontal Curves	Maximum Gradients	Pulling Force	IS Specification
Electro-hydraulic-operated, roof hanged, endless type, and SCHARF make	3 ph, 50 Hz,110 KW/550 Volt, IP-55, IS 4691	0–3 m/s	90°	1:4.5 or 45 degrees	Less than ten times the minimum breaking strength of rope	IS 17242 2019

.

The embarking and disembarking stations are used to pick up and drop off riders as well as to ensure reliable chair uncoupling and pick-up by the wire rope at the transition area from wire rope to rail, shown in Figure 3. The return station and tensioning tower weight are erected at the conclusion of the transit section. Curve stations hung in the transport segment by anchoring chains can address horizontal course variations effectively.

The individual rides on the MRCL in the mine use a chair to get from one location to the desired destination and back. The man-riding chairs on an infinite wire rope are held in place by positive friction. The wire is steered by rollers spaced at no more than fifteen-meter intervals. The driving station and return pulleys are securely connected to withstand forces up to the rope’s minimum breaking force. A roof hanging system with a return pulley and proper rope tensioning configuration is used for the return end installation. The return end installation and tensioning column with internal tensioning weight are installed at the downhill end. It is supported by rails and is used to adjust the tensioning distance of the counterweight. This system is also equipped with many safety features such as over-travel and over-speed switch, pull cord rope and switch, pre start alarm, emergency brake, hydraulic brake, telephone and pager phones, etc.

We planned to build a man-rider chair lift system in two stages as part of the mine’s expansion plan. In phase I, MRCL was placed from the surface to the D level, and in phase II, it was expanded up to the G level. When constructing and installing MRCL, the lowest breaking force and applied force on the steel wire are critical criteria. The breaking force must be at least ten times greater than the applied resultant force [8,9,10].

2. Literature Review

The design of mechanical systems can be a very complex task involving the mechanical design itself but also the organization of the shop floor [11,12] as well the respective controllers [13,14] and communications techniques and possibilities [15].

In this work, authors devoted attention to the mechanical part of the system as well as safety and reliability issues concerning design and practical implementation in the coal mine.

Ren Zhiqian et al. [16] used a double Pareto lognormal distribution to examine the fatigue life of steel wire rope under impact stresses. They postulated that the double Pareto lognormal distribution model could accurately reflect the reliability degradation process of wire ropes, providing guidance on wire rope fatigue life computation under diverse impact loads. Shuai Wand et al. [17] conducted a stress study of steel wire rope under bending with various structural shapes. Based on rope failure and fatigue failure situations, life characterization metrics were provided. They concluded that the structural integrity of the cross-twisted wire rope is superior to that of the co-twisted steel wire rope when bent. Where wear degradation and fatigue stress are dominant, Seale-type co-twisted and cross-twisted steel wire rope is chosen. Juan Felipe Beltran et al. [18] used experimental and analytical methodologies to investigate the static response of asymmetrical damage to metallic strands of steel wire rope. Damage strands of multilayer strands are regarded as uncoupled biaxial bending and axial stress 1D nonlinear beams. Rope types 1 × 7 and 1 × 19 were employed, with damage levels and strand diameters ranging from 5% to 40% and 3.5 mm to 22.2 mm, respectively. The static response of asymmetrical strand breakage was well-predicted by a nonlinear beam. M. Giglio et al. [19] investigated the mechanical strength of steel wire rope exposed to axial and bending stresses using stress and strain analysis. The study takes into account the rope used in helicopter rescue hoists that is subjected to swinging off the recovery hook. The analytical results and experimental data were compared in order to forecast the reliability and fatigue life of steel wire rope. Failure analysis of steel wire rope used in overhead cranes was performed by L. Guerra-Fuentes et al. [20]. They examined wire damage using a visual examination, stereoscopic analysis, scanning electron microscopy, and a micro hardness test to correlate operating conditions with suspected failure causes. Localized plastic distortion occurred in steel wire rope, which was followed by wire wear, stress concentrations, and, eventually, fatigue failure. Using a new technique to failure analysis and prediction, Achraf Wahid et al. [21] evaluated three damage models for steel wire rope. The first model relies on the modified unified theory, and the second and third models use residual energy models for static damage. The area under the tensile curve for each test is calculated for this one using trapezoidal numerical integration. Based on the obtained results, we can characterize the mechanical behavior of the rope and predict its damage course. Predictive maintenance and cable maintenance were aided by these stages of deterioration. SonglingXue et al. [22] investigated the slip effects between rope wires when bending and fatigue forces are applied to them using the concept of share-splitting slip. The input parameters were acquired from steel wire rope research. The suspension wire was fatigue tested under tension and bending fatigue using a self-developed testing apparatus. Individual steel wires from the rope were studied under an electron microscope.

3. Research Methodology

It is critical to address risk assessment and safety during the design, installation, and extension stages of MRCL in accordance with the DGMS recommendations as per CMR Regulation 93(6). To relieve the strain pressures produced by travelling long and unequal distances up to the working faces in underground mines, an MRCL was devised to be installed in the mine, with the processes outlined below in Figure 4.

4. Research Methodology

4.1. Load Calculation for Man Rider

The MRCL was installed at the mines according to the IS 17242-2019 [23]. The drive head of MRCL is grouted at the pit top of the incline, and its tail end is grouted in the below-ground mine at the desired place up to the length of the installation. The distance between two tubes and two riders is 15 m.

Gradient = Ratio of one meter drop in RL to horizontal distance covered (1:X)

∅ = tan⁻¹ (Gradient)

(1)

4.2. Calculation of Slope Forces

F₁ and F₂ are the forces resulting from the weight of persons (assumed average weight 80 kgf/pers);

F₃ and F₄ are the resulting forces from the weight of chairs (13 kgf/chair);

F₁ and F₃ are the forces acting in the direction from the drive unit to the return unit.

F₂ and F₄ are the forces acting in the direction from the return to the drive unit, as shown in Figure 5.

F_P.D = (80 × 9.81 × Horizontal Distance × sin∅)/15

(2)

F_P.U = (80 × 9.81 × Horizontal Distance × sin∅)/15

(3)

F_C.D = (13 × 9.81 × Horizontal Distance × sin∅)/15

(4)

F_C.U = (13 × 9.81 × Horizontal Distance × sin∅)/15

(5)

Slope forces acting on the wire rope of MRCL due to the weight of riders and chairs are calculated by the Equations (2)–(5).

F₁ = ∑ F_P.D; F₂ = ∑ F_P.U; F₃ = ∑ F_C.D; F₄ = ∑ F_C.U;

Resulting slope force:

F_H = (F₁ + F₂ + F₃ + F₄)

(6)

4.3. Calculation of Man-Riding Capacity (Mc)

Travelling speed: S (m/s);

Distance between two chairs: Lc = 15 m;

Mc = (S × 3600)/Lc    [Person/hour]

(7)

4.4. Calculation of Required Rope Pulling Force (F_R)

Summation of the angles of all the horizontal curves of MRCL: α_H;

Summation of the angles of all the vertical curves of MRCL: α_V;

Rolling resistance of each pulley station in straight section of the installation: R_PS;

Rolling resistance due to a rope deviation of 3° (curves, synclines, anticlines): R_θ

Resulting rolling resistance of pulley on either side:

F_R = R_PS × L/L_P + R_θ × (α_H + α_V)/3

(8)

Required pulling force (F_P):

F_P = F_H + 2 × F_R   [N]

(9)

4.5. Calculation for the Required Output of Drive Unit

The drive unit of MRCL is comprised of an electrical motor, hydraulic power pack, hydraulic motor, and drive pulley combined to drive the steel wire rope, as shown in Figure 6.

Required output of the drive unit (P_O):

P_O = F_P × S/(9.8 × 10²)    [KW]

(10)

Efficiency of the drive unit η;

Required input of the drive unit (electric motor) (P_i):

P_i = P_O/η    [KW]

(11)

Required capacity of induction motor = P_i × 1.1 (considered factor 1.1);

Select the nearest and effective capacity of the motor to the calculated value.

4.6. Calculation of Required output of the Rope Safety Factor

Rope safety factor (S.F_R) = Ultimate strength/Working stress (F_B/F_H) must be higher than 10.

Overall maximum inclination (Average) α_m:

α_m = ((L₁x ∅₁ + L₂x ∅₂ + L₃x ∅₃₊ … + L_nx ∅_n))/L

(12)

Effective length of installation for total vertical deflection of α_m:

L_E = L/Cos α_m     [m]

(13)

Maximum number of riders for the installation:

N_R = L_E/L_C × 2

(14)

Horizontal component of force acting on the wire rope:

F_HC = F_P × Sin 0°

(15)

Vertical component of forces acting on suspension tubes at full capacity of the chair lift system:

F_VS = ((N_R × (W_P + W_C) × g) + L_E × 2 × (WR/100) × g) × Cos α_m°   [N]

(16)

4.7. Calculation of Maximum Permissible Load-Bearing Capacity of Holding Bolt/Roof Bolt of Suspension Tubes

Number of suspension tubes for the total length of chairlift system:

T = L_E/L_P

(17)

Self-weight of suspension tube with carrying and depression pulley (W_ST):

W_ST = 115 kgf   (approx.)

(18)

Force acting on each suspension tube due to its own weight:

F_SS = W_ST × g     [N]

(19)

Force on each suspension tube at maximum capacity of chairlift system:

F_ST = F_VS/T + F_SS    [N]

(20)

Force on each suspension tube with two passing at the same time:

F_SP = (F_P.D + F_P.U + F_C.D + F_C.U) + F_SS + (W_R15 × g × 2)

(21)

Since F_SP > F_ST, we will be considering this force for calculating the load-bearing capacity of roof bolts.

Load test of each roof bolt done with minimum 5000 N;

Two roof bolts are used to fix each suspension tube, and the suspension tube arrangement is shown in Figure 7.

4.8. Factor of Safety for Each Suspension Tube

See below

F_ST = 5000 × 2/F_SP

(22)

4.9. Calculation of Factor of Safety of Tensioning Rope

Figure 8 shows the rope tensioning arrangement along with counter weight.

Weight of counter weight W_C = 1500 kgf;

Force on tensioning rope due to counter weight:

F_Cw = W_C × 9.81

(23)

Forces acting on tensioning rope:

F_WR = F_CW + F_HC

(24)

Minimum breaking force of the tensioning rope B_F:

B_F = 167,000 N for 16 mm steel wire rope;

B_F = 191,000 N for 18 mm steel wire rope.

Factor of safety of tensioning rope:

F.S_TR = Ultimate strength/Working stress = B_F/F_WR

(25)

5. Engineering Calculation for the Design and Installation MRCL at Actual Mining Conditions

Figure 9 shows a side and top perspective of the layout of the MRCL installation and extension phases at underground mines. The technical parameters of Phase I Man-rider installation are mentioned in

Table 2. Phase I Man-rider Installation.

Phase-I
Sections of the Chairlift in Sequence from the Drive Unit to the Return Unit					Inclination	Sine of Inclination	Slope Force
		Horizontal Distance	Curve Station	Gradient (1 m RL: Horizontal Distance)	ϕ	Sinϕ	Person		Chair
Level	Level	(m)		1:X			F1 (N)	F2 (N)	F3 (N)	F4 (N)
Level A to Level B = $l_1$		930		1:5	11.31	0.196	9527		1548
Level B to Level C = $l_2$		140	90° to $l_1$	1:50	1.15	0.020	146		24
Level D to Level D = $l_3$		326	90° to $l_2$	1:10	5.72	0.100	1703		277
Total		1396	180o		18.16		11,377		1849

, while,

Table 3. Phase II Man-rider Extension.

PHASE-II
Sections Of The Chairlift In Sequence From The Drive Unit To The Return Unit					Inclination	Sine of Inclination	Slope force
		Horizontal Distance	Curve Station	Gradient (1 m RL: Horizontal Distance)	ϕ	Sinϕ	Person		Chair
Level	Level	(m)		1:X			F1 (N)	F2 (N)	F3 (N)	F4 (N)
Level D to Level E = $l_4$		40		1:10	5.71	0.10	209		34
Level E to Level F = $l_5$		53	12° to $l_4$	1:10	5.71	0.10	277		45
Level F to Level G = $l_6$		1330	64.5° to $l_5$	1:50	1.14	0.02	1390		226
Total		1423	76.5°		12.56		1876		305

implies the parameters of Phase II Man-rider Extension. All parameters of the mine were considered for the load calculation in both phases and combined parameters of both the phases are mentioned in the

Table 4. Combined Framework of Phase I and Phase II.

Phase I	Horizontal Distance (m)	Curve Station (°)	Inclination Ø (°)	Slope Force Person	Slope Force Chair
+
Phase II				F1 (N)	F2(N)	F3(N)	F4(N)
Total	2819	256.5	30.733	13,254	2154

[24].

5.1. Phase-I

The MRCL was installed in two phases; the drive head was installed at pit top with an initial length of 1396 m, and all the technical parameters of this installation are mentioned in Table 2.

5.2. Phase II Engineering Calculation for the Extension MRCL at Actual Mining Conditions

Further, the MRCL was extended up to the total length of 2819 m in phase II; Table 3 states all the parameters of phase II.

5.3. Calculation of Power Requirement and Factor of Safety for Man-Riding Lift Chair System in Both Phase I and Phase II

Comparison of phase I and phase II, including all engineering calculation parameters, is given in

Table 5. Power and Factor of Safety Calculation.

Calculation of Power and Rope Safety Factor		Phase I	Phase II	Unit
Diameter of drive unit sheave	$D$	1500	1500	mm
Rope diameter	$D_R$	16	16	mm
Minimum breaking force for 16 sq. mm rope	$F_{RB}$	167	167	KN
Weight of wire rope	$W_R$	91.5	91.5	kg/100 m
Weight of 15 m wire rope	$W_{R15}$	13.73	13.73	kg
Travelling speed	S	1.5	1.5	m/s
Distance between two chairs	$L_c$	15	15	m
Man-riding capacity	$M_c$	360	360	Pers/h
Total length of installation	L	1396	2819	m
Over all maximum inclination over the span	α max	11.3	11.3	Deg
Distance between the pulley station	$L_P$	15	15	m
Summary of the angles of all the horizontal curves	${\alpha }_H$	180	256	Deg
Summary of the angles of all the vertical curves	${\alpha }_V$	36	61	Deg
Rolling resistance of each pulley station	$R_{PS}$	20	20	N
Rolling resistance due to a rope deviation of 3 degrees (curves, synclines, anticlines)	$R_{\theta }$	39	39	N
Resulting slope force	$F_H$	13,226	15,407	N
Resulting in the rolling resistance of pulleys on either side	$F_R$	4752	8043	N
Efficiency of the drive unit	ɳ	0.9	0.9
Required pulling force	$F_P$	23	32	KN
Required output of the drive unit	$P_o$	65	90	KW
Required input of the drive unit (e-motor)	$P_i$	72	100	KW
Required capacity of electric motor	$P_E$	80	110	KW
Capacity of L motor to be selected	M	110	110	KW
Rope safety factor	$S.F_R$	12.6	10.8
Effective length of installation for total vertical deflection of 60 (approx.)	LE	1454	2936	M
Maximum number of riders for the installation	$N_R$	186	376	Nos.
Horizontal component of force acting on wire rope	FHC	−1165	−2630	N
Vertical component of force acting on suspension tubes at full capacity of the chair lift system	FVS	195,795	395,743	N
Number of suspension tubes for the total of chairlift system	T	100	202	N
Self-weight of suspension tube with carrying and depression pulley	WST	100	100	kg
Force acting on each suspension tube due to its own weight	FSS	981	981	N
Force on each suspension tube at maximum capacity of chairlift system	FST	2939	2940	N
Force acting on each suspension tube with two persons passing at the same time	FSP	3212	3212	N
Maximum permissible load bearing of each roof blot of two numbers fixed in suspension tube	ST	3.11	3.11	N
Force on tensioning rope due to counter weight	FCW	14,715	14,715	N
Force acting on tensioning rope	FWR	13,550	12,084	N
Minimum breaking force of the tensioning rope	$F_{TB}$	167,000	167,000	N
Factor of safety of tensioning rope	$S.F_{TR}$	12.32	13.81

.

The rope should be galvanized and have a long life under typical conditions. The rope’s speed should be changeable between 0 and 3 m/s. The breaking load of the rope should be at least ten times greater than the maximum static load. The time length was set at one year, and it must be assured that this rope life is not exceeded. The rope must adhere to the Indian Standard for aerial ropeways as well as the applicable clause of the Coal Mines Regulations, 2017 [25].

Table 6. Steel Wire Rope Specifications.

Steel Wire Rope	Nominal Diameter	Length	Construction	Strand Construction	Tensile Grade	Type of Core	Lay Direction	Minimum Breaking Force
IS-1855/2003 (Marked)	16 mm IS 6594	Phase I—3 km Phase II—6 km	6 × 7, preformed, galvanized	6-1	1960 N/mm2	SISAL	RHL IS 6594	16 mm2 = 167 KN IS 1608

contains the technical specifications for steel wire rope.

If the rope diameter falls below 10% of its original value, and there are more than 17 broken wires in a 1.5 m length or more than 8 broken wires in a 0.24 m length, the rope must be replaced [26].

6. Analytical Approaches

In the deterministic approach of design considered the strength of the material and the stress applied on it, under this assumption, FOS will be:

Factor of Safety (FOS) = Strength/Stress

(26)

Design margin (M) = Strength − Stress

(27)

However, the reality of the situation is portrayed in the probabilistic method, where stress and strength both vary during operation. The stress fluctuates according to loading cycles, whereas the strength varies due to material deterioration associated with aging, fatigue, corrosion, temperature, and so on. Given that the steel wire rope’s strength and the force applied in phases I and II are normally distributed, the interaction between load and strength in Figure 10 shows that the greater the safety margin, the safer the system and vice versa. The selection and customization of the range of safety margins is dependent on the system’s applicability and standard norms. High safety factor at a high design margin results in low failure rate [27,28,29,30].

Safety Margin M = Strength − Load

As far as the safety of the steel wire rope is concerned, the difference between strength and load will be ten times the load, i.e., FOS is 10.

Steel wire rope should be replaced when the strength is less than ten times the load, or S − L < 10 L.

When ten times the load increases the figure of strength:

S > 10 L

(28)

μ_M = μ_S − μ_L

σ_m² = σ_s² + σ_L² + 2σ_SL

2σ_SL = 0

if S and L are independent variables.

Therefore,

σ_m² = σ_s² + σ_L²

Probability of failure (Pf):

Z = (M × μ_m)/σ_m

Pf = φ (Z)

Pf = φ (μ_m/σ_m)

= 1 − φ (μ_m/σ_m)

(29)

Reliability of a system:

Reliability = 1 − probability of failure

R = 1 − Pf

= 1 − (1 − φ (μ_m/σ_m))

= φ (μ_m/σ_m)

= φ (β), β = Reliability index

β = μ_m/σ_m = (μ_s − μL)/(σ_s² + σ_l²)^1/2

(30)

Probability of safety or reliability:

Ps = ∅(β)

Probability of failure:

1 − ∅(β)

In Figure 11, the green area represents the MRCL operation’s reliable and safe zone, where the F.O.S. is greater than 10.

7. Computational Approach

The Creo 8.0 version was used to create a model of a 16 mm², seven-strand, right-hand-lay steel wire rope for analysis in Ansys R16. 2 software. Figure 12 depicts a rope model that was produced for use in the program.

Figure 13 and Figure 14 depict the equivalent stress and normal stress that resulted from applying the mathematically predicted required pulling force in phase I.

Figure 15 and Figure 16 depict the equivalent stress and normal stress that resulted from applying the mathematically predicted required pulling force in phase II.

Table 7. Summary of computational approach.

Sr. No.	Phase	Normal Stress (Mpa)	Equivalent Stress (MPa)
1	Phase I (22.7 KN)	1.25	15.27
2	Phase II (31.4 KN)	2.62	18.75

has illustrated the overall summary of computational approach.

8. Results and Discussion

In this research, mathematical calculations were performed to account for the undulation of underground mines during the design, installation, and extension stages of the MRCL. The minimal breaking force of steel wire rope and the consequent applied force are critical components of design, installation, and extension [31,32,33]. According to the OEM test certificate, the minimum breaking force of 16 sq. mm steel wire rope is 167 KN. The resulting slope forces in phases I and II are 13.226 KN and 15.407 KN, respectively, and the factor of safety is above the recommended limits, i.e., FOS = 10, in both situations and the results are comparable with the existing studies [34,35,36]. It was demonstrated using an analytical approach that the likelihood of failure is about equal to zero, and the probability of safety is approximately equal to one at the reliability index (β) ≥ 3. The steel wire rope’s recommended safety factor is 10; therefore, the MRCL must run at 10 times and above the maximum practically applied resulting slope forces on it [37,38]. For the reliability index value of β = 8.95, shown in Figure 10, the evaluated FOS is 10, beyond which the MRCL must operate. The outcome of a steel wire rope simulation model in Ansys R 16.2 software indicates a very minor difference in equivalent stresses, 15.27 MPa and 18.75 MPa in phase I and phase II, respectively, when the appropriate pulling forces of both phases are applied to it and the findings are superior than existing studies [38,39].

9. Conclusions

The MRCL system is a man-riding arrangement designed to move workers in and out of underground mines. It is an endless machine that uses two pulleys, drive and return, to rotate steel wire rope. Curve, carrying, and depression pulleys are used to guide and support the rope of the MRCL installation all the way along its length. As a result of the rope rotating over them, these pulleys are constantly in motion when the MRCL is operating. Following extensive research, it has been determined that the design of a 110 KW electrohydraulic power pack, installation of 1396 m, and extension of the MRCL to a total length of 2819 m is viable in Saoner underground mine no. 1. The steel wire rope must be operated at or above FOS 10 to comply with safety regulations. The minimum breaking strength of a 16 sq mm steel wire rope is 167 KN, and the rope can only be operated with slope forces as high as 16.7 KN. The steel wire rope must be replaced after one year of continuous usage consisting of a minimum of 12 h a day, i.e., 12 × 365 = 4380 h, or every 10% reduction in the original cross-sectional area, whichever comes first. The strength of the steel wire rope decreases as its cross-sectional area decreases, and the impact of the practically resulting slope forces increases as the rope length and angles increase. Both occurrences reduce the factor of safety below ten, which violates the safety norms established by DGMS for the use of steel wire rope in the MRCL. Risk assessment while using the MRCL is negligible, and it is safe for operation for miners while going in and out and to and from the mines.

The novel aspect of this research is that the load was computed mathematically for each and every load-bearing portion of the MRCL and was then validated experimentally and analytically. For both stages, a simulation model of steel wire was examined under the established stresses under loading conditions. This study can aid in the resolution of real-world issues involving the consideration of safety factors for design requirements that include stress and strength characteristics. The study could be useful for any system that deals with changing loads. Studies show that the maximum load applied is below the required factor of safety or the safety standards of the design criteria.