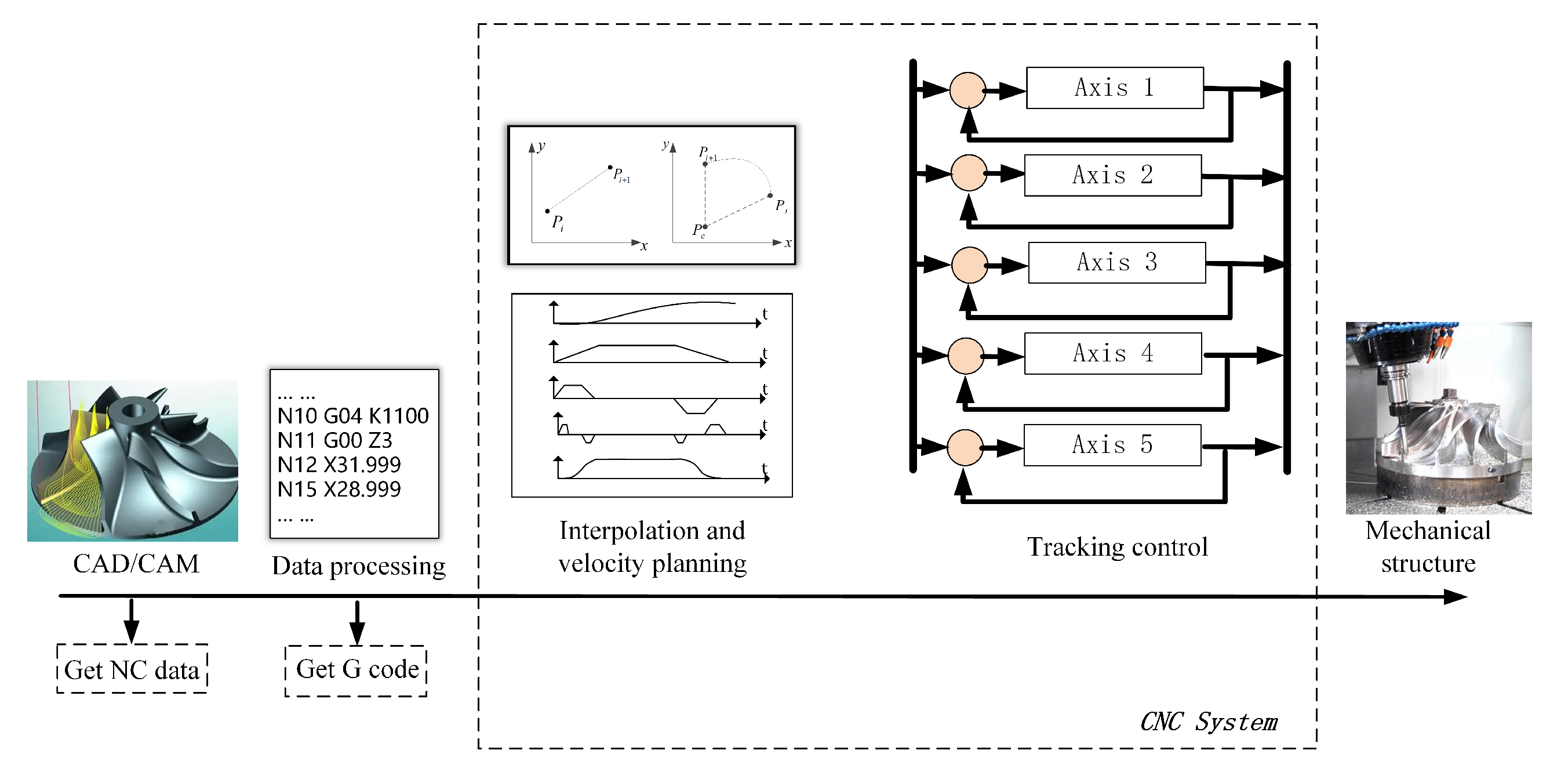
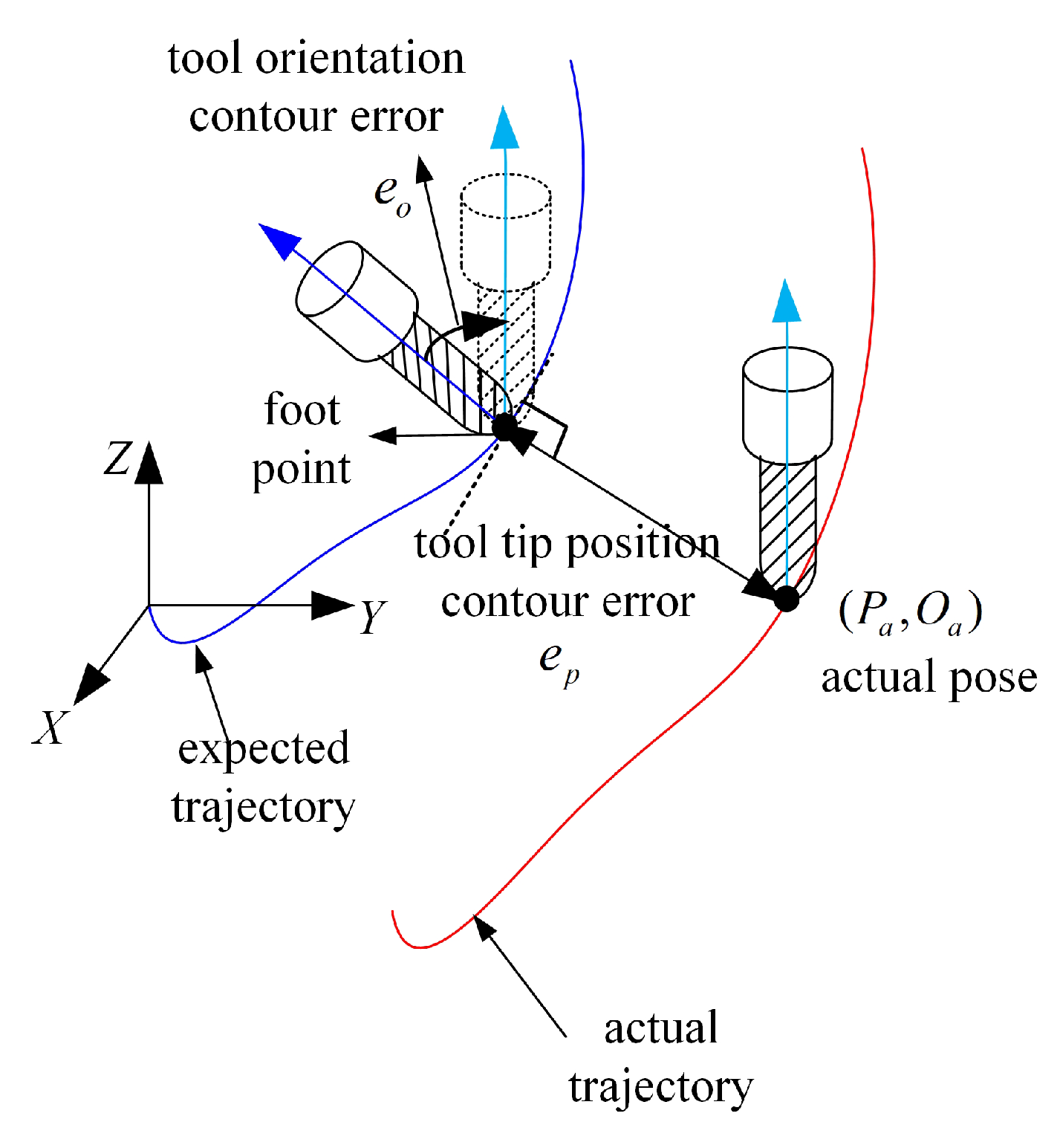
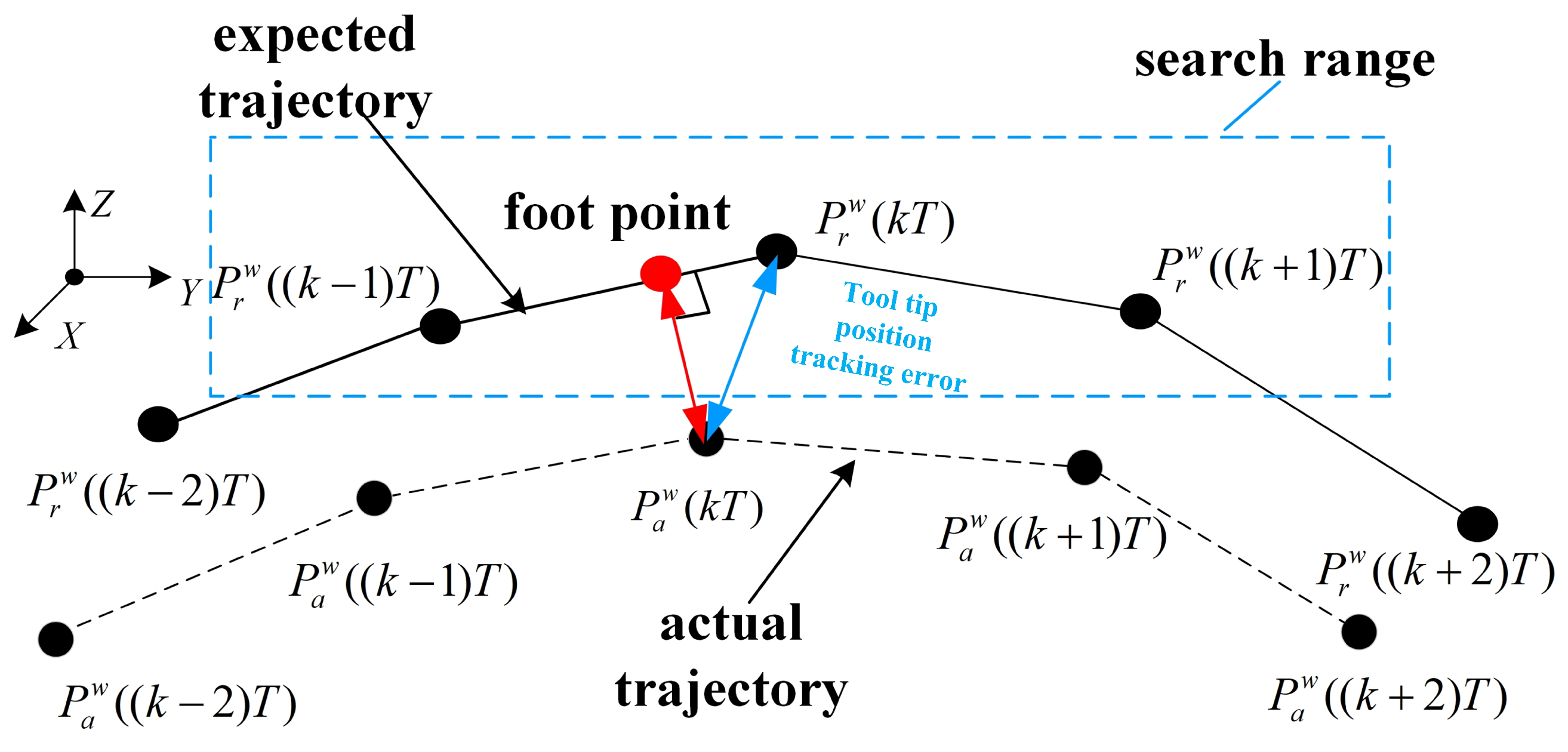
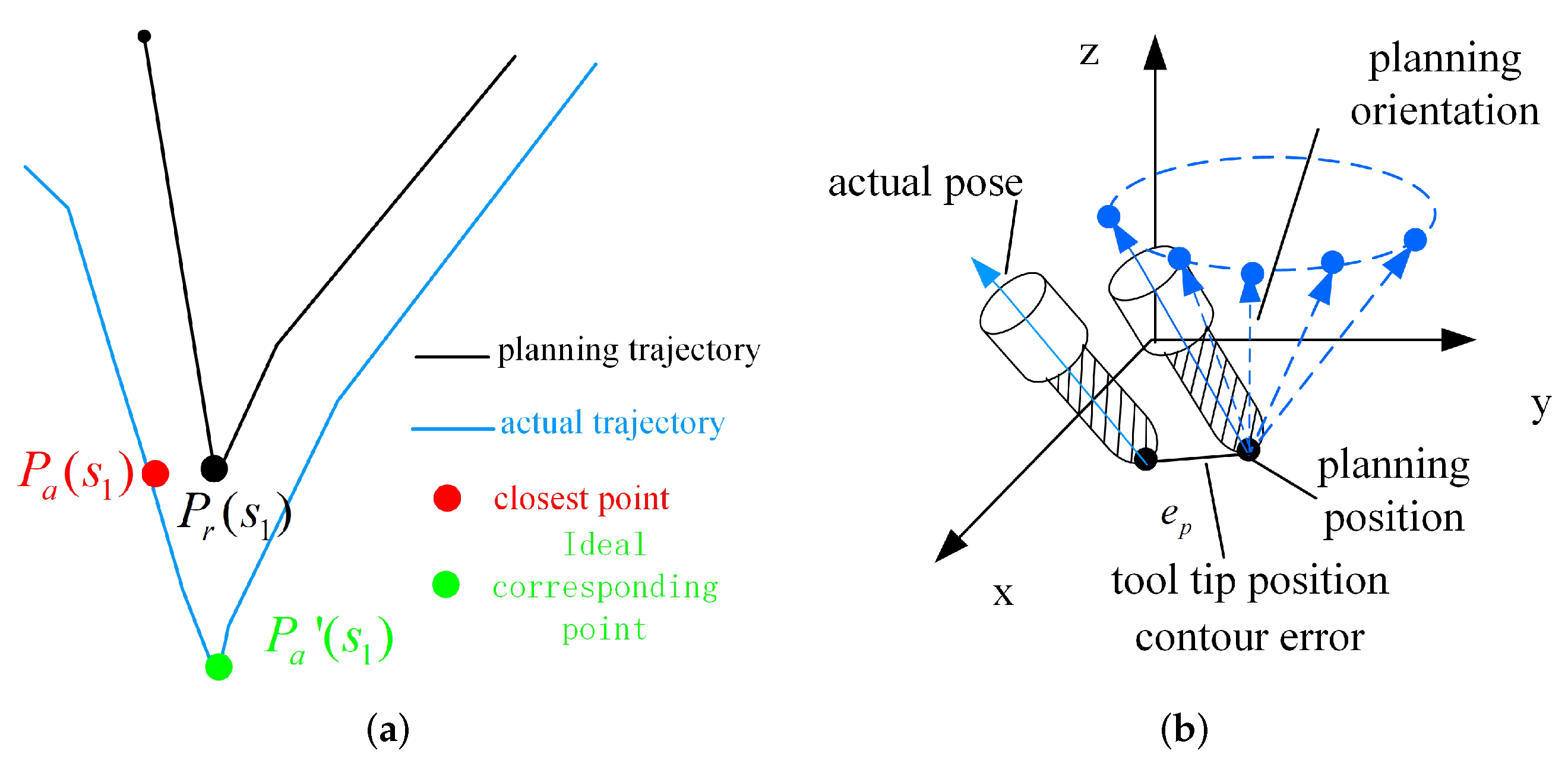
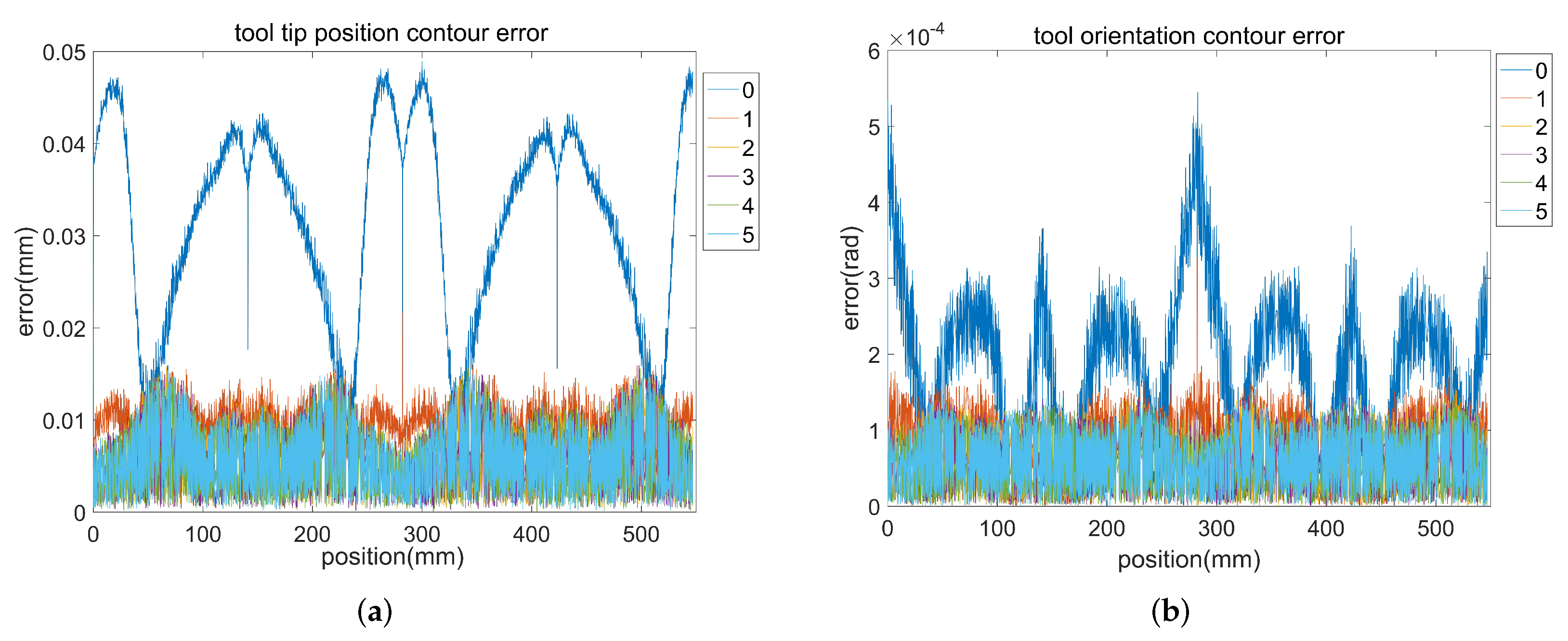
Therefore, this paper improves the current estimation method into a hybrid form to solve the problems above.
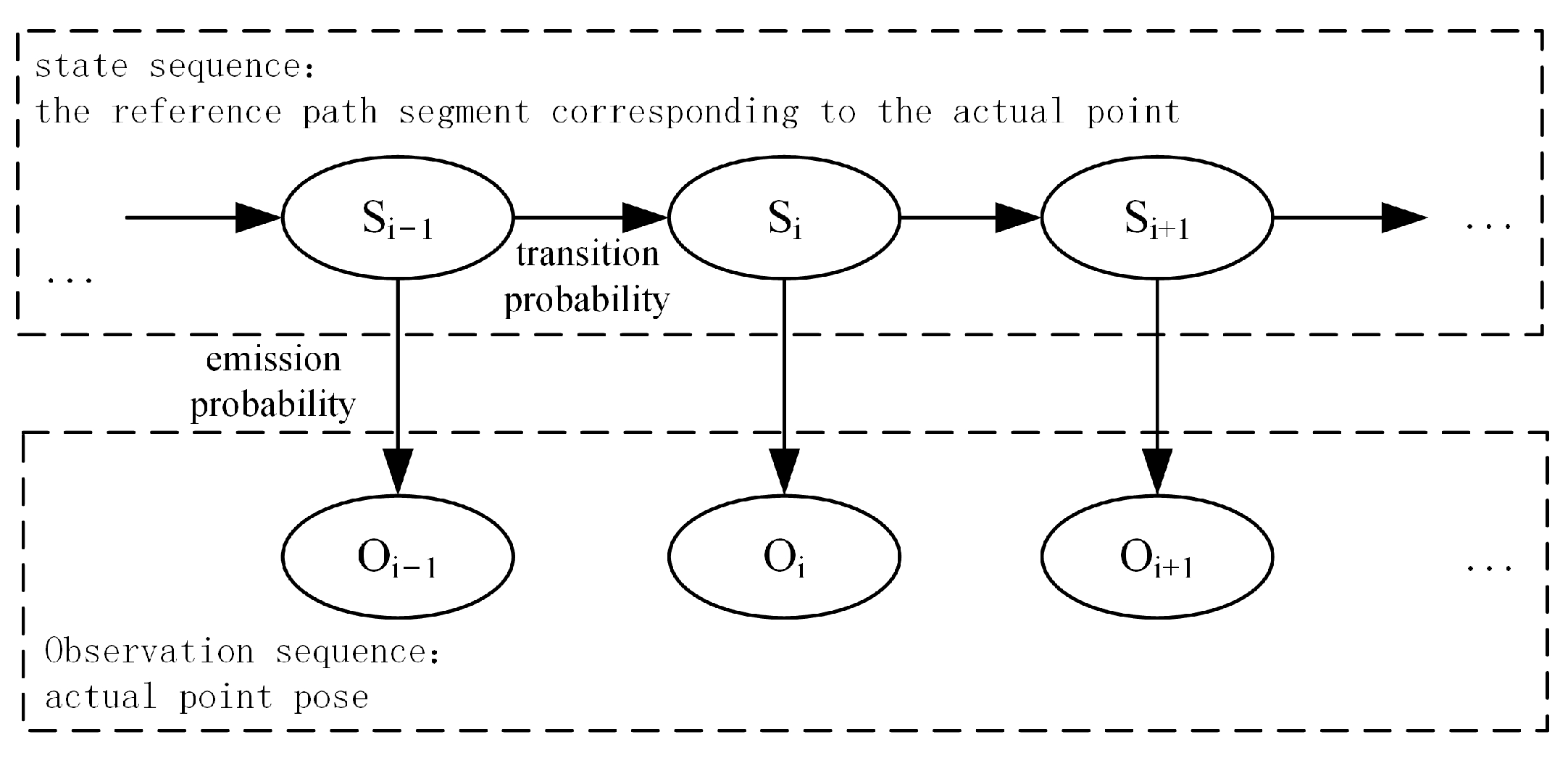
3.1. Establishment of Spatial Mapping Relationship Based on Hidden Markov Model
Before calculating the contour error, we need to establish a mapping relationship between actual trajectory and expected path so that we can determine the range of finding foot points. In this paper, we uses the hidden Markov model to map the actual trajectory points to the expected path segment.
In this application, the discrete points of the actual trajectory are regarded as the observation sequence
, the expected path segment is regarded as the state sequence
. One of the fundamental problems that the hidden Markov model can solve is estimating the state sequence with the highest probability under the premise of knowing the observation sequence, emission probability, and transition probability, so it can obtain the most possible sequence of the expected path segment corresponding to the actual points. The model structure is shown in
Figure 6.
In this model, the transition probability refers to the probability of transferring from one state to another state, and the emission probability refers to the probability that the state corresponds to the observation. Based on empirical considerations, the closer the actual point is to the expected path segment, the more possible it is that it corresponds to the segment. So, the emission probability is mainly based on the distance between the actual point and the expected path. Considering the geometric characteristics of the path, the probability of transferring from one segment to the next segment depends on the derection of the path and point’s movement. The transition probability depends on the sum of the deviations between the motion direction of actual points and the possible corresponding path. The specific calculation method is as follows.
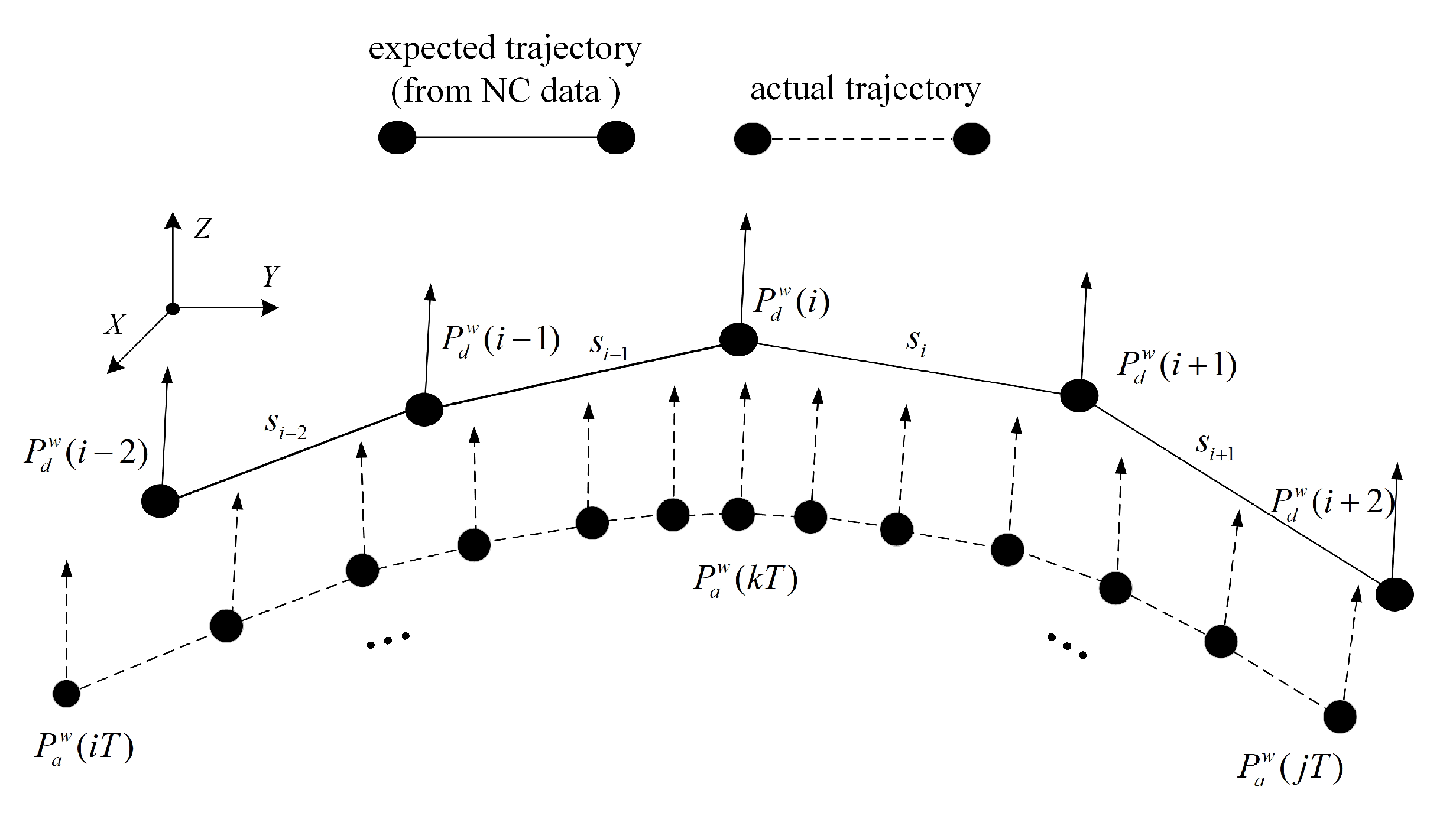
As shown in
Figure 7, assume that the sensor takes
T as the sampling period. The actual points are
. The discrete points
on the expected path have only order but no time stamp. Here, we represent segment
with
and represent the segment corresponding to
with
. According to the hidden Markov model, (
4) expresses the probability that all actual points correspond to the possible expected path. The expected path sequence with the maximal probability calculated by (
4) is the sequence that the actual points sequence corresponds to.
In (
4), the first part
represents the probability that the actual point
corresponds to
. The second part
is the transition probability. Among them,
and
may be the same segment or two adjacent segments.
k only means that is corresponding to the actual point at the moment
.
Since the probability range is , multiplying multiple probabilities may result in overflow or inaccurate results. Therefore, this paper uses cost instead of probability such that the problem of finding the expected path sequence with the maximal probability is transformed into the problem of finding the expected path sequence with the minimum cost.
The emission cost is defined as the distance from the actual point to the expected path.
indicates that the cost of
corresponding to the actual point
is the expected path
.
v represents that it is the emission cost. Its formula is shown in (
5):
The transition cost is denoted by
, where
indicates that the expected path segment corresponding to
is
, and the expected path segment corresponding to
is
. Its formula is shown in (
6):
Among them,
is the angle difference between the motion direction of the actual point
and its corresponding path
. In the example in
Figure 8, corresponding path
is
.
It is assumed that the first actual point corresponds to the first segment , so . Then the second actual point has two possible situation. One is that corresponds to the same segment as , i.e., both of them correspond to . In this case, . The other is that corresponds to the next segment of , i.e., corresponds to . In this case, . The costs of the two corresponding sequences can be calculated separately.
In the first case: both
and
correspond to
, and the cost is shown in (
7), where
is the distance from point
to segment
,
is the sum of the two angles, i.e.,
and
,
is the angle difference between the motion direction of
and the direction of
, and
is the angle difference between the motion direction of
and the direction of
.
Second possible case:
corresponds to
, and
corresponds to
. The cost, in this case, is shown in (
8). Where
is the distance from point
to line segment
;
is the sum of two angles, i.e.,
and
,
is the angle difference between the motion direction of point
and the direction of line segment
, and
is the angle difference between the motion direction of point
and the direction of line segment
.
Next, continue to calculate the segment that may correspond to. In the first case above, there are two corresponding situations: and correspond to the same segment or corresponds to the next segment of , . In the second case above, there are also two situations: and correspond to the same segment or corresponds the next segment of , . From this, calculate all possible planned path segment costs when reaching .
When
correspond to the expected path sequence
, this sequence is under the condition of the first corresponding case of
above, and its cost is shown in (
9), where
can be obtained from (
7).
When
correspond to the expected path sequence
, this sequence is also under the condition of the first corresponding case of
above, and its cost is shown in (
10).
When
correspond to the expected path sequence
, this sequence is under the condition of the second corresponding case of
above, and its cost is shown in (
11).
When
correspond to the expected path sequence
, this sequence is also under the condition of the second corresponding case of
above, and its cost is shown in (
12).
For a five-axis CNC system, another point is selected to consider the influence of the tool orientation. For example, for point
shown in
Figure 9, calculate the distance and direction deviation between it and point
on the expected tool orientation to form a line segment. When calculating the emission cost and transition cost, (
13) and (
14) are used for calculation.
Finally, the Vertibe algorithm can calculate the sequence with the maximal probability. In this case, a certain mapping relationship can be established between the actual point and the expected path. Then the contour error can be calculated based on the contents of this section.
3.2. Tool Tip Position and Tool Orientation Contour Error Estimation
To address the problem that the current contour error estimation algorithm uses the closest tool tip position as the basis to calculate the overall contour error, this paper proposes an evaluation function that comprehensively considers the influence of tool tip position and orientation. The evaluation function is shown in (
15). When calculating the contour error at a reference point, the actual point for calculating the contour error is no longer determined by the minimum tool tip position distance, but by the minimum evaluation function.
In (
15),
and
are the tool tip position and tool orientation deviation from a reference point to a actual point and
is the modulus of
.
and
are two coefficients change with the changing trend of the tool tip position and tool orientation. If the position of the tool tip changes sharply,
will be larger, and
plays a major role in (
15). Otherwise,
will be larger, and
F is mainly affected by
. Since the dimensions and magnitudes of the two deviations of
and
are not uniform, the coefficient
R is used for adjustment. The calculation method of the above coefficients is described below.
As shown in
Figure 10, the tool tip position changing speed at the reference point
can be estimated as (
16). Tool orientation changing speed can be calculated by (
17).
In the workpiece coordinate, the tool tip position coordinates of point
can be expressed as
, and the tool orientation vector is expressed as
,
in (
16) can be calculated by (
18) and
can be calculated by (
19).
Finally, the coefficients are normalized, and the parameters
and
are calculated using (
20) and (
21), respectively. Finally, the coefficient R is determined according to the tool position and orientation changes of the machining reference path. So far, all the parameters in (
15) except the angle deviation
and distance deviation
have been obtained.
In
Section 3.1, each actual point corresponds to the expected path segment. As shown in
Figure 10, assume that all points between point
and
correspond to the reference path segment
, and points
to
correspond to the reference path segment
. Then, when calculating the contour error of
, the estimation range is narrowed down to the actual points corresponding to the adjacent segments of
. For example, for
, actual points
,
, and
respectively correspond to segments
and
. We select
,
, and
to fit the actual trajectory with a quadratic polynomial. Taking the x-axis as an example, when the x-axis displacements corresponding to
,
, and
are
,
, and
, respectively, the fitting is performed with a quadratic polynomial:
Substitute
into (
23) to obtain (
23).
Substitute the coordinates of each point and (
23) can be solved:
Therefore, the actual trajectory from
to
is decomposed to the x-axis and can be fitted by (
21), and the fitting parameters can be obtained. Similarly, the above methods can solve the fitting equations of the actual points
to
in the sliding window interval corresponding to the reference point
for other axes.
After substituting (
25) into the kinematics forward solution conversion formula obtained from the machine tool structure, the tool tip position and tool orientation of the actual trajectory used to calculate contour error can be converted into a function of
t. The tool tip position coordinates and tool orientation vectors of the trajectory between the actual point
and
in the workpiece coordinate can be expressed as:
, i.e., a function with
t as a variable.
For each reference point
, the actual trajectory for calculating the contour error can be expressed. Then, the position distance from the current reference point to the trajectory can be calculated by (
27), (
26) can represent the tool orientation deviation from the current reference point to the actual trajectory.
After substituting (
26) and (
27) into (
15), the current evaluation function can be expressed as an expression with
t as the variable shown in (
28).
Calculate the value of
t to the minimum evaluation function and get
. Take
into (
24) and (
23). The obtained
and
are the tool orientation and tool tip position contour errors at the reference point. If the reference point is
, the tool orientation and tool tip position contour error are denoted as
and
, respectively.