CHBS-Net: 3D Point Cloud Segmentation Network with Key Feature Guidance for Circular Hole Boundaries
Abstract
:1. Introduction
- A novel segmentation network is proposed, which aims to achieve accurate segmentation of circular hole boundary points and improve the accuracy of fitting parameters.
- An encoding–decoding–attention fusion mechanism is designed. This mechanism utilizes key features in the boundary region of the circular hole to guide the point cloud segmentation.
- An LSTM parallel structure is introduced for modeling contour continuity and temporal relationships between boundary points.
- Feature extraction in neighborhoods of different scales is performed by considering point cloud features in neighborhoods of different ranges. This reduces the interference of neighboring points at boundary points on the segmentation results.
2. Related Work
2.1. Convolutional Neural Network-Based Point Cloud Segmentation Algorithm
2.2. Graph Neural Network-Based Point Cloud Segmentation Algorithm
2.3. Attention-Based Point Cloud Segmentation Algorithm
2.4. Transformer-Based Point Cloud Segmentation Algorithm
2.5. Practical Considerations
3. Methodology
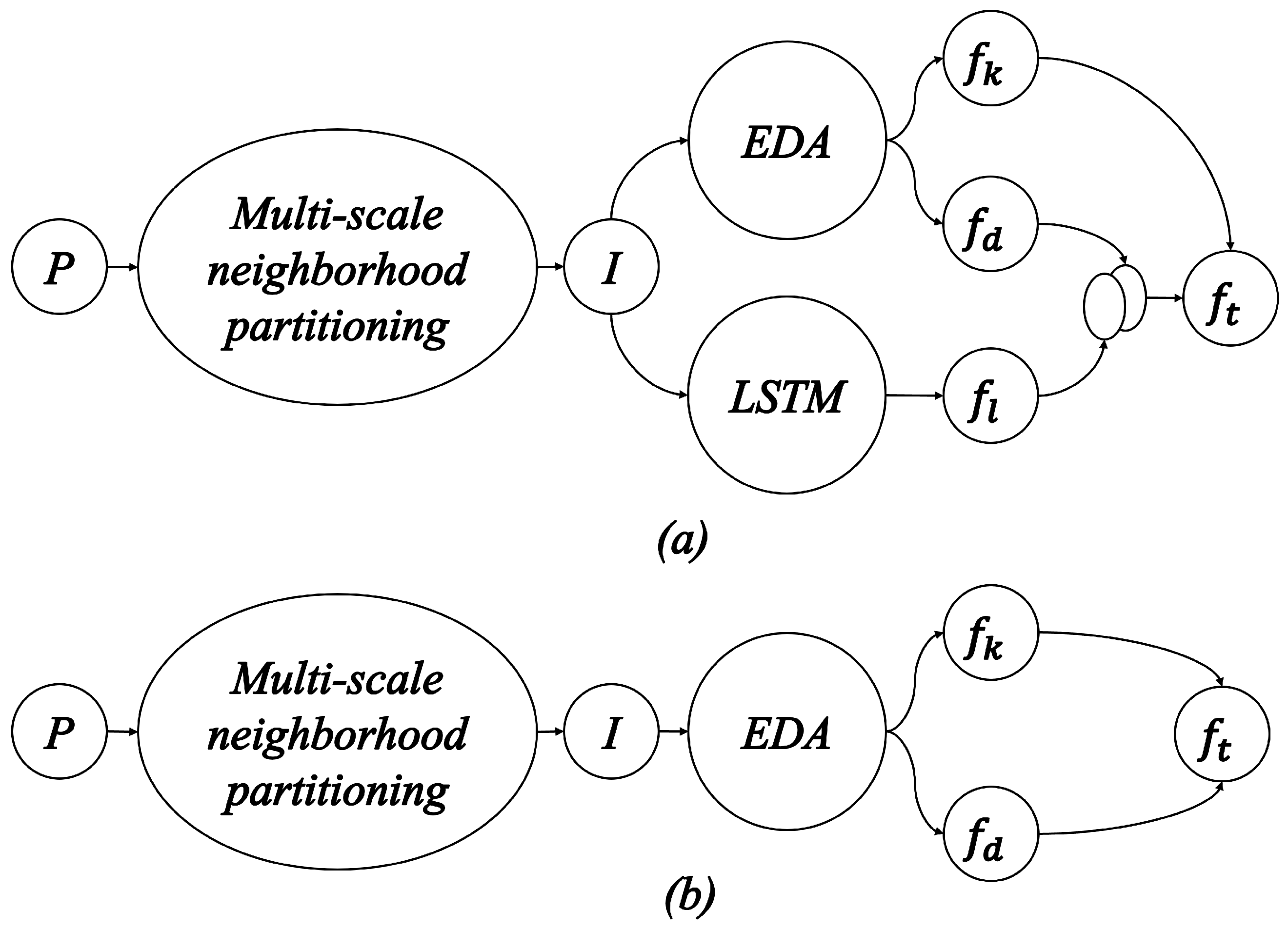
3.1. Encoding–Decoding–Attention Fusion Guidance Mechanism
- Encoder: The encoder comprises multiple layers responsible for extracting the circular hole boundary region from , as expressed in Equation (1).where is the learnable parameter of the encoder. The encoder consists of a series of convolutional layers, batch normalization layers, LeakyReLU activations, and random downsampling layers. The encoding features from each layer of the encoder are shared, and these features serve as inputs not only to the next layer but also to the decoder. The encoder is responsible for roughly delineating the circular hole boundary region from I.
- Spatial-channel attention module: This module consists of both spatial and channel statistical feature attention mechanisms, emphasizing different aspects of point cloud data importance. The spatial attention mechanism focuses on the significance of various locations in the point cloud data, while the channel attention mechanism accentuates the relevance of distinct channels within the point cloud data, as specified in Equations (2) and (3).where represents the learnable parameter of the spatial statistical feature attention mechanism, and represents the learnable parameter of the channel statistical feature attention mechanism.
- Decoder: The decoder is comprised of convolutional layers, batch normalization layers, LeakyReLU activations, and upsampling layers. Initially, undergoes upsampling, and the result is fused with features from the corresponding encoder layers. This fusion aims to recover essential details for the segmentation task, eventually yielding high-level semantic decoding features , as indicated in Equation (4).where is the learnable parameter of the decoder.
- Guidance information generation process: First, average pooling is applied to along the channel dimension. Subsequently, a multi-layer perceptron is applied to linearly transform the pooling result. Finally, the linear transformation result undergoes nonlinear activation using the tanh function to generate the W. The fusion process described above successfully empowers the training process to simultaneously optimize feature selection and spatial relationship modeling. It allocates more attention to key boundary points that contain important semantic information, thus alleviating the class imbalance problem as follows:where is the weight needed for in W. is the weight needed for in W. ⨀ denotes the Hadamard product of matrices.
3.2. LSTM Parallel Structure
3.3. Multi-Scale Neighborhood Partitioning
3.4. Circular Hole Boundary Segmentation-Net
3.5. Experiment Settings
4. Experimental Results Analysis
4.1. Implementation Details
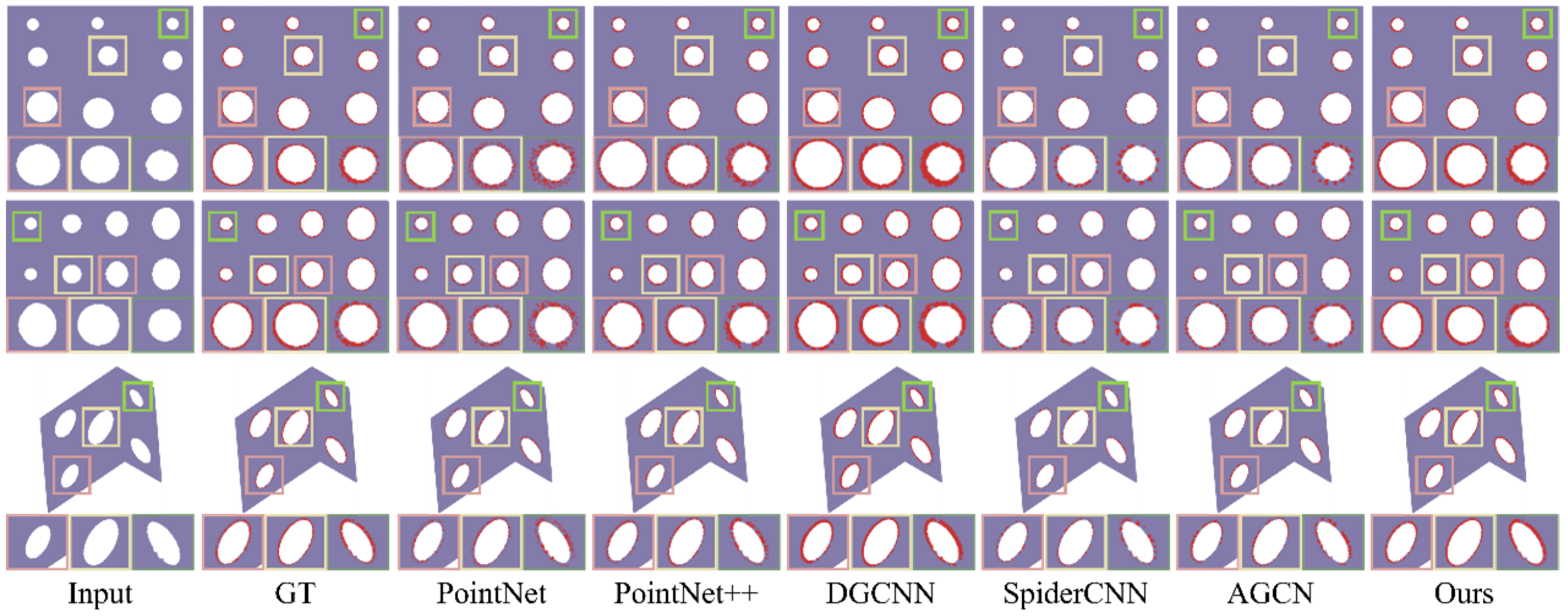
4.2. Experimental Results on the Sheet Metal Parts Dataset
4.3. Ablation Experiment
4.3.1. Effects of LSTM Parallel Structure
4.3.2. Effects of Multi-Scale Neighborhood Partitioning
5. Conclusions
6. Limitation Discussion and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, C.; Yu, H.; Gu, B.; Lin, Y. Modeling and analysis of assembly variation with non-uniform stiffness condensation for large thin-walled structures. Thin-Walled Struct. 2023, 191, 111042. [Google Scholar] [CrossRef]
- Li, Y.; Ma, L.; Zhong, Z.; Liu, F.; Chapman, M.A.; Cao, D.; Li, J. Deep Learning for LiDAR Point Clouds in Autonomous Driving: A Review. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3412–3432. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Lepetit, V.; Woo, W. Multiple 3D Object tracking for augmented reality. In Proceedings of the 2008 7th IEEE/ACM International Symposium on Mixed and Augmented Reality, Cambridge, UK, 15–18 September 2008; pp. 117–120. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; He, Q.; Fang, Z.; Fu, J. Grasping pose estimation for SCARA robot based on deep learning of point cloud. Int. J. Adv. Manuf. Technol. 2020, 108, 1217–1231. [Google Scholar] [CrossRef]
- Zhang, Z.; Malashkhia, L.; Zhang, Y.; Shevtshenko, E.; Wang, Y. Design of Gaussian process based model predictive control for seam tracking in a laser welding digital twin environment. J. Manuf. Process. 2022, 80, 816–828. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Y.; Zhang, L.; Gao, R.X.; Wu, D. Deep learning for smart manufacturing: Methods and applications. J. Manuf. Syst. 2018, 48, 144–156. [Google Scholar] [CrossRef]
- Yin, J.; Zhao, W. Fault diagnosis network design for vehicle on-board equipments of high-speed railway: A deep learning approach. Eng. Appl. Artif. Intell. 2016, 56, 250–259. [Google Scholar] [CrossRef]
- Li, C.; Sanchez, R.V.; Zurita, G.; Cerrada, M.; Cabrera, D.; Vásquez, R.E. Gearbox fault diagnosis based on deep random forest fusion of acoustic and vibratory signals. Mech. Syst. Signal Process. 2016, 76–77, 283–293. [Google Scholar] [CrossRef]
- Cheng, X.; Yu, J. RetinaNet with Difference Channel Attention and Adaptively Spatial Feature Fusion for Steel Surface Defect Detection. IEEE Trans. Instrum. Meas. 2021, 70, 2503911. [Google Scholar] [CrossRef]
- He, Y.; Song, K.; Meng, Q.; Yan, Y. An End-to-End Steel Surface Defect Detection Approach via Fusing Multiple Hierarchical Features. IEEE Trans. Instrum. Meas. 2020, 69, 1493–1504. [Google Scholar] [CrossRef]
- Xie, Y.; Tian, J.; Zhu, X.X. Linking Points with Labels in 3D: A Review of Point Cloud Semantic Segmentation. IEEE Geosci. Remote Sens. Mag. 2020, 8, 38–59. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.; Koltun, V. Point Transformer. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 16239–16248. [Google Scholar] [CrossRef]
- Zhang, C.; Wan, H.; Shen, X.; Wu, Z. PVT: Point-Voxel Transformer for Point Cloud Learning. arXiv 2022, arXiv:2108.06076. [Google Scholar] [CrossRef]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. Pct: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, J.; Peng, B. Point clouds learning with attention-based graph convolution networks. Neurocomputing 2020, 402, 245–255. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. arXiv 2019, arXiv:1801.07829. [Google Scholar] [CrossRef]
- Liang, Z.; Yang, M.; Deng, L.; Wang, C.; Wang, B. Hierarchical Depthwise Graph Convolutional Neural Network for 3D Semantic Segmentation of Point Clouds. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8152–8158. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Red Hook, NY, USA, 4–9 December 2017; pp. 5105–5114. [Google Scholar]
- Wu, B.; Zhou, X.; Zhao, S.; Yue, X.; Keutzer, K. SqueezeSegV2: Improved Model Structure and Unsupervised Domain Adaptation for Road-Object Segmentation from a LiDAR Point Cloud. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4376–4382. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Liu, Y. Three-Dimensional Point Cloud Segmentation Based on Context Feature for Sheet Metal Part Boundary Recognition. IEEE Trans. Instrum. Meas. 2023, 72, 2513710. [Google Scholar] [CrossRef]
- Choy, C.; Gwak, J.; Savarese, S. 4D Spatio-Temporal ConvNets: Minkowski Convolutional Neural Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3070–3079. [Google Scholar] [CrossRef]
- Komarichev, A.; Zhong, Z.; Hua, J. A-CNN: Annularly Convolutional Neural Networks on Point Clouds. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7413–7422. [Google Scholar] [CrossRef]
- Xu, M.; Ding, R.; Zhao, H.; Qi, X. PAConv: Position Adaptive Convolution with Dynamic Kernel Assembling on Point Clouds. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 3172–3181. [Google Scholar] [CrossRef]
- Lei, H.; Akhtar, N.; Mian, A. Spherical Kernel for Efficient Graph Convolution on 3D Point Clouds. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3664–3680. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Sun, X.; Wu, C.Y.; Wang, P.; Neumann, U. Grid-GCN for Fast and Scalable Point Cloud Learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5660–5669. [Google Scholar] [CrossRef]
- Li, G.; Müller, M.; Qian, G.; Delgadillo, I.C.; Abualshour, A.; Thabet, A.; Ghanem, B. DeepGCNs: Making GCNs Go as Deep as CNNs. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 6923–6939. [Google Scholar] [CrossRef] [PubMed]
- Lei, H.; Akhtar, N.; Mian, A. SegGCN: Efficient 3D Point Cloud Segmentation with Fuzzy Spherical Kernel. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11608–11617. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Ni, B.; Li, L.; Liu, J.; Zhou, M.; Tian, Q. Modeling Point Clouds with Self-Attention and Gumbel Subset Sampling. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3318–3327. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, W.; Lu, L.; Zhao, Q. Pooling Scores of Neighboring Points for Improved 3D Point Cloud Segmentation. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1475–1479. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11105–11114. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, X.; Li, J.; Fang, Z.; Jiang, X.; Huq, K.M.S. LFT-Net: Local Feature Transformer Network for Point Clouds Analysis. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2158–2168. [Google Scholar] [CrossRef]
- Thyagharajan, A.; Ummenhofer, B.; Laddha, P.; Omer, O.J.; Subramoney, S. Segment-Fusion: Hierarchical Context Fusion for Robust 3D Semantic Segmentation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–23 June 2022; pp. 1226–1235. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. SpiderCNN: Deep Learning on Point Sets with Parameterized Convolutional Filters. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Switzerland, 2018; pp. 90–105. [Google Scholar]
- Zhang, Y.; Zhou, Z.; David, P.; Yue, X.; Xi, Z.; Gong, B.; Foroosh, H. PolarNet: An Improved Grid Representation for Online LiDAR Point Clouds Semantic Segmentation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 9598–9607. [Google Scholar] [CrossRef]
- Wen, S.; Wang, T.; Tao, S. Hybrid CNN-LSTM Architecture for LiDAR Point Clouds Semantic Segmentation. IEEE Robot. Autom. Lett. 2022, 7, 5811–5818. [Google Scholar] [CrossRef]



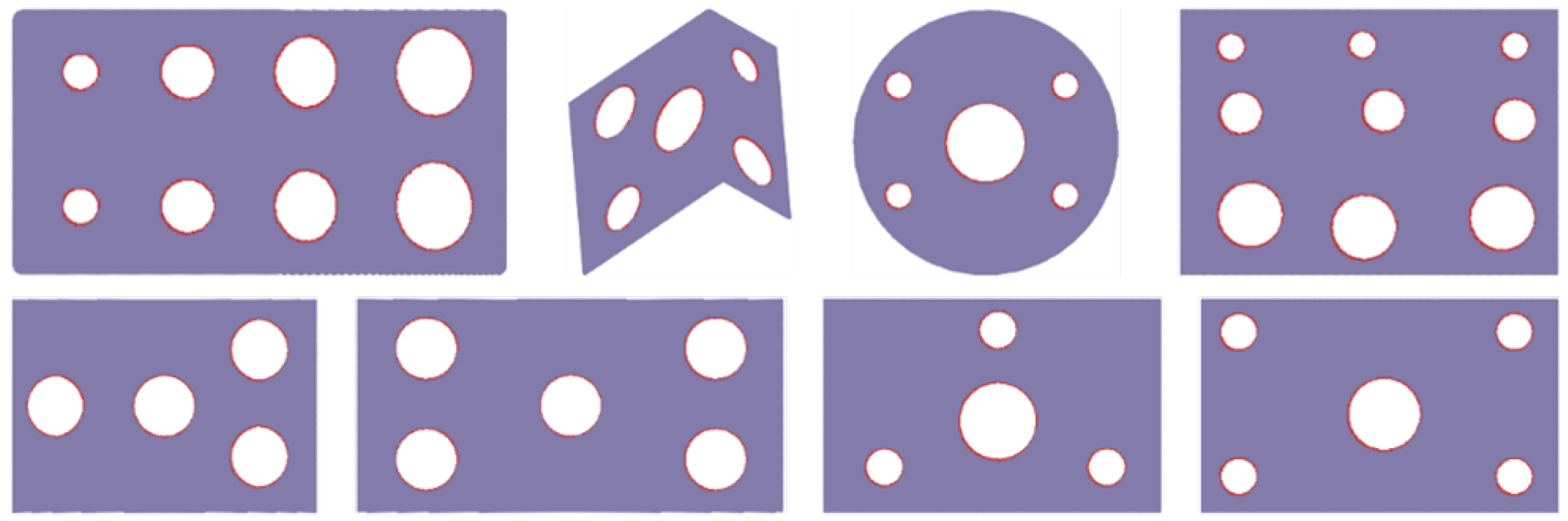

| Average Length of Parts (mm) | Average Width of Parts (mm) | Diameter of Circular Hole (mm) | FOV of the Camera (mm) | Maximum Number of Sampling Points | X-Direction Resolution (mm) | Scanning Speed (mm/s) |
|---|---|---|---|---|---|---|
| 450 | 200 | 10–100 | 145–425 | 1800 | 0.100–0.255 | 80 |
| Method | mIoU |
|---|---|
| PointNet [18] | 76.7 |
| PointNet++ [19] | 80.0 |
| DGCNN [16] | 83.6 |
| SpiderCNN [35] | 79.5 |
| AGCN [15] | 85.5 |
| Ours | 87.1 |
| Method | AD(c) | AD(r) | MSE(r) |
|---|---|---|---|
| PointNet [18] | 0.668 | 0.271 | 0.076 |
| PointNet++ [19] | 0.509 | 0.239 | 0.093 |
| DGCNN [16] | 0.467 | 0.297 | 0.090 |
| SpiderCNN [35] | 0.439 | 0.309 | 0.104 |
| AGCN [15] | 0.469 | 0.278 | 0.080 |
| Ours | 0.381 | 0.181 | 0.034 |
| Method | mIoU | AD(c) | AD(r) | MSE(r) |
|---|---|---|---|---|
| Net-S | 87.1 | 0.381 | 0.181 | 0.034 |
| Net-M | 85.3 | 0.494 | 0.298 | 0.103 |
| Index | Method | mIoU | AD(c) | AD(r) | MSE(r) |
|---|---|---|---|---|---|
| case.1 | - | 83.8 | 0.469 | 0.298 | 0.103 |
| case.2 | , | 83.2 | 0.482 | 0.283 | 0.096 |
| case.3 | , | 87.1 | 0.381 | 0.181 | 0.034 |
| case.4 | , | 85.1 | 0.431 | 0.325 | 0.111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, X.; Li, Y.; Liu, Y. CHBS-Net: 3D Point Cloud Segmentation Network with Key Feature Guidance for Circular Hole Boundaries. Machines 2023, 11, 982. https://doi.org/10.3390/machines11110982
Zhang J, Wang X, Li Y, Liu Y. CHBS-Net: 3D Point Cloud Segmentation Network with Key Feature Guidance for Circular Hole Boundaries. Machines. 2023; 11(11):982. https://doi.org/10.3390/machines11110982
Chicago/Turabian StyleZhang, Jiawei, Xueqi Wang, Yanzheng Li, and Yinhua Liu. 2023. "CHBS-Net: 3D Point Cloud Segmentation Network with Key Feature Guidance for Circular Hole Boundaries" Machines 11, no. 11: 982. https://doi.org/10.3390/machines11110982
APA StyleZhang, J., Wang, X., Li, Y., & Liu, Y. (2023). CHBS-Net: 3D Point Cloud Segmentation Network with Key Feature Guidance for Circular Hole Boundaries. Machines, 11(11), 982. https://doi.org/10.3390/machines11110982





