Damage Identification for Railway Tracks Using Onboard Monitoring Systems in In-Service Vehicles and Data Science
Abstract
:1. Introduction
- Detecting early-stage damage to railway tracks using artificial intelligence and simulated railway vehicle vibration measurements, recorded by in-service vehicles;
- Create conditions for the operational and technical integration of railway track dynamic monitoring and maintenance for different railway networks;
- Validate the developed artificial intelligence algorithm for damage detection to railway track using axle box accelerations registered by a freight wagon, considering an optimized number of accelerometers, big data, and operational and simulated environmental conditions, for railway decisionmakers in order to be integrated, later, into an in-service wagon.
2. Numerical Modeling of Vehicle–Track Dynamic System
2.1. Vehicle Model
2.2. Track Model
2.3. Modeling of Vehicle–Track Dynamic Interaction
3. Simulation of Baseline and Damage Scenarios
3.1. Baseline
3.2. Damage
4. Vehicle Dynamic Responses
5. AI-Based Methodology for Railway Track Damage Detection
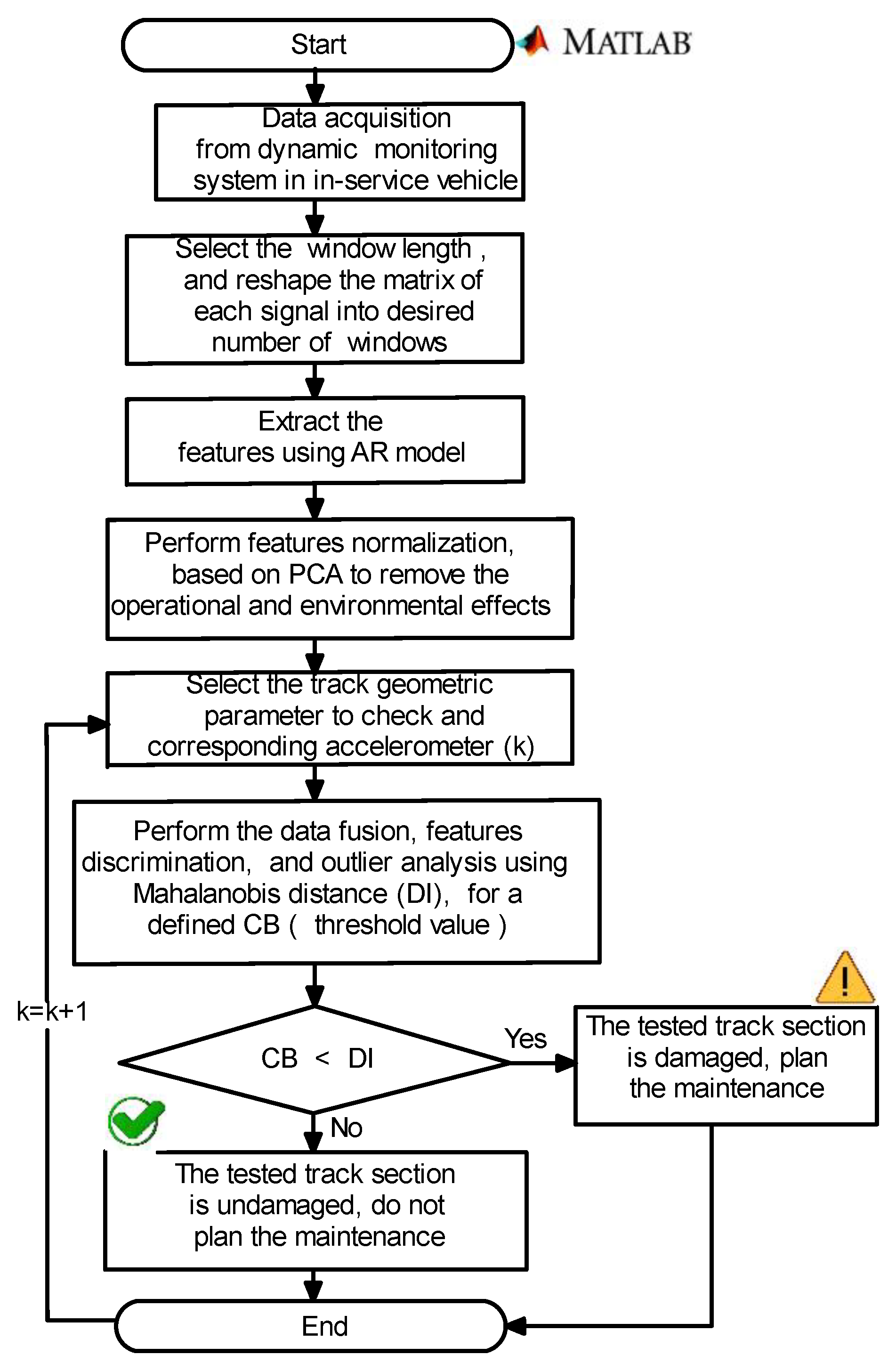
5.1. Overview
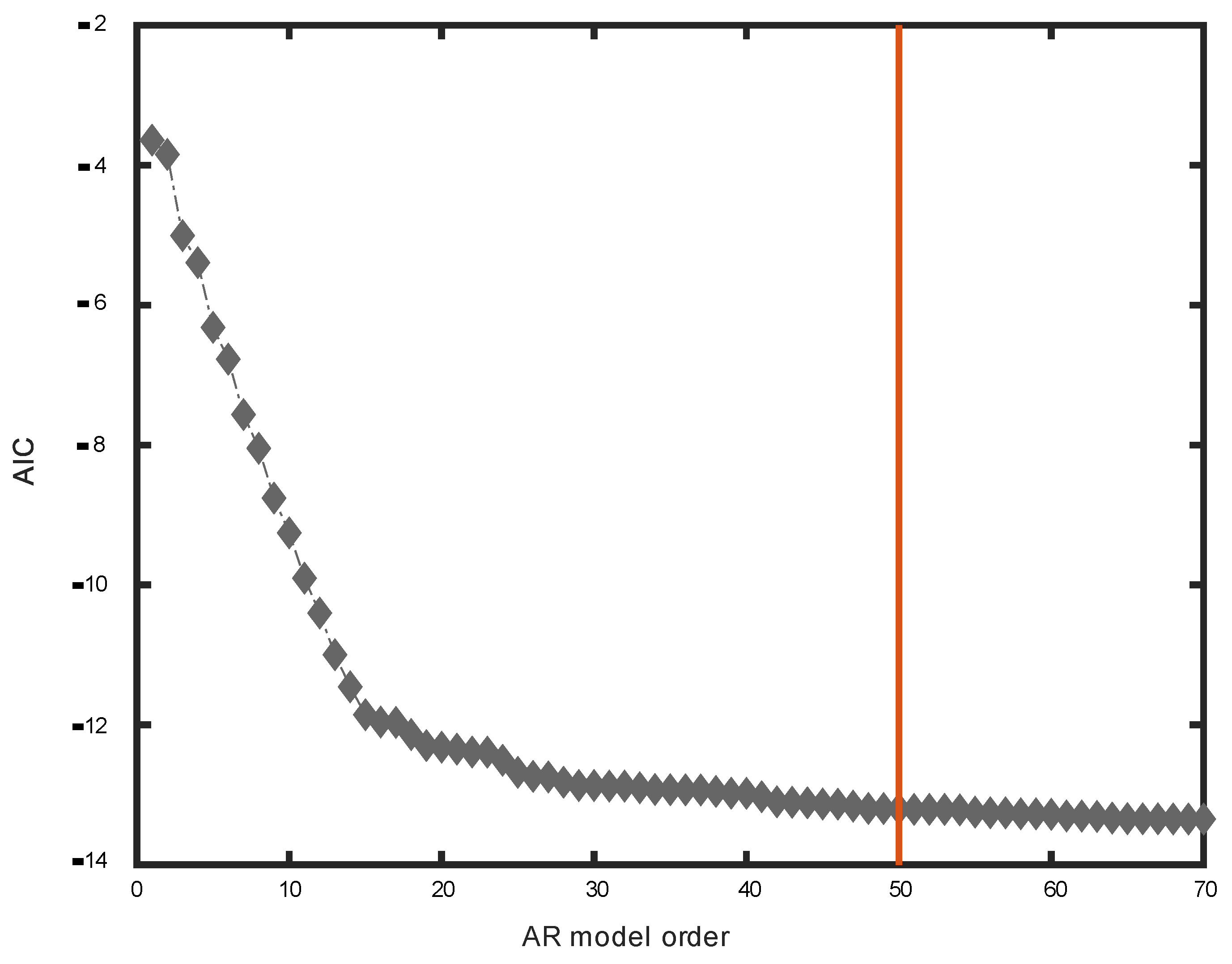
5.2. Feature Extraction
5.3. Feature Normalization
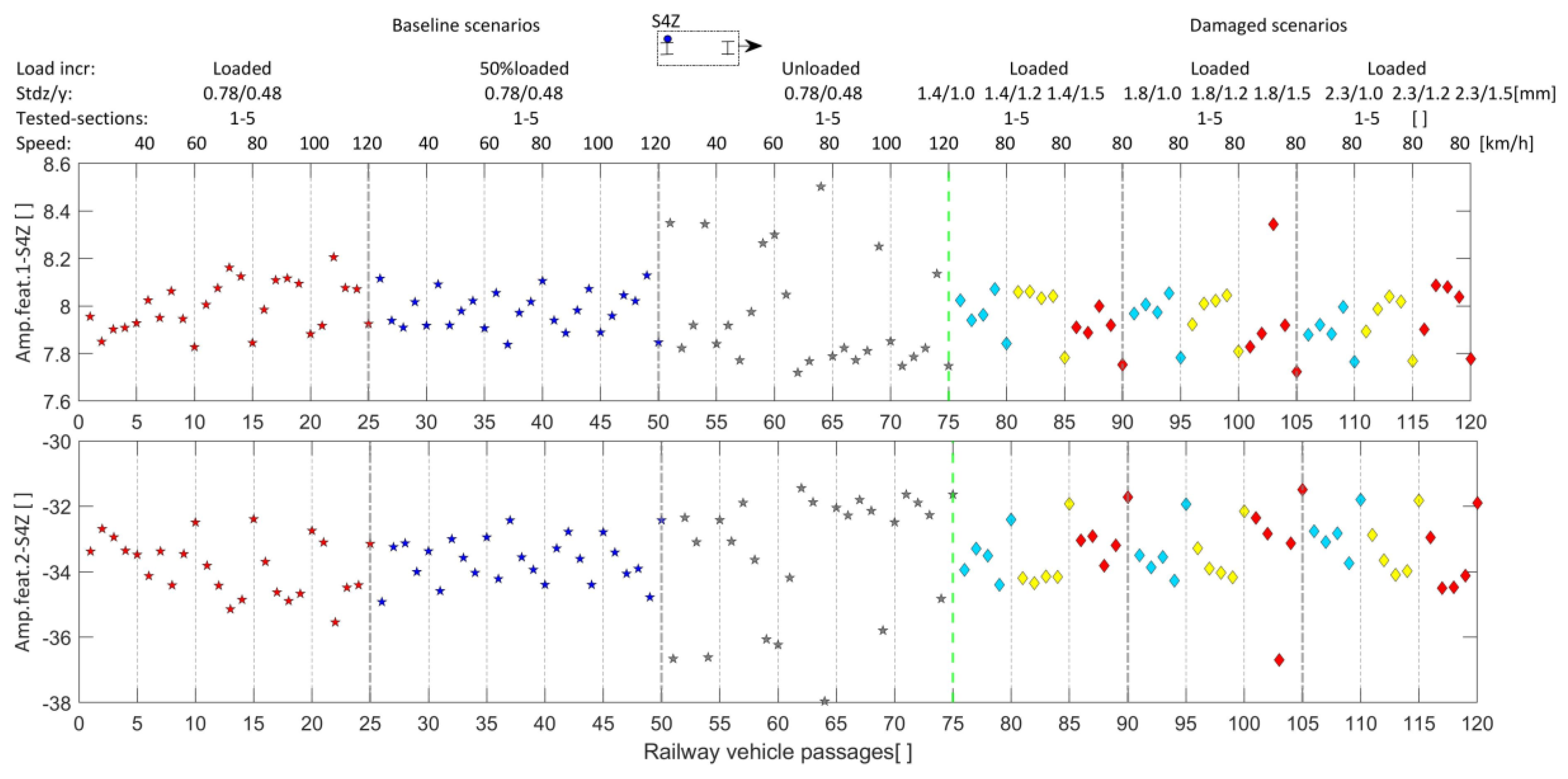
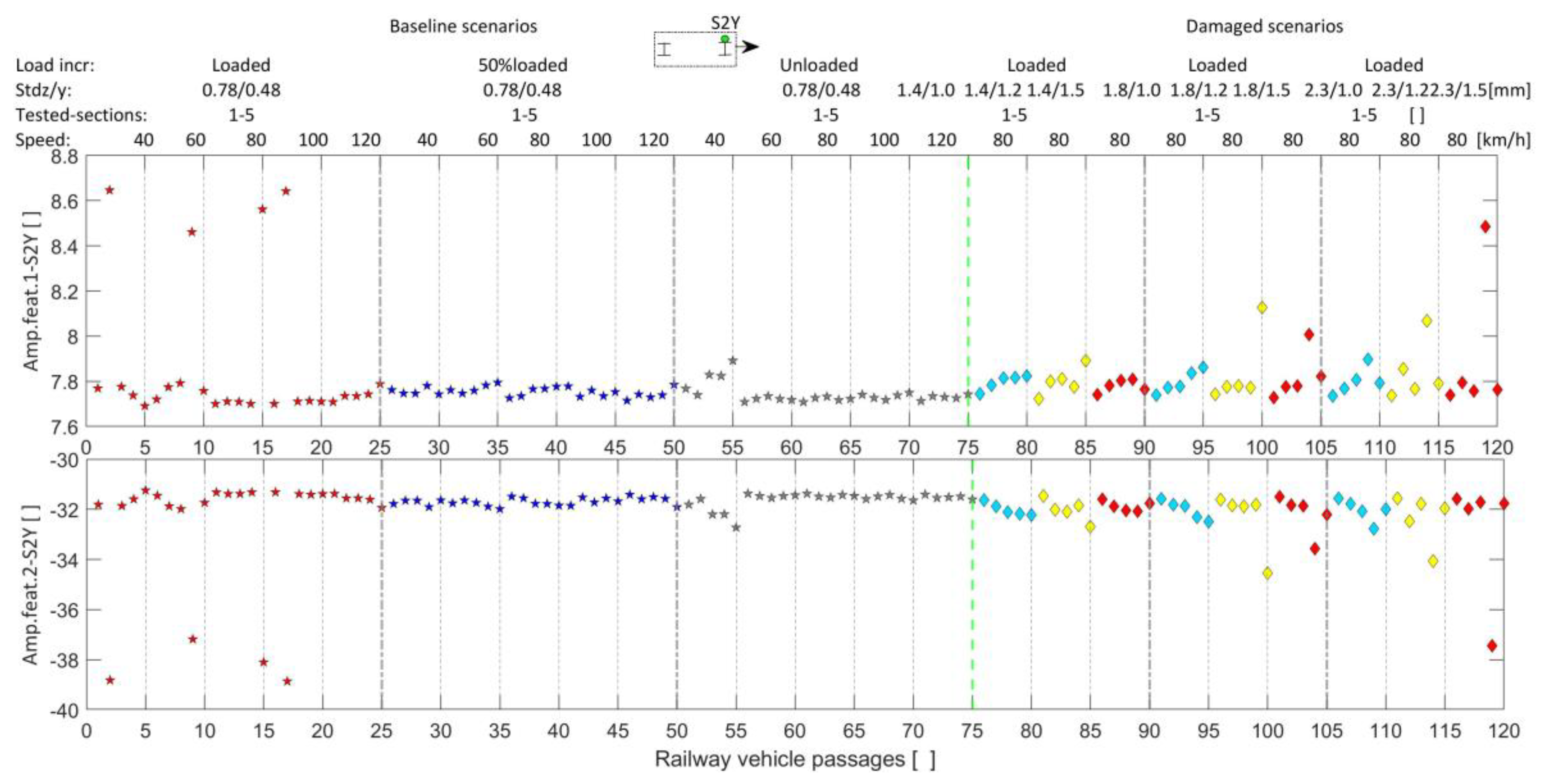
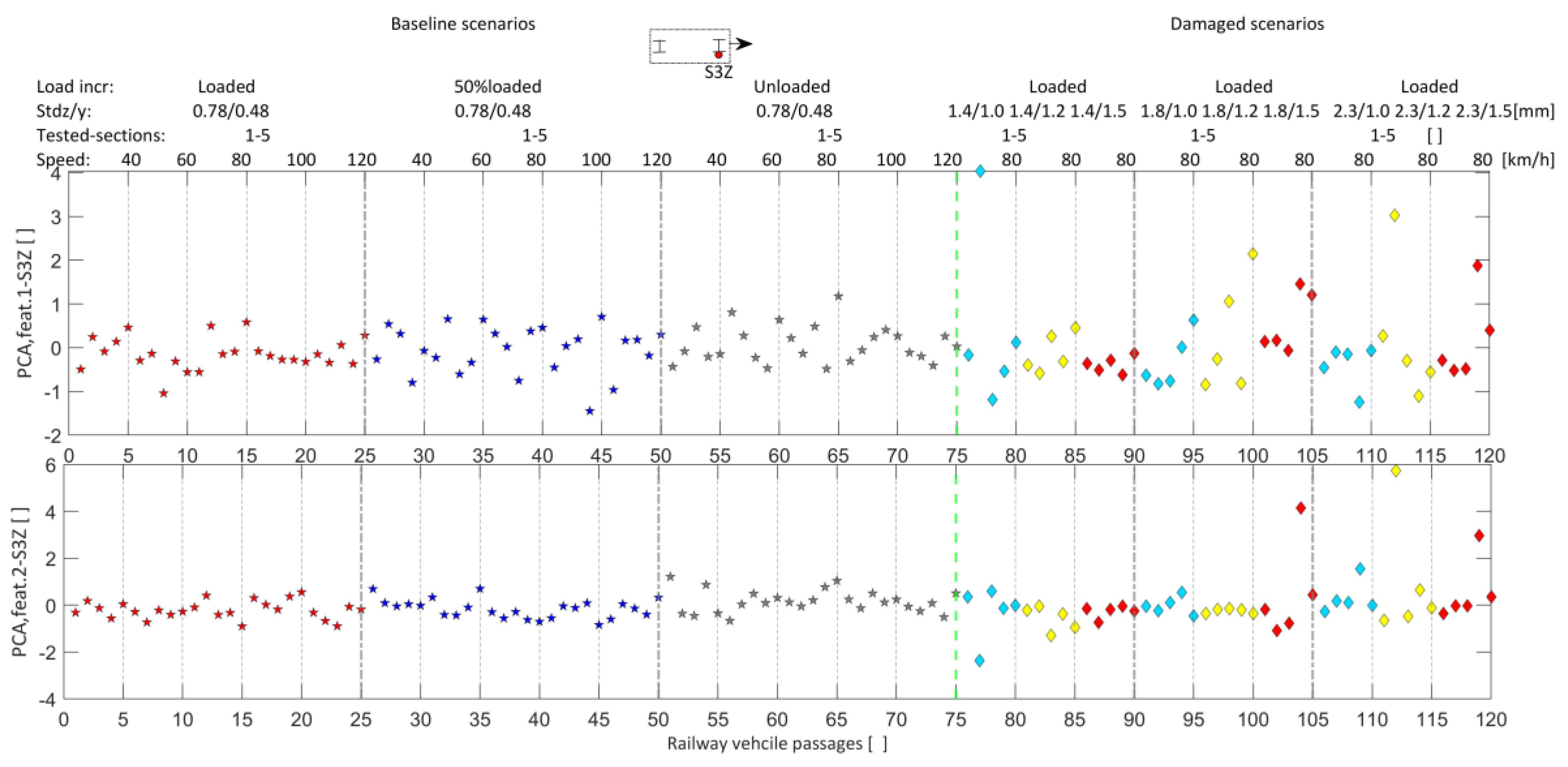
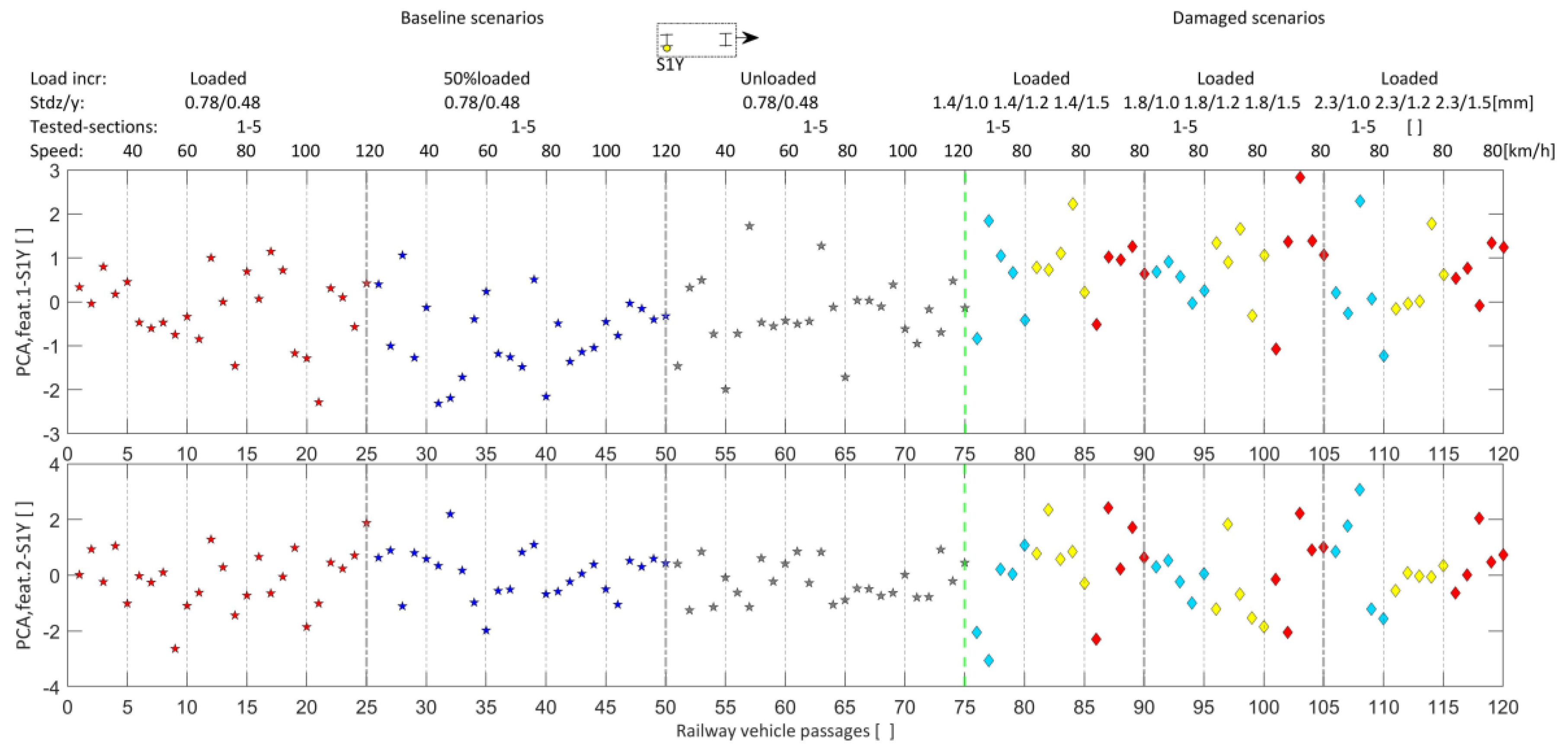
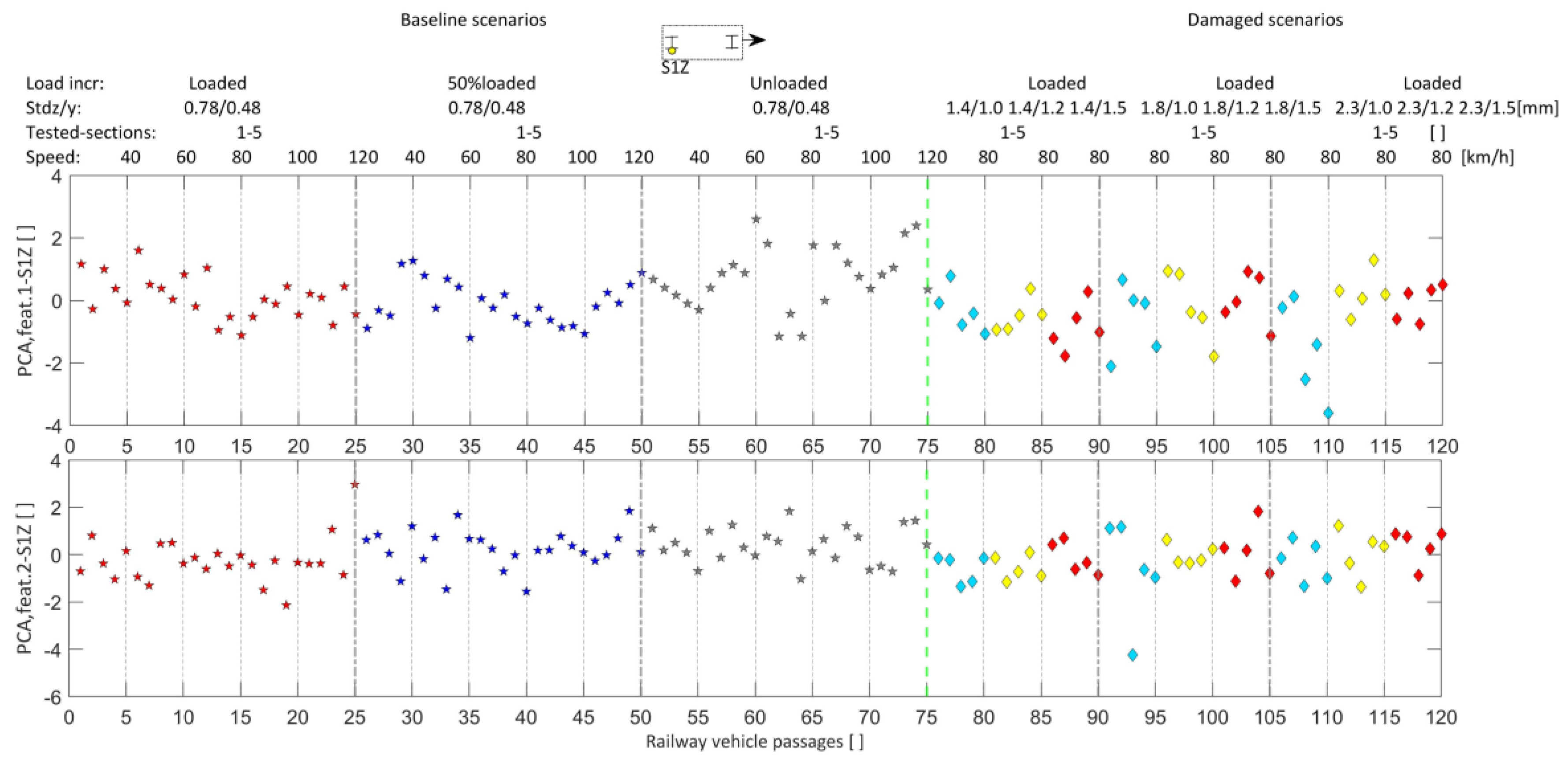
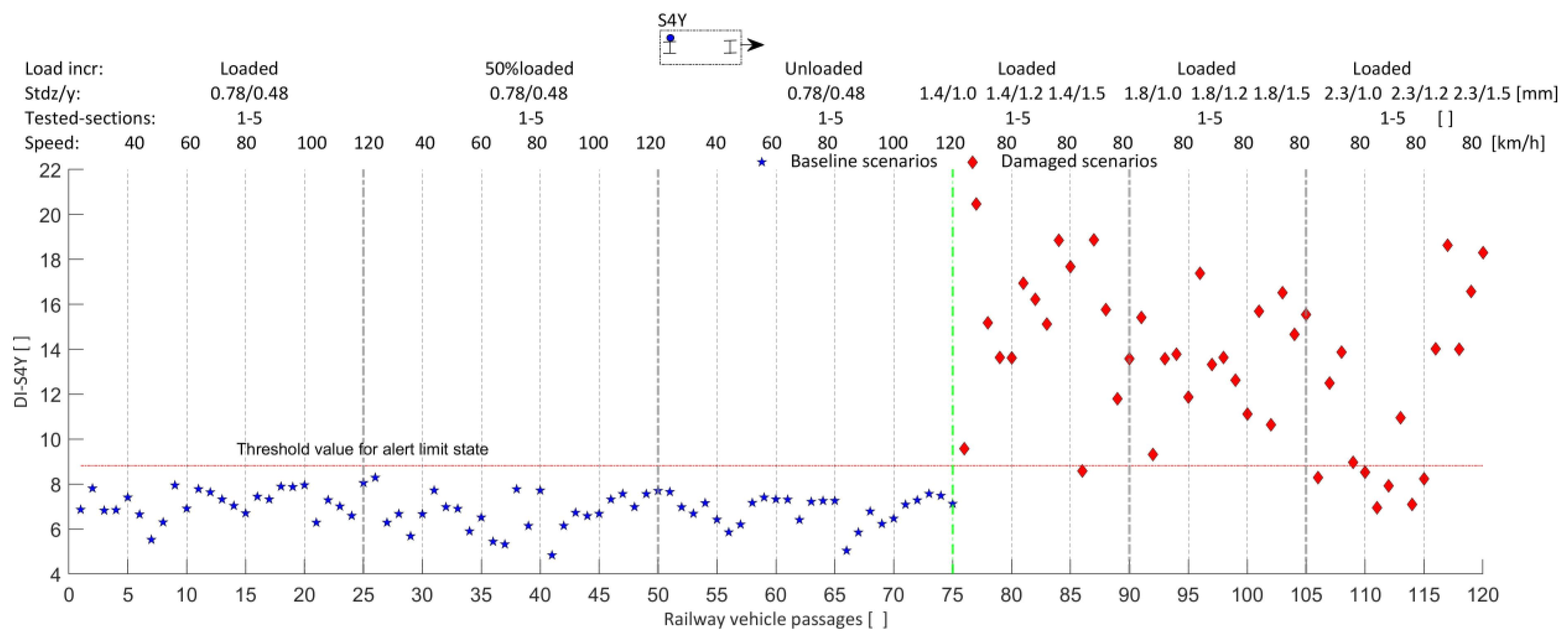
5.4. Data Fusion, Features Discrimination, and Outlier Analysis
5.5. Accuracy Assessment Based on Different Sensor Layouts
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vale, C.; Lurdes, S.M. Stochastic Model for the Geometrical Rail Track Degradation Process in the Portuguese Railway Northern Line. Reliab. Eng. Syst. Saf. 2013, 116, 91–98. [Google Scholar] [CrossRef]
- Abadi, T.; Le Pen, L.; Zervos, A.; Powrie, W. Effect of Sleeper Interventions on Railway Track Performance. J. Geotech. Geoenviron. Eng. 2019, 145, 04019009. [Google Scholar] [CrossRef]
- Harris, D.K.; Lutch, R.H.; Ahlborn, T.M.; Duong, P. Optimization of a Prestressed Concrete Railroad Crosstie for Heavy-Haul Applications. J. Transp. Eng. 2011, 137, 815–822. [Google Scholar] [CrossRef]
- Frýba, L. Dynamics of Railway Bridges, 2nd ed.; Academy of Scientes of Sciences Czeh Republic: Prague, Czeh Republic, 1996; p. 332. [Google Scholar] [CrossRef]
- Claus, H.; Schiehlen, W. Modeling and Simulation of Railway Bogie Structural Vibrations. Veh. Syst. Dyn. 1998, 29, 538–552. [Google Scholar] [CrossRef]
- Tsunashima, H. Condition Monitoring of Railway Tracks from Car-Body Vibration Using a Machine Learning Technique. Appl. Sci. 2019, 9, 2734. [Google Scholar] [CrossRef]
- Balouchi, F.; Bevan, A.; Formston, R. Development of Railway Track Condition Monitoring from Multi-Train in-Service Vehicles. Veh. Syst. Dyn. 2021, 59, 1397–1417. [Google Scholar] [CrossRef]
- Choi, S. Identifying Parametric Models Used to Estimate Track Irregularities of a High-Speed Railway. Machines 2023, 11, 6. [Google Scholar] [CrossRef]
- Tan, C.; Elhattab, A.; Uddin, N. “Drive-by’’ Bridge Frequency-Based Monitoring Utilizing Wavelet Transform. J. Civ. Struct. Health Monit. 2017, 7, 615–625. [Google Scholar] [CrossRef]
- Souza, E.F.; Bragança, C.; Meixedo, A.; Ribeiro, D.; Bittencourt, T.N.; Carvalho, H. Drive-by Methodologies Applied to Railway Infrastructure Subsystems: A Literature Review—Part I: Bridges and Viaducts. Appl. Sci. 2023, 13, 6940. [Google Scholar] [CrossRef]
- Bragança, C.; Souza, E.F.; Ribeiro, D.; Meixedo, A.; Bittencourt, T.N.; Carvalho, H. Drive-by Methodologies Applied to Railway Infrastructure Subsystems: A Literature Review—Part II: Track and Vehicle. Appl. Sci. 2023, 13, 6982. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Obrien, E.J.; Quirke, P.; Cantero, D.; Golpayegani, F. Railway Track Loss-of-Stiffness Detection Using Bogie Filtered Displacement Data Measured on a Passing Train. Infrastructures 2021, 6, 93. [Google Scholar] [CrossRef]
- Sun, L.; Shang, Z.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of Bridge Structural Health Monitoring Aided by Big Data and Artificial Intelligence: From Condition Assessment to Damage Detection. J. Struct. Eng. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Bosso, N.; Magelli, M.; Trinchero, R.; Zampieri, N. Application of Machine Learning Techniques to Build Digital Twins for Long Train Dynamics Simulations. Veh. Syst. Dyn. 2023, 1–20. [Google Scholar] [CrossRef]
- Memon, T.R.; Memon, T.D.; Chowdhry, B.S.; Kalwar, I.H.; Mal, K. Development of Specialized IoT Cloud Platform for Railway Track Condition Monitoring. In Proceedings of the 2021 International Conference on Robotics and Automation in Industry (ICRAI), Rawalpindi, Pakistan, 26–27 October 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Ren, J.-J.; Liu, W.; Du, W.; Zheng, J.-L.; Wei, H.; Zhang, K.-Y.; Ye, W.-L. Identification Method for Subgrade Settlement of Ballastless Track Based on Vehicle Vibration Signals and Machine Learning. Constr. Build. Mater. 2023, 369, 130573. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite-Element Model Calibration of a Railway Vehicle Based on Experimental Modal Parameters. Veh. Syst. Dyn. 2013, 51, 821–856. [Google Scholar] [CrossRef]
- Lederman, G.; Chen, S.; Garrett, J.H.; Kovačević, J.; Noh, H.Y.; Bielak, J. Track Monitoring from the Dynamic Response of a Passing Train: A sparse Approach. Mech. Syst. Signal Process. 2017, 90, 141–153. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Obrien, E.; Quirke, P.; Bowe, C. Railway Track Monitoring Using Train Measurements: An Experimental Case Study. Appl. Sci. 2019, 9, 4859. [Google Scholar] [CrossRef]
- Li, J.; Shi, H. Rail Corrugation Diagnosis of High-Speed Railway Based on Dynamic Responses of the Vehicle. In Proceedings of the 2020 Prognostics and Health Management Conference (PHM-Besançon), Besancon, France, 4–7 May 2020; pp. 148–152. [Google Scholar] [CrossRef]
- Kostić, B.; Gül, M. Vibration-Based Damage Detection of Bridges under Varying Temperature Effects Using Time-Series Analysis and Artificial Neural Networks. J. Bridge Eng. 2017, 22, 04017065. [Google Scholar] [CrossRef]
- Lee, K.; Jeong, S.; Sim, S.-H.; Shin, D.H. Damage-Detection Approach for Bridges with Multi-Vehicle Loads Using Convolutional Autoencoder. Sensors 2022, 22, 1839. [Google Scholar] [CrossRef]
- Huang, M.-S.; Gül, M.; Zhu, H.-P. Vibration-Based Structural Damage Identification under Varying Temperature Effects. J. Aerosp. Eng. 2018, 31, 04018014. [Google Scholar] [CrossRef]
- Silva, R.; Guedes, A.; Ribeiro, D.; Vale, C.; Meixedo, A.; Mosleh, A.; Montenegro, P. Early Identification of Unbalanced Freight Traffic Loads Based on Wayside Monitoring and Artificial Intelligence. Sensors 2023, 23, 1544. [Google Scholar] [CrossRef] [PubMed]
- Meixedo, A.; Santos, J.; Ribeiro, D.; Calçada, R.; Todd, M. Damage Detection in Railway Bridges Using Traffic-Induced Dynamic Responses. Eng. Struct. 2021, 238, 112189. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Sarrabezolles, C.; Khan, M.; Golpayegani, F. A Machine-Learning-Based Approach for Railway Track Monitoring Using Acceleration Measured on an In-Service Train. Sensors 2023, 23, 7568. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A Spatial Coupling Model to Study Dynamic Performance of Pantograph-Catenary with Vehicle-Track Excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Xia, X.; Meng, Z.; Han, X.; Li, H.; Tsukiji, T.; Xu, R.; Zheng, Z.; Ma, J. An Automated Driving Systems Data Acquisition and Analytics Platform. Transp. Res. Part C Emerg. Technol. 2023, 151, 104120. [Google Scholar] [CrossRef]
- Xia, X.; Bhatt, N.P.; Khajepour, A.; Hashemi, E. Integrated Inertial-LiDAR-Based Map Matching Localization for Varying Environments. IEEE Trans. Intell. Veh. 2023, 99, 1–12. [Google Scholar] [CrossRef]
- Tsunashima, H.; Hirose, R. Condition Monitoring of Railway Track from Car-Body Vibration Using Time-Frequency Analysis. Veh. Syst. Dyn. 2022, 60, 1170–1187. [Google Scholar] [CrossRef]
- Quirke, P.; Bowe, C.; Obrien, E.J.; Cantero, D.; Antolin, P.; Goicolea, J.M. Railway Bridge Damage Detection Using Vehicle-Based Inertial Measurements and Apparent Profile. Eng. Struct. 2017, 153, 421–442. [Google Scholar] [CrossRef]
- SIMPACK®, Multibody System Simulation, Dassault Systemes Simulia Corp.: Eagan, MN, USA, 2021.
- Chang, C.; Ding, X.; Ling, L.; Li, F.; Liu, T.; Wang, K.; Zhai, W. Mechanism of High-Speed Train Carbody Shaking Due to Degradation of Wheel-Rail Contact Geometry. Int. J. Rail Transp. 2022, 11, 289–316. [Google Scholar] [CrossRef]
- Ng, A.K.; Martua, L.; Sun, G. Dynamic Modelling and Acceleration Signal Analysis of Rail Surface Defects for Enhanced Rail Condition Monitoring and Diagnosis. In Proceedings of the 2019 4th International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 6–8 September 2019; pp. 69–73. [Google Scholar] [CrossRef]
- Belov, I.V.; Shalymov, R.V.; Tkachenko, A.N.; Larionov, D.Y.; Podgornaya, L.N. Development of an Algorithm for Detecting Railway Corrugations in Acceleration Data. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), St. Petersburg and Moscow, Russia, 26–29 January 2021; pp. 1609–1613. [Google Scholar] [CrossRef]
- Zhuang, L.; Qi, H.; Zhang, Z. The Automatic Rail Surface Multi-Flaw Identification Based on a Deep Learning Powered Framework. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12133–12143. [Google Scholar] [CrossRef]
- Erduran, E.; Pettersen, F.M.; Gonen, S.; Lau, A. Identification of Vibration Frequencies of Railway Bridges from Train-Mounted Sensors Using Wavelet Transformation. Sensors 2023, 23, 1191. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, Y.; Ni, Y.; Ni, Y.; Wang, X.; Wang, X. Real-Time Defect Detection of High-Speed Train Wheels by Using Bayesian Forecasting and Dynamic Model. Mech. Syst. Signal Process. 2020, 139, 106654. [Google Scholar] [CrossRef]
- Flynn, E.B.; Todd, M.D. A Bayesian Approach to Optimal Sensor Placement for Structural Health Monitoring with Application to Active Sensing. Mech. Syst. Signal Process. 2010, 24, 891–903. [Google Scholar] [CrossRef]
- Sun, Z.; Lu, J.; Sun, J. Online Dynamic Detection of Hazardous Cracks in Train Wheels by Probe Combination: Based on Classical Piezoelectric Ultrasonic Technology. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Auersch, L. Simultaneous Measurements of the Vehicle, Track, and Soil Vibrations at a Surface, Bridge, and Tunnel Railway Line. Shock Vib. 2017, 2017, 11959286. [Google Scholar] [CrossRef]
- König, P.; Salcher, P.; Adam, C.; Hirzinger, B. Dynamic Analysis of Railway Bridges Exposed to High-Speed Trains Considering the Vehicle–Track–Bridge–Soil Interaction. Acta Mech. 2021, 232, 4583–4608. [Google Scholar] [CrossRef]
- Silva, R.; Ribeiro, D.; Bragança, C.; Costa, C.; Arêde, A.; Calçada, R. Model Updating of a Freight Wagon Based on Dynamic Tests under Different Loading Scenarios. Appl. Sci. 2021, 11, 10691. [Google Scholar] [CrossRef]
- Bragança, C.; Neto, J.; Pinto, N.; Montenegro, P.A.; Ribeiro, D.; Carvalho, H.; Calçada, R. Calibration and Validation of a Freight Wagon Dynamic Model in Operating Conditions Based on Limited Experimental Data. Veh. Syst. Dyn. 2022, 60, 3024–3050. [Google Scholar] [CrossRef]
- Zhai, W.; Han, Z.; Chen, Z.; Ling, L.; Zhu, S. Train–Track–Bridge Dynamic Interaction: A State-of-the-Art Review. Veh. Syst. Dyn. 2019, 57, 984–1027. [Google Scholar] [CrossRef]
- Zhang, D.; Zhai, W.; Wang, K. Dynamic Interaction between Heavy-Haul Train and Track Structure Due to Increasing Axle Load. Aust. J. Struct. Eng. 2017, 18, 190–203. [Google Scholar] [CrossRef]
- Lou, P.; Gong, K.; Zhao, C.; Xu, Q.; Luo, R.K. Dynamic Responses of Vehicle-CRTS III Slab Track System and Vehicle Running Safety Subjected to Uniform Seismic Excitation. Shock Vib. 2019, 2019, 5308209. [Google Scholar] [CrossRef]
- Wu, X.; Liang, S.; Chi, M. An Investigation of Rocking Derailment of Railway Vehicles under the Earthquake Excitation. Eng. Fail. Anal. 2020, 117, 104913. [Google Scholar] [CrossRef]
- Choi, J.-Y.; Chung, J.-S.; Kim, S.-H. Experimental Study on Track-Bridge Interactions for Direct Fixation Track on Long-Span Railway Bridge. Shock Vib. 2019, 2019, 1903752. [Google Scholar] [CrossRef]
- Yin, X.; Wei, X.; Zheng, H. Applying System Dynamics of Discrete Supported Track to Analyze the Rail Corrugation Causation on Curved Urban Railway Tracks. Discret. Dyn. Nat. Soc. 2021, 2021, 9958163. [Google Scholar] [CrossRef]
- Carnevale, M.; Collina, A.; Peirlinck, T. A Feasibility Study of the Drive-By Method for Damage Detection in Railway Bridges. Appl. Sci. 2019, 9, 160. [Google Scholar] [CrossRef]
- Bernal, E.; Spiryagin, M.; Vollebregt, E.; Oldknow, K.; Stichel, S.; Shrestha, S.; Ahmad, S.; Wu, Q.; Sun, Y.; Cole, C. Prediction of Rail Surface Damage in Locomotive Traction Operations Using Laboratory-Field Measured and Calibrated Data. Eng. Fail. Anal. 2022, 135, 106165. [Google Scholar] [CrossRef]
- Chang, C.; Ling, L.; Han, Z.; Wang, K.; Zhai, W. High-Speed Train-Track-Bridge Dynamic Interaction Considering Wheel-Rail Contact Nonlinearity Due to Wheel Hollow Wear. Shock Vib. 2019, 2019, 5874678. [Google Scholar] [CrossRef]
- Mosleh, A.; Montenegro, P.; Costa, P.A.; Calçada, R. An Approach for Wheel Flat Detection of Railway Train Wheels Using Envelope Spectrum Analysis. Struct. Infrastruct. Eng. 2021, 17, 1710–1729. [Google Scholar] [CrossRef]
- Xue, R.; Ren, Z.; Fan, T.; Rakheja, S. Vertical Vibration Analysis of a Coupled Vehicle-Container Model of a High-Speed Freight EMU. Veh. Syst. Dyn. 2020, 60, 1228–1252. [Google Scholar] [CrossRef]
- Bernal, E.; Spiryagin, M.; Cole, C. Onboard Condition Monitoring Sensors, Systems and Techniques for Freight Railway Vehicles: A Review. IEEE Sens. J. 2019, 19, 4–24. [Google Scholar] [CrossRef]
- EN13848-5:2008+A1:2015; Via-Qualidade Geométrica, Parte 5: Níveis De Qualidade Da Geometria Da Via-Plena Via. European Committee for Standarization, CEN: Brussels, Belgium, 2015; p. 20. (In Portuguese)
- Bezin, Y.; Iwnicki, S.D.; Cavalletti, M.; de Vries, E.; Shahzad, F.; Evans, G. An Investigation of Sleeper Voids Using a Flexible Track Model Integrated with Railway Multi-Body Dynamics. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 597–607. [Google Scholar] [CrossRef]
- Carlberger, A.; Torstensson, P.T.; Nielsen, J.C.; Frid, A. An Iterative Methodology for the Prediction of Dynamic Vehicle–Track Interaction and Long-Term Periodic Rail Wear. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 1718–1730. [Google Scholar] [CrossRef]
- Bezin, Y.; Sambo, B.; Magalhaes, H.; Kik, W.; Megna, G.; Costa, J.N. Challenges and methodology for pre-processing measured and new rail profiles to efficiently simulate wheel-rail interaction in switches and crossing. Veh. Syst. Dyn. 2023, 61, 799–820. [Google Scholar] [CrossRef]
- Neto, J.; Montenegro, P.A.; Vale, C.; Calçada, R. Evaluation of the Train Running Safety under Crosswinds—A Numerical Study on the Influence of the Wind Speed and Orientation Considering the Normative Chinese Hat Model. Int. J. Rail Transp. 2020, 9, 204–231. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, K.; Cai, C. Fundamentals of Vehicle–Track Coupled Dynamics. Veh. Syst. Dyn. 2009, 47, 1349–1376. [Google Scholar] [CrossRef]
- Montenegro, P.; Neves, S.; Calçada, R.; Tanabe, M.; Sogabe, M. Wheel–Rail Contact Formulation for Analyzing the Lateral Train–Structure Dynamic Interaction. Comput. Struct. 2015, 152, 200–214. [Google Scholar] [CrossRef]
- Polach, O. A Fast Wheel-Rail Forces Calculation Computer Code. Veh. Syst. Dyn. 2021, 33, 728–739. [Google Scholar] [CrossRef]
- Yan, W.; Fischer, F.D. Applicability of the Hertz Contact Theory to Rail-Wheel Contact Problems. Arch. Appl. Mech. 2000, 70, 255–268. [Google Scholar] [CrossRef]
- Kalker, J.J. A Fast Algorithm for the Simplified Theory of Rolling Contact. Veh. Syst. Dyn. 1982, 11, 1–13. [Google Scholar] [CrossRef]
- Six, K.; Meierhofer, A.; Müller, G.; Dietmaier, P. Physical Processes in Wheel–Rail Contact and Its Implications on Vehicle–Track Interaction. Veh. Syst. Dyn. 2015, 53, 635–650. [Google Scholar] [CrossRef]
- Liu, B.; Mei, T.; Bruni, S. Design and Optimisation of Wheel–Rail Profiles for Adhesion Improvement. Veh. Syst. Dyn. 2018, 54, 429–444. [Google Scholar] [CrossRef]
- MATLAB6®, Version 2018; Themathworks Inc.: Natick, Ma, USA, 2018.
- Mosleh, A.; Meixedo, A.; Ribeiro, D.; Montenegro, P.; Calçada, R. Automatic Clustering-Based Approach for Train Wheels Condition Monitoring. Int. J. Rail Transp. 2022, 11, 639–664. [Google Scholar] [CrossRef]
- Tamhane, A.C. Statistical Analysis of Designed Experiments; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; p. 708. [Google Scholar] [CrossRef]





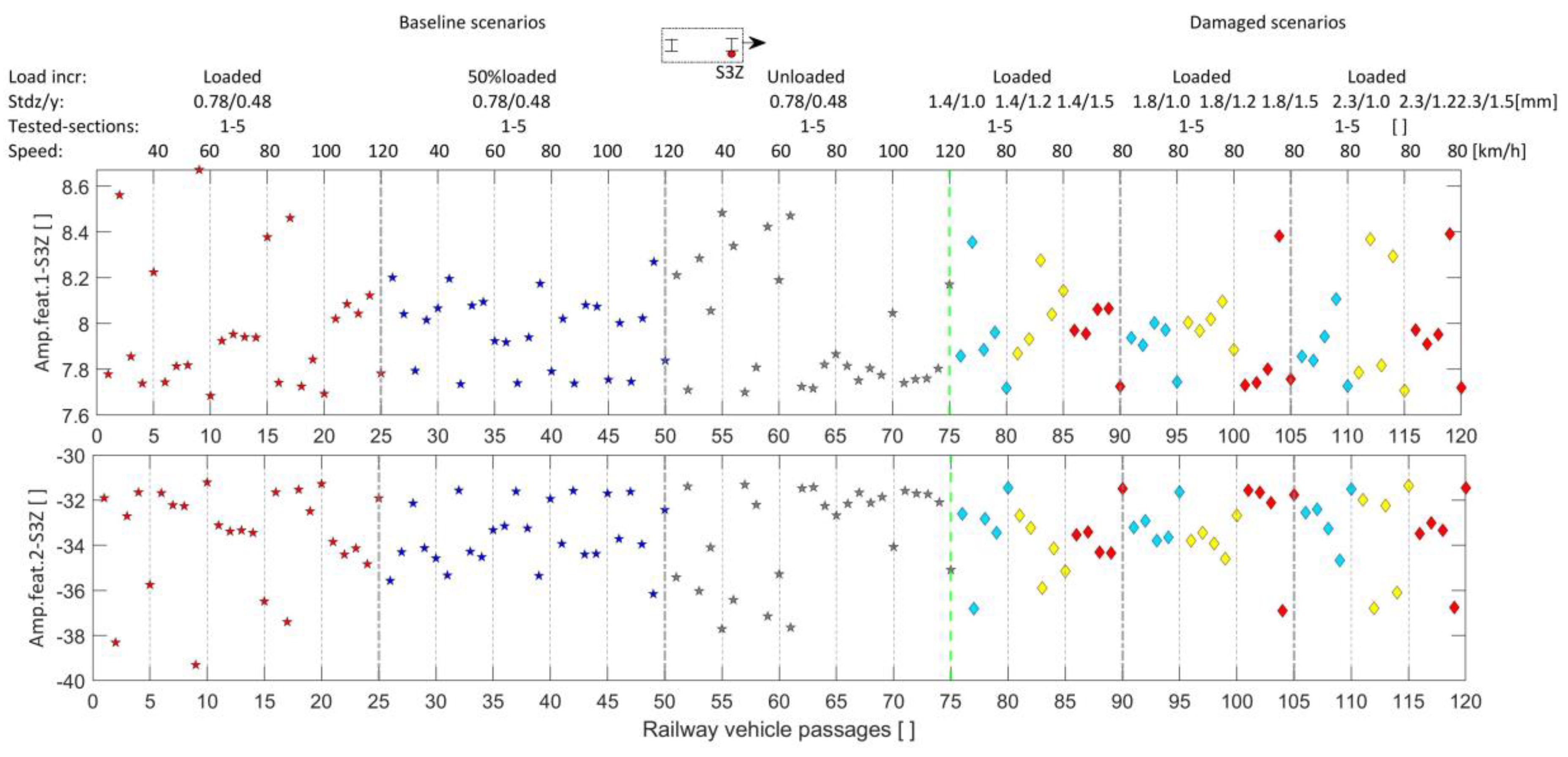
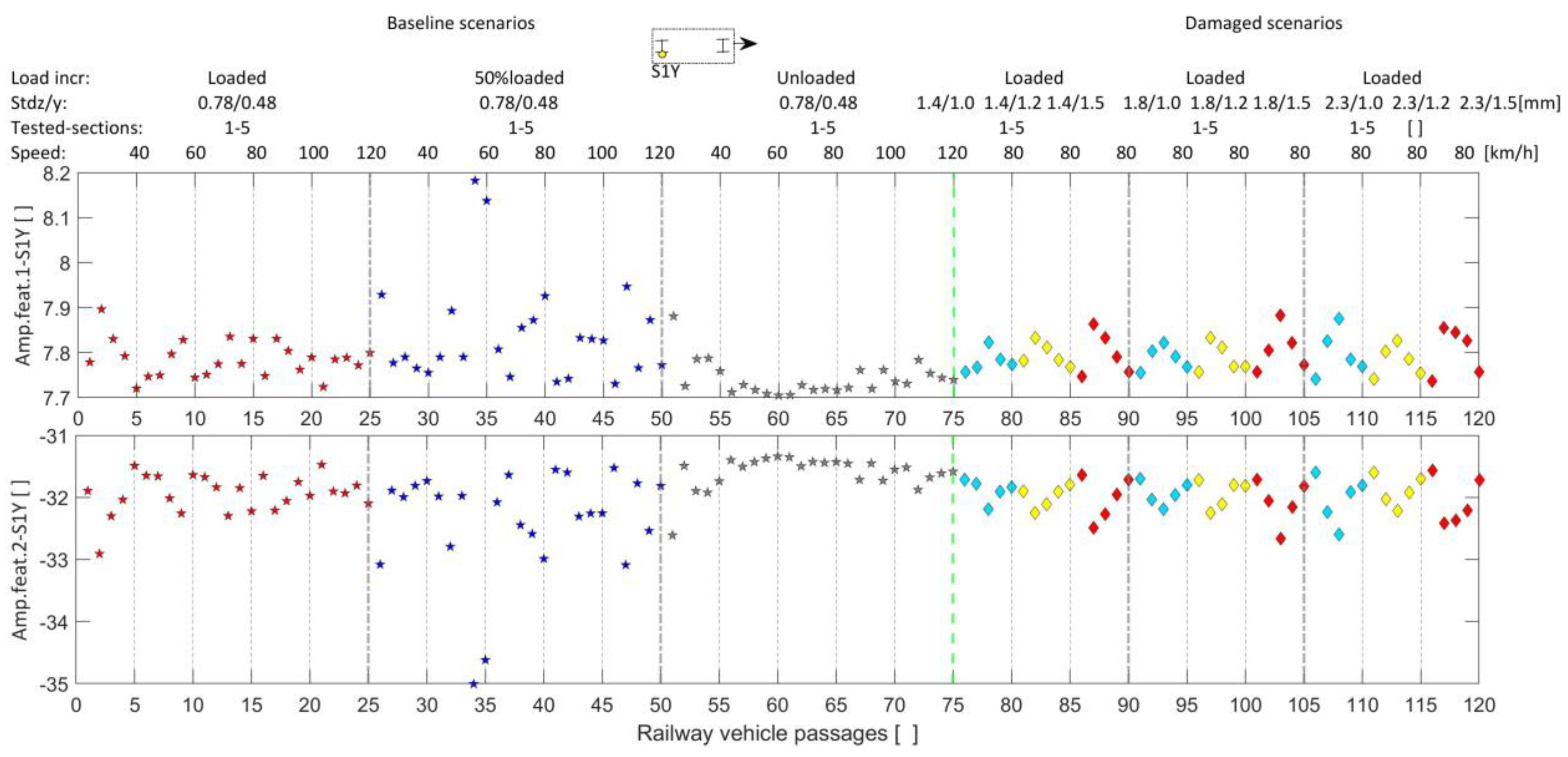
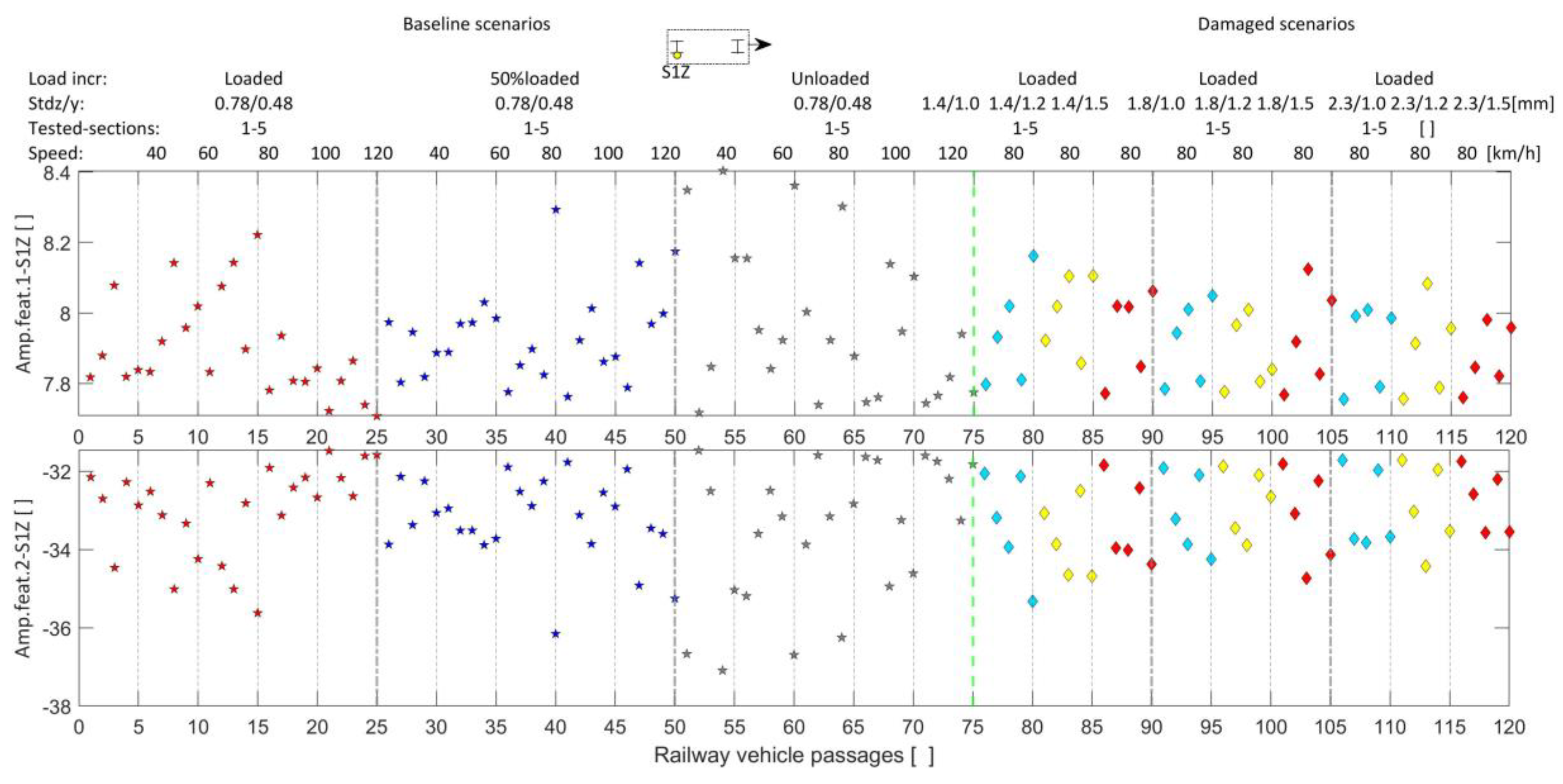


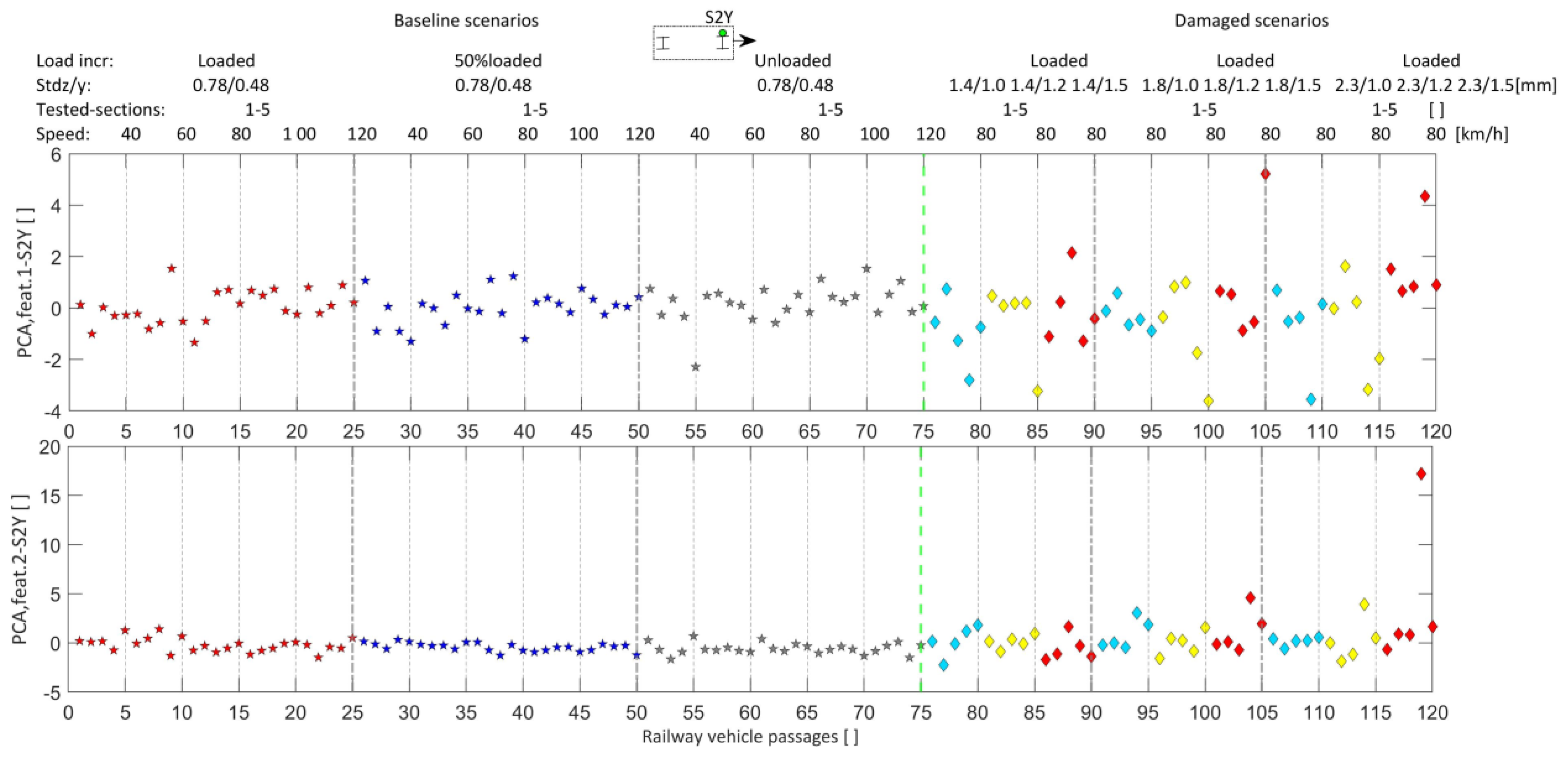




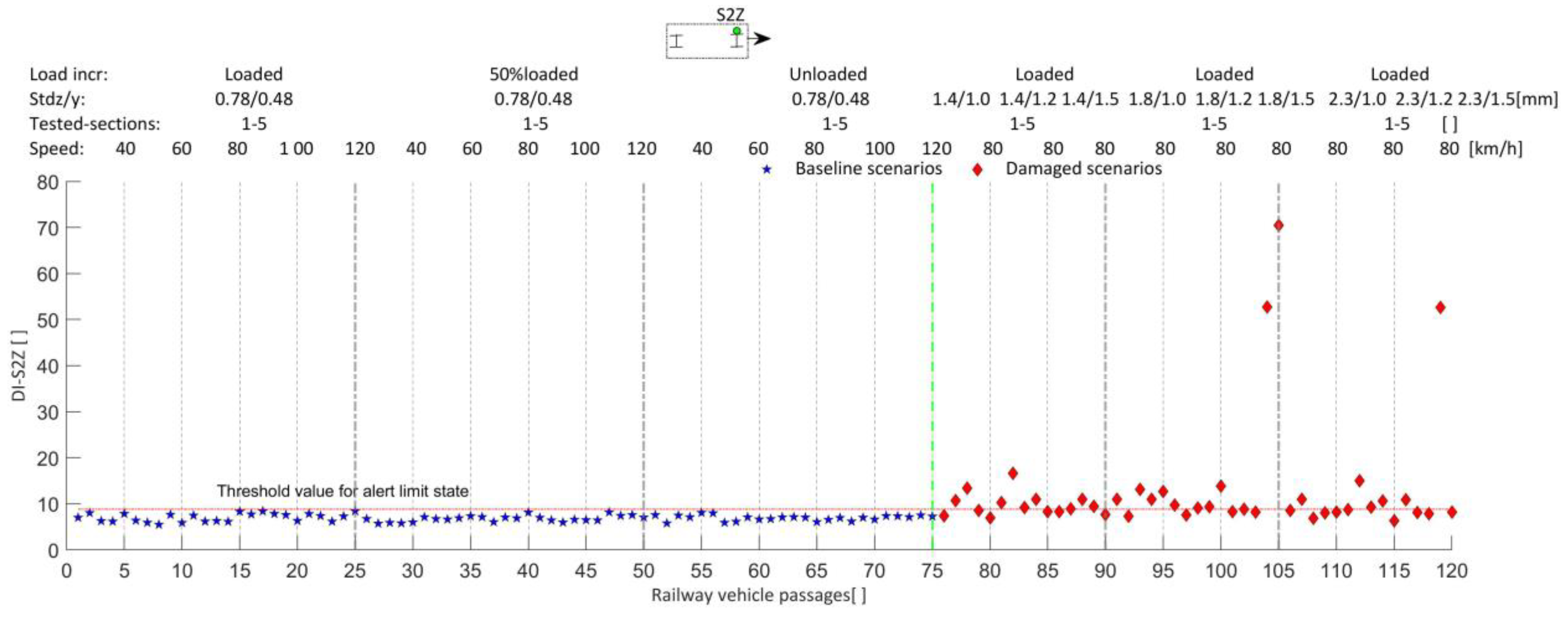
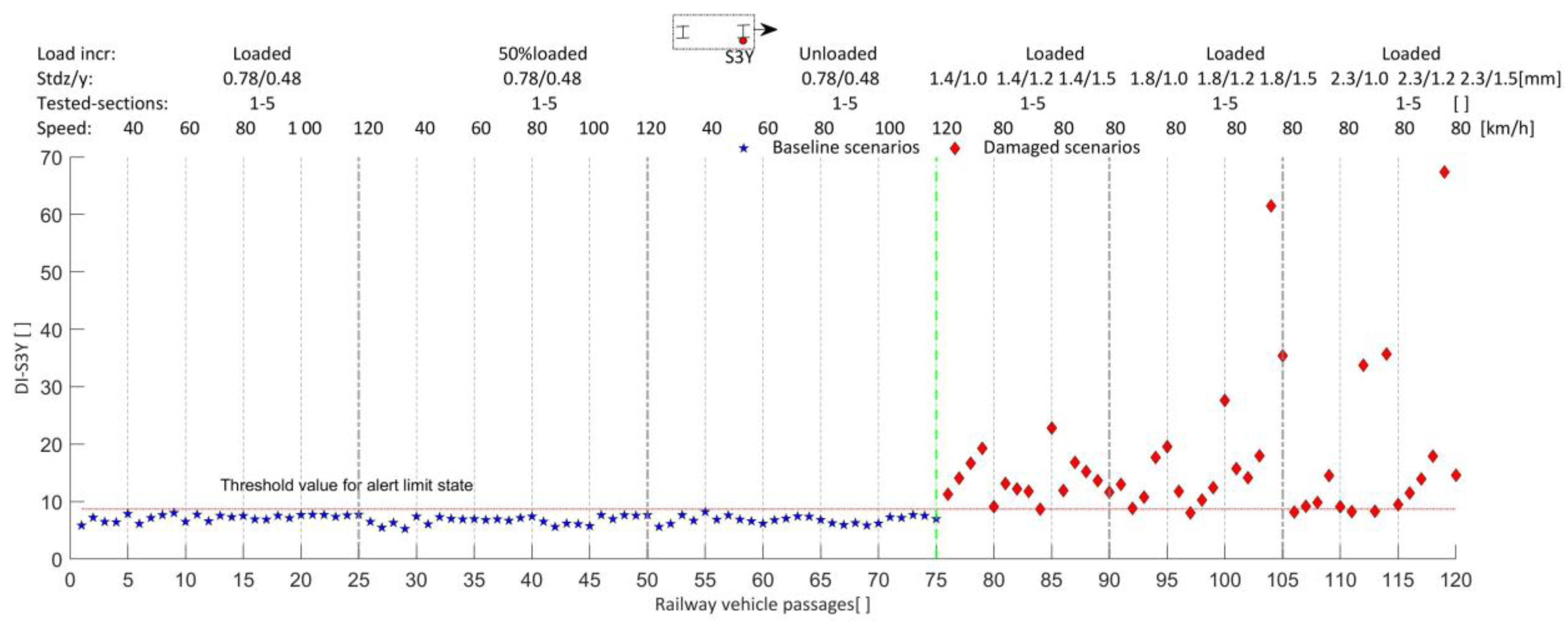

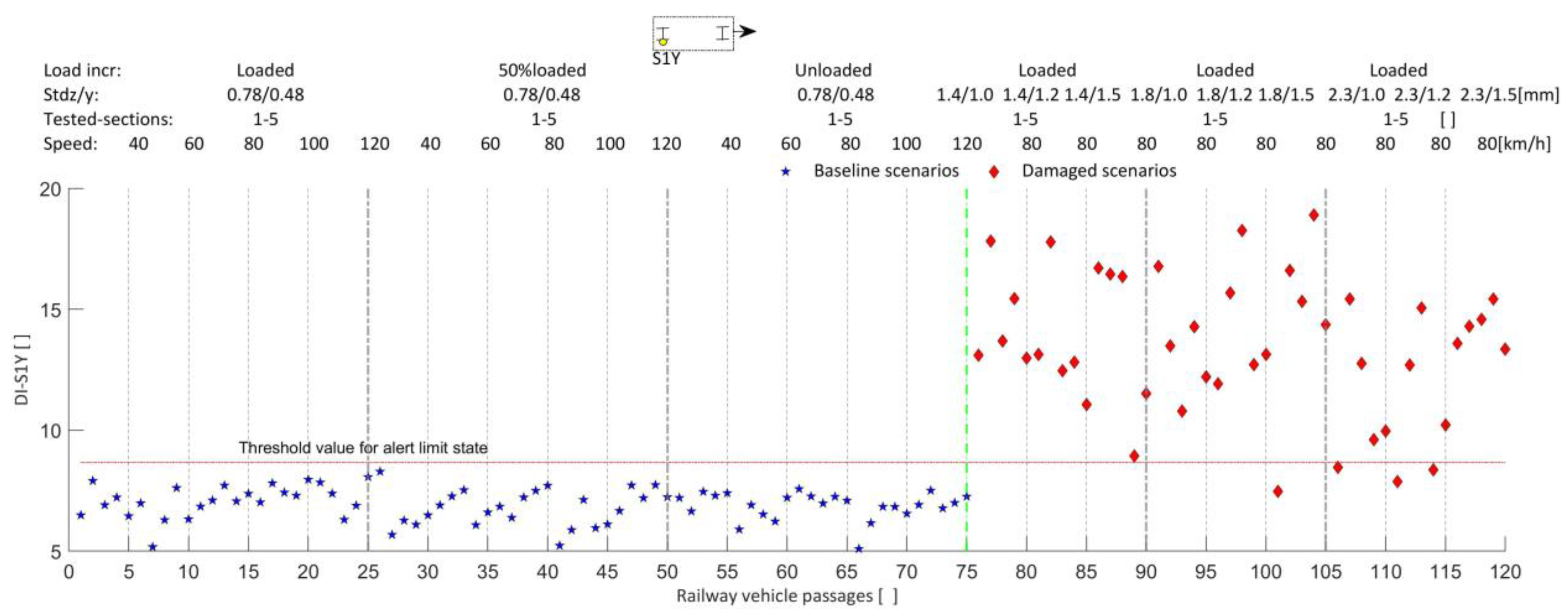
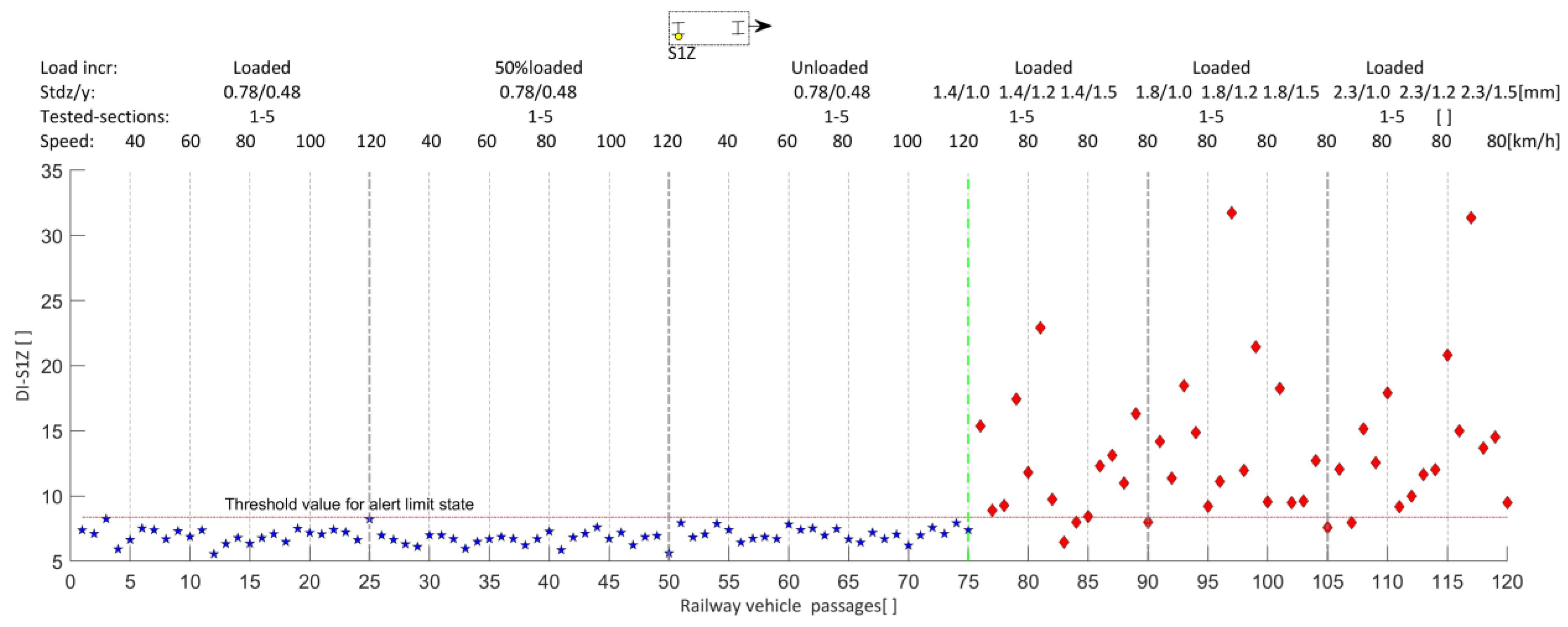
| Geometric and Dynamic Properties | Limit Bounds (Lower/Upper) | Adopted Value | Unit |
|---|---|---|---|
| Car body mass (mc) | 41,100 | [ | |
| ) | 49,000 | ||
| ) | 673,000 | ||
| ) | 665,000 | ||
| ) | −/− | ||
| ) | −/− | ||
| ) | −/− | ||
| Wheel set mass | |||
| ) | −/− | ||
| ) | −/− | ||
| ) | [m] | ||
| ) | 44,981 | ||
| ) | 30,948 | ||
| ) | 1860 | ||
| ) | −/− |
| Description of the Properties | Value | Unit | References | |
|---|---|---|---|---|
| Rail | ) | 87.7 | [] | [61] |
| Density | 7850 | [] | [61] | |
| Moment of inertia | 0.309 | [] | [61] | |
| Elasticity modulus (E) | [] | [44] | ||
| Poisson’s ratio (ν) | 0.28 | [-] | [61] | |
| Rail pad and fastening system | ) | ] | [61] | |
| ) | [] | [44] | ||
| ) | [ | [61] | ||
| ) | [] | [44] | ||
| Sleeper | Area of the cross section | [] | [44] | |
| Moment of inertia of the cross section | [] | [44] | ||
| Density | [] | [61] | ||
| ) | [] | [44,61] | ||
| Poisson’s ratio (ν) | 0.2 | [-] | [61] | |
| Ballast | ) | [] | [44] | |
| ) | 0.11 | [] | [62] | |
| ) | [ | [61] | ||
| ) | [] | [61] | ||
| ) | 50 | [] | [61] | |
| ) | 15 | [] | [61] | |
| Foundation | ) | [] | [61] | |
| ) | 0.501 | [] | [61] |
| Speed (km/h) | ALSTD for LL (mm) | ALSTD for LA (mm) |
|---|---|---|
| 2.3 to 3.0 | 1.5 to 1.8 | |
| 1.8 to 2.7 | 1.2 to 1.5 | |
| 1.4 to 2.4 | 1.0 to 1.3 | |
| 1.2 to 1.9 | 0.8 to 1.1 | |
| 1.0 to 1.5 | 0.7 to 1.0 |
| Description | Baseline Scenarios | Damage Scenarios |
|---|---|---|
| Type of railway vehicle | Freight Laagrss vehicle | Freight Laagrss vehicle |
| Load increment of wagon | 3 types | 1 type |
| Noise ratio | 5% | 5% |
| Vehicle speeds [km/h] | 40–120 | 80 |
| Track geometric irregularities | 1 profile | 9 profiles |
| ALSTD for longitudinal level (z) | 0.78 | 1.4, 1.8, 2.3 |
| ALSTD for lateral alignment (y) | 0.48 | 1, 1.2, 1.5 |
| Total number of analyses | 45 | 75 |
| Sampling frequency for acceleration, . | ||
| Low-pass digital filter for acceleration (Chebyshev II) | ||
| Damage | Detection Accuracy for Each Sensor | |||||||
|---|---|---|---|---|---|---|---|---|
| S4Y | S1Y | S2Y | S3Y | S2Z | S3Z | S4Z | S1Z | |
| LRLL | ---- | ---- | ---- | ---- | 94% | ---- | 98% | ---- |
| RRLL | ---- | ---- | ---- | ---- | ---- | 99% | ---- | 98% |
| LRLA | ---- | 98% | 99% | ---- | ---- | ---- | ---- | ---- |
| RRLA | 95% | ---- | ---- | 100% | ---- | ---- | ---- | ---- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traquinho, N.; Vale, C.; Ribeiro, D.; Meixedo, A.; Montenegro, P.; Mosleh, A.; Calçada, R. Damage Identification for Railway Tracks Using Onboard Monitoring Systems in In-Service Vehicles and Data Science. Machines 2023, 11, 981. https://doi.org/10.3390/machines11100981
Traquinho N, Vale C, Ribeiro D, Meixedo A, Montenegro P, Mosleh A, Calçada R. Damage Identification for Railway Tracks Using Onboard Monitoring Systems in In-Service Vehicles and Data Science. Machines. 2023; 11(10):981. https://doi.org/10.3390/machines11100981
Chicago/Turabian StyleTraquinho, Nelson, Cecília Vale, Diogo Ribeiro, Andreia Meixedo, Pedro Montenegro, Araliya Mosleh, and Rui Calçada. 2023. "Damage Identification for Railway Tracks Using Onboard Monitoring Systems in In-Service Vehicles and Data Science" Machines 11, no. 10: 981. https://doi.org/10.3390/machines11100981
APA StyleTraquinho, N., Vale, C., Ribeiro, D., Meixedo, A., Montenegro, P., Mosleh, A., & Calçada, R. (2023). Damage Identification for Railway Tracks Using Onboard Monitoring Systems in In-Service Vehicles and Data Science. Machines, 11(10), 981. https://doi.org/10.3390/machines11100981










