A Novel Tooth Modification Methodology for Improving the Load-Bearing Capacity of Non-Orthogonal Helical Face Gears
Abstract
:1. Introduction
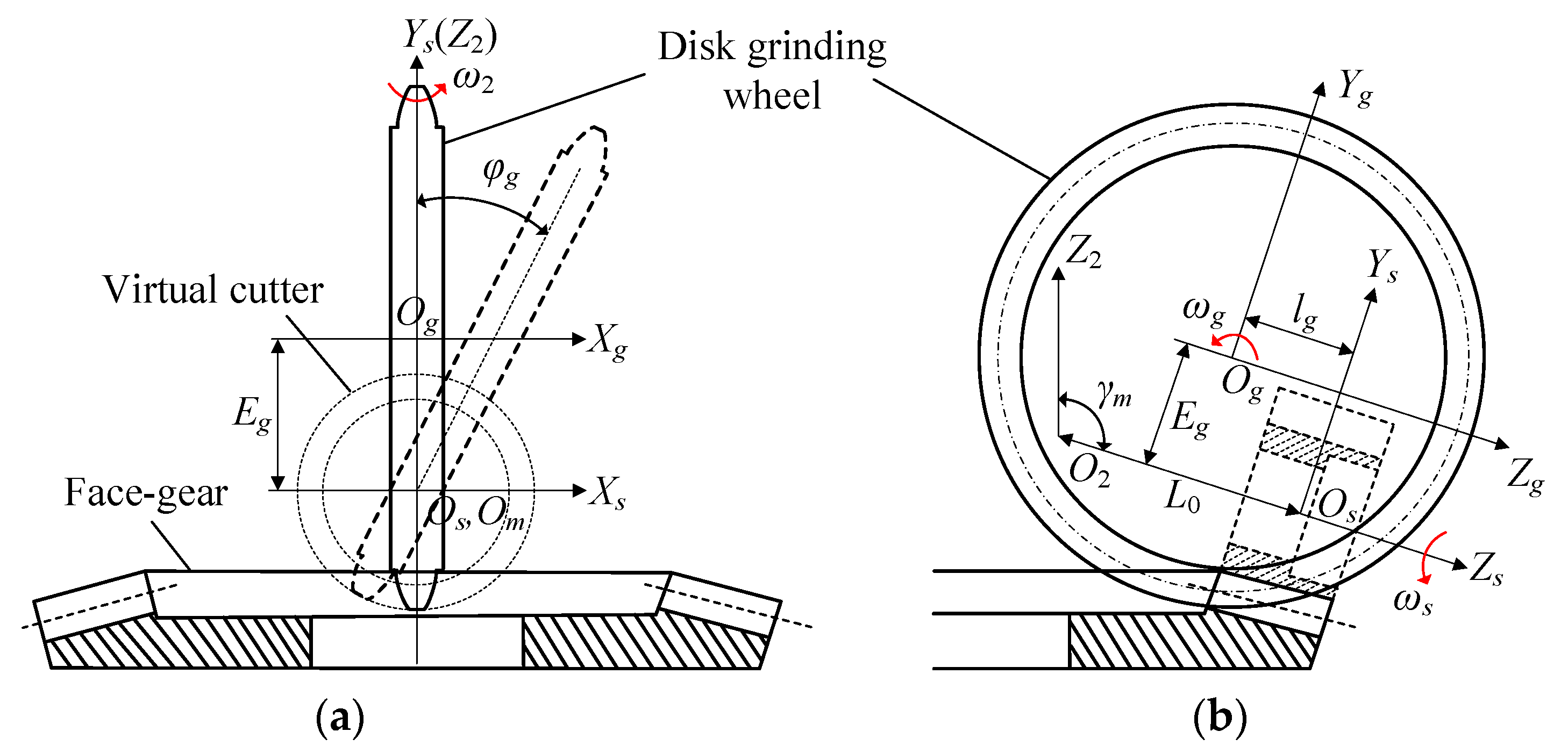
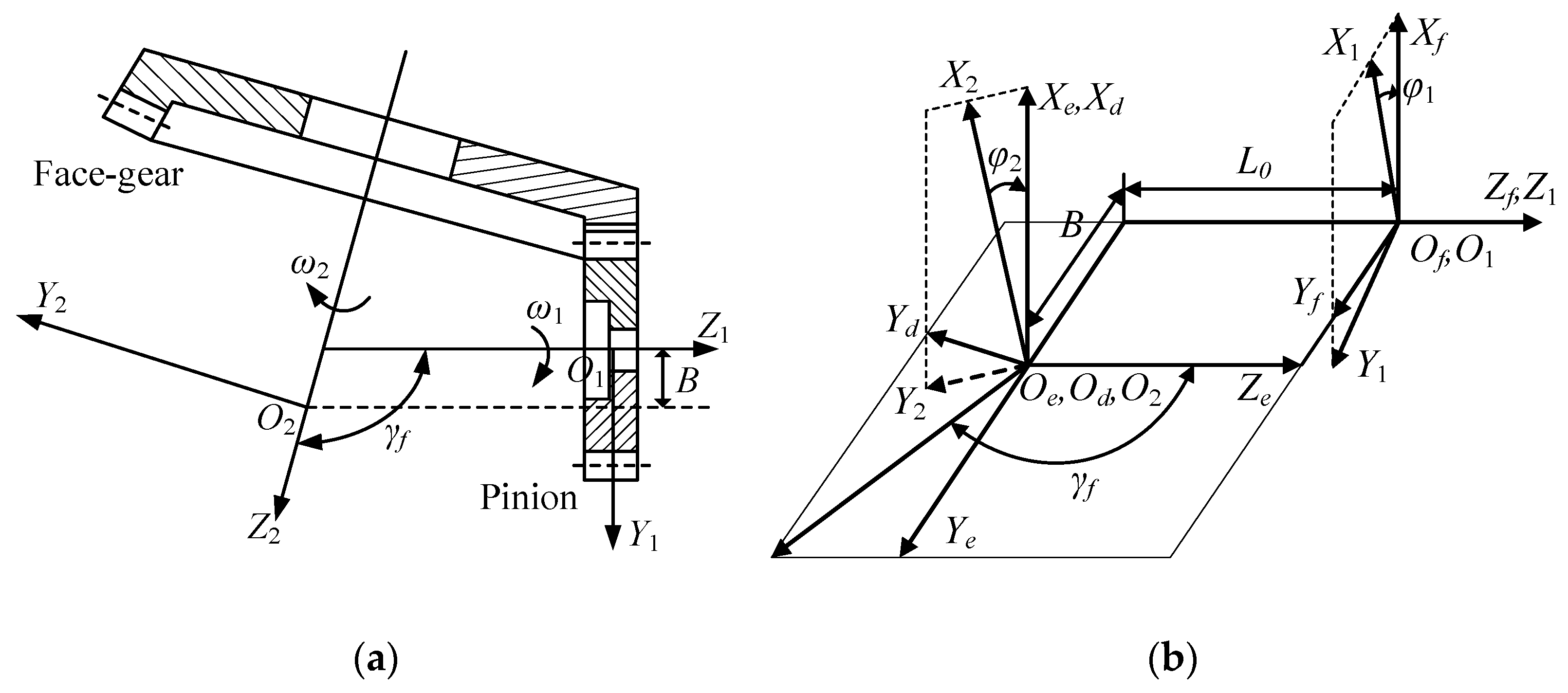
2. Generation of Non-Orthogonal Helical Face Gear Pair
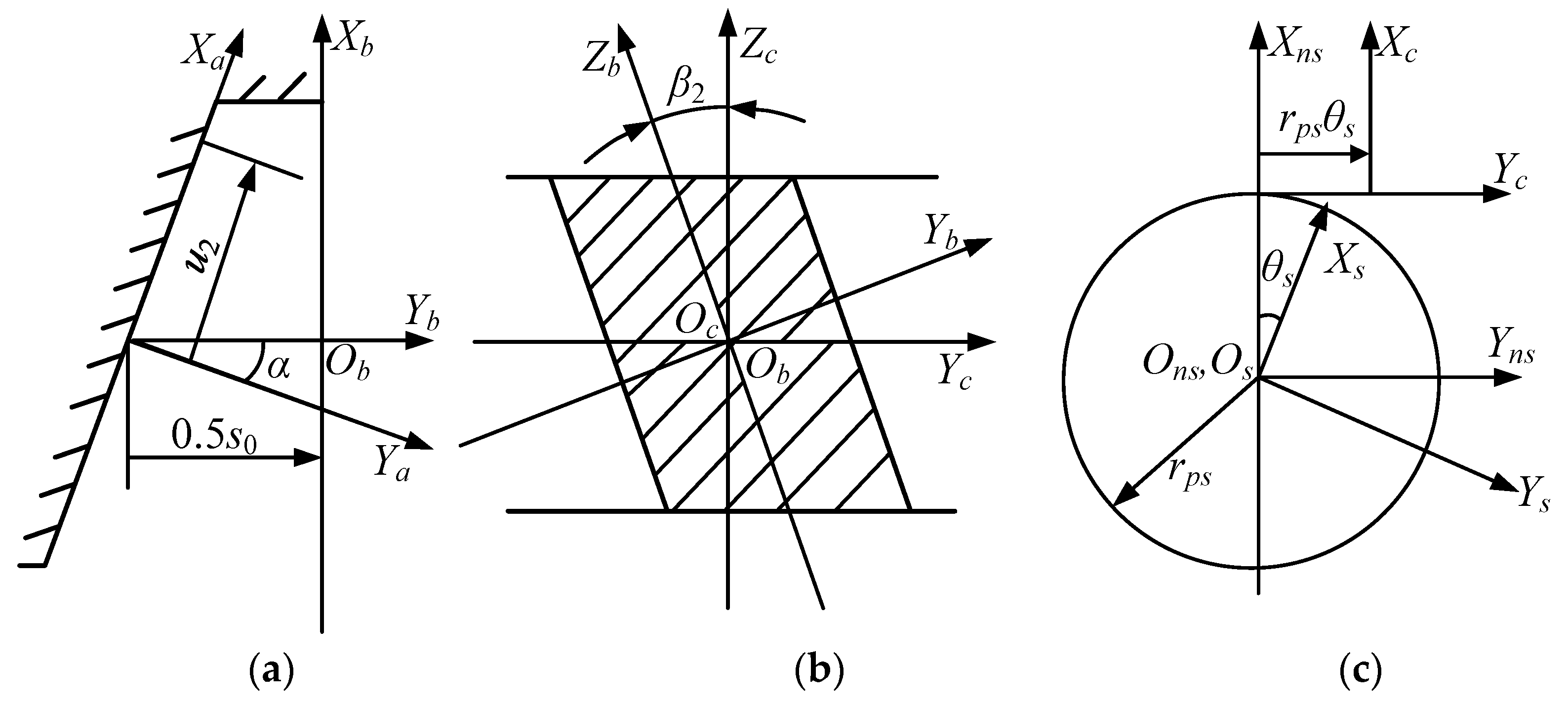
2.1. Generation of Tooth Surface of Face Gear
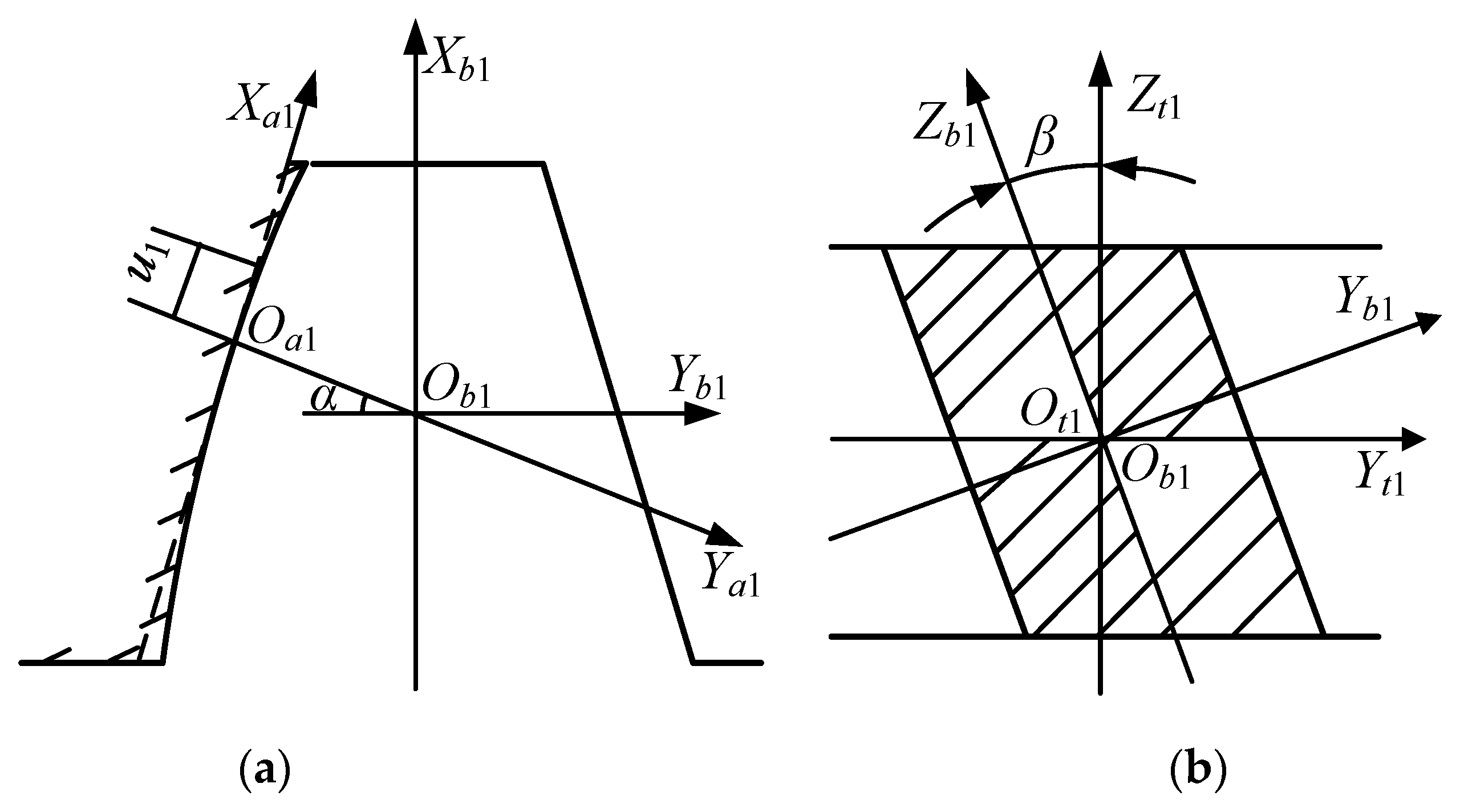
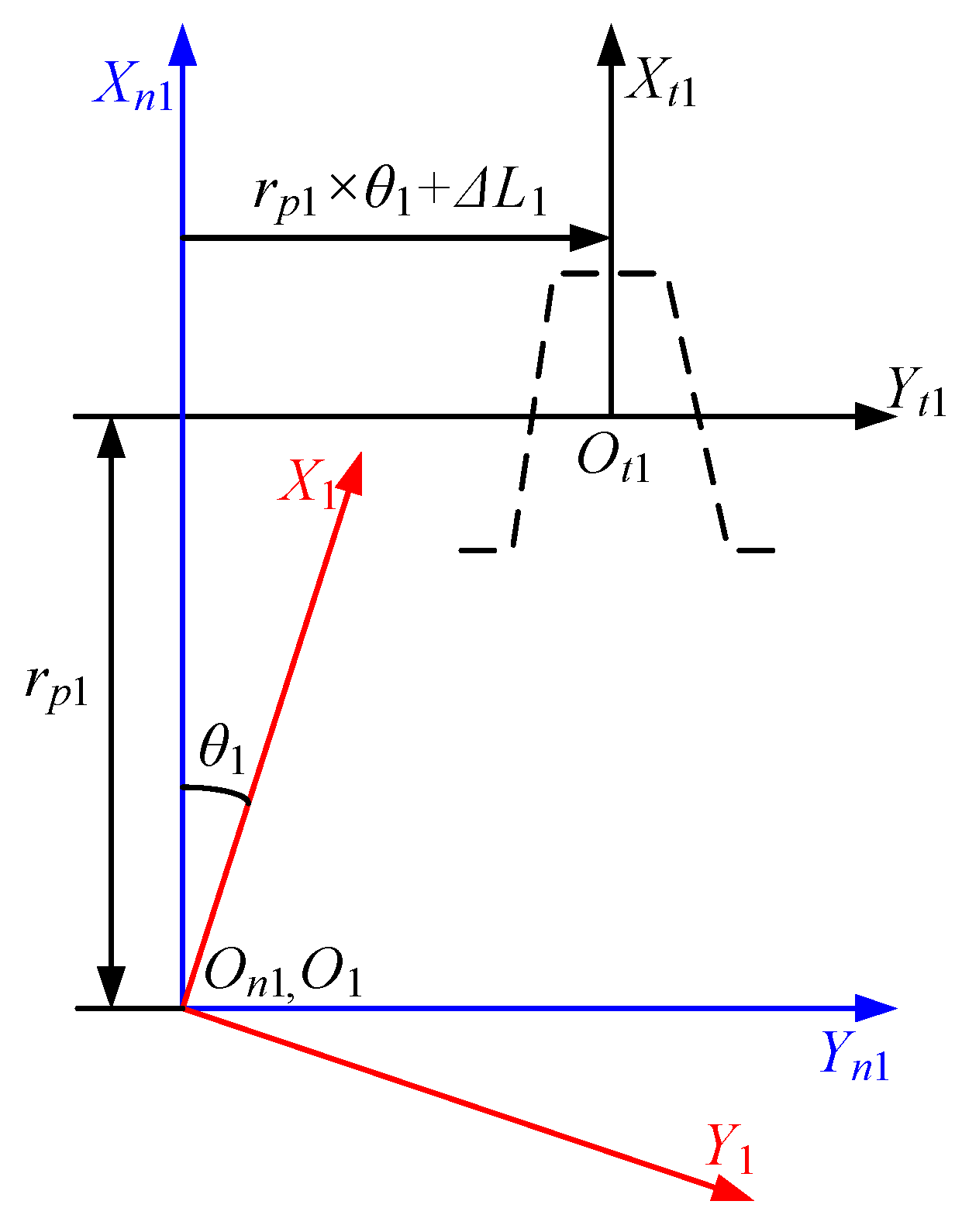
2.2. Generation of Novel Double-Crowned Tooth Surface of Pinion
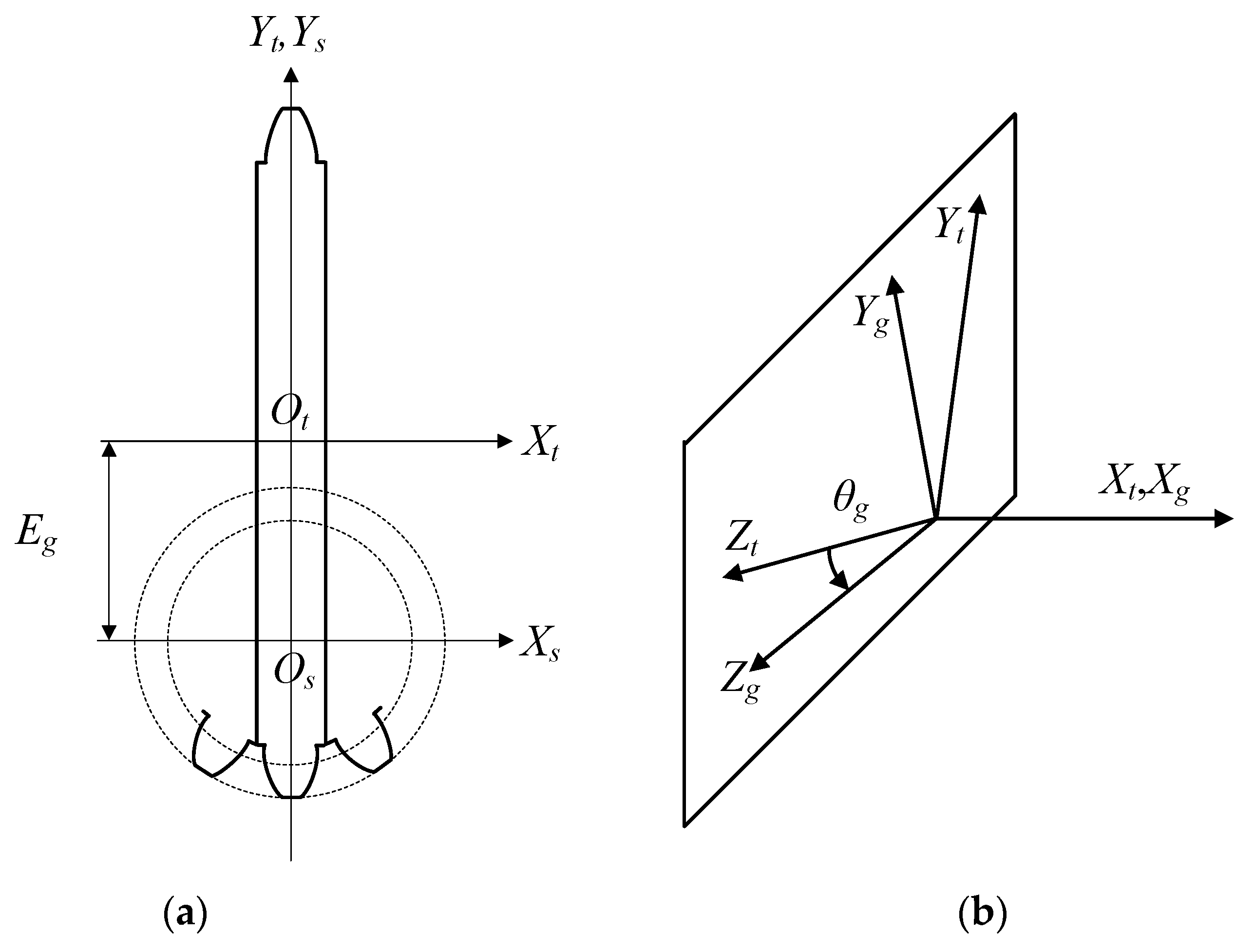
3. Analysis of Meshing Performance of Face Gears
3.1. Tooth Contact Analysis
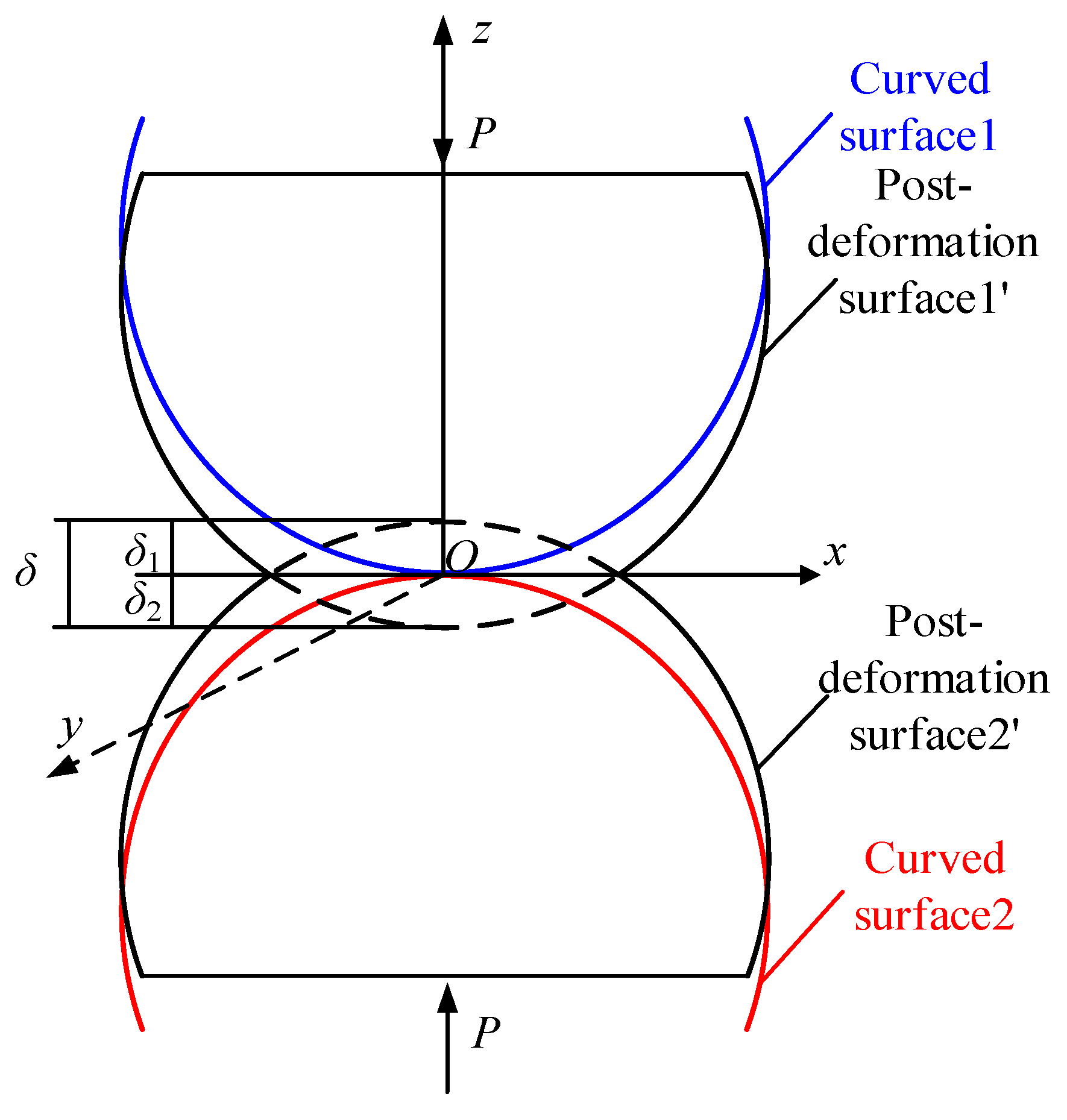
3.2. Calculation of Hertzian Contact Stress
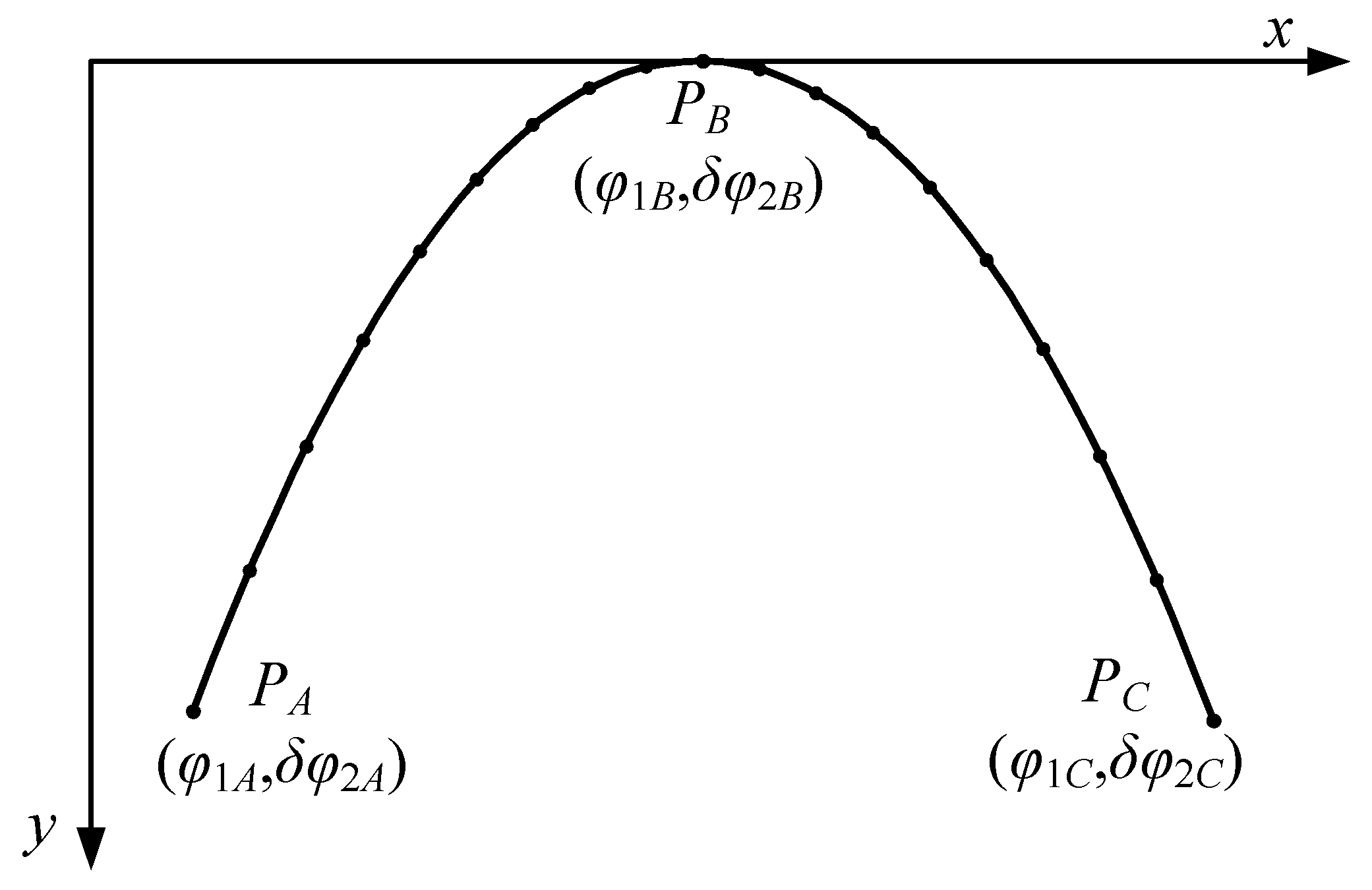
4. Designation of Intentional High-Order Transmission Error
5. Numerical Examples and Discussions
- (1)
- Parameter calculation. According to the tooth height of the gear shaping cutter, the tooth height parameter z2 of the face gear in the coordinate system S2 is derived;
- (2)
- Calculate the tooth width. Find the minimum inner diameter R1 of the gear undercut and the maximum outer diameter R2 without tooth tip sharpening, and select an appropriate tooth width within the range of R1 and R2 as the known quantity y2;
- (3)
- Discrete y2 and z2. Through discretization, i discrete values of y2i (y21, y22, y23, …, y2i) and j discrete values of z2j (z21, z22, z23, …, z2j) are obtained; based on the y2i and z2j, which are used as the input values and substituted into the tooth surface equation, we can obtain i × j values of θSij (θSi1, θSi2, θSi3, …, θSij) and i × j values of φSij (φSi1, φSi2, φSi3, …, φSij);
- (4)
- Visualization of the working tooth surface. Back-substitute the i × j group (θSij, φSij) into the non-orthogonal asymmetric surface gear tooth surface equation to obtain i × j discrete coordinate points (xij, yij, zij) on the corresponding tooth surface, and apply MatLab instructions to generate work surfaces for gears with non-orthogonal faces.
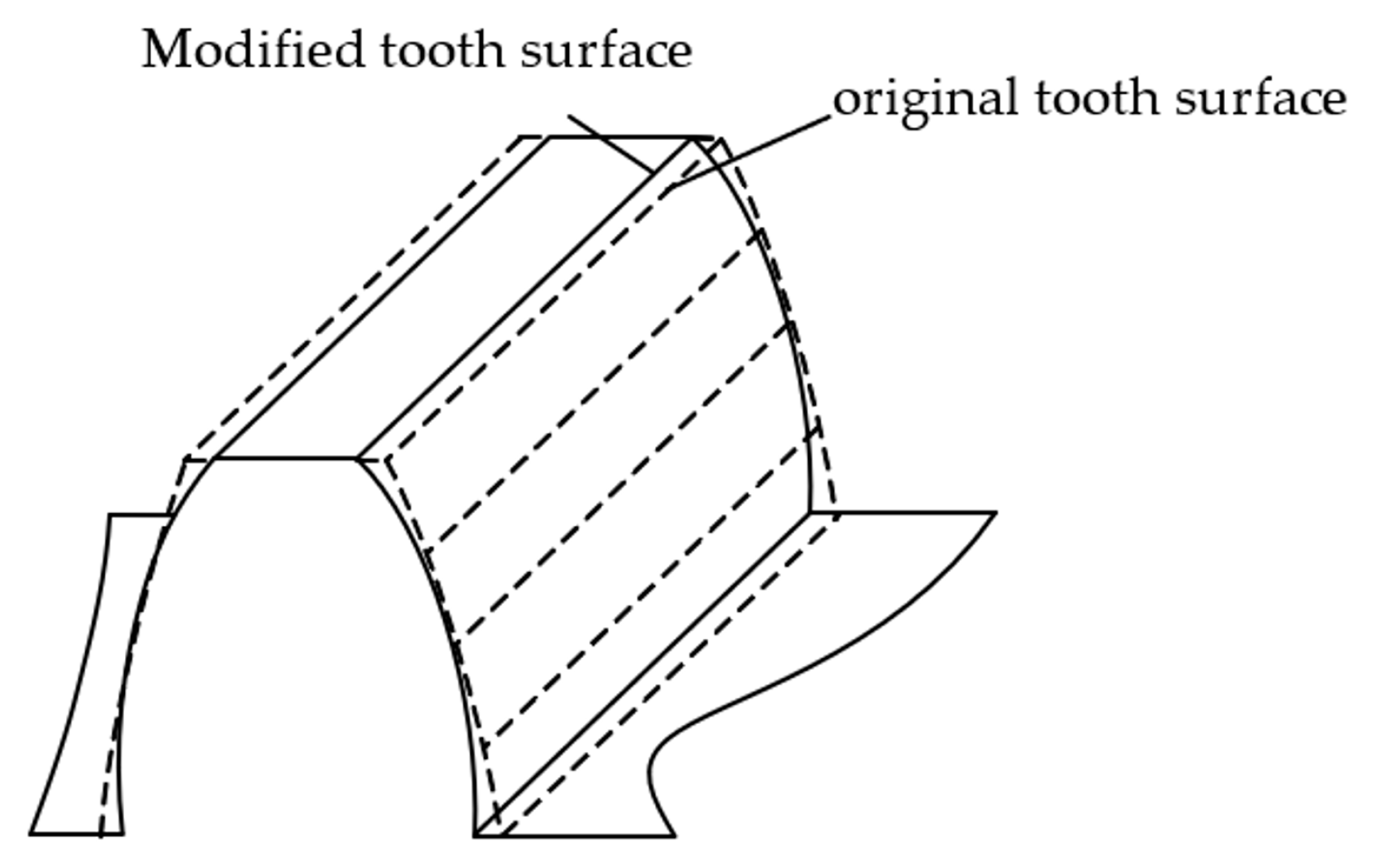
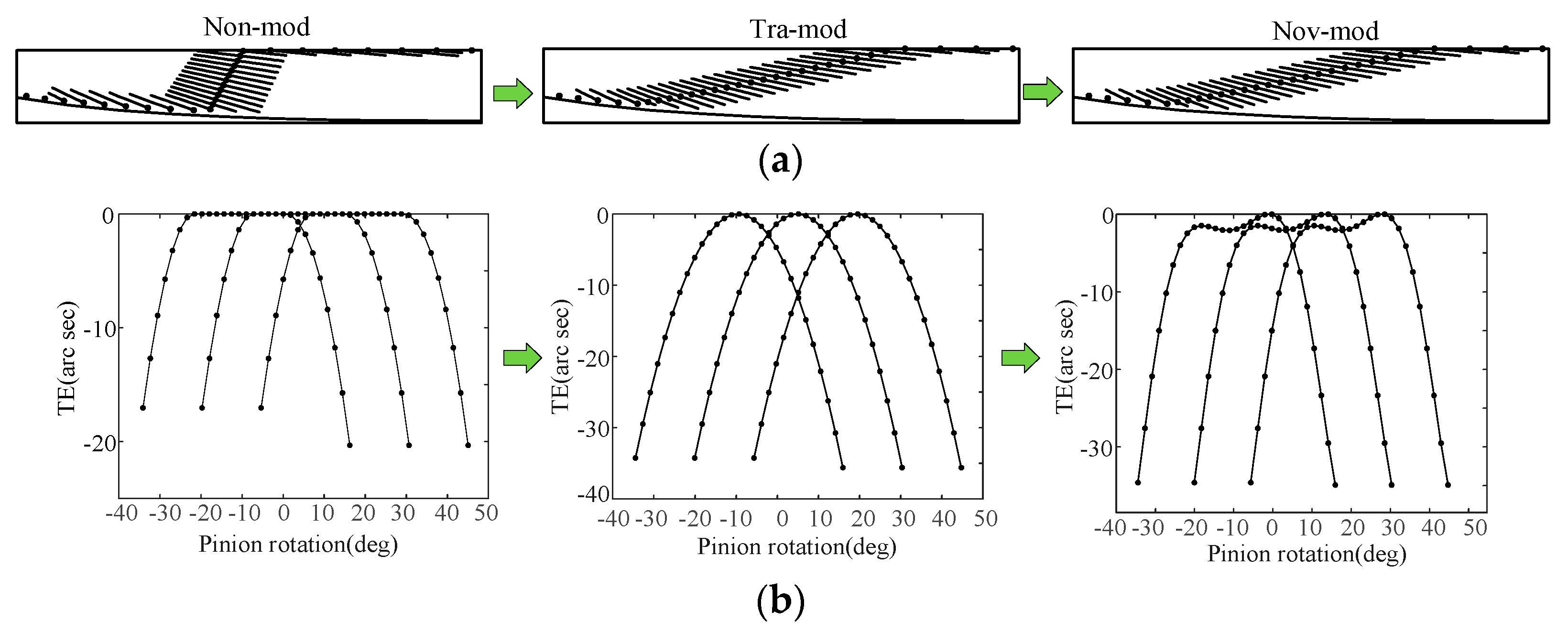
5.1. Tooth Modification
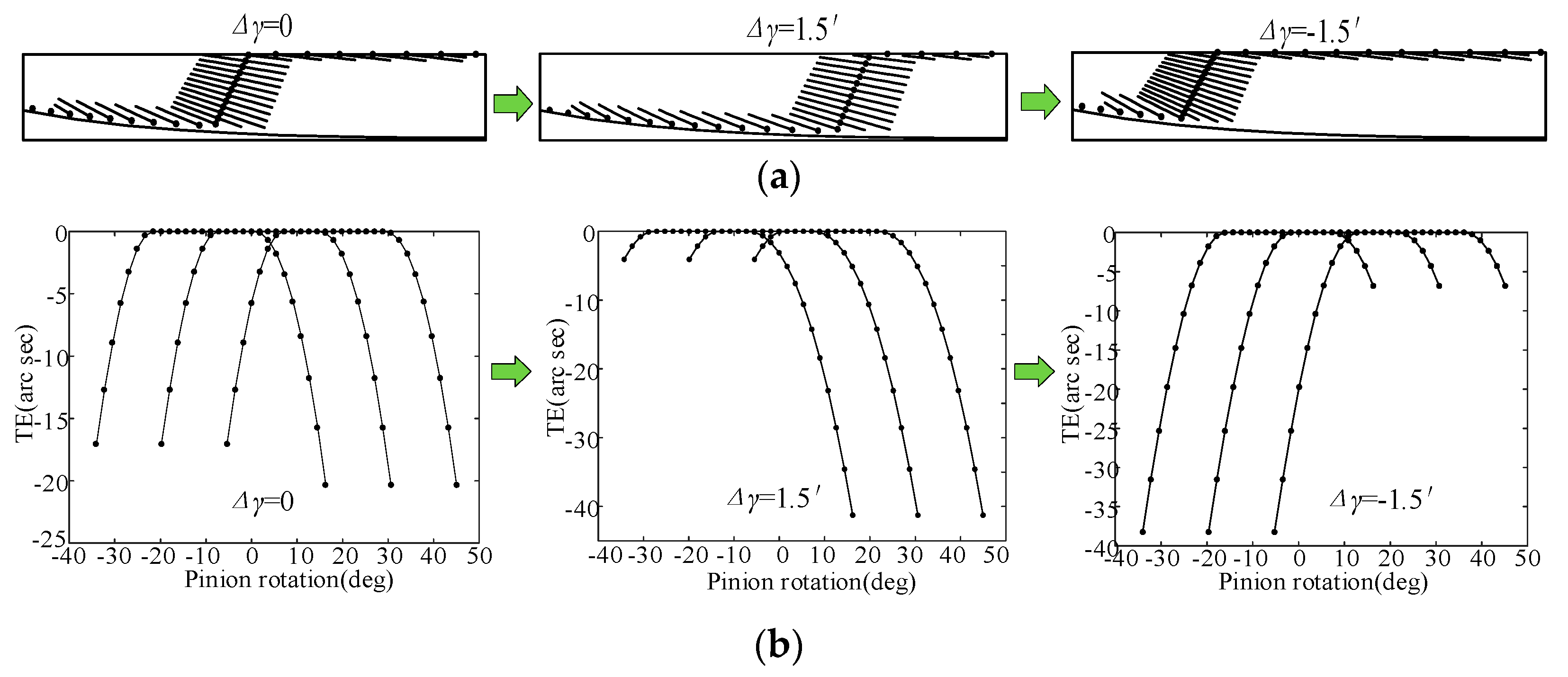
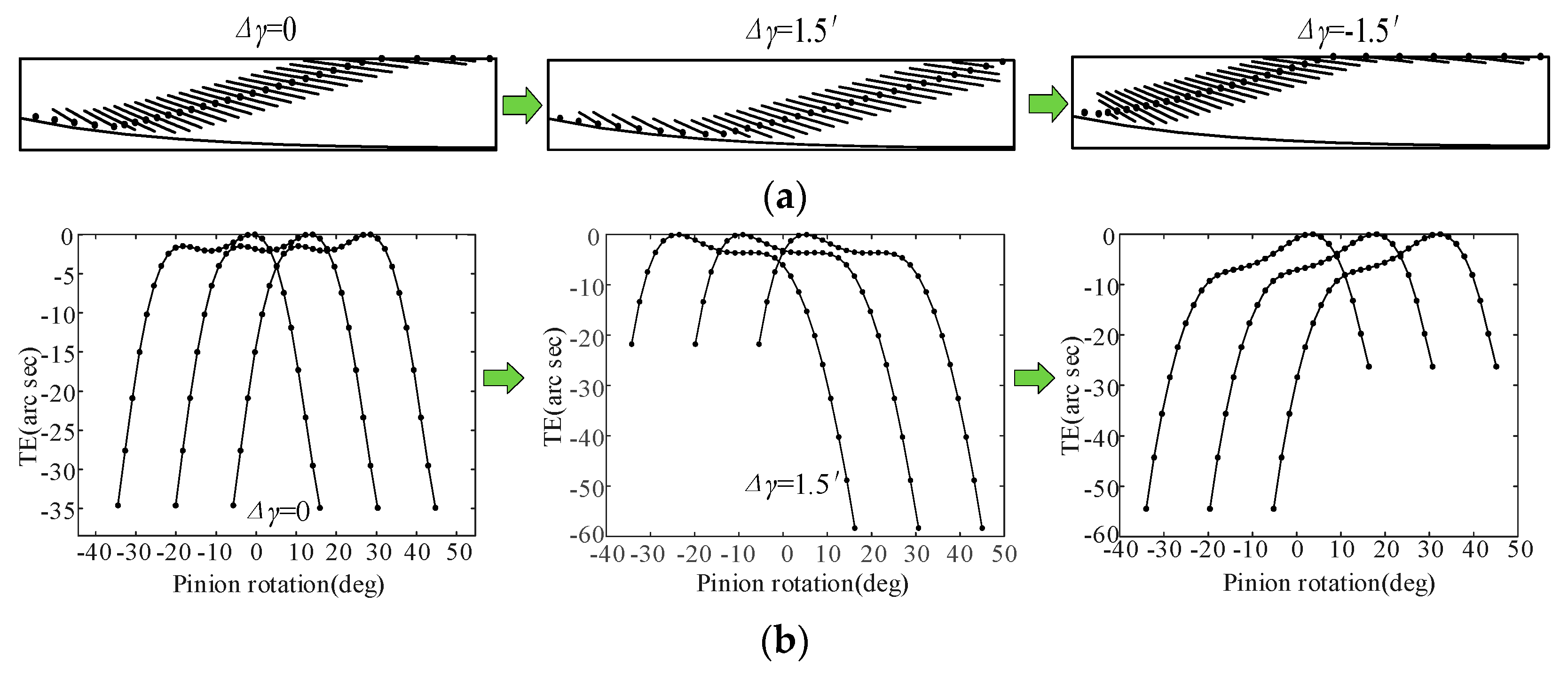
5.2. Tooth Contact Analysis
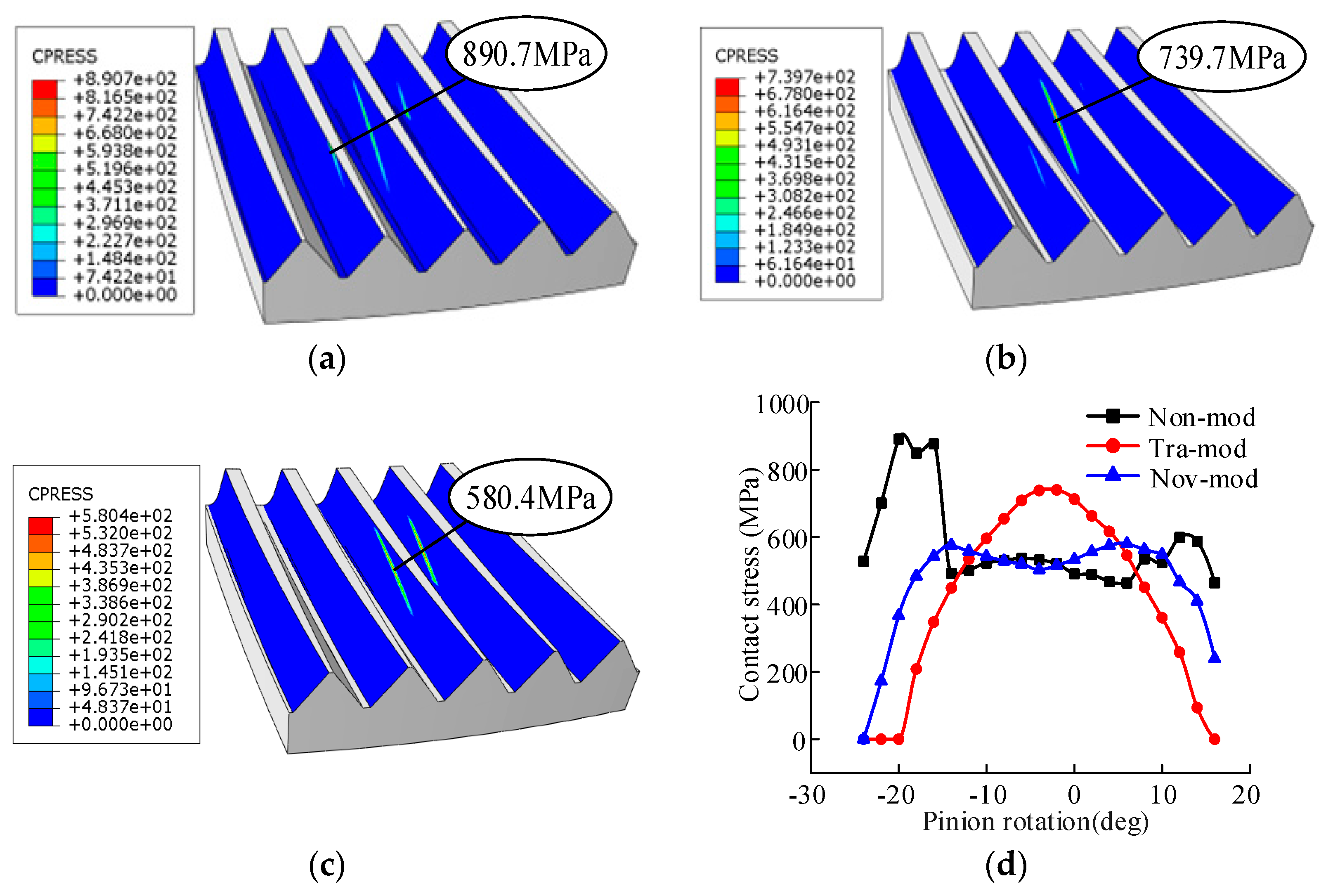
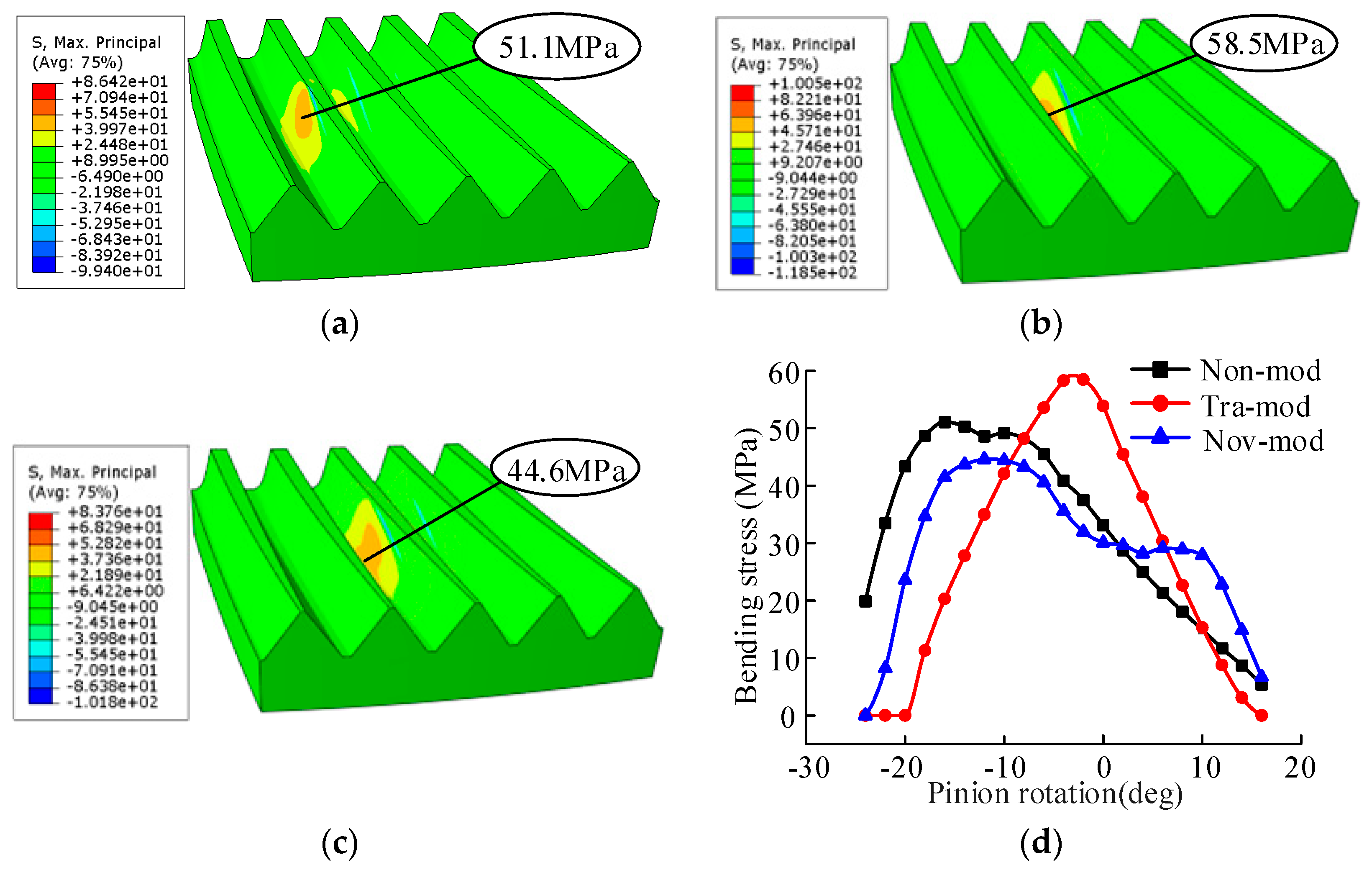
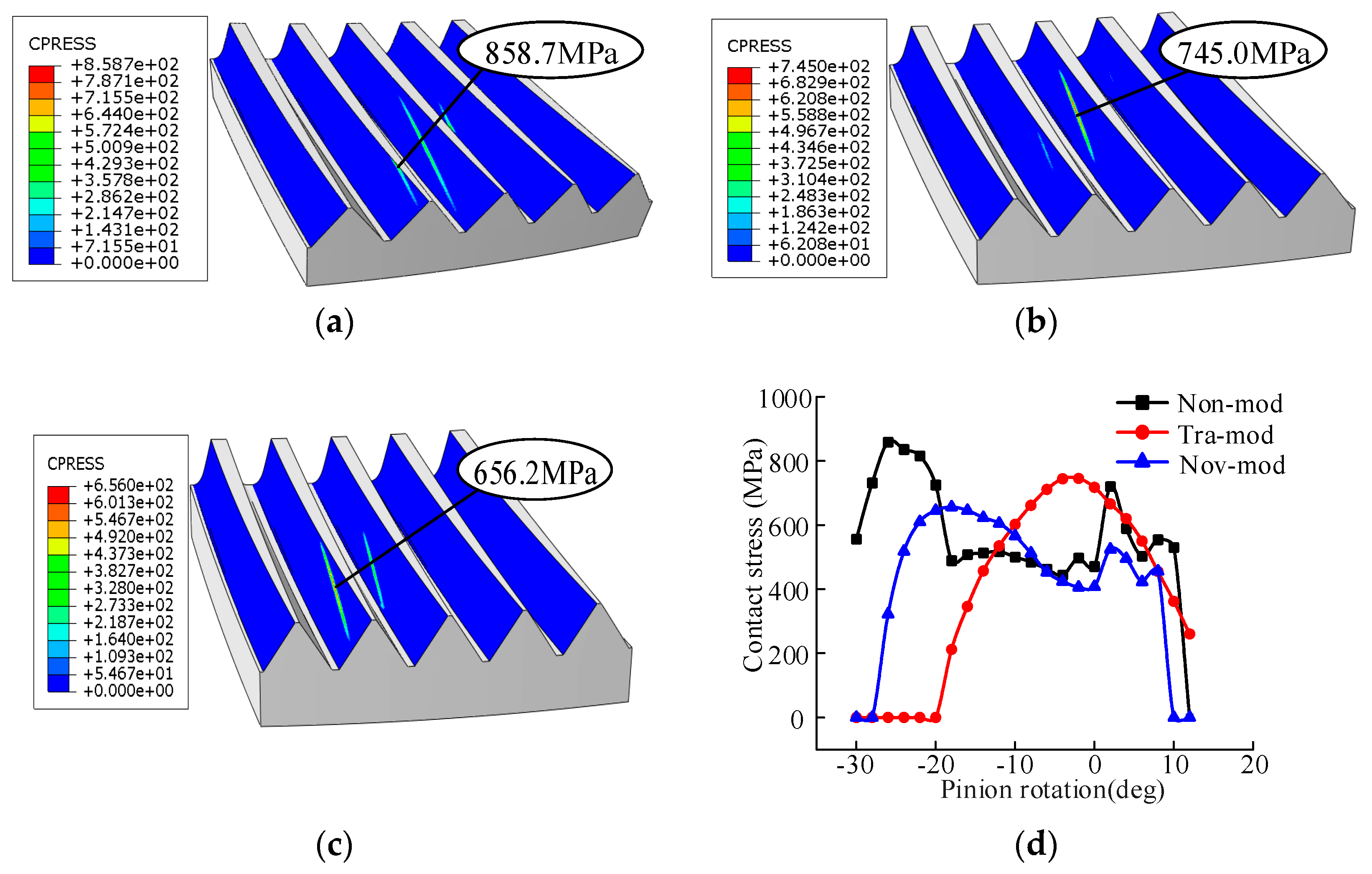
5.3. Loaded Tooth Contact Analysis
6. Conclusions
- (1)
- This paper proposes a new bidirectional gear modification method. The tooth modification is determined by the modified rack-cutter, and its feed motion is related to an intentionally designed transmission error. The novelty of the tooth modification design is that the transmission error can be predesigned.
- (2)
- The performance of the introduced novel tooth modification is studied through TCA and LTCA. Under the non-misalignment error working conditions, the contact stress and bending stress of the novel tooth modification decrease by as much as 34.83% and 12.72%, which shows better meshing performance compared to the traditional tooth modification.
- (3)
- Under the misalignment error working conditions, the contact stress and bending stress of the novel tooth modification decrease by as much as 26.24% and 7.98%. The introduced new gear modification method has lower tooth profile contact stress and tooth root bending stress both with and without misalignment errors.
- (4)
- The introduced novel tooth modification in this paper is universal, and not limited to face gears but can be extended to other types of gears.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a1 | modification parameter for tooth profile modification |
| Si | coordinate system i |
| ui, li | surface parameter of ∑i |
| [M]i,j | coordinate transmission matrix (from Sj to Si) |
| position vector and unit normal vector of surface ∑i | |
| β | base helix angle |
| ΔL1 | parameter of additional translation motion of rack-cutter |
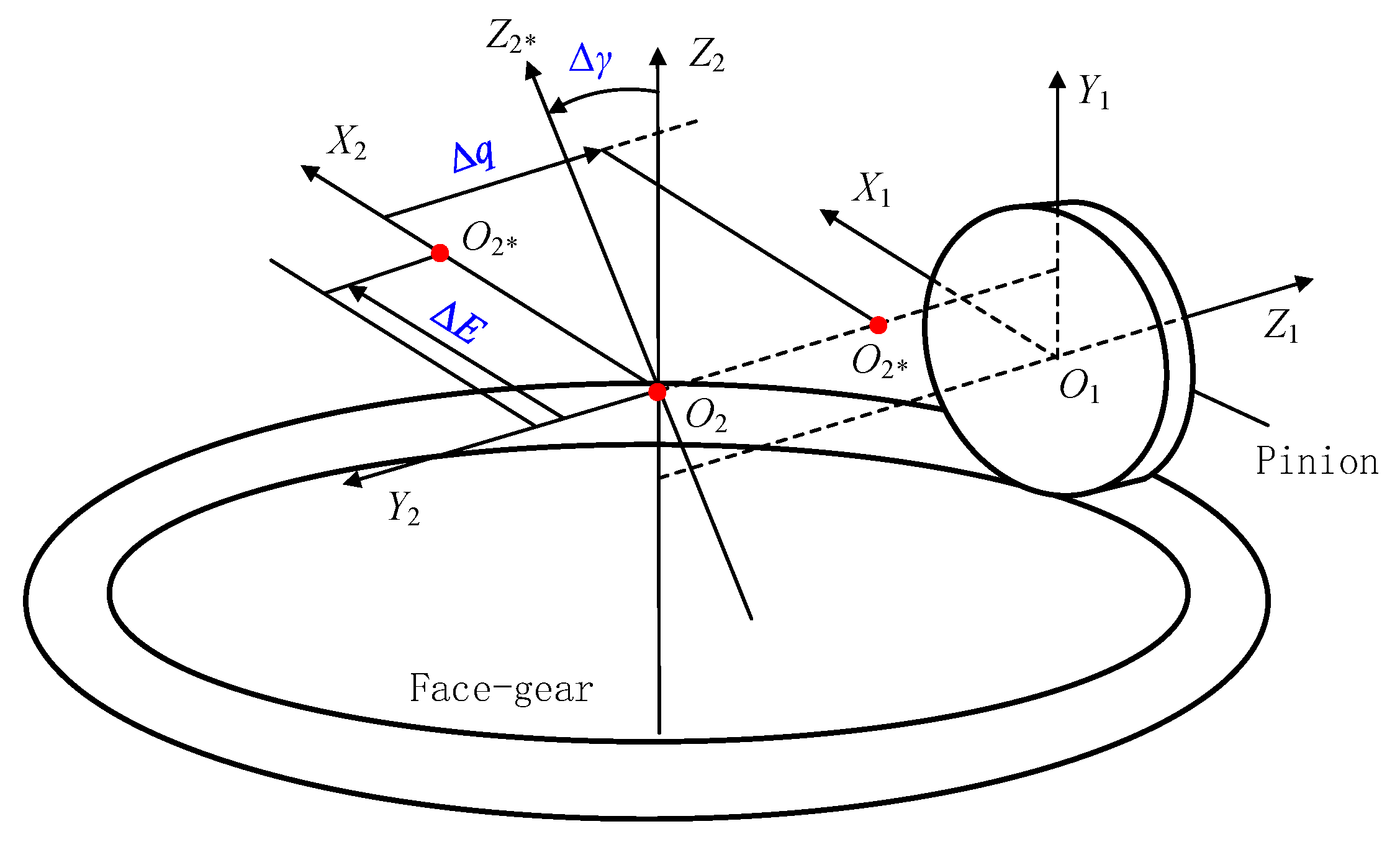
| Δγ | misalignment angle error |
| δφ2 | transmission error |
| θ1 | rotation angle of generated pinion |
| p0 | maximum contact stress |
| φ1, φ2 | rotation angle of pinion and face gear |
| Abbreviations | |
| Nov-mod | novel modification |
| Non-mod | non-modification |
| Tra-mod | traditional modification |
| TE | transmission error |
References
- He, Z.; Lin, H.; Han, X. Computerized design and simulation of meshing of modified double circular-arc helical gears by tooth end relief with helix. Mech. Mach. Theory 2010, 45, 46–64. [Google Scholar]
- Chapron, M.; Velex, P.; Bruyère, J.; Becquerelle, S. Optimization of Profile Modifications with Regard to Dynamic Tooth Loads in Single and Double-Helical Planetary Gears with Flexible Ring-Gears. J. Mech. Des. 2016, 138, 023301. [Google Scholar] [CrossRef]
- Tran, V.-Q.; Wu, Y.-R. A novel method for closed-loop topology modification of helical gears using internal-meshing gear honing. Mech. Mach. Theory 2019, 145, 103691. [Google Scholar] [CrossRef]
- Deng, J.; Nie, S.; Deng, X.; Jiang, C. Tooth surface mismatch modification method of cycloidal bevel gear based on conjugate tooth surface modification. J. Adv. Mech. Des. Syst. Manuf. 2020, 14, JAMDSM0017. [Google Scholar] [CrossRef]
- Li, T.; An, X.; Deng, X.; Li, J.; Li, Y. A New Tooth Profile Modification Method of Cycloidal Gears in Precision Reducers for Robots. Appl. Sci. 2020, 10, 1266. [Google Scholar] [CrossRef]
- Wang, H.; Tang, L.; Zhou, C.; Shi, Z. Wear life prediction method of crowned double helical gear drive in point contact mixed elas-tohydrodynamic lubrication. Wear 2021, 484, 204041. [Google Scholar] [CrossRef]
- Feng, Z.; Chen, Y.; Zhao, Y. Analysis of Influence of Pinion Tooth Trace Modification on Tooth Surface of Curved Tooth Face Gear. Mech. Transm. 2022, 46, 50–55. [Google Scholar]
- Huangfu, Y.; Zhao, Z.; Ma, H.; Han, H.; Chen, K. Effects of tooth modifications on the dynamic characteristics of thin-rimmed gears under surface wear. Mech. Mach. Theory 2020, 150, 103870. [Google Scholar] [CrossRef]
- Yang, J.; Lin, T.; He, Z.; Chen, M. Novel calculation method for dynamic excitation of modified double-helical gear transmission. Mech. Mach. Theory 2022, 167, 104467. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Mao, S.M.; Guo, W.C.; Guo, Z. Tooth modification and dynamic performance of the cycloidal drive. Mech. Syst. Signal Process. 2017, 85, 857–866. [Google Scholar] [CrossRef]
- Zschippang, H.; Weikert, S.; Küçük, K.; Wegener, K. Face-gear drive: Geometry generation and tooth contact analysis. Mech. Mach. Theory 2019, 142, 103576. [Google Scholar] [CrossRef]
- Dongsheng, H. Research on Numerical Analysis Modeling Method for Gear Meshing and Its Applications; Dalian University of Technology: Dalian, China, 2012. [Google Scholar]
- Yunbo, S. Novel Design Process for Face Gear Drive with a High Order Polynomial Function of Transmission Error. J. Xi’an Technol. Univ. 2013, 33, 7. [Google Scholar]
- Li, D.; Wu, S.; Zhao, R.; Deng, X. Design of the high-order curve tooth profile and analysis on the face gear’s tooth contact. Mech. Des. 2020, 37, 109–114. [Google Scholar]
- Fu, X.; Fang, Z.; Cui, Y.; Hou, X.; Li, J. Modelling, design and analysis of offset, non-orthogonal and profile-shifted face gear drives. Adv. Mech. Eng. 2018, 10, 1687814018798250. [Google Scholar] [CrossRef]
- Fu, X.; Fang, Z.; Xiang, L.; Li, J. Assembly errors tolerance and sensitivity of offset face gears. J. Harbin Eng. Univ. 2018, 39, 1227–1232. [Google Scholar]
- Feng, G.; Xie, Z.; Zhou, M. Geometric design and analysis of face-gear drive with involute helical pinion. Mech. Mach. Theory 2019, 134, 169–196. [Google Scholar] [CrossRef]
- Wang, C. Multi-objective optimal design of modification for helical gear. Mech. Syst. Signal Process. 2021, 157, 107762. [Google Scholar] [CrossRef]
- Gao, P.; Liu, H.; Yan, P.; Xie, Y.; Xiang, C.; Wang, C. Research on application of dynamic optimization modification for an involute spur gear in a fixed-shaft gear transmission system. Mech. Syst. Signal Process. 2022, 181, 109530. [Google Scholar] [CrossRef]
- Zheng, F.; Zhang, M.; Zhang, W.; Tan, R.; Guo, X. On the deformed tooth contact analysis for forged bevel gear modification. Mech. Mach. Theory 2019, 135, 192–207. [Google Scholar] [CrossRef]
- Yuan, B.; Liu, G.; Yue, Y.; Liu, L.; Shen, Y. A novel tooth surface modification methodology for wide-faced double-helical gear pairs. Mech. Mach. Theory 2021, 160, 104299. [Google Scholar] [CrossRef]
- Yan, P.; Liu, H.; Gao, P.; Zhang, X.; Zhan, Z.; Zhang, C. Optimization of distributed axial dynamic modification based on the dynamic characteristics of a helical gear pair and a test verification. Mech. Mach. Theory 2021, 163, 104371. [Google Scholar] [CrossRef]
- Yang, Y.C.; Wu, Y.R.; Tsai, T.M. An analytical method to control and predict grinding textures on modified gear tooth flanks in CNC generating gear grinding. Mech. Mach. Theory 2022, 177, 105023. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, Z.; Tong, S.; Li, S.; Tong, Z. Gear tribodynamic modeling and analysis considering tooth profile modification. Tribol. Int. 2023, 178, 108023. [Google Scholar] [CrossRef]
- Su, J.; Fang, Z.; Cai, X. Design and analysis of spiral bevel gears with seventh-order function of transmission error. Chin. J. Aeronaut. 2013, 26, 1310–1316. [Google Scholar] [CrossRef]
- Jiang, J.; Fang, Z. Design and analysis of modified cylindrical gears with a higher-order transmission error. Mech. Mach. Theory 2015, 88, 141–152. [Google Scholar] [CrossRef]
- Jia, C.; Fang, Z.; Zhang, Y. Topography of modified surfaces based on compensated conjugation for the minimization of trans-mission errors of cylindrical gears. Mech. Mach. Theory 2017, 116, 145–161. [Google Scholar] [CrossRef]
- Yu, B.; Ting, K.L. Compensated conjugation and gear tooth design and modification. J. Mech. Des. 2016, 138, 073301. [Google Scholar] [CrossRef]
- Yang, J.; Shi, Z.; Zhang, H.; Li, T.; Nie, S.; Wei, B. Dynamic analysis of spiral bevel and hypoid gears with high-order transmission errors. J. Sound Vib. 2018, 417, 149–164. [Google Scholar] [CrossRef]
- Mu, Y.; Li, W.; Fang, Z.; Zhang, X. A novel tooth surface modification method for spiral bevel gears with higher-order transmission error. Mech. Mach. Theory 2018, 126, 49–60. [Google Scholar] [CrossRef]
- Samani, F.S.; Molaie, M.; Pellicano, F. Nonlinear vibration of the spiral bevel gear with a novel tooth surface modification method. Meccanica 2019, 54, 1071–1081. [Google Scholar] [CrossRef]
- Korta, J.A.; Mundo, D. Multi-objective microgeometry optimization of gear teeth supported by response surface methodology. Mech. Mach. Theory 2017, 109, 278–295. [Google Scholar] [CrossRef]
- Lu, G.; Fan, S.; Li, G.; Tong, S.; Xiao, R. Research on Design and Pitch surface shape of New Type High-order Non-conical gears. Chin. Mech. Eng. 2015, 26, 2989–2995. [Google Scholar]
- Zhao, X.; Ye, J.; Chu, M.; Dai, L.; Chen, J. Automatic Scallion Seedling Feeding Mechanism with an Asymmetrical High-order Transmission Gear Train. Chin. J. Mech. Eng. 2020, 33, 10. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Guo, K., Ye, L., Fan, L., Jr., Eds.; Shanghai Scientific and Technical Publishers: Shanghai, China, 2008; pp. 484–485. [Google Scholar]
- Vouaillat, G.; Noyel, J.P.; Ville, F.; Kleber, X.; Rathery, S. From Hertzian contact to spur gears: Analyses of stresses and rolling contact fatigue. Mech. Ind. 2019, 20, 626. [Google Scholar] [CrossRef]
- Guingand, M.; Vaujany, J.; Jacquin, C.Y. Quasi-static analysis of a face gear under torque. Comput. Methods Appl. Mech. Eng. 2005, 194, 4301–4318. [Google Scholar] [CrossRef]

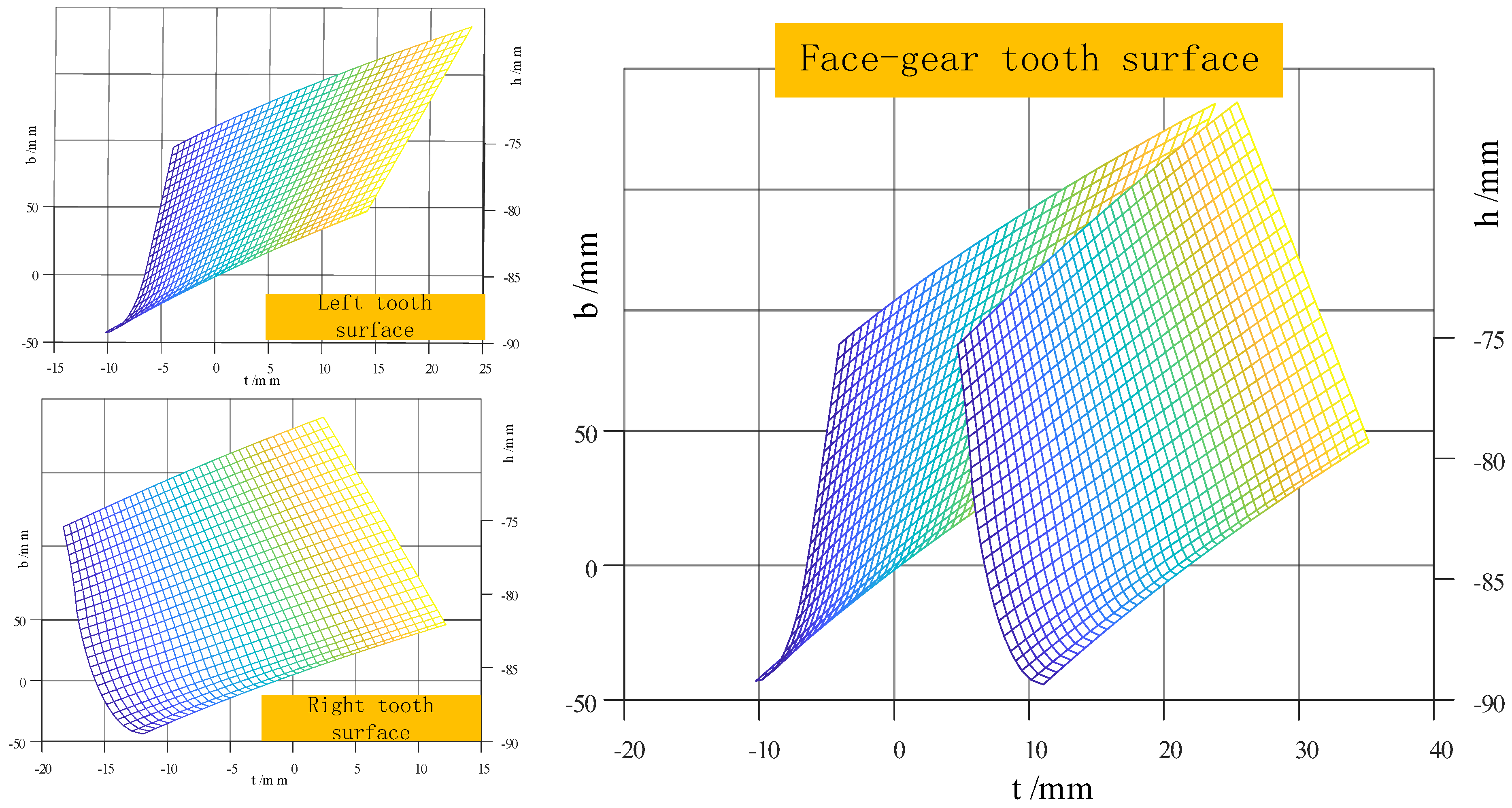
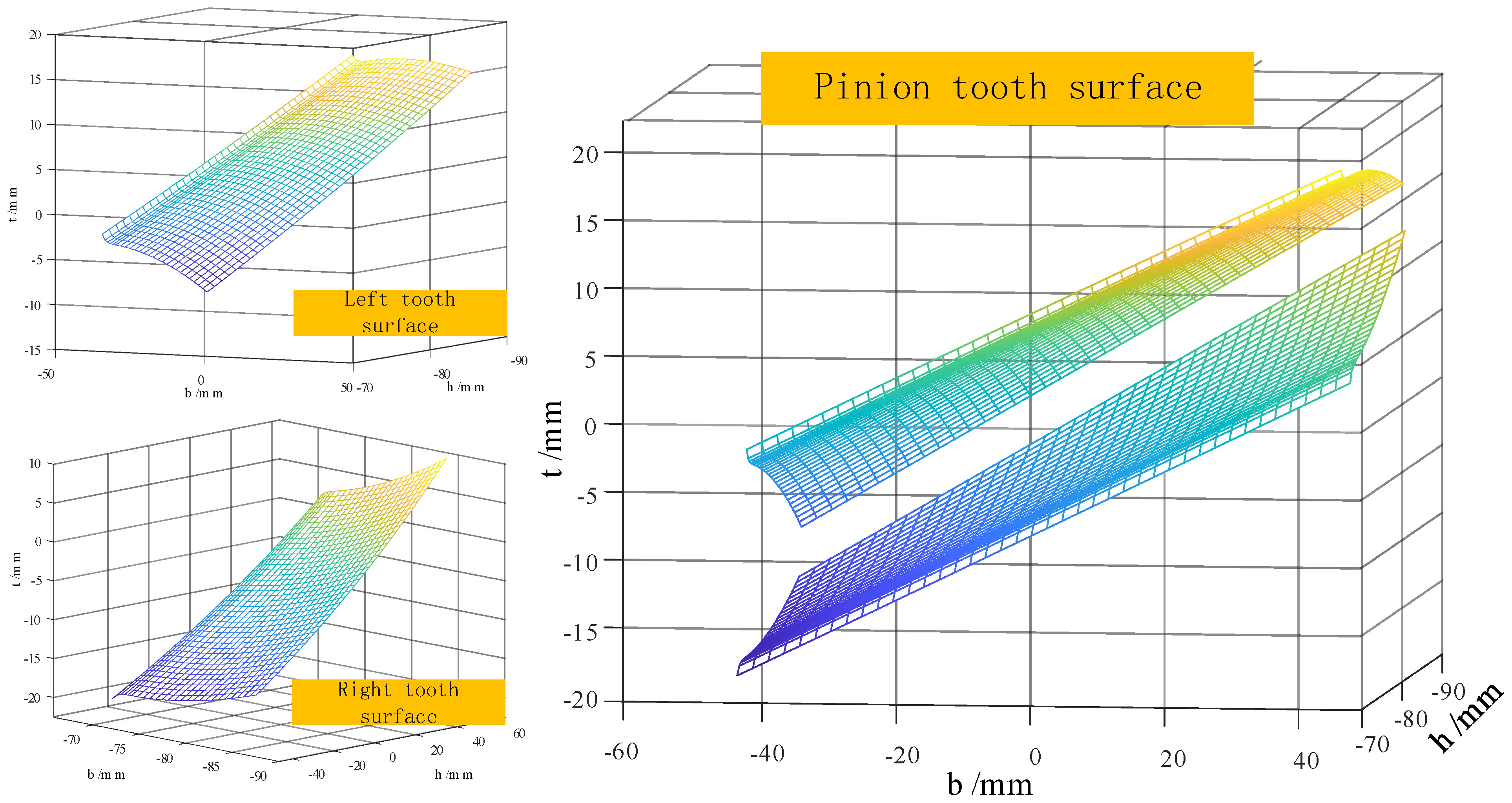
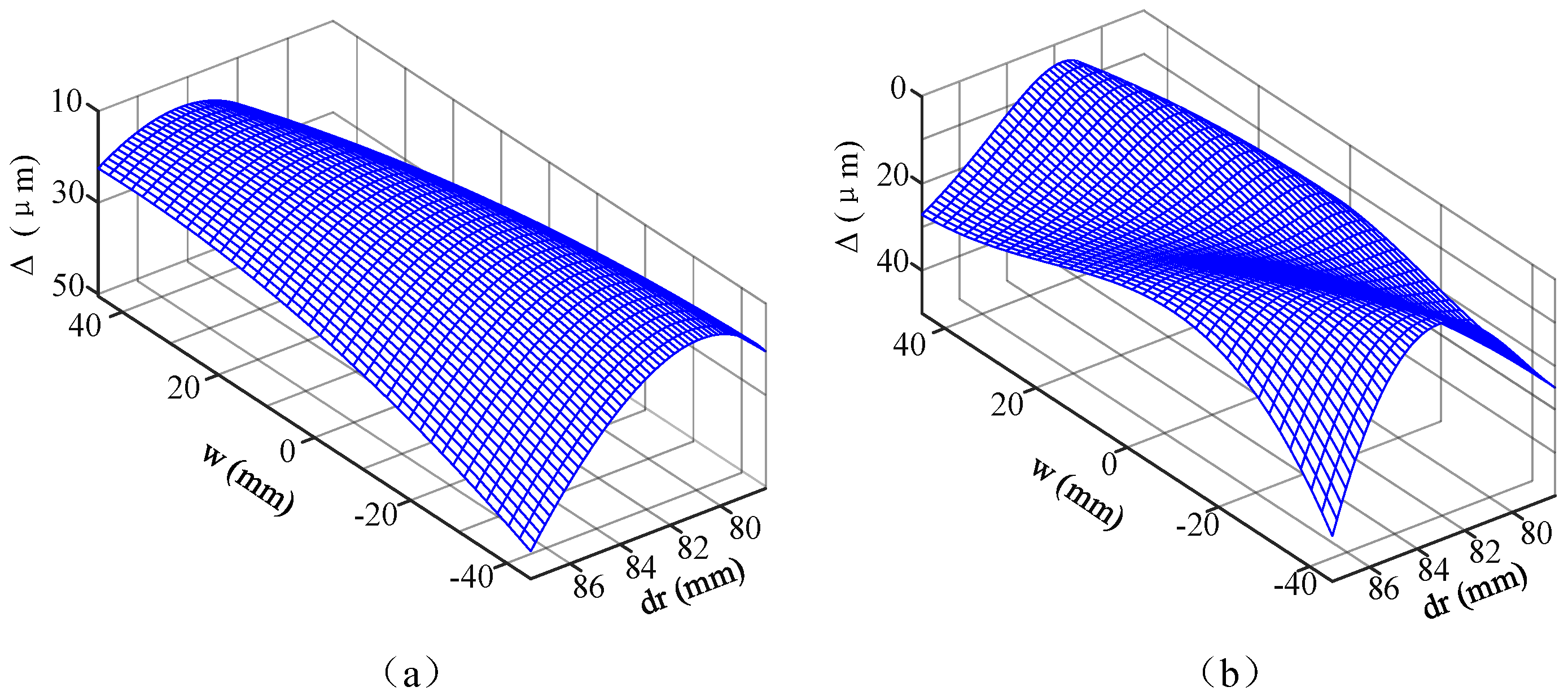


| Parameter | Value |
|---|---|
| Pinion tooth number | 25 |
| Cutter tooth number | 28 |
| Face gear tooth number | 160 |
| Normal module (mm) | 6.35 |
| Pressure angle (degree) | 25 |
| Helix angle (degree) | 15 |
| Shaft angle (degree) | 100 |
| Inner radius (mm) | 510 |
| External radius (mm) | 600 |
| Items | Contact Stress | Bending Stress | ||
|---|---|---|---|---|
| Results (MPa) | Variation | Results (MPa) | Variation | |
| Non-mod | 890.7 | — | 51.1 | — |
| Tra-mod | 739.7 | −16.95% | 58.5 | +14.48% |
| Nov-mod | 580.4 | −34.83% | 44.6 | −12.72% |
| Items | Contact Stress | Bending Stress | ||
|---|---|---|---|---|
| Results (MPa) | Variation | Results (MPa) | Variation | |
| Non-mod | 940.9 | — | 63.9 | — |
| Tra-mod | 774.2 | −17.73% | 80.6 | +26.13% |
| Nov-mod | 694.5 | −26.24% | 58.8 | −7.98% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, C.; Li, B.; Xu, J. A Novel Tooth Modification Methodology for Improving the Load-Bearing Capacity of Non-Orthogonal Helical Face Gears. Machines 2023, 11, 1077. https://doi.org/10.3390/machines11121077
Jia C, Li B, Xu J. A Novel Tooth Modification Methodology for Improving the Load-Bearing Capacity of Non-Orthogonal Helical Face Gears. Machines. 2023; 11(12):1077. https://doi.org/10.3390/machines11121077
Chicago/Turabian StyleJia, Chao, Bingquan Li, and Junhong Xu. 2023. "A Novel Tooth Modification Methodology for Improving the Load-Bearing Capacity of Non-Orthogonal Helical Face Gears" Machines 11, no. 12: 1077. https://doi.org/10.3390/machines11121077
APA StyleJia, C., Li, B., & Xu, J. (2023). A Novel Tooth Modification Methodology for Improving the Load-Bearing Capacity of Non-Orthogonal Helical Face Gears. Machines, 11(12), 1077. https://doi.org/10.3390/machines11121077





