Failure of Threaded Connections: A Literature Review
Abstract
:1. Introduction
2. Loosening and Preload Loss (Dynamic or Static)
2.1. Theories of Loosening Process
2.2. Analytical Modelling
2.3. Vibrational Loading
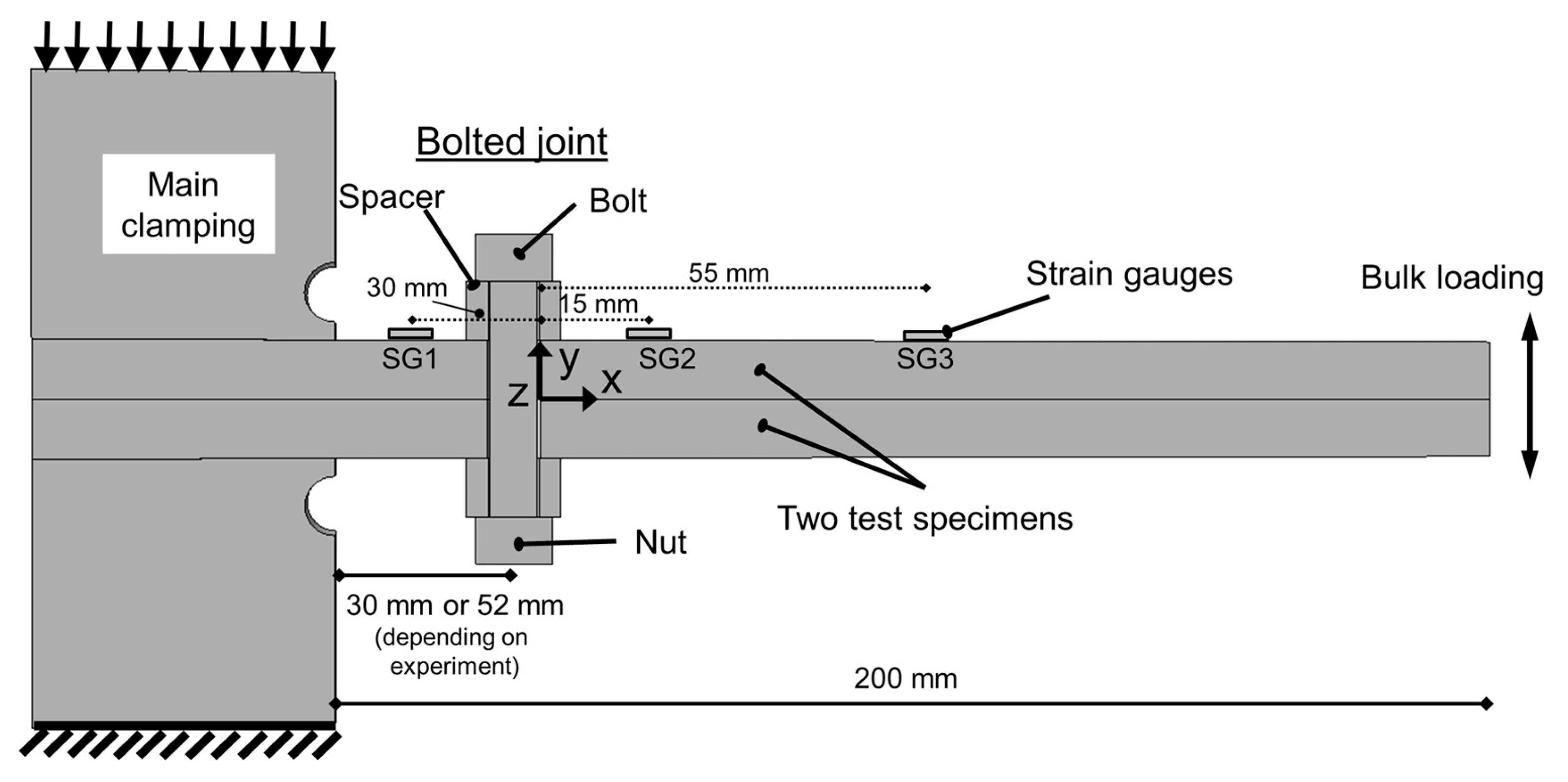
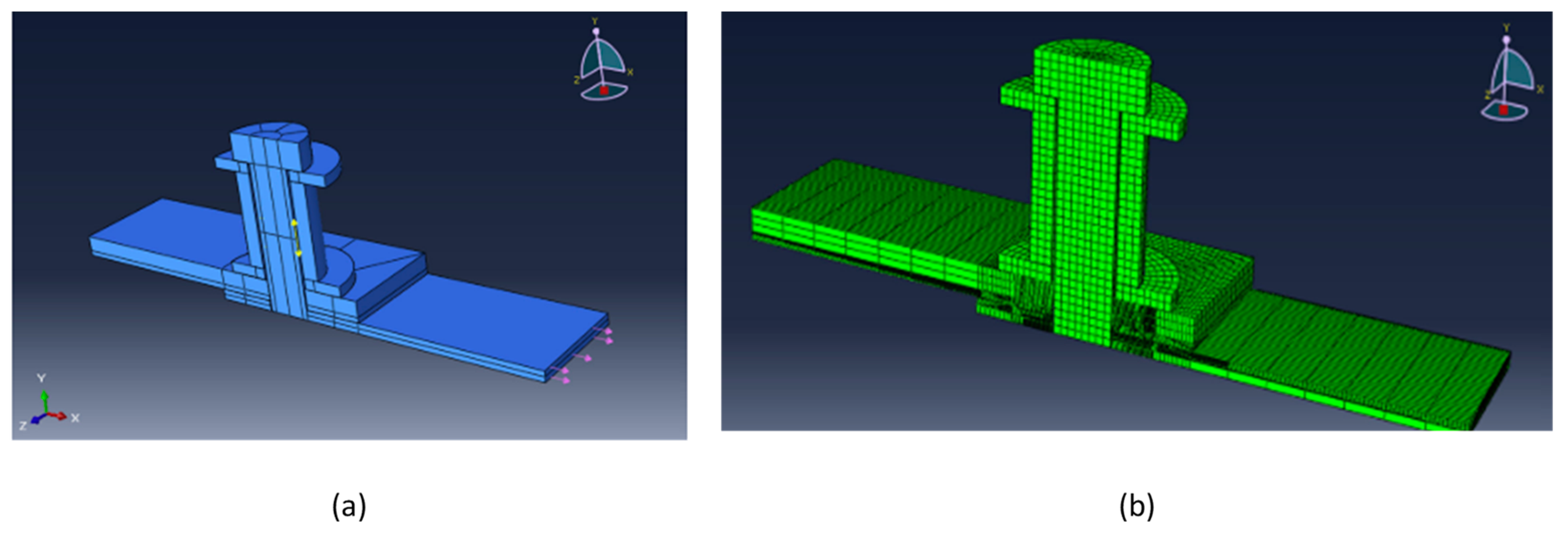
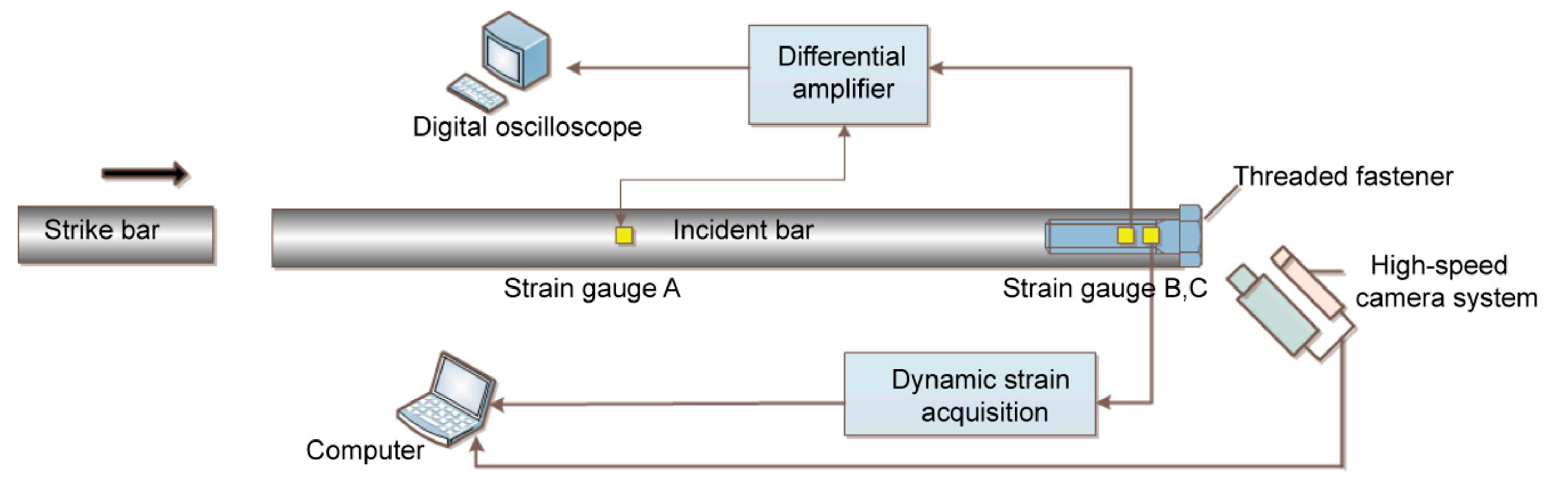
2.4. Impact Loading
2.5. Thermal Loading
3. Incorrect Assembly
4. Improper Design Parameters
5. Material Properties
5.1. Type of Material
5.2. Nonconformity of the Material
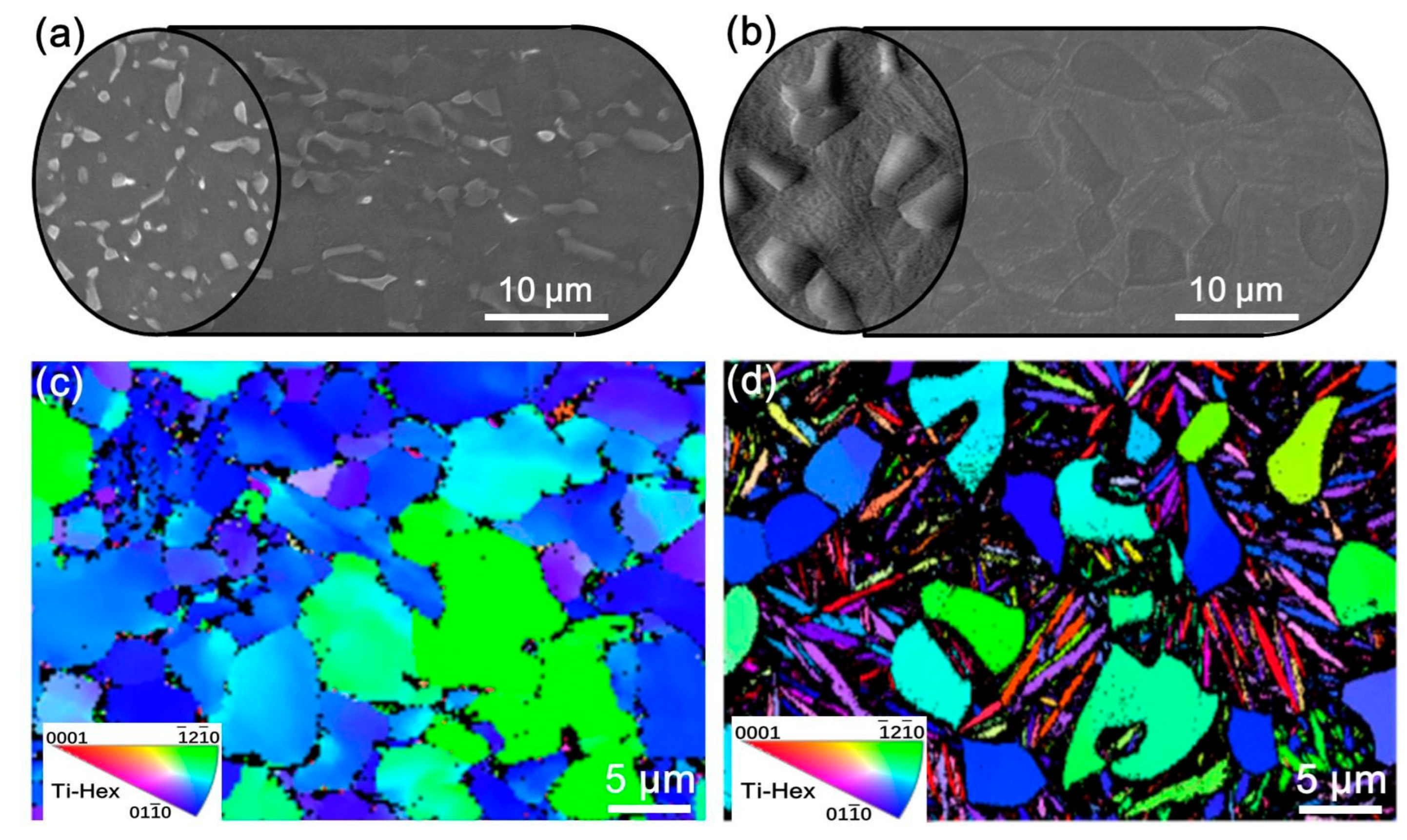
5.3. Material Texture
5.4. Viscoplasticity
5.5. Corrosion
5.6. Supplier
6. Fretting Fatigue
6.1. Experimental Analyses
6.2. Numerical Analyses
7. Fatigue Failure
8. Overload
9. Corrosion and Other Environmental Effects
9.1. Theories of Stress Corrosion Cracking
9.2. Experimental Analyses
10. Impact Loading
11. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Failure Type | Common Causes | Preventions |
|---|---|---|
| Loosening | Vibrational loading exceeding design limits. Preload loss due to any other factor | Use of threadlockers Application of adequate torque during assembly Use of mechanical retention devices |
| Incorrect assembly | Application of improper initial preload. | Clearly state the proper bolting sequences for assembly of joints having more than one bolt in the installation drawings. Measuring the initial torque application to avoid the overtightening of bolts. Carry out experimentation to characterize the friction coefficient of the joint. Provide technicians with suitable instruments. |
| Improper design parameters | Allowing high stress concentration regions such as sharp radius of head to shank, the sharp thread root radius. Manufacturing non-standardized shapes of bolt parts such as bolt thread shape. Unknown changes in friction coefficients upon first tightening and retightening operations. | Using rolled threads to have an additional compressive stress layer, which prevents crack formation. Using bolts with smoother head-to-shank transition. Rounded thread roots and standardized thread shape to provide proper fitting of the threads. Periodic replacement of bolts. Use of appropriate lubrication. Carry out experimentation to characterize the friction coefficient of the joint. |
| Material properties | Uncontrolled match between material specifications and actual components Improper heat treatment Use of unsuitable lubricants | Use high corrosion-resistant material such as stainless steel in humid environments. Carry out heat treatment in insulated environments especially for sensitive materials such as titanium. Refer to relevant standards to define adequate safety factors for specific material combinations, such as stainless steel and aluminium. For critical applications, set up a control strategy for inspection of the supplied parts. |
| Fretting fatigue | Sliding frictional contacts characterized by high stress concentration. | Removing high stress concentration regions by design. Using appropriate adhesives between matching surfaces. |
| Fatigue failure | Inappropriate geometry of bolted connections. Improper design. Material defects. Inadequate initial preload. | Apply appropriate initial preload. Decrease bolt stiffness (material of cross-section modification). Apply appropriate surface treatments (e.g., shot peening). Provide accurate design of the most critical parts of the fastener (1st engaged thread, runout thread, head-to-shank transition). |
| Overload | Uncontrolled preload (unsuitable torque wrench, or uncalibrated torque wrench). Unsuitable type and application of lubricant. Loading on the system greater than the design loads or error in estimating the external loads during the design phase. | Controlled application of lubricant, only after suitable experimentation of COF on the same combination of materials. Thorough estimation of the loading conditions during the design phase (use standards, load cycles from previous products, experimentation on prototypes). |
| Corrosion and other environmental effects | Presence of hydrogen in the environment and a suitable material in which it could be adsorbed (e.g., steel) Presence of sulphate-reducing bacteria (SRB) Presence of corners during cold working, inducing stress concentration | Using materials which are resistant to hydrogen embrittlement. Removing hydrogen by employing proper material processing Using dry raw material for steel production with high-quality processes such as vacuum melting Allowing enough time in solidification to free up the entrapped hydrogen Using appropriate coatings on the surfaces of the bolts Controlling the production of H2S. Use of microorganism inhibitors in bolted connections |
References
- Chen, J.-H.; Hsieh, S.-C.; Lee, A.-C. The failure of threaded fasteners due to vibration. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 299–314. [Google Scholar] [CrossRef]
- Haynes, G. Fasteners: A beginner’s guide. Cyber Press: Santa Clara, CA, USA.
- Milan, M.T.; Spinelli, D.; Filho, W.W.B.; Montezuma, M.F.V.; Tita, V. Failure analysis of a SAE 4340 steel locking bolt. Eng. Fail. Anal. 2004, 11, 915–924. [Google Scholar] [CrossRef]
- Avellon, G. Fastener Failures Prove Surprisingly Common in the Automotive Industry. 2014. Available online: https://boltfailure.com/fastener-failures-prove-surprisingly-common-in-the-automotive-industry/ (accessed on 5 December 2022).
- Epower Metals. Failure Analysis of Bolt Corrosion. 2020. Available online: https://www.epowermetals.com/failure-analysis-of-bolt-corrosion.html (accessed on 5 December 2022).
- QC-FIT Evaluation of Connector and Bolt Failures—Summary of Findings. 2014. Available online: https://www.bsee.gov/sites/bsee.gov/files/ (accessed on 5 December 2022).
- Bickford, J.H. An Introduction to the Design and Behavior of Bolted Joint Marcel Dekker; Raven Press: New York, NY, USA, 1995. [Google Scholar]
- Camillo, J. Why Threaded Fasteners Fail. Assembly. 2018. Available online: https://www.assemblymag.com/articles/94240-why-threaded-fasteners-fail (accessed on 6 December 2022).
- Pai, N.G. Vibration Induced Loosening of Threaded Fasteners: Mechanisms, Modeling and Design Guidelines. University of South Florida: Tampa, FL, USA, 2002. [Google Scholar]
- Olmi, G. An experimental investigation on a crack propagating from a geartrain housing in an asphalt milling machine. Eng. Fail. Anal. 2014, 38, 38–48. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Fini, S.; Olmi, G. A numerical and experimental approach to the design and failure analysis of a pinion shaft for wheel loaders. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1493–1504. [Google Scholar] [CrossRef]
- Otter, C.D.; Maljaars, J. Preload loss of stainless steel bolts in aluminium plated slip resistant connections. Thin-Walled Struct. 2020, 157, 106984. [Google Scholar] [CrossRef]
- Kharmanda, G.; Olhoff, N.; El-Hami, A. Optimum values of structural safety factors for a predefined reliability level with extension to multiple limit states. Struct. Multidiscip. Optim. 2004, 27, 421–434. [Google Scholar] [CrossRef]
- Wileman, J.; Choudhury, M.; Green, I. Computation of Member Stiffness in Bolted Connections. J. Mech. Des. Trans. ASME 1991, 113, 432–437. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Sen, A.; Das, S. An investigation on the anti-loosening characteristics of threaded fasteners under vibratory conditions. Mech. Mach. Theory 2010, 45, 1215–1225. [Google Scholar] [CrossRef]
- Sakai, T. Investigations of bolt loosening mechanisms. Bull. JSME 1978, 21, 1391–1394. Available online: http://www.mendeley.com/research/geology-volcanic-history-eruptive-style-yakedake-volcano-group-central-japan/ (accessed on 15 December 2022). [CrossRef]
- Junker, G.H. New Criteria for Self-Loosening of Fasteners Under Vibration. SAE Tech. Pap. 1969, 78, 314–335. [Google Scholar] [CrossRef]
- Yamamoto, A.; Kasei, S. Investigation on the self loosening of threaded fasteners under transverse vibration-A solution for self-loosening mechanism. J. Jpn. Soc. Precis. Eng. 1977, 43, 470–475. [Google Scholar] [CrossRef]
- Pai, N.; Hess, D. Three-dimensional finite element analysis of threaded fastener loosening due to dynamic shear load. Eng. Fail. Anal. 2002, 9, 383–402. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Sun, W.; Jiang, P.; Pan, J.; Guan, Z. Study on self-loosening mechanism of bolted joint under rotational vibration. Tribol. Int. 2021, 161, 107074. [Google Scholar] [CrossRef]
- Bretl, J.L.; Cook, R.D. Modelling the load transfer in threaded connections by the finite element method. Int. J. Numer. Methods Eng. 1979, 14, 1359–1377. [Google Scholar] [CrossRef]
- Miller, D.L.; Marshek, K.M.; Naji, M.R. Determination of load distribution in a threaded connection. Mech. Mach. Theory 1983, 18, 421–430. [Google Scholar] [CrossRef]
- Daadbin, A. Static and dyamic analysis of knuckle shape threaded joints. Mech. Mach. Theory 1990, 25, 225–232. [Google Scholar]
- Daadbin, A.; Chow, Y. A theoretical model to study thread loosening. Mech. Mach. Theory 1992, 27, 69–74. [Google Scholar] [CrossRef]
- Casanova, F. Failure analysis of the draft tube connecting bolts of a Francis-type hydroelectric power plant. Eng. Fail. Anal. 2009, 16, 2202–2208. [Google Scholar] [CrossRef]
- Nassar, S.A.; Housari, B.A. Effect of Thread Pitch and Initial Tension on the Self-Loosening of Threaded Fasteners. J. Press. Vessel. Technol. Trans. ASME 2005, 128, 590–598. [Google Scholar] [CrossRef]
- Housari, B.A.; Nassar, S.A. Effect of Thread and Bearing Friction Coefficients on the Vibration-Induced Loosening of Threaded Fasteners. J. Vib. Acoust. Trans. ASME 2007, 129, 484–494. [Google Scholar] [CrossRef]
- Yang, X.; Nassar, S. Analytical and Experimental Investigation of Self-Loosening of Preloaded Cap Screw Fasteners. J. Vib. Acoust. 2011, 133, 031007. [Google Scholar] [CrossRef]
- Nassar, S.A.; Yang, X. A Mathematical Model for Vibration-Induced Loosening of Preloaded Threaded Fasteners. J. Vib. Acoust. Trans. ASME 2009, 131, 021009. [Google Scholar] [CrossRef]
- Nassar, S.A.; Yang, X. Modeling the effect of nut thread profile angle on the vibration-induced loosening of bolted joint systems. In Advanced Joining Processes; Öchsner, A., da Silva, L.F.M., Altenbach, H., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2020; pp. 29–54. [Google Scholar]
- Liu, Z.; Wang, B.; Li, Y.; Zhang, C.; Wang, Y.; Chu, H. Analysis of self-loosening behavior of high strength bolts based on accurate thread modeling. Eng. Fail. Anal. 2021, 127, 105541. [Google Scholar] [CrossRef]
- Goodier, J.N. Loosening by Vibration of Threaded Fastenings. Mech. Eng. 1945, 67, 798. [Google Scholar]
- Sauer, J.A.; Lemmon, D.C.; Lynn, E.K. Bolts: How to prevent their loosening. Mach. Des. 1950, 22, 133–139. [Google Scholar]
- Paland, E.G. Investigation of the Locking Features of Dynamically Loaded Bolted Connections. Doctoral Dissertation, Hannover University, Hannover, Germany, 1966. [Google Scholar]
- Zaki, A.M.; Nassar, S.A.; Yang, X. Effect of Conical Angle and Thread Pitch on the Self-Loosening Performance of Preloaded Countersunk-Head Bolts. J. Press. Vessel. Technol. Trans. ASME 2012, 134, 021210. [Google Scholar] [CrossRef]
- DIN 65151:2002-08; Aerospace Series—Dynamic Testing of the Locking Characteristics of Fasteners under Transverse Loading Conditions (Vibration Test). Deutsche Institut für Normung E.V. (DIN): Berlin, Germany, 2002.
- Dinger, G. Design of multi-bolted joints to prevent self-loosening failure. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2564–2578. [Google Scholar] [CrossRef]
- Dinger, G. and Friedrich, G. Avoiding self-loosening failure of bolted joints with numerical assessment of local contact state. Eng. Fail. Anal. 2011, 18, 2188–2200. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Q.; Guan, Z. Self-Loosening Failure Analysis of Bolt Joints under Vibration considering the Tightening Process. Shock. Vib. 2017, 2017, 2038421. [Google Scholar] [CrossRef]
- Du, J.; Qiu, Y.; Wang, Z.; Li, J.; Wang, H.; Wang, Z.; Zhang, J. A three-stage criterion to reveal the bolt self-loosening mechanism under random vibration by strain detection. Eng. Fail. Anal. 2022, 133, 105954. [Google Scholar] [CrossRef]
- Baubles, R.C.; Mccormick, G.J.; Faroni, C.C. Loosening of Fasteners by Vibration; Report No. ER272-2177; Elastic Stop Nut Corp. Am. (ESNA): Union, NJ, USA, 1966. [Google Scholar]
- Zhang, M.; Jiang, Y.; Lee, C.-H. An Experimental Investigation of the Effects of Clamped Length and Loading Direction on Self-Loosening of Bolted Joints. J. Press. Vessel. Technol. Trans. ASME 2005, 128, 388–393. [Google Scholar] [CrossRef]
- Miller, M.; Johnson, C.; Sonne, N.; Mersch, J.; Kuether, R.J.; Smith, J.; Ortiz, J.; Castelluccio, G.; Moore, K. Bolt Preload Loss Due to Modal Excitation of a C-Beam Structure. In Nonlinear Structures & Systems; Springer: New York, NY, USA, 2020; pp. 203–214. [Google Scholar] [CrossRef]
- Eraliev, O.M.U.; Zhang, Y.-H.; Lee, K.-H.; Lee, C.-H. Experimental investigation on self-loosening of a bolted joint under cyclical temperature changes. Adv. Mech. Eng. 2021, 13, 1–8. [Google Scholar] [CrossRef]
- Casanova, F.; Mantilla, C. Fatigue failure of the bolts connecting a Francis turbine with the shaft. Eng. Fail. Anal. 2018, 90, 1–13. [Google Scholar] [CrossRef]
- Fonte, M.; Reis, L.; Infante, V.; Freitas, M. Failure analysis of cylinder head studs of a four stroke marine diesel engine. Eng. Fail. Anal. 2019, 101, 298–308. [Google Scholar] [CrossRef]
- Jawwad, A.K.A.; Alshabatat, N.; Mahdi, M. The effects of joint design, bolting procedure and load eccentricity on fatigue failure characteristics of high-strength steel bolts. Eng. Fail. Anal. 2021, 122, 105279. [Google Scholar] [CrossRef]
- O’Brien, M.J.; Metcalfe, R.G. High Strength Engineering Fasteners: Design for Fatigue Resistance. J. Fail. Anal. Prev. 2009, 9, 171–181. [Google Scholar] [CrossRef]
- Van Campen, D.H. A Systematic Bolt-Tightening Procedure for Reactor Vessel Flanges; University of Technology: Delft, The Netherlands, 1969. [Google Scholar]
- Bibel, G.D. Method of Tightening Threaded Fasteners. U.S. Patent No. 5,278,775,, 11 January 1994. [Google Scholar]
- Nassar, S.A.; Wu, Z.; Yang, X. A New Tightening Methodology for Gasketed Joints Based on Nonlinear Finite Element Analysis. Am. Soc. Mech. Eng. Press. Vessel. Pip. Div. PVP 2008, 2, 127–137. [Google Scholar] [CrossRef]
- Abasolo, M.; Aguirrebeitia, J.; Avilés, R.; De Bustos, I.F. Methodology for the Optimization of Bolting Sequences for Wind Generator Flanges. J. Press. Vessel. Technol. Trans. ASME 2014, 136, 061202. [Google Scholar] [CrossRef]
- Zheng, M.; Li, Y.; Liu, Z.; Zhao, Y.; Yang, C. A multi-bolt tightening method based on elastic interaction coefficient and gasket creep relaxation. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 9639–9647. [Google Scholar] [CrossRef]
- Shiba, R.; Chao, E.Y.S.; Kasman, R. Fatigue Properties of the Hoffmann-Vidal External Fixation Apparatus. Orthopedics 1984, 7, 443–456. [Google Scholar] [CrossRef] [PubMed]
- Curtis, L.R. Metallurgical failure analysis of fasteners in an impeller assembly. J. Fail. Anal. Prev. 2006, 6, 17–22. [Google Scholar] [CrossRef]
- Eraslan, O.; Inan, O. The effect of thread design on stress distribution in a solid screw implant: A 3D finite element analysis. Clin. Oral Investig. 2009, 14, 411–416. [Google Scholar] [CrossRef] [PubMed]
- Alemayehu, D.-B.; Jeng, Y.-R. Three-Dimensional Finite Element Investigation into Effects of Implant Thread Design and Loading Rate on Stress Distribution in Dental Implants and Anisotropic Bone. Materials 2021, 14, 6974. [Google Scholar] [CrossRef] [PubMed]
- Stevenson, M.; McDougall, J.; Cline, K. Metallurgical Failure Analysis of Titanium Wing Attachment Bolts. Pract. Fail. Anal. 2003, 3, 75–80. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure (VDI). Systematic Calculation of High Duty Bolted Joints Joints with One Cylindrical Bolt; VDI 2230; Verein Deutscher Ingenieure (VDI): Düsseldorf, Germany, 2003. [Google Scholar]
- Croccolo, D.; De Agostinis, M.; Vincenzi, N. Failure analysis of bolted joints: Effect of friction coefficients in torque–preloading relationship. Eng. Fail. Anal. 2011, 18, 364–373. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Vincenzi, N. Influence of tightening procedures and lubrication conditions on titanium screw joints for lightweight applications. Tribol. Int. 2012, 55, 68–76. [Google Scholar] [CrossRef]
- De Agostinis, M.; Fini, S.; Olmi, G. The influence of lubrication on the frictional characteristics of threaded joints for planetary gearboxes. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2553–2563. [Google Scholar] [CrossRef]
- Han, X.; Thrush, S.J.; Zhang, Z.; Barber, G.C.; Qu, H. Tribological characterization of ZnO nanofluids as fastener lubricants. Wear 2020, 468–469, 203592. [Google Scholar] [CrossRef]
- Kumar, M.; Persson, E.; Sherrington, I.; Glavatskih, S. Changes in friction of zinc flake coated threaded fasteners due to humidity, temperature and storage duration. Tribol. Int. 2022, 170, 107498. [Google Scholar] [CrossRef]
- Rezvani, S.; Zhou, L.; Ni, C. Experimental evaluation of angle bracket connections in CLT structures under in- and out-of-plane lateral loading. Eng. Struct. 2021, 244, 112787. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Vincenzi, N. Recent improvements and design formulae applied to front motorbike suspensions. Eng. Fail. Anal. 2010, 17, 1173–1187. [Google Scholar] [CrossRef]
- Chen, W.-H.; Lee, S.-S.; Yeh, J.-T. Three-dimensional contact stress analysis of a composite laminate with bolted joint. Compos. Struct. 1995, 30, 287–297. [Google Scholar] [CrossRef]
- Riccio, A. Effects of Geometrical and Material Features on Damage Onset and Propagation in Single-lap Bolted Composite Joints under Tensile Load: Part II—Numerical Studies. J. Compos. Mater. 2005, 39, 2091–2112. [Google Scholar] [CrossRef]
- Valenza, A.; Fiore, V.; Borsellino, C.; Calabrese, L.; Di Bella, G. Failure Map of Composite Laminate Mechanical Joint. J. Compos. Mater. 2007, 41, 951–964. [Google Scholar] [CrossRef]
- Xiao, Y.; Ishikawa, T. Bearing strength and failure behavior of bolted composite joints (part I: Experimental investigation). Compos. Sci. Technol. 2005, 65, 1022–1031. [Google Scholar] [CrossRef]
- Chang, F.-K.; Lessard, L.B. Damage Tolerance of Laminated Composites Containing an Open Hole and Subjected to Compressive Loadings: Part I—Analysis. J. Compos. Mater. 1991, 25, 2–43. [Google Scholar] [CrossRef]
- Chang, F.-K.; Chang, K.-Y. A Progressive Damage Model for Laminated Composites Containing Stress Concentrations. J. Compos. Mater. 1987, 21, 834–855. [Google Scholar] [CrossRef]
- Dano, M.-L.; Gendron, G.; Picard, A. Stress and failure analysis of mechanically fastened joints in composite laminates. Compos. Struct. 2000, 50, 287–296. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. Stress analysis and strength prediciton of mechanically fastened joints in FRP: A review. Compos. Part A Appl. Sci. Manuf. 1997, 28, 529–547. [Google Scholar] [CrossRef]
- Hashin, Z. Fatigue Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Olmedo, Á.; Santiuste, C. On the prediction of bolted single-lap composite joints. Compos. Struct. 2012, 94, 2110–2117. [Google Scholar] [CrossRef]
- Camanho, P.; Lambert, M. A design methodology for mechanically fastened joints in laminated composite materials. Compos. Sci. Technol. 2006, 66, 3004–3020. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. A Progressive Damage Model for Mechanically Fastened Joints in Composite Laminates. J. Compos. Mater. 1999, 33, 2248–2280. [Google Scholar] [CrossRef]
- Hart-Smith, L.J. Bolted Joints in Graphite-Epoxy Composites; Mcdonnell Douglas Corp Long Beach CA Douglas Aircraft DIV: Long Beach, CA, USA, 1976. [Google Scholar]
- ASTM D 7248/D 7248M-08; Standard Test Method for Bearing/Bypass Interaction Response of Polymer Matrix Composite Laminates Using 2-Fastener Specimens. American Society for Testing and Materials (ASTM) International: West Conshohocken, PA, USA, 2008.
- Liu, F.; Zhao, L.; Mehmood, S.; Zhang, J.; Fei, B. A modified failure envelope method for failure prediction of multi-bolt composite joints. Compos. Sci. Technol. 2013, 83, 54–63. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, S.; Zhang, J.; Huang, W.; Cheng, Y.; Zhang, J. Effect of damage on failure mode of multi-bolt composite joints using failure envelope method. Compos. Struct. 2017, 160, 8–15. [Google Scholar] [CrossRef]
- Zhao, L.; Shan, M.; Liu, F.; Zhang, J. A probabilistic model for strength analysis of composite double-lap single-bolt joints. Compos. Struct. 2017, 161, 419–427. [Google Scholar] [CrossRef]
- Davidson, P.; Waas, A.M. Probabilistic defect analysis of fiber reinforced composites using kriging and support vector machine based surrogates. Compos. Struct. 2018, 195, 186–198. [Google Scholar] [CrossRef]
- Liu, F.; Fang, Z.; Zhao, L.; Zhang, J.; Hu, N. A failure-envelope-based method for the probabilistic failure prediction of composite multi-bolt double-lap joints. Compos. Part B Eng. 2019, 172, 593–602. [Google Scholar] [CrossRef]
- ISO 898-1; Mechanical Properties of Fasteners Made of Carbon Steel and Alloy Steel—Part 1: Bolts, Screws and Studs with Specified Property Classes—Coarse Thread and Fine Pitch Thread. ISO (International Organization of Standardization): London, UK, 2018.
- Lee, H.-C.; Jin, Y.-G.; Lee, Y.-H.; Son, I.-H.; Lee, D.-L.; Im, Y.-T. Process design of high-strength bolt of fully pearlitic high-carbon steel. J. Mater. Process. Technol. 2010, 210, 1870–1875. [Google Scholar] [CrossRef]
- Kodur, V.; Yahyai, M.; Rezaeian, A.; Eslami, M.; Poormohamadi, A. Residual mechanical properties of high strength steel bolts subjected to heating-cooling cycle. J. Constr. Steel Res. 2017, 131, 122–131. [Google Scholar] [CrossRef]
- Hu, Y.; Tang, S.-L.; George, A.K.; Tao, Z.; Wang, X.-Q.; Thai, H.-T. Behaviour of stainless steel bolts after exposure to elevated temperatures. J. Constr. Steel Res. 2019, 157, 371–385. [Google Scholar] [CrossRef]
- Ban, H.; Yang, Q.; Shi, Y.; Luo, Z. Constitutive model of high-performance bolts at elevated temperatures. Eng. Struct. 2021, 233, 111889. [Google Scholar] [CrossRef]
- Cai, W.-Y.; Jiang, J.; Li, G.-Q.; Wang, Y.-B. Fracture behavior of high-strength bolted steel connections at elevated temperatures. Eng. Struct. 2021, 245, 112817. [Google Scholar] [CrossRef]
- Li, D.; Uy, B.; Wang, J.; Song, Y. Assessment of titanium alloy bolts for structural applications. Steel Compos. Struct. 2022, 42, 553–568. [Google Scholar] [CrossRef]
- Adeoti, G.O.; Fan, F.; Huihuan, M.; Shen, S. Investigation of aluminium bolted joint (HBJ) system behavior. Thin-Walled Struct. 2019, 144, 106100. [Google Scholar] [CrossRef]
- Cui, Y.; Meng, Q.; Zhang, B.; Yan, F. Fracture analysis of Ti–6Al–4V bolts. Eng. Fail. Anal. 2006, 13, 669–672. [Google Scholar] [CrossRef]
- Jha, A.K.; Singh, S.K.; Kiranmayee, M.S.; Sreekumar, K.; Sinha, P. Failure analysis of titanium alloy (Ti6Al4V) fastener used in aerospace application. Eng. Fail. Anal. 2010, 17, 1457–1465. [Google Scholar] [CrossRef]
- Gong, Y.; Ding, Q.; Yang, Z.-G. Failure analysis on premature fracture of anchor bolts in seawater booster pump of nuclear power plant. Eng. Fail. Anal. 2018, 97, 10–19. [Google Scholar] [CrossRef]
- Grimmer, P.W.; Mersch, J.P.; Smith, J.; Veytskin, Y.; Susan, D. Modeling Empirical Size Relationships on Load-Displacement Behavior and Failure in Threaded Fasteners. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 2268. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, X.; Shan, L.; Jiao, G.; Gao, Q.; Lin, Z.; Zheng, W.; Zhao, S. Design and fabrication of isotropic high-strength Ti-6Al-4V fastener. Mater. Lett. 2022, 323, 132554. [Google Scholar] [CrossRef]
- Radouani, R.; Echcharqy, Y.; Essahli, M. Numerical Simulation of Galvanic Corrosion between Carbon Steel and Low Alloy Steel in a Bolted Joint. Int. J. Corros. 2017, 2017, 6174904. [Google Scholar] [CrossRef]
- Zhang, J.; Ebrahimi, N.; Lai, D. Galvanic Corrosion Risk of Using Galvanized A325 Bolts in Corrosion-Resistant Steel Bridges. J. Bridg. Eng. 2019, 24, 06019001. [Google Scholar] [CrossRef]
- Abid, M.; Al-Grafi, M.W.; Wajid, H.A. Effect of bolt behaviour on the performance of a bolted joint. World Appl. Sci. J. 2013, 26, 89–96. [Google Scholar] [CrossRef]
- Lacalle, R.; Cicero, S.; Ferreño, D.; Álvarez, J. Failure analysis of a bolt in a scaffolding system. Eng. Fail. Anal. 2008, 15, 237–246. [Google Scholar] [CrossRef]
- Korsunsky, A.M. (Ed.) Chapter 11—Eigenstrain Methods in Structural Integrity Analysis. In A Teaching Essay on Residual Stresses and Eigenstrains; Elsevier Inc.: Cambridge, MA, USA, 2017; pp. 167–172. [Google Scholar]
- Walker, P.B. Fretting in the Light of Aircraft Experience. J. R. Aeronaut. Soc. 1959, 63, 293–298. [Google Scholar] [CrossRef]
- Sandifer, J.P. Evaluation of methods for reducing fretting fatigue damage in 2024-T3 aliminium lap joints. Wear 1973, 26, 405–412. [Google Scholar] [CrossRef]
- Wagle, S.; Kato, H. Ultrasonic detection of fretting fatigue damage at bolt joints of aluminum alloy plates. Int. J. Fatigue 2009, 31, 1378–1385. [Google Scholar] [CrossRef]
- Chakherlou, T.; Razavi, M.; Aghdam, A.; Abazadeh, B. An experimental investigation of the bolt clamping force and friction effect on the fatigue behavior of aluminum alloy 2024-T3 double shear lap joint. Mater. Des. 2011, 32, 4641–4649. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Fini, S.; Olmi, G.; Robusto, F.; Scapecchi, C. Fretting fatigue in mechanical joints: A literature review. Lubricants 2022, 10, 53. [Google Scholar] [CrossRef]
- Ungar, E.E. Energy Dissipation at Structural Joints; Mechanisms and Magnitudes; Bolt Beranek and Newman Inc.: Cambridge, MA, USA, 1964. [Google Scholar] [CrossRef]
- Rogers, P.F.; Boothroyd, G. Damping at Metallic Interfaces Subjected to Oscillating Tangential Loads. J. Eng. Ind. 1975, 97, 1087–1093. [Google Scholar] [CrossRef]
- Eriten, M.; Polycarpou, A.A.; Bergman, L.A. Development of a Lap Joint Fretting Apparatus. Exp. Mech. 2011, 51, 1405–1419. [Google Scholar] [CrossRef]
- Gaul, L.; Lenz, J. Nonlinear dynamics of structures assembled by bolted joints. Acta Mech. 1997, 125, 169–181. [Google Scholar] [CrossRef]
- Ovcharenko, A.; Halperin, G.; Etsion, I.; Varenberg, M. A novel test rig for in situ and real time optical measurement of the contact area evolution during pre-sliding of a spherical contact. Tribol. Lett. 2006, 23, 55–63. [Google Scholar] [CrossRef]
- Kartal, M.E.; Mulvihill, D.M.; Nowell, D.; Hills, D.A. Determination of the Frictional Properties of Titanium and Nickel Alloys Using the Digital Image Correlation Method. Exp. Mech. 2010, 51, 359–371. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Song, Y.; McFarland, D.; Bergman, L.; Vakakis, A. Experimental study of non-linear effects in a typical shear lap joint configuration. J. Sound Vib. 2004, 277, 327–351. [Google Scholar] [CrossRef]
- Smallwood, D.O.; Gregory, D.L.; Coleman, R.G. A three parameter constitutive model for a joint which exhibits a power law relationship between energy loss and relative displacement. In Proceedings of the 72nd Shock and Vibration Symposium, Destin, FL, USA, 12–16 November 2001; pp. 12–16. [Google Scholar]
- Mutoh, Y.; Jayaprakash, M. Tangential stress range–compressive stress range diagram for fretting fatigue design curve. Tribol. Int. 2011, 44, 1394–1399. [Google Scholar] [CrossRef]
- Murugesan, J.; Mutoh, Y. Fretting fatigue strength prediction of dovetail joint and bolted joint by using the generalized tangential stress range–compressive stress range diagram. Tribol. Int. 2014, 76, 116–121. [Google Scholar] [CrossRef]
- Juoksukangas, J.; Lehtovaara, A.; Mäntylä, A. Experimental and numerical investigation of fretting fatigue behavior in bolted joints. Tribol. Int. 2016, 103, 440–448. [Google Scholar] [CrossRef]
- Jiménez-Peña, C.; Talemi, R.H.; Rossi, B.; Debruyne, D. Investigations on the fretting fatigue failure mechanism of bolted joints in high strength steel subjected to different levels of pre-tension. Tribol. Int. 2017, 108, 128–140. [Google Scholar] [CrossRef]
- Li, D.; Xu, C.; Botto, D.; Zhang, Z.; Gola, M. A fretting test apparatus for measuring friction hysteresis of bolted joints. Tribol. Int. 2020, 151, 106431. [Google Scholar] [CrossRef]
- Szlosarek, R.; Kröger, M. Fatigue behavior of bolted boreholes under various preloads. Mater. Test. 2022, 64, 195–201. [Google Scholar] [CrossRef]
- Ferjaoui, A.; Yue, T.; Wahab, M.A.; Hojjati-Talemi, R. Prediction of fretting fatigue crack initiation in double lap bolted joint using Continuum Damage Mechanics. Int. J. Fatigue 2015, 73, 66–76. [Google Scholar] [CrossRef]
- Aghababaei, R.; Warner, D.H.; Molinari, R.A.J.-F. Critical length scale controls adhesive wear mechanisms. Nat. Commun. 2016, 7, 11816. [Google Scholar] [CrossRef] [PubMed]
- Leonard, B.D.; Ghosh, A.; Sadeghi, F.; Shinde, S.; Mittelbach, M. Third body modeling in fretting using the combined finite-discrete element method. Int. J. Solids Struct. 2014, 51, 1375–1389. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, M.H.A.L.; Abascal, R. Anisotropic Fretting Wear Simulation Using the Boundary Element Method. Comput. Model. Eng./Sci. 2012, 87, 127–156. [Google Scholar] [CrossRef]
- McColl, I.R.; Ding, J.; Leen, S.B. Finite element simulation and experimental validation of fretting wear. Wear 2004, 256, 1114–1127. [Google Scholar] [CrossRef]
- Armand, J.; Pesaresi, L.; Salles, L.; Wong, C.; Schwingshackl, C.W. A modelling approach for the nonlinear dynamics of assembled structures undergoing fretting wear. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 20180731. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yang, J. Fatigue Behavior of Bolted Joints: Comparative Analysis for the Effect of Fretting and Stress Concentration. Mater. Perform. Charact. 2020, 9, 309–323. [Google Scholar] [CrossRef]
- Antaki, G.; Gilada, R. (Eds.) Chapter 2—Design Basis Loads and Qualification. In Nuclear Power Plant Safety and Mechanical Integrity; Butterworth-Heinemann: Boston, MA, USA, 2015; pp. 27–102. [Google Scholar]
- Garcia, T.; Cicero, S.; Ibáñez, F.; Álvarez, J.; Martín-Meizoso, A.; Bannister, A.; Klimpel, A.; Aldazabal, J. Fatigue Performance of Thermally Cut Bolt Holes in Structural Steel S460M. Procedia Eng. 2015, 133, 590–602. [Google Scholar] [CrossRef]
- Croccolo, D.; Bogojević, N.; De Agostinis, M.; Fini, S.; Olmi, G.; Robusto, F.; Šoškić, Z.; Ćirić-Kostić, S. Fatigue response of additively manufactured as-built 15-5 PH stainless steel and effects of machining and thermal and surface treatments. Fatigue Fract. Eng. Mater. Struct. 2022, 46, 433–451. [Google Scholar] [CrossRef]
- Fini, S.; Croccolo, D.; De Agostinis, M.; Olmi, G.; Robusto, F.; Scapecchi, C. Experimental Investigation on the Fatigue Strength for Different Tightening Procedures and Materials in Metric Screws. Press. Vessel. Pip. Conf. 2022, 86151, V002T02A031. [Google Scholar]
- Oskouei, R.; Chakherlou, T. Reduction in clamping force due to applied longitudinal load to aerospace structural bolted plates. Aerosp. Sci. Technol. 2009, 13, 325–330. [Google Scholar] [CrossRef]
- Albrecht, P.; Sahli, A.H.; Wattar, F. Fatigue Strength of Bolted Joints. Eng. Struct. 1987, 113, 1834–1849. [Google Scholar] [CrossRef]
- Huhn, H.; Valtinat, G. Bolted connections with hot dip galvanized steel members with punched holes. In Proceedings of the ECCS/AISC Workshop, Connections in Steel Structures V: Innovative Steel Connections, Amsterdam, The Netherlands, 3–4 June 2004; pp. 3–5. [Google Scholar]
- Chakherlou, T.N.; Oskouei, R.; Vogwell, J. Experimental and numerical investigation of the efect of clamping force on the fatigue behaviour of bolted plates. Eng. Fail. Anal. 2008, 15, 563–574. [Google Scholar] [CrossRef]
- Esmaeili, F.; Chakherlou, T.; Zehsaz, M. Investigation of bolt clamping force on the fatigue life of double lap simple bolted and hybrid (bolted/bonded) joints via experimental and numerical analysis. Eng. Fail. Anal. 2014, 45, 406–420. [Google Scholar] [CrossRef]
- Esmaeili, F.; Barzegar, S.; Jafarzadeh, H. Evaluation of fatigue life reduction factors at bolt hole in double lap bolted joints using volumetric method. J. Solid Mech. 2017, 9, 1–11. [Google Scholar]
- Abazadeh, B. Failure mode prediction of single lap bolted Joints. Int. Res. J. Adv. Eng. Sci. 2016, 1, 95–99. [Google Scholar]
- Munse, W.H.; Wright, D.T.; Newmark, N.M. Laboratory Tests of Bolted Joints. Trans. Am. Soc. Civ. Eng. 1955, 120, 1299–1318. [Google Scholar] [CrossRef]
- Griza, S.; da Silva, M.E.G.; dos Santos, S.V.; Pizzio, E.; Strohaecker, T.R. The effect of bolt length in the fatigue strength of M24×3 bolt studs. Eng. Fail. Anal. 2013, 34, 397–406. [Google Scholar] [CrossRef]
- Birkemoe, P.C.; Meinheit, D.; Munse, W.H. Fatigue of a 514 steel in bolted connections. J. Struct. Div. 1969, 95, 2011–2030. [Google Scholar] [CrossRef]
- Atzori, B.; Lazzarin, P.; Quaresimin, M. A re-analysis on fatigue data of aluminium alloy bolted joints. Int. J. Fatigue 1997, 19, 579–588. [Google Scholar] [CrossRef]
- Zhou, S.; Sun, Y.; Ge, J.; Chen, X. Multiaxial fatigue life prediction of composite bolted joint under constant amplitude cycle loading. Compos. Part B Eng. 2015, 74, 131–137. [Google Scholar] [CrossRef]
- Vogt, J.-B.; Boussac, O.; Foct, J. Prediction of fatigue resistance of a hot-dip galvanized steel. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 33–39. [Google Scholar] [CrossRef]
- Cicero, S.; García, T.; Álvarez, J.; Martín-Meizoso, A.; Aldazabal, J.; Bannister, A.; Klimpel, A. Definition and validation of Eurocode 3 FAT classes for structural steels containing oxy-fuel, plasma and laser cut holes. Int. J. Fatigue 2016, 87, 50–58. [Google Scholar] [CrossRef]
- Dragoni, E. Effect of anaerobic threadlockers on the fatigue strength of threaded connections. Int. J. Mater. Prod. Technol. 1999, 14, 445. [Google Scholar] [CrossRef]
- Taylor, D.S.; Pan, J. Fatigue Crack Initiation in Threaded Fasteners Using the Critical Plane Approach. SAE Trans. 2003, 112, 318–325. [Google Scholar] [CrossRef]
- Hareyama, S.; Manabe, K.; Shimodaira, T.; Hoshi, A. Working load analysis and strength estimation for bolted joints. In Proceedings of the ASME 2014 International Mechaical Engineering Congress and Exposition (IMECE2014), Montreal, QC, Canada, 14–20 November 2014; pp. 1–10. [Google Scholar]
- Sorg, A.; Utzinger, J.; Seufert, B.; Oechsner, M. Fatigue life estimation of screws under multiaxial loading using a local approach. Int. J. Fatigue 2017, 104, 43–51. [Google Scholar] [CrossRef]
- Nassar, S.A.; Li, T. Novel Modeling of Mean Stress Effect on the High-Cycle Fatigue Performance of Preloaded Threaded Fasteners. Am. Soc. Mech. Eng. Press. Vessel. Pip. Div. (Publ.) PVP 2019, 2, 1–7. [Google Scholar] [CrossRef]
- Baggerly, R.G. Evaluating the Effects of Overtorque in Bolts. J. Fail. Anal. Prev. 2001, 1, 41–46. [Google Scholar] [CrossRef]
- Eliaz, N.; Gheorghiu, G.; Sheinkopf, H.; Levi, O.; Shemesh, G.; Ben-Mordechai, A.; Artzi, H. Failures of bolts in helicopter main rotor drive plate assembly due to improper application of lubricant. Eng. Fail. Anal. 2003, 10, 443–451. [Google Scholar] [CrossRef]
- Xue, X.; Tang, X.; Lu, H.; Geng, X. Failure Analysis of a Reactor after Explosion Accident. Procedia Eng. 2015, 130, 1397–1403. [Google Scholar] [CrossRef]
- Chen, H.; Ramandi, H.L.; Walker, J.; Crosky, A.; Saydam, S. Failure of the threaded region of rockbolts in underground coal mines. Min. Technol. 2018, 127, 146–154. [Google Scholar] [CrossRef]
- Neidel, A.; Gädicke, T.; Ullrich, T. Torsional Overload Fracture of Twist-off Bolts During Assembly. Pract. Metallogr. 2022, 59, 39–49. [Google Scholar] [CrossRef]
- Vandermaat, D.; Elias, E.; Craig, P.; Saydam, S.; Crosky, A. Experimental protocol for stress corrosion cracking of rockbolts. In Proceedings of the 2012 Coal Operators’ Conference, Mining Engineering, University of Wollongong, Wollongong, Austrilia, 16–17 February 2012; pp. 129–136. [Google Scholar]
- Craig, P.; Saydam, S.; Hagan, P.; Crosky, A.; Hebblewhite, B. Australian rock bolt steel chemistry and stress corrosion cracking. In Proceedings of the Second Australasian Ground Control in Minig Conference, Sydney, NSW, Australia, 23–24 November 2010; pp. 40–44. [Google Scholar]
- Crosky, A.; Smith, B.; Hebblewhite, B. Failure of rockbolts in underground mines in Australia. J. Fail. Anal. Prev. 2003, 3, 70–78. [Google Scholar] [CrossRef]
- Escobar, J.; Romero, A.; Lobo-Guerrero, J. Failure analysis of submersible pump system collapse caused by assembly bolt crack propagation by stress corrosion cracking. Eng. Fail. Anal. 2015, 60, 1–8. [Google Scholar] [CrossRef]
- Craig, P.H.; Hagan, P.; Vandermaat, D. Premature failure of australian coal mine rock bolts. Int. J. Min. Sci. Technol. 2016, 26, 59–64. [Google Scholar] [CrossRef]
- Neidel, A.; Gädicke, T.; Hartanto, V.; Wallich, S.; Wöhl, E. Austenitic Stainless Steel Bolt Failure by Stress Corrosion Cracking. Pract. Metallogr. 2018, 55, 97–109. [Google Scholar] [CrossRef]
- Hagarová, M.; Peterka, P.; Mantič, M.; Vojtko, M.; Baranová, G.; Matvija, M. Failure analysis of leaded brass bolt. Eng. Fail. Anal. 2023, 143, 106899. [Google Scholar] [CrossRef]
- Perrin, M.; Gaillet, L.; Tessier, C.; Idrissi, H. Hydrogen embrittlement of prestressing cables. Corros. Sci. 2010, 52, 1915–1926. [Google Scholar] [CrossRef]
- Ćwiek, J. Prevention methods against hydrogen degradation of steel. J. Achiev. Mater. Manuf. Eng. 2010, 43, 214–221. [Google Scholar]
- Biezma, M. The role of hydrogen in microbiologically influenced corrosion and stress corrosion cracking. Int. J. Hydrogen Energy 2001, 26, 515–520. [Google Scholar] [CrossRef]
- Toribio, J.; Valiente, A. Failure analysis of cold drawn eutectoid steel wires for prestressed concrete. Eng. Fail. Anal. 2006, 13, 301–311. [Google Scholar] [CrossRef]
- Jha, A.K.; Narayanan, P.R.; Sreekumar, K.; Mittal, M.; Ninan, K. Hydrogen embrittlement of 3.5Ni–1.5Cr–0.5Mo steel fastener. Eng. Fail. Anal. 2008, 15, 431–439. [Google Scholar] [CrossRef]
- Villalba, E.; Atrens, A. Hydrogen embrittlement and rock bolt stress corrosion cracking. Eng. Fail. Anal. 2009, 16, 164–175. [Google Scholar] [CrossRef]
- Al-Nabulsi, K.M.; Al-Abbas, F.M.; Rizk, T.Y.; Salameh, A.E.M. Microbiologically assisted stress corrosion cracking in the presence of nitrate reducing bacteria. Eng. Fail. Anal. 2015, 58, 165–172. [Google Scholar] [CrossRef]
- AlAbbas, F.M.; Williamson, C.; Bhola, S.M.; Spear, J.R.; Olson, D.L.; Mishra, B.; Kakpovbia, A.E. Influence of sulfate reducing bacterial biofilm on corrosion behavior of low-alloy, high-strength steel (API-5L X80). Int. Biodeterior. Biodegrad. 2013, 78, 34–42. [Google Scholar] [CrossRef]
- Chen, H.; Kimyon, Ö.; Ramandi, H.L.; Craig, P.; Gunawan, C.; Wu, S.; Manefield, M.; Crosky, A.; Saydam, S. Microbiologically influenced stress corrosion cracking responsible for catastrophic failure of cable bolts. Eng. Fail. Anal. 2022, 131, 105884. [Google Scholar] [CrossRef]
- Atrens, A.; Brosnan, C.C.; Ramamurthy, S.; Oehlert, A.; O Smith, I. Linearly increasing stress test (LIST) for SCC research. Meas. Sci. Technol. 1993, 4, 1281–1292. [Google Scholar] [CrossRef]
- Gamboa, E.; Atrens, A. Environmental influence on the stress corrosion cracking of rock bolts. Eng. Fail. Anal. 2003, 10, 521–558. [Google Scholar] [CrossRef]
- Villalba, E.; Atrens, A. An evaluation of steels subjected to rock bolt SCC conditions. Eng. Fail. Anal. 2007, 14, 1351–1393. [Google Scholar] [CrossRef]
- Aziz, N.; Craig, P.; Nemcik, J.; Hai, F. Rock bolt corrosion—An experimental study. In 2013 Coal Operators’ Conference; Mining Engineering, University of Wollongong: Wollongong, Australia, 2013; pp. 144–151. [Google Scholar]
- Vandermaat, D.; Saydam, S.; Hagan, P.; Crosky, A. Examination of rockbolt stress corrosion cracking utilising full size rockbolts in a controlled mine environment. Int. J. Rock Mech. Min. Sci. 2016, 81, 86–95. [Google Scholar] [CrossRef]
- Grimsmo, E.L.; Clausen, A.; Aalberg, A.; Langseth, M. Beam-to-column joints subjected to impact loading. In Proceedings of the Nordic Steel Construction Conference, Tampere, Finland, 23–25 September 2015. [Google Scholar]
- Mohotti, D.; Ali, M.; Ngo, T.; Lu, J.; Mendis, P.; Ruan, D. Out-of-plane impact resistance of aluminium plates subjected to low velocity impacts. Mater. Des. 2013, 50, 413–426. [Google Scholar] [CrossRef]
- Hongo, K. Loosening of Bolt and Nut Fastenings. Trans. Jpn. Soc. Mech. Eng. 1964, 30, 934–939. [Google Scholar] [CrossRef]
- Koga, K. Loosening by Repeated Impact of Threaded Fastenings. Trans. Jpn. Soc. Mech. Eng. 1969, 35, 1104–1111. [Google Scholar] [CrossRef]
- Koga, K.; Isono, H. Study on Self-loosening of Bolted Joints Taking Account of Characteristics of Impulsive Friction. Bull. JSME 1986, 29, 1004–1012. [Google Scholar] [CrossRef]
- Saleem, M.; Nasir, M. Bond evaluation of steel bolts for concrete subjected to impact loading. Mater. Struct. 2015, 49, 3635–3646. [Google Scholar] [CrossRef]
- Moore, K.J. A Reduced-Order Model for Loosening of Bolted Joints Subjected to Axial Shock Excitation. J. Appl. Mech. 2019, 86, 1–37. [Google Scholar] [CrossRef]
- Moore, K.J.; Kurt, M.; Eriten, M.; Dodson, J.C.; Foley, J.R.; Wolfson, J.C.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Nonlinear Parameter Identification of a Mechanical Interface Based on Primary Wave Scattering. Exp. Mech. 2017, 57, 1495–1508. [Google Scholar] [CrossRef]
- Saleem, M. Cyclic Shear-Lag Model of Steel Bolt for Concrete Subjected to Impact Loading. J. Mater. Civ. Eng. 2018, 30, 04018023. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, F.; Zhang, D.; Yu, Y.; Li, L.; Guo, X. Failure mechanisms of bolted flanges in aero-engine casings subjected to impact loading. Chin. J. Aeronaut. 2021, 34, 125–144. [Google Scholar] [CrossRef]
- Tanlak, N.; Sonmez, F.; Talay, E. Detailed and simplified models of bolted joints under impact loading. J. Strain Anal. Eng. Des. 2011, 46, 213–225. [Google Scholar] [CrossRef]
- Guo, Y.; Wei, Y.; Yang, Z.; Huang, C.; Wu, X.; Yin, Q. Nonlinearity of interfaces and force transmission of bolted flange joints under impact loading. Int. J. Impact Eng. 2017, 109, 214–223. [Google Scholar] [CrossRef]
- Zheng, Q.; Guo, Y.; Wei, Y.; Wang, Y.; Wang, X. Loosening of steel threaded connection subjected to axial compressive impact loading. Int. J. Impact Eng. 2020, 144, 103662. [Google Scholar] [CrossRef]
- Ngo, T.T.; Pham, T.M.; Hao, H.; Chen, W.; Elchalakani, M. Performance of monolithic and dry joints with GFRP bolts reinforced with different fibres and GFRP bars under impact loading. Eng. Struct. 2021, 240, 112341. [Google Scholar] [CrossRef]
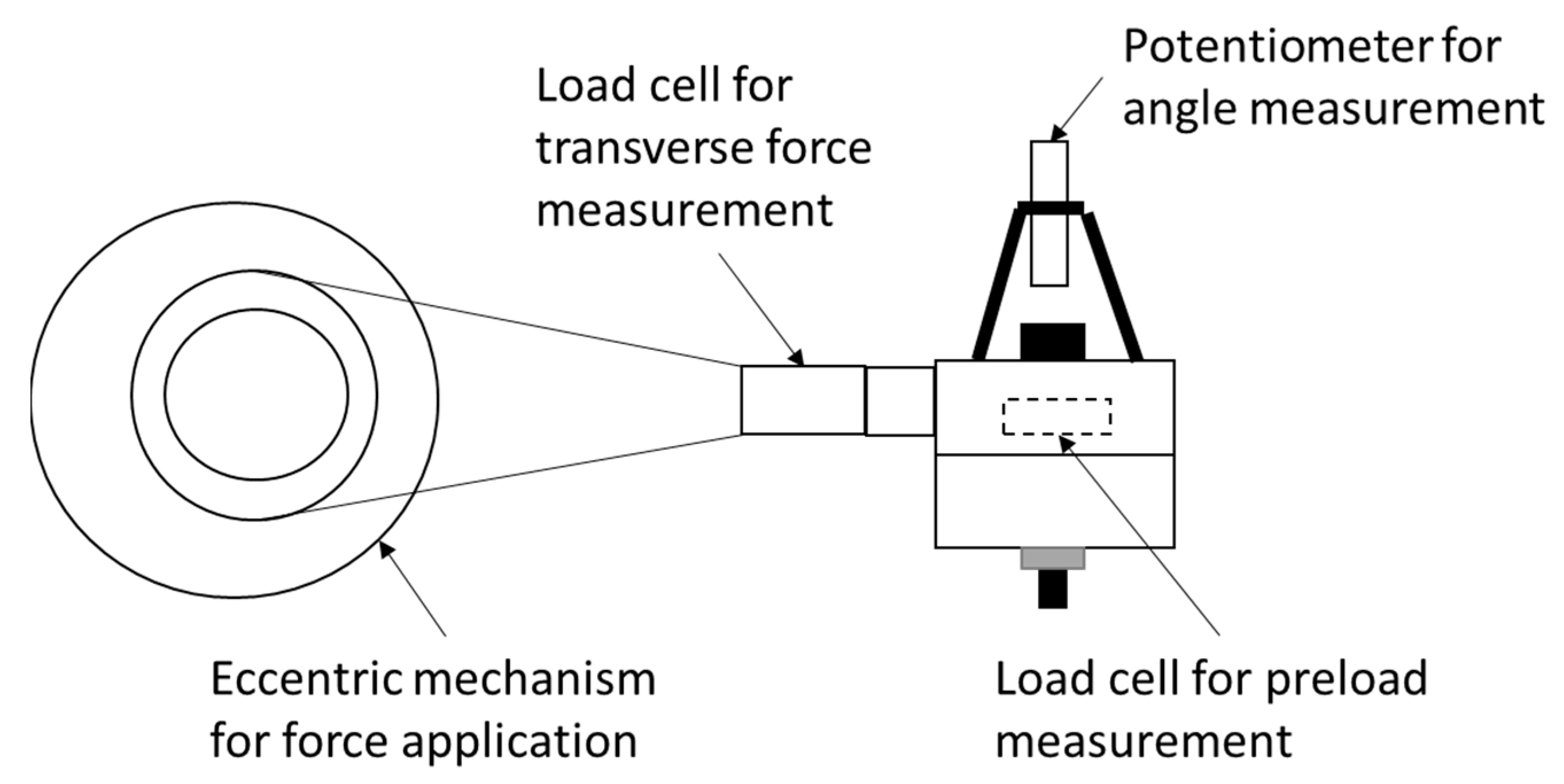
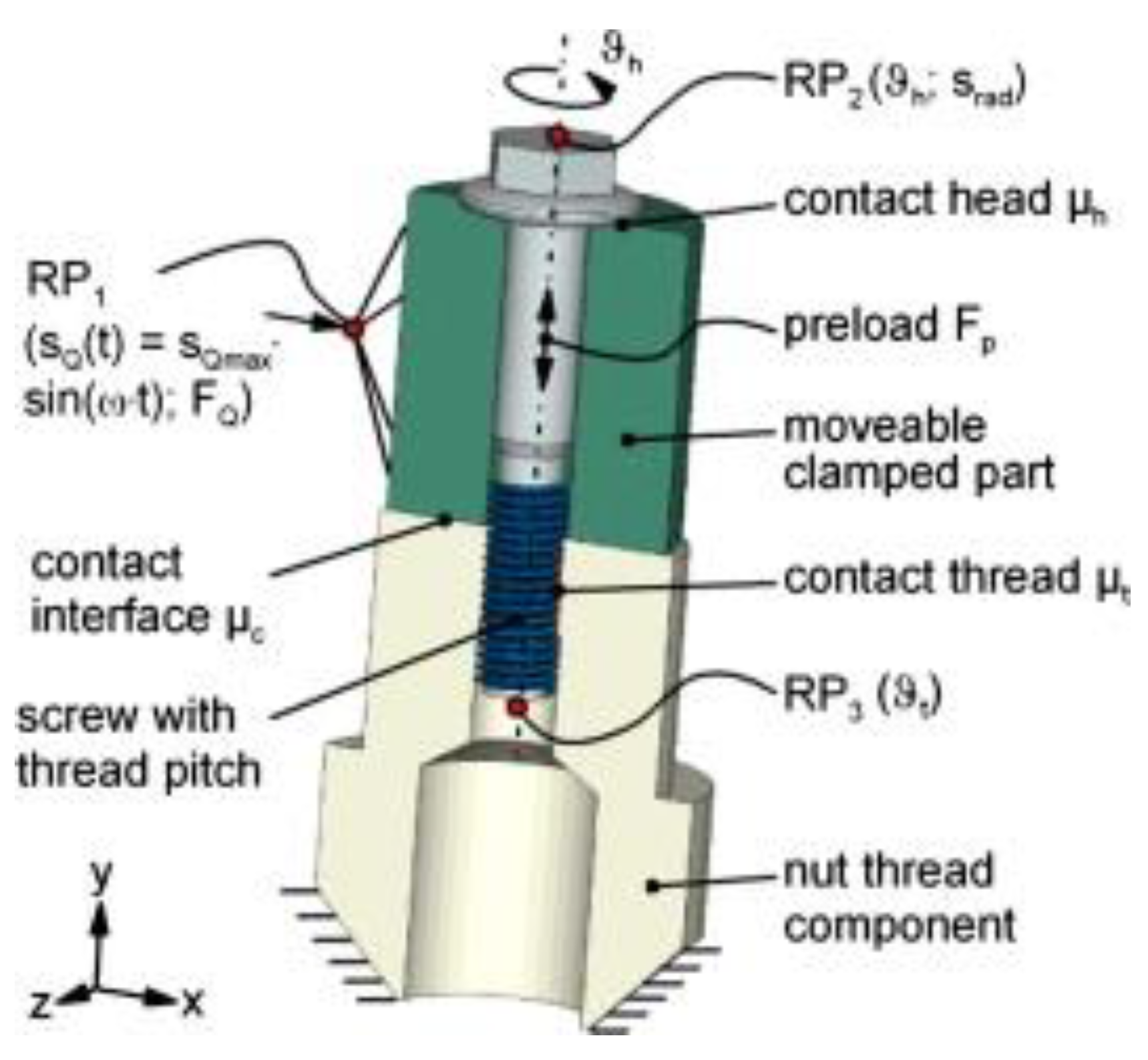



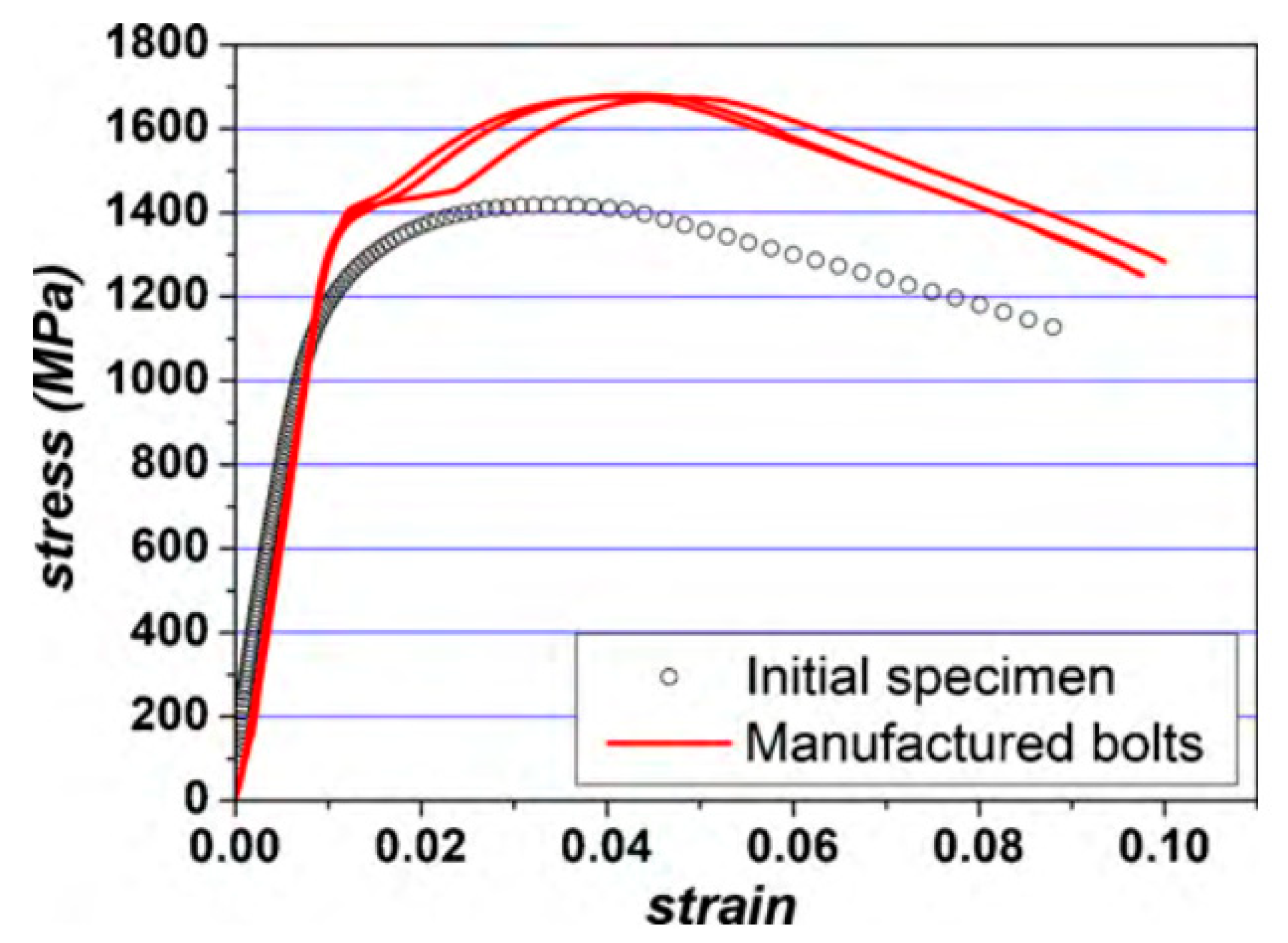
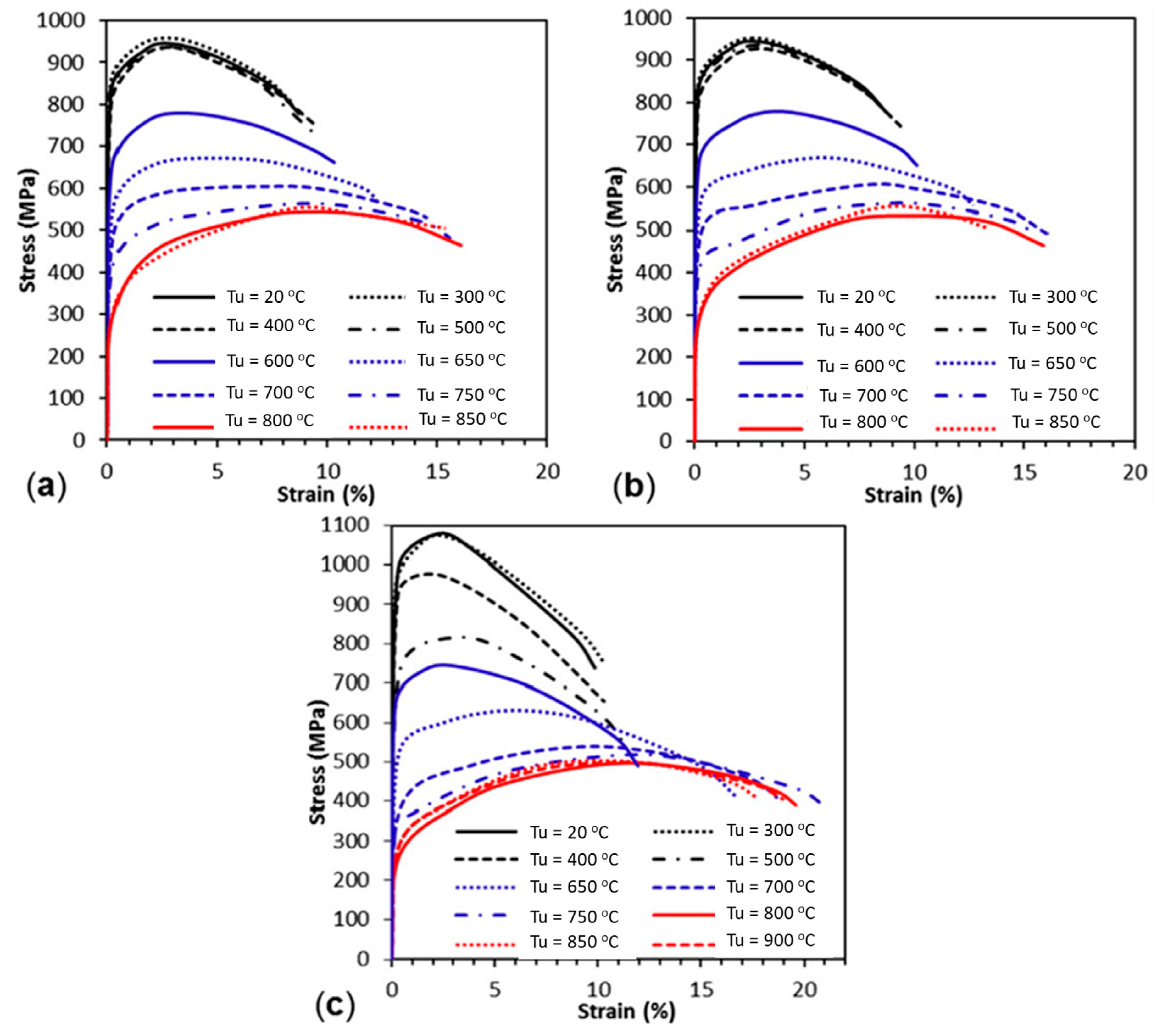
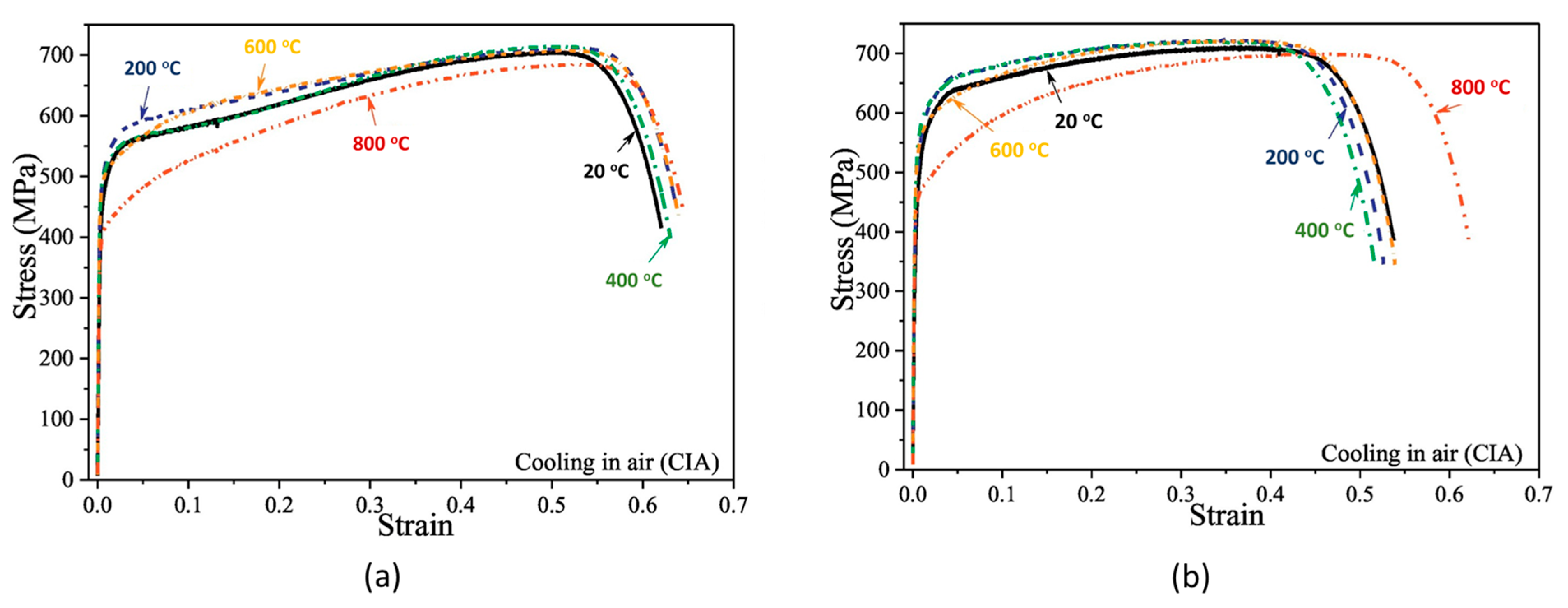
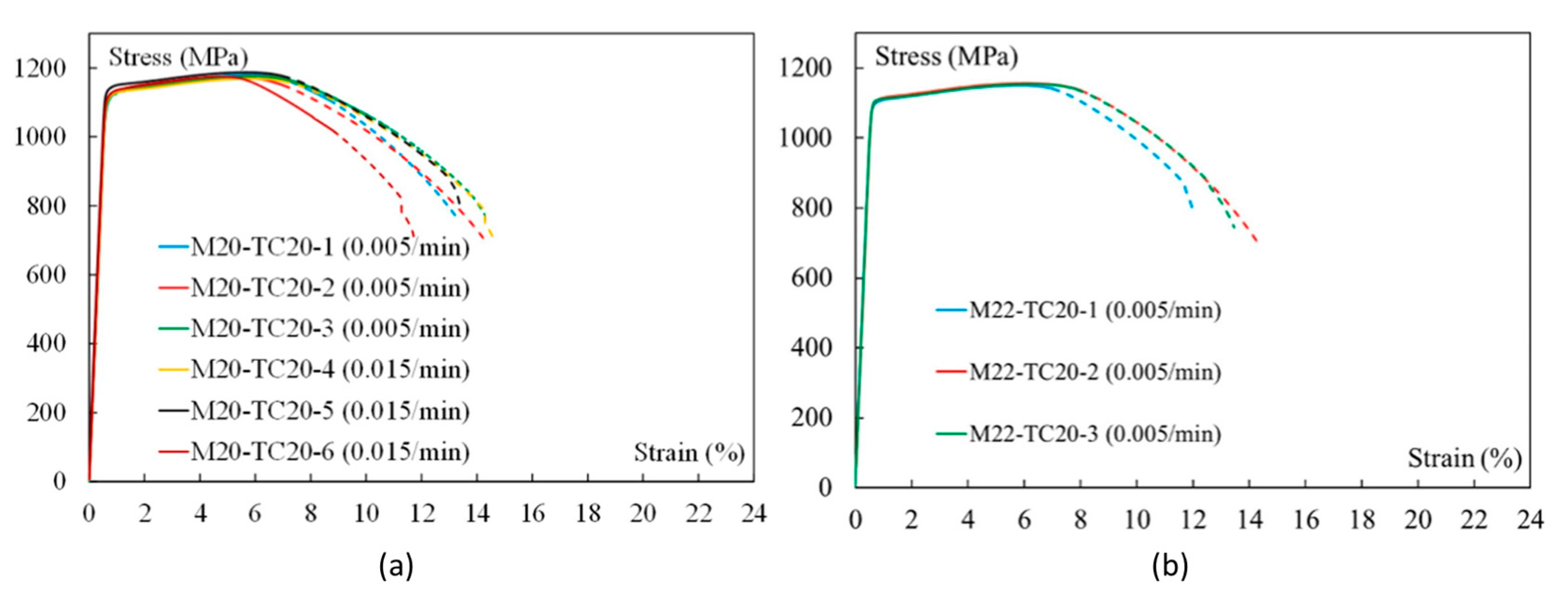
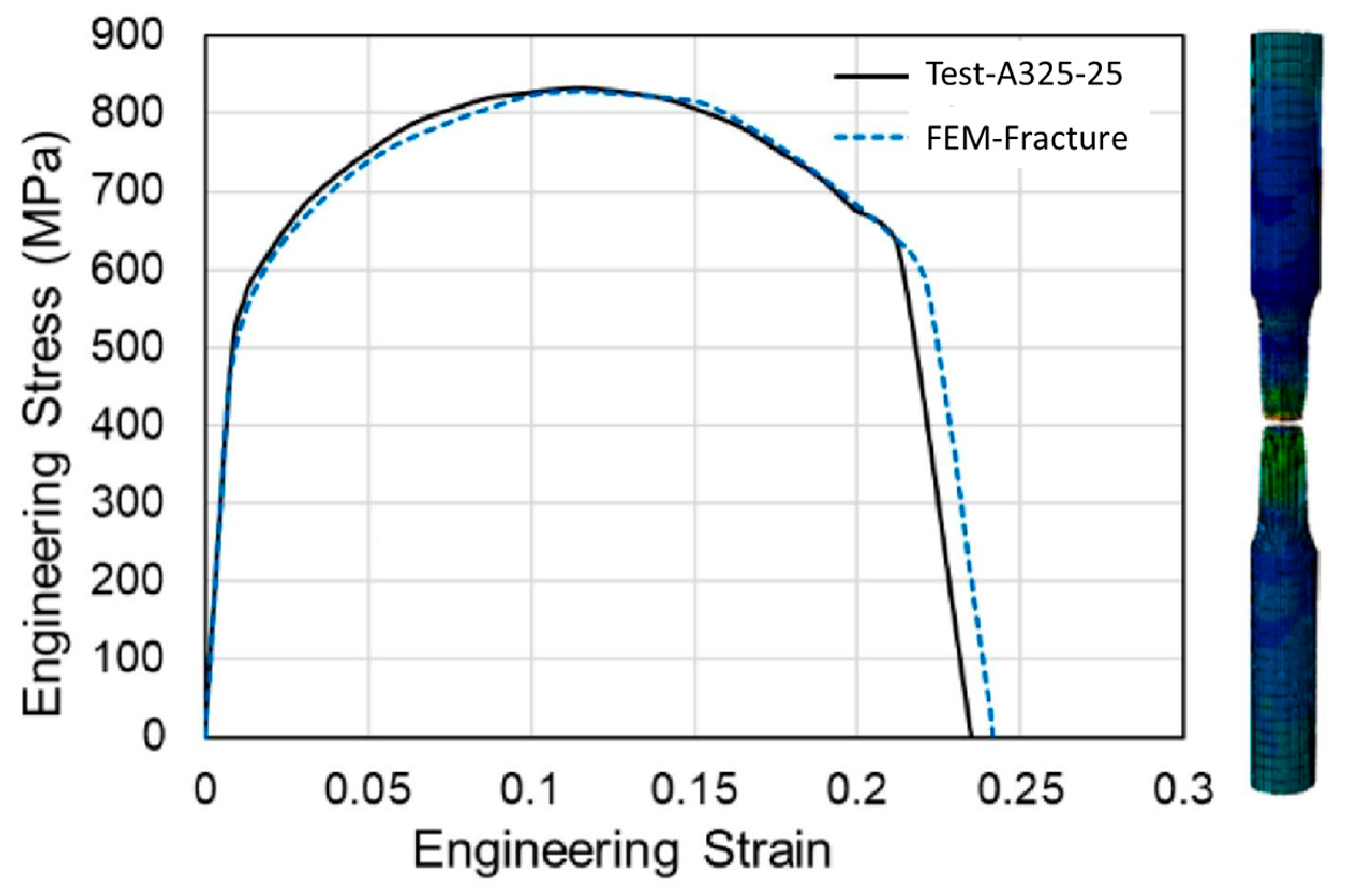
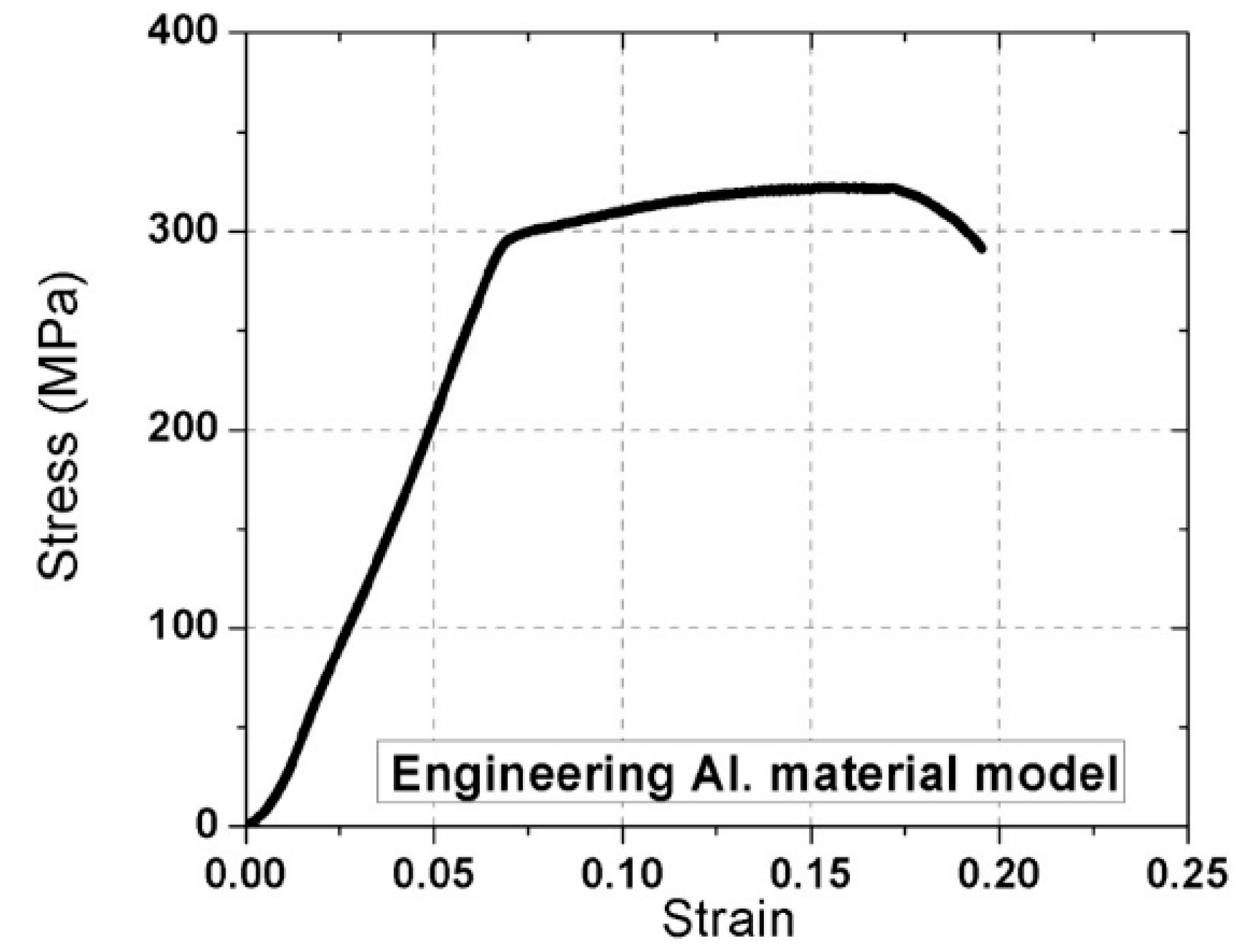






| Initial Clamping Force (kN) | Percentage of Loosening |
|---|---|
| 8 | 16 |
| 9 | 6.4 |
| 10 | 6.0 |
| 11 | 5.9 |
| 12 | 3.4 |
| 13 | 3.0 |
| 14 | 2.5 |
| 15 | 2.5 |
| 16 | 2.7 |
| 17 | 3.0 |
| 18 | 3.6 |
| Theory | Reference |
|---|---|
| Sakai’s fixed nut and free bolt head theory | [16] |
| Junker’s complete slippage theory | [17] |
| Two-stage theory by Yamamoto and Kasei | [18] |
| Local slippage theory | [19] |
| Theory for rotational loading | [20] |
| Mathematical Models | Reference |
|---|---|
| Linear self-loosening mathematical model | [26,27] |
| Non-linear self-loosening mathematical model | [28,29] |
| Incorporation of nut thread effect in a non-linear self-loosening model | [30] |
| Experimental Analysis | Reference |
| Use of microscopes to measure nut rotation | [32] |
| Junker’s apparatus for transverse excitation | [17] |
| Dinger’s apparatus for transverse and rotational excitation | [37] |
| Experimental configuration for PCB subjected to random vibrations | [40] |
| Thread Type | Static Loading | Quasi-Static Loading | Dynamic Loading |
|---|---|---|---|
| Square | 121.04 | 126.49 | 159.77 |
| Buttress (CF) | 173.24 | 182.33 | 239.41 |
| Reverse buttress (CF) | 205.79 | 214.42 | 298.60 |
| Trapezoidal | 237.23 | 247.06 | 358.69 |
| Triangular | 313.81 | 313.81 | 496.48 |
| Serial Number | Material of Bolt | Reference |
|---|---|---|
| 1. | Carbon steel | ISO 898-1 [86] |
| 2. | Fully pearlitic high-carbon steel | Lee et al. [87] |
| 3. | SAE 10B38 steel and SAE 10B21 steel | Kodur et al. [88] |
| 4. | Stainless steel, A2–70 and A4–70 | Hu et al. [89] |
| 5. | Grade 10.9 high-performance (HP) steel | Ban et al. [90] |
| 6. | ASTM A325 bolt and A572 Grade 50 steel | Cai et al. [91] |
| 7. | Titanium alloy (Ti6Al4V) | Li et al. [92] |
| 8. | Aluminium 6082-T6 | Adeoti et al. [93] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Croccolo, D.; De Agostinis, M.; Fini, S.; Mele, M.; Olmi, G.; Scapecchi, C.; Tariq, M.H.B. Failure of Threaded Connections: A Literature Review. Machines 2023, 11, 212. https://doi.org/10.3390/machines11020212
Croccolo D, De Agostinis M, Fini S, Mele M, Olmi G, Scapecchi C, Tariq MHB. Failure of Threaded Connections: A Literature Review. Machines. 2023; 11(2):212. https://doi.org/10.3390/machines11020212
Chicago/Turabian StyleCroccolo, Dario, Massimiliano De Agostinis, Stefano Fini, Mattia Mele, Giorgio Olmi, Chiara Scapecchi, and Muhammad Hassaan Bin Tariq. 2023. "Failure of Threaded Connections: A Literature Review" Machines 11, no. 2: 212. https://doi.org/10.3390/machines11020212
APA StyleCroccolo, D., De Agostinis, M., Fini, S., Mele, M., Olmi, G., Scapecchi, C., & Tariq, M. H. B. (2023). Failure of Threaded Connections: A Literature Review. Machines, 11(2), 212. https://doi.org/10.3390/machines11020212











